5. The Evidence Approximation

완전한 ( full ) 베이지언 패러다임의 선형 기저 함수 모델에서는 초모수 $ \alpha $ , $ \beta $ 가 사용된다.
- 여기서 $ \alpha $ 는 파라미터 $ {\bf w} $ 에 대한 분산을, $ \beta $ 는 $ {\bf t} $ 에 대한 분산을 의미한다.
- 또한 파라미터 $ {\bf w} $ 를 추정하는 것 외에 하이퍼 파라미터(초모수)들을 이용하여 예측 분포를 만드는 것을 살펴보았다.
- 하지만 이들을 주변화(marginalization)하는 것는 수학적으로 무척이나 힘든 것이라는 것도 확인하였다.
- 그리고 이런 경우를 analytically intractible 하다고 한다.
따라서 이 식을 바로 구할 수 있는 방법이 없기 때문에 이 식을 근사(approximation)하는 방법에 대해 이야기할 것이다.
- 주변 가능도 함수(marginal likilihood function) 를 최대화시키는 방식을 이용할 것이다.
이 프레임워크는 empirical Bayes 라고도 알려져있다.
- 혹은 “type2 MLE” 혹은 “evidence approximation” 이라고도 한다.
초모수 $ \alpha $ 와 $ \beta $ 를 이용하여 완전한 형태의 베이지언 예측분포를 나타내어 보자.

$p(t|{\bf t}) = \iiint p(t|{\bf w}, \beta) p({\bf w}|{\bf t}, \alpha, \beta) p(\alpha, \beta | {\bf t}) d{\bf w}d\alpha d\beta \qquad{(3.74)}$

여기서 $ p(t|{\bf w}, \beta) $ 는 식 (3.8) 에서 주어졌다. 그리고 $ p({\bf w}|{\bf t}, \alpha, \beta) $ 는 식 (3.49) 를 살펴보면 된다.
- 이 때 $ {\bf m}_N $ , $ {\bf S}_n $ 은 식(3.53) 과 식(3.54)에 나와있다.
여기서 입력 변수 $ {\bf x} $ 는 모든 영역에 대해 영향을 미치고 있으므로 생략한다.
이 때 사후분포 $ p(\alpha, \beta|{\bf t}) $ 가 특정한 지점 $ \widehat{\alpha} $ 와 $ \widehat{\beta} $ 에서 최고점을 만든다고 생각해보자.
- 이 때 우리는 $ \alpha $ 와 $ \beta $ 를 각각 $ \widehat{\alpha} $ 와 $ \widehat{\beta} $ 라 가정하고 파라미터 $ {\bf w} $ 를 주변화하면 된다.
- 이런 가정을 근사(approximation) 과정이라고 생각하는 것이다.
이러면 식을 다음과 같이 좀 더 간단하게 기술할 수 있다.

$p(t|{\bf t}) \simeq p(t|{\bf t}, \widehat{\alpha}, \widehat{\beta}) = \int p(t|{\bf w}, \widehat{\beta})p({\bf w}|{\bf t}, \widehat{\alpha}, \widehat{\beta})d{\bf w} \qquad{(3.75)}$

이제 적당한 $ \widehat{\alpha} $ 와 $ \widehat{\beta} $ 를 구하면 된다. (당연히 mode 값 등을 사용할 것이다.)
이를 구하기 위해 베이즈 이론으로 식을 전개하도록 하자.

$p(\alpha, \beta | {\bf t}) \propto p({\bf t}|\alpha, \beta)p(\alpha, \beta) \qquad{(3.76)}$

이 때 하이퍼 파라미터의 사전분포는 동일하다고 가정해보자.
따라서 이제 첫번째 텀에만 집중한다. $ p({\bf t}|\alpha, \beta) $ 를 주변 가능도 함수(marginal likelihood function)라고 한다.
- 우리는 선형 기저 함수모델을 위한 가능도 함수 전개 방식을 그대로 사용할 것이다.
- 이로부터 초모수를 추정할 수 있다.
  - cross-validation 등을 사용하지 않고 단일 샘플 집합으로부터 이 값을 추정하도록 한다.
  - 참고로 이 때 $ \alpha\;/\;\beta $ 식이 정칙화 파라미터로 사용된다.
이와 별개로, $ \alpha $ 와 $ \beta $ 의 사전 분포로 감마 분포를 사용하는 경우 식 (3.74)에서 $ {\bf w} $ 에 대한 함수는 스튜어트 $ {\bf t} $ 분포로 주어진다.
- 이런 경우 작업이 가능한 형태로 전개가 된다고 생각할 수 있으나 최종 $ {\bf w} $ 에 대한 적분식은 여전히 처리 불가능하다.(intractible)
- 물론 이 때의 적분식은 가우시안 근사를 기본으로 하는 라플라스 근사 방식을 도입하여 풀 수 있기는 하다.
  - 4.4절에 이와 관련된 내용을 설명한다.
  - 그리고 사실 이게 좀 더 현실적인 대안이기는 하다.
  - 하지만 라플라스 근사법도 분포가 한쪽으로 심하게 쏠린(skewed) 경우에는 잘 맞지 않는 근사법이다.
다시 evidence 방식으로 돌아가 이야기를 해보자면 크게 2가지 방식으로 나눌 수 있다.
- 3.5.2 절에서 설명하고 있는 미분 최대화 방식과,
- 9.3.4 절에서 설명하고 있는 EM 알고리즘을 사용하는 방식이다.
- 걱정하지 말자. 이후에 모두 살펴볼 것이다.

3.5.1 증거(evidence) 함수의 평가

주변 가능도 함수 $ p({\bf t}|\alpha, \beta) $ 는 다음의 식으로 얻을 수 있다.

$p({\bf t}|\alpha, \beta) = \int p({\bf t}|{\bf w}, \beta) p({\bf w}|\alpha) d{\bf w} \qquad{(3.77)}$

위의 식은 식(2.15)에서 언급한 선형 가우시안 모델의 조건부 분포를 이용하여 구할 수 있다.
하지만 여기서는 적분을 수행하는 대신 지수부에 포함된 제곱식을을 이용하여 일반화된 형태로 전개할 것이다.
- 정규화된 가우시안 계수를 가지는 표준 형태로 만든다.
책에는 전개 식이 안 나와있다. 최종 식을 보도록 하자.

$p({\bf t}|\alpha, \beta) = \left(\frac{\beta}{2\pi}\right)^{N/2}\left(\frac{\alpha}{2\pi}\right)^{M/2} \int \exp\{-E({\bf w})\}d{\bf w} \qquad{(3.78)}$

여기서 $ M $ 은 $ {\bf w} $ 의 차원을 나타낸다.

$E({\bf w}) = \beta E_D({\bf w}) + \alpha E_w({\bf w}) = \frac{\beta}{2}\|{\bf t} - \Phi{\bf w}\|^2 + \frac{\alpha}{2}{\bf w}^T{\bf w} \qquad{(3.79)}$

이 식은 식(3.27)과 상수만 다를 뿐 동일한 식이다.
참고삼아 식(3.27)을 간단히 보고 넘어가도록 하자.

$E({\bf w})=\dfrac{1}{2}\sum_{n=1}^{N}\{t_n-{\bf w}^T\phi({\bf x}_n)\}^2+\dfrac{1}{2}{\bf w^Tw} \qquad{(3.27)}$

따라서 이 식을 앞서 전개한 방식과 동일하게 처리 가능하다.

$E({\bf w}) = E({\bf m}_N)+\frac{1}{2}({\bf w}-{\bf m}_N)^T {\bf A} ({\bf w} - {\bf m}_N) \qquad{(3.80)}$

이 때,

${\bf A} = \alpha {\bf I} + \beta \Phi^T\Phi \qquad{(3.81)}$

이 식은 사실 식(3.51) 에 대응되는 식이다.

$E({\bf m}_N) = \frac{\beta}{2}\| {\bf t} - \Phi{\bf m}_N\|^2 + \frac{\alpha}{2}{\bf m}_N^T{\bf m}_N \qquad{(3.82)}$

식을 잘 살펴보면 $ {\bf A} $ 는 다음과 같이 에러 함수를 두번 미분한 것과 같다.

${\bf A} = \nabla \nabla E({\bf w}) \qquad{(3.83)}$

이 식은 헤시안 행렬(Hessian matrix)로 잘 알려져있다.
이 때 $ {\bf m}_N $ 은 다음과 같이 정의된다.

${\bf m}_N = \beta {\bf A}^{-1}\Phi^T{\bf t} \qquad{(3.84)}$

식(3.54)에서 보면 $ {\bf A} = {\bf S}_N^{-1} $ 로 생각할 수 있다.
이제 $ {\bf w} $ 에 대한 적분식을 살펴보도록 한다.

$\int \exp\left(-E({\bf w})\right) d{\bf w} = \exp(-E({\bf m}_N))\int \exp\left\{ -\frac{1}{2}({\bf w}-{\bf m}_N)^T {\bf A} ({\bf w}-{\bf m}_N) \right\}d{ \bf w}\\=\exp\left\{-E({\bf m}_N)\right\}(2\pi)^{M/2}|{\bf A}|^{-1/2} \qquad{(3.85)}$

이제 최종적으로 로그 주변 가능도 함수를 구해보도록 한다.

$\ln p({\bf t}|\alpha, \beta) = \frac{M}{2}\ln \alpha + \frac{N}{2}\ln \beta - E({\bf m}_n) - \frac{1}{2}\ln |{\bf A}| - \frac{N}{2}\ln(2\pi) \qquad{(3.86)}$

이 값을 이용하여 적절한 $ M $ 값을 찾는 방법을 살펴보자.

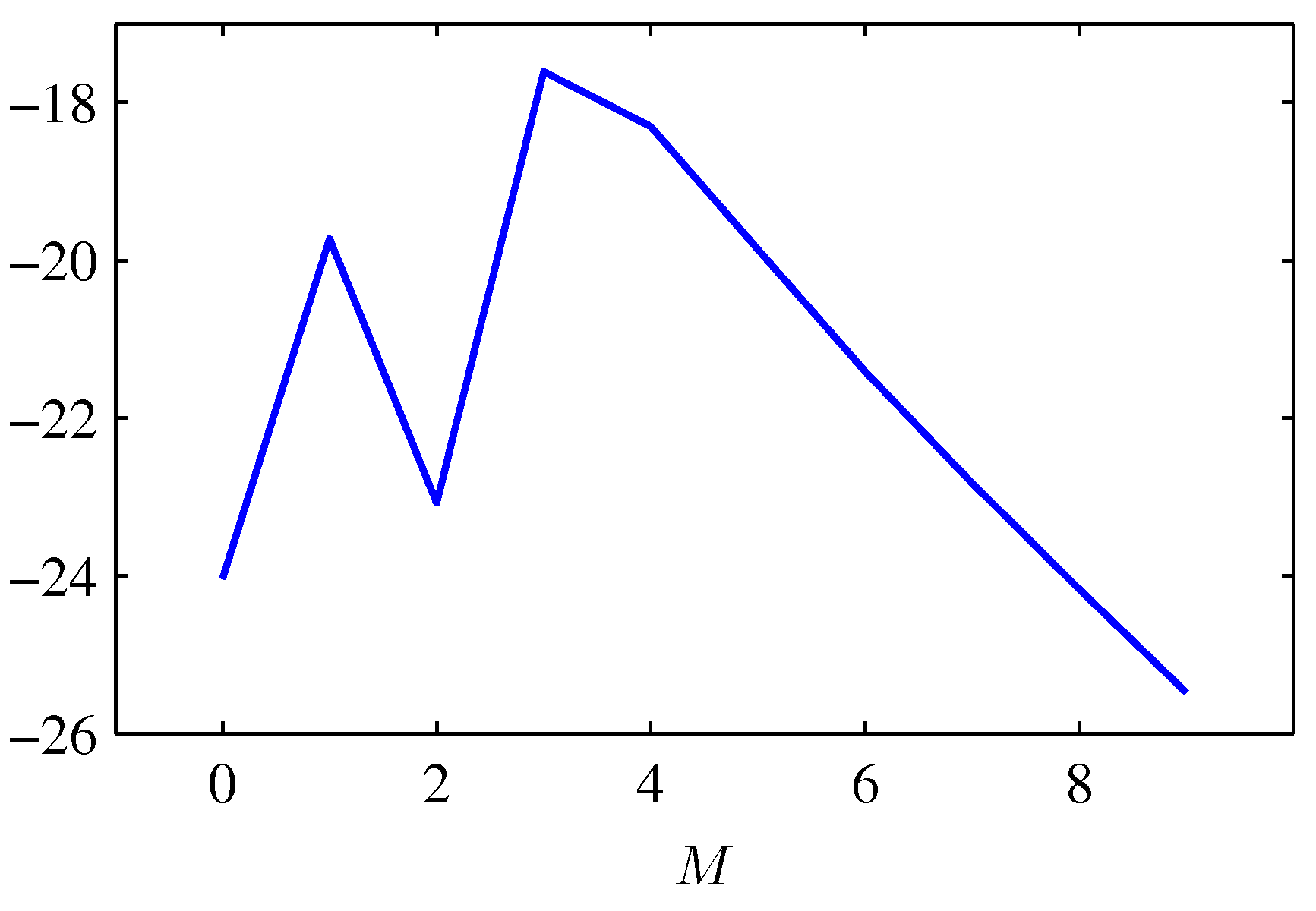
figure3.14

위의 그림은 polynomial regression 문제를 위의 식을 통해 구한 결과이다.
이 때 $ \alpha = 5 \times 10^{-3} $ 으로 고정되어 있다.
여러가지 $ M $ 값을 이용하여 로그 가능도 함수 값을 살펴본다.
- 식을 통해 $ M=3 $ 일 때 가장 높은 확률 값을 찾아낼 수 있었다.

3.5.2 증거(evidence) 함수 최대화하기

$ \alpha $ 에 관한 $ p({\bf t}|\alpha, \beta) $ 를 최대화하던 문제를 좀 더 생각해보자.

$(\beta \Phi^T \Phi) {\bf \mu}_i = \lambda_i{\bf \mu}_i \qquad{(3.87)}$

고유(eigen) 벡터 식에 의해 $ (\beta \Phi^T \Phi) $ 는 위와 같은 조건을 만족하게 된다.
따라서 $ {\bf A} $ 는 식 (3.81) 식에 의해 $ {\bf A} = \alpha + \lambda_i $ 로 생각할 수 있다.
이제 식 (3.86)에서 사용되는 $ \ln |{\bf A} $ 에 이를 대입하여 미분해보자.

$\frac{d}{d\alpha}\ln |{\bf A}| = \frac{d}{d\alpha}\ln \prod_{i}(\lambda_i+\alpha) = \frac{d}{d\alpha}\sum_i \ln(\lambda_i+\alpha) = \sum_i \frac{1}{\lambda_i + \alpha} \qquad{(3.88)}$

이제 위의 식을 포함하여 최종적으로 식 (3.86)을 $ \alpha $ 로 미분한 식을 살펴보자.

$0 = \frac{M}{2\alpha} - \frac{1}{2}{\bf m}_N^T{\bf m}_N - \frac{1}{2}\sum_i \frac{1}{\lambda_i+\alpha} \qquad{(3.89)}$

우리는 $ \alpha $ 에 관한 식을 알고 싶기 때문에 이 변수에 대해 정리를 한다.

$\alpha {\bf m}_N^T{\bf m}_N = M - \alpha\sum_i \frac{1}{\lambda_i+\alpha} = \gamma \qquad{(3.90)}$

예전에 비슷한 식을 본 적이 있긴 하다.
일단 한 변수로 완전히 정리가 되지 않기 때문에 $ \gamma $ 를 도입한다.
이제 $ \gamma $ 를 다음과 같이 정리 가능하다.

$\gamma = \sum_i \frac{\lambda_i}{\alpha + \lambda_i} \qquad{(3.91)}$

이제 최종적으로 $ \alpha $ 에 대한 식을 $ \gamma $ 를 통해 정리 가능하다.

$\alpha = \frac{\gamma}{ {\bf m}_N^T{\bf m}_N} \qquad{(3.92)}$

식을 잘 보면 $ \alpha $ 값을 구하기 위해 $ \gamma $ 가 필요한데 다시 이 내부에서 $ \alpha $ 가 필요한 상황이다.
결국은 Iterative 모델로 이 값을 결정하게 된다.
값이 반복되기 때문에 $ \alpha $ 의 값이 수렴될 때까지 반복하면 된다.
- 우선 초기값으로 $ \alpha $ 값을 임의로 정한 다음 이 때의 $ {\bf m}_N $ 과 $ \gamma $ 값을 구해 다시 $ \alpha $ 값 구하는 것을 반복한다.
- 계산이 복잡해보이지만 실제로는 $ \Phi^T\Phi $ 는 고정값이므로 그리 높은 연산을 요구하지는 않는다.

이제 $ \beta $ 에 대해서도 비슷한 방식으로 전개 가능하다.
식 (3.87)에서 사용된 고유값(eigen value) $ \lambda_i $ 에 대한 $ \beta $ 의 미분식은 $ d\lambda_i/d\beta = \lambda_i/\beta $ 로 처리하면 된다.

$\frac{d}{d\beta} \ln |{\bf A}| = \frac{d}{d\beta}\sum_i \ln(\lambda_i+\alpha) = \frac{1}{\beta}\sum_i\frac{\lambda_i}{\lambda_i+\alpha} = \frac{\gamma}{\beta} \qquad{(3.93)}$

편의상 식 전개가 좀 생략되어 있다.
이제 미분을 해보자. (stationary point 찾기)

$0 = \frac{N}{2\beta} - \frac{1}{2}\sum_{n=1}^N\{t_n-{\bf m}_N^T\phi({\bf x}_n)\}^2 - \frac{\gamma}{2\beta} \qquad{(3.94)}$

정리하면 다음과 같다.

$\frac{1}{\beta} = \frac{1}{N-\gamma}\sum_{n=1}^N \{t_n-{\bf m}_N^T\phi({\bf x}_N)\}^2 \qquad{(3.95)}$

앞선 식을 생각하여 $ \alpha $ 와 $ \beta $ 를 정한뒤 다시 $ \gamma $ 를 구하고 반복하는 방식을 사용할 수 있다.

3.5.3 효율적인 파라미터 수 (Effective number of parameters)

(참고) 이번 절은 내용을 대략적으로만 이해할 수 있어서 잘못된 내용이 포함될 가능성이 많다.
베이지언 추론 방식에서 식 (3.92) 의 $ \alpha $ 가 주는 의미가 무엇인지를 살펴보기로 하자.
아래 그림을 보자.

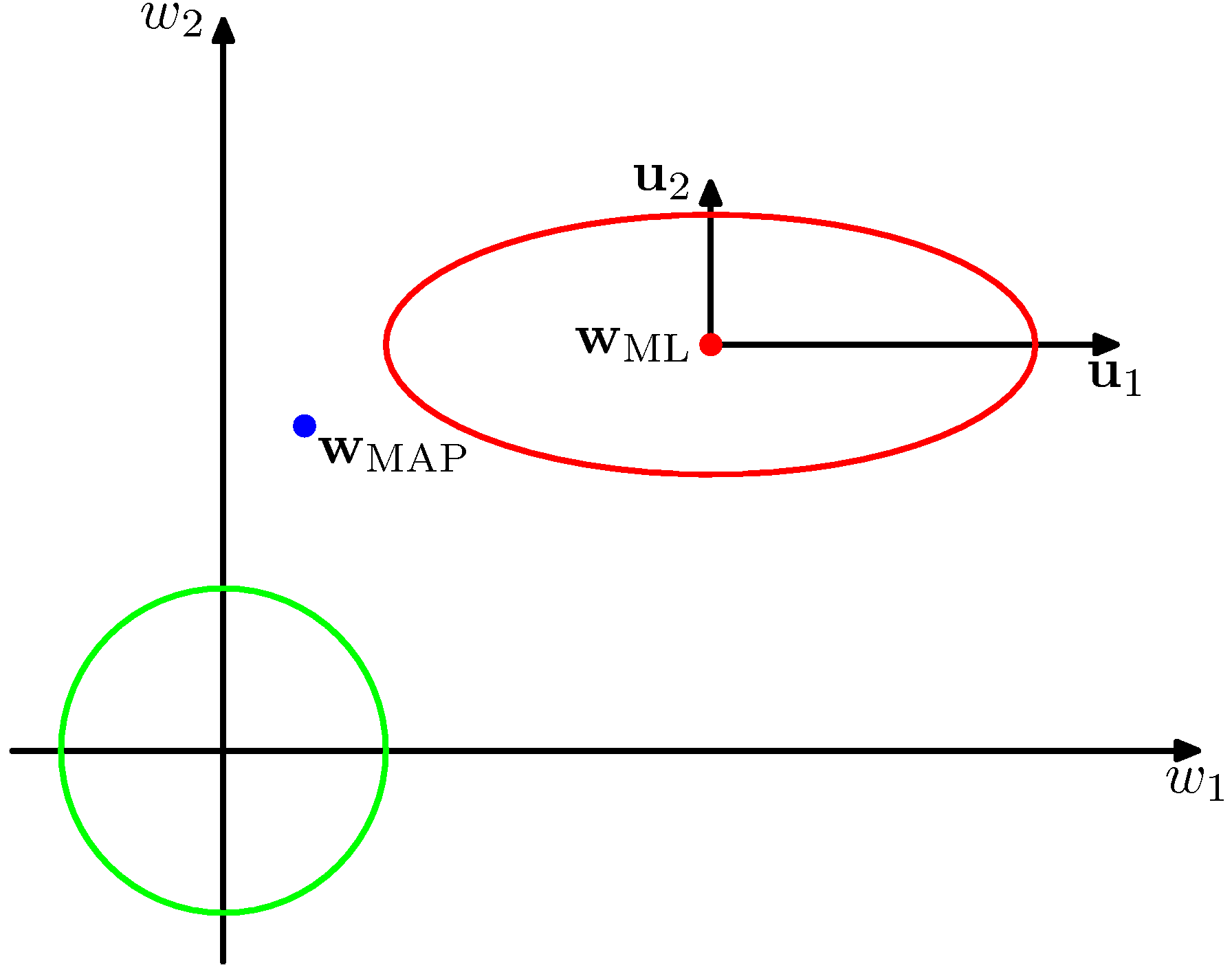
figure3.15

붉은 색의 컨투어는 가능도 함수를 의미한다.
- 일단 $ {\bf w}_i $ 에 대하여 상관 계수가 0 인 형태의 컨투어를 형성하고 있다.
- 이는 $ {\bf w}_i $ 가 $ \beta \Phi^T\Phi u_i = \lambda_i u_i $ 식과 같이 고유 값으로 변환 가능하므로 이를 고유 벡터 차원으로 변환한 뒤 나타낸 그림이다.
- 개념적으로 보면 어차피 이 가능도 함수는 $ {\bf w} $ 에 대한 이차형식(quadratic)으로 주어진다.
- $ \beta \Phi^T\Phi $ 가 대칭 행렬이므로 양의 정방향 행렬(positive definite matrix)이기 때문에 때문에 고유 값은 양수이다.
- 만약 $ \alpha = 0 $ 이면 사후 분포의 모드(mode) 값은 $ {\bf w}_{ML} $ 로 사용하면 된다.
- 만약 $ \alpha $ 가 0 이 아니라면 모드(mode) 값은 $ {\bf w}_{MAP} = {\bf m}_N $ 이다.
  - 가우시안 분포를 사용했기 때문에 모드와 기대값이 값다.
식 (3.92) 를 통해 $ \gamma $ 로부터 가장 효율적인 파라미터 수를 확인할 수 있다.
- 만약 $ \alpha « \lambda_i $ 인 경우 $ \gamma_i=1 $ 이 된다.
- 반면 $ \alpha » \lambda_i $ 인 경우 $ \gamma_i=0 $ 이 된다.
- 따라서 $ \gamma $ 는 $ 0 \le \gamma \le M $ 이 되게 된다. ( $ i=M $ 이므로 )
그리고 식 (3.95) 를 보면 $ \beta $ 를 추정하는데 있어서 $ N-\gamma $ 가 사용된다는 것을 알 수 있다.
1장에서 다루었던 가우시안 분산에 대한 MLE 추적을 잠시 떠올려보자. (식 (1.56)이다.)
- 이 때 분산 값은 다음과 같이 추정되었다.

$\sigma_{ML}^2 = \frac{1}{N}\sum_{n=1}^N (x_n - \mu_{ML})^2 \qquad{(3.96)}$

사실 이것은 샘플에 의해 편향(bias)된 결과이고 이미 비편향된 결과는 다음과 같다는 사실을 이미 알고 있다.

$\sigma_{MAP}^2 = \frac{1}{N-1}\sum_{n=1}^N (x_n - \mu_{ML})^2 \qquad{(3.96)}$

이것은 분명 우리가 얻은 결과인 $ \frac{1}{N-\gamma} $ 와 연결되어 있다.
- 바로 베이지언 방식은 이미 자유도(degree of freedom)의 개념이 식 자체에 포함되어 있다는 것이다.
- 그리고 앞선 식에서 $ -1 $ 이 추가된 것은 파라미터 평균(means) 때문이다.
- 결국 파라미터의 수를 제어하는 요소처럼 반영된다는 것.
지금까지 예로 들었던 것처럼 우리는 일단 $ 9 $ 개의 가우시언 기저 함수를 (Gauyssian basis fucntion) 사용할 것이다.
- 잘 기억이 나지 않는다면 1.1절을 참고해보자.
- 따라서 bias 를 반영하여 총 $ 10 $ 개의 파라미터를 가진 모델을 생ㅇ각하자.
- 그리고 베이지언 방식을 사용한다고 하였으므로 초모수(hyper-parameter) $ \alpha $ 와 $ \beta $ 도 사용된다.
일단 샘플의 개수는 $ N $ 이고 $ N » M $ 이라고 가정하자.
- 사용할 모델의 개수를 $ \gamma = M $ 이라고 해서 식을 전개해보면,

$\alpha = \frac{M}{2E_W({\bf m}_N)} \qquad{(3.98)}$ $\beta = \frac{N}{2E_D({\bf m}_N)} \qquad{(3.99)}$

여기서 $ E_W $ 와 $ E_D $ 는 각각 식 (3.25)와 식 (3.26) 에서 주어진 식이다.

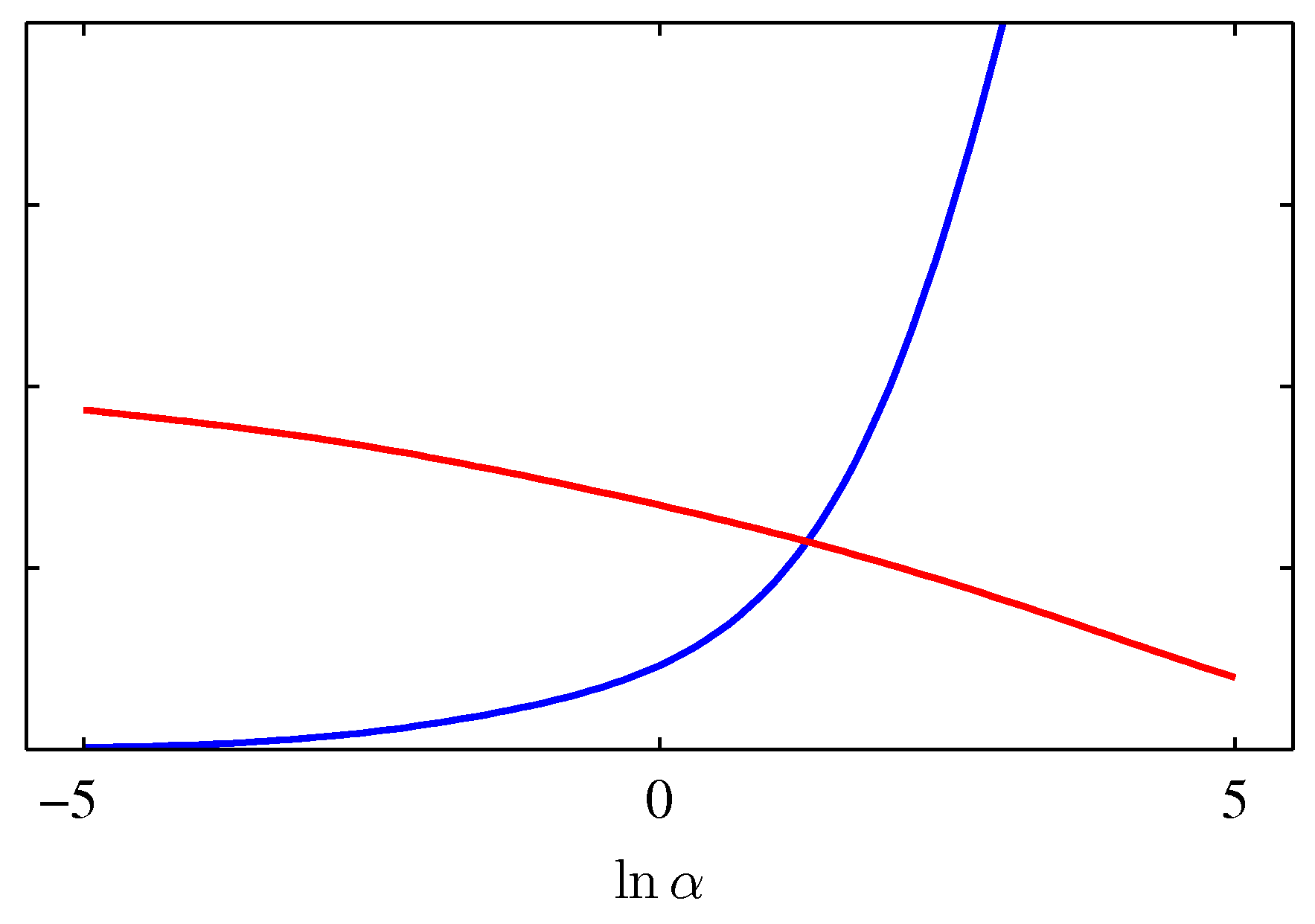
왼쪽
- 붉은 색 선은 $ \gamma $ 값이고, 파란 색은 $ 2\alpha E_W({\bf m}_N) $ 의 값이다.
- 두 점이 만나는 지점을 주목하자.
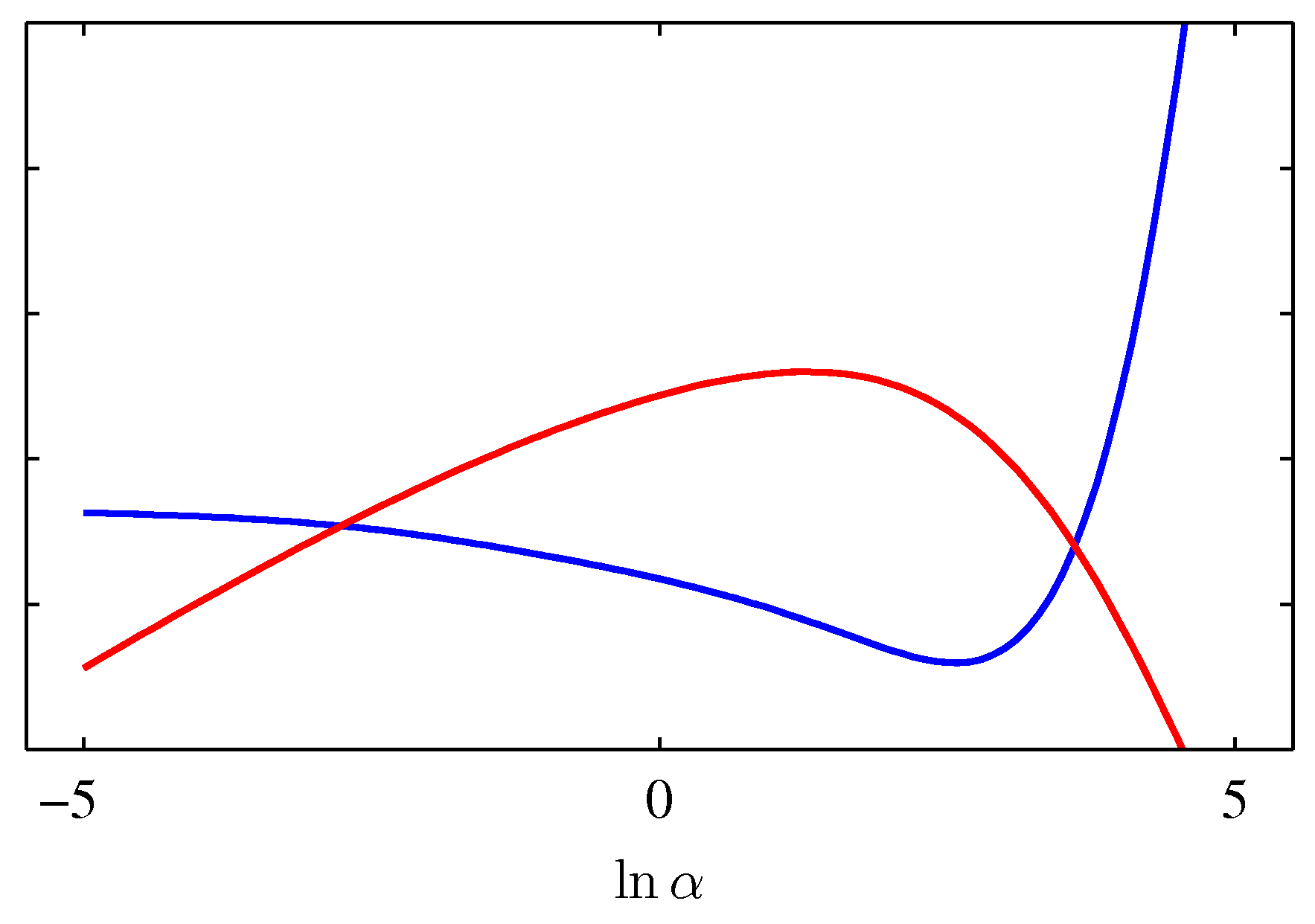
오른쪽
- 붉은 색 선은 $ \ln p(t|\alpha, \beta) $ 이고 파란 색은 테스트 에러 값이다.
두 그림 다 동일한 지점에서의 $ \alpha $ 값을 표현할 수 있다.
- 왼쪽은 두 점이 만나는 지점.
- 오른 쪽은 $ \ln p(t|\alpha, \beta) $ 가 최대가 되는 지점.
마지막으로 $ \alpha $ 값이 어떻게 $ w_i $ 값을 조절하게 되는지 그림으로 확인해보자.

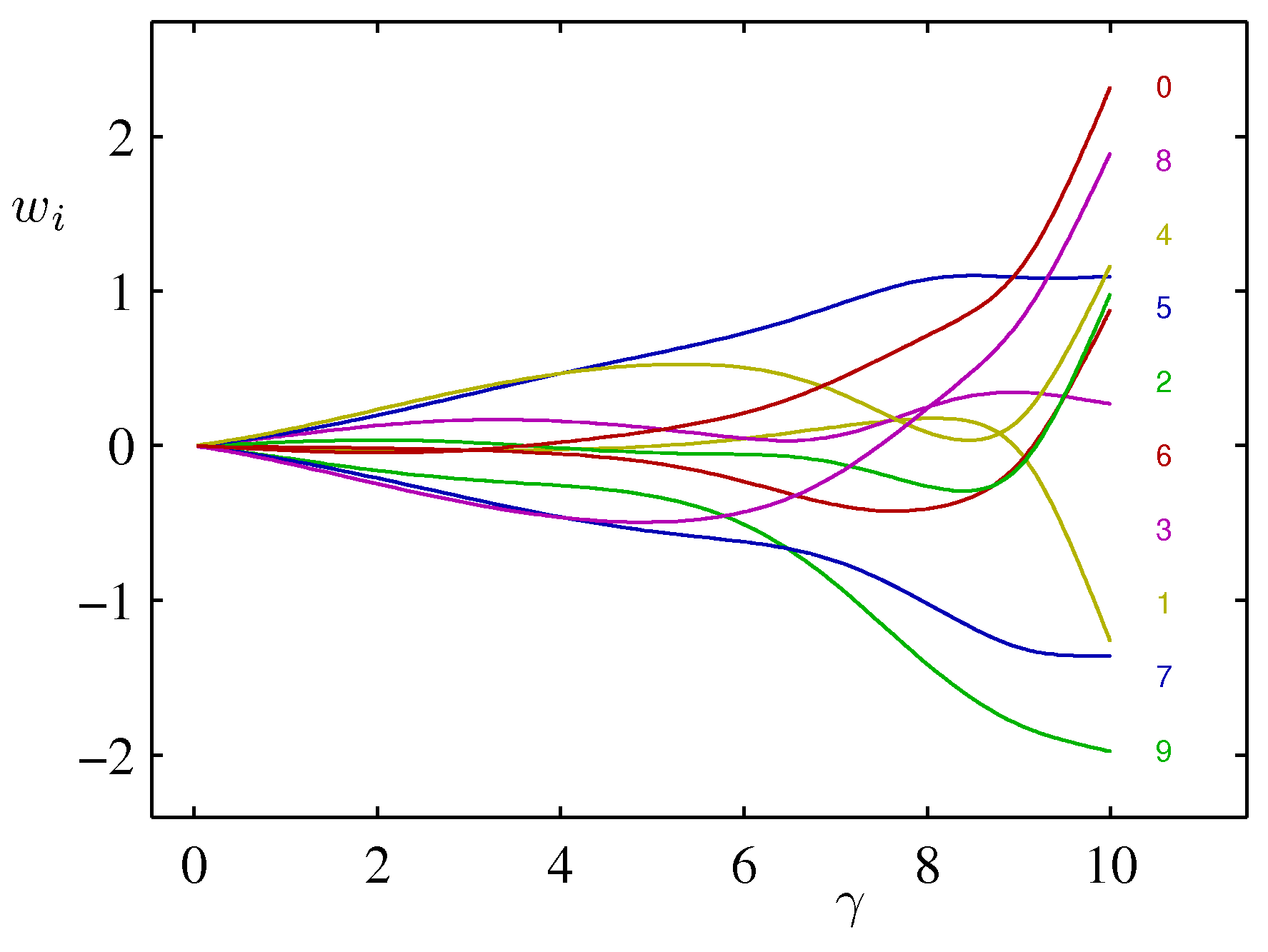
figure3.17

총 10개의 파라미터가 있다. (가우시안 기저 함수에 대한 계수)
$ \gamma $ 에 따라 $ w_i $ 값이 달라지게 된다.
솔직하게 이번 절의 후반부는 자세히 보지를 못했다.

Chapter. 3

3.5.1 증거(evidence) 함수의 평가

3.5.2 증거(evidence) 함수 최대화하기

3.5.3 효율적인 파라미터 수 (Effective number of parameters)