1. Linear Basis Function Models

목표 : 실수 범위의 입력 변수 \( x \) 를 관찰한 후에 이 관찰 값을 바탕으로 실수 범위의 타겟 \( t \) 의 값을 예측하고 싶다.

• 가장 기본적인 선형 모델은 다음과 같다.

• 여기서 \( {\bf x}=(x_1,…,x_D)^T \) 이고 이 때의 식을 이를 선형 회귀 (linear regression)식이라고 부른다.
  • 이 함수는 직선이나 하이퍼 평면을 만들어내며, 보통 분류(Classification) 문제에서 많이 활용된다.
  • 이 모델의 파라미터는 \( {\bf w} \) 벡터이다. : \( {\bf w}=(w_0,…,w_D)^T \)
  • 이 식은 입력 데이터 \( x_i \) 에 대해 선형식이다. 이 식을 좀더 일반화하여 표기할 수 있다.

• 일반화된 식으로 변경되면서 \( x \) 에 함수 \( \phi(\cdot) \) 가 추가된 형태가 되었다.
  • 특히 이 함수를 기저함수(basis function)라고 부른다.
  • 기저 함수의 도입으로 기존에는 \( x \) 에 대해 선형 식이었던 \( y({\bf x}, {\bf w}) \) 함수가 \( x \) 에 대해 비선형 함수가 될 수도 있다.
  • 마지막으로 \( w_0 \) 는 바이어스(bias)라고 부른다.
  • 표기의 편리성을 위해 \( \phi_0(x)=1 \) 로 정의하고 좀 더 간략한 식으로 기술하기도 한다.

• 일반적으로 전처리 과정 등을 통해 입력 데이터 \( x \) 에 대해 차원 축소가 수행되기도 한다.
  • 결국 feature 선별 작업을 수행하여 \( {\bf \phi}=(\phi_0,…,\phi_{M-1})^T \) 의 차수가 결정한다.
• 1장의 기억을 떠올려보면 우리는 다항식을 사용해서 이런 회귀식을 만들었다. 여기서 문제는,
  • 위에서 제시한 다항식은 \( x \) 에 대해서는 선형식(linear)이 아니다.
  • \( x \) 는 \( N \) 차원의 데이터가 아니라 1차원의 데이터였다.
• 1장에서 했던 것처럼 이번 장에서도 위 식을 그대로 사용하는 것이 아니라 회귀 분석에 적합하도록 특별한 형태로 제한하여 사용한다.

• 우리는 1장에서 사용된 식과 유사하게 다음과 같은 조건으로 작업을 진행할 것이다.
  • \( x \) 의 입력 범위는 1차원 실수값이다. 물론 출력 값인 \( t \) 또한 1차원 실수 값이다.
  • 기저 함수(basis function)가 적용된 회귀식을 사용한다.
    • 이는 비록 \( x \) 에 대해 비선형 함수일 수 있지만, \( w \) 에 대해 선형이므로 선형식이라고 부른다.
  • 따라서 1장에서 살펴보았던 다항식(polynomial)의 형태를 기본으로 식을 전개할 것이다.
    • 결국 1차원 벡터의 \( x \) 와 D 차원 벡터의 \( w \) 를 다룬다.
• 참고로 1장에서 사용했던 다항식(polynomial) 기저 함수는 \( \phi_j(x)=(x)^{\;j} \) 였다.
  • 이 함수는 약간 문제가 있는데, 이러한 기저함수는 Global Function 의 조건을 만족한다.
  • Global Function 이 뭘까?
    • 입력 값의 범위가 약간만 변하더라도 함수 전체 수식에서 다르게 적용되어 최종 출력 값이 크게 변하는 함수를 의미한다.
  • 이런 경우 함수 근사에 대한 한계점이 존재하게 된다.
  • 좀 더 정확한 함수 근사를 위해 보통은 Spline 이라는 기법을 이용하여 이를 보정하는데, 여기서는 자세히 다루지 않는다.
    • 간단하게만 언급하자면 Spline 함수는 함수를 구간 별로 나누어 구간 별로 서로 다른 근사 함수를 만들어내는 것이다.
• 이제 새로운 기저 함수 형태를 좀 살펴보도록 한다. 가장 먼저 정규 분포 형태의 기저 함수를 살펴보자.

• 정규 분포와 다른 점은 정규화 계수(normalization coefficient) 가 없다는 점인데 사실 필요가 없다.
  • 이는 회귀식에 계수 \( w_j \) 가 존재하기 때문에 이것이 정규화 역할을 함께 수행할 수 있어 생략한 것이다.
• 시그모이드(sigmoid) 형태의 기저 함수도 있다.

• 이 두 함수는 모두 \( u_j \) 와 \( s \) 를 가지고 있다.
  • \( u_j \) : 입력 데이터 범위 내의 특정한 위치를 의미한다. 일정한 간격마다 점을 찍는다고 생각해도 된다.
    • \( u \) 는 보통 평균을 의미하는 \( greek \) 문자로 인해 오해할 수 있는데 여기서는 평균을 의미하는 것이 아니다.
      • 정확히 말하자면 \( \mu \) 가 평균을 의미하는 \( greek \) 문자이다. (문자셋이 약간 다르다.)
      • 여기서 \( u_j \) 는 주어진 데이터의 범위 안에 있는 임의의 한 값을 의미한다.
    • 아래 그림을 참고하면, 일정 간격으로 \( u_j \) 들을 구성할 수 있다.
    • 가변적인 크기를 가지는 \( u_j \) 들을 만들어낼 수도 있다.
  • \( s \) : 스케일을 의미하며 하나의 기저 함수가 영향력을 미칠수 있는 범위를 산정하는데 사용된다고 생각하면 된다.

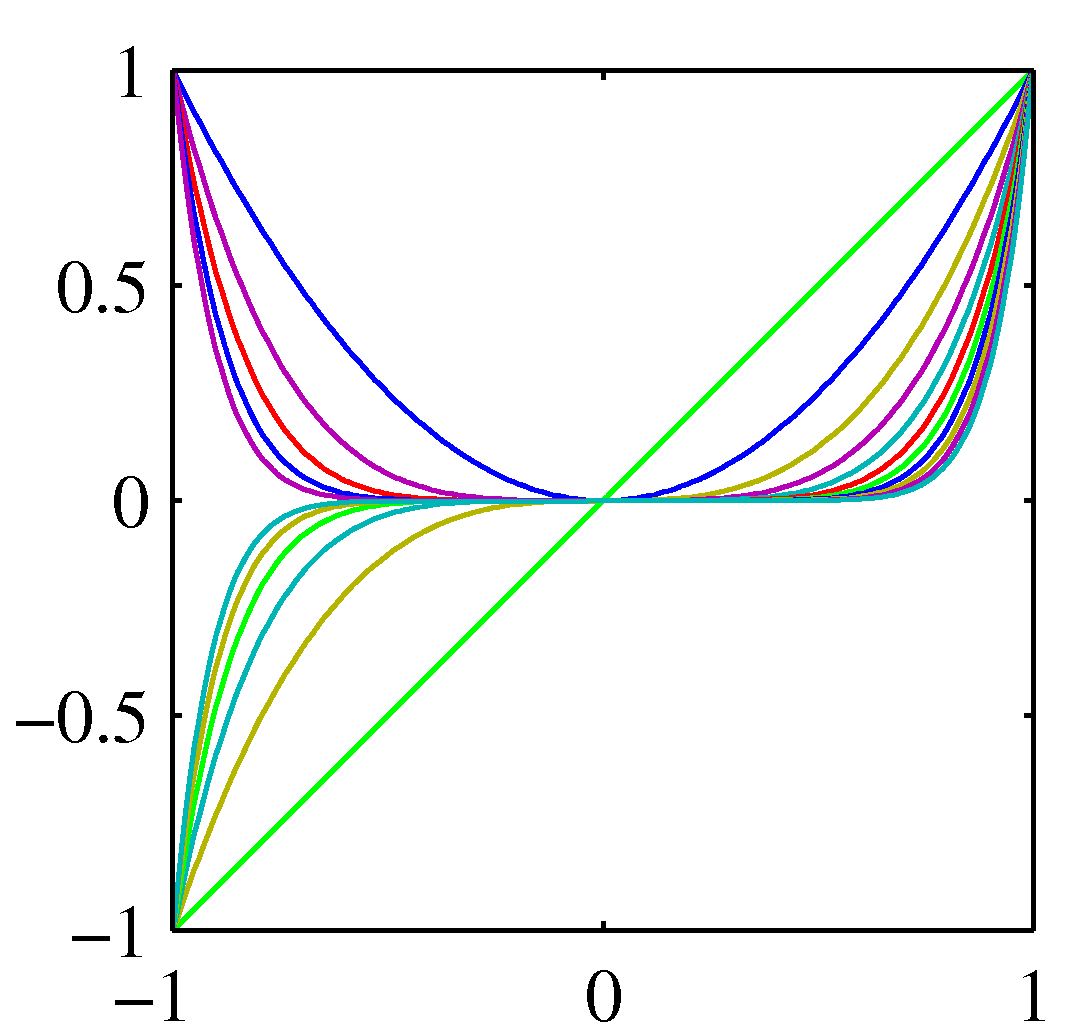
• 위의 그림을 보면 좀 더 이해하기 쉽다.
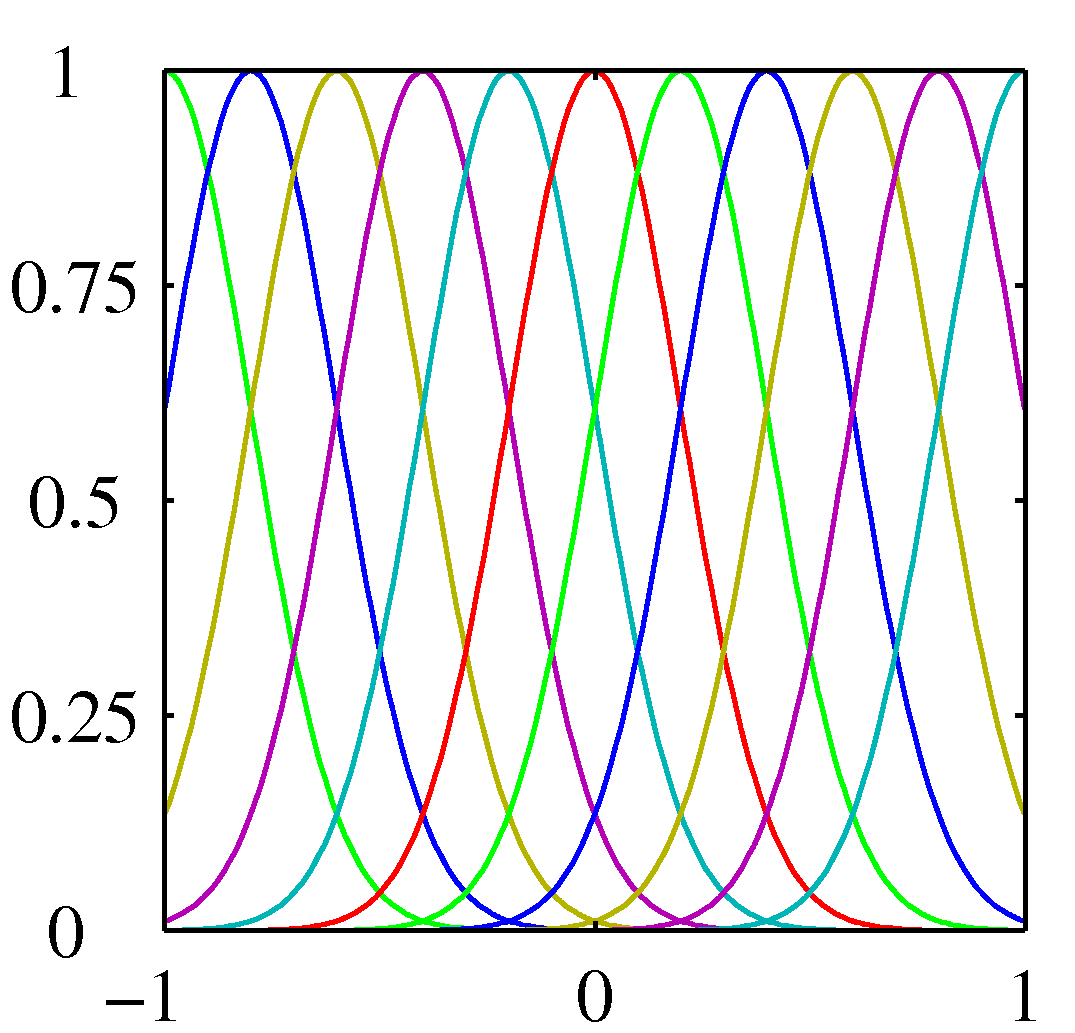
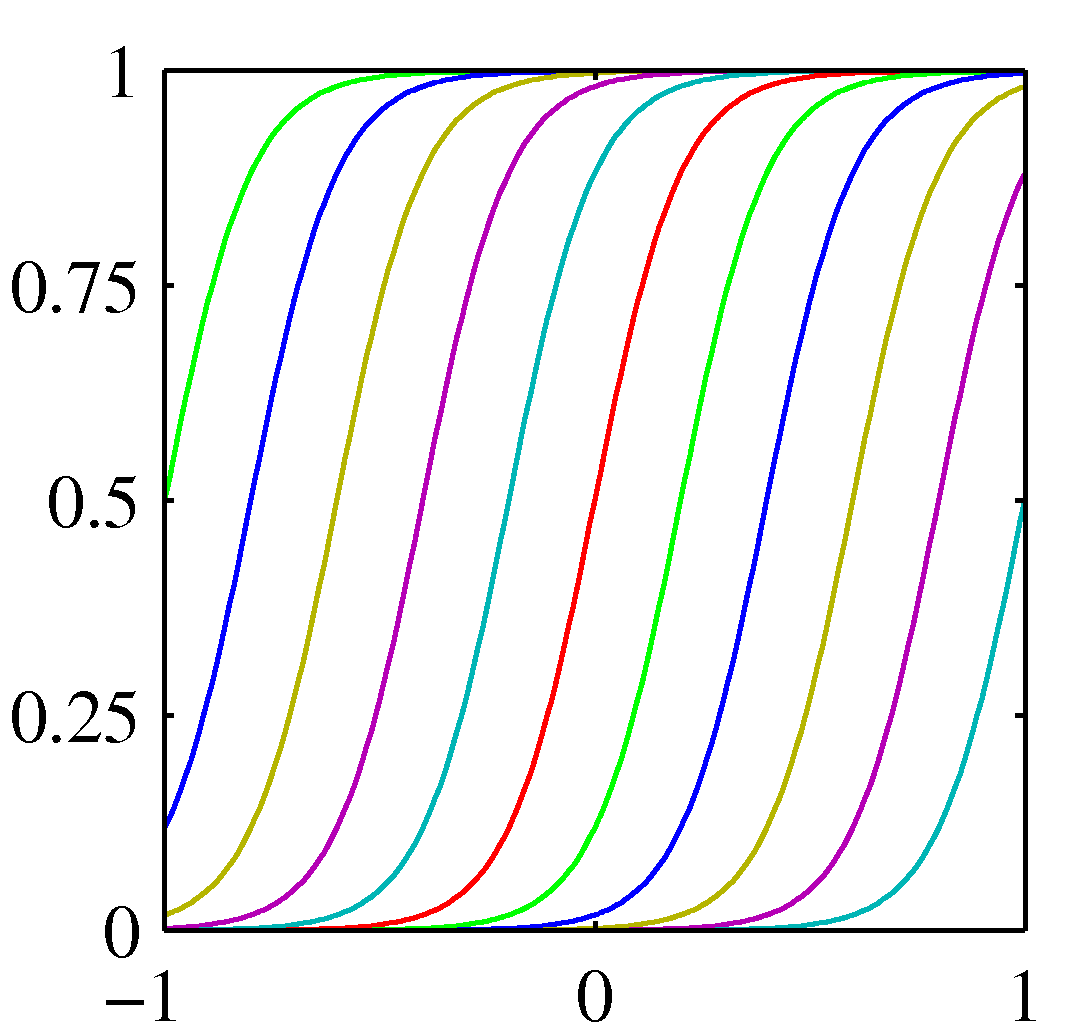
  • 첫번째는 다항식, 두번째는 가우시안, 세번째는 시그모이드 기저 함수를 나타낸다.
  • 그림을 보면 색깔마다 서로 다른 기저 함수를 의미하게 된다. 즉 \( \phi_j \) 에서 \( j \) 를 의미하게 된다.
  • 가우시안, 시그모이드의 경우 각각의 기저 함수의 중간 값의 위치가 \( u_j \) 가 된다. 일정한 간격으로 구성됨을 알 수 있다.
  • 가우시안, 시그모이드의 경우 하나의 기저 함수의 퍼짐 혹은 기울기 정도를 \( s \) 를 이용하여 조절할 수 있다.
  • 이 그림을 통해 Global Function 개념을 약간 이해할 수 있다.
    • 만약 임의의 \( x \) 한 점을 고려해보자.
    • 예를 들어 \( x=0.5 \) 이런 식으로 생각을 하면 이 때 y축에 존재하는 기저 함수의 개수를 보면 된다.
    • 다항식의 경우 나타난 모든 기저 함수가 연관되어 있다.
    • 가우시안과 시그모이드는 \( x=0.5 \) 인 주변의 기저 함수만이 실제 값을 가지게 되고 나머지는 0또는 1의 값을 반환하게 된다.
    • 즉, 한 점에 대해 연관되어진 기저 함수의 개수가 얼추 정해지게 된다. (전체 기저 함수 개수보다 작거나 같다.)
• 기저 함수는 여기서 언급한 것 외에도 다양하게 만들어 낼 수 있다.
  • 가장 간단한 꼴의 기저 함수는 \( \phi(x)=x \) 인 기저함수이다.
    • 이 경우 \( w \) 가 D 개의 벡터라도 결국 하나의 직선으로 근사식이 만들어지게 된다.
    • 즉, \( f=w_0+w_1x+…w_Dx=(\sum_{n=1}^{D}w_n){x}+w_0 \) 인 직선의 방정식
• 이후에 등장하는 예제들은 특별히 어떤 기저 함수를 사용해야 된다는 제약이 없다.
  • 즉, 최대한 일반화된 모델로 설명을 진행할 예정이다.

3.1.1. 최대 가능도와 최소 제곱법 (Maximum likelihood and least squares)

• 우리는 이미 1장에서 다항식의 기저 함수를 이용하여 커브 피팅을 하는 방식을 살펴 보았다.
  • 이 때 사용한 기법이 최소 제곱법(Least Square)이다.
• 또한 우리는 가우시안 노이즈 모델을 적용하여 최소 제곱법을 이용해 MLE 를 구하는 것도 살펴보았다.
• 우리는 이것에 대해 좀 더 자세히 살펴볼 예정이다.
• 자, 일단 가우시안 노이즈가 포함된 타겟 \( t \) 에 대한 함수를 표현해 보자.

• 여기서 \( e \) 는 평균이 0이고 분산 값이 \( \beta^{-1} \) 인 가우시안 랜덤 변수이다. (즉, \( N(e|0, \beta^{-1}) \) 분포를 따른다.)
  • 1장에서도 언급했지만 \( \beta \) 에 대한 역(inverse)을 분산 값으로 사용하는 것은 계산의 편리성 때문이다.
  • 분산(variance)에 대한 역(inverse) 값을 정밀도(precision)이라고 부른다.
• 이제 모델을 만들어보자.
• 현재 우리가 고민해야 할 것은 입력 값 \( x \) 에 대한 \( t \) 값의 관계이므로 다음과 같은 확률식으로 이를 표현할 수 있다.

• \( x \) 는 하나의 샘플 데이터이다. 이 때의 결과 값은 \( t \) 가 된다.
  • 따라서 위의 식은 “주어진 입력 데이터 \( x \) 에 대해 얻어질 결과 \( t \) 에 대한 확률 분포”라고 생각하면 된다.
  • 식을 보면 알겠지만 가우시안 분포를 따른다.
• \( w \) 는 벡터로서 보통 샘플 데이터를 통해 얻어내야 하는 값이지만, 일단은 최적의 \( w \) 를 찾았다고 생각하자.
  • 그러면 상수 값인 고정된 파라미터가 된다.
• \( \beta \) 는 샘플 하나가 가진 노이즈 요소로 이 또한 가우시안 분포를 따른다고 한다.
  • 이 말은 \( \beta \) 를 랜덤 변수로 고려할 수 있다.
  • 즉, 평균이 0이고 일정한 크기의 분산 값을 가진 정규 분포에 의해 에러가 생성된다고 가정한다. ( \( N(\beta|0, s^{-1}) \) )
  • 물론 이것은 노이즈에 대한 하나의 가정일 뿐이다.
    • 상황에 따라 적합하지 않은 가정일 수 있으나 여기서는 그냥 이해를 돕기위해 사용된다.
  • \( w \) 와 마찬가지로 이것도 최적의 값을 구해야 하지만, 일단은 최적의 \( \beta \) 를 알고 있다고 해보자.
    • 그럼 고정된 파라미터가 된다.
    • 베이지안 방식을 사용할지라도 mode 나 mean 값을 그냥 파라미터의 값으로 사용하기도 한다.
• 이제 이 식을 풀어서 기술해보자.
  • 임의의 \( x \) 데이터가 주어졌을 때, 이미 최적의 \( w \) 벡터와 노이즈 정보 \( \beta \) 가 존재한다.
  • 따라서 이를 이용해서 그 때 얻을 수 있는 \( t \) 를 확률 식으로 표현할 수 있다.
  • 고정된 \( w \) 와 \( \beta \) 로 인해 최적의 근사 식 \( y \) 가 만들어졌으므로,
  • 얻을 수 있는 \( t \) 값은 최적의 근사 식 \( y(x,w) \) 를 통해 얻어진 값과 일치할 확률이 가장 크다.
  • 그러나 샘플이 노이즈를 가질 수 있으므로 예측한 값 주변 근처에 생성될 수 있다.
  • 이것 또한 노이즈 팩터 \( \beta \) 를 통해 어느 범위까지 노이즈를 포함하여 발현될 지를 예측할 수 있다.
• 그림 1.16에 이에 대한 개념이 잘 표현되어 있다.

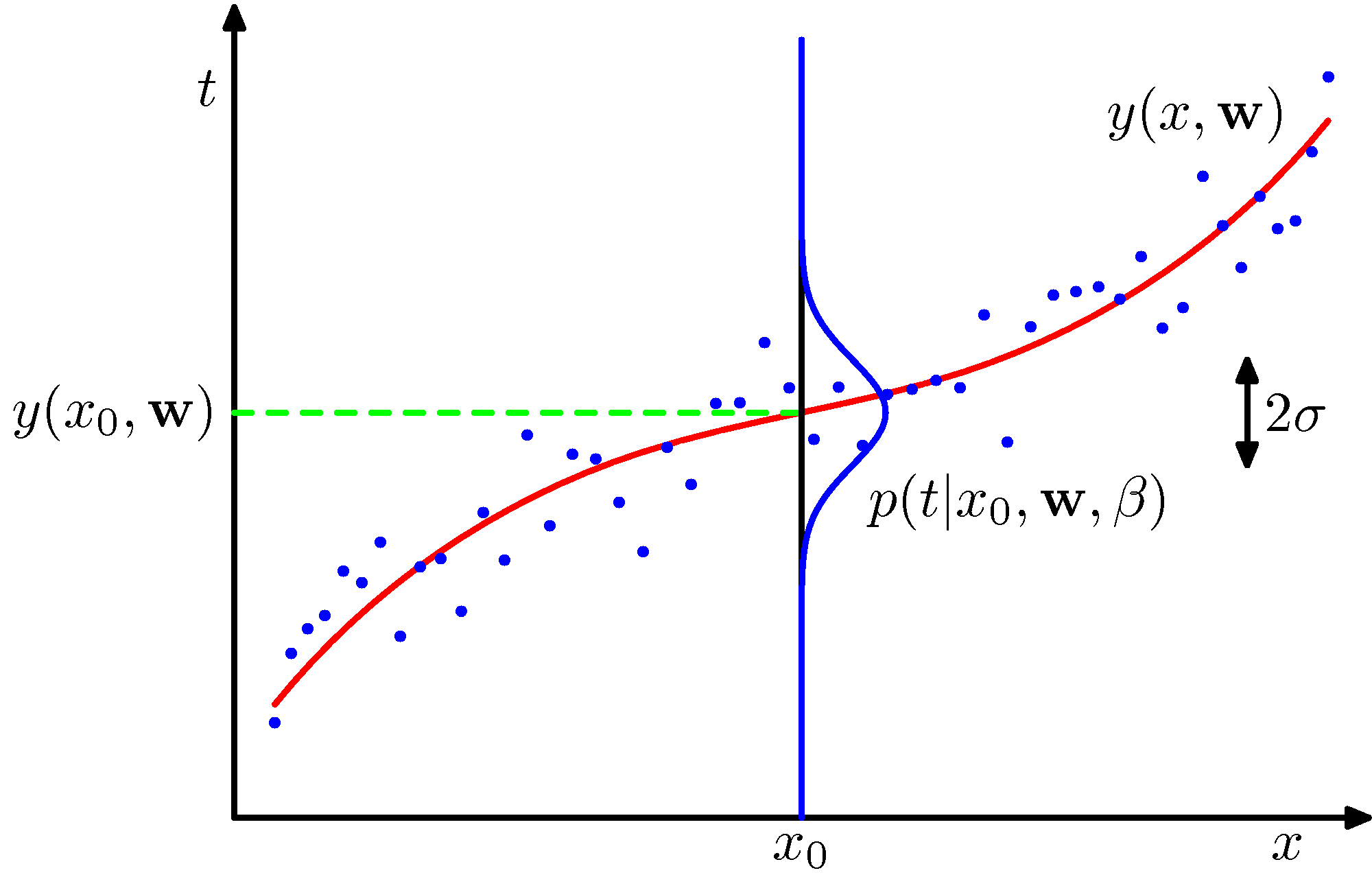
• 그런데 임의의 \( x \) 데이터에 대해 \( y(x,{\bf w}) \) 에서 \( t \) 의 값이 가장 많이 발현될 가능성이 높다고 이야기할 수 있을까?
• 이는 \( p(t|x) \) 의 평균 값이 \( y(x,w) \) 가 되기 때문인데, 이에 대한 사항은 1.5.5 절을 참고하도록 한다. (식 1.89)
  • 참고로 정규 분포에서는 최빈값( mode )은 1개만 존재하며 평균 값과 같고 분포 식 가운데에 위치하게 된다.

• 이제 MLE 를 구하기 위한 단계로 전개를 해보도록 한다.
• 가장 먼저 샘플 데이터에 대한 식을 정의한다.
  • 입력 데이터 \( X \) 는 \( X={x_1,…,x_N} \) 으로 주어진다.
  • 이에 대응되는 출력 값은 \( {\bf t}={t_1,…,t_N} \) 이다.
• 각각의 데이터가 발현될 가능성은 모두 독립적이라 가정한다. ( i.i.d )
  • 따라서 우리가 샘플 데이터를 얻는 확률은 다음과 같이 기술할 수 있다.

• \( x \) 는 전 영역에 걸쳐 등장하기 때문에, 좀 더 깔끔한 표기를 위해 확률 표현에서는 생략하도록 한다.
  • 엄밀히 말하면 \( x \) 는 여기서 랜덤 변수가 아니기 때문에 생략이 가능하다.
• 로그 함수를 도입하여 수식을 좀 더 간단하게 만든다.

• 이 함수를 가능도 함수(likelihood function)로 사용하여 최적의 모수를 찾을 수 있다.
• 여기서 사용되는 파라미터는 \( w \) 와 \( \beta \) 가 되고 각각에 대해 간단하게 편미분하여 값을 구할 수 있다.
  • 최종적으로 \( w \) 에 대해 Convex 함수 꼴이 된다.
• \( w \) 에 대해 미분하면,

• 좌변을 0으로 두고(식 3.14) 전개하면 다음과 같은 식을 얻을 수 있다.

• 이를 최소 제곱법의 일반 방정식(normal equation) 이라고 부른다.
  • 파라미터의 추정 방식이 업데이트 방식이 아닌 일반 방정식으로 풀이되는 방식이다.
• 이 때 사용되는 \( \Phi \) 는 \( N\times{M} \) 크기의 행렬로 디자인 행렬(design matrix) 이라고 한다.
  • 실제 식은 다음과 같다.

• 참고로 아래와 같이 식을 줄여서 표현하기도 한다.

• 여기서 \( \Phi^{\dagger} \) 와 같은 값을 \( \Phi \) 의 Moore-Penrose pseudo-inverse 라고 부른다.

• 다음으로 \( w_0 \) 에 대해 좀 살펴보자.
• 만약 \( w_0 \) 를 함수에서 분리해 기술한다면 에러 함수가 다음과 같이 변하게 된다.

• 만약 이 식이 \( w_0 \) 로 인해 0이 된다고 가정해보자. 그럼 식을 다음과 같이 전개할 수 있다.

• 결국 에러 함수를 최소로 만들어 낼 수 있는 \( w_0 \) 의 값의 의미를 보자.
  • 이는 실제 얻어지는 샘플들의 타겟 값들의 평균과,
    이 때 기저함수에 가중치를 곱하여 얻어진 결과의 평균값의 차이를 보정하는 역할을 하게 된다.
  • 따라서 bias 라는 이름이 괜히 만들어진게 아니다.
• 마지막으로 노이즈에 대해서도 MLE 값을 구할 수 있다.
  • 원래 식이었던 3.11 을 \( \beta \) 에 대해 편미분하면 다음과 같은 결과를 얻는다. (결국 분산을 구하는 식을 얻는다.)

3.1.2. 최소 제곱법의 기하학적 의미 (Geometry of least squares)

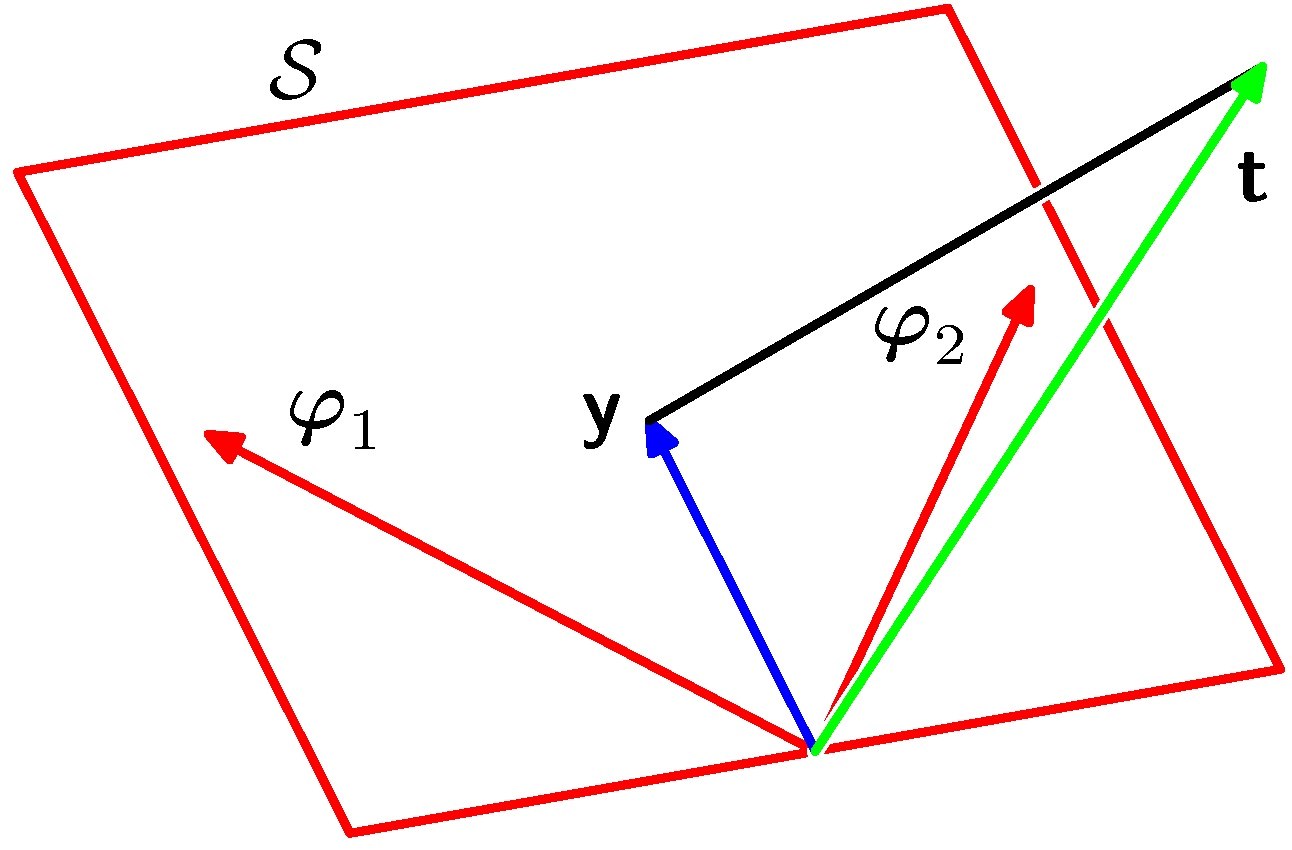
• 여기서는 최소 제곱법이 가지는 기하학적 의미를 생각해본다.
• 우리가 N개의 샘플 데이터를 통해 얻을 수 있는 모든 \( t \) 는 N차원의 벡터 공간 놓여있는 하나의 벡터라고 생각할 수 있다.
  • 식으로 표현하면 \( {\bf t}=(t_1,…,t_n)^T \) 이다.
• 이제 이 차원에다가 우리가 사용한 기저함수를 표현할 수 있는 벡터를 상상해보자.
  • 하나의 \( j \) 에 대해서 총 N개의 샘플을 적용하여 얻은 결과를 생각하면 N차원에 표현할 수 있는 하나의 벡터가 된다.
  • 즉 어떤 벡터 \( {\bf v1} \) 이 \( \phi_1 \) 을 적용하는 벡터라고 하면,
    모든 샘플 데이터에 대해 \( {\bf v1}=(\phi_1(x_1),…,\phi_1(x_n))^T \) 를 가지는 하나의 벡터가 된다.
  • 이는 앞서 정의한 design matrix 에서 하나의 컬럼에 대응된다.
• \( j \) 에 대해 샘플에 기저함수를 적용한 벡터를 \( \Phi_j \) 하고 정의하면,
  • 이 벡터들은 N차원의 공간에 M-1개의 벡터로 표현된다.
  • 위의 그림에서는 빨간색 벡터가 된다.
• 내용을 전개하기에 앞서 간단하게 기초 선형대수 성질을 기술해보자.
  • \( N \) 차원 위에서 표현된 임의의 벡터는 \( N \) 개의 기저 벡터의 선형 합으로 표현될 수 있다.
    • 기저 함수와 기저 벡터를 혼동하지 말것. 다른 개념이다.
  • 이 의미를 반대로 생각해보면, \( N \) 차원에서 \( N \) 개의 기저 벡터를 모두 가지고 있지 않다면 임의의 한 점을 나타내는 벡터를 모두 표현하기는 불가능이다.
  • 만약 \( N-1 \) 개의 기저 벡터만을 가지고 있다면 \( N \) 차원 내에서 일부 점들은 이 기저 벡터만으로는 표현할 수 없다.
  • 따라서 이런 벡터들의 집합을 하나의 공간으로 생각한다면 \( N \) 차원의 서브(sub) 공간으로 구성된 영역을 가지게 됨을 유추할 수 있다.
• 다음으로 우리가 만든 모델(즉, 근사식)을 통해 얻어진 결과 벡터를 \( {\bf y} \) 라고 하면 마찬가지로 \( N \) 차원의 공간에 하나의 벡터로 표현 가능하다.
• 이 \( {\bf y} \) 벡터는 \( {\bf t} \) 벡터와는 다르게 \( N \) 차원의 모든 위치에서 발현될 수 있는 것은 아니다.
  • 왜냐하면 수식 전개상 \( \phi_j(x_n) \) 벡터들의 선형 합으로 표현되기 때문이다.
• 따라서 벡터 \( {\bf t} \) 는 \( N \) 차원의 모든 영역 내에서 발현될 수 있지만, \( {\bf y} \) 는 정해진 공간 내에서만 발현된다.
  • 앞선 수식에서 알 수 있듯 기저 함수의 차원은 \( M \) 이다. 보통 이 값은 전체 샘플 데이터 \( N \) 보다 작다.
• 이를 선형 대수에서는 벡터 공간이라고 표현한다.
  • \( \Phi_j \) 벡터들의 조합으로 만들어 낼 수 있는 벡터 공간을 \( S \) 라고 정의하면 \( S{\subseteq}Space(N) \) 이 된다.

• 위의 그림을 보면 대략적으로 이해 할수 있다.
• 결국 우리가 구하고자 하는 것은 \( {\bf y} \) 벡터가 놓일 수 있는 공간 \( S \) 로부터 실제 결과 값 \( {\bf t} \) 벡터 사이에 가장 가까운 거리를 가지는 한 점을 찾는 것이다.
  • 이 점이 바로 \( {\bf y} \) 벡터가 된다.
• 현실적인 입장에서 볼 때, 최소 제곱법의 일반식(normal equation)은 약간의 제약이 존재한다.
  • 이는 기저 함수 연산식에서 \( \Phi^T\Phi \) 가 특이 행렬(singular)이 될 수 있기 때문이다. (즉, 역행렬이 존재 안 함)
  • 이는 \( \Phi^T\Phi \) 의 결과로 정방 행렬이 얻어지고, 정방 행렬의 경우 행 또는 열 중 2개 이상의 값이 동일하거나 배수인 경우 역행렬이 없는 경우가 발생한다.
  • 간단하게 생각해보면 방정식에서 \( K \) 개의 근을 찾기 위해서는 서로 다른 \( K \) 개의 식이 필요하다는 이야기.
  • 실제 구현에 있어서는 완벽하게 Singular 조건을 만족하지 않더라도 정방 행렬이 너무 크거나 실수 연산 범위의 제약으로 역행렬을 못 구하는 일이 생기기도 한다.
    • 계산시 수치 연산의 overflow , underflow 등으로 인해.
• 이를 해결하기 위해 SVD(singular value decomposition)을 도입할 수 있다. (차원 축소의 효과가 있음)
• 뒤에 나오지만 정칙화(regularization)를 도입해서 문제를 해결할 수도 있다.
  • 자세히 설명을 하지 않지만 정방 행렬에 대각 행렬을 더한 뒤 역행렬을 구하는 방식을 사용한다.

3.1.3. 시퀀스 학습 (Sequential learning)

• 지금까지 살펴본 MLE 기법은 전체 데이터를 한번에 사용해서 처리하는 배치(batch) 방식이었다.
• 그러나 데이터 규모가 커지거나, 데이터가 순차적인 입력으로 이루어질 때에는 이러한 방식을 사용하기 힘들다.
• 따라서 데이터가 순차적으로 입력될 때에 모델의 파라미터를 학습하는 방법을 살펴보도록 하자
  • 이런 방식을 on-line 방식이라고 한다.
  • 당연히 데이터는 순차적인 스트리밍 방식으로 입력되어야 하고,
  • 따라서 구해야 할 파라미터 값이 계속해서 갱신되어야 한다.
• 여기서는 Stochastic gradient decent 라는 방식을 확인한다. (이를 Sequential Learning 이라고도 한다)
• 방식은 매우 간단하다. 에러함수 \( E_D \) 를 \( E_D=\sum_{n}E \) 로 정의하여 파라미터를 업데이트되도록 식을 만든다.

• 여기서 ( \)\tau \))는 데이터가 반복적으로 입력된 횟수이다. \( \eta \) 는 학습률(learning rate) 파라미터이다.
• 사실 \( \eta \) 를 무엇으로 정해야 하는지는 매우 신중하게 결정되어야 한다.
• 위와 같은 알고리즘을 LMS(least mean square) 라고 한다.

3.1.4. 정칙화가 포함된 최소 제곱법 (Regularized least squares)

• 우리는 이미 1.1 장에서 정칙화(regularization)에 대한 개념을 다루어 보았다.
  • 학습시 오버피팅을 방지하기 위해 사용되는 방법이다.
• 에러 함수는 다음과 같이 정의된다.

• 여기서 \( \lambda \) 는 정칙화 계수(regularization coefficient)로서 \( E_D({\bf w}) \) 와 \( E_W({\bf w}) \) 사이의 가중치를 조절하게 된다.
  • 이 식을 정리하면 다음과 같다.

• 정칙자(regularizer)중 특별한 케이스에 대해 기계 학습 분야에서 weight decay 로 불리는 기법이 있다.
  • 이는 가중치가 반복 횟수에 따라 점점 작아지는 경우를 의미한다.
  • 또한 parameter shinkage 방식이라고도 하는데, 파라미터의 값이 점점 작아지기 때문이다.
• 에러 함수가 \( {\bf w} \) 에 대해 이차 함수(quadratic) 형태로 남게되어 유일한 해를 가지는 닫힌 구조(closed form)가 된다.
• 최종적으로 식을 정리하면 다음과 같다.

• 앞서 설명한대로 정방 행렬에 어떤 대각 행렬을 더해 역행렬을 구하는 식이 만들어진다.
• 여기에 좀 더 일반화된 형태의 정칙화 기능을 적용할 수 있다.

• 이 경우 \( q=2 \) 인 경우 맨 처음 보았던 형태를 적용하는 이차형식 정칙화(quadratic regularizer)가 된다.
• 아래 그림을 보면 다양한 \( q \) 에 대해 실제 파라미터가 가지게 되는 값의 범위 모양을 기술하고 있다.

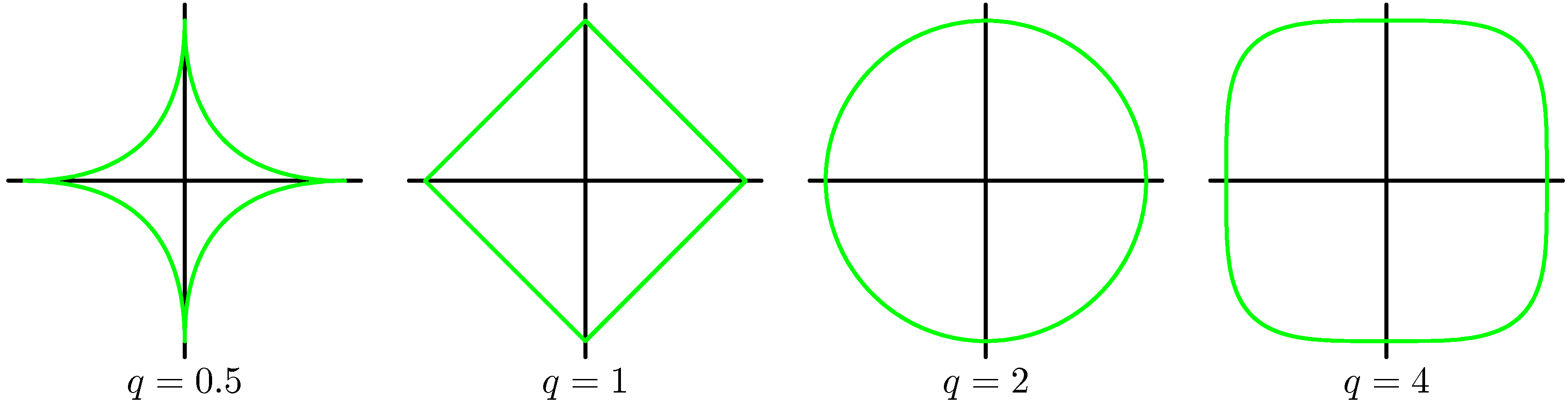
• 이 중 \( q=1 \) 인 경우를 Lasso 라고 한다.
  • 이 경우 \( \lambda \) 값이 충분히 크다면 \( M-1 \) 개의 \( w \) 중에 많은 수가 0이 되거나 0 값에 가까운 값을 가지게 된다.
  • 자연스럽게 feature selection 이 된다.
  • 결국 이런 모델은 sparse 모델의 형태가 되는데, 몇개의 기저 함수만이 모델의 식을 만드는데 사용되게 된다.

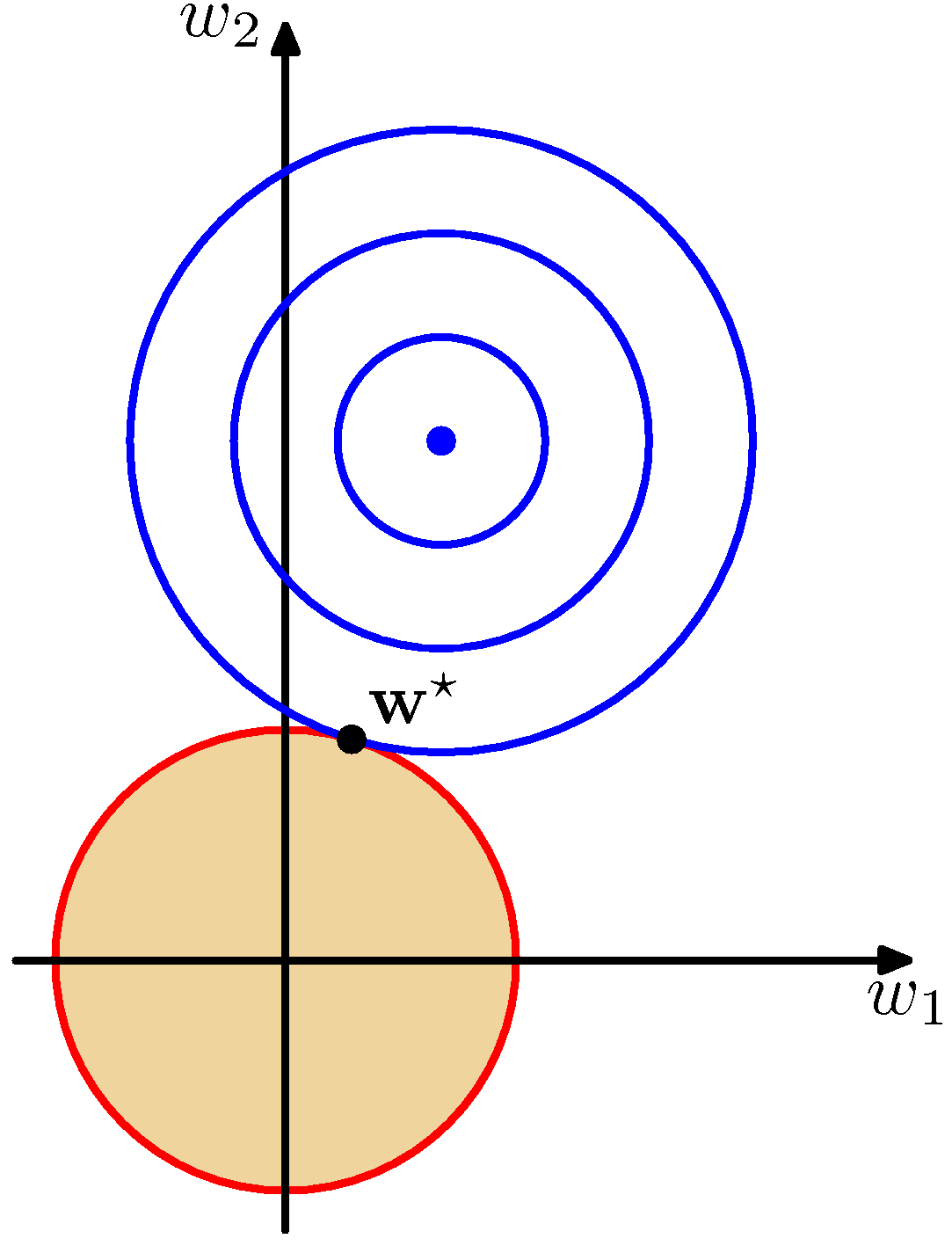
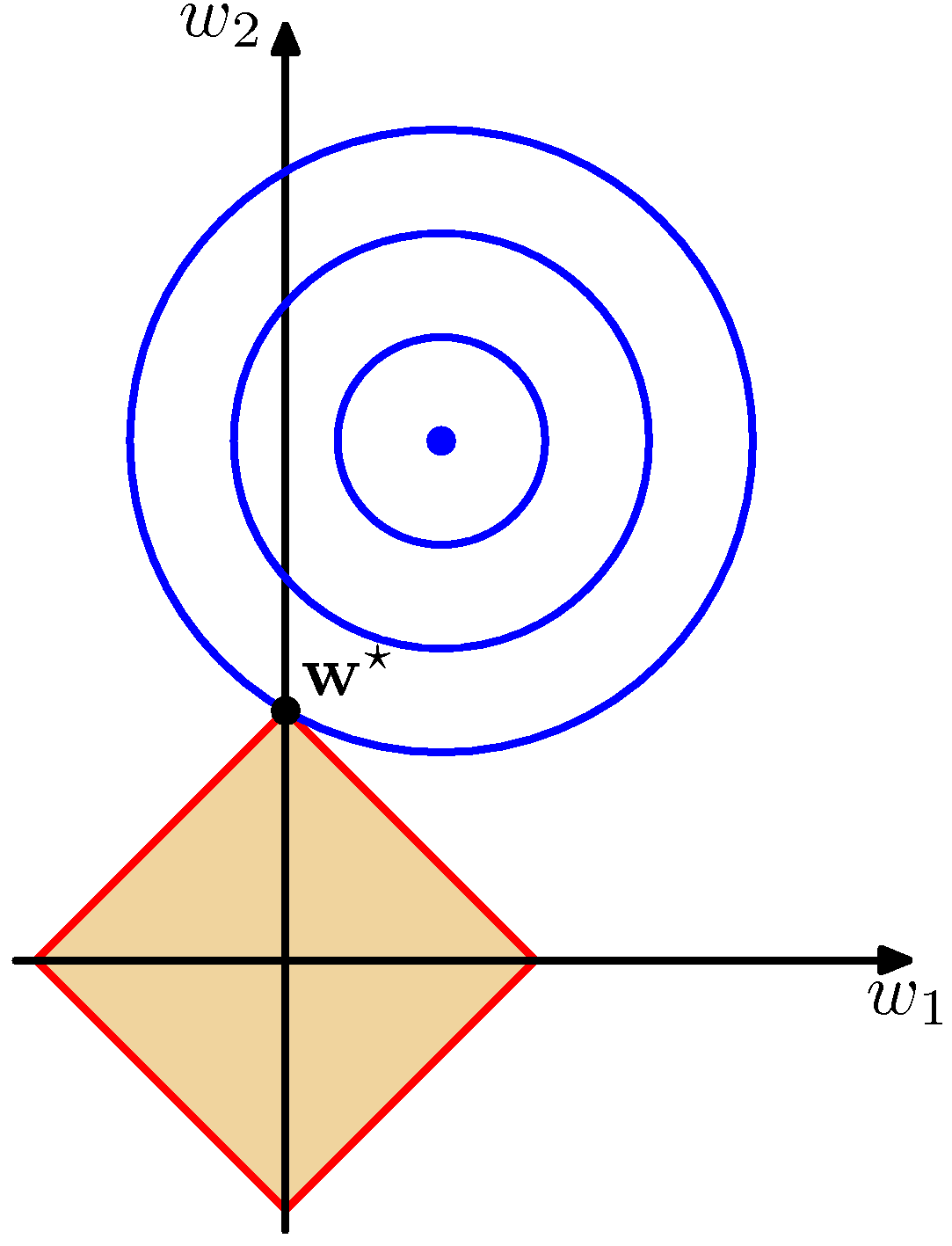
• 위의 그림에 대해 유심히 살펴보도록 하자.
  • 왼쪽은 \( q=2 \) 인 경우이고, 오른쪽은 \( q=1 \) 인 경우를 의미한다.
  • 이 때 사용되는 파라미터는 \( w_0 \) 와 \( w_1 \) 뿐인 아주 간단한 모델이다.
  • 이런 경우 얻게 되는 \( y(x, {\bf w}) \) 식은 직선 식이 된다.
  • 위의 좌표는 오로지 \( w \) 벡터에 대해서만 표현하고 있다.
  • 상단 파란 원의 중심이 \( E({\bf w}) \) 를 최소로 만드는 \( {\bf w} \) 벡터 값을 표현한 것이다.
  • 보통 정칙화 요소가 없는 경우 이 값을 모델의 파라미터로 사용하게 된다.
  • 그러나 정칙화(regularization) 기능이 추가되면, \( w \) 가 가질수 있는 값의 범위가 제한되게 된다.
    • 즉, 위의 그림에서는 노란색 영역에서만 \( w \) 값을 취할 수 있다.
  • \( w \) 에 대한 정칙화 요소식을 잘 생각해보자.
  • 파란 색의 컨투어는 동일한 \( E({\bf w}) \) 값을 가지는 \( w \) 값들을 연결한 것이다.
    • 이 값이 원(타원)으로 만들어지는 것은 \( E \) 에 대해 \( w \) 는 이차 형식이기 때문이다.
  • 정칙화 요소가 포함된 경우 \( w \) 는 \( E_D({\bf w}) \) 를 최소화하는 위치가 아니라 노란 색 영역 범위 내에 존재하는 \( w^* \) 로 정해지게 된다.
  • 이는 사실 라그랑지앙 승수와 관련이 있다.
    • 따라서 두 식을 미분한 값이 같아야 한다. 물론 이 때 부호(방향)는 상관없음.
  • 그림을 보면 노란색의 범위는 원점을 중심으로 크기가 결정되므로 보통 파라미터 값을 작게 만드는 성질이 있음을 알 수 있다.
  • 라소(lasso)의 경우( \( q=1 \) ) 확률적으로 \( w^* \) 지점이 한 축 위에 위치할 가능성이 커진다.
    • 따라서 위의 그림을 보면 \( w_1 \) 의 값은 0이 됨을 알 수 있다.
  • 즉, \( q \) 값이 작을 수록 임의의 \( w_j \) 값이 0에 수렴될 가능성이 더 커진다는 것을 유추해 볼 수 있다.
  • 노란 색의 범위는 고정된 상수 값이 된다.

• 이 식은 라그랑지안 승수로부터 얻어진다.
  • 여기서 사용된 \( \eta \) 는 결국 \( \lambda \) 와 연결되어 있다. (역의 관계)
  • 따라서 \( \lambda \) 값이 0이 되는 경우 결국 이 값은 \( E_D({\bf w}) \) 에서 얻어진 \( w \) 값의 범위까지 확장된다.
  • 반대로 \( \lambda \) 값이 커지는 경우 \( \eta \) 값은 점점 줄어들어 원점까지 작아지게 된다. 이 경우 모든 \( w \) 값은 0이 되게 된다.

3.1.5. 다중 출력값 (Multiple outputs)

• 지금까지 출력값 \( t \) 가 단일 차원의 실수 값이라고 가정했다.
  • 이를 벡터로 확장하는 것을 기술한다.
• 이 챕터는 별로 어렵지 않다. 수식만 봐도 대부분 이해할 수 있다.
• \( {\bf t} \) 벡터의 크기가 \( K \) 라고 할 때 각각의 값은 서로 영향을 주지 않는다.
• 따라서 기존의 식 중 \( t \) 와 \( w \) 에 추가로 \( K \) 개의 차원이 추가되는 수준이다.

• Likeilhood 함수를 정의해보자.

• 이렇게 얻은 식에 대해 MLE 를 구하면 다음과 같다.

• 개별적인 값은 다음과 같다.

• 식 자체로의 변화는 없고, 스칼라 변수가 벡터로 확장되었다는 것만 유의하도록 하자.