2. Bias-Variance Decomposition

우리는 지금까지 회귀모형을 작성할 때 해당 모델의 형태와 이 때 사용되는 기저함수의 개수가 고정되어 있다고 가정했다.
그리고 이 문제를 풀기 위해 최소 제곱법을 도입하여 식을 전개했다.
작은 크기의 샘플 데이터에 대해 복잡한 모델을 사용하는 경우 오버 피팅이 발생하는 현상도 확인했다.
- 그러나 오버 피팅을 줄이기 위해 모델의 파라미터 수를 줄이면 모델의 유연성이 떨어지는 현상이 발생한다.
- 따라서 파라미터의 수는 유지하되 오버피팅을 막기 위한 수단으로 정칙화(regularization) 기능을 도입했다.
이 때 정칙화 계수 $ \lambda $ 값의 변화에 따라 어떻게 모델이 제약되는지도 살펴보았다.
- 하지만 어떻게 하면 가장 좋은 $ \lambda $ 값을 찾을 수 있는지는 아직 언급되지 않았다.
- 만약 $ \lambda $ 의 값이 0이 되면 어떻게 될까?
- 이런 경우 정칙화(regularization) 요소가 사라짐으로써 비정칙화(unregularization)와 결과와 동일하게 된다.
우리는 이전 장에서 MLE 에서 발생하는 오버 피팅 현상이 썩 좋은 현상은 아니며
베이즈 추론을 사용하는 경우 이 문제를 어느 정도 해결할 수 있다는 것을 배웠다.
따라서 당연히 지금까지 했던 내용들을 자연스럽게 베이즈 추론을 사용하는 버전까지 확장을 하게 될 것이다.
그러나 이번 장에서는 이를 살펴보기에 앞서,
- 우선 빈도론자(frequentist)의 입장에서 bias-variance 트레이드-오프(trade-off)에 대해 좀 살펴보기로 하자.
우리는 이미 1.5.5절에서 회귀식에서 사용하는 결정 이론에 대해 논의했다.
- 기억이 나지 않는다면 반드시 해당 절에서 관련 내용 확인할 것.
우리는 최적의 예측 모델을 찾기 위한 방안으로 조건부 분포 $ p(t|x) $ 함수를 이용하여 Loss 함수를 정의하여 식을 전개했다.
최종적으로 다음과 같은 식을 얻었음을 상기하자.

$h(x)=E[t|x]=\int{tp(t|x)\;dt} \qquad{(3.36)}$

여기서 중요한 포인트는 다음의 두 가지를 구별해 볼 필요가 있다는 것이다.
- 결정 이론으로 부터 얻어진 Squared Loss 함수
- 파라미터 MLE 추정 과정에서 얻어진 Sum-of-Squre 에러 함수
우리가 1.1.5절에서 다룬 식을 잠시 꺼내어 보자.

$E[L]=\int{\{y(x)-h(x)\}^2p(x)\;dx}+\iint{\{h(x)-t\}^2p(x,t)}\;dx\;dt \qquad{(3.37)}$

이 중에서 두번 째 텀(term)은 $ y(x) $ 와 직접적인 관련이 없다.
- 이 영역은 데이터의 노이즈(noise)를 의미하게 된다.
첫번 째 텀(term)을 보면 우리가 선택해야 할 $ y(x) $ 가 어떤 값으로 수렴해야 하는지를 이해할 수 있다.
- 왜냐하면 제곱 식에 의해 이 값은 항상 0이거나 0보다 큰 값을 가지게 된다.
- 우리의 목표는 에러를 최소화해야 하는 것이기 때문에 최대한 $ h(x) $ 와 동일한 $ y(x) $ 를 찾아야 한다.
- 데이터가 충분히 많다면, $ h(x) $ 에 매우 근사된 $ y(x) $ 를 쉽게 찾을 수 있을 것이다.
- 하지만 우리에게 주어진 데이터는 고정된 크기 $ N $ 을 가진 데이터 $ D $ 일 뿐이다. (즉, 샘플이다.)
이제 논의를 확장하기 위해 몇 가지 가정을 해보자.
- 우리는 분포 $ p(t, x) $ 를 통해 생성된 $ N $ 개의 샘플로 구성된 데이터 집합 $ D $ 를 얻을 수 있음.
- 또한 여러 개의 데이터 집합을 얻을 수 있으며 모든 샘플은 서로 독립적으로 생성된다고 가정할 수 있음. ( i.i.d )
- 우리는 각각의 데이터 집합을 이용하여 예측 함수 $ y(x;D) $ 를 만들어 낼 수 있다.
이런 경우 서로 다른 데이터 집합은 서로 다른 손실(loss) 함수와 결과를 만들어 낼 것이다.
아까 사용했던 식의 첫번 째 텀에 이 내용을 반영해 보자.

$\{y(x;D)-h(x)\}^2 \qquad{(3.38)}$

하나의 데이터 집합을 이용하여 손실 함수를 구할 수 있기 때문이다.
이제 여러 개의 데이터 집합으로 구해진 함수의 평균값 $ E_D[y(x;D)] $ 를 이용해서 식을 전개해보자.

$\{y(x;D)-E_D[y(x;D)]+E_D[y(x;D)]-h(x)\}^2\\=\{y(x;D)-E_D[y(x;D)]\}^2+\{E_D[y(x;D)-h(x)]\}^2\\\\+2\{y(x;D)-E_D[y(x;D)]\}\{E_D(x;D)-h(x)\} \qquad{(3.39)}$

위의 식을 통해 우리는 데이터로 얻어진 $ y(x;D) $ 와 회귀식 $ h(x) $ 사이의 차이는 2개의 속성으로 나누어짐을 확인할 수 있다.
첫번 째 텀은 바이어스(bias)라고 하고, 두번 째 텀은 분산(variance)이라고 한다.

$E_D[\{y({\bf x};D)-h({\bf x})\}^2]\\ = \{E_D[y({\bf x};D)]-h({\bf x})\}^2+ E_D[\{y({\bf x};D)-E_D[y({\bf x};D)]\}^2] \qquad{(3.40)}$

최종적으로 우리는 기대 손실(expected loss) 값을 다음과 같이 정의할 수 있다.

${Expected}\;{loss} = (bias)^2 + variance + noise \qquad{(3.41)}$

각각의 값들은 다음과 같다.

$(bias)^2=\int{\{E_D[y(x;D)]-h(x)\}^2p(x)\;dx} \qquad{(3.42)}$ $variance = \int{E_D[\{y(x;D)-E_D[y(x;D)]\}^2]p(x)\;dx} \qquad{(3.43)}$ $noise=\iint{\{h(x)-t\}^2p(x,t)\;dx\;dt} \qquad{(3.44)}$

우리의 목표는 기대 손실 $ E[L] $ 값을 최소화하는 것이다. 그리고 이 값은 위의 3가지 요소로 나누어(decomposed) 고려할 수 있다.
이 중 노이즈 값은 관찰 데이터 자체에 포함된 에러로서 우리가 제어하기 힘든 영역이다.
따라서 우리는 바이어스(bias) 와 분산(variance) 값을 적절히 조절하여 기대 손실이 가장 작은 값을 만들어야 한다.
- 보통 이 두 요소는 서로 trade-off 관계를 가진다.
- 따라서 유연한 모델은 낮은 바이어스, 높은 분산도를 가지게 되며,
- 엄격한 모델은 높은 바이어스, 낮은 분산도를 가지게 된다.

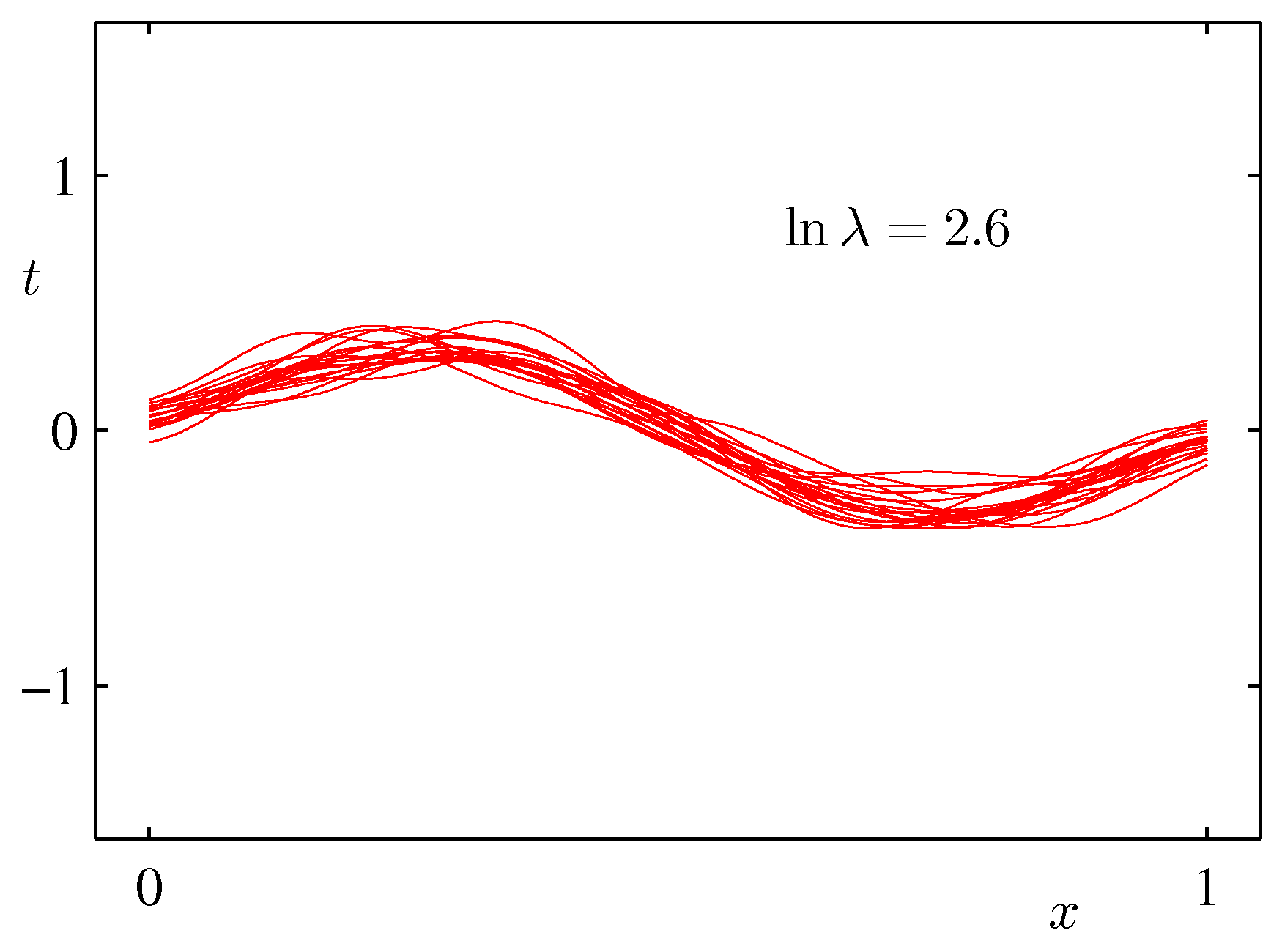
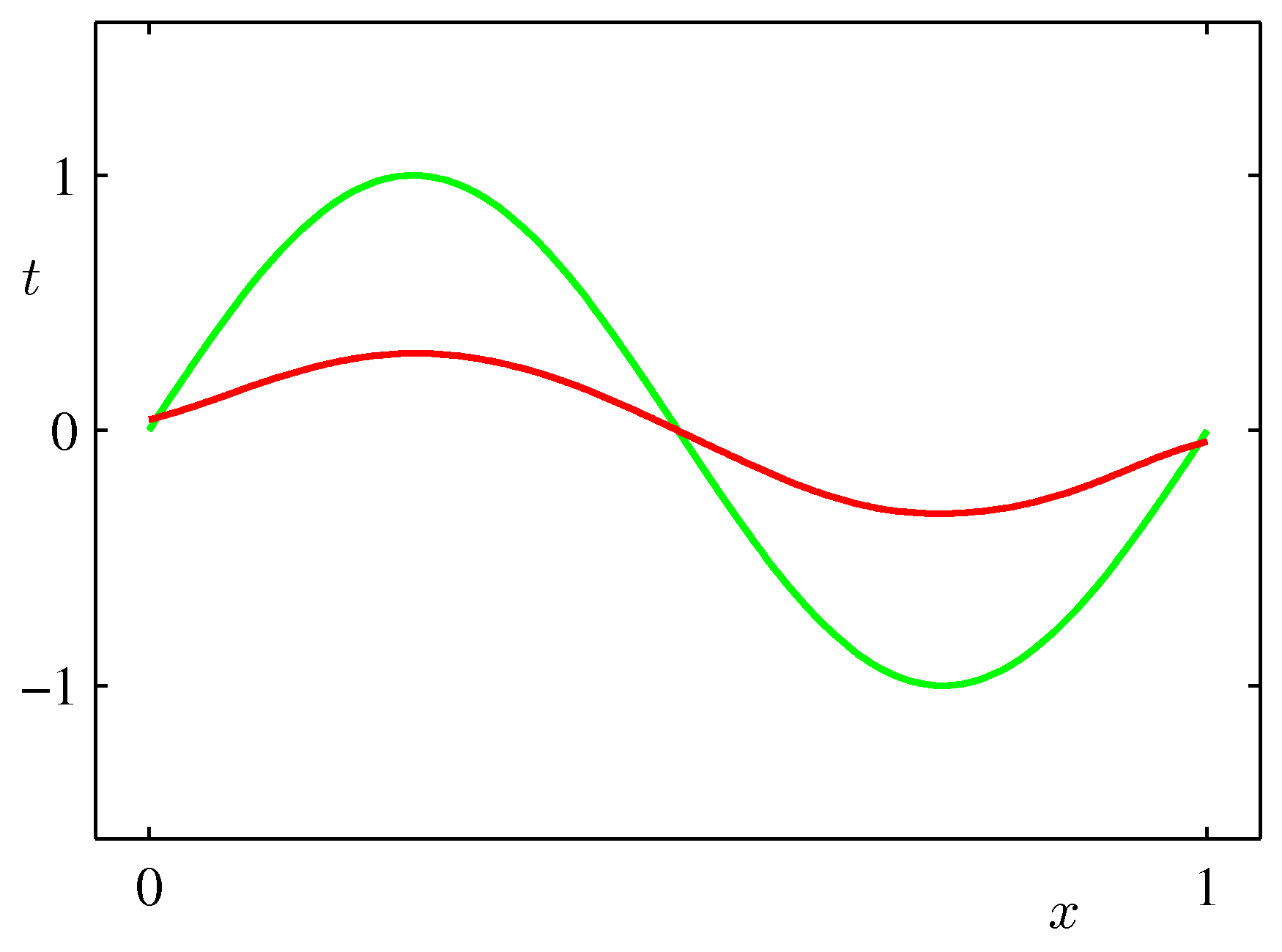
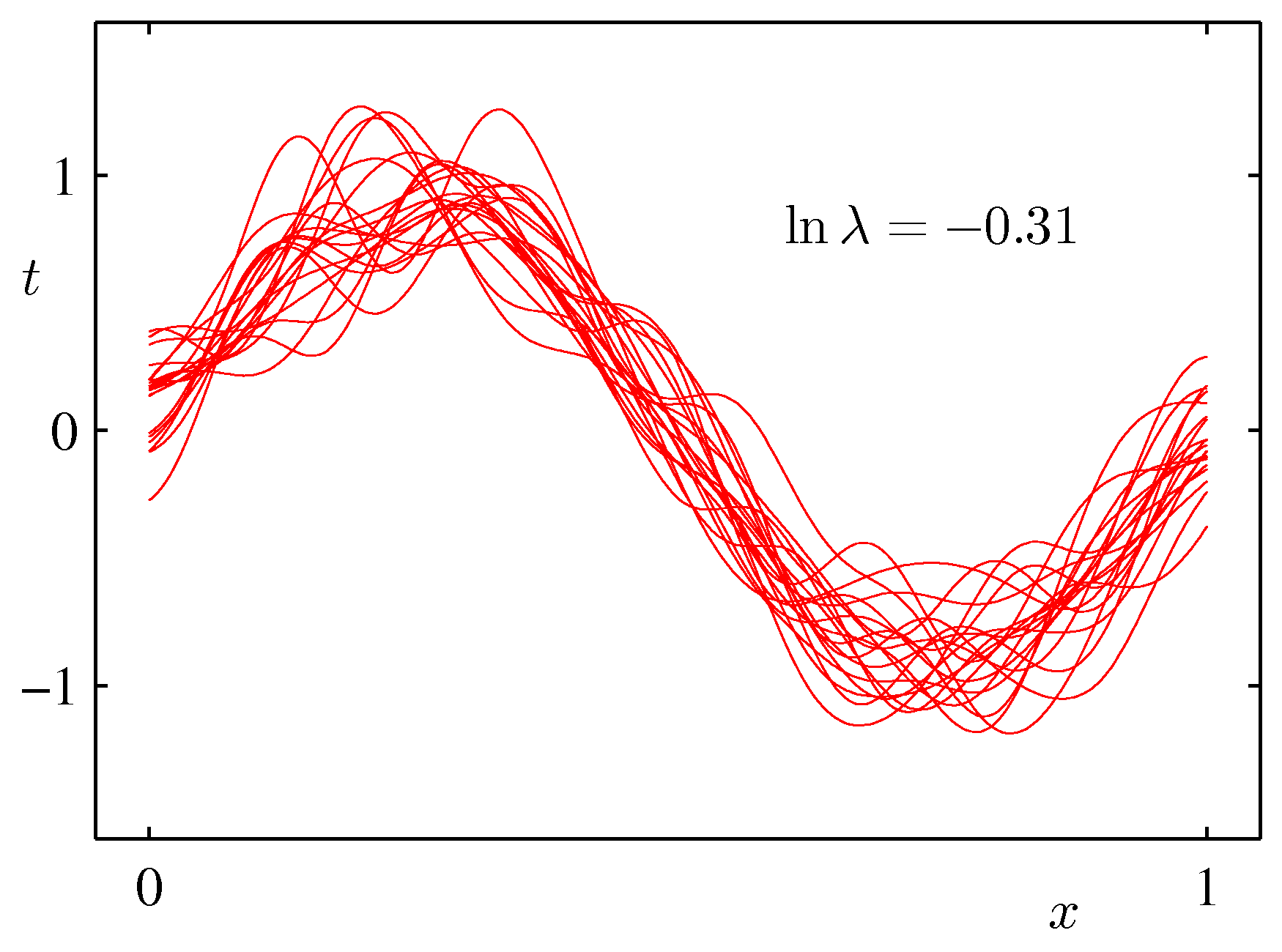
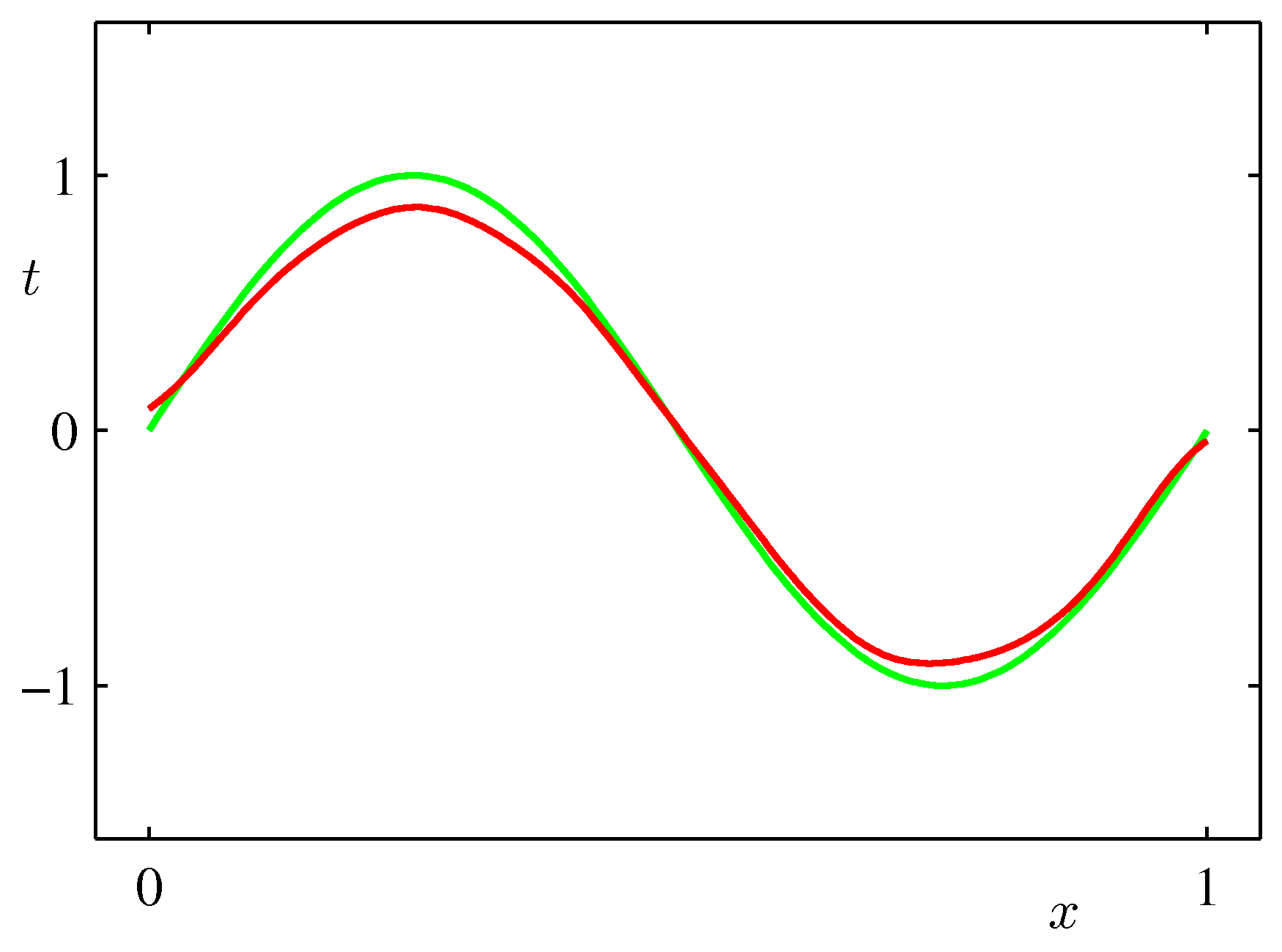
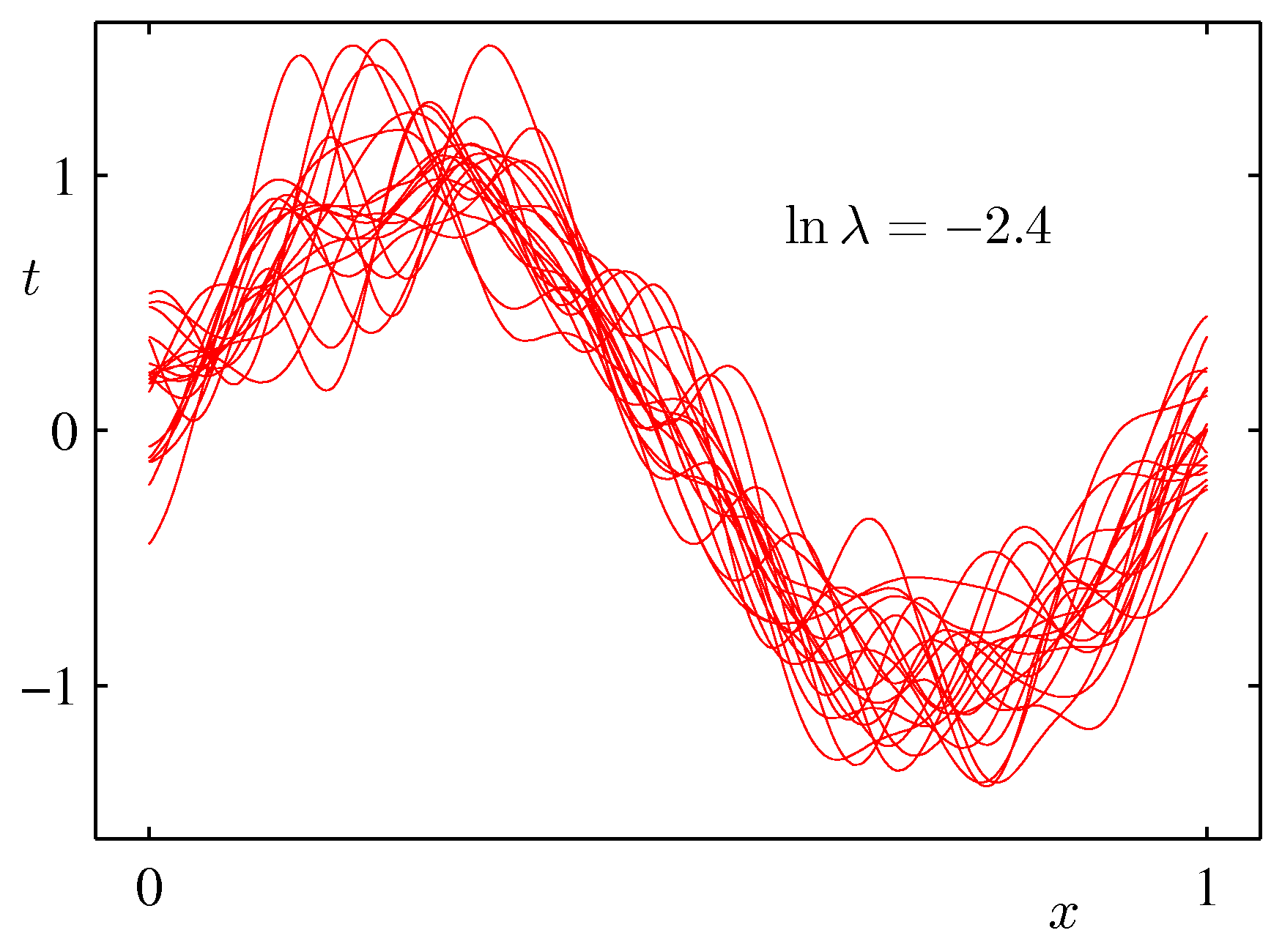
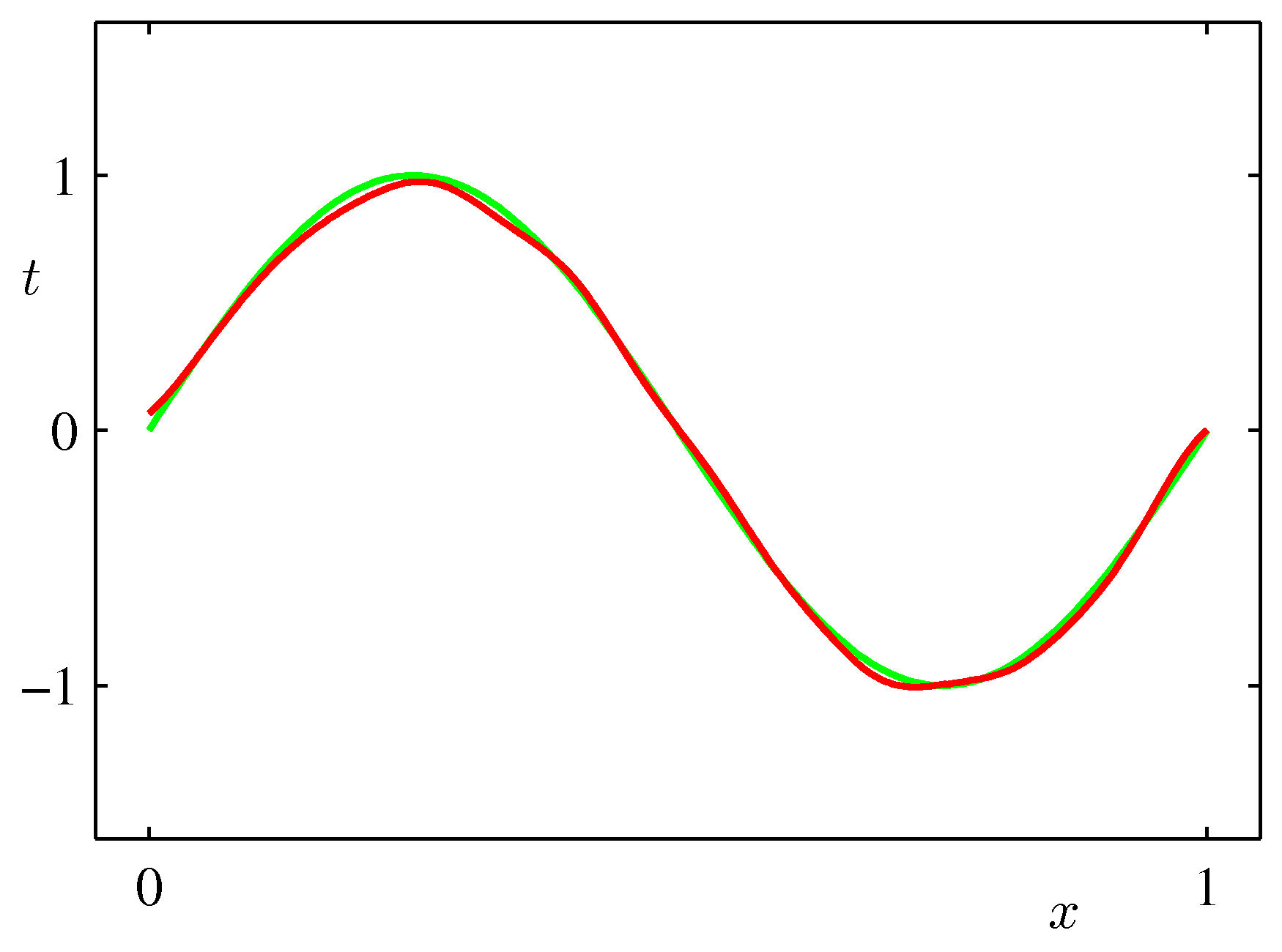
위의 그림은 바이어스와 분산 사이의 trade-off 관계를 잘 나타태는 그림이다.
- 하나의 샘플은 25개의 데이터로 구성된다. (일정 위치로부터 샘플 데이터를 추출하였다.)
- 이러한 샘플 집합은 총 $ L=100 $ 개로 구성된다. 각각의 학습 결과는 왼쪽 그림의 붉은 색 선이 된다.
- 오른쪽 그림의 붉은 색 그래프는 왼쪽 샘플 집합 결과의 평균 값이다.
- 오른쪽 그림의 녹색 선은 우리가 예측해야 할 $ \sin2\pi $ 곡선이다.
- $ \lambda $ 값을 변화시켜 가면서 결과를 확인하였다.
$ \ln\lambda $ 값이 큰 경우 높은 바이어스와 낮은 분산 값을 가진다.
- 따라서 각각의 샘플 집합들 사이의 분산도가 작은 것을 알 수 있다.
- 대신 실제 예측할 수 있는 값의 범위가 제한적이어서 최종 결과가 잘못 도출될 수도 있다.
- 샘플 수를 충분히 확보하지 못하는 경우에는 가급적 이러한 안정된 모델을 선호하기도 한다.
$ \ln\lambda $ 값이 작은 경우에는 낮은 바이어스와 높은 분산 값을 가진다.
- 따라서 최종 결과로 사용된 예측 값(평균값)은 실제 결과와 매우 유사한 것을 확인할 수 있다.
- 하지만 개별 샘플 집합의 결과를 보면 분산도가 매우 큰 것을 알 수 있다.
- 따라서 샘플 수가 충분하지 못한 경우 실제 결과와 매우 큰 편차를 보이는 잘못된 결과를 얻을 수 있다.
- 샘플 수가 충분하기만 하다면 이런 방식이 좋다.

위와 같은 bias-variance 의 trade-off 관계를 다음과 같은 식으로도 확인할 수 있다.

$\bar{y}(x) = \frac{1}{L}\sum_{l=1}^{L}y^{(l)}(x) \qquad{(3.45)}$

squared-bias 와 variance 에 대한 합은 다음과 같이 주어진다.

$(bias)^2 = \frac{1}{N}\sum_{n=1}^{N}\{\bar{y}(x_n)-h(x_n)\}^2 \qquad{(3.46)}$ $variance = \frac{1}{N}\sum_{n=1}^{N}\frac{1}{L}\sum_{l=1}^{L}\{y^{(l)}(x_n)-\bar{y}(x_n)\}^2 \qquad{(3.47)}$

이 식을 도식화한 결과를 보도록 하자.

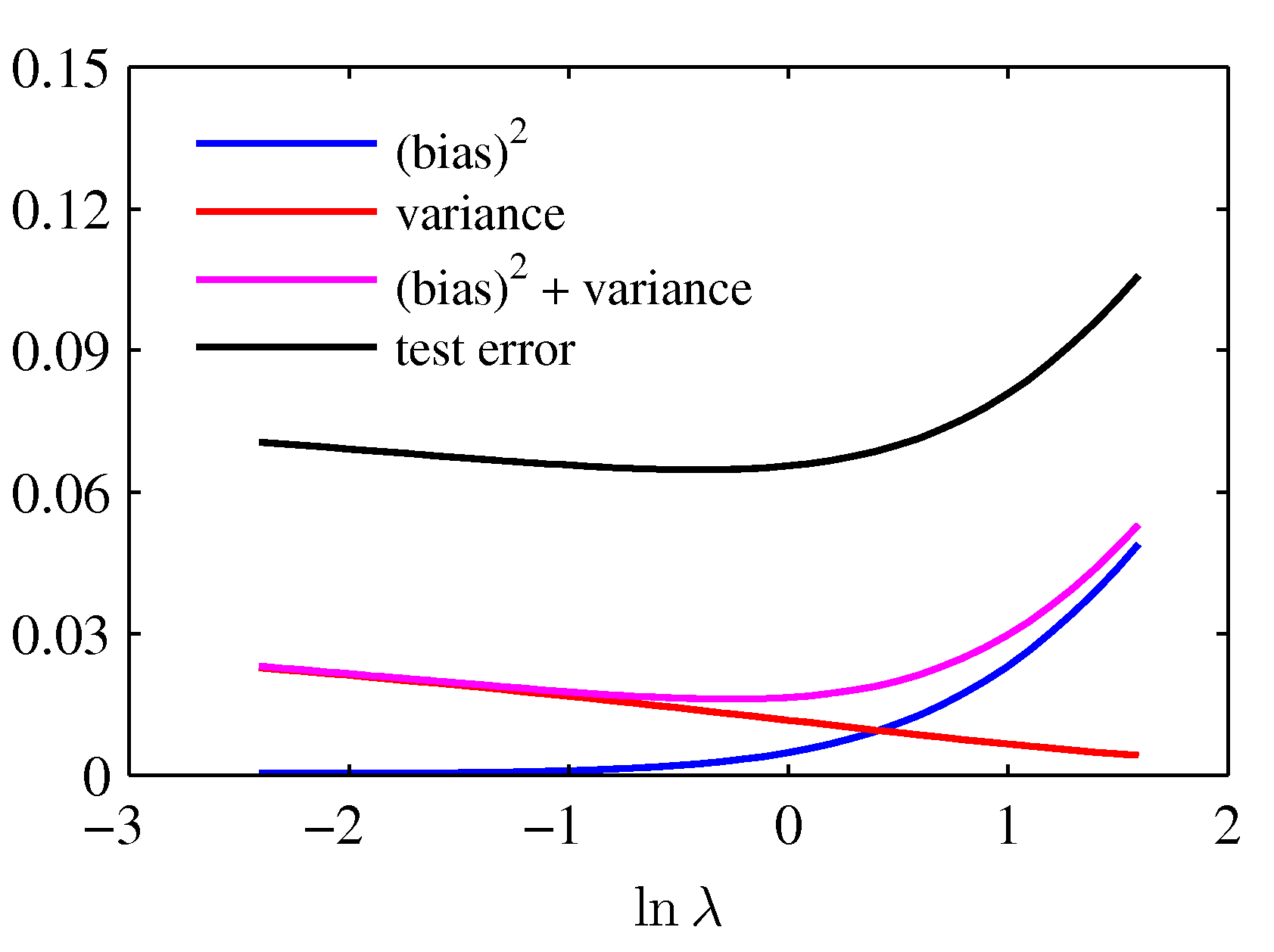
figure3.6

결국 분홍색 선이 가장 최소가 되는 지점의 $ \lambda $ 를 고르는 문제가 된다.
이 위치에서 테스트 에러도 최소가 되는 것을 확인할 수 있다.
이러한 관점은 빈도론자가 모델을 어떻게 바라보고 있는지에 대한 좋은 해석점이 된다.
- 다만 위의 수식에서는 여러 데이터 집합에 대한 앙상블 형태로 식이 전개되기 때문에 충분한 데이터가 확보되어야 한다.
- 결국 데이터 자체가 모델의 중요한 요소가 된다.

Chapter. 3