- 확률 모델을 계산하는데 있어 현실적으로는 정확한 값을 추론할 수 없는 경우가 대다수이다.
- 따라서 정확한 값을 추출하기 보단 근사적인(approximation) 방식이 더 선호된다.
- 우리는 앞 장에서 결정론적인 근사 방식인 변분 베이즈(VB)와 기대값 전파(EP) 기법을 살펴보았다.
- 이번 장에서는 수치적인 샘플링 기법을 통한 모델의 근사 방식을 다룰 것이다. 이를 Monte Carlo 방식이라고 한다.
- 우리는 지금까지 알려지지 않은 랜덤 변수에 대한 사후 분포를 구하는 문제에 매달렸었다.
- 하지만 실제 많은 경우에는 랜덤 변수의 사후 분포가 필요한 문제가 아니라 이에 대한 기대값을 요구하는 경우가 많았다.
- 예를 들어 예측 분포의 경우 모든 잠재변수들의 가능한 확률값의 주변 확률 분포의 형태로 계산되게 된다.
- 이 값을 계산하기 위해 사후 분포가 필요했던 것이다.
- 본격적으로 들어가기에 앞서, 여기서는 특정한 예를 이용해서 우리가 접근하고자 하는 방식이 무엇인지 간단하게 살펴보고 시작할 것이다.
- 현재 우리의 목표는 함수 \(f(z)\) 에 대한 기대값을 구하는 것이다.
- 하지만 단순하게 함수 \(f(z)\) 에 대해 \(z\) 가 발현될 확률이 모두 동일한 것이 아니라 특정한 분포의 형태를 취하고 있다.
- 따라서 이를 고려한 기대값을 구해야 한다.
- 함수에 대한 기대값을 구하는 식은 이미 예전에 다루었었다.
- 현재 우리의 목표는 함수 \(f(z)\) 에 대한 기대값을 구하는 것이다.
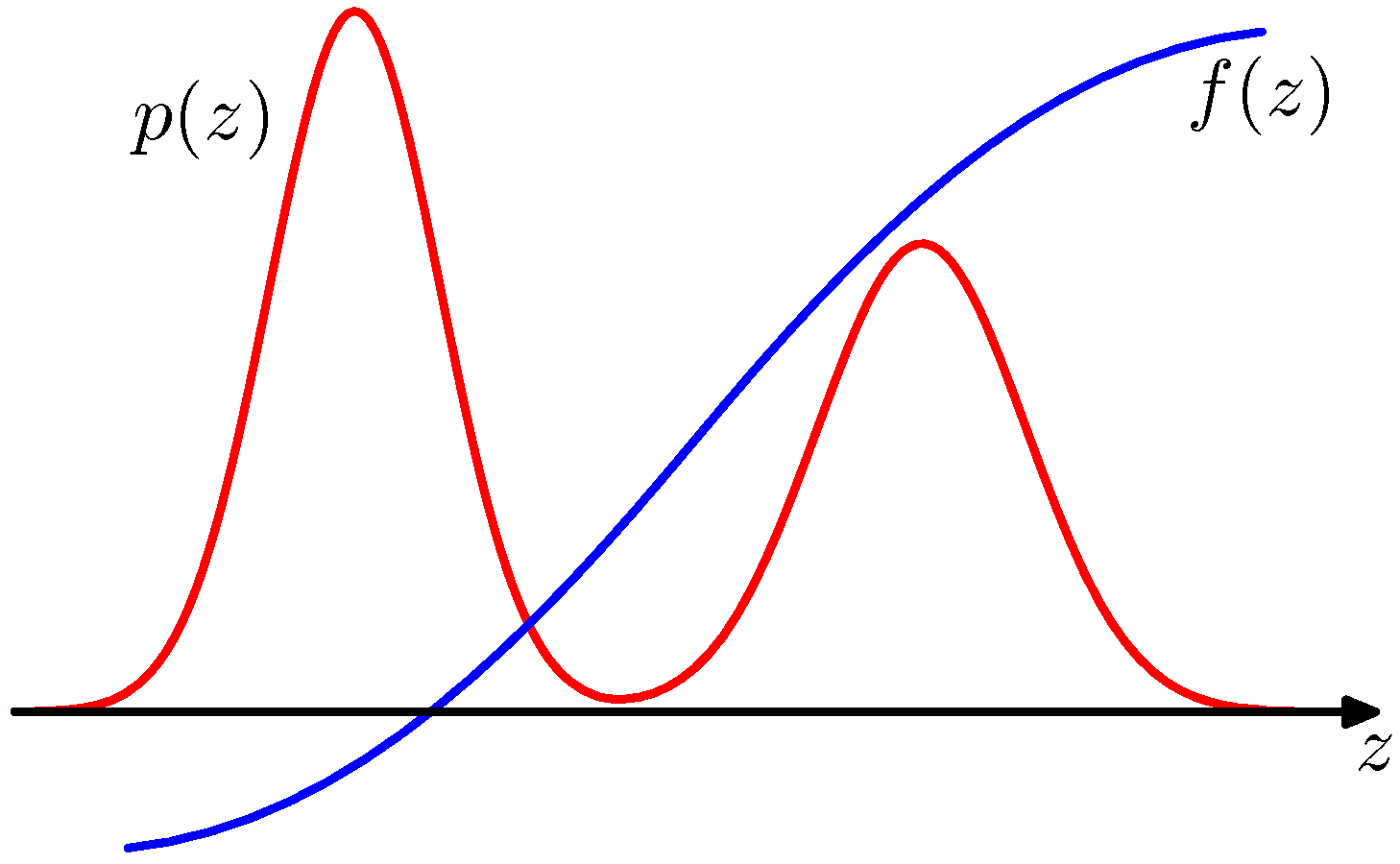
- 아래 그림을 보자.
- 만약 변수 \(z\) 가 이산 확률 변수였다면, 이 식은 적분 식이 아니라 합(sum)의 공식으로 표현되었을 것이다.
- 위와 같은 적분식이 그동안 참 많이도 등장했었는데 실제로는 다루기가 어려운 식이다.
- 베이지안 회귀 문제를 보면
- \(p(t|\mathbf{z}) = \int p(t|\mathbf{x, w})p(\mathbf{w}) d{\mathbf{w}}\) 를 구할 때에 첫번째 텀에 \(N(y(\mathbf{x,w}), \beta^{-1})\) 를 사용했었다.
- 하지만 실제 전개를 해보면 식이 그리 만만하지 않게 전개되었다.
-
당장 그림에서 주어진 \(p(z)\) 조차 그리 쉬운 형태가 아니어서 기대값을 구하기 쉽지 않다.
- 이제 샘플링을 통한 기대값 근사를 다루어보자.
- 일단 샘플을 정의한다.
- \(\mathbf{z}^{l}\) 로 정의한다. ( \(l = 1,…,L\) )
- 샘플은 서로 독립적이다. 따라서 분포 \(p(z)\) 로부터 독립적으로 발생된다.
- 기대값 근사식은 다음과 같다.
- 샘플을 확률 분포를 이용하여 생성하였기 때문에 다음이 성립한다.
- 이를 이용하면 분산도 정의할 수 있다.
- 위에서 제시한 샘플링 방식에 대해 살펴보자.
- 장점
- 식을 보면 \(z\) 의 차원에 무관하다. 따라서 이상적으로는 아주 적은 샘플을 이용해서도 정확한 추정이 가능하다.
- 실제 경험에 따르면 겨우 10~20 개의 샘플을 이용해서 좋은 결과를 얻는다.
- 단점
- 얻어지는 샘플들이 사실은 서로 독립적이 아니다.
- 이게 무슨 말인고 하니 위의 그림을 보면 \(p(z)\) 가 높은 경우에는 \(f(z)\) 가 작고
- 반대로 \(f(z)\) 가 클 때에는 \(p(z)\) 가 작다.
- 작은 확률값을 가지는 위치에서 샘플이 발현되는 경우, \(f(z)\) 값은 매우 크므로 기대값에 미치는 영향이 커질 수 있다.
- 따라서 좋은 정확도를 얻기 위해서는 적어도 많은 샘플이 요구되는 경우가 있을 수 있음
- 장점
- DAG 에서의 샘플링
- 뜬금없이 이게 여기서 왜 등장하는지 모르겠다.
- 예전에 잠깐 살펴보았던 ancestral sampling 방식에 대한 설명이다.
- 결합 확률 \(p(z)\) 가 방향성 그래프라고 생각해보자.
- 그러면 Markov식에 의해 다음과 같이 기술된다.
- 여기서 \(z_i\) 는 i 번째 노드와 관련있는 모든 변수의 집합이다.
- 여기서 \(pa_i\) 는 부모 노드와 관련있는 모든 변수의 집합이다.
- 이로부터 샘플을 어떻게 생성할까?
- 8장에서 배운 그대로 각 \(z\) 에 번호를 붙여 부모 노드로부터 각 분포로부터 샘플을 하나씩 생성하면 된다.
- 다시 설명할 필요가 없을 듯.
- 그런데 만약 그래프 노드 중 일부 노드가 관찰(observed)된 경우에는 어떻게 할까?
- 기억나실지 모르겠지만 중간 노드가 관찰되면 ancestral sampling 을 사용할 수 없다.
- 방법은 생각보다 아주 단순하다.
- 똑같이 ancestral sampling 을 이용하여 샘플을 생성해간다.
- 중간에 이미 관찰된 노드를 만나는 경우 이 때의 관찰값이 앞서 샘플링되었던 결과와 잘 부합되면 통과, 도저히 나올 수 없는 결과가 도출되었다고 판단되면 보류하고 중간까지 생성된 샘플을 모두 버린다.
- 처음부터 다시 시작
- 이러한 방식은 importance sampling 방식의 특별한 예라 하겠다.
- 하지만 실제로 위와 같은 방식은 사용 안함. (근데 왜 이렇게 길게 설명을…)
- 비방향성 그래프도 가능하지만, 보통 Gibbs 샘플링이 사용되므로 이후에 보자.