- 1장에서 오버-피팅(over-fitting)을 막을 수 있는 방안으로 Cross-Validation 기법이나 정칙화 파라미터를 사용하는 방법들을 설명했다.
- 이번 절에서는 베이지안 관점에서의 모델 선택 문제를 다루어보고자 한다.
- 뜬금없이 왜 모델 선택 문제인가?
- 1장에서 모델을 \( M \) 파라미터로 구별했고 \( M \) 값이 증가할수록 오버피팅 현상이 발생하는 것을 확인했다.
- 이를 막기 위한 방법으로 \( M \) 값을 조절하는 방법이 아닌 Cross-Validation이나 정칙화를 다루었다.
- 물론 모델을 변경하면 오버 피팅이 줄어든다는 것도 잠깐 보긴 봤다.
- 이번 절에서는 모델 자체를 변경하는 것을 다루게 될 것이다.
- 하지만 좀 더 구체적인 내용은 다음 절에서 다루도록 하고 여기서는 우선 일반적인 내용만 다루도록 한다.
- 베이지안 관점에서는 모델 선택의 문제 또한 확률적인 문제로 다루게 된다.
- 선택 가능한 모델의 수를 \( L \) 이라고 정의하면 모델 \( {M_i} \) 는 \( i=1,…,L \) 이 된다.
- 즉, 이를 랜덤 변수로 놓는다.
- 다항 커브 피팅 문제에서는 타겟 \( t \) 를 랜덤 변수로 놓고 입력 데이터 \( {\bf X} \) 을 주어진 (알려진) 데이터라고 가정했다.
- 이와는 조금 다른 모델로 입력 데이터도 하나의 랜덤 변수로 놓고 두 변수 \( {\bf X} \) 와 \( {\bf t} \) 에 대한 결합 분포를 구하는 모델도 있다.
- 이제 데이터 \( D \) 가 주어졌을 때 사용할 하나의 모델을 표현해보자.
- 이 모델이 나올수 있는 확률을 확률 함수로 표현 가능하다. 즉, \( p(M_i) \)
- 자, 이제 데이터 집합 \( D \) 가 주어졌을 때 사후 확률을 다음과 같이 정의 가능하다.
- 여기서 사전( prior ) 분포는 특정 모델의 초기 선호도가 된다.
- 물론 이 값이 모두 같다고 가정해도 크게 문제가 될게 없다.
- 따라서 우리가 집중해서 볼 요소는 \( p(D|M_i) \) 이다.
- 이 영역을 model evidence 라고 한다.
- model evidence 를 주변 가능도 ( marginal likelihood ) 함수라고도 부른다.
- 왜냐하면 주어진 모델 공간에서의 가능도 함수를 의미하기 때문
- Bayes Factor
- 한 모델의 model evidence 에 대한 다른 모델의 model evidence 비율을 Bayes Factor 라고 한다.
- \( p(D|M_i) / p(D|M_j) \) 로 정의된다.
- 이는 모델 \( M_i \) 가 모델 \( M_j \) 보다 선호될 비율이라고 생각하면 된다.
- 모델을 통해 사후 분포를 알아내기만 하면 예측 분포를 만들어 낼 수도 있다.
- 사실 위와 같은 방식은 여러 모델을 이용하여 Mixture 분포를 만들어내는 형태라고 생각할 수 있다.
- 각각의 모델의 확률 \( p(t|{\bf x}, M_i, D) \) 의 평균 확률이 된다.
- 즉 위의 식은 mixture 모델을 일반화한 식이라고 생각하면 된다.
- 만약 사후 확률 값이 동일한 2개의 모델이 주어졌다고 하자.
- 자신들의 파라미터의 예측값을 각각 \( \alpha \) 와 \( \beta \) 라 예측했다면,
- 위의 결과에서는 \( t=(\alpha+\beta)/2 \) 와 같은 형태로 모수의 값이 얻어지는 것이 아니라,
- 두 개의 봉우리가 생기는 형태(다봉)의 확률 분포를 얻게 될 것이다. (mixture model)
- 평균적인 모델을 사용하는 가장 손 쉬운 방법은 가장 적합한 모델 하나만을 선택하여 사용하는 것이다.
- 그리고 이렇게 여러 모델 중 하나의 모델을 선택하는 작업을 model selection 이라고 한다.
- 어떤 모델이 더 좋은지는 주어진 데이터가 발현된 확률이 더 큰 모델이 무엇인지 확인하여 이를 선택하면 된다.
- 어떤 모델의 파라미터 집합 \( {\bf w} \) 가 주어졌을 때, model evidence 를 살펴보자.
- 이를 합의 법칙과 곱의 법칙을 이용하여 표현 가능하다.
- 샘플링의 관점에서 본다면 사전 분포로 랜덤하게 샘플링된 파라미터를 가지는 모델로부터 데이터가 생성되었다고 생각할 수 있다.
- 게다가 이 수식을 분모로 하는 (즉, 정규화 요소로 사용하는) 파라미터의 사후 확률을 기술할 수 있다.
- 위에서 사용한 model evidence 의 적분 식을 이용하여 우리는 파라미터와 관련한 통찰을 얻을 수 있다.
- 논의를 쉽게 하기 위해 일단은 1차원의 파라미터 \( w \) 만을 고려하도록 하자.
- 그리고 특정 모델을 가정하고 나서 이를 잠시 수식에서 생략해보자. ( \( M_i \) 를 생략 )
- 그러면 우리가 구해야 할 사후 확률 값은 \( p(D|w)p(w) \) 로 생각하면 된다.
- 이 식은 모수 \( w \) 가 하나의 값으로 거의 수렴해서 높은 피크를 이루는 경우를 가정한 것이다.
- 또한 \( w \) 의 사전 분포는 모두 동일하다고 가정하여 \( p(w) = \frac{1}{\Delta w_{prior}} \) 로 놓았다.
- 이 식에 \( \ln \) 함수를 취한다. 식은 다음과 같이 전개된다.
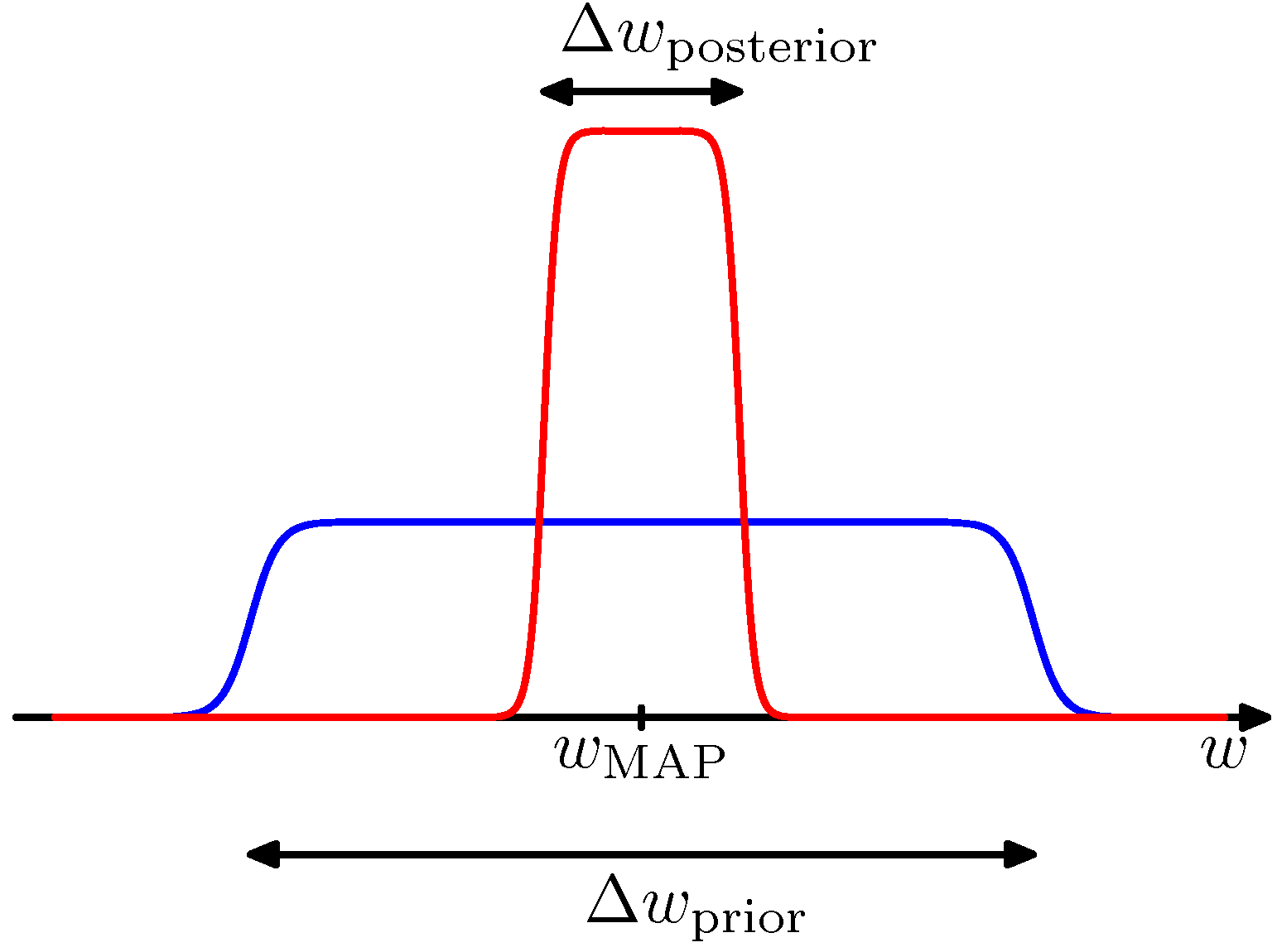
- 위 그림은 \( w \) 의 사후 분포가 한 점에서 높은 피크를 그릴 때의 모습을 대략적으로 나타낸 것이다.
- 이제 이 식을 분석해보도록 하자.
- 첫번째 텀(term)은 이 데이터를 가장 잘 표현하는 파라미터에 대한 확률값으로 결국 로그 가능도 함수가 된다.
- 두번째 텀(term)은 모델의 복잡성에서 기인하는 페널티 텀(penalty term)이 된다.
- 이 텀은 음수인데 사후 확률이 피크를 이루기 때문에 결국 로그로 들어가는 값이 1보다 작기 때문이다.
- 이런 이유로 사후 확률이 고정된 특정 값으로 점점 수렴해 갈수록 두번째 텀은 값의 비율이 더 커지게 된다.
- 이제 사용되는 파라미터의 개수가 \( M \) 개라고 생각해보자.
- 그리고 비슷한 방식으로 식을 전개하면 쉽게 다음의 식을 얻을 수 있다.
- 이 식은 \( p(D) \) 를 추정하기 위한 가장 손쉬운 방식의 전개이다.
- 식의 복잡도가 모델 파라미터 수 \( M \) 에 대해 선형으로 증가한다.
- 이제 \( M \) 의 수가 변함에 따라 어떻게 식이 달라질지 생각해보자.
- 보통 복잡한 모델을 사용하는 경우 파라미터의 수가 증가하게 된다.
- 하지만 이 경우 가능도 함수의 확률 값이 증가하게 된다. (모델 피팅이 대개 더 잘되므로)
- 하지만 위의 식에 의해 패널티 텀도 \( M \) 에 의해 증가하게 되므로 \( p(D) \) 값을 감소시키는 요인으로 작용된다.
- 따라서 \( M \) 값을 통해 모델 파라미터의 수를 결정하는게 문제의 핵심이 된다.
- 결국 모델의 선택은 maximum evidence 와 관련이 있다.
- 모델에 의해 파라미터의 복잡도가 결정되기 때문.
- 참고로 실제 이 식은 다음과 같이 기술하는 경우가 많다.
- 실제로는 변형 식이 꽤나 많은데, 이미 1장에서 AIC 를 살펴보았다. ( \( \ln p(D|w_{MAP})-M \) )
-
이제 베이지언 모델에서 모델 비교를 통해 가능도 함수의 주변 확률이 어떻게 선호되는 모델을 찾을 수 있는 것인지를 이해하도록 해보자.
-
우선 3개의 모델이 주어졌다고 가정해보자. ( \( M_1, M_2, M_3 \) )
- 가로 축은 가능한 데이터 집합 공간을 하나의 1차원으로 표현한 정보이다.
- 모든 샘플 데이터 공간을 하나의 차원 값으로 매핑한 것이다.
- 따라서 가로 축의 한 점은 얻을 수 있는 하나의 데이터 집합을 의미하게 된다.
- 이 모델들로부터 샘플을 얻을 수 있는 확률을 한 번 상상해 보자.
- 가로 축은 가능한 데이터 집합 공간을 하나의 1차원으로 표현한 정보이다.
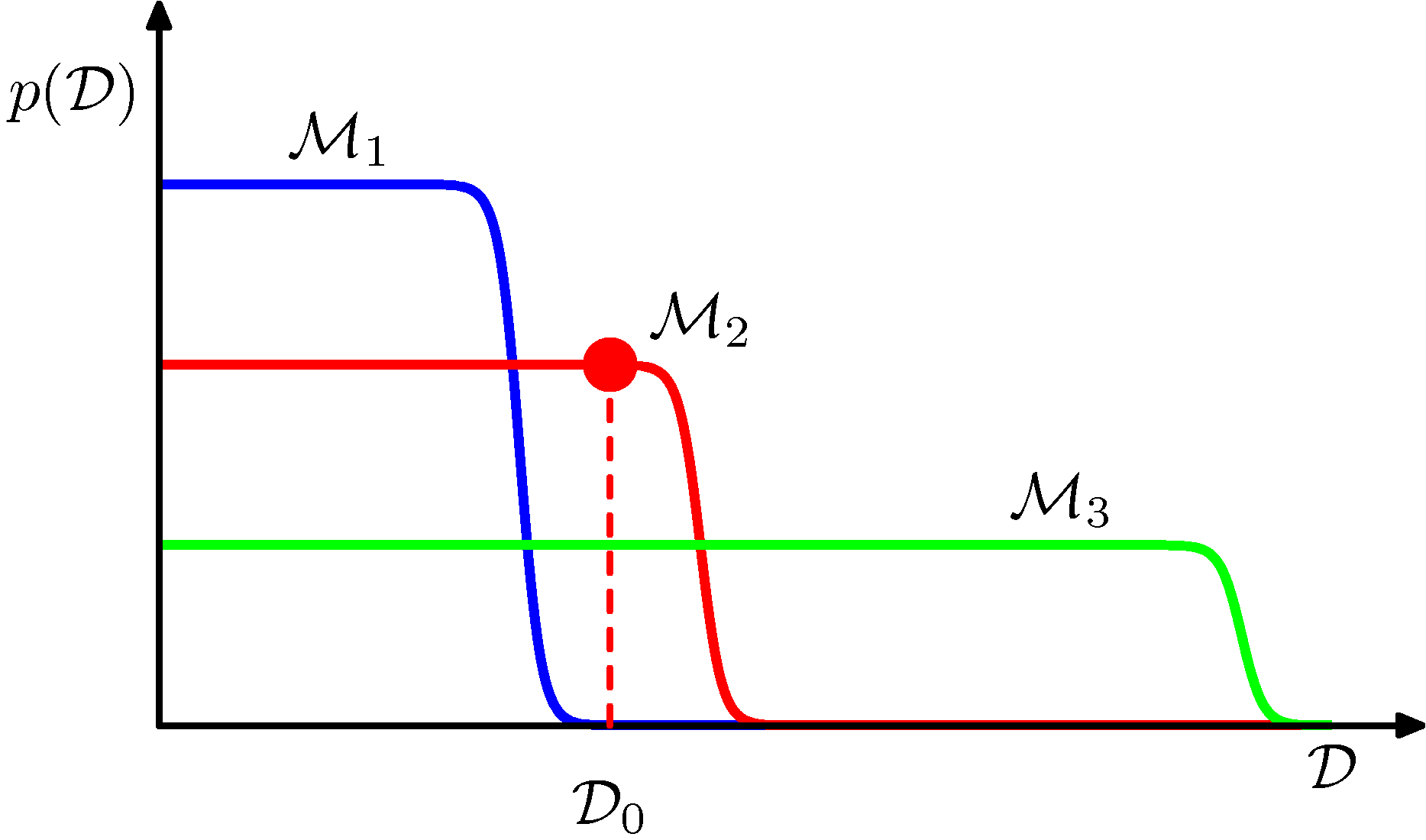
- 그림을 보면 \( M_1 \) 이 가장 단순한 모델이고, \( M_3 \) 가 가장 복합한 모델임을 알 수 있다.
- 모든 확률은 정규화되어 있으며 특정한 샘플 집합 \( D_0 \) 는 그림에서 보듯 모델 \( M_2 \) 에서 발현된 확률이 가장 크다.
- 위와 같이 주어진 모델에서 샘플을 생성하는 방법은 간단하다.
- 우선 먼저 모델별로 주어진 \( p(w) \) 로부터 임의의 \( w \) 값을 하나 구하고 \( p(D|w) \) 로부터 샘플을 얻어낸다.
- 단순한 모델(예를 들어 1차원 다항식 모델)에서는 대부분 비슷한 값을 가지는 데이터만을 얻을 수 있다.
- 따라서 이 경우는 위의 그림에서 가로 축의 일부 지역만을 포함하는 확률 분포를 얻게 될 것이다.
- 반면 복잡한 모델(예를 들어 9차수의 다항식 모델)에서는 \( p(w) \) 로부터 생성된는 \( w \) 가 다양하기 때문에 \( p(D|w) \) 로부터 얻어지는 샘플의 범위도 훨씬 다양하게 된다.
- 결국 \( p(D|M_i) \) 는 확률 함수이고 이로인해 정규화되어야 하므로 데이터 공간에 대한 확률 분포를 얻을 수 있다.
- 그림 3.13 에서 데이터 \( D_0 \) 의 경우 따라서 가장 가능성이 높은 모델은 \( M_2 \) 가 됨을 알 수 있다.
- evidence 의 확률 값이 가장 높기 때문이다.
- 본질적으로는,
- 간단한 모델의 경우 임의로 주어진 데이터에 적합하게 될 확률이 매우 작고,
- 복잡한 모델의 경우 임의의 데이터에 대해 일정 부분 대응할 수 있으나 실제 모델일 가능성은 매우 낮아진다.
- 베이지언 모델 비교 프레임워크에서는,
- 암묵적으로 고려되는 모델 중에 진짜 모델 분포가 존재하고 여기로부터 데이터가 생성되었다고 가정한다.
- 이 가정이 맞다면 베이지먼 모델 비교 프레임워크는 항상 가장 올바른 모델을 선호하게 된다.
- 이걸 확인하기 위해서 두 개의 모델 \( M_1 \) 과 \( M_2 \) 를 고려하되 실제 진짜 모델은 \( M_1 \) 이라고 가정해보자.
- 이 때의 베이즈 팩터의 평균 값은 다음과 같은 형태를 취하게 된다.
- 이 식은 \( KL\;divergence \) 만족하므로 항상 양수이다.
- 물론 두 모델이 같은 경우 0이지만 여기서는 모델이 다르다는 가정이다.
- 따라서 베이즈 펙터는 항상 올바른 모델을 선호하게 된다.
- 지금까지 우리는 베이지언 방식이 오버피팅을 피하고 모델간 비교를 하는 과정을 살펴보았다.
- 하지만 베이지언 방식을 포함해 모든 패턴 인식 접근에 있어 모델의 형태를 가정하고 시작한다.
- 결국 잘못된 모델의 선택은 잘못된 결과를 얻게 된다.
- 게다가 그림 3.12에서 보았듯이 모델 evidence 영역은 사전 분포의 영향을 많이 받는다.
- 게다가 부적절한 사전 분포(improper prior)를 선택하는 경우 어떻게 될지 알 수가 없다.
- 여기서 부적절한 사전 분포는 사용자가 선택한 분포 중 확률 조건을 만족하지 못하는 분포를 의미한다.
- 베이지언 관련 자료를 찾아보면 나온다.
- 게다가 부적절한 사전 분포(improper prior)를 선택하는 경우 어떻게 될지 알 수가 없다.
- 현실적으로는 학습데이터와는 독립적인 테스트 데이터 집합을 이용하여 모델의 성능을 평가하게 된다.