- 지금까지 MLE를 이용하여 선형 회귀 문제를 해결하는 방법을 살펴보았다.
- 또한 기저함수의 개수를 조절하여 가장 효율적인 모델 복잡도에 대해서도 살펴보았다.
- 또한 정칙화 요소의 의미와 정칙화 계수를 조절하여 모델의 복잡도를 조절하는 방법도 배웠다.
- 여기서는 베이지안 추론 기법을 이용하여 MLE에서 발생하던 오버 피팅의 문제를 해결하는 방법을 살펴볼 것이다.
- 이번 절에서도 마찬가지로 1차원 실수 값인 타겟 \( t \) 를 예측하는 문제를 다루어 볼 것이다.
3.3.1. 파라미터 분포 (Parameter distribution)
- 이제 베이지안 관점을 살펴보기 위해 모델의 파라미터에 대한 사전 분포(prior distribution)를 다룰 것이다.
- 여기서는 앞서 소개된 \( {\bf w} \) 파라미터에 대한 분포를 고려하게 된다.
- 물론 노이즈와 관련된 파라미터 \( \beta \) 는 앞서 사용했던 방식 그대로 사용하게 된다.
- 가능도 함수 또한 앞절에서 사용한 \( p({\bf t}|{\bf w}) \) 가 된다.
- 이는 \( {\bf w} \) 에 대한 이차 형식(quadratic)의 식이다.
- 이제 파라미터 \( {\bf w} \) 에 대한 공액 사전 분포(conjugate prior ditribution)로 가우시안 분포를 고려해 본다.
- 즉, \( {\bf w} \) 는 랜덤 변수로 고려된다.
-
여기서 사전 분포에 대한 평균은 \( {\bf m}_0 \) 이고 공분산은 \( S_0 \) 이다.
- 이제 사후(posterior) 분포에 대해 고려해보자. 이 분포는 가능도 함수와 사전 분포의 곱으로 표현된다.
- 공액 사전 분포를 가우시안 분포로 선택했기 때문에 사후 분포도 마찬가지로 가우시안 분포이다.
- 사전 분포에 공액 사전 분포를 사용하는 경우 사후 분포와 켤레 관계가 된다. (동일한 분포)
- 따라서 사후 분포를 다음과 같이 정의할 수 있다.
- 이 때 평균과 공분산은 다음과 같다.
- 교재에서는 이에 대한 수식 전개는 생략되어 있음
-
베이지안 추론과 관련된 다른 책자에서는 대부분 위와 관련된 식의 전개가 포함되어 있으니 참고바람
- 사후 분포 또한 가우시안 분포를 따르므로 이 값을 최대화하는 \( {\bf w} \) 를 구하는 것은 매우 쉽다. (편미분)
- 결국 \( {\bf w}_{MAP} = {\bf m}_N \) 을 얻을 수 있음.
- MAP은 사전 분포를 고려한 사후 분포의 최빈값(mode)으로 가우시안의 경우 평균값과 최빈값이 같다.
- 만약 사전 분포를 좀 더 간단한 형태로 놓는다면 사후 분포 또한 좀 더 간단한 형태의 식을 얻을 수 있다.
- 사전 분포를 평균이 0이고 공분산이 \( \alpha^{-1}{\bf I} \) 인 가우시안 분포로 고려해보자.
- 이 때의 사후 분포의 파라미터는 다음과 같이 된다.
- 이 때 로그 가능도 함수(log likelihood fucntion)은 다음과 같다.
- 사후 분포를 가장 크게 하는 값은 이전에 봤던 최소 제곱합(sum-of-squared) 에러 함수와 차이가 없다.
- 다만 \( \lambda \) 값을 \( \lambda=\alpha/\beta \) 로 처리하기만 하면 된다.
- 이제 실제 사후 분포를 이용하여 얻어지는 결과를 그림을 통해 살펴보도록 한다.
- 이 그림이 이번 절의 핵심 내용이다.
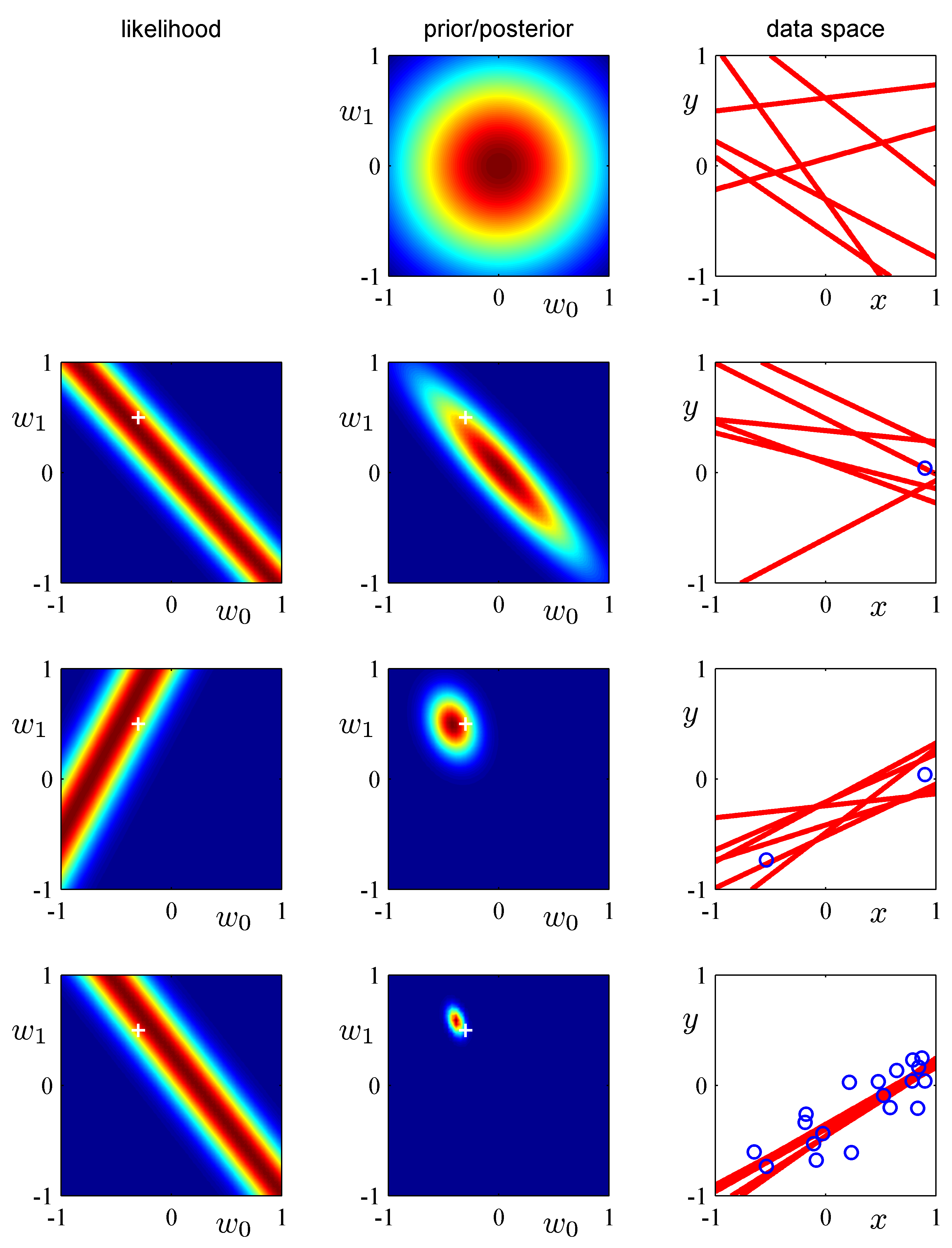
- 위의 그림은 순차적인 베이지안 사후 분포 적용을 그림으로 나타낸 것이다.
- 이 데이터는 1차원의 \( x \) 데이터에 대한 회귀 모델을 나타낸 것으로 사용되는 파라미터는 \( w_0 \) 와 \( w_1 \) 이 된다.
- 데이터가 순차적으로 발생하면서 사후 분포가 업데이트되는 모델을 나타내고 있다.
- 맨 왼쪽 그림은 가능도 함수를 \( {\bf w} \) 에 관해 표현한 그림이고, 가운데는 사전 및 사후 분포를 나타낸다.
- 사전 분포, 사후 분포 모두 가우시안 분포이다. (공액 사전 분포임)
- 오른쪽 그림은 데이터가 관찰된 후 예측된 파라미터 값을 이용하여 랜덤하게 5개의 모델을 만들어낸 것이다.
- 즉, 얻어진 사후분포로부터 가능한 파라미터를 랜덤하게 선정하여 붉은 색 선으로 그려놓았다.
- 직선이 되는 이유는 \( w_0 \) 와 \( w_1 \) 파라미터만 존재하기 때문이다.
- 가장 첫줄의 경우에는 사후분포가 주어지는 것이 아니므로 사전분포로부터 샘플을 랜덤 생성한 것이다.
- 맨 첫출부터 시작해서 하나의 샘플이 추가될 때마다 변화되는 양상을 순서대로 나타내고 있다.
- 가장 먼저 첫 줄 그림을 보면 가능도 함수는 존재하지 않고, 사전 분포만 주어진다.
- 이 때 사전 분포는 평균이 0이고 공분산이 1인 가우시안 분포가 된다.
- 그림을 보더라도 완전한 구의 형태로 그 중심은 평균 0인 값이 된다.
- 이 상태에서 임의의 모델을 선택하는 경우 \( {\bf w} \) 가 가우시안 분포에 의해 랜덤하게 생겨난다.
- 오른쪽 그림을 보면 알 수 있듯 무작위적으로 직선이 생겨난다.
- 물론 가우시안 분포를 따르고 있으므로 0 근처의 값이 랜덤하게 배정되는 가능성이 높을 것이라 예측할 수 있다.
- 이 때 사전 분포는 평균이 0이고 공분산이 1인 가우시안 분포가 된다.
- 그 다음 줄(2번째 줄)은 첫번 째 샘플이 발현된 후의 결과이다.
- 오른쪽 그림을 보면 샘플이 파란색 원으로 표기되고 있음을 알 수 있다.
- 이 경우 가능도 함수를 통해 \( {\bf w} \) 의 확률을 결정할 수 있다. (즉, 확률 분포의 모양이 만들어진다.)
- 이를 이용하여 사후 분포를 구한 것이 가운데 그림이다.
- 베이지안 추론이 가지는 특징 중 하나는 업데이트 모델이 가능하다는 것이다.
- 여기서는 업데이트 모델이 사용되고 있다.
- 사전 분포와 사후 분포가 같은 형태의 분포를 사용하기 때문에 관찰 데이터를 이용해 얻어진 사후 분포를,
- 다시 새로운 데이터가 입력될 때의 사전 분포로 활용할 수 있다.
- 따라서 여기서는 샘플 하나가 추가되어 얻어진 사후 분포를 다시 사전 분포로 이용하여 사용하게 된다.
- 샘플이 발현될수록 사후 분포는 특정 값으로 피크가 만들어진다.
- 물론 MLE 와 다르게 사전 분포가 계속 반영되는 형태를 취하게 된다.
- 마지막 줄을 보면 많은 샘플을 적용한 경우 거의 한 점에 수렴하는 것을 알 수 있다.
- 물론 데이터가 이상하게 일정한 패턴을 가지지 않는다면 특정 값에 수렴하는게 보장이 안될수도 있다.
- 여기서는 그냥 예제이므로 이해해주자.
- 그림에서 알 수 있듯 실제 값(하얀색 플러스 위치)과 예측 값(붉은 색 분포)이 매우 가까워지는 것을 알 수 있다.
- 다음과 같은 형태의 사전 분포를 고려해 볼 수도 있다.
- 이 때 \( q=2 \) 인 경우 가우시안 분포가 된다.
- 이는 이전에 봤던 정칙화(regularization) 과정과 동일한 형태이다.
- 정규화된 에러 함수를 최소화하는 \( {\bf w} \) 를 찾아 사후 분포를 최대화시킨다.
- 여기서는 \( q\neq2 \) 이더라도 최빈값(mode)이 평균(mean)이 됨을 알 수 있다.
3.3.2. 예측 분포 (Predictive distribution)
- 실제 사용에 있어서는 \( {\bf w} \) 값을 예측하는 작업보다 임의의 입력 값 \( {\bf x} \) 에 대한 예측값을 제공하는 작업이 더 빈번하게 발생한다.
- 베이지안 추론 방식에서는 이를 이해 예측 분포(predictive distribution)라는 편리한 기능을 제공한다.
- 여기서 \( {\bf t} \) 는 학습 데이터의 타겟값을 의미한다.
- 사실 앞서 다 언급한 내용이기는 하다.
- 이를 통해 얻어진 예측 분포 식은 다음과 같다.
- 이 때의 분산 값은 다음과 같이 주어진다.
- 분산 값에 대해 좀 살펴보도록 하자.
- 첫번째 항목은 정확도의 역수, 즉 원래의 노이즈의 분산 값을 의미하게 된다.
- 즉, 가우시안 분포 형태를 취하는 노이즈(noise)의 요소가 그대로 적용이 되어 있음을 알 수 있다.
- 두번째 항목이 문제인데, 여기서는 파라미터 \( {\bf w} \) 의 불확실성이 반영된 수식이라 할 수 있다.
- 식의 형태를 잘 보면 샘플 데이터가 추가될 수록 두번째 항목이 점점 좁아지는(narrower) 것을 알 수 있다.
- 즉, \( \sigma_{N+1}^2({\bf x}) \le \sigma_N^2({\bf x}) \) 를 만족하게 된다.
- 이 결과로, 만약 \( N\rightarrow\infty \) 이면 이 값은 0이 된다.
- 첫번째 항목은 정확도의 역수, 즉 원래의 노이즈의 분산 값을 의미하게 된다.
- 아래 그림은 예측 분포에서 얻어지는 분산값의 변화를 그림으로 나타낸 것이다.
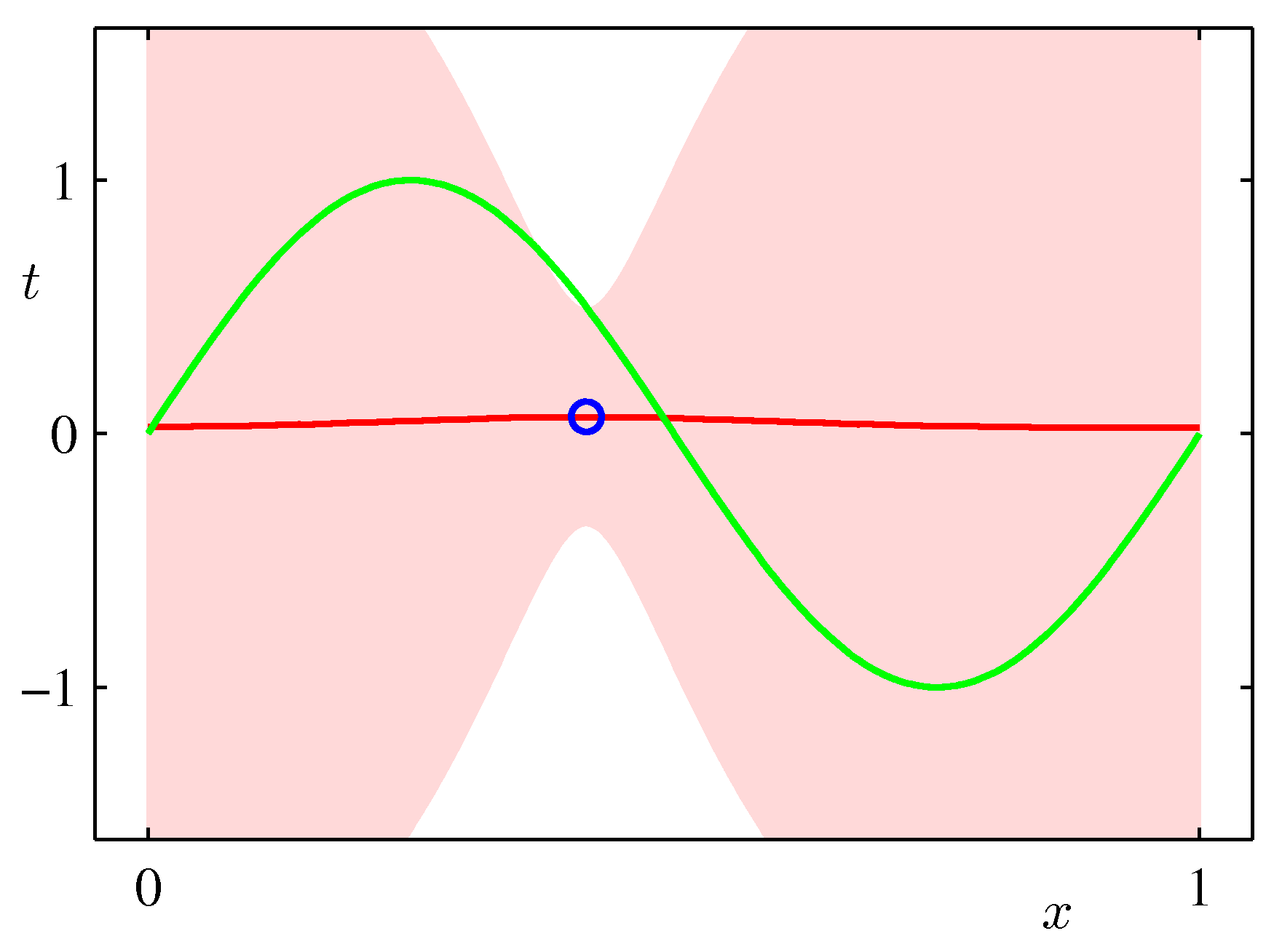
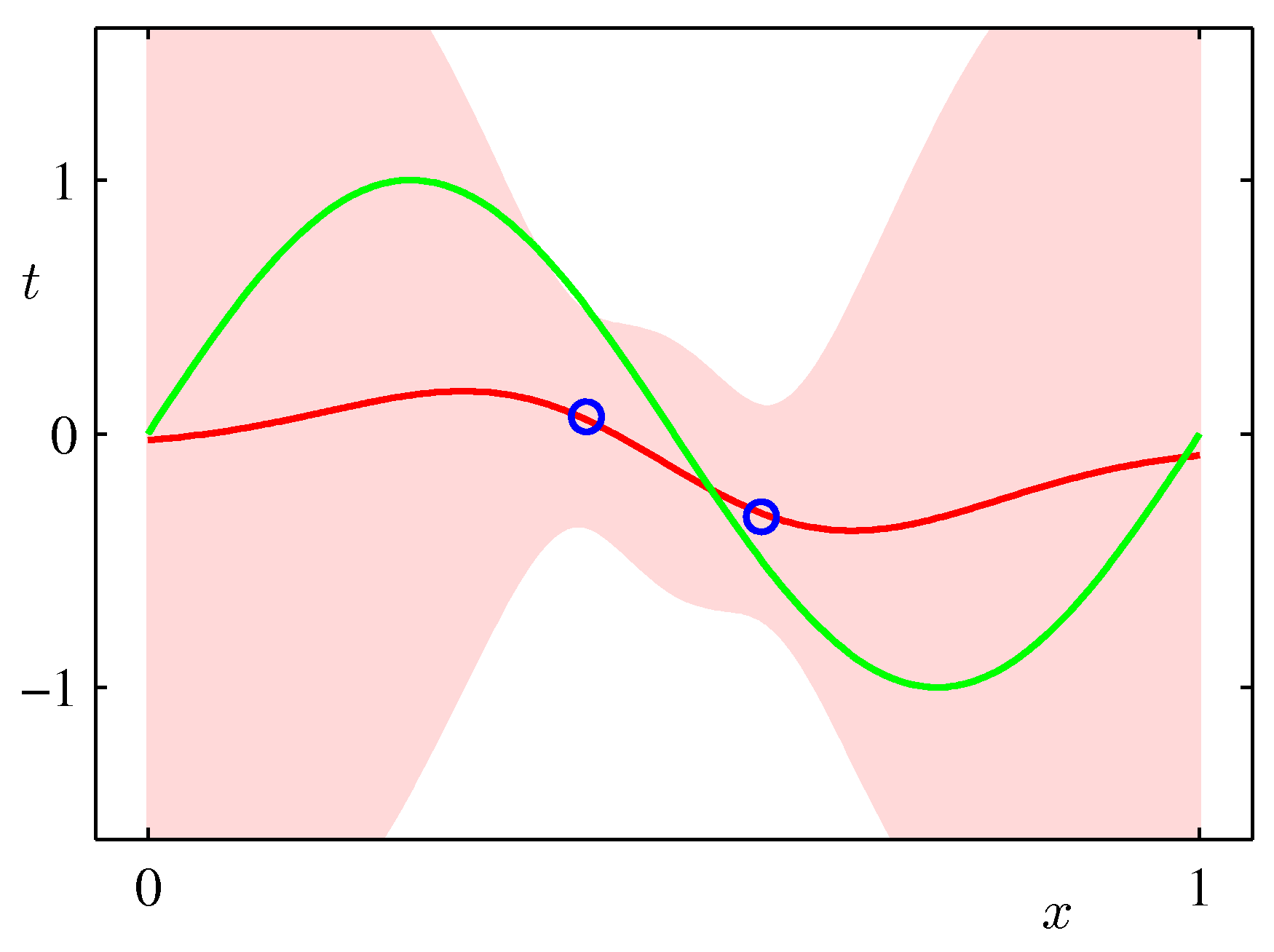
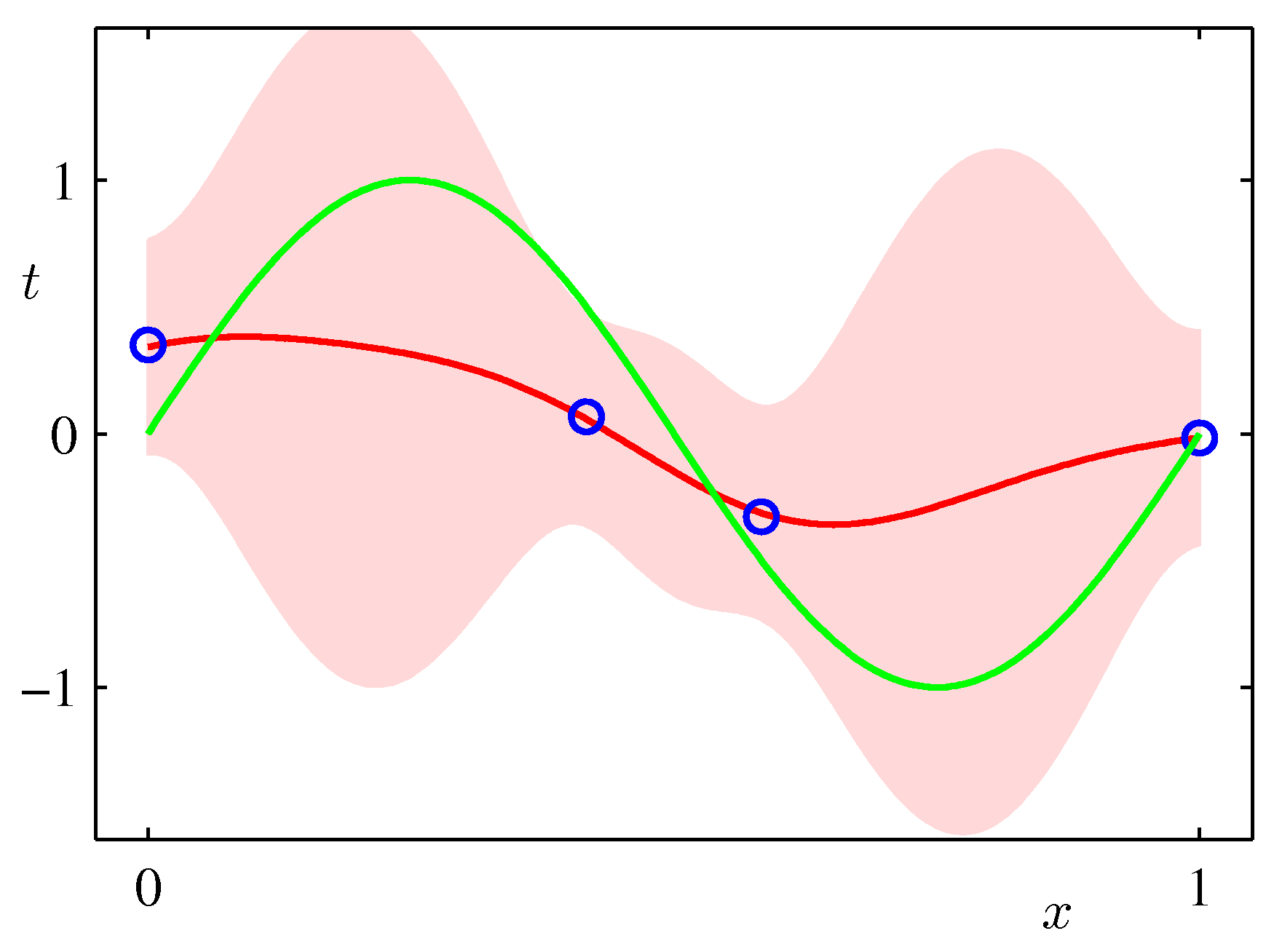
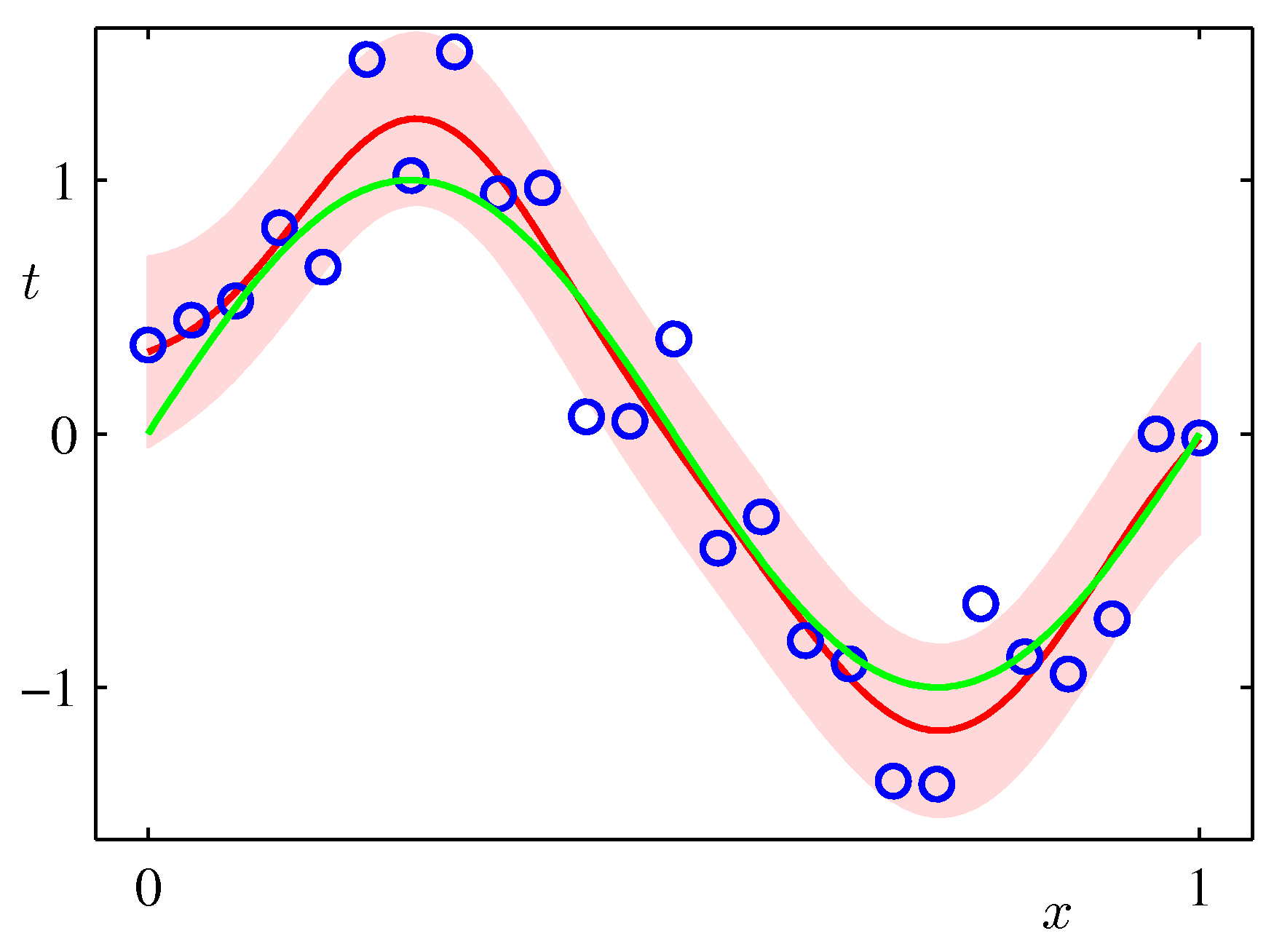
- 위의 그림은 9개의 가우시안 기저 함수를 선형 결합하여 만든 모델이다.
- 샘플을 순차적으로 생성하면서 그림을 표현하고 있다. 가장 처음 그림은 \( N=1 \) 이고 최대 \( N=25 \) 까지 샘플을 늘려가면서 실험한 결과이다.
- 붉은 색의 영역이 샘플수에 따른 분산 값의 범위값을 그림으로 나타낸 것이다.
- 샘플이 증가할수록 최초 정의한 노이즈(noise)의 분산 범위로 범위가 좁혀지는 것을 알 수 있다.
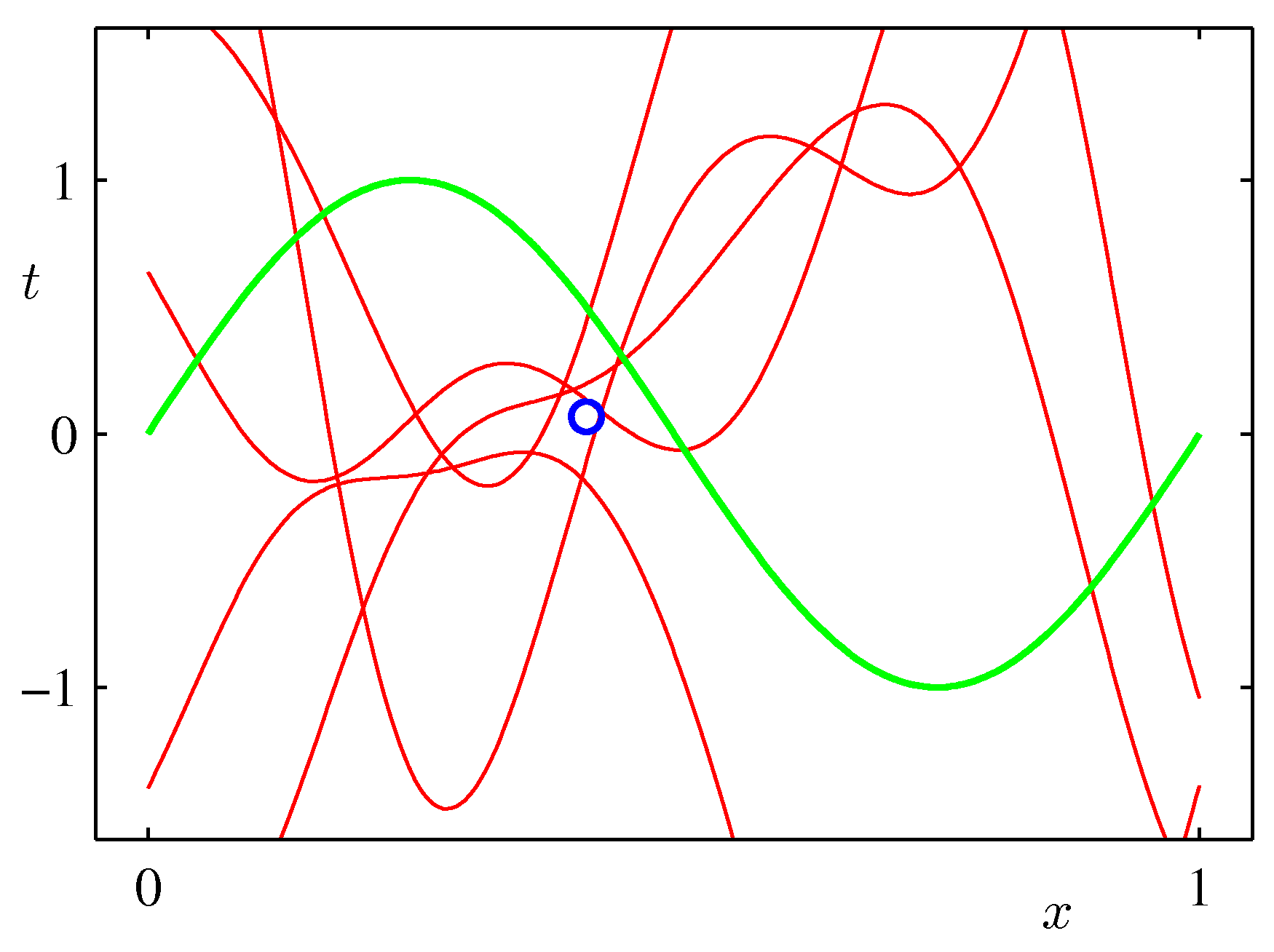
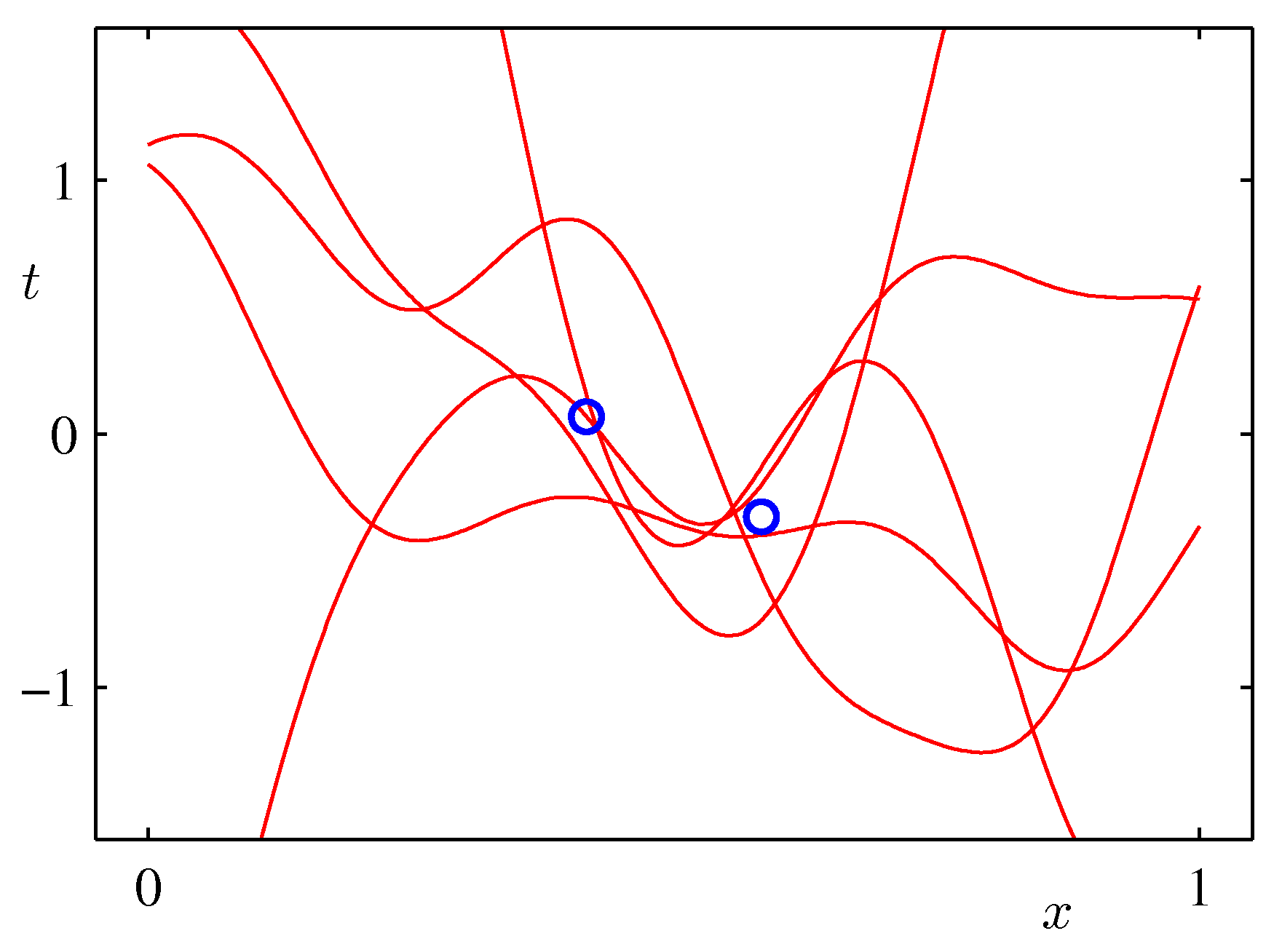
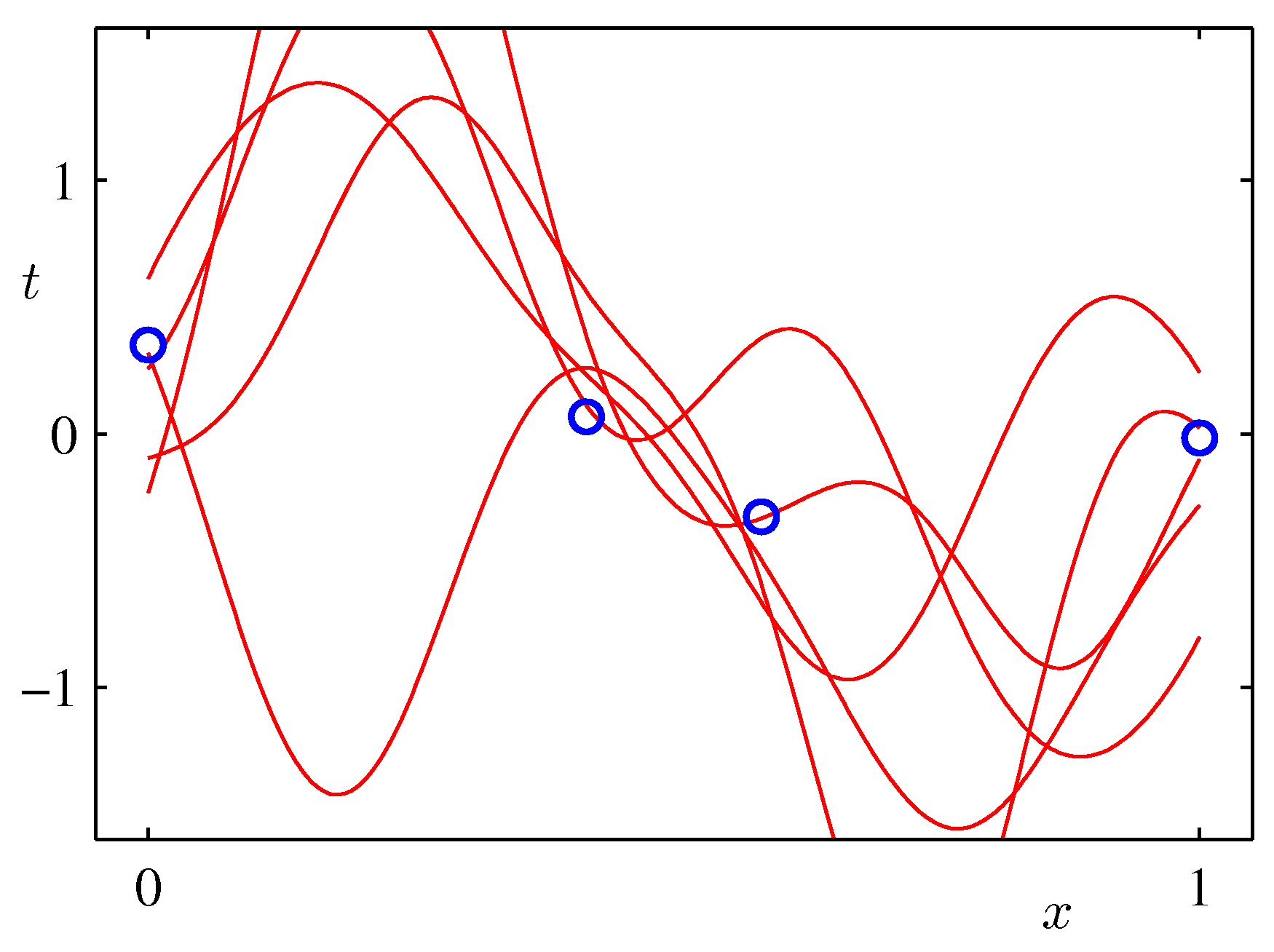
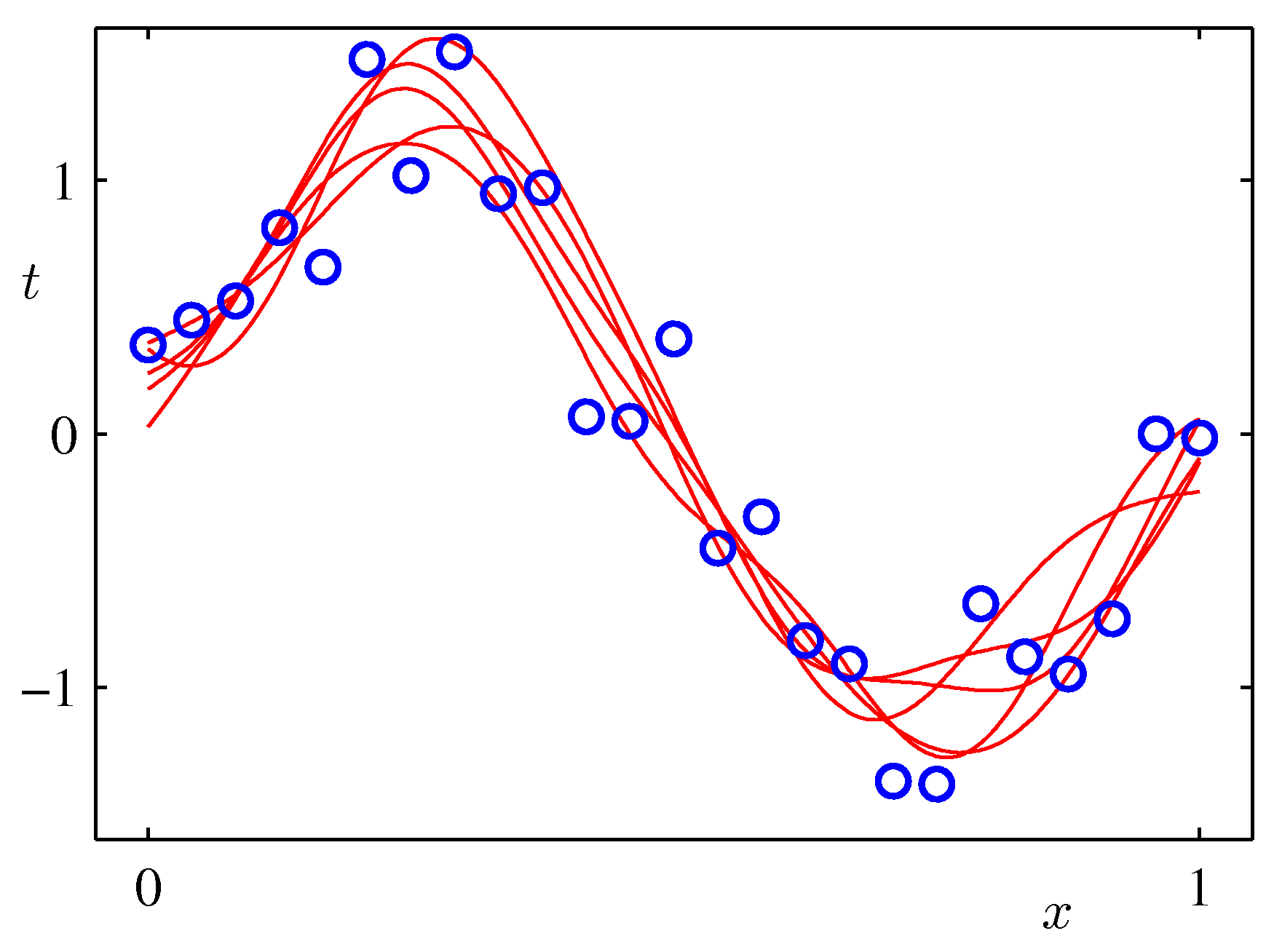
- 위의 그림은 실제 얻어진 결과를 이용하여 랜덤하게 파라미터를 추출하여 얻어진 결과를 나타내고 있다.
- 발현된 샘플이 적은 경우 가능한 분산 범위가 크기 때문에 variance 가 큰 결과를 얻게 된다.
- 샘플 수가 증가할 수록 안정된 범위의 모델을 얻게 된다.
3.3.3. 동등커널 (Equivalent Kernel)
- 선형 기저 함수 모델에서의 사후 분포의 평균 값을 구하는 문제는 커널 함수를 도입하는 문제로 대체하여 해결할 수 있다.
- 이러한 방식을 알아보기 위해서 간단하게 식을 변형해 보도록 하자.
- 여기서 \( S_N \) 은 식 3.51에서 정의한 식이다.
- 이 식의 의미는 임의의 한 점 \( {\bf x} \) 에 대한 예측 분포의 기대값은 타겟 변수 \( t_n \) 의 선형 결합식으로 주어지게 된다.
- 이 때 함수 \( k() \) 는 다음과 같다.
- 이 식을 smoother matrix 또는 동등커널 (equivalent kernel) 이라고 부른다.
- 특히나 회귀 분석에서 사용되는 위와 같은 선형 커널을 linear smoother 라고 부른다.
- 가우시안 기저 함수에 대한 동등 커널의 모양은 아래 그림을 참고하도록 하자.
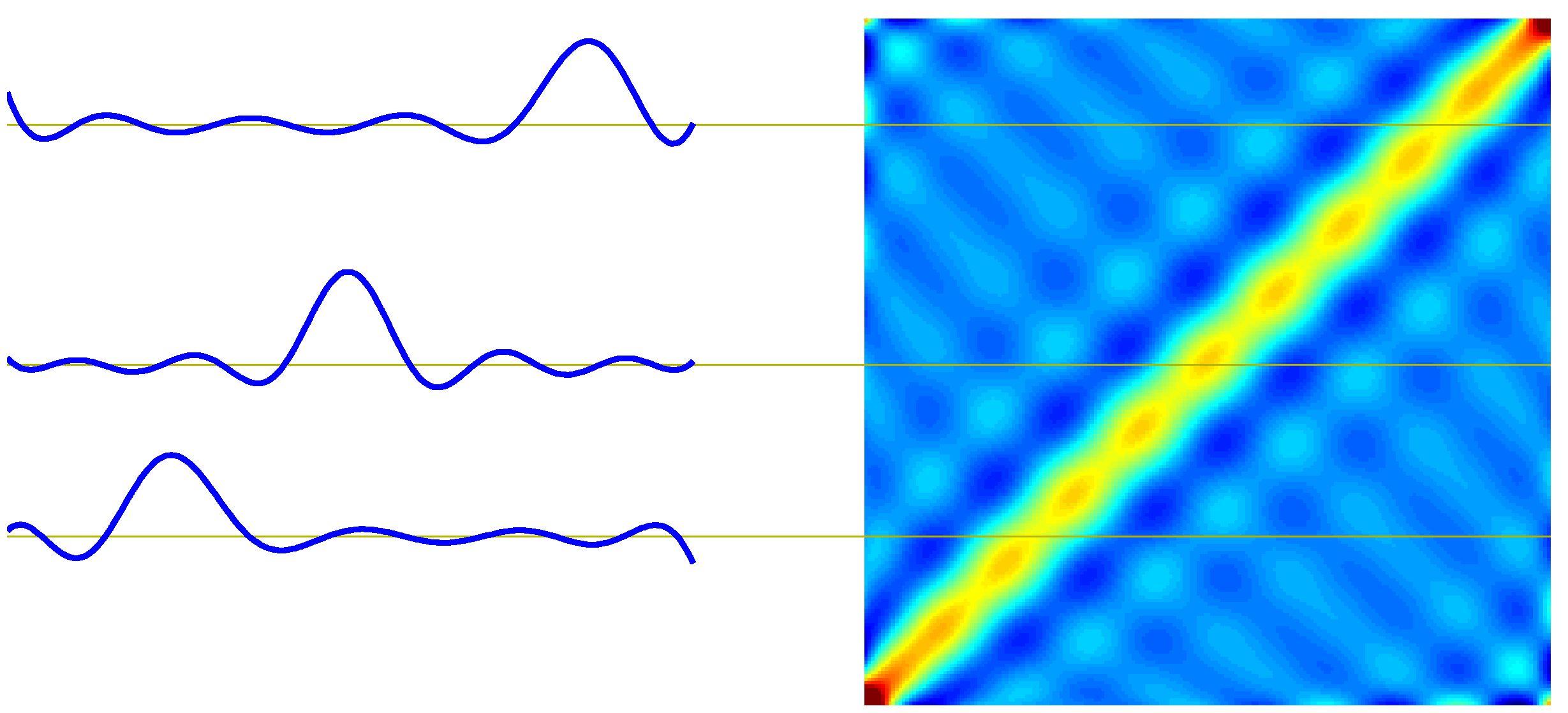
- 위의 그림은 3개의 위치에서 각각의 커널 함수의 모양을 살펴보는 그림이다.
- 이게 뭔가 싶겠지만 실제 정의된 커널 함수를 직접 도식화하면 위와 같은 그림을 얻을 수 있다.
- 어떤 형태의 기저 함수를 사용하던지 커널 함수의 그림은 비슷하게 도출된다.
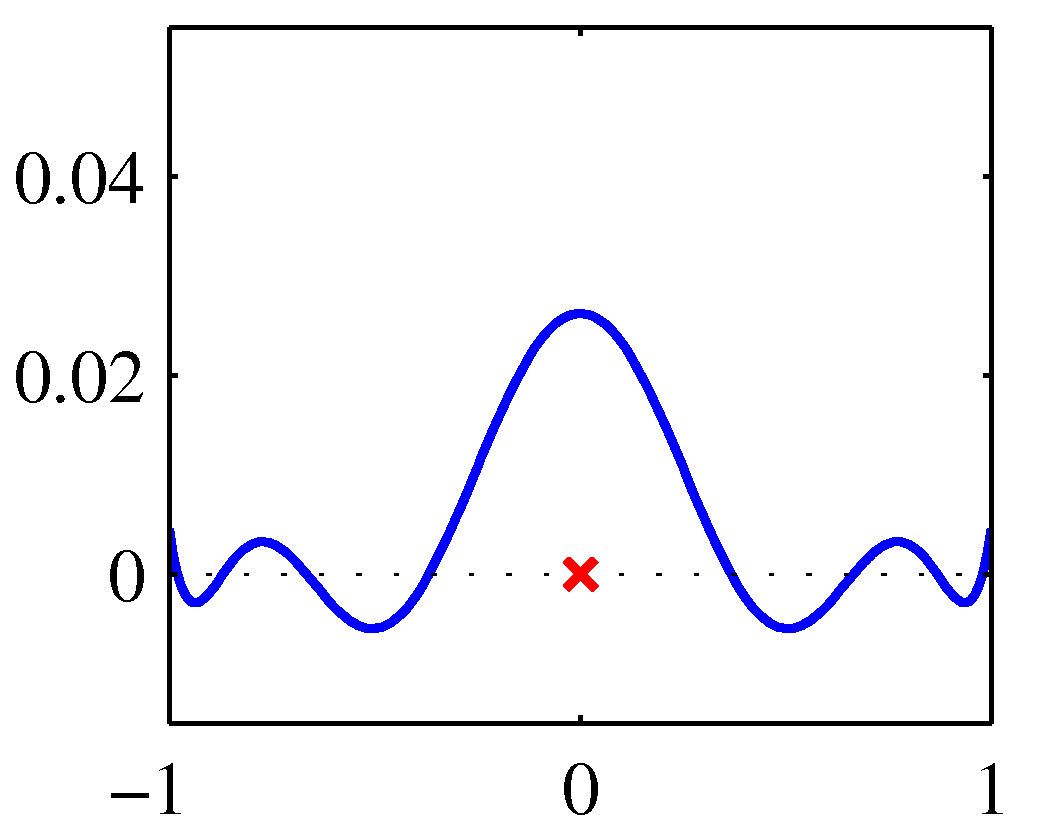
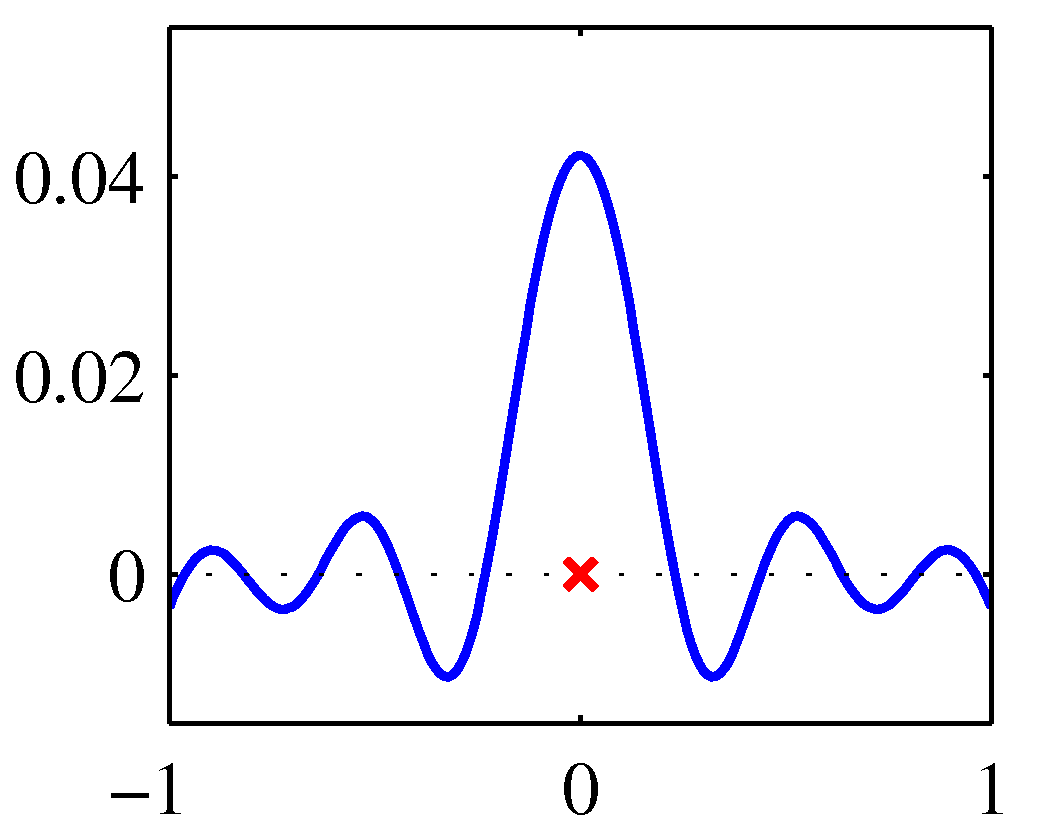
- 위의 그림은 \( x=0 \) 일 때의 커널 함수 모양으로 왼쪽은 polynomial , 오른쪽은 sigmodal 이다.
- 실제 함수의 모양은 거의 차이가 없다는 것을 알 수 있다.
- 원래 \( x \) 값을 중심으로 대칭의 모습이다.
- 이러한 사실로부터 실제 기저 함수를 이용하여 커널 함수를 얻는 방법 대신에,
- 이와 유사한 커널 함수를 사용자가 정의해서 대입할 수도 있다.
- 이는 6장에서 다시 자세히 언급할 것이다.
- 동등 커널에 중요한 특징이 하나 더 있다.
- 이 식은 (식3.19)와 (식3.62)을 조합하여 만들어낸 식이다.
- 예측한 평균 값에 가까운 경우에 큰 함수 값을 가지고 그 외에는 작은 값을 가진다는 것을 알 수 있다.
- (그림 8)은 (식3.59)를 통해 얻어진 결과를 그림으로 나타낸 것이다.
- (그림 9)는 샘플들로부터 구해진 파라미터 \( {\bf w} \) 를 통해 얻어진 사후 분포를 이용하여 그린 결과이다.
- 이 그림은 \( y \) 와 \( {\bf x} \) 간의 동등 커널로 부터 얻어진 것이다.
- 앞서 언급한대로 임의의 커널을 이용해 이를 대체함으로서 선형 회귀와 관련된 식을 만들 수 있다.
- 즉, 기저 함수를 사용하지 않고 바로 커널 함수를 설정해서 쓴다.
- 6.4절을 참고하자.
- 우리는 앞서 동등 커널이 학습 데이터와, 예측할 새로운 데이터 \( x \) 의 결합으로 이루어져 있다는 것을 확인했다.
- 그리고 이는 다음과 같은 조건을 만족해야 한다.
- 이는 \( t_n=1 \) 의 값을 가지는 모든 데이터 \( n \) 이용하여 평균 \( \widehat{y}({\bf x}) \) 를 구하면 쉽게 확인 가능하다.
- 기저 함수들의 선형 독립성을 보장하기 위해서는 기저 함수의 개수보다 샘플의 수가 더 많아야 한다.
- 그리고 적어도 하나의 기저 함수는 상수값이어야 한다. (바이어스 파라미터로 작용한다.)
- 이 값으로 인해 합이 1이 되도록 적절하게 보정된다.
- 잊지 말아야 할 것은 커널 함수의 값이 양수도 될 수 있고 음수도 될 수 있다는 것이다.
- 따라서 합이 1인 제약을 맞추기 위해 convex 함수의 조합만을 요구하지는 않는다.
- 마지막으로 동등 커널 함수는 일반적인 커널 함수의 특징을 가진다. 바로 다음과 같은 성질이다.
- 여기서 \( \psi({\bf x}) = \beta ^{1/2}{\bf S}_N^{1/2}\phi({\bf x}) \) 이다.