6. Infomation Theory

• 정보 이론 분야는 언제나 그렇듯 쉽지 않다.
• 여기서는 정말 간단한 개념만을 살짝 맛보고 지나가도록 하자.
• 간단한 예제를 통해 설명하도록 한다.
  • 어떤 이산 랜덤 변수 \( x \) 가 있다고 하자.
  • 여기서 우리가 \( x \) 의 구체적인 값을 관찰하는 경우 얼마만큼의 정보(information)를 얻는지를 정량화하도록 한다.
• 우선 정보라는 개념을 구체화해야 하는데 간단하게 생각하면 “학습에 있어 필요한 놀람의 정도(degree of surprise)” 로 해석하면 된다.
  • 조금 추상적인 표현이지만 예제를 통해 좀 더 구체적으로 이해하도록 하자.
  • 잘 일어날 것 같지 않은 사건을 관찰하는 경우, 빈번하게 일어나는 사건보다 더 많은 정보를 취득했다고 고려하는 것이다.
  • 따라서 항상 발생하는 일이라면, 사건 발생 후 얻는 정보의 양은 \( 0 \) 이다.
• 정보가 이런 속성을 가지고 있기 때문에 결국 확률에 종속적인 모양새가 된다.
• 정보의 양을 \( h(x) \) 라고 정의하면 정보는 결국 확률 함수의 조합으로 표현이 되게 될 것이다.

• 정보의 양을 나타내는 함수 \( h(x) \) 는 확률 함수 \( p(x) \) 의 음의 로그 값(logarithm)으로 볼 수 있다.
  • 정보의 값은 0 이상이어야 하므로 0~1 사이의 확률값에 로그를 붙이는 경우 앞에 음수가 붙어야 한다.
  • 그리고 낮을 확률 값을 가지는 사건이 높은 정보량을 가져야 하므로 이러한 식을 유도하는 것은 당연한 선택이다.
  • 사실 로그의 밑수(base)가 어떤 값인지는 상관 없으나 조건에 따라 적절한 것을 선택한다.
  • 현재는 \( b=2 \) 를 사용한다. 이런 경우 \( h(x) \) 의 기본 단위가 비트(bit)라고 생각하면 된다.
• 이제 랜덤 변수 하나를 송신자가 수신자에게 전달한다고 가정해보자.
• 이 때 전송되는 데이터 양의 평균을 고려하면 어떻게 될까? 이 때의 값을 정의해보자.

• 이 식은 매우 중요한데 이를 엔트로피(entropy)라고 정의한다.
• 랜덤 변수 \( x \) 에 대한 엔트로피- \( \lim_{p\to0}p\log_2p=0 \) 이므로 \( p(x)=0 \) 이면 \( p(x)\log_2 p(x)=0 \) 이다.
• 엔트로피는 평균 정보량을 의미하며, \( p(x) \) 인 분포에서 \( h(x) \) 함수의 기대값을 의미하게 된다.
• 엔트로피의 정의가 애매하고 임의적인 것처럼 보이는 것도 사실이나 이런 정의가 유용한 속성들을 담고 있다는 것은 부정하기 어려운 사실.
• 이제 예를 이용하여 엔트로피의 개념을 습득해 본다.
• 랜덤 변수 \( x \) 가 \( 8 \) 개의 가능한 값을 가지는 경우
• 각각의 경우가 발현될 확률이 모두 동일하게 \( \frac{1}{8} \) 인 경우 하나의 데이터 \( x \) 를 전송하기 위해 필요한 평균 비트 수는 3이 된다.

• 이것으로 엔트로피에 대한 감을 익혔으면 한다.
  • 현재 확률 분포가 Uniform 분포를 따르게 되므로 실제 데이터를 표현할 때 동일한 정보량을 가지는 형태로 표현되게 된다.
  • 앞서 언급한데로 bit 단위로 정보량을 표현하므로 임의의 데이터 한개를 전송하기 위한 평균 bit 량은 3이 된다는 의미로 받아들이면 된다.
• 각각의 경우가 발현될 확률이 \( (\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{64},\frac{1}{64},\frac{1}{64},\frac{1}{64}) \) 이면 필요한 비트 수는 2가 된다.

• 호프만 코딩법과 같은 표현 기법을 이미 알고 있는 사람이라면 위의 결과가 의미하는 것이 어떤 것인지 쉽게 알아챌 수 있다.
  • 발현 빈도가 높은 데이터는 더 짧은 bit 를 가지는 데이터로 표현하여 전체 전송량을 줄일 수 있게 된다.

• 결국 Non-Uniform 분포의 엔트로피가 Uniform 분포의 엔트로피보다 낮다는 것을 의미한다.

• 또 다른 예제를 들어보자.
  • \( {a,b,c,d,e,f,g,h} \) 데이터를 전송하고자 한다.
  • 이 때 앞서 설명했던 Non-Uniform 분포를 고려해서 각각의 인코딩 코드를 0, 10, 110, 1110, 111100, 111101, 1111110, 111111 로 만든다.
  • 이러면 코드를 만드는 평균 길이는 다음과 같이 계산할 수 있다.

• 위의 경우는 앞서 보았던 \( H(x) \) 를 구한 것과 동일한 결과를 얻는다.
• Noiseless coding theorem (Shannon, 1948)
  • 엔트로피는 랜덤 변수의 상태를 전송하는데 필요한 비트 수의 Lower Bound 가 된다.
  • 예를 들어 엔트로피가 3.4 라면 결국 실제 필요한 비트는 4비트가 필요하게 되므로 Lower Bound임.
• 원래 엔트로피는 물리학에서 주로 통용되던 개념으로 통계 역학(statistical mechanics) 관점에서 엔트로피는,
• “어떤 계의 무질서도” 또는 “거시 상태에 대응되는 미시 상태의 가짓 수” 정도로 이해된다.
• 이러한 관점을 잘 설명하고 있는 예제를 통해 엔트로피 개념을 좀 더 확인해 보자.
• \( N \) 개의 물체를 여러 개의 통에 나누어 놓는 문제를 고려하자.
  • 여기서 물체는 분자 등으로 생각하면 될 것 같다. 이러한 계의 상태를 나타내는 엔트로피 값을 표현할 것이다.
  • 그리고 이거 잘 찾아보면 공업 수학인지 일반 물리인지 대학 초급 교과에 나오는 내용이다.
  • \( n_i \) : \( n \) 개의 물체가 \( i^{th} \) 번째 통에 배치된 상태.
  • 전체 Bin 영역에 \( N \) 개의 물체가 무작위로 놓여있다고 해보자. 이 때 총 나타날 수 있는 가지 수는 \( N! \) 이 된다.
    • \( N \) 개의 집합에서 \( N \) 개를 뽑는 순열과 같다. \(_nP_n=\frac{n!}{0!}=n! \)
  • 그런데 같은 Bin 에 들어간 물체들은 어디에 속해있느냐가 중요한게 아니라 개수만 의미가 있음.
    • 즉, 두 통의 물체가 일부 바뀌더라도 갯수만 유지되면 상관 없음.
  • 최종적으로 만들어낼 수 있는 총 가지 수는 다음과 같이 정의할 수 있다.

• 이걸 multiplicity 라고 부른다.
• 로그를 붙이고 적당한 상수를 넣어 식을 정리하자.

• Stirling’s approximation

• 이걸 적용하면,

• \( N\to\infty \) 이고 \( n_i/N \) 이 고정된 상수라고 하면,

• 결국 통계역학 관점의 엔트로피 식을 얻는다.
  • \( p_i \) 는 \( i \) 번 째 통에 물체가 할당되었을 확률 : \( p_i=\lim_{N\to\infty}\frac{n_i}{N} \)
  • \( \sum_i n_i = N \)
• 이제 이산 랜덤 변수 \( X \)의 엔트로피를 기술해 보자. (물론 \(p(X=x_i)=p_i\) 이다. )

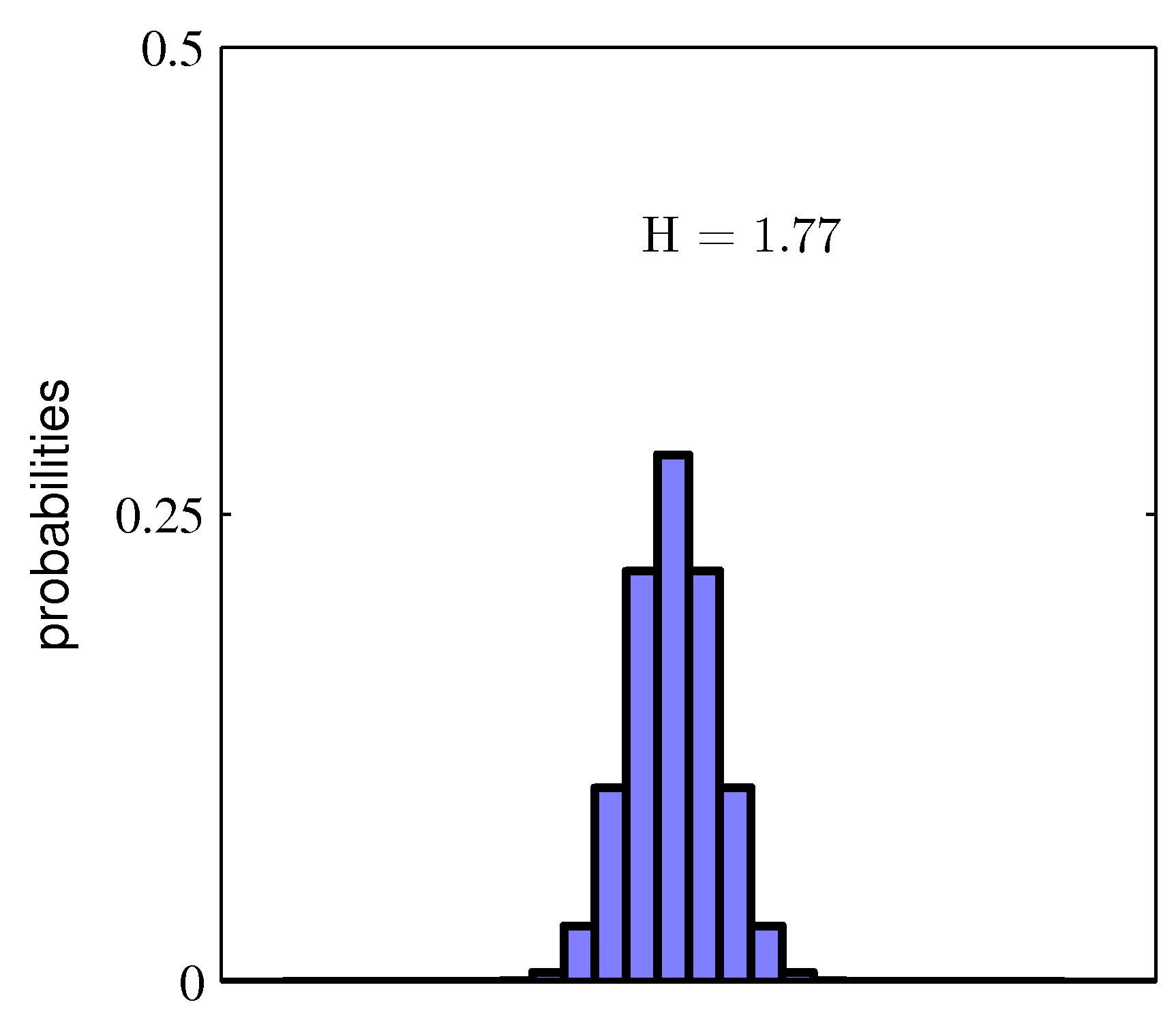
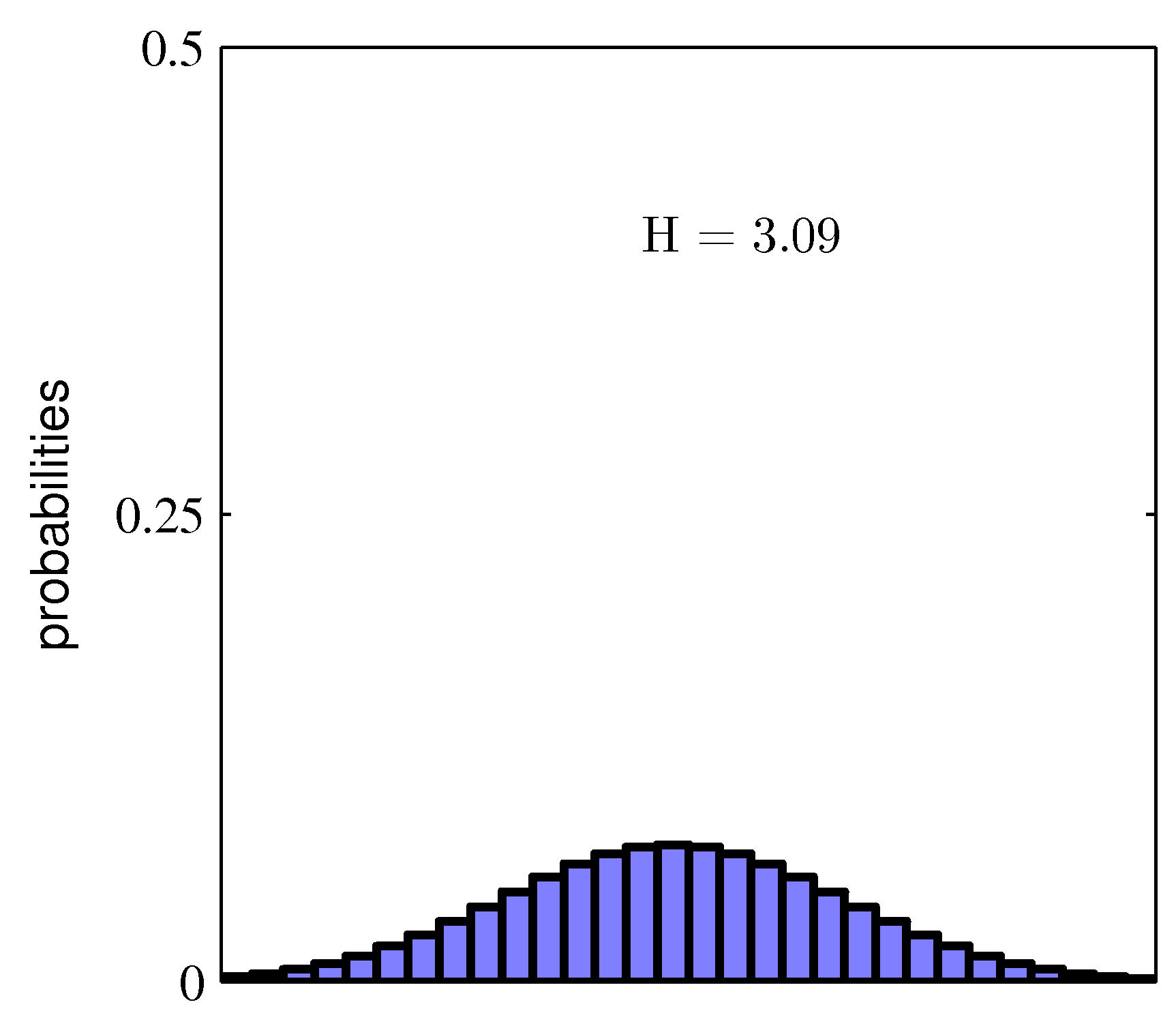
• 이 식을 보면, \( p(x) \) 가 특정 지점에서 높게 피크를 치면 낮은 엔트로피를 얻게 되는 것을 알 수 있다.
  • 이건 이미 Non-uniform 분포가 Uniform 분포보다 엔트로피가 낮다고 설명한 것과 같은 내용이다.

• 최대 엔트로피 값을 만드는 식은 어떻게 될까?
• 확률의 합은 1이라는 제약 조건을 이용해서 라그랑지앙 승수를 이용하면 쉽게 계산 가능하다.
  • 라그랑지앙 승수는 제약 조건이 주어졌을 때의 함수의 최소값을 찾는 문제를 해결하기 위한 수단으로,
  • 관련 자료는 다른 교재를 참고하도록 한다.

• 결국 엔트로피가 최대가 되는 경우는 \( p(x_i) = \frac{1}{M} \) 임을 알 수 있다.
• 여기서 \( M \) 은 상태 \( x_i \) 에 속한 물체의 개수를 의미한다.
• 이 때의 엔트로피 값은 \( H = \ln M \) 이 된다.
• 이 결과는 Jensen’s Inequality 로도 유도 가능하다.
• 최대값이 존재하는지 여부는 해당 함수를 두 번 미분하면 된다. (음수이면 최대값 존재)

연속 변수

• 자, 이제 \( p(x) \) 를 연속적인 변수 \( x \) 에 대해서도 확장을 해보도록 하자.
• 우선 앞서 사용했던 Bin 의 너비를 \( \Delta \) 이라고 정의하자.
• \( p(x) \) 가 연속이면, 다음과 같이 식을 기술할 수 있다.

• 이게 왜 가능할까?

• mean value theorem
  • 함수 \( f \)가 닫힌 구간 \( [a, b] \) 에서 연속이고 열린 구간 \( (a, b) \) 에서 미분 가능하면 \( f’(c) = \frac{f(b)-f(a)}{b-a} \) 를 만족하는 \( c \) 가 존재.
  • 이를 확장하면 \( \int_a^bf(t)dt=f(c)(b-a) \) 도 가능함.
• 식에 mean value theorem 을 적용한다.
• \( f(c)=p(x_i) \) 가 되는 이유는 해당 구간에서 입력 값은 모두 \( x_i \) 로 균일하기 때문이다. (같은 Bin에 속함)
• 이제 \( x_i \) Bin 에 대한 확률 값은 \( p(x_i)\Delta \) 임을 확인했다. 최종 엔트로피 식에 넣어보자.

• \( \sum_i p(x_i)\Delta = 1 \) 이므로 마지막 텀이 분리되었다. (로그 내 값이 분리된 후 식에 의해 전개)

• 이제 마지막 텀인 \( -\ln\Delta \) 은 제거하도록 한다. 왜냐하면 \( \Delta \to 0 \) 을 사용할 것이기 때문이다.
• 이제 최종 식을 구해보자. 이산 합을 적분으로 변경하는 전형적인 식이다.

• 이런 식을 미분 엔트로피 (differential entropy) 라고 부른다.
• 앞서 정보를 나타낼 때 비트(bit) 로 정보의 크기를 표현한 것을 봤는데, 여기서는 비트로 정보를 표기하는 경우 매우 많은 비트가 필요하게 된다.
  • 실수 영역을 bit로 표현해야 하기 때문.
• 자, 이제 최종 식은 다음과 같다.

• 입력 벡터 \( {\bf x} \) 에 대한 엔트로피 값을 얻을 수 있다.

• 이산 랜덤 변수의 경우 \( p(x) \) 가 Uniform 분포일 때 가장 높은 엔트로피 값을 가지는 것을 확인했다.
• 연속 랜덤 변수일 경우에도 동일할까? 확인해보자.
• 마찬가지로 라그랑지랑 승수로 문제를 푼다. 하지만 이산 변수일 때보다 다른 제약들이 추가로 존재한다.

• 정규화 문제로 인해 1차, 2차 적률(moment) 에 대한 제약 사항이 필요하다.
  • 당연히 이러한 조건이 필요하다는 것은 느낌이 오는데, 왜 제약이 더 늘어나는 것일까?
    • 이거 왜 그런지 사실 잘 모르겠음. 정보 이론을 좀 더 살펴보야 할 듯
  • 어쨌거나 1차 적률은 평균, 2차 적률은 분산과 관련된 식이고 확률적 조건이 맞아떨어져야 한다는 것이다.
    • 일견 타당한 이야기인 한데 왜 이산 데이터에서는 이를 고려하지 않는 것인가? 오로지 합이 1이라는 제약 사항만 고려함.
• 어쨌거나 이런 제약들을 모두 라그랑지앙 승수에 넣고 풀면,

• 미분한 식의 우변 값을 0으로 놓고 전개하면 다음과 같은 식을 얻는다.

• 이 식은 마찬가지로 처음에 언급했던 제약 사항을 만족해야 한다.
• 따라서 해당 식에 대입해서 넣고 다시 풀면 아래와 같은 최종 식을 구한다. (증명은 생략)

• 삽질 끝에 얻은 식이 겨우 가우시안 분포이다.
• 이 이야기는 엔트로피를 최대로 하는 확률은 정규 분포를 따른다는 것.
  • 입력 변수가 연속일 경우 가우시안 분포가 엔트로피를 최대로 만들어내고,
  • 입력 변수가 이산일 경우 균일(uniform) 분포가 엔트로피를 최대로 만든다.
  • 이제 \( p(x) \) 가 가우시안 분포를 따를 때의 엔트로피 값을 보자. 앞서 살펴본 differential entropy 식에 대입하면 다음을 얻게 된다.

• 이 식은 오로지 분산(여기서는 \( \sigma^2 \) )에만 영향을 받는다.
• 따라서 분산도가 커지면 엔트로피가 증가하는 것을 알 수 있다.
• 마찬가지로 분산 값이 \( \infty \) 로 증가한다면 균일 분포가 됨을 알 수 있다.
• 이 식에서 재미있는 것은 이산 변수와는 다르게 연속 변수에서는 엔트로피의 값이 0보다 작을 수 있다는 것이다.
  • \( \sigma^2 \) 의 값이 \( \sigma^2 < \frac{1}{2\pi e} \) 인 경우
• 결합 확률 \( p(x,y) \) 에 대한 엔트로피 값은 어떻게 될까?
• \( x \) 가 이미 알려져 있다면 필요한 정보는 \( -\ln p({\bf y}|{\bf x}) \) 이고 \( {\bf y} \) 에 대한 식으로 전개하면 된다.

• 이를 \( {\bf x} \) 가 주어졌을 때 \( {\bf y} \) 에 대한 조건부 엔트로피(conditional entory)라고 한다.

• 역시나 뒷 부분으로 오면 올 수록 자세한 설명 없이 대충 이런게 있다 정도로만 설명이 진행된다.

• 조건부 엔트로피는 다음과 같은 성질을 만족한다.

• 위의 식은 직관적으로 이해할 수 있다.
• \( ({\bf x}, {\bf y}) \) 를 기술하기 위해 필요한 정보는 \( {\bf x} \) 만 기술하기 위한 정보와
• \( {\bf x} \) 가 주어졌을 때 \( {\bf y} \) 를 기술하기 위한 정보의 합으로 이루어진다.
• 곱이 아니라 합이라는 사실이 중요한데, 사실 내부적으로 로그가 포함되어 있기 때문.
• 이후 좀 더 식이 나올 것이다.

1.6.1 연관 엔트로피와 상호 정보 (Relative entropy and mutual information)

• 이번 절에서는 정보 이론에 관한 여러 썰을 좀 풀것이다. 긴장하기 바란다.
• 거창하게 패턴 인식에 대한 아이디어부터 좀 이야기하자.
• 정확한 형태를 모르는 확률 분포 \( p({\bf x}) \) 가 있다고 해보자. 그리고 이 확률 분포를 최대한 근사한 \( q({\bf x}) \) 가 있다고 하자.
• 그럼 당연히 데이터의 실 분포는 \( p({\bf x}) \) 이고, 우리가 예측한 분포는 \( q({\bf x}) \) 라는 생각을 할 수 있을 것이다.
• 이제 해당 데이터를 \( q(x) \) 의 코딩 스킴으로 인코딩해서 데이터를 전송한다고 해보자.
  • 이러면 이 데이터의 실 분포인 \( p(x) \) 에 의해 얻을 수 있는 정보량과 우리가 실제 사용한 \( q({\bf x}) \) 사이의 정보량은 다를 수 있다.
  • \( p({\bf x}) \) 가 아닌 \( q({\bf x}) \) 를 사용했기 때문에 추가적으로 필요한 정보량의 기대값을 정의해보자.
    • 이 때 정보의 양은 bit 가 아니라 nat를 쓴다. ( \( \log_2 \) 가 아니라 \( \ln \) 을 사용한다. )
    • 정보량을 \( -\ln p(\bf x) \) 로 정의하였고, 정보량의 기대값을 엔트로피라고 정의하였으므로 최종 식을 엔트로피의 식으로 기술할 수 있다.

• 이러한 정의를 relative entropy 또는 Kullback-Leibler divergence 라고 부른다.
• 그냥 \( KL \) divergence 라고도 한다.
  • 어쨌거나 근사 분포인 \( q({\bf x}) \) 를 사용했기 때문에 정보량은 \( -\ln q({\bf x}) \) 를 사용한다.
  • 하지만 데이터의 실 분포는 \( p(x) \) 이므로 기대값은 실분포를 대상으로 구하게 된다.
• 식을 보면 알겠지만 \( KL(p||q) \neq KL(q||p) \) 이다. (non-symmetric)
• \( KL \) 은 항상 \( KL[p|q] \ge 0 \) 을 만족한다.
  • 만약 \( p({\bf x}) = q({\bf x}) \) 이면 \( KL(p||q) = 0 \) 이다. 반대도 성립한다.
• 이를 증명하기 위해 먼저 간단한 개념을 좀 살펴보자.

• 가장 먼저 convex 함수라는 것이 무엇인지 알아야 한다. (이제야 convex 의 개념이 나온다.)
  • 우리 나라 말로는 볼록 으로 변역할 수 있으나 의미 전달이 이상하므로 그냥 convex 라는 용어를 계속 사용하도록 하자.
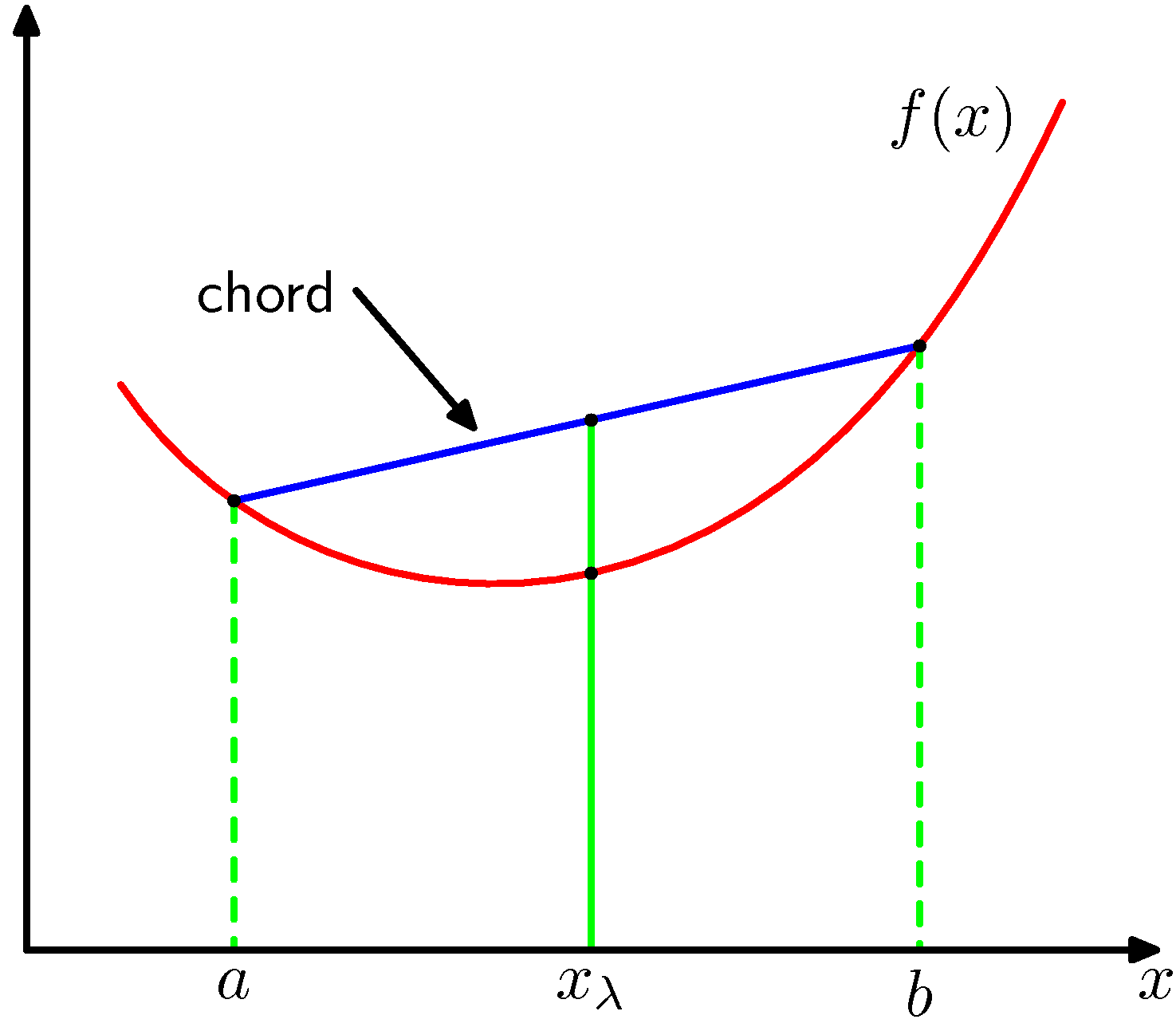
• 어떤 함수 \( f(x) \) 내에서 임의의 두 점 사이의 chord 가 함수 \( f(x) \) 와 같거나 혹은 더 위쪽으로 형성된다면 이를 convex 라고 한다.
  • 말이 어려우니 위의 그림을 보면, 파란색의 선이 chord 가 된다.
  • 즉, 함수 내 임의로 정한 서로 다른 두개의 점을 연결한 선이다.
  • 붉은 색 선이 실제 함수 값이다.
  • 따라서 위의 그림에서 표현된 \( f(x) \) 도 convex 하다고 할 수 있다.
• 자, 이제 이걸 식으로 만들어보자.
• 임의의 구간 \( x=a \) 와 \( x=b \) 를 정한다. ( \( a<b \) )
• 그럼 그 사이의 임의의 \( x_{\lambda} \) 는 \( x_{\lambda}=\lambda{a}+(1-\lambda)b \) 로 정할 수 있다.
• 이제 Convexity 를 구하는 식을 정리해보자.

• convex를 만족하는 함수로 \( f(x)=x\ln(x) \) , \( f(x)=x^2 \) 등을 들 수 있다.
• \( \lambda=1 \) 또는 \( \lambda=0 \) 인 경우에만 등호( \( = \))가 성립하는 경우 이를 strictly convex 라고 부른다.
• 부등호가 반대이면 이를 concave 라고 한다.
  • 즉, \( f(x) \) 가 convex 이면, \( -f(x) \) 는 concave 가 된다.
• 이는 수학적 귀납법을 이용해 증명 가능하다.
• 앞서 언급한 식을 일반화하여 기술해보자.

• 여기서 모든 \( x_i \) 의 집합에 대해 \( \lambda_i \ge 0 \) 이고 \( \sum_i\lambda_i=1 \) 을 만족한다.
• 이 식을 옌센부등식 (Jensen’s inequality) 이라고 한다.
  • 이 사람이 어느 나라 사람인지 모르겠으나 젠센 부등식 이라고도 부른다. 뭐가 맞는 것인지 모르겠다.
• 만약 위 식에서 \( \lambda_i \) 를 이산 변수 \( x \) 에 대한 확률 분포라고 고려하면, 식을 다음과 같이 정리할 수 있다.

• 연속 변수에 대해서도 확장 가능하다.

• 이 식은 생각보다 많이 사용되므로 꼭 눈도장 찍어놓기 바란다.

• 이제 Jensen’s inequality 를 이용해서 실제 KL divergence 를 유도하는 식을 보자.

• \( f(x) = -\ln(\frac{q({\bf x})}{p({\bf x})}) \) 로 놓는다.
  • 만약 이 함수가 convex 또는 concave 인 경우 이 식은 Jensen 부등식으로 확장 가능하다.
    • 물론 \( -\ln(\cdot) \) 은 당연히 convex 함수. 따라서 위와 같은 부등식을 얻을 수 있다. (위의 식은 전개 후 정리가 되어 있다.)
  • 이 때 \( \int q({\bf x})d{\bf x}=1 \) 이다. ( \( q \) 가 확률 식이므로) 따라서 \( -\ln\int q({\bf x})d{\bf x}=0 \) 을 얻는다.
  • 이렇게 하면 \( KL \) 의 결과를 유도할 수 있다. (즉, \( KL[p||q] \ge 0 \) )
• 이제 \( f(x)=-\ln(t(x)) \) 와 같은 형태의 함수에 대한 성질을 좀 살펴보도록 하자.
  • 이 함수는 strictly convex 함수이다.
  • 따라서 위의 식에서 \( KL[p||q]=0 \) 이 만족되기 위해서는 \( p=q \) 인 경우밖에 없다.
  • 따라서 정의에 따라 \( KL[p||q]=0 \) 인 경우에만 \( p({\bf x})=q({\bf x}) \) 가 성립한다.
• 이런 성질을 이용하면 \( KL \) divergence를 두 확률분포 간의 차이점(dissimilarity)의 척도로 생각해 볼 수 있다.
  • 좀 쉽게 이야기하자면 \( KL \) 값이 0인 경우에는 두 분포가 같고 다른 경우에는 양수의 실수 값을 가지게 된다.
• data compression
  • 앞서 언급했던 데이터 인코딩 문제를 \( KL \) 과 함게 생각해보면,
  • 이론적으로 생각해봤을 때 가장 효율적인 압축은 데이터의 실 분포를 정확히 알고 모델을 만들었을 때 이다.
  • 실 분포와 다른 분포가 사용되면 \( KL \)만큼의 추가 정보가 만들어져 덜 효율직인 인코딩이 이루어진다.
• 다음으로 모델링하고자 하는 확률 분포 \( p({\bf x}) \)를 따르는 데이터를 생성하고 싶다고 하자.
• 물론 우리가 만들어내는 분포는 조정 가능한 파라미터 \( {\pmb \theta} \) 를 이용해 만든 \( q({\bf x}|{\pmb \theta}) \) 분포이다. ( \( p({\bf x}) \)의 근사 분포)
• 이 경우 \( KL \) divergence 를 최소화하는 \( {\pmb \theta} \) 가 결정되어야 한다.
• 우리는 \( p({\bf x}) \)를 알 수 없지만, 이를 통해 생성된 샘플 \( {\bf x}_n \) 은 얻을 수 있다.
• 이 때 이 샘플의 평균을 이용해서 \( p({\bf x}) \)기대값을 근사하자.
  • 이와 관련된 식은 이미 1장에서 살펴보았다. (식 1.35) : \( E[f] \simeq \frac{1}{N}\sum_n f(x_n) \)

• \( KL \) 자체가 \( f({\bf x})=-ln(\frac{q({\bf x})}{p({\bf x})}) \) 에 대한 평균함수 형태이므로 위와 같이 기술할 수 있다.
• 여기서 두번 째 텀은 \( {\pmb \theta} \) 값과 무관하고 첫번 째 텀은 학습 데이터로부터 계산 가능한 음 로그 가능도 함수(negative log likelihood)이다.
• 그러므로 \( KL \) divergence를 최소화하는 것은 결국 가능도 함수(likelihood)를 최대화 시키는 것과 동일하다.
  • 어찌보면 당연한 결과라 하겠다.
  • 이제 중요한 이유는 \( KL \) 이 가능도 함수를 이용한 MLE 와 연관성을 가지게 된다는 것이다.
  • 즉, MLE를 최대화 하는 관점을 \( KL \) 을 최소화하는 관점으로 전환하여 사용할 수 있다는 것.
  • 9.4절에 \( EM \) 알고리즘을 설명하면서 이와 관련된 내용이 함께 언급된다.
  • 위의 식이 생각보다 중요한데 10장의 변분 추론과 많은 관련이 있다.

• 이제 두 변수 \( {\bf x} \) 와 \( {\bf y} \)가 주어졌을 때 결합 확률 분포와 관련된 내용을 좀 살펴보자.
• \( {\bf x} \)와 \( {\bf y} \)가 서로 독립적이라면 결합 분포는 각각 주변화(marginalize)된 확률의 곱으로 표현할 수 있다. : \( p({\bf x}, {\bf y}) = p({\bf x})p({\bf y}) \)
• \( {\bf x} \) 와 \( {\bf y} \)가 서로 독립적이지 않다면 주변화된 곱의 확률값과 결합 확률간의 차리로 둘 사이의 거리를 측정할 수 있다.
  • 즉, \( p({\bf x})p({\bf y}) \) vs. \( p({\bf x}, {\bf y}) \)
  • 이 때 사용할 수 있는 것이 \( KL \) divergence 이다.

• 이를 상호 정보(mutual information) 라고 한다.
• 항상 \( I[{\bf x}, {\bf y}] \ge 0 \)을 만족한다.
• 만약 \( {\bf x} \) 와 \( {\bf y} \)가 서로 독립적이라면 \( I[{\bf x}, {\bf y}] = 0 \) 이 된다.
• 합(sum) 과 곱(product)의 법칙도 사용할 수 있다.

• mutual information 은 조건부 엔트로피(conditional entropy)와 연관이 있다.
  • \( {\bf y} \) 를 알고 난 후에 \( {\bf x} \)의 불확실성을 줄이는 과정으로 볼 수 있다.
• 베이지안 관점으로 접근하자면 \( p({\bf x}) \) 는 사전(prior) 분포, \( p({\bf x}|{\bf y}) \) 는 관찰 값 \( {\bf y} \) 를 측정한 이후의 사후(posterior) 분포로 볼 수 있다.