- 지금까지 최소 제곱법(Least square)을 이용한 다항식 커브 피팅의 예를 살펴보았다.
- 또한 다항식에서 최적의 차수(order)를 구해 강건한 모델을 만드는 것도 살펴보았다.
- 정칙화 계수(regularization coefficient) \( \lambda \) 를 조절하여 모델의 복잡도를 조절할 수 있다는 것을 확인했다.
-
실제 이를 적용하기 위해서는 이런 파라미터들을 실제로 직접 구할 수 있어야 한다.
- MLE (Maximum likelihood estimation) 방식은 오버피팅이 쉽게 발생할 수 있음을 확인했다.
- 물론 데이터가 충분하다면 다양한 모델을 학습하여 가장 적당한 파라미터 값을 추정할 수 있다.
- 별도의 validation 데이터를 구성하여 테스트를 해보는 등의 방법이 있다고 설명했다.
-
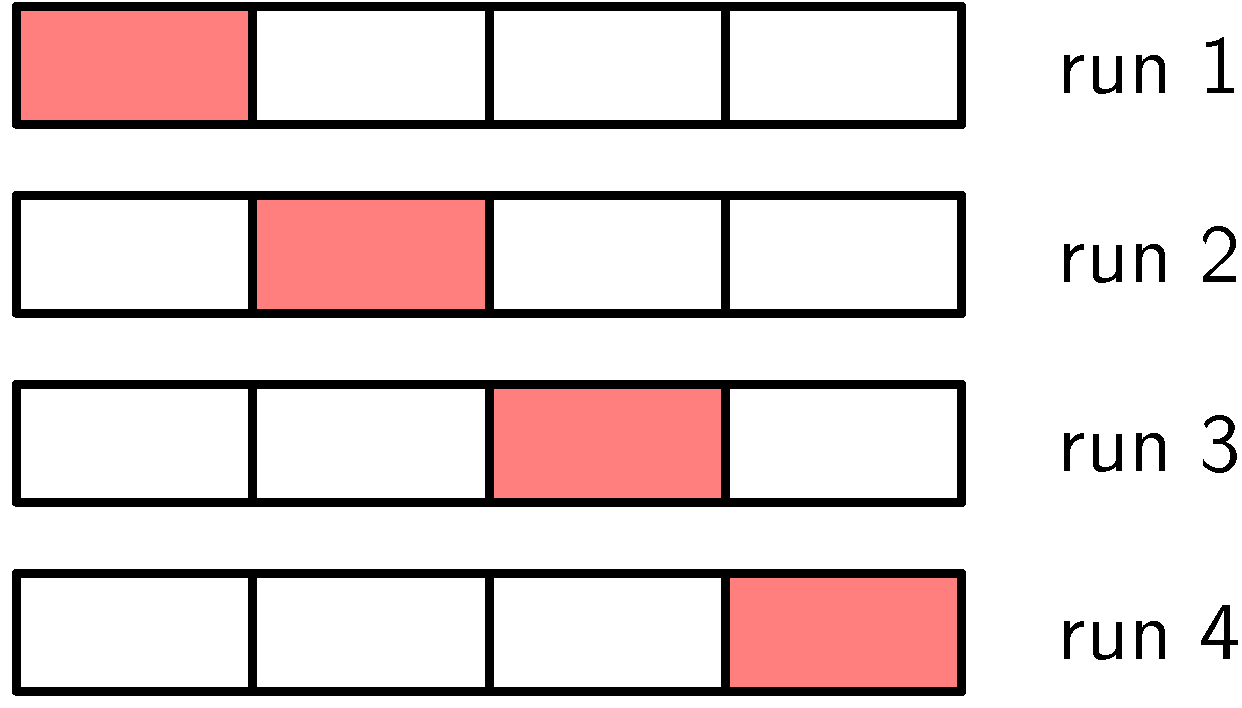
기계학습 분야에서는 학습된 모델의 정확도를 판단하는 기준으로 cross-validation 기법을 자주 활용한다.
- cross validation
- 임의(random)로 고른 \( (S-1)/S \) 를 학습 집합으로, \( 1/S \) 를 테스트 집합으로 하여 학습 진행
- \( S \) 를 하나씩 번갈하가면서 총 \( N \) 번 테스트
- \( S \) 가 증가하면 반복해야 할 횟수도 함께 증가한다는 단점이 존재
- 초모수(hyper-parameter) 조합까지 테스트해보려면 초모수의 개수에 지수 승만큼 테스트를 반복해야 한다.
- 여기서 초모수란 베이안 추론에서의 hyper-parameter를 의미하는 것은 아님.
- 모델 선택에 있어 사용되는 모든 메타 파라미터들을 의미한다.
- 예를 들어 K-NN 알고리즘에서 K 값은 모델에서 고정되어 있으나 cross-validation을 통해 K 값을 결정할 수 있다.
- 이 때의 K 값은 결국 모델의 초모수가 된다.
- 이 정도로 설명했으면 대충 의미는 파악했을 것이다.
- 이상적으로는 학습 데이터 집합만 사용하면서 반복되는 작업 없이 한번에 여러 모델을 비교해볼 수 있어야 한다.
- 정말 원하는 것은 학습 데이터에만 종속적이고 오버피팅으로 인한 bias 가 발생하지 않는 측정값을 찾는 것.
- 전통적인 정보 이론 (infomation criteria) 영역에서는 MLE 로 인해 발생되는 bias를 막기 위해 페널티 조건을 추가하는 방식을 사용한다.
- 예를 들어 AIC(Akaike information criterion) 라는 기법은 좋은 모델을 선정하는 기준으로 다음과 같은 값을 사용한다.
- 여기서 \( M \) 은 모델에서 사용한 파라미터(parameter)의 개수를 의미한다.
- 대략적인 의미는 현재 주어진 데이터를 가장 적합하게 만드는 모수를 추정하되 모델이 복잡해서는 안된다는 것이다. (occam’s razor)
- 즉, 동일한 성능을 내는 모델 두개가 제공된다면 여기서 덜 복잡한 모델을 선택할 수 있어야 한다.
- 원래 모델 성능을 측정하는데 \( p(D | \theta) \) 가 사용되는 것은 당연한 것이다. 여기에 페널티 조건으로 \( M \) 이 추가된 형태이다.
- 모델 선택시에 위의 식이 사용되는 이유는 4.4.1 절에서 다시 언급되므로 그 때 확인을 하자.