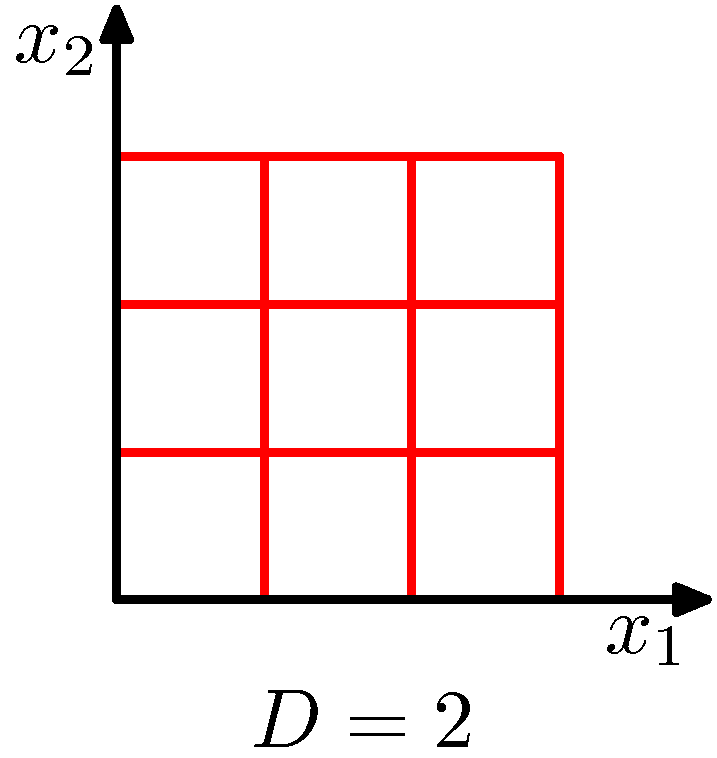
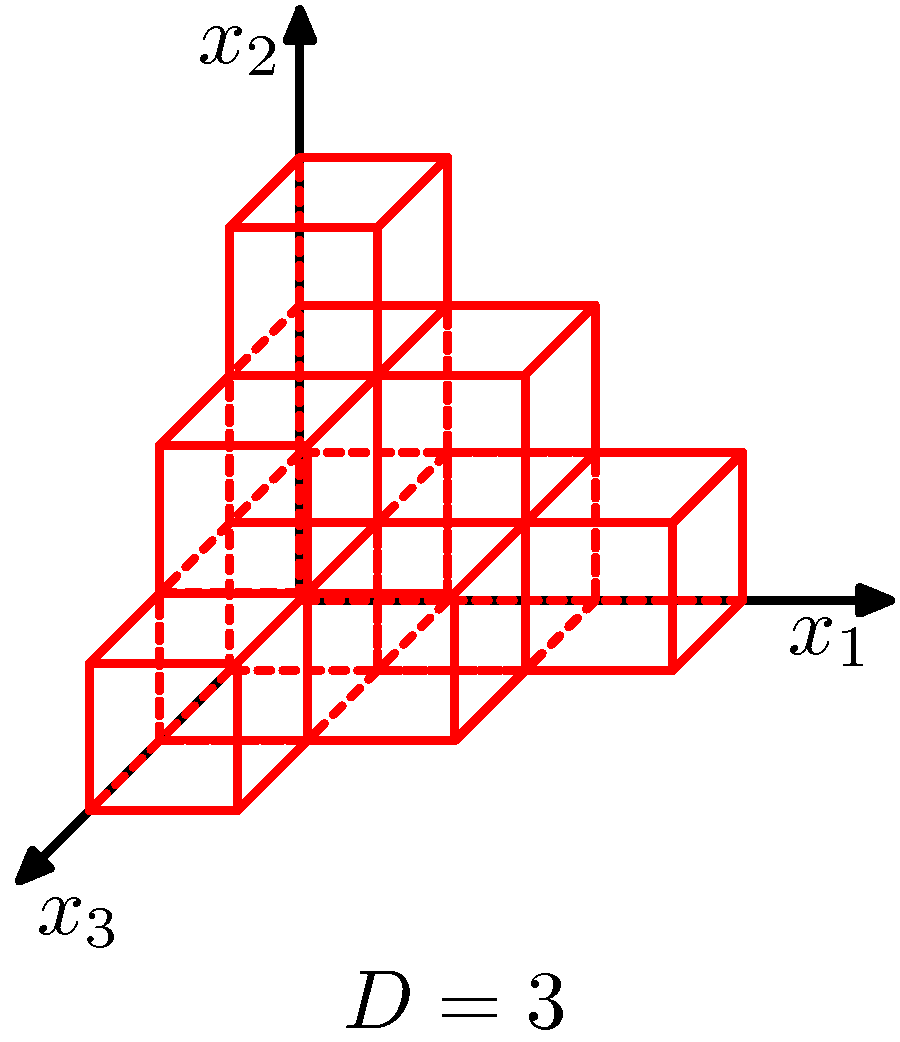
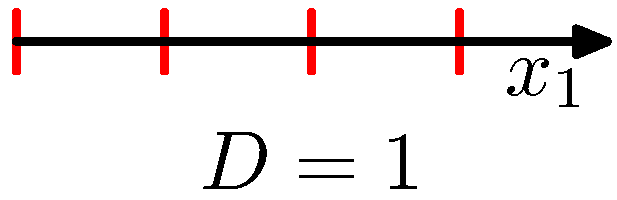4. The Curse of Dimensionality
- 앞서 살펴본 커브 피팅 예제에서는 입력변수 \( x \) 의 범위가 1차원 데이터었다.
- 하지만 현실은? 이런 경우가 거의 없다.
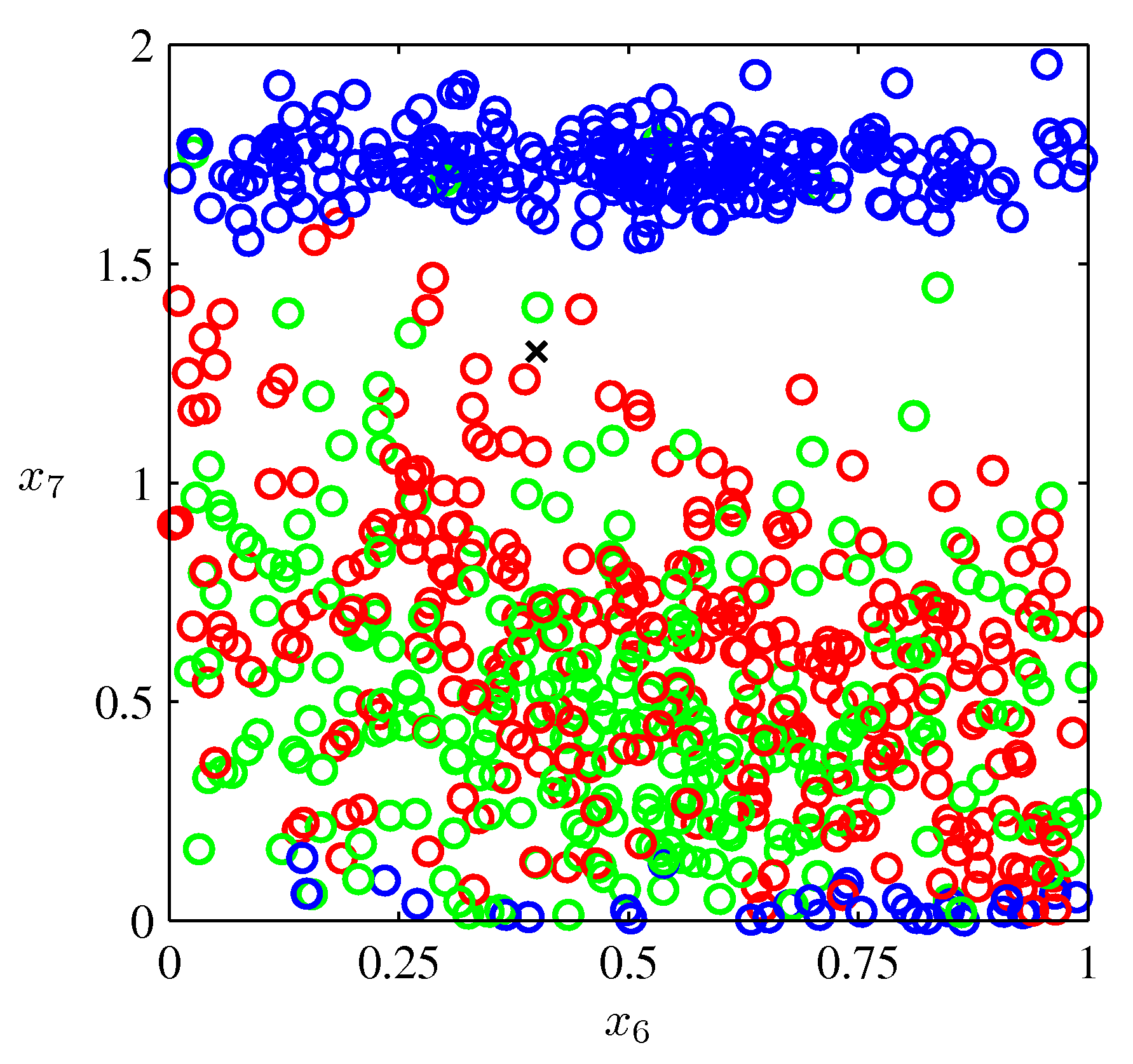
- 위의 그림은 PRML 교재 Appendix. A 데이의 일부를 나타낸 그림이다. (Oil 데이터)
- 이 데이터는 총 12 차원의 입력 범위를 가지고 있다.
- 그림에서 표기한 차원은 각각 \( x_6 \) 과 \( x_7 \) 의 데이터이다.
- 포인트의 색깔은 데이터의 클래스를 의미한다. 현재 3 종류의 클래스가 존재한다고 확인할 수 있다.
- 이 중 \( x \) 로 표기한 영역에서 이 데이터가 어떤 클래스에 속할지를 판단하는 문제이다.
- 가장 손쉬운 방식은 무엇일까?
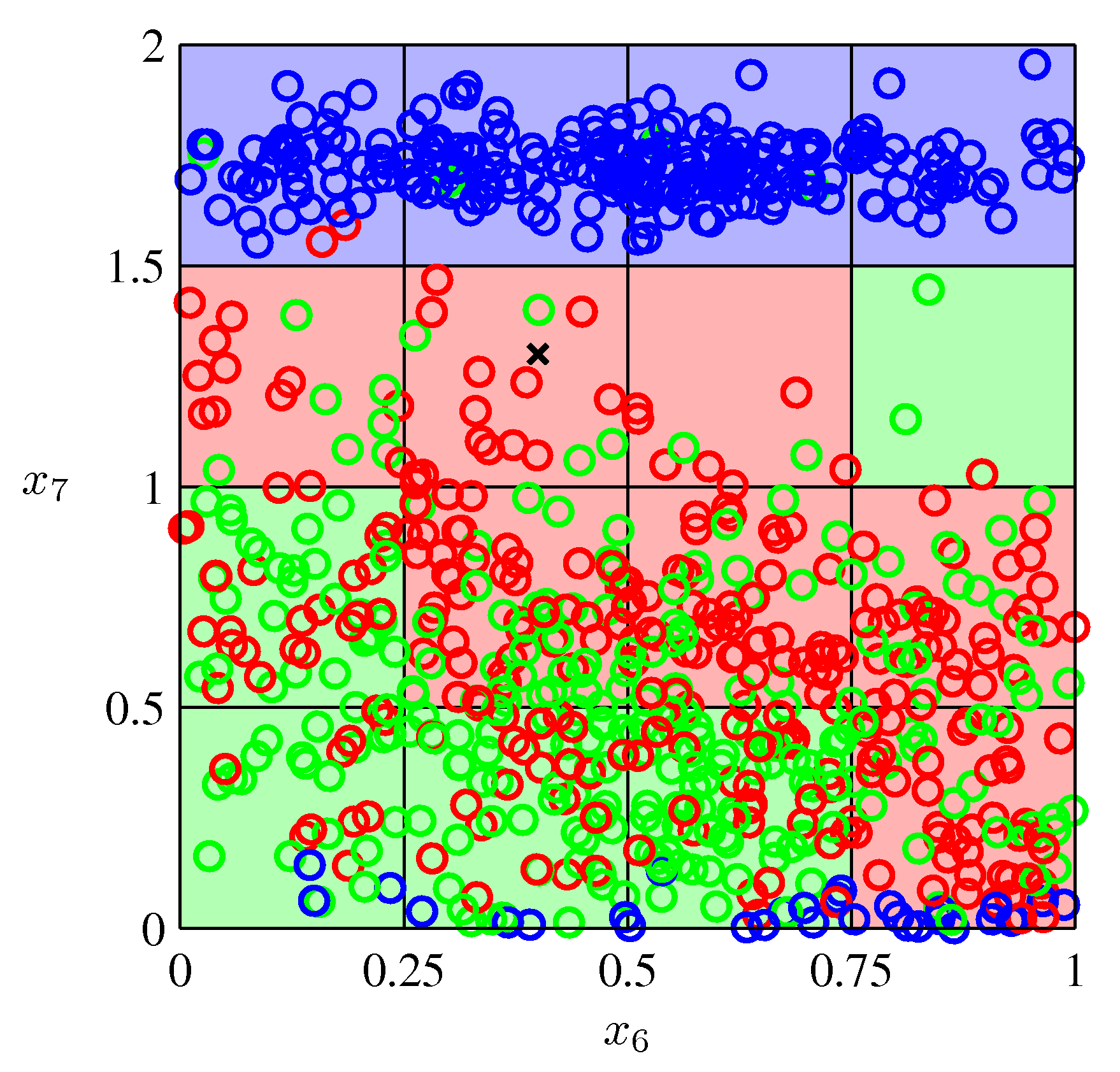
- 전체 입력 범위를 작은 단위의 셀(cell)로 나누어 \( x \) 가 속한 셀 내에서 가장 많은 클래스를 확인한 뒤 그 클래스로 분류를 하는 방법이다.
- 위의 그림에서 하나의 색깔 박스에 해당하는게 셀(cell)이 된다.
- 간단히 생각해보면 꽤나 괜찮은 접근 방식이다.
- 하지만 입력 데이터의 차원이 증가하게 되면 이런 방식을 적용하기가 어려워진다.
- 셀의 개수가 지수(exponential)로 증가함.
- 우리가 앞서 사용한 다항식 방식의 식을 도입하게 되면 구해야할 차원은 \( D^M \) 까지 증가하게 된다.
- 이걸 기하학적인 관점에서 기술하면 다음과 같다.
- 반지름의 길이가 \( r=1 \) 인 구를 생각해보자. 물론 차원은 \( D \) 차원이다.
- 이 때의 구의 부피는? (이 때 입력 차원에 독립적인 일반식을 생각해보자.)
- 참고로 3차원에서 구의 부피는 \( (4/3)\pi r^3 \) 이다. (기억들이 나시는지?)
- 그리고 거리가 \( r=1 \) 인 경우의 구의 부피에서 \( r=1-e \) 인 구의 부피를 빼는 것을 상상해보자.
- 이 때 \( e \) 는 보통 매우 작은 값을 사용할 것이다.
- 이러면 다차원 구의 부피는 표면 층의 부피가 된다.
- 물론 \( e \) 값을 어느 정도의 작은 값으로 취하는 가에 따라 표피만 의미하는 것이 아니라 수박 껍질처럼 고려될수도 있다.
- 그럼 이제 \( e \) 값을 조절하면서 이 구간의 부피비를 생각해볼 수 있을 것이다.
- 식은 매우 단순한데, 원래 구의 부피를 분모로 놓고 \( e \) 로 인해 결정되는 겉 껍질의 부피를 분자로 놓게 된다.
- 즉, 원래의 부피와 겉면의 부피의 비를 확인하고 싶은 것이다.
- 이 때 \( e \) 값이 변화할 때 원래 부피와의 비율을 살펴보자.
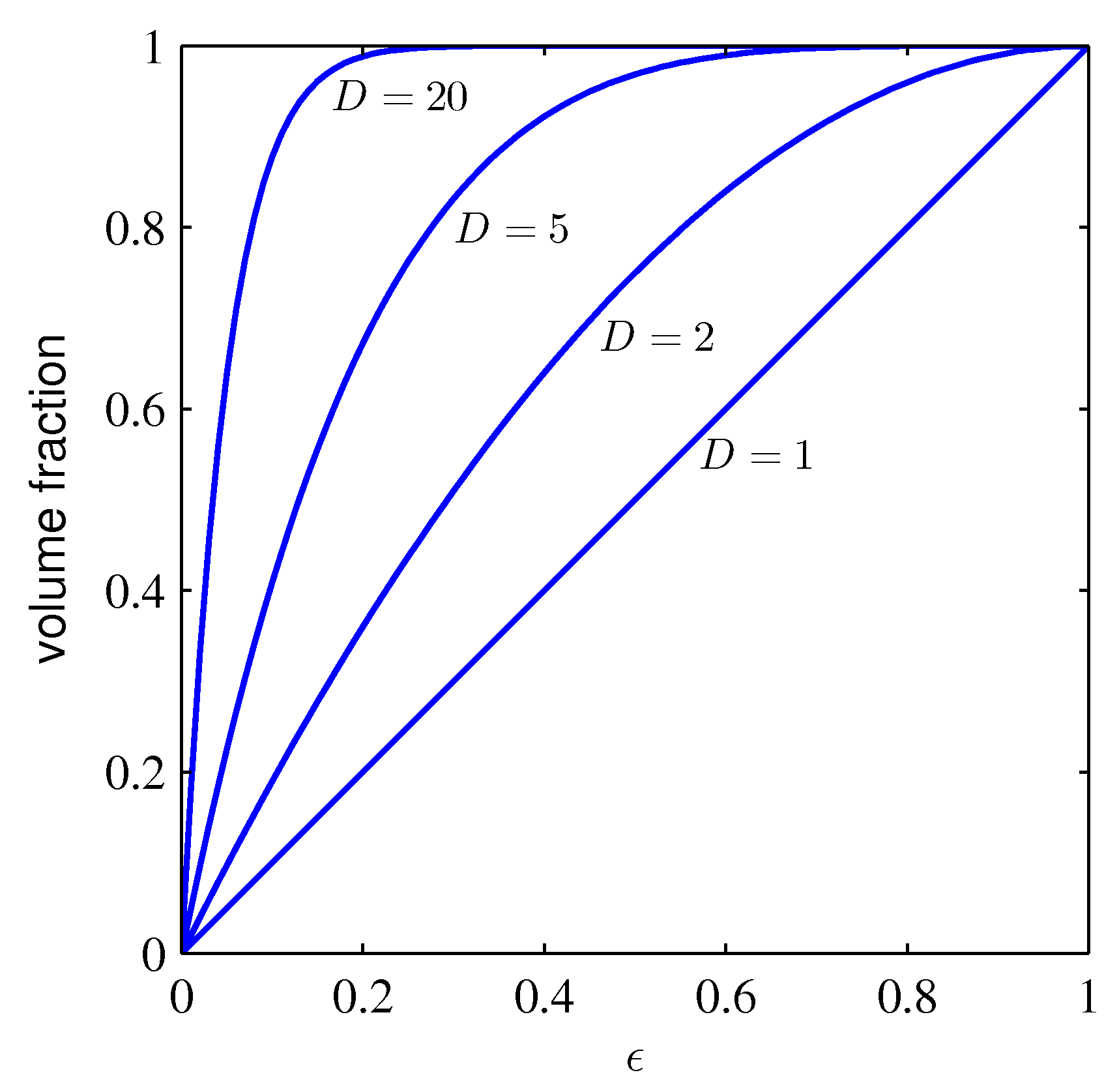
- 그림을 잘 보면 차원이 증가할수록(D가 커질수록) \( e \) 값이 작더라도 원래 볼륨 크기와 근접하게 됨을 알 수 있다.
- 이걸 다른 관점에서 이야기하자면 차원이 증가할수록 전체 볼륨 크기의 대부분은 표면에 위치하게 된다는 것이다.
- 3차원까지만 머릿속에 그릴 수 있는 우리로서는 약간 이해하기 어렵지만 그래도 상상을 해 볼수는 있다.
- 이걸 다시 다차원 공간에서의 가우시안 분포로 고려해보자.
- D차원을 가진 샘플 \( x \) 가 있다고 해보자. 이 샘플은 원점으로부터 임의의 거리 \( r \) 만큼 떨어져 있을 것이다.
- 이 데이터 \( x \) 를 하나의 차원으로 축소한다. 새로운 차원은 \ r \) 로, 원점으로부터 떨어진 거리를 의미하는 변수이다.
- 단위가 거리이므로 여기서 사용되는 값은 양수이다.
- 결국 \( D \) 차원의 정보가 하나의 차원으로 축약된다.
- 이제 샘플을 랜덤하게 생성해보자. (물론 가우시안 분포를 따라서 생성되어야 한다.)
- 데이터 \( x \) 가 원래 가지고 있던 차원을 증가하면서 랜덤하게 생성해본다.
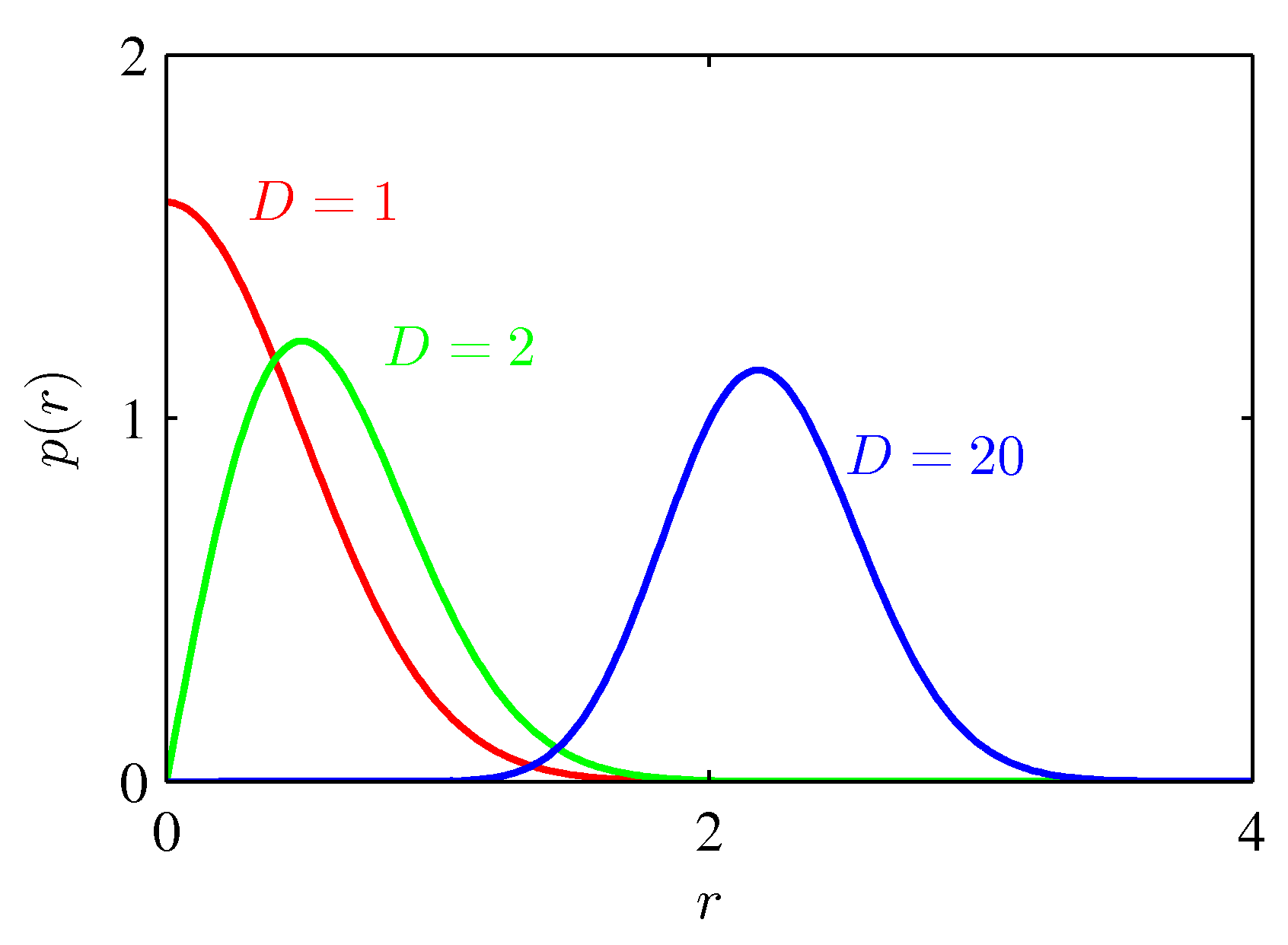
- 그리고 실제 데이터가 어느 거리에 많이 존재하는지를 확인해본다.
- 차원이 증가하는 경우 반지름 \( r \) 의 위치에 데이터의 분포가 집중이 되고 있는 것을 확인할 수 있다.
- 즉, 차원이 증가할수록 전제 부피 중 표면 쪽의 부피 비율이 증가하기 때문에 실제 샘플이 등장할 비율도 표면에 가까워지도록 변화할 것이다.
- 처음에 보았던 직관(insight)과 일맥상통하는 결과이다.
- 차원의 저주 ( curse of dimensionality )
- 저차원 공간에서 얻은 직관이 고차원 공간에서도 통용될 것이라는 것을 믿으면 안된다.
- 물론 고차원 공간을 다루는 것이 쉬운 일은 아니지만, 고차원 공간에서 적용 가능한 테크닉들이 존재하는 것도 사실.
- 왜냐하면 실제 데이터는 이 고차원 공간을 모두 사용하는 것이 아니라 부분적인 저차원 지역에 국한된 경우가 많다.
- 게다가 실제 데이터는 평활화(smoothness) 요소가 포함되어 있음
- 약간의 데이터 위치의 변경으로도 전체 차원의 정보가 변경되는 것은 아니므로 국한된 지역으로 보간(interpolation)하는 방식을 사용할 수 있음
- 예) 이미지에서 객체의 방향을 확인하고자 한다.
- 컨베이어 벨트 위에 있는 평면의 객체의 이동 방향을 확인한다.
- 이미지를 고차원 공간에서의 점들로 전환 (10x10 사이즈인 경우 100차원 데이터)
- 객체가 이미지 내에서 다른 위치에 나타날 것이므로 3개의 자유도를 가짐 (위치, 방향, 명암)
- 이 고차원의 데이터는 3차원 매니폴드(manifold) 위에 존재하며 객체의 위치, 방향, 명암의 합으로 만들어진 관계로 인해 매니폴드는 비선형적으로 구성된다.
- 매니폴드(manifold)는 일단 하나의 차원(dim)이라고 생각하면 된다. 실제 더 높은 차원이 존재하지만 우리에게 필요한 영역만 별도의 차원으로 인식해서 생각할 때 사용되는 개념이라 생각하면 되겠다.
- 우리가 필요한 것은 방향성이므로, 3차원 매니폴드 내에서 1차원의 자유 변수만 집중하면 된다.
- 이 예제는 설명이 너무 어려워 무슨 말인지 잘 모르겠다. 이게 여기에 꼭 맞는 예제인가 싶기도 하고.
- 이와 관련된 내용은 5장 즈음에 탄젠트 벡터를 설명하면서 조금 나오기는 한다.