5. Nonparametric Methods

• 이번 장에서는 데이터로부터 추론할 수 있는 적은 수의 파라미터를 가지는 특별한 함수 형태의 확률 분포들을 다루었다.
  • 이런 접근 방법을 모수적 (parametic) 접근법이라고 부른다.
• 이러한 접근법의 한계는 데이터를 잘 표현하지 못하는 모델을 사용하는 경우 엉망의 결과를 예측하는 모델이 만들어질 수 있다는 것이다.
• 예를 들어 데이터 자체가 multi-modal 형태의 출력 결과를 만들어냄에도 불구하고 가우시안 모델을 고집한다면 결코 좋은 결과를 얻을 수 없다.
• 이제 이번 장의 마지막 절에서는 비모수적(nonparametric) 방법론에 대해 다루어 볼 것이다.
  • 여기서는 아주 간단한 형태의 빈도론자적(frequentist) 입장만을 다루도록 한다.
  • 하지만 베이지안 방식을 사용하는 비모수적 방법론도 존재하므로 관심있는 사람은 찾아보도록 한다.
• 가장 간단한 형태인 히스토그램(histogram) 모델을 먼저 알아보도록 하자.
  • 사실 이미 1장에서 히스토그램과 관련된 내용을 다루어보기는 했다.
  • 여기서 좀 더 자세히 다루어보자.
  • 가장 기본적인 히스토그램은 입력 변수 \(x \) 의 영역을 일정한 크기의 단위로 나누게 된다.
  • 이 때 하나의 단위를 빈(Bin)이라고 하고 이 때의 크기를 \(\Delta_i \) 라고 한다. ( \( i \) 마다 크기는 가변적)
  • 하나의 Bin 안에 속한 샘플의 개수를 \(n_i \) 라고 하면 이 때의 확률 값은 다음과 같이 정의할 수 있다.

• 물론 일반적인 경우 하나의 Bin 크기는 모두 동일하게 취급한다. ( \( \Delta_i=\Delta \))
• 확률값의 총 합은 1이므로 \(\int p(x)dx =1 \) 도 성립해야 한다.

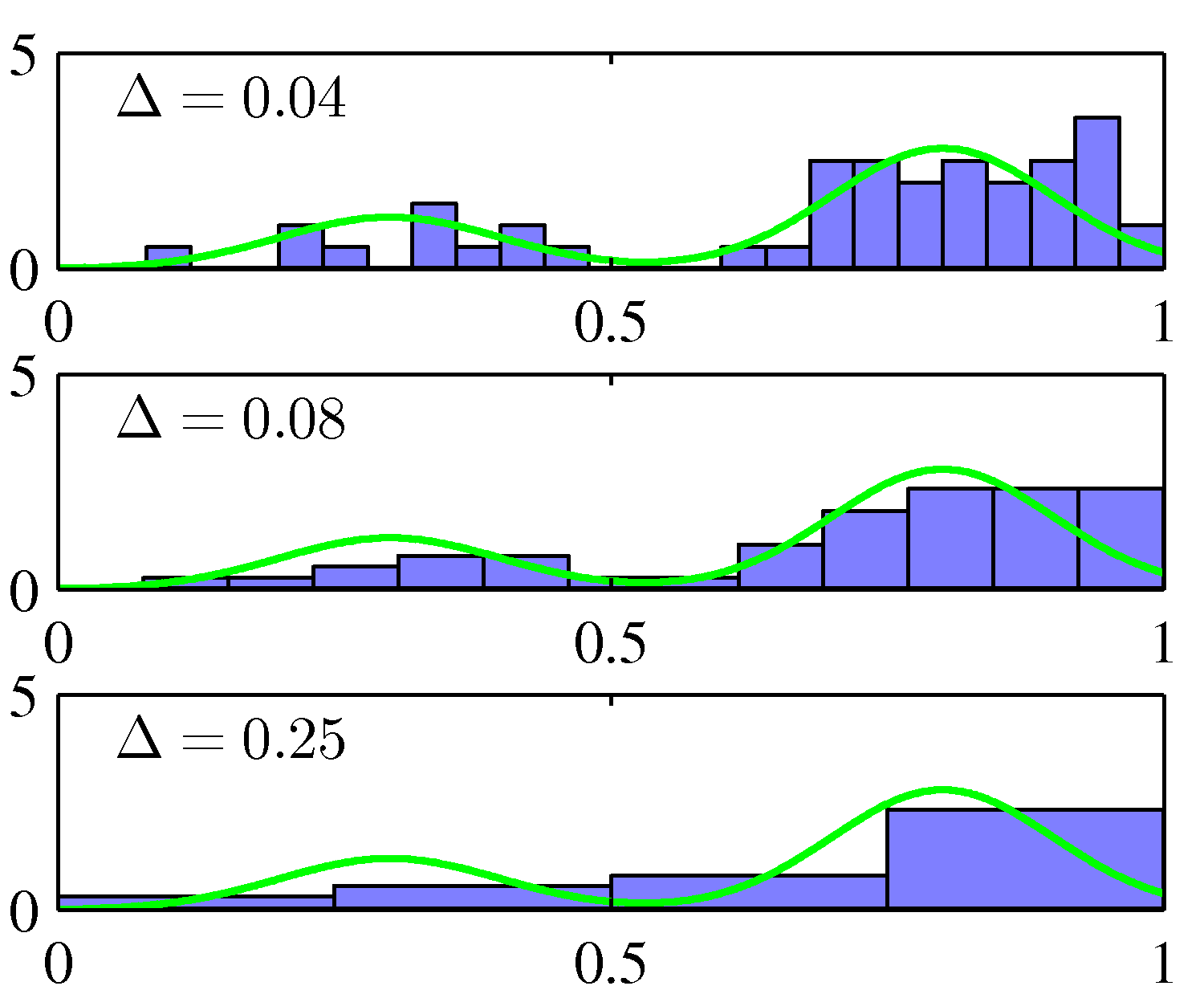
• 위의 그림은 총 50개의 관찰 데이터를 여러 크기의 \(\Delta \) 값을 이용하여 표기한 것이다.
• 모두 동일한 데이터임에도 불구하고 Bin 의 크기에 따라 얻어지는 모양들이 서로 다른 것을 알 수 있다.
• 따라서 \(\Delta \) 값을 어떻게 정하느냐가 매우 중요한 요소가 됨을 알 수 있다.
  • \(\Delta \) 가 매우 작으면 튀는 지점(spike)이 발생하기 쉽다.
  • \(\Delta \) 가 매우 큰 경우 지나치게 평탄화(smooth)되어 데이터의 특징점을 찾아내기가 힘들다
  • 가장 적당한 \(\Delta \) 를 찾아내야 한다.
• 히스토그램의 특징
  • 한번 히스토그램을 구성하고 나면 관찰 데이터가 필요 없다.
  • 데이터를 순차적으로 처리가 가능하다.
  • 데이터 가시화에 좋은 효과를 지닌다. (사용자가 데이터를 명확하게 이해하기 좋다.)
• 히스토그램이 주는 2개의 직관이 있는데,
  • 지역적(local)인 밀도 추정이 가능하다는 것이다.
    • 특정 위치의 확률 밀도 추정을 위해 해당 지점과 가까이 있는 데이터만을 고려하게 된다.
    • 이를 위해서는 점들 사이의 거리 측정 방식을 도입해야 한다.
      • 히스토그램에서는 Bin 의 크기가 이를 충족시키고 있다.
      • 다른 방법도 얼마든지 제안 가능하다.
  • 평탄화(smoothing)를 위한 파라미터 값 조절이 매우 중요하다.
    • 실제 데이터에 대해 너무 크지도, 너무 작지도 않은 파라미터 값을 선정해야 한다.
• 히스토그램의 한계점
  • 추정된 밀도가 불연속적이므로 응용에 어려움이 좀 있다.
  • \(D \) 차원의 데이터를 각각 \(M \) 개의 Bin 으로 나누면 전체 Bin 수는 \(M^D \) 가 된다. (지수 증가)

2.5.1. 커널 밀도 추정 (Kernel density estimators)

• 히스토그램이 많은 문제를 가지고 있다고 언급했으므로 당연히 이에 대한 해결책을 언급할 것이다.
  • 차수가 증가하면 연산량이 지수로 증가한다거나, 불연속 점이 발생한다거나, Bin 크기에 많은 영향을 받는다거나 등
• 여러 방법론들을 제시하기 전에 비모수적 방법론이 공통적으로 포함 하고 있는 개념들을 직관적으로 이해해 보자.
• 문제 공간 정의
  • 확률 밀도는 \(p({\bf x}) \)
  • \(D \) 차원의 입력 공간
  • 거리 측정 방식은 Euclidian 방식
  • \(R \) : 임의의 데이터 \({\bf x} \) 를 포함하게 되는 어떤 단위의 region
  • \(V \) : \(R \)의 공간상의 부피
  • \(K \) : 데이터를 \(N \) 번 관찰한 뒤 얻은 데이터 중 그 데이터가 공간 \(R \) 에 속하게 되는 관찰 데이터 개수
• 히스토그램과 유사하게 확률를 정의할 수 있다.
• 공간 \(R \) 에서의 확률 값

• 우선 히스토그램의 문제는 불연속점이 생긴다는 것인데 여기서는 확률 밀도 함수 \(p({\bf x}) \) 를 도입하여 이 문제를 해결하자.
  • 즉, 특정 벡터 \({\bf x} \) 가 어떠한 확률 분포 \(p({\bf x}) \) 에 의해 발생한다.
  • 적분이 된다는 이야기는 적어도 \(R \) 범위 내에서는 \(p({\bf x}) \) 함수가 연속인 밀도이다.
    • 히스토그램 내 Bin 크기와 대응되는 개념으로 생각하면 된다.
• 여기에 \(N \) 개의 벡터 집합 \({\bf X}=({\bf x}_1, …, {\bf x}_n)^T \) 가 있다고 하자.

• 이 \(N \) 개의 벡터 중 \(K \) 개가 영역 \(R \) 에 속할 확률을 고려하도록 한다.

• \(K \) : 데이터를 \(N \) 번 관찰한 뒤 \(R \) 에 속하게 되는 샘플의 수
  • 이 때 \(K \)의 확률은 이항 분포(binomial distribution)을 따르게 될 것이다.
  • 이를 모델링하면 다음과 같다.

• 이 때 \(R \) 내에 위치하는 값들의
  • 평균 : \(E[K/N] = P \)
  • 분산 : \(var[K/N] = P(1-P)/N \)
  • 이는 이항 분포의 파라미터 값이다.
• \(N\rightarrow\infty \) 라면 분산은 0이 되고, 이 확률 분포는 특정 점에서 피크를 만들어 낼 것이다. (즉, 평균)
  • 이렇게 하면 다음 식이 성립하게 된다.

• 물론 \(R \) 은 충분히 작아서 확률 밀도 \(p({\bf x}) \) 가 상수 값이 될 정도로 작아야 한다고 가정하자.
  • 이게 무슨 이야기인고 하니 \(R \) 영역이 너무 작아져 이 범위 내의 \(p({\bf x}) \) 결과가 상수화된다는 의미이다.
  • 결국 확률은 사각형을 구하는 식이 된다. 그럼 아래와 같이 식을 기술할 수 있다.

• 이 두 식을 결합하면 다음과 같은 식을 얻을 수 있다.

• 이거 사실 히스토그램 식과 차이가 없다. 그냥 좀 더 일반화된 버전이다.
• 이 때 사용된 가정들을 좀 정리하자면 두 가지 상충되는 요건이 존재함을 알 수 있다.
  • \(R \) 에 포함된 \(p({\bf x}) \) 의 값이 특정 상수 값이 될 정도로 \(R \) 이 충분히 작아야 하고 (가정에 의해)
  • \(N \) 개의 샘플 중에 \(K \) 개의 샘플이 \(R \) 영역에 안착될만큼 \(R \) 이 충분히 커야 한다. (현실적인 계산을 위해)
  • 서로 모순이 있는 것 같은데 두 조건을 다 만족하는 적당한 크기의 \(R \) 이 필요하다는 것.
• 실제 위 식을 적용하기 위한 방법은 크게 2가지가 있다.
  • \(K \) 를 고정시키고 값 \(V \) 를 결정 : K-nearest-neighbour
  • \(V \) 를 고정시키고 값 \(K \) 를 결정 : Kernel approach

• 일단 커널 메소드에 대해 좀 더 알아보도록 한다.
• 커널 메소드에서는 \(R \) 은 매우 작은 크기의 입방체 (hyper-cube)로 정의된다. ( \(V_n=h_n^d \) )
  • 이 큐브의 중심에 포인트 \({\bf x} \) 가 있다.
• 우리는 이에 대한 확률 밀도를 결정하고자 한다.
  • 만약 이 입방체에서 \(K \) 개의 샘플이 포함된다면 이 대의 개수를 세기 위한 커널 함수는 다음과 같이 기술할 수 있다.

• 갑자기 커널 함수가 왜 등장했는지는 신경쓰지 말고 커널 함수가 어떻게 동작하는지만 보자.
  • 입력 값을 \({\bf u} \) 벡터를 입력받는다.
  • 식이 좀 혼동되는데 \({\bf u} \) 의 모든 벡터 요소의 절대값이 \(1/2 \) 이하여야 1이 반환되는 함수이다.
  • 결국 \(K(\cdot) \) 는 1 차원의 실수 값을 반환하는 함수이다.
• 이제 이 함수를 이용해서 입방체 내에 점의 수를 다음과 같이 계산 가능하다.

• 결국 주어진 \({\bf x} \) 를 중심으로 입방체 내에 몇 개의 샘플이 존재하는지를 확인하게 된다.
  • 잘 상상이 안 될수도 있다. 임의의 한 점 \({\bf x} \) 가 주어지면 각 차원으로 \(h/2 \) 거리 내에 존재하는 모든 샘플을 센다.
  • 한 점을 중심으로 거리를 계산하는 것이므로 실제 계산에서는 모든 샘플 데이터의 비교가 필요하다. \(O(N) \)
• 위와 같은 함수는 일종의 커널 함수(kernel method)로 파젠 윈도우(Parzen window)라고 한다.
• 이제 위의 \(K \) 에 관한 식을 원래 식 \(p({\bf x})=K/NV \) 에 대입하여 전개해보자.

• 여기서 \(V=h^D \) 를 사용하였다.
• 사실 식을 조금만 변경하면 \({\bf x} \) 가 중심이 되는 하나의 큐브를 고려하는 식이 아닌 \({\bf x}_n \) 을 중심으로 하는 \(N \) 개의 큐브를 만들어 낼 수 있다.

• 위와 같은 식에서도 여전히 히스토그램과 같은 단점이 발생한다.
  • 바로 큐브의 가장자리 영역에서는 불연속적인 값을 가지게 된다.
  • 이는 위와 같은 방식이 사실은 히스토그램의 전개 방식을 일반화시킨 것에 지나지 않기 때문이다.
• 이제부터 본격적으로 각 지점에서 연속인 함수를 도입하는 방법을 살펴볼 것이가.
• 이런 기법을 스무딩(smoothing)이라고 하는게 가장 간단한 방법은 가우시안 함수를 씌우는 것
• 이렇게 하면 평탄화(smoother)된 확률 밀도를 얻을 수 있다.

• 교재가 좀 불친절해서 이런 식이 왜 등장했는지에 대한 언급이 없다.
  • 간단하게 생각해보면 하나의 샘플 데이터를 기준으로 가우시안 함수를 고려하는 것이다.
  • 즉 하나의 샘플 \({\bf x}_n \) 에 대해 중심이 \({\bf x}_n \) 이고 표준 편차가 \(h \) 인 가우시안을 만들고,
  • 이를 합하여 새로운 밀도 함수를 만들어내는 것이다. (이 때 정규화를 위해 \(1/N \) 이 곱해짐)
  • 그낭 간단히 상상을 해보면 각 관찰 데이터 별로 하나의 가우시안 분포가 만들어지고 이를 선형 결합한 함수가 최종 함수가 된다.
  • 결국 중요한 요소는 관찰 데이터가 실제 얼마나 분포되어 있는지 여부와 \(h \) 값을 어떻게 설정하느냐에 따라 분포 모양이 많이 달라질 것임.

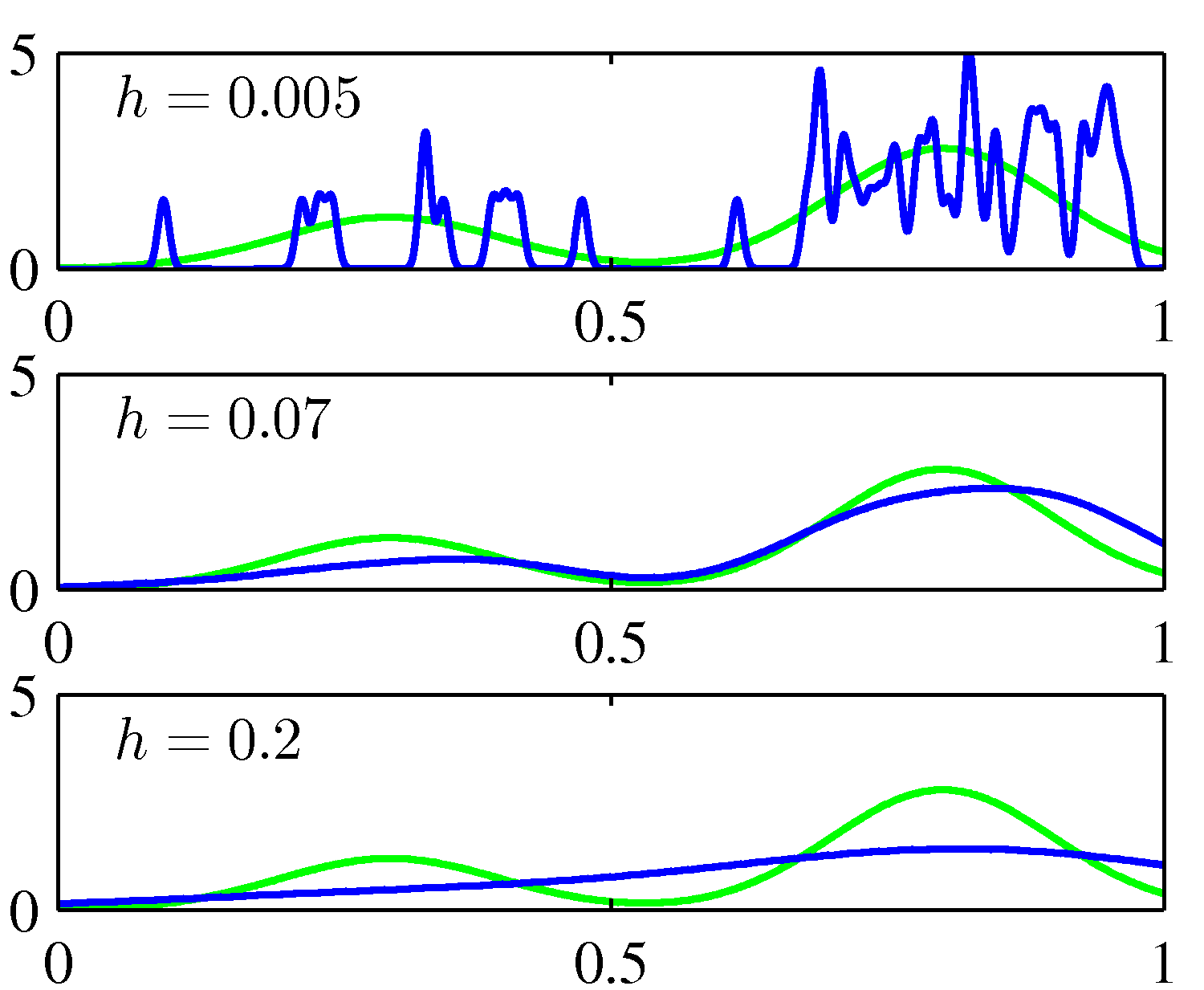
• 위의 그림을 보면 \(h \) 값을 어떻게 조절하는가에 따라 스무딩 효과가 달라지는 양상을 확인할 수 있다.
  • \(h \) 가 너무 작은 경우 분석하기 어려울 정도로 엉성하게 피크가 형성되고(undersmooth),
  • \(h \) 가 너무 큰 경우 밀도가 과도하게 부드러워져서 데이터의 구조를 덮어버리게 된다.(oversmooth)

• 사실 커널 모델이 한 가지 형태로 국한된 것은 아니고 다양항 형태의 커널을 사용할 수 있다.
• 여기서는 다음과 같은 조건을 가진 커널을 사용해야 한다.

• 커널 밀도 추정 (KDE) 방식의 특징
  • 장점
    • 학습 단계에 계산 작업이 필요 없다. 데이터만 저장되어 있으면 된다.
  • 단점
    • 데이터 크기에 비례하여 연산 비용이 증가한다.
    • 사용되는 \(h \) 가 고정되어 있다.
      • 각 차수마다 최적의 \(h \) 가 다를 수 있으므로 이에 대한 한계점이 존재
      • 데이터 밀집도가 큰 영역에서는 over-smooth 현상이 발생하고,
      • 데이터 밀집도가 작은 영역에서는 under-smooth 가 발생한다.

2.5.2. 최근접-이웃 방법 (Nearest-neighbour methods)

• 이 방식은 \(K \) 를 고정하고 데이터로부터 \(V \) 를 결정하는 방식을 취한다.
• \({\bf x} \) 를 중심으로 하는 구(sphere)를 고려한다.
• 이 구가 \(K \) 개의 샘플을 포함할 때까지 구의 반지름을 계속 늘려간다.
• 정확히 \(K \) 개의 샘플이 포함된 구의 부피를 \(V \) 하고 하고 이 때의 확률 밀도 \(p({\bf x}) \) 를 추정한다.
• 이러한 방식을 K-nearest neighboures 방법이라고 부른다.

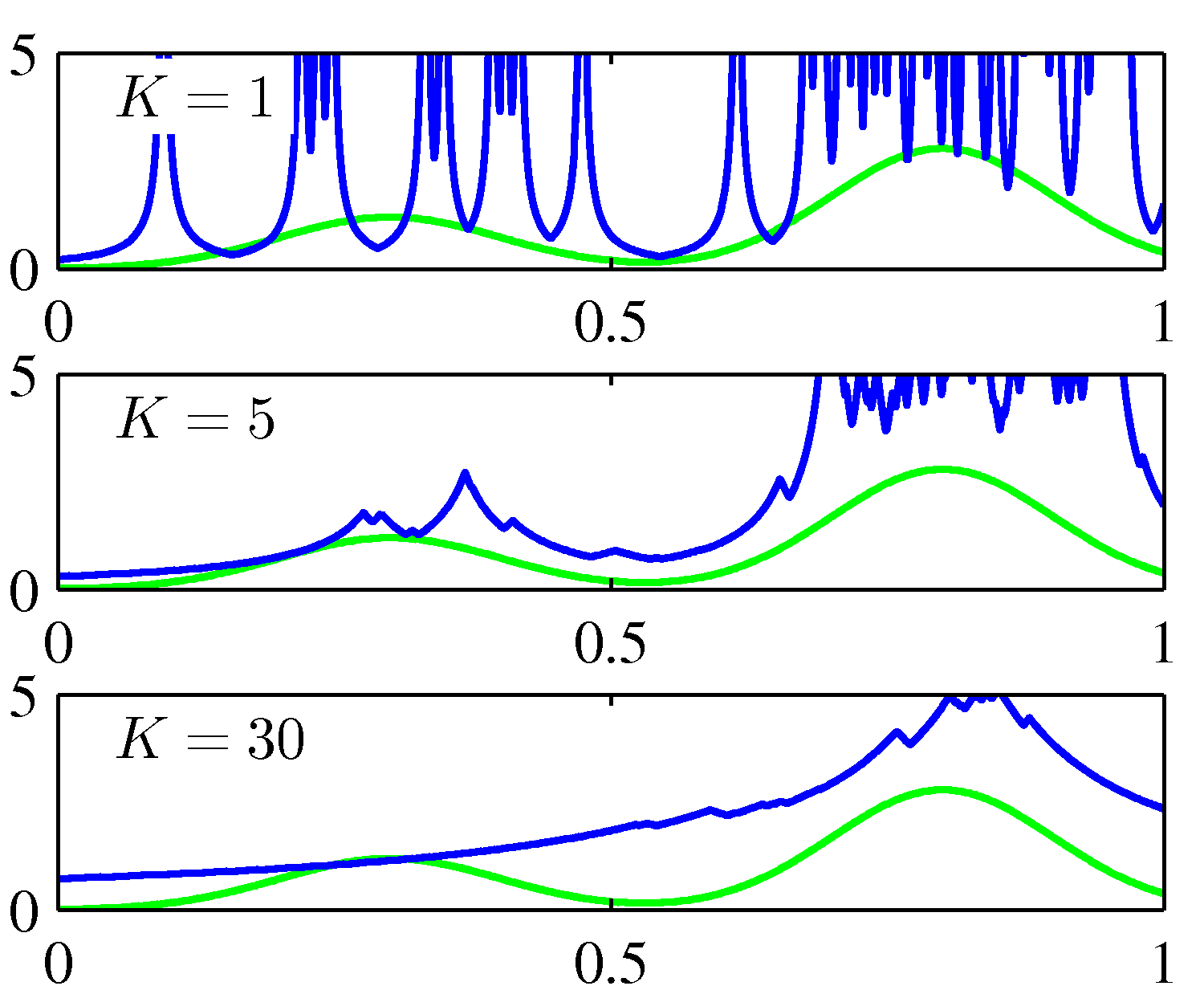
• 별로 어려운 점이 없기 때문에 그림부터 좀 살펴보도록 하자.
  • 커널 방식과 마찬가지로 \(K \) 의 값을 어떻게 설정하느냐에 따라 커널 메소드의 결과와 유사한 결과를 얻는다.
  • 결국 \(K \) 값을 어떻게 선택하느냐에 따라 스무딩 효과가 달라지게 된다.
• 이번 절에서는 이 기법을 이용하여 분류(classification) 문제를 해결하는 과정을 살펴볼 것이다.
• 간단하게 문제 정의부터 하도록 하자.
  • \(N \) : 전체 데이터 샘플 집합의 크기
  • \(C_k \) : 분류시 사용할 클래스 종류
  • \(N_k \) : 특정 클래스 \(C_k \) 에 포함되는 샘플 집합의 크기
  • 이 때 새로운 데이터 \({\bf x} \) 가 주어질 때 이 데이터가 속할 클래스를 판별
• 입력 데이터 \({\bf x} \) 를 중심으로 어떤 클래스에 속하는 데이터인지 상관하지 않고, 샘플 데이터 중 \(K \) 개가 속하는 구를 구한다.
• 이때 구의 부피는 \(V \) 이고, 구 안에서 각 클래스별로 샘플의 갯수를 구한다. (이 때 각 클래스의 샘플 수를 \(K_k \) 라 하자.)

• 특정 조건이 없는 확률 밀도는 다음과 같다.

• 각 클래스에 대한 사전 확률값은 간단하게 빈도값을 이용하자. $p(C_k) = \frac{N_k}{N} \qquad{(2.255)}$

• 이 식을 최종 결합하면 다음과 같은 결과를 얻게 된다.

• 최종 결과가 매우 간단한 형태로 도출된다.
  • 결국 각 클래스에 속할 확률 값들은 \(K_k/K \) 로 얻어지게 되고,
  • 분류를 위해 특정 클래스에 속할 경우를 구하기 위해서는 해당 확률 값이 가장 큰 클래스에 할당하면 된다.
  • 그냥 구 안에서 각 클래스 별로 몇 개의 샘플이 속하는지 세어 보고 가장 많은 클래스를 \({\bf x} \) 의 클래스로 할당하면 된다.

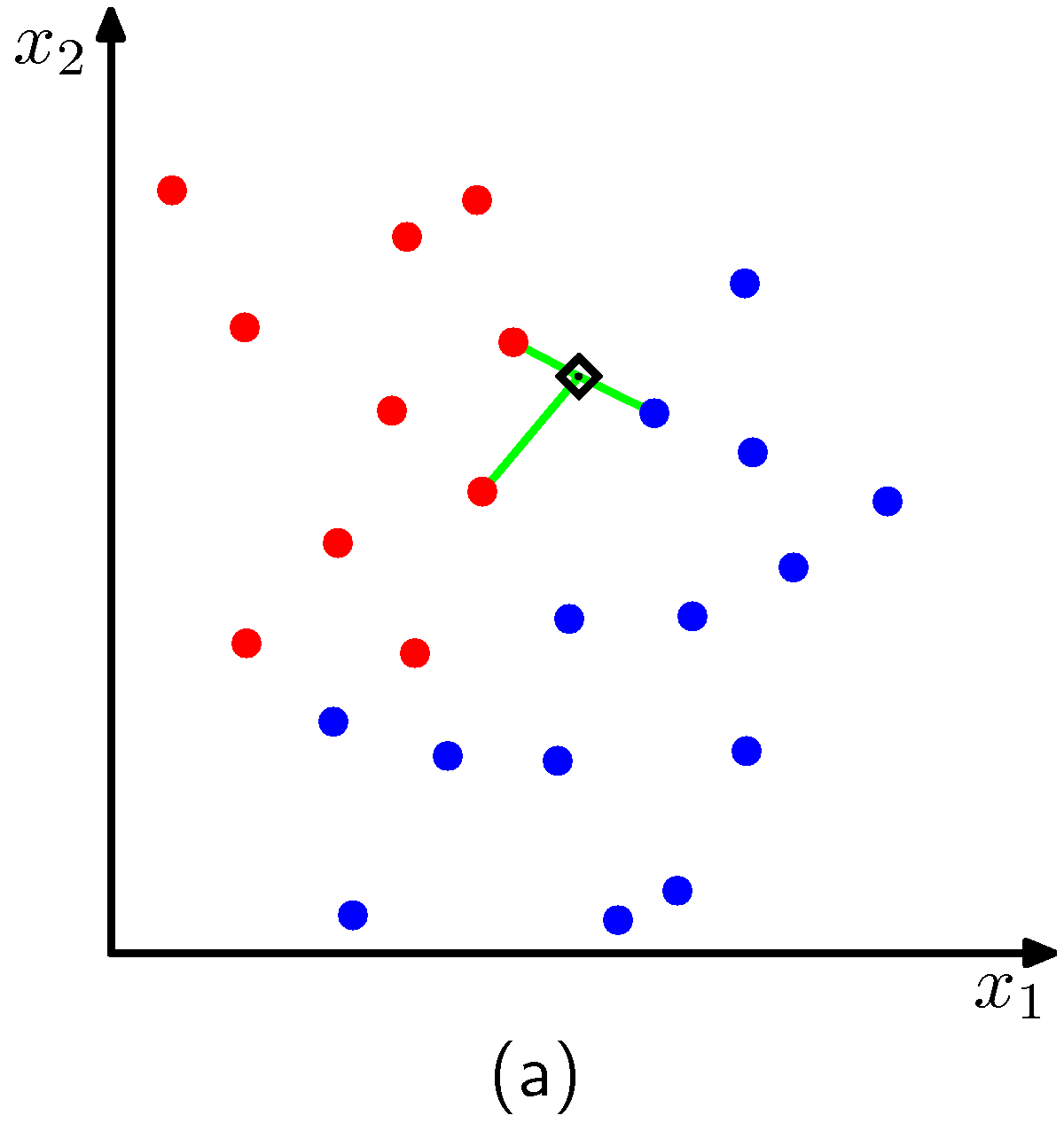
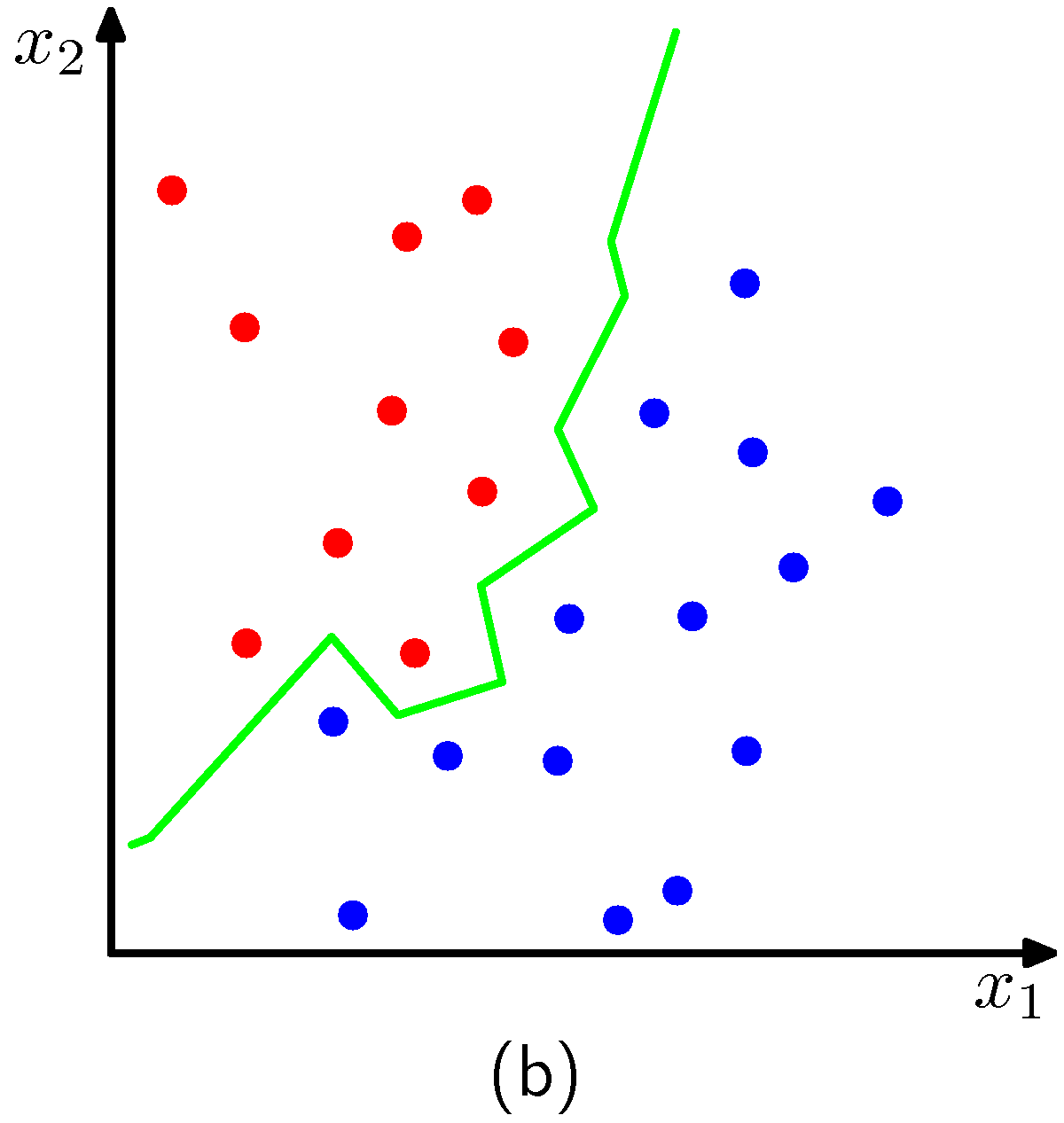
• 우선 그림 (a) 는 임의의 한 점(검은색 다이아몬드 모양) 위치에서 어떤 클래스에 속할지를 결정하게 된다.
• \(K=3 \) 인 경우에는 해당 위치에서는 붉은 색의 클래스로 판별되게 된다.
• 최종적으로 \(K=3 \) 인 경우 판별 영역은 그림 (b)와 같이 되게 된다.

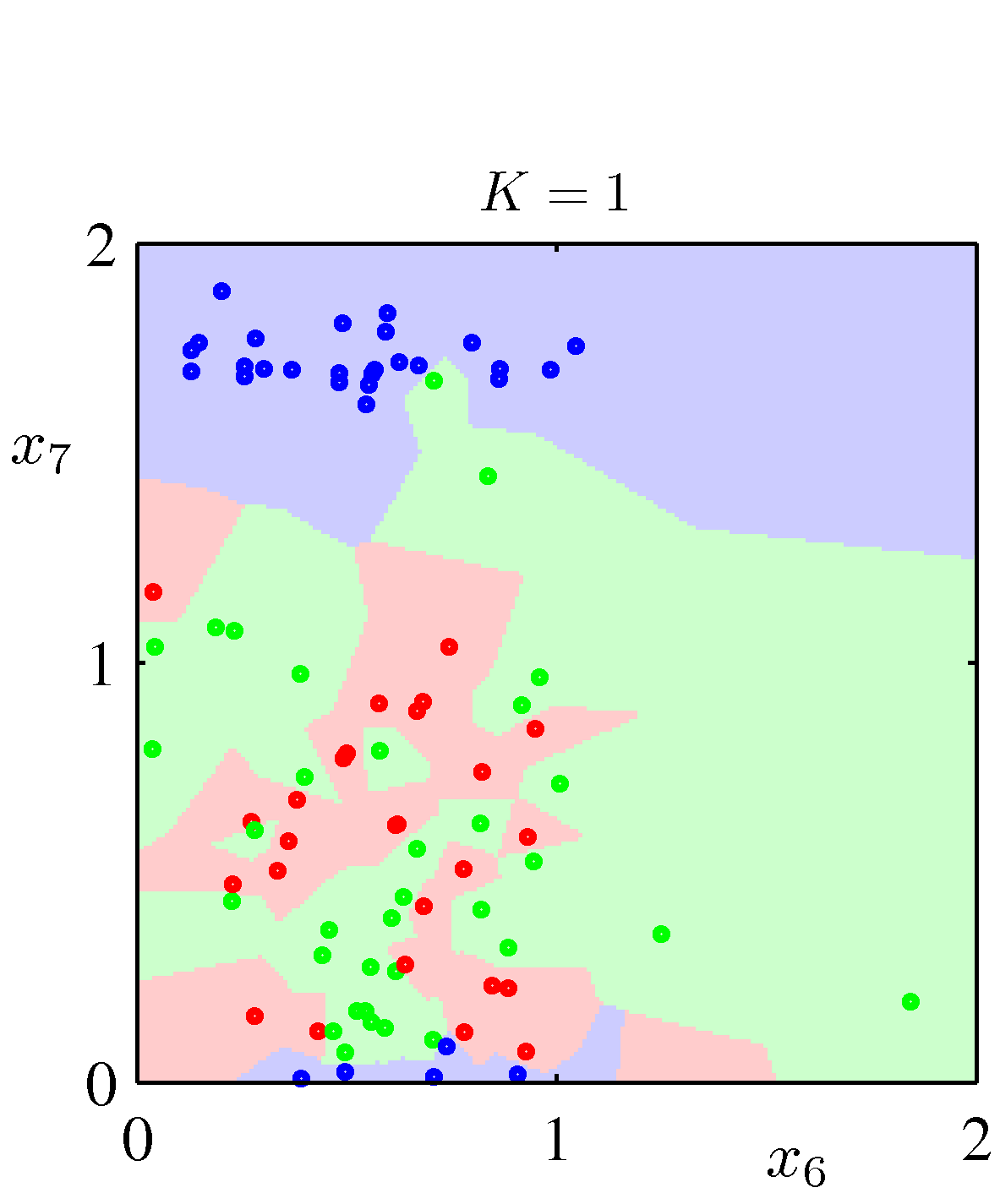
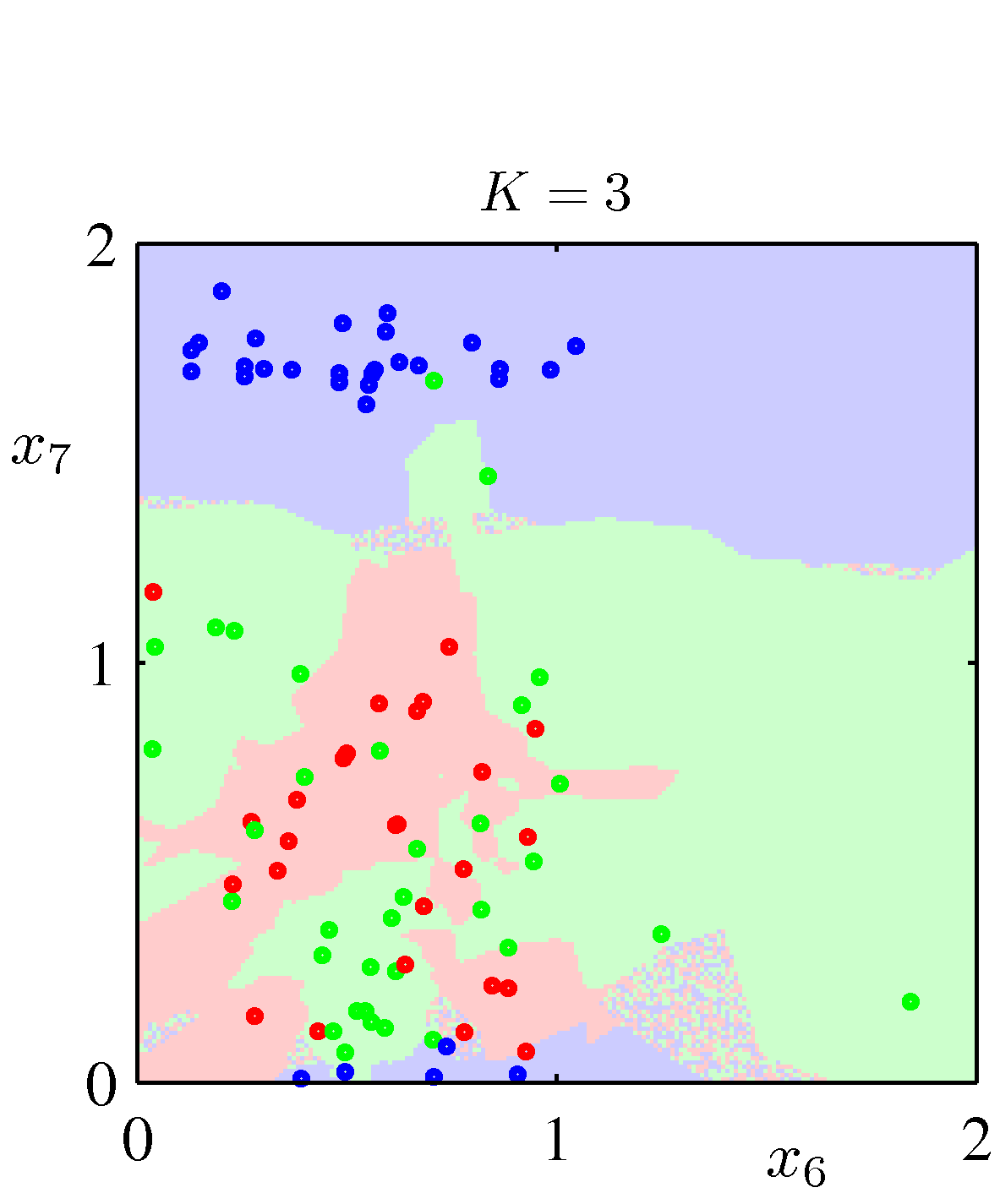
• 이제 마지막으로 \(K \) 값이 달라짐에 따라 판별식이 어떻게 달라지는지 그림으로 살펴보도록 하자.
• \(K=1 \) 인 경우 단순하게 가장 가까운 점에 속한 클래스를 선택하는 형태가 되고,
  • 이 경우에 \(N\rightarrow\infty \) 이면 에러율이 최적의 분류기가 가지는 최소 에러율보다 에러가 두 배 이상 커지지 않음이 증명되어 있다.
• 그냥 \(K \) 값으로 스무딩 정도를 조절할 수 있다는 것만 알고 넘어가도 무리가 없을 듯 하다.

• 마지막으로 지금까지 살펴본 비-파라미터적인 방식들은,
  • 전체 데이터를 메모리에 저장하고 있어야 하는 단점이 존재한다. (물론 보통 데이터를 트리 기반으로 저장함)
  • 학습 데이터가 점점 방대해지는 요즘 추세엔 좀 안 맞는 경향이다.
  • 따라서 좀 더 유연하면서 학습 데이터 크기에 영향을 받지 않는 새로운 방법이 요구된다.
  • 이후 챕터에 이런게 등장할 것이니 걱정하지 않아도 된다. (보통 근사 방식의 기법들)