2. Multinomial Variables

지금까지 살펴보았던 이항 분포는 2개의 가능한 변수 중 하나를 선택하는 문제였다.
이제부는 $ K $ 개의 가능성 중 하나를 선택하는 문제를 다루어 볼 것이다.
문제를 간단하게 하기 위해 $ K $ 차원의 크기를 가지는 입력 변수를 고려해보자.
여기서 하나의 요소를 $ x_k $ 로 정의하고, $ x_k $ 의 값이 1이라면 나머지 값은 모두 0인 상태로 가정한다.
만약 $ K=6 $ 인 상태에서 $ x_3=1 $ 인 경우를 표현하면 다음과 같다.

${\bf x} = (0,0,1,0,0,0)^T \qquad{(2.25)}$

이제 $ \sum_{k=1}^{K}x_k=1 $ 임을 알 수 있다. (1-to-K 모델이므로)
$ x_k=1 $ 일때의 확률을 모수 $ \mu_k $ 를 이용하여 표현하면 $ p(x_k=1)=\mu_k $ 가 된다.
이 식으로 하나의 데이터 $ {\bf x} $ 에 대한 확률 값은 다음과 같이 정의 가능하다.

$p({\bf x}|{\pmb \mu}) = \prod_{k=1}^{K}\mu_k^{x_k} \qquad{(2.26)}$

모수도 벡터가 되으로 $ {\pmb \mu} = (\mu_1, …, \mu_K)^T $ 와 같이 정의된다. ( $ \mu_k\ge0 $, $ \sum_k\mu=1 $)
앞서 설명한 정의들에 의해 다음의 식을 얻게 된다.

$\sum_{\bf x}p({\bf x} | {\pmb \mu})=\sum_{k=1}^{K}\mu_k =1 \qquad{(2.27)}$ $E[{\bf x}|{\pmb \mu}] = \sum_{\bf x}p({\bf x}|{\pmb \mu}){\bf x} = (\mu_1, ..., \mu_K)^T = {\pmb \mu} \qquad{(2.28)}$

이제 모든 관찰값(즉, 샘플)에 대한 확률 값을 고려해보자. (가능도 함수는 이렇게 정의된다.)

$p(D|{\pmb \mu}) = \prod_{n=1}^{N}\prod_{k=1}^{K}\mu_k^{x_{nk}} = \prod_{k=1}^{K}\mu_k^{\sum_n x_{nk}}=\prod_{k=1}^{K}\mu_k^{m_k} \qquad{(2.29)}$

식을 보면 가능도 함수는 $ K $ 개의 종류를 가지는 샘플 $ N $ 개에만 의존한다.

$m_k = \sum_n{x_{nk}} \qquad{(2.30)}$

이를 충분 통계(sufficient statistics)라고 한다.
- 모수 정보를 모두 포함한 식을 충분통계량이라고 한다.
- 이런 경우 모수 대신 이 식을 이용해서 분포를 표현 가능하다. (예를 들어 가능도함수비 등)
가능도 함수(likelihood)를 이용해서 모수를 추정하는 것은 당연한 수순.
여기서는 라그랑지앙 승수를 이용하여 처리한다. (혹, 라그랑지앙 승수를 잘 모르겠다면 별도의 자료를 찾아볼 것)

$\sum_{k=1}^{K}m_k\ln \mu_k + \lambda\left(\sum_{k=1}^{K}\mu_k-1\right) \qquad{(2.31)}$

$ \mu $ 에 대해 미분하고 이 값을 0으로 놓고 전개한다.

$\mu_k = -\frac{m_k}{\lambda} \qquad{(2.32)}$

$ \sum_k\mu_k=1 $ 에 의해 $ \lambda=-N $ 이 성립되므로 최종 식은 다음과 같아진다.

$\mu_k^{ML} = \dfrac{m_k}{N} \qquad{(2.33)}$

이항 분포가 다항 분포에도 그대로 확장되고 있다는 걸 쉽게 이해할 수 있다.
이제 $ m_1,…m_K $ 를 가지는 결합 분포를 고려해보자. 그러면 식은 다음과 같아진다.

$Mult(m_1, m_2, ..., m_K|{\pmb \mu}, N) = \binom{N}{m_1m_2...m_k}\prod_{k=1}^{K}\mu_k^{m_k} \qquad{(2.34)}$

이게 바로 다항분포(multinomial distribution) 이다.
여기서 정규화 계수는 다음과 같다.

$\binom{N}{m_1m_2...m_k} =\dfrac{N!}{m_1!m_2!...m_K!} \qquad{(2.35)}$

참고로 $ m_k $ 는 다음과 같은 제약이 따른다.

$\sum_{k=1}^{K}m_k=N \qquad{(2.36)}$

별로 어려운 내용은 없다. 이항 분포를 $ K $ 개의 그룹으로 확장한 것이다.

2.2.1. 디리슈레 분포 (The Dirichlet distribution)

이제 다항 분포에 어울리는 사전 분포로 디리슈레 분포를 다루어보자.
- 표기가 “디리슈레”가 맞는 것인지는 항상 의문이다.
이항 분포에 대한 공액사전 분포로 베타 분포가 사용되듯, 다항 분포에 대한 공액사전 분포로 디리슈레 분포가 사용된다.
다항 분포의 모수 추정을 위한 모수의 사전 분포로 다음과 같은 형태를 생각하면 된다.

$p({\pmb \mu}|{\pmb \alpha}) \propto \prod_{k=1}^{K}u_k^{a_k-1} \qquad{(2.37)}$

여기서 $ 0 \le \mu_k \le 1 $ 이고 $ \sum_k \mu_k=1 $ 의 성질을 만족한다.
또, $ {\pmb \alpha}=(\alpha_1,…,\alpha_K)^T $ 를 만족한다.
이런 합의 제약으로 인해서 $ {\mu_k} $ 에 대한 분포를 심플렉스(simplex) 라고 불리우는 방식으로 표현 가능하다.
- 심플렉스(simplex)는 $ K-1 $ 개의 차원으로 이루어진 공간에 정보를 표현한다.
- $ K=3 $ 일 때의 심플렉스 샘플은 아래와 같다.

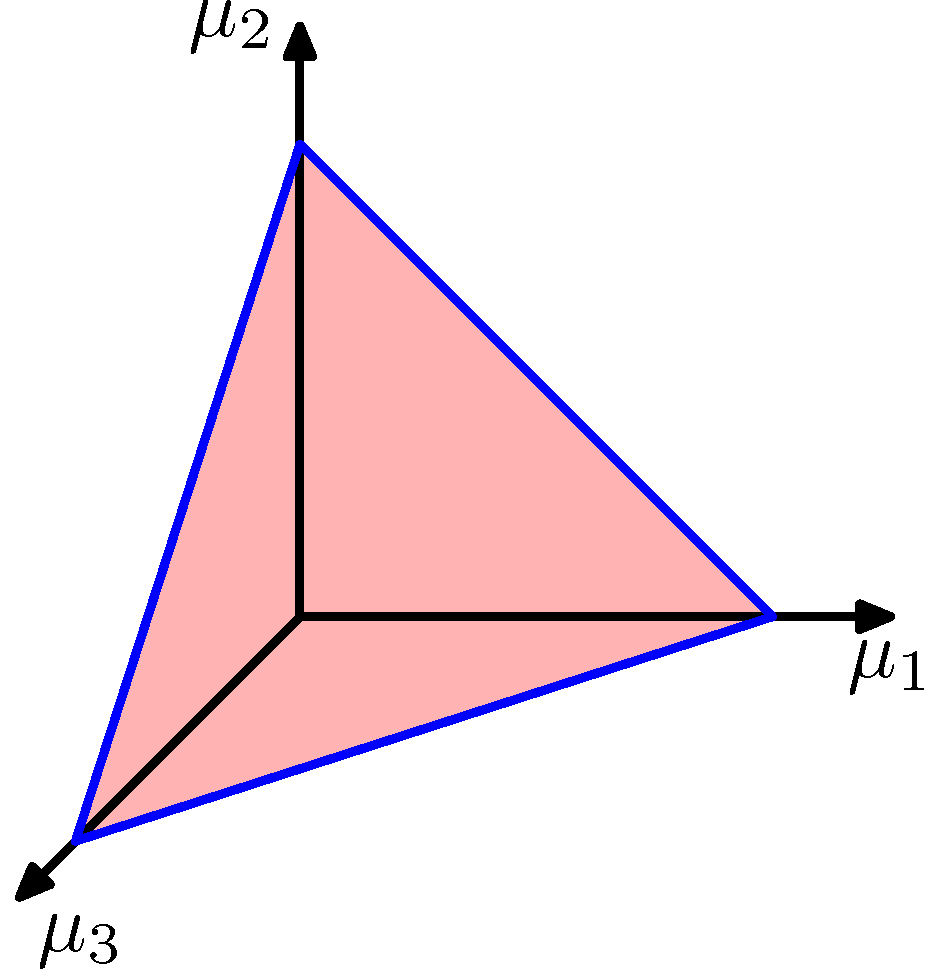
figure2.4

위의 그림을 보면 붉은 색 평면 위 한 점에 $ {\pmb \mu} $ 벡터가 존재해야 한다. (총 합이 고정된 상수이므로)
이 때의 분포의 표현은 다음과 같다.

$Dir({\pmb \mu}|{\pmb \alpha})=\dfrac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)}\prod_{k=1}^{K}\mu_k^{\alpha_k-1} \qquad{(2.38)}$

이를 디리슈레(Dirichlet) 분포라고 한다.
이 때 $ \Gamma(x) $ 는 다음과 같다.

$\Gamma(x)=\int_{0}^{\infty}\mu^{x-1}e^{-u}du$

또 $ \alpha_0 $ 는 다음과 같다.

$\alpha_0=\sum_{k=1}^{K}\alpha_k \qquad{(2.39)}$

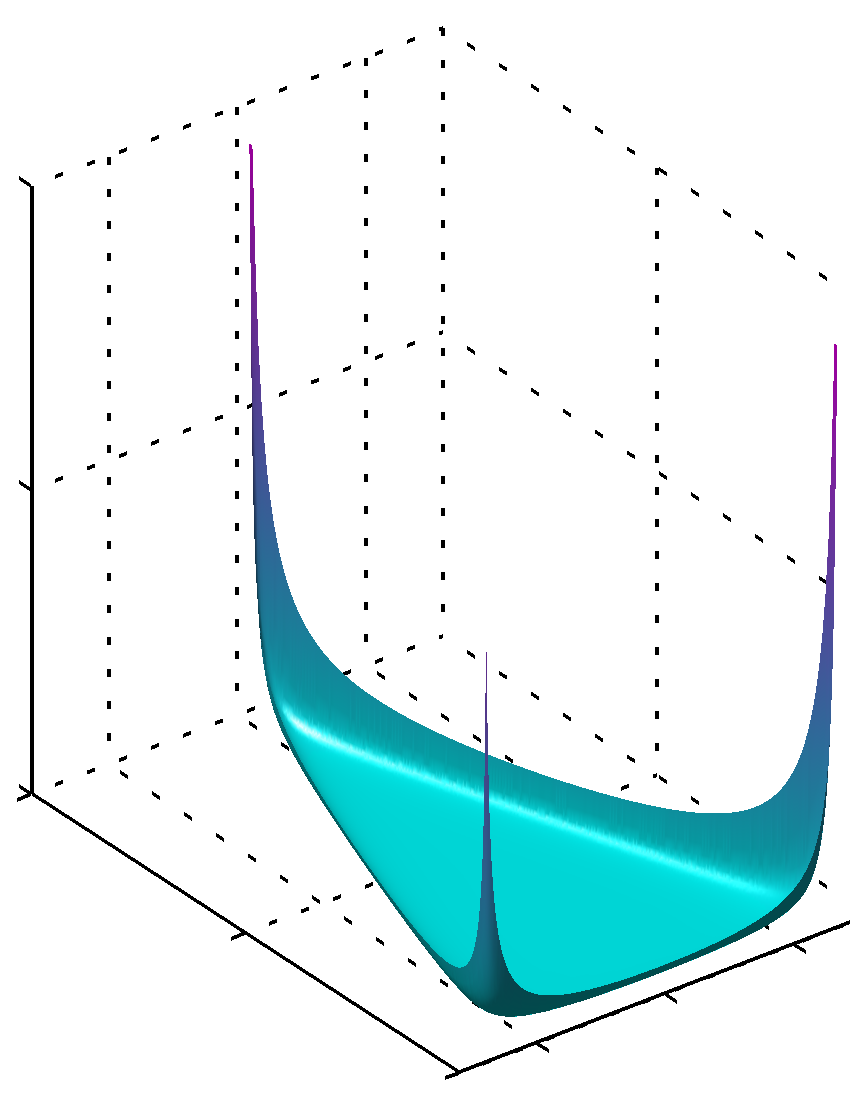
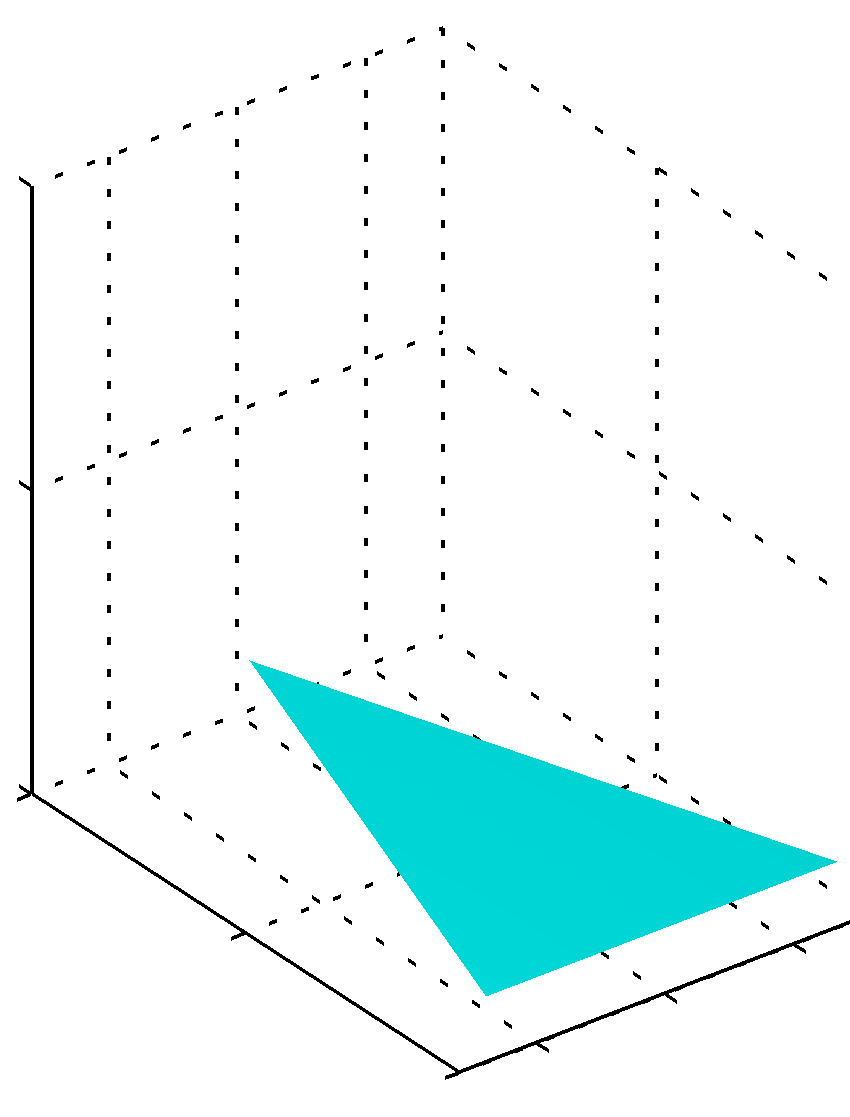
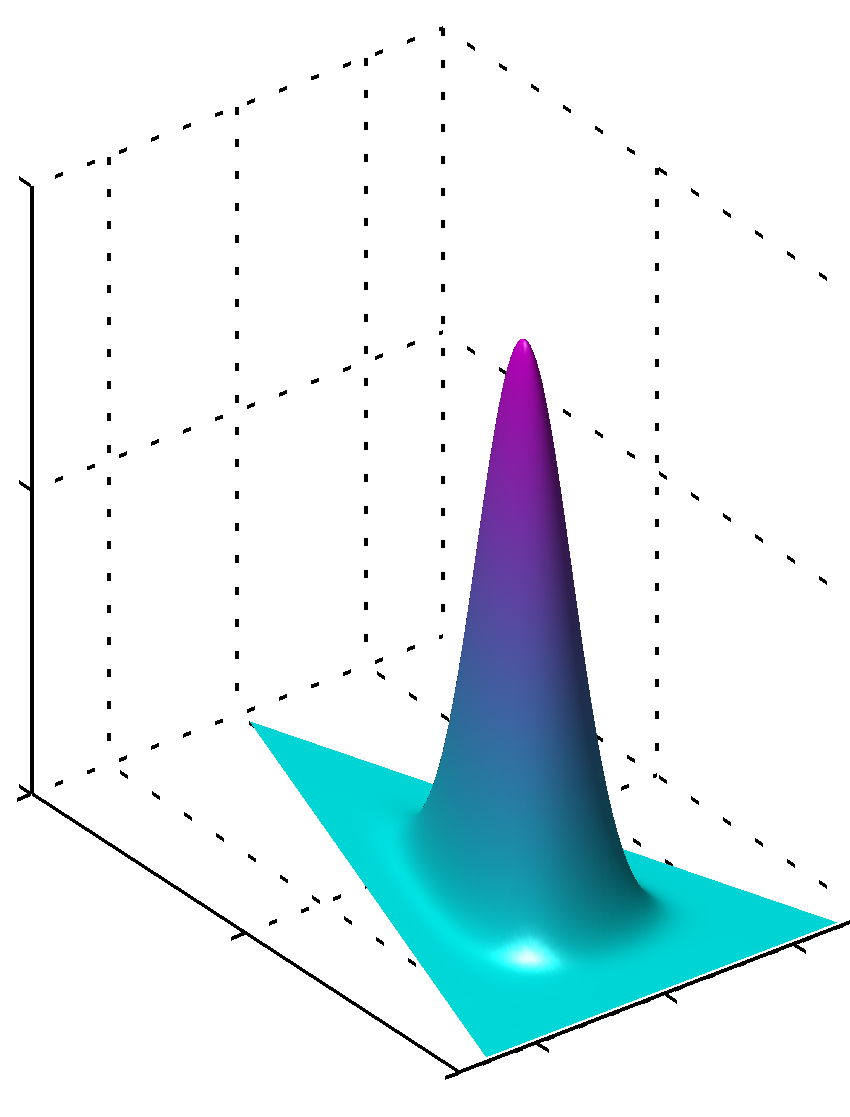
위의 그림은 심플렉스 위에 존재할 수 있는 확률의 값들에 대한 예를 간단하게 표기한 것이다.
왼쪽은 $ {a_k}=0.1 $ , 중간은 $ {a_k}=1 $ , 오른쪽은 $ {a_k}=10 $ 일때 확률 분포를 표기한 것이다.
간단히 살펴봐도 베타 분포를 $ K $ 개의 차원으로 확장한 것이라고 쉽게 확인할 수 있다.
이제 가능도함수(likelihood)를 살펴보도록 하자.

$p({\pmb \mu}|D, {\pmb \alpha}) \propto p(D|{\pmb \mu})p({\pmb \mu}|{\pmb \alpha}) \propto \prod_{k=1}^{K} \mu_k^{\alpha_k+m_k-1} \qquad{(2.40)}$

디리슈레 분포가 공액 사전 분포로 사용되었기 때문에 사후분포(posterior distibution) 또한 디리슈레 분포를 따를 것이라는 걸 알 수 있다.
따라서 이를 계산하면 다음과 같다.

$p({\pmb \mu}|D, {\pmb \alpha}) = Dir({\pmb \mu}|{\pmb \alpha}+{\bf m}) = \dfrac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\prod_{k=1}^{K}\mu_k^{a_k+m_k-1} \qquad{(2.41)}$

식을 봐서도 짐작할 수 있지만 $ K=2 $ 인 경우 베타 분포와 동일해진다.

Chapter. 2

2.2.1. 디리슈레 분포 (The Dirichlet distribution)