3. The Gaussian Distribution [I]

가우시안 분포는 보통 정규분포(standard distribution)로 알려져있다.
왜냐하면 연속 확률 분포 중 가장 널리 알려진 분포이기 때문이다.
단일 변수 $ x $ 에 대해 가우시안 분포는 다음과 같이 기술된다.

$N(x|\mu, \sigma^2) = \dfrac{1}{(2\pi\sigma^2)^{1/2}}\exp\left\{-\frac{1}{2\sigma^2}(x-\mu)^2\right\} \qquad{(2.42)}$

여기서 $ \mu $ 는 평균, $ \sigma^2 $ 은 분산이다.
입력 변수가 $ D $ 차원의 벡터인 경우를 다변량 가우시안 분포라 하며 다음과 같은 식으로 기술한다.

$N({\bf x}|{\pmb \mu}, {\bf \Sigma}) = \dfrac{1}{(2\pi)^{D/2}|{\bf \Sigma}|^{1/2}}\exp\left\{-\frac{1}{2}({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu})\right\} \qquad{(2.43)}$

여기서 $ {\pmb \mu} $ 는 $ D $ 차원의 평균 벡터이고, $ {\bf \Sigma} $ 는 $ D\times D $ 크기를 가지는 공분산 행렬이다.
참고로 $ |{\bf \Sigma}| $ 는 $ {\bf \Sigma} $ 의 행렬식(determinant)가 된다.
앞서도 살펴보았지만 연속형 확률 변수에서 가우시안 분포는 변수의 엔트로피를 최대화하는 분포이다.
가우시안 분포가 가지는 또다른 중요한 성질은 중심 극한 정리(central limit theorem)이다.
중심 극한 정리
- 표본 평균(sample mean)들이 이루는 분포는 샘플 크기가 큰 경우 모집단의 원래 분포와 상관없이 가우시안 분포를 따름.
- 동일한 확률 분포를 따르는 $ N $ 개의 독립 확률 변수의 평균 값은 $ N $ 이 충분이 크다면 가우시안 분포를 따름.
- $ N $ 개의 확률 변수가 어떤 확률 분포를 따르든지 상관없이 $ N $ 이 충분이 크다면 그 합은 가우시안 분포를 따름.
- 문장을 잘 읽어볼 것. 표본의 값을 랜덤 변수로 놓는 것이 아니라 표본의 평균 값을 랜덤 변수로 놓는 것이다.

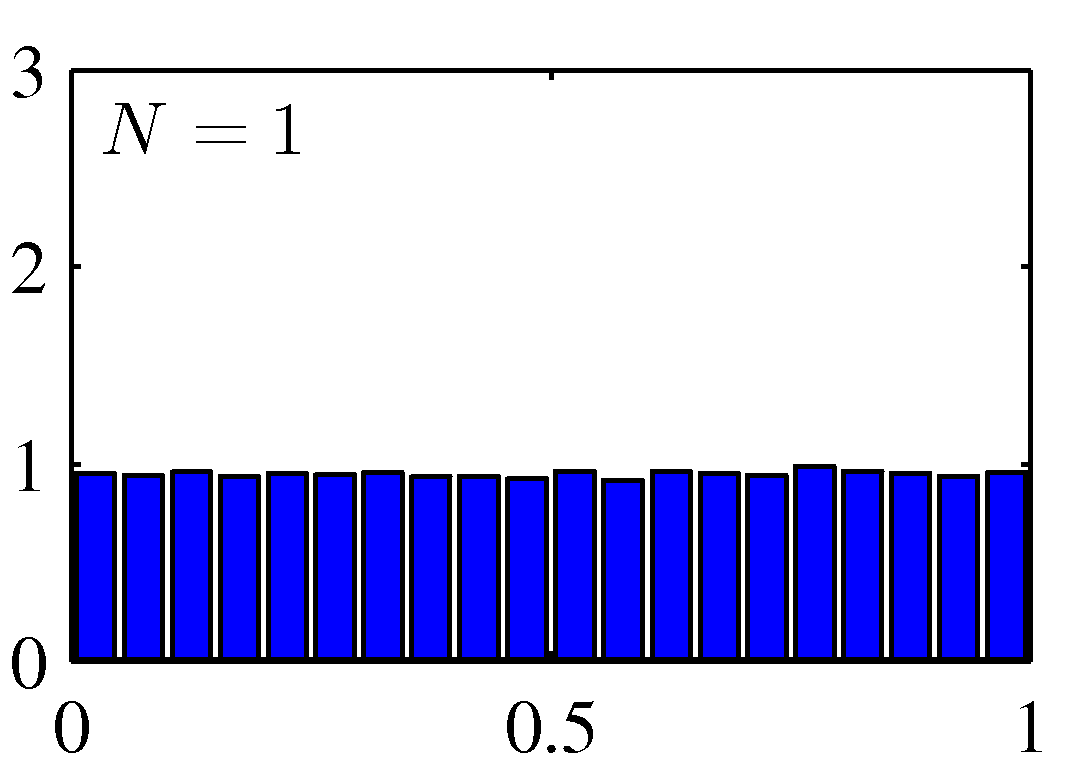
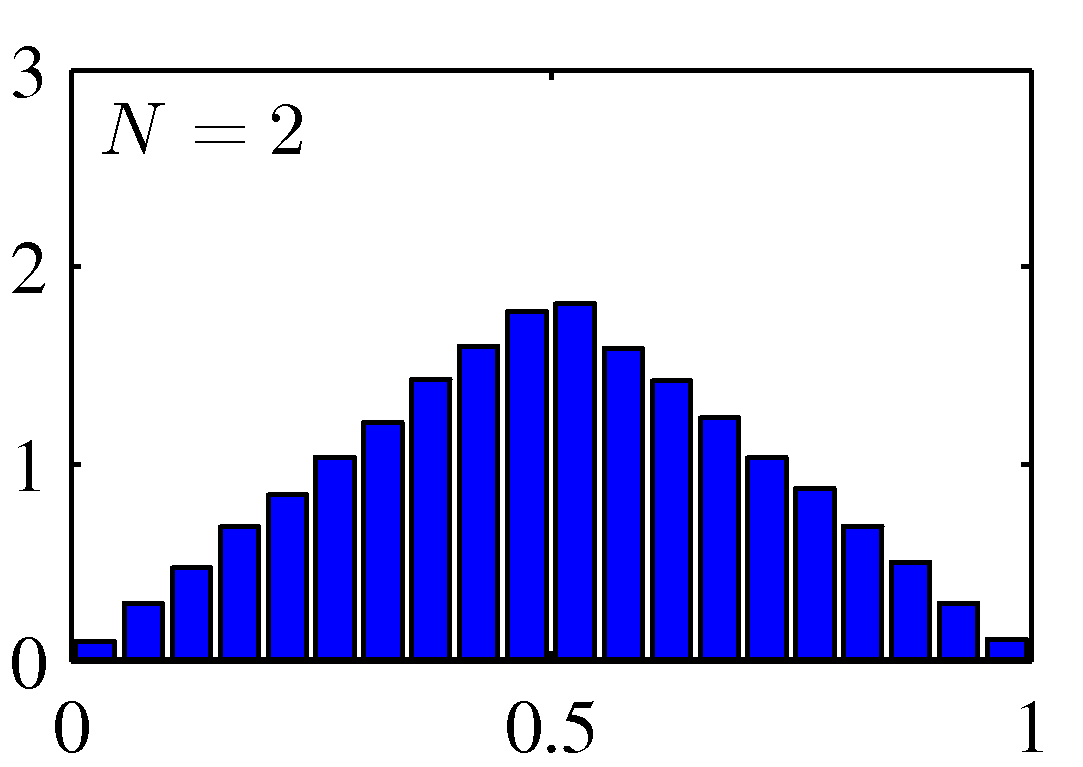
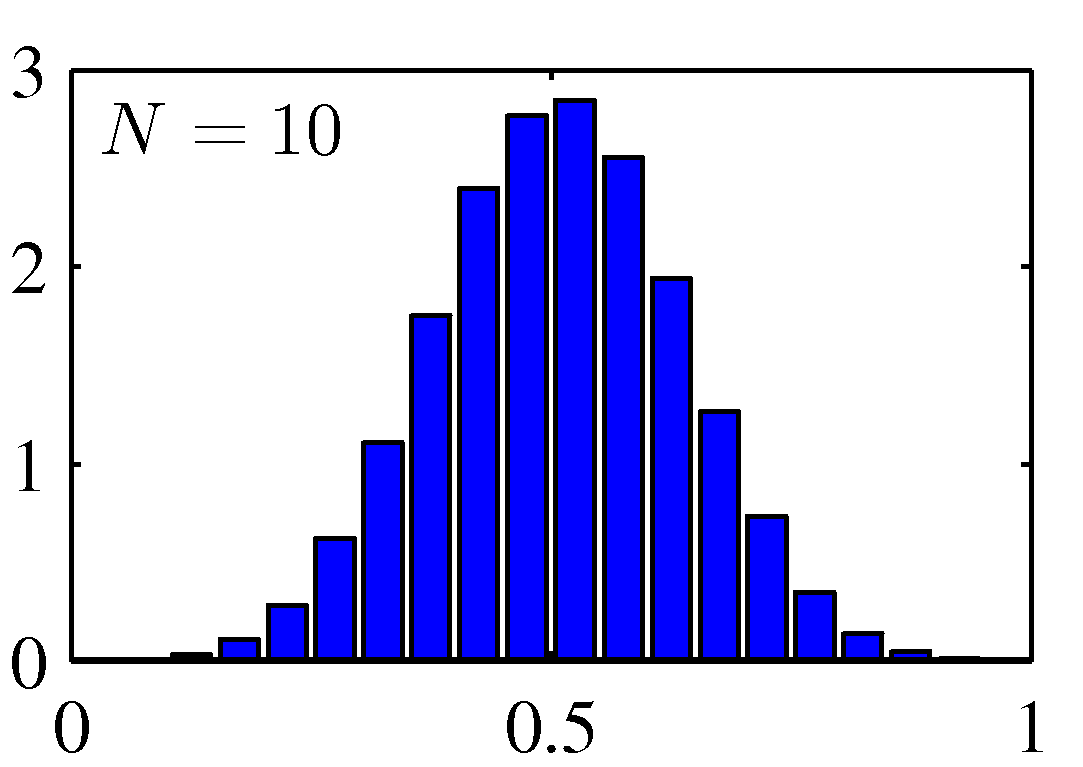
위의 그림은 $ [0,1] $ 범위에서 균등분포(uniform distribution)를 가지는 분포에서 얻은 결과의 평균 값의 히스토그램을 그린 것이다.
$ N $ 이 커질수록 정규 분포의 모양을 만들는 것을 확인할 수 있다.
마찬가지로 이항 분포(binomial distribution) 에서 관찰값 $ N $ 개의 합 $ m $ 이 분포를 이루는데,
- 이 때 관찰값 $ N $ 이 $ N\to\infty $ 가 되면, 이 분포는 결국 가우시안 분포가 된다.
가우시안 분포는 매우 중요하고 분석해볼만한 중요한 요소들을 포함하고 있다.
우리는 이번 장에서 이를 꼼꼼하게 살펴볼 것이다. (1장에 비해 기술적인 내용이 더 나온다.)
이후 장에서 이를 응용한 내용들이 많이 등장하니까 여기서 확실하게 익히고 가야 한다.

가우시안 분포의 기하학적인 형태를 살펴보자.
$ x $ 에 대한 가우시안의 함수적 종속성은 $ exp $ 지수부에 등장하는 이차형식(quadratic)에 있음.
- 이번 기회에 아래 식을 자세히 좀 보도록 하자.
- 이 식이 중요한 이유는, 이후에 자주 등장할 가우시안 분포 수식의 구조 때문이다.
- 이후로 계속 가우시안 분포에 로그를 취하는 형태가 등장하게 될 터인데 지수부의 식이 로그로 인해 자주 사용되게 됨.
  - $ \ln e^{(a)} \equiv a $
- 자주 등장할 터이니 여기서 외우려고 노력 할 필요는 없다.

$\Delta^2 = ({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu}) \qquad{(2.44)}$

여기서 $ \Delta $ 를 $ \mu $ 에서 $ x $ 까지의 마할라노비스 거리(Mahalanobis distance) 라고 부른다
만약 공분산이 단위 행렬(identity matrix) $ I $ 인 경우 이 값은 유클리디안 거리(Euclidean distance)와 동일해진다.
결국 이 값은 평균과의 거리를 측정할 때 분산도를 고려한다는 의미가 된다.
$ x $ 공간에 놓인 가우시안 함수의 표면은 모두 동일한 상수 값을 가지게 되는데, (컨투어를 그리면 함수의 결과값이 동일함)
이는 위의 이차식의 결과 값이 마찬가지로 동일한 상수 값이 되기 때문이다.
무엇보다도 중요한 점은 공분산 행렬 $ {\bf \Sigma} $ 가 대칭행렬(symmetric matrix)이라는 점이다.
이로 인해 지수(exponent) 연산에 의해서 비대칭적인 요소가 모두 사라진다. (종모양의 좌우 대칭 함수가 된다.)
공분산이 대칭행렬이므로 이 행렬에 대해 아주 잘 알려진 고유벡터(eigen-vector) 식을 적용할 수 있다.

${\bf \Sigma}{\bf u}_i = \lambda_i {\bf u}_i \qquad{(2.45)}$

교재에서는 직접적으로 언급하지 않고 있지만, 고유(eigen) 벡터에 관련된 식을 좀 이해하고 있어야 한다.
따라서 다른 교재를 좀 참고하기 바란다. 참고로 간단히만 언급하면,
- 고유식은 오로지 정방 행렬 ( $ N\times N $ ) 에만 적용가능하다.
- $ N\times N $ 크기의 정방 행렬에서는 최대 $ N $ 개의 고유벡터, 고유값을 얻을 수 있다.
- $ N\times N $ 크기의 대칭 행렬의 경우 $ N $ 개의 고유벡터를 얻을 수 있다.
따라서 위의 식은 공분산 행렬의 고유벡터, 고유값을 정의한 식이 된다.
공분산은 대칭 행렬이며 실수 값(real number)만 가진다.
- 굳이 실수임을 강조하는 이유는 허수 값을 가지는 행렬에 대한 고유식도 존재하기 때문이다.
- 그러나 여기서 허수를 고려한 고유벡터까지 고려할 필요는 없다.
공분산 행렬에 대한 모든 고유 벡터는 단위 직교(orthonormal)한다. (공분산 행렬이 대칭 행렬이므로)
- 따라서 위에서 언급한 식 중 $ {\bf u}_i $ 는 단위 직교 벡터를 의미한다.

${\bf u}_i^T{\bf u}_j=I_{ij} \qquad{(2.46)}$ $I_{ij}=\left\{\begin{array}{lr}1 & if\;i=j\\0 & otherwise\end{array}\right. \qquad{(2.47)}$

이제 공분산 행렬을 고유벡터로 표현해보자.
- ‘고유’ 라는 표현에서도 알 수 있듯이 선형 변환 후에도 변하지 않는 성질과 직교 벡터의 성질로 인해,
- 공분산 행렬을 고유 벡터의 선형 결합 형태로 표현 가능하다.

${\bf \Sigma}=\sum_{i=1}^{D}{\lambda_i}{\bf u}_i{\bf u}_i^T \qquad{(2.48)}$

역행렬도 쉽게 구할 수 있다.

${\bf \Sigma}^{-1}=\sum_{i=1}^{D}\dfrac{1}{\lambda_i}{\bf u}_i{\bf u}_i^T \qquad{(2.49)}$

이제 맨 위의 quadratic 식에 이 값을 대입하면 다음과 같은 식이 된다.

$\Delta^2 = \sum_{i=1}^{D}\frac{y_i^2}{\lambda_i} \qquad{(2.50)}$ $y_i={\bf u}_i^T({\bf x}-{\pmb \mu}) \qquad{(2.51)}$

이것을 벡터식으로 확장할 수 있다.

${\bf y} = {\bf U}({\bf x}-{\pmb \mu}) \qquad{(2.52)}$

이제 $ {\bf y} $ 를 어떻게 해석해야 할까?
- 위의 식으로 $ {\bf y} $ 를 $ {\bf x} $ 에 대해 새로운 좌표로 변환한 좌표로 볼 수있다.
- 아마 고등학교 즈음해서 벡터에 대한 변환식을 배웠던 기억이 있을 것이다.
- 결국 이 식은 가우시안 함수의 원점을 $ {\pmb \mu} $ 로 옮기고 고유 벡터를 축으로 회전 변환되는 식이 된다.
- $ {\bf U} $ 는 직교 행렬이고 $ {\bf U}^T{\bf U}=I $, $ {\bf U}{\bf U}^T=I $ 를 만족한다. ( $ I $ 는 단위행렬)
사실 이러한 변환을 주축 변환이라고 한다. 선형대수 교재에 많이 나온다.

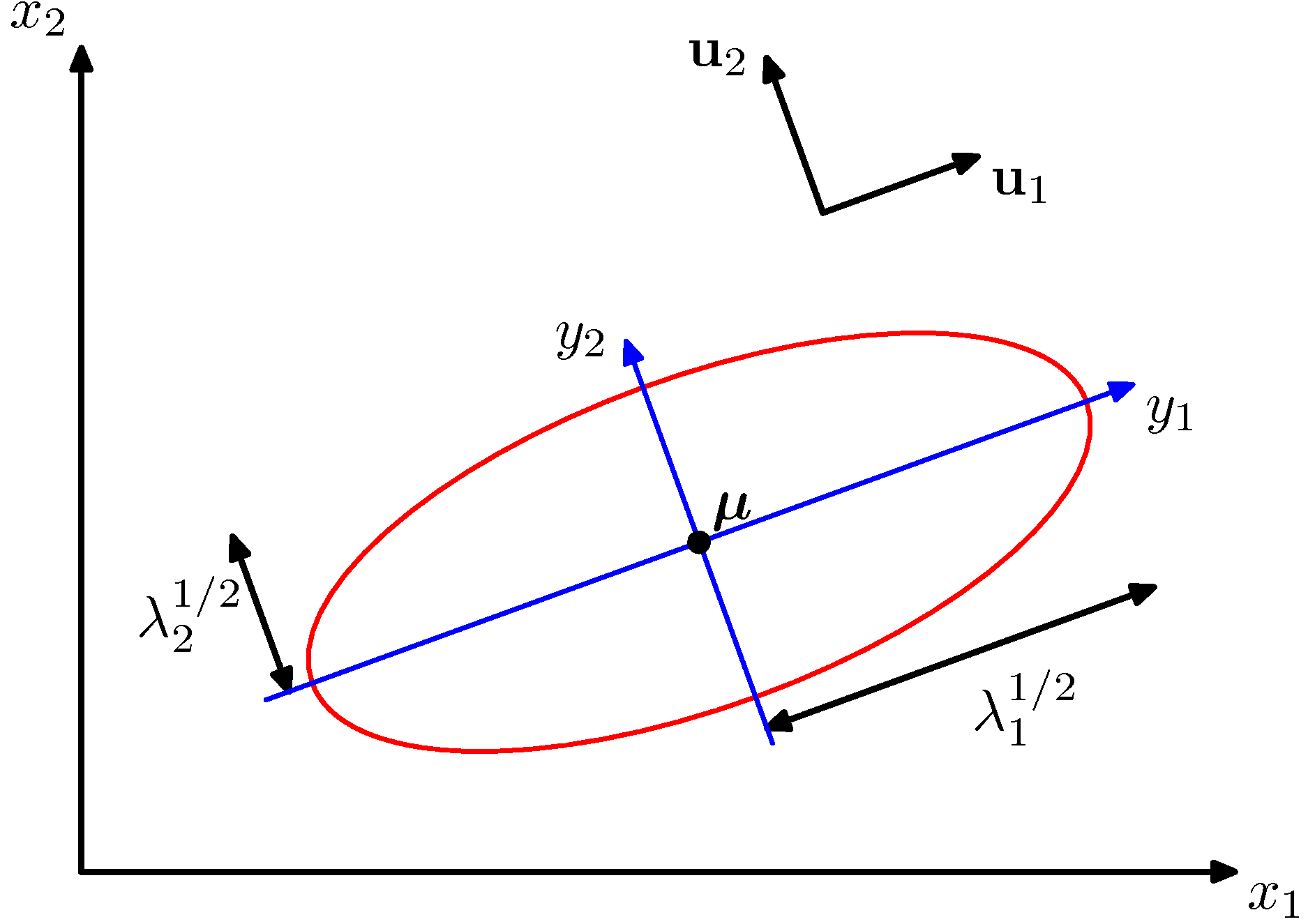
figure2.7

그림 설명
- 그림에서 사용되는 데이터는 2차원 데이터로 $ (x_1, x_2) $ 이다.
- 붉은 선은 타원 표면(surface)으로 동일한 확률 값을 가지는 위치가 된다. (이를 컨투어라고 한다.)
- $ {\bf u} $ 는 고유 벡터로 정의되며 이 축으로 타원이 형성된다.
- 이 때 고유벡터를 축으로 하는 타원에 대한 공분산은 고유값 $ \lambda $ 의 영향을 받는다.
- 그림을 보면 쉽게 이해될 것이다.
그림에서 붉은 선처럼 동일한 상수 확률값을 가지는 위치에서 $ \Delta^2=\sum_D\frac{y_i^2}{\lambda_i} $ 식도 동일한 상수 값을 가지게 된다.
만약 고유값 $ \lambda_i $ 가 모두 양수라면 컨투어는 타원(ellipsoid) 형태가 된다.
- 위의 그림이 이를 잘 나타내고 있다. (즉, 가우시안에서는 고유값이 모두 양수임)
- 이 때에는 타원의 중심이 $ {\pmb \mu} $ 가 되고 고유값 $ \lambda_i^{1/2} $ 스케일로 타원이 형성되게 된다.
가우시안 분포의 경우 이에 대한 정의가 명확한데,
- 공분산에 대한 고유값은 모두 양수여야만 한다. (0보다 모두 커야 한다.)
- 만약 모두 양수가 아닌 경우를 정규화되지 못했다고 하며 이런 경우를 12장에서 좀 다루고 있다. (0이 되는 값)
- 모든 고유값이 양수이면 이런 행렬을 양의 정부호 행렬(positive definite matrix)이라고 한다.
  - 선형 대수에서는 이런 성질을 주요하게 다루고 있는데, 양의 정부호를 만족하는 경우 할 수 있는 것들이 많기 때문이다.
이번 절에서는 여기까지만 들어가도록 하자.
- 이와 관련된 내용은 선형 대수 책에서 더 자세하게 설명하고 있다.
- 다만 여기서는 일반적인 대칭 행렬에 대한 고유식 속성을 공분산에 적용한 것 뿐이다.
- 궁금하신 분들은 선형 대수 책을 좀 더 찾아보도록 하자.

이제 가우시안 분포를 $ {\bf y} $ 좌표로 전환하는 것에 대해 좀 살펴보자.
$ {\bf x} $ 좌표계에서 $ {\bf y} $ 좌표계로 전환하는 것은 야코비안(Jacobian) 행렬 $ {\bf J} $ 를 이용한다.
- 이 식을 야코비안으로 발음할지 쟈코비안으로 발음할지 애매하기는 하다.

$J_{ij}=\dfrac{\partial x_i}{\partial y_i}=U_{ji} \qquad{(2.53)}$

야코비안이 좌표 축 변환을 만들어 낼 때 어떻게 변화하는지 좀 알아야 하는데, 여기서는 간단하게 다음의 성질만을 기술해본다.
- 아주 간단하게만 이야기하자면 공간의 선형 변환시 발생되는 부피의 변화율을확률 식에 반영하자는 것.

$\int_{\bf x} f({\bf x})d{\bf x} = \int_{\bf y} f({\bf y})|{\bf J}|d{\bf y}$

식을 전개하기 앞서 필요한 식들을 좀 정리하자. 이미 앞서서 $ {\bf y} = {\bf U}({\bf x}-{\pmb \mu}) $ 는 확인을 했다.

${\vert}{\bf J}{\vert}^2 = {\vert}{\bf U}^T{\vert}^2 = {\vert}{\bf U}^T{\vert}\;{\vert}{\bf U}{\vert} = {\vert}{\bf U}^T{\bf U}{\vert} = {\vert}{\bf I}{\vert} = 1 \qquad{(2.54)}$

$ U $ 는 직교 행렬이므로 식을 전개하면 결국 $ |J|=1 $ 을 얻게 된다.
이제 $ \left|\Sigma\right| $ 값을 구하면,

$\left|\Sigma\right|^{\frac{1}{2}}=\prod_{j=1}^{D}\lambda_j^{\frac{1}{2}} \qquad{(2.55)}$

이제 식을 $ x $ 축에서 $ y $ 축으로 전환하여 본다. $ {\bf y} = {\bf U}({\bf x}-{\pmb \mu}) $ 을 대입하고 기타 식들을 추가하면,

$p({\bf y}) = p(x)|{\bf J}| = \prod_{j=1}^{D}\dfrac{1}{(2\pi\lambda_j)^{1/2}}\exp\left\{-\dfrac{y_j^2}{2\lambda_j}\right\} \qquad{(2.56)}$

식을 잘 살펴보면 서로 독립적인 $ D $ 개의 정규 분포의 확률 값이 단순 곱으로 이루어져 있다는 것을 알 수 있다.
고유 벡터를 이용해서 축을 변환시켜 얻은 식은 결국 차원간 서로 독립적인 정규 분포를 만들어낸다.
이 식을 적분해보자.

$\int p({\bf y})d{\bf y} = \prod_{j=1}^{D} \int_{-\infty}^{\infty}\dfrac{1}{(2\pi\lambda_j)^{1/2}}\exp \left\{-\dfrac{y_j^2}{2\lambda_j}\right\}dy_i=1 \qquad{(2.57)}$

역시나 확률 값이므로 각각의 차원에 대해 전구간 적분하면 크기가 1이고, 이를 $ D $ 차원만큼 곱해도 여전히 결과는 1이다.
- 이건 확률식이라 당연하다.
- 실제 얻어진 결과는 위의 그림에서 $ {\bf y} $ 축을 대상으로 회전 변환한 식이라 상상해보자.
이제 가우시안 분포의 적률(moment)을 좀 살펴보도록 하자.
- 참고로 적률(moment)은 고전 통계학에서 사용되었던 파라미터이다.
$ {\bf x} $ 축에 대해 평균값을 살펴볼 예정인데 우선 식 전개를 편하게 하기 위해 $ {\bf z} = ({\bf x}-{\pmb \mu}) $ 를 놓고 식을 전개한다.

$E[{\bf x}] = \dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\int\exp\left\{-\frac{1}{2}({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu})\right\}{\bf x}d{\bf x}\\ = \dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\int\exp\left\{-\frac{1}{2}({\bf z})^T{\bf \Sigma}^{-1}({\bf z})\right\}({\bf z}+{\pmb \mu})d{\bf z} \qquad{(2.58)}$

위의 식은 $ {\bf z} $ 에 의해 좌우 대칭인 함수가 만들어진다.
여기에 $ ({\bf z}+{\pmb \mu}) $ 식이 추가되어 있으므로 $ {\pmb \mu} $ 만큼 평행이동한 함수이다.
따라서 중심이 $ {\pmb \mu} $ 이고 좌우 대칭인 정규 함수가 만들어진다. 따라서 평균은 다음과 같다.

$E[{\bf x}]={\pmb \mu} \qquad{(2.59)}$

이제 2차 적률(second order moments)에 대해 살펴보자.

$E[{\bf x}{\bf x}^T]=\dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\int\exp\left\{-\frac{1}{2}({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu})\right\}{\bf x}{\bf x}^Td{\bf x}\\ = \dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\int\exp\left\{-\frac{1}{2}({\bf z})^T{\bf \Sigma}^{-1}({\bf z})\right\}({\bf z}+{\pmb \mu})({\bf z}+{\pmb \mu})^Td{\bf z}$

여기서 $ ({\bf z}+{\pmb \mu})({\bf z}+{\pmb \mu})^T $ 를 전개할 수 있다.
이를 전개한 수식에서 $ {\pmb \mu}{\bf z}^T $ 와 $ {\bf z}{\pmb \mu}^T $ 는 서로 대칭 관계이므로 제거된다.
$ {\bf u}{\bf u}^T $ 는 수식에서 상수의 역할이므로 적분 바깥 쪽으로 나오게 된다.
결국 우리가 집중해야 할 요소는 $ {\bf z}{\bf z}^T $ 이다.
참고로 $ {\bf z} $ 는 다음과 같이 고유벡터로 표현 가능하다. ${\bf z}=\sum_{j=1}^{D}y_j{\bf u}_j \qquad{(2.60)}$
여기서 $ y_j={\bf u}_j^T{\bf z} $ 이다.
따라서 식을 다음과 같이 전개 가능하다.

$\dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\int\exp\left\{-\frac{1}{2}({\bf z})^T{\bf \Sigma}^{-1}({\bf z})\right\}{\bf z}{\bf z}^Td{\bf z}$ $=\dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}{\bf u}_i{\bf u}_j^T\int \exp \left\{-\sum_{k=1}^{D}\frac{y_k^2}{2\lambda_k}\right\}y_iy_jd{\bf y}\\ =\sum_{i=1}^{D}{\bf u}_i{\bf u}_j^T\lambda_i=\Sigma \qquad{(2.61)}$

원 식에 대입하면 다음과 같은 결과를 얻는다.

$E[{\bf x}{\bf x}^T]={\pmb \mu}{\pmb \mu}^T + \Sigma \qquad{(2.62)}$

뭐, 원래 알고 있던 2차 적률 값이다. (평균의 제곱과 분산의 합)
이제 공분산(covariance) 값도 한번 구해보자.
$ E[{\bf x}]={\pmb \mu} $ 이므로 어차피 동일한 결과를 얻게 된다.

$cov[{\bf x}]=E[({\bf x}-E[{\bf x}])({\bf x}-E[{\bf x}])^T] \qquad{(2.63)}$ $cov[{\bf x}]=\Sigma \qquad{(2.64)}$

가우시안 모델은 정말 널리 사용되는 모델이지만 몇 가지 제약들을 가지고 있다.
제약(1) : 모수(parameter)의 개수
- $ D $ 개의 차원을 가진 데이터에서 총 $ D(D+3)/2 $ 개의 독립적인 파라미터를 가지게 된다.
  - $ \mu $ 파라미터 $ D $ 개, 공분산은 $ D(D+1)/2 $ 개를 가지게 된다. (공분산은 대칭 행렬임)
- 따라서 $ D $ 가 증가하게 되면 차수에 대해 제곱에 비례하여 모수의 개수가 증가하게 된다.
- 이런 경우 여러가지 계산이 어려워지고 공분산의 역행렬 등을 구하기가 어려워 진다.
- 가능한 대안점들
  - 공분산을 대각행렬(diagonal matrix)로만 제한한다.
    - $ \Sigma=diag(\sigma^2) $ 형태로만 사용함.
    - 이런 경우 총 $ 2D $ 개의 독립적인 파라미터를 가지게 된다.
    - 컨투어는 각 축들에 평행한 타원으로만 주어지게 된다.
  - 공분산을 단위행렬(I)에 비례하도록 제한
    - $ \Sigma=\sigma^2\cdot I $ 형태로만 사용함.
    - 이런 경우 총 $ D+1 $ 개의 독립적인 파라미터를 가지게 된다.
    - 이런 형태의 공분산을 등방성 공분산(isotropic covariance)이라고 부름
    - 밀도가 구(concentric circle)의 형태를 취하게 된다.

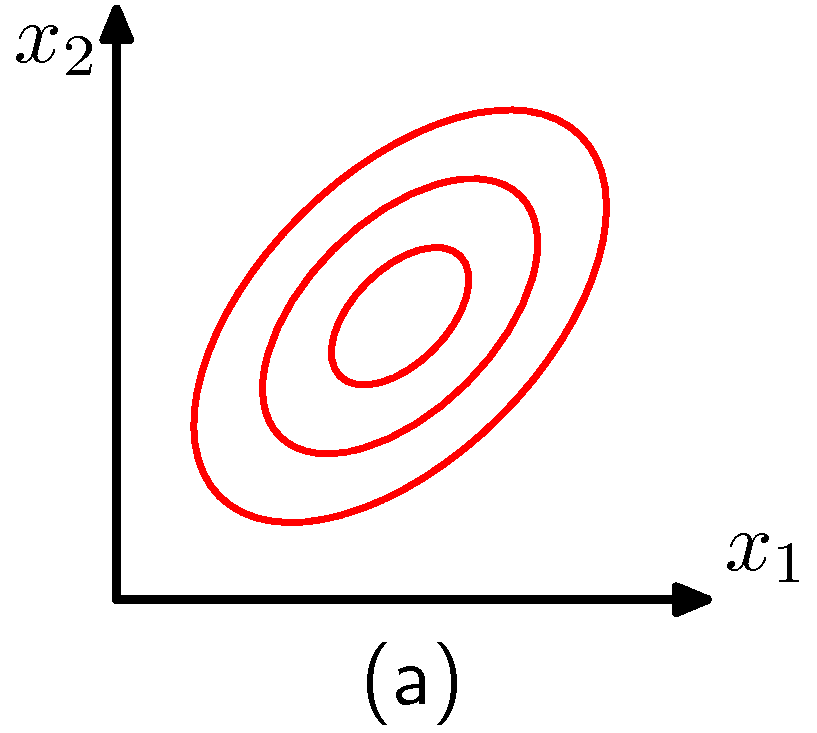
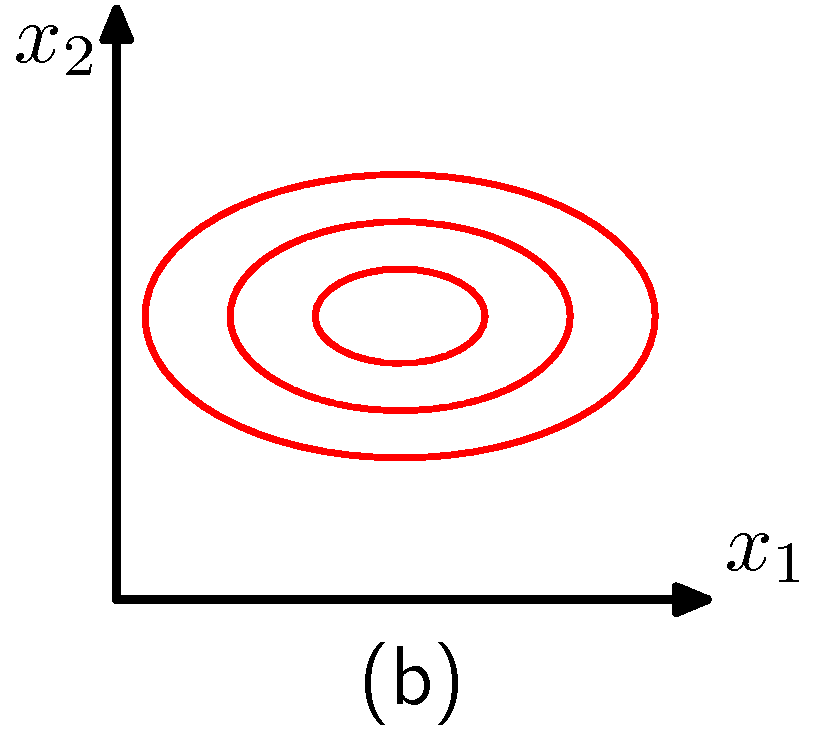
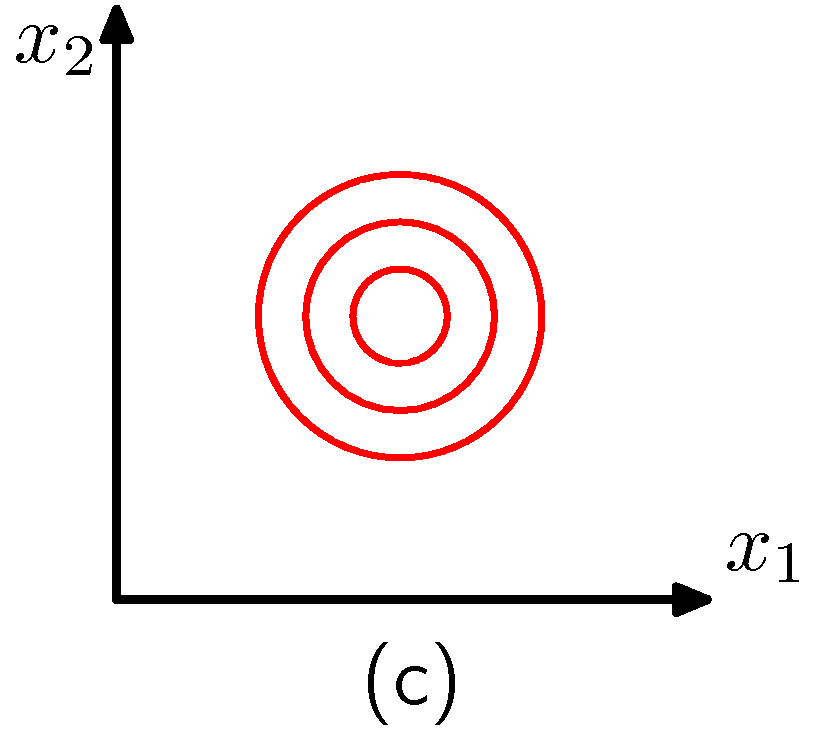
(a) 는 일반적인 2차원 가우시안 분포
(b) 는 공분산이 대각 행렬인 2차원 가우시안 분포
(c) 는 공분산이 등방성 공분산인 2 차원 가우시안 분포
모수 개수의 자유도를 제한하는 접근 형태는 공분산을 빠르게 계산할 수 있기 때문에 좋은 성능을 가짐
하지만 확률 밀도의 형태를 제한하기 때문에 데이터 사이의 연관 관계를 파악할 수 있는 능력을 제한하게 된다.
제약(2) : 분포의 모양이 단봉(unimodal)의 형태만 올 수 있음
- 봉우리가 하나만 생기는 형태의 분포만을 근사할 수 있음.
- 따라서 다봉(multimodal) 형태를 취하는 확률 분포를 근사할 수 없다.
- 가능한 대안점들
  - 이후에 살펴볼 Latent, Hidden, Un-observed 변수들을 사용해서 이런 문제를 해결할 수 있다. (이후에 등장할 것임)
  - 가우시안 분포 여러 개를 혼합(mixture)하여 만드는 모델도 이후에 언급할 것이다.
계층 모델(hierarchical model)을 이용하여 좀 더 좋음 모델을 제시할 수 있다. 예를 들어,
- MRF (Markov Random Field) :
  - 이미지 처리를 위한 확률 모델로 많이 사용됨
  - 픽셀의 공간적 구성을 반영한 구조를 도입하여 쉽게 랜더링할 수 있는 장점이 있다.
- Linear Dynmaic System
  - 시계열 데이터 모델링
  - 매우 큰 관측 모델과 잠재 변수(latent variable)의 사용
8장에서 이와 관련된 내용을 좀 다룰 것이다.

2.3.1. 조건부 가우시안 분포 (Conditional Gaussian distributions)

다차원 가우시안 확률 분포의 중요한 특징을 살펴보자.
스포일러를 조금 하자면,
- 두개의 확률 변수의 결합 확률 분포가 가우시안이면, 조건부 확률 분포도 가우시안 분포가 된다.
- 이 때 두 개의 주변(marginal) 확률 분포도 가우시안 분포가 된다.
조건부 분포의 경우를 먼저 살펴보자.
- 즉, 가우시안 분포를 따르는 두 개의 변수에 대해 조건부 분포가 어떤 분포를 따르게 되는지를 증명하여 볼 것이다.
$ D $ 차원을 가진 어떤 입력 벡터 $ {\bf x} $ 가 있고, 이 데이터는 $ N({\bf x}\;|\; {\pmb \mu}, \Sigma) $ 분포를 따른다고 하자.
이 때 입력 벡터 $ {\bf x} $ 를 두개의 집합으로 나누면 다음과 같이 표기 가능하다.

${\bf x}=\dbinom{ {\bf x}_a }{ {\bf x}_b} \qquad{(2.65) }$

이러면 $ a $ 는 $ M $ 개의 차원을 가지게 되고, $ b $ 는 $ D-M $ 개의 차원을 가지게 된다.
이 때 대응되는 평균은 다음과 같다.

$\mu=\dbinom{ {\pmb \mu}_a }{ {\pmb \mu}_b } \qquad{(2.66)}$

공분산도 표시해보자.

$\Sigma=\left(\begin{array}{cc}\Sigma_{aa} & \Sigma_{ab}\\ \Sigma_{ba} & \Sigma_{bb}\end{array}\right) \qquad{(2.67)}$

위의 식이 처음에는 이해가 안될수도 있는데(나만 그런건가?), 잘 생각해보면 잘 들어 맞는다.
공분산은 대칭행렬이므로 $ \Sigma^T=\Sigma $ 임을 잊지 말자. 따라서 $ \Sigma_{ba}=\Sigma_{ab}^T $ 이다.
많은 경우 공분산을 그대로 사용하기 보다 공분산의 역행렬을 사용하기도 한다.
- 수식 전개를 할 때 훨씬 편리하기 때문
- 따라서 여기서도 간단하게 공분한의 역행렬, 즉 정확도 행렬(precision matrix)을 정의하도록 한다.

$\Lambda=\Sigma^{-1} \qquad{(2.68)}$

이제 공분산 행렬의 관계식을 정확도 행렬을 통해 다시 정리해보자.

$\Lambda = \left(\begin{array}{cc}\Lambda_{aa} & \Lambda_{ab}\\ \Lambda_{ba} & \Lambda_{bb}\end{array}\right) \qquad{(2.69)}$

마찬가지로 $ \Lambda_{ab}^T=\Lambda_{ba} $ 가 성립한다.
단, $ \Lambda_{aa} $ 가 단순하게 $ \Sigma_{aa} $ 의 역행렬을 구하면 얻어지는 것은 아니다.
- 공분산의 부분 행렬의 역행렬이 부분 행렬의 정확도 행렬이라고는 할 수 없음. 혼동하지 말것.
우리가 찾고자하는 식은 $ p({\bf x}_a | {\bf x}_b) $ 에 대한 확률 분포이다.
여기서 현재의 결합 확률 분포는 $ p({\bf x})=p({\bf x}_a, {\bf x}_b) $ 로 나타낼 수 있다.
- 만약 여기서 $ {\bf x}_b $ 가 고정된 관찰값이라고 가정하면 이 때의 $ {\bf x}_a $ 에 대한 확률 분포를 예측해볼 수 있다.
  - 조건부 분포를 구하기 위해서는 당연한 가정이다.
- 좀 더 효율적으로 계산 결과를 얻어내기 위해 가우시안 분포에서 지수의 이차형식(quadratic) 부분을 살펴보도록 한다.
- 앞서 언급했던 아래 식을 의미한다.

$\Delta^2 = ({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu})$

식을 전개해보자.

$-\dfrac{1}{2}({\bf x}-{\pmb \mu})^T\Sigma^{-1}({\bf x}-{\pmb \mu})=\\ -\dfrac{1}{2}({\bf x}_a-{\pmb \mu}_a)^T\Lambda_{aa}({\bf x}_a-{\pmb \mu}_a) - \dfrac{1}{2}({\bf x}_a-{\pmb \mu}_a)^T\Lambda_{ab}({\bf x}_b-{\pmb \mu}_b)\\ -\dfrac{1}{2}({\bf x}_b-{\pmb \mu}_b)^T\Lambda_{ba}({\bf x}_a-{\pmb \mu}_a) - \dfrac{1}{2}({\bf x}_b-{\pmb \mu}_b)^T\Lambda_{bb}({\bf x}_b-{\pmb \mu}_b) \qquad{(2.70)}$

앞서 $ {\bf x}_b $ 는 특정한 값으로 고정되어 있다고 생각한다고 이야기 했다.
따라서 위의 식은 그냥 $ {\bf x}_a $ 에 대한 식으로 고려할 수 있는데 마찬가지로 이차형식(quadratic)이 된다.
이 식을 통해 결국 $ p({\bf x}_a|{\bf x}_b) $ 는 가우시안 분포를 따르게 될 것임을 짐작할 수 있다.
- 일반적인 가우시안 분포가 $ \exp(\cdot) $ 의 지수부에 이차형식(quadratic)의 식을 가지고 있으며, 별도의 상수부는 $ \exp(\cdot) $ 외부로 나올 수 있다.
- 따라서 위의 식은 다시 정리를 해봤자 가우시안 분포의 형태가 나오게 될 것이다.
실제 이것이 가우시안 분포를 따른다고 하면 평균과 공분산을 구할 수 있어야 할 것이다.
- 이걸 한번 구해 보도록 하자.
좀 더 직관적으로 문제를 해결하기 위해서 일반적인 가우시안 분포에서의 이차형식(quadratic) 영역의 구조를 좀 살펴보자.
- 혹시나 해서 적어놓는데 이차형식(quadratic)의 정의를 잘 모르겠으면 선형 대수를 참고하도록 하자.

$-\dfrac{1}{2}({\bf x}-{\pmb \mu})^T\Sigma^{-1}({\bf x}-{\pmb \mu})=-\dfrac{1}{2}{\bf x}^T\Sigma^{-1}{\bf x} + {\bf x}^T\Sigma^{-1}{\pmb \mu}+const \qquad{(2.71)}$

위와 같은 전개 방식을 completing the square 라고 부른다.
- 가우시안 분포와 관련된 일반적인 작업 중 하나이다.
- $ \exp(\cdot) $ 내의 이차형식(quadratic)을 이용해서 평균(mean)과 공분산(covariance)을 구할 수 있다.
전개 식을 살펴보자. const 영역은 사실 $ {\bf x} $ 와는 독립적인 영역이다.
공분산 $ \Sigma $ 는 대칭 행렬임을 잘 알고 있다.
자, 이제 일반적인 가우시안 분포에서 이차 형식(quadratic) 내의 값들로부터 어떻게 평균과 분산이 연관되어 있는지 확인해본다.
- 위의 식에서 이차 형식을 일반화시켜 전개한 부분이 우변이다.
- 이걸 두번 미분한 값은 (즉, 2차식의 계수에 주목해야 한다.) 바로 $ \Sigma^{-1} $ 이 된다.
  - 이를 통해 공분산의 역행렬을 구할 수 있다. (즉, 두번 미분해서 얻은 행렬이 공분산이 되어야 한다.)
- 다음으로 1차식의 계수는 $ \Sigma^{-1}{\pmb \mu} $ 가 된다.
  - 따라서 공분산을 구한 다음 1차 계수를 이용해서 평균의 벡터를 구할 수 있다.
이제 조건부 분포에서의 평균과 분산을 구해보도록 하자.
$ {\bf x}_a $ 와 $ {\bf x}_b $ 로 표현된 이차 형식 영역을 $ {\bf x}_a $ 에 대해 두번 미분한다고 할 때 의미가 있는 영역은 다음과 같다.

$-\dfrac{1}{2}{\bf x}_a^T\Lambda_{aa}{\bf x}_a \qquad{(2.72)}$

$ {\bf x}_b $ 와 관련된 영역은 모두 상수 취급하면 된다.
자, 이제 두번 미분한 값이 공분산의 역행렬이 되어야 하므로 조건부 분포 $ p({\bf x}_a|{\bf x}_b) $ 에 대한 공분산은 다음과 같이 정의할 수 있다.

$\Sigma\_{a|b} = \Lambda_{aa}^{-1} \qquad{(2.73)}$

이제 당연히 $ {\bf x}_a $ 의 1차식과 관련된 텀들을 모아 이 계수를 확인해야 한다. (평균을 구하기 위해)

${\bf x}_a^T\{\Lambda_{aa}{\pmb \mu}_a - \Lambda({\bf x}_b-{\pmb \mu}_b)\} \qquad{(2.74)}$

$ \Lambda_{ba}^T=\Lambda_{ab} $ 임을 이미 알고 있다.
위의 식은 결국 $ \Sigma_{a|b}^{-1} \; {\pmb \mu}_{a|b} $ 와 같아져야 한다.
식을 전개하면 다음과 같게 된다.

$\Sigma_{a|b}^{-1}\; {\pmb \mu}_{a|b} = \{\Lambda_{aa}{\pmb \mu}_a - \Lambda({\bf x}_b-{\pmb \mu}_b)\}$ ${\pmb \mu}_{a|b} = \Sigma_{a|b}\{\Lambda_{aa}{\pmb \mu}_a - \Lambda_{ab}({\bf x}_b-{\pmb \mu}_b)\}\\ = {\pmb \mu}_a - \Lambda_{aa}^{-1}\Lambda_{ab}({\bf x}_b-{\pmb \mu}_b) \qquad{(2.75)}$

다 괜찮은데 한 가지 걸리는 부분은 현재 평균과 공분산이 정확도(precision) 행렬로 표현이 되었다는 것이다.
최종 출력시에는 공분산으로 표현을 해 놓는 것도 좋을 듯 하다.
이를 위해 역행렬을 구하는 다음 식을 고려해보자.

$\left(\begin{array}{cc}A & B \\ C & D \end{array}\right)^{-1} = \left(\begin{array}{cc} M & -MBD^{-1} \\ -D^{-1}CM & D^{-1}CMBD^{-1} \end{array}\right) \qquad{(2.76)}$

이 중 $ M^{-1} $ 은 Schur completment 라고 불리는 행렬을 의미한다.

$M = (A-BD^{-1}C)^{-1} \qquad{(2.77)}$

이 식을 아래 행렬에 대입해서 풀 수 있다.

$\begin{pmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix}^{-1} = \begin{pmatrix} \Lambda_{aa} & \Lambda_{ab} \\ \Lambda_{ba} & \Lambda_{bb} \end{pmatrix} \qquad{(2.78)}$

전개하면 다음과 같은 식을 얻게 된다.

$\Lambda_{aa} = (\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1} \qquad{(2.79)}$ $\Lambda_{ab} = -(\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1}\Sigma_{ab}\Sigma_{bb}^{-1} \qquad{(2.80)}$

최종적으로 $ p({\bf x}_a|{\bf x}_b) $ 에 대한 평균과 분산을 정리해보자.

${\pmb \mu}_{a|b} = {\pmb \mu}_a + \Sigma_{aa}\Sigma_{bb}^{-1}({\bf x}_b-{\pmb \mu}_b) \qquad{(2.81)}$ $\Sigma_{a|b} = \Sigma_{aa} - \Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba} \qquad{(2.82)}$

아오, 기나긴 전개 과정이 끝났다.
위의 식을 좀 살펴보면,
- 평균의 경우 $ {\bf x}_b $ 에 대한 선형 함수의 꼴로 나오게 되며,
- 공분산의 경우 $ {\bf x}_b $ 에 대해 독립적인 식이 된다.
조건부 분포 $ p({\bf x}_a|{\bf x}_b) $ 에 대한 평균과 공분산 값은 $ {\bf x}_a $ 와 $ {\bf x}_b $ 에 대한 부분 공분산 행렬이 아닌 부분 정확도 행렬로 표현하는게 더 간결하다는 것도 알 수 있다.

결론

$ p({\bf x}_a, {\bf x}_b) $ 가 가우시안 분포를 따르는 경우, $ p({\bf x}_a|{\bf x}_b) $ 도 가우시안 분포를 따르게 된다.
- 이거 하나 확인하자고 꽤 많은 양의 수식을 전개해 보았다.

2.3.2. 주변 확률 가우시안 분포 (Marginal Gaussian distributions)

지금까지 결합확률분포인 $ p({\bf x}_a, {\bf x}_b) $ 의 확률 분포가 가우시안 분포이면 $ p({\bf x}_a|{\bf x}_b) $ 분포도 가우시안 분포임을 확인하였다.
이제 이 식을 이용하여 주변 확률 분포에 대해서도 살펴볼 예정이다.
주변확률 분포
- 결합 확률 분포에서 한 쪽의 변수가 사라지거나 무시되는 것.
- $ p(x, y) $ 에서 $ x $ 에 대한 주변 확률 분포는 $ p(x) $ 가 되며, $ y $ 에 대한 주변 확률 분포는 마찬가지로 $ p(y) $ 가 된다.
- 이 때 한쪽의 변수는 합산하여 사라지게 되는데 이산 변수는 모든 확률 값의 합으로, 연속 변수의 경우 적분을 통해 진행된다.
주변(marginal) 확률 분포에 대해 살펴보도록 하자.

$p({\bf x}_a) = \int p({\bf x}_a, {\bf x}_b)d{\bf x}_b \qquad{(2.83)}$

주변 확률 분포 또한 가우시안 분포가 되는지를 확인하는 과정이 필요.
마찬가지로 우리의 전략은 이차형식(quadratic) 내에서 평균과 분산을 얻어낼 수 있는지 여부를 확인하는 것.
가우시안 분포 내 이차 형식을 다시 한번 보자.

$-\dfrac{1}{2}({\bf x}-{\pmb \mu})^T\Sigma^{-1}({\bf x}-{\pmb \mu})=-\dfrac{1}{2}{\bf x}^T\Sigma^{-1}{\bf x} + {\bf x}^T\Sigma^{-1}{\pmb \mu}+const$

여기서 우리는 $ {\bf x}_b $ 에 대한 적분을 수행해야 한다.
따라서 이번에는 $ {\bf x}_b $ 텀에 대해 각각의 계수를 모아본다.
따라서 마찬가지로 completing the square 를 사용하게 된다.

$-\dfrac{1}{2}{\bf x}_b^{T}\Lambda_{bb}{\bf x}_b + {\bf x}_b^T{\bf m} = -\dfrac{1}{2}({\bf x}_b-\Lambda_{bb}^{-1}{\bf m})^T\Lambda_{bb}({\bf x}_b-\Lambda_{bb}^{-1}{\bf m}) + \dfrac{1}{2}{\bf m}^T\Lambda_{bb}^{-1}{\bf m} \qquad{(2.84)}$

위의 식은 $ {\bf x}_b $ 에 대해 완전 제곱식을 이용해서 전개한 식이다.
- 완전 제곱식이란 말을 너무 오랜만에 들어서 기억이 안 날수도 있는데,
- 이차식을 어떻게든 제곱의 형태 즉, 이차 형식으로 만들어내고 이를 만들기 위해 추가한 텀을 다시 빼는 텀으로 넣어 식을 보정하는 것.
- 위의 식을 보면 $ {\bf x}_b $ 에 대한 이차식을 만들어내 내고 이 때 필요한 $ \frac{1}{2}{\bf m}^T\Lambda_{bb}^{-1}{\bf m} $ 가 보정된 형태.
여기서 $ {\bf x}_b $ 의 1차 계수인 $ {\bf m} $ 은 다음과 같이 정의된다.

${\bf m} = \Lambda_{bb}{\pmb \mu}_b - \Lambda_{ba}({\bf x}_a-{\pmb \mu}_a) \qquad{(2.85)}$

자, 이제 이 식을 가지고 실제 적분을 수행해보자. (적분은 $ {\bf x}_b $ 에 대한 적분이다.)
- 첫번째 텀 $ -\frac{1}{2}({\bf x}_b-{\bf m})^T\Lambda_{bb}({\bf x}_b-\Lambda_{bb}^{-1}{\bf m}) $ 은 $ {\bf x}_b $ 에 대한 식으로 생각할 수 있다.
- 두번째 텀 $ \frac{1}{2}{\bf m}^T\Lambda_{bb}^{-1}{\bf m} $ 은 $ {\bf x}_b $ 에는 종속적이지 않으나 $ {\bf x}_a $ 에는 종속적이다.
이제 첫번 째 텀을 적분하는 식을 기술해보자.

$\int\exp\left\{-\dfrac{1}{2}({\bf x}_b-\Lambda_{bb}^{-1}{\bf m})^T\Lambda_{bb}({\bf x}_b-\Lambda_{bb}^{-1}{\bf m})\right\}d{\bf x}_b \qquad{(2.86)}$

결국 위의 적분식은 Unnormalize 가우시안 적분이 되며 실제 값은 정규화 계수의 역수가 된다.
- 가우시안 분포의 경우 적분의 합이 1이 되어야 하므로, 적분의 결과에 역수를 취한 값이 정규화 계수가 된다.
- 위의 식 자체가 하나의 정규식으로 완전한 꼴을 가지고 있으므로 독립적인 값으로 생각하고 계산해도 문제 없음.
- 이런 정규화 계수는 평균에 독립적이고 단지 공분산에 대한 행렬식에 의존하게 된다. (가우시안 분포의 정의에 의해)
- 사실 첫번째 텀은 그냥 적분이 가능하다고 생각하기만 하면 큰 무리 없음.
이제 두번째 텀에 관심을 가져보자.두번 째 텀은 $ {\bf x}_a $ 에 종속적인 텀이다.
- 따라서 $ {\bf x}_b $ 에 대한 적분식에서는 관여하지 않고 적분식 밖으로 나오게 된다.
- 하지만 이후에는 $ {\bf x}_a $ 에 대한 식으로 사용되게 된다.
- 왜냐하면 적분 이후에는 $ p({\bf x}_a) $ 식의 꼴이 되고 $ {\bf x}_a $ 에 대한 확률 함수로 고려할 수 있기 때문이다.
이제 이 식을 $ {\bf x}_a $ 에 대해 정리해보도록 하자.

$\dfrac{1}{2}[\Lambda_{bb}{\pmb \mu}_b-\Lambda_{ba}({\bf x}_a-{\pmb \mu}_a)]^T\Lambda_{bb}^{-1}[\Lambda_{bb}{\pmb \mu}_b-\Lambda_{ba}({\bf x}_a-{\pmb \mu}_a)]\\ - \dfrac{1}{2}{\bf x}_a^T\Lambda_{aa}{\bf x}_a + {\bf x}_a^T(\Lambda_{aa}{\pmb \mu}_a+\Lambda_{ab}{\pmb \mu}_b) + const\\ = - \dfrac{1}{2}{\bf x}_a^T(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}){\bf x}_a + {\bf x}_a^T(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}){\pmb \mu}_a+const \qquad{(2.87)}$

최종적으로 위의 결과는 지부수 $ \exp(\cdot) $ 에 놓이게 된다.
const 영역은 일단 $ {\bf x}_a $ 와 무관한 식이므로 잠시 머릿속에서 비워 둔다.
근데 이런 형태의 꼴은 어디선가 봤던 식이다. (식 2.71)

$-\dfrac{1}{2}({\bf x}-{\pmb \mu})^T\Sigma^{-1}({\bf x}-{\pmb \mu})=-\dfrac{1}{2}{\bf x}^T\Sigma^{-1}{\bf x} + {\bf x}^T\Sigma^{-1}{\pmb \mu}+const$

그렇다. 이 식도 사실 이차 형식(quadratic)의 풀이 식과 동일한 형태의 모양을 취하고 있다.
결국은 $ \exp(quadratic) $ 와 같은 형태가 되므로 정규식이 된다.
조건부 분포를 구할 때 사용한 방식을 그대로 적용하면 여기서 평균과 분산을 구할 수 있다.
- 공분산은 이차형식(quadratic) 내 2차식의 계수로, 평균은 1차식의 계수로 얻을 수 있음을 확인했다.
이를 이용해서 분산과 평균을 각각 구해보자.

$\Sigma_a = (\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1} \qquad{(2.88)}$ $\Sigma_a(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}){\pmb \mu}_a = {\pmb \mu}_a \qquad{(2.89)}$

마찬가지로 정확도 행렬보다는 공분산 행렬로 표기하는 것이 더 편할 수 있다.
- 수식 계산에는 정확도 행렬이 편하지만 최종적으로 사용할 때에는 공분산 행렬이 더 편하다.

$\begin{pmatrix}\Lambda_{aa} & \Lambda_{ab} \\ \Lambda_{ba} & \Lambda_{bb} \end{pmatrix}^{-1} =\begin{pmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix} \qquad{(2.90)}$

아래 식을 이용해서 전개해보자.

$\begin{pmatrix}A & B \\ C & D \end{pmatrix}^{-1} =\begin{pmatrix} M & -MBD^{-1} \\ -D^{-1}CM & D^{-1}CMBD^{-1} \end{pmatrix}$

우리는 이제 다음과 같은 식을 얻을 수 있다.

$(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1} = \Sigma_{aa} \qquad{(2.91)}$

최종적으로 전개를 하면 다음과 같은 식을 얻는다.

$E[{\bf x}_a] = {\pmb \mu}_a \qquad{(2.92)}$ $cov[{\bf x}_a] = \Sigma_{aa} \qquad{(2.93)}$

엄청나게 복잡한 수식 전개를 했지만 얻는 결과는 너무 깔끔하다.
게다가 직관적으로 너무나 타당한 식을 얻었다.

Partitioned Gaussians

이제 정리의 시간을 가져보자.
가우시안 분포를 취하는 어떤 결합 분포가 다음과 같이 주어졌을 때 (단, $ N({\bf x}|{\pmb \mu}, \Sigma) $ with $ \Lambda \equiv \Sigma^{-1} $ )

${\bf x}=\dbinom{ {\bf x}_a }{ {\bf x}_b } \qquad{(2.94)}$ ${\pmb \mu}=\dbinom{ {\pmb \mu}_a }{ {\pmb \mu}_b } \qquad{(2.94)}$ $\Sigma=\begin{pmatrix}\Sigma_{aa} & \Sigma_{ab}\\ \Sigma_{ba} & \Sigma_{bb}\end{pmatrix} \qquad{(2.95)}$ $\Lambda = \begin{pmatrix}\Lambda_{aa} & \Lambda_{ab}\\ \Lambda_{ba} & \Lambda_{bb}\end{pmatrix} \qquad{(2.95)}$

조건부 확률 분포 (Conditional distribution)

$p({\bf x}_a|{\bf x}_b) = N({\bf x}_a\;|\;{\pmb \mu}_{a|b}, \Lambda_{aa}^{-1}) \qquad{(2.96)}$ ${\pmb \mu}_{a|b} = {\pmb \mu}_a - \Lambda_{aa}^{-1}\Lambda_{ab}({\bf x}_b-{\pmb \mu}_b) \qquad{(2.97)}$

결합 확률 분포 (Marginal distribution)

$p({\bf x}_a) = N({\bf x}_a\;|\;{\pmb \mu}_a, \Sigma_{aa}) \qquad{(2.98)}$

그림으로 살펴보자.

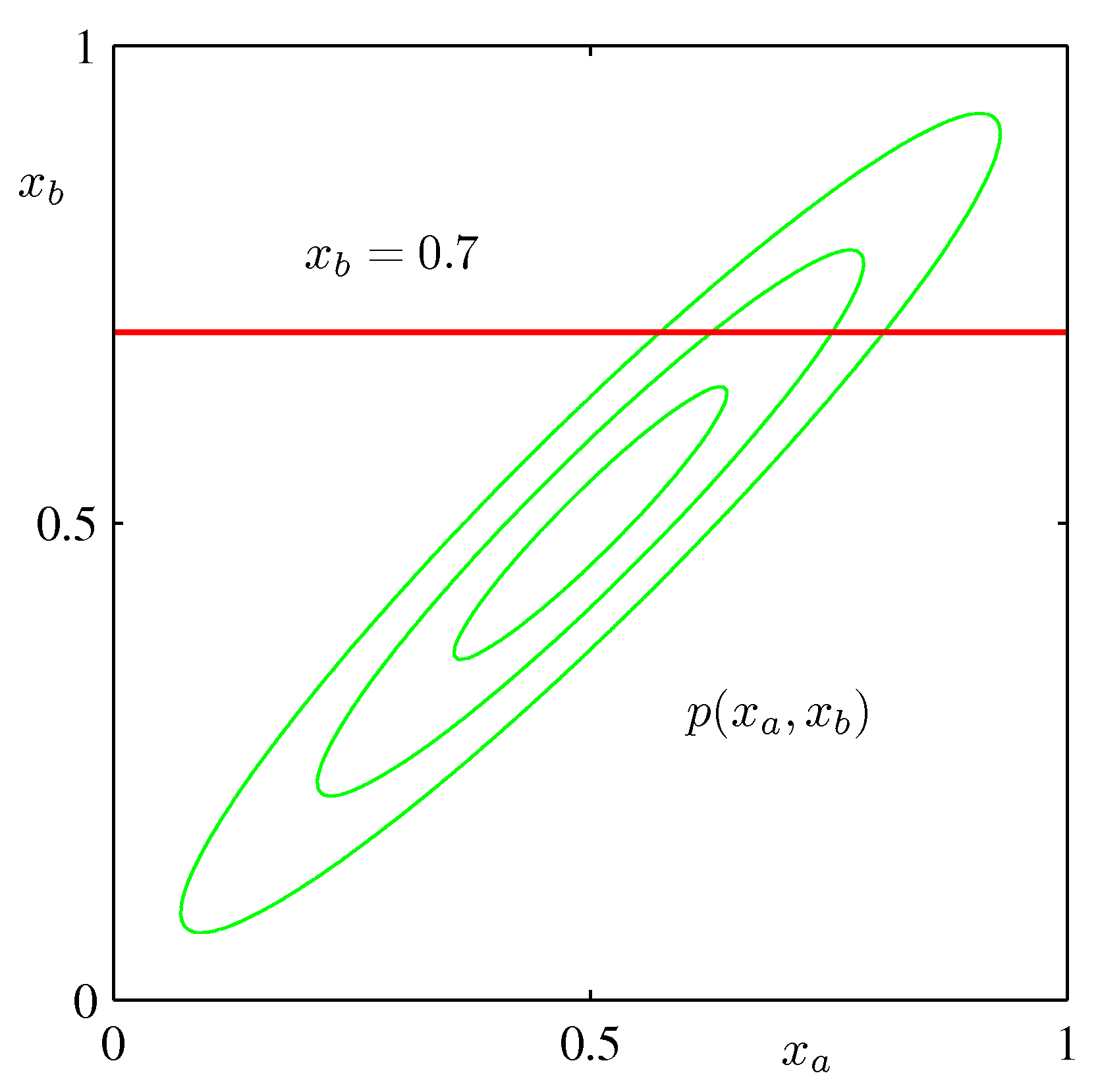
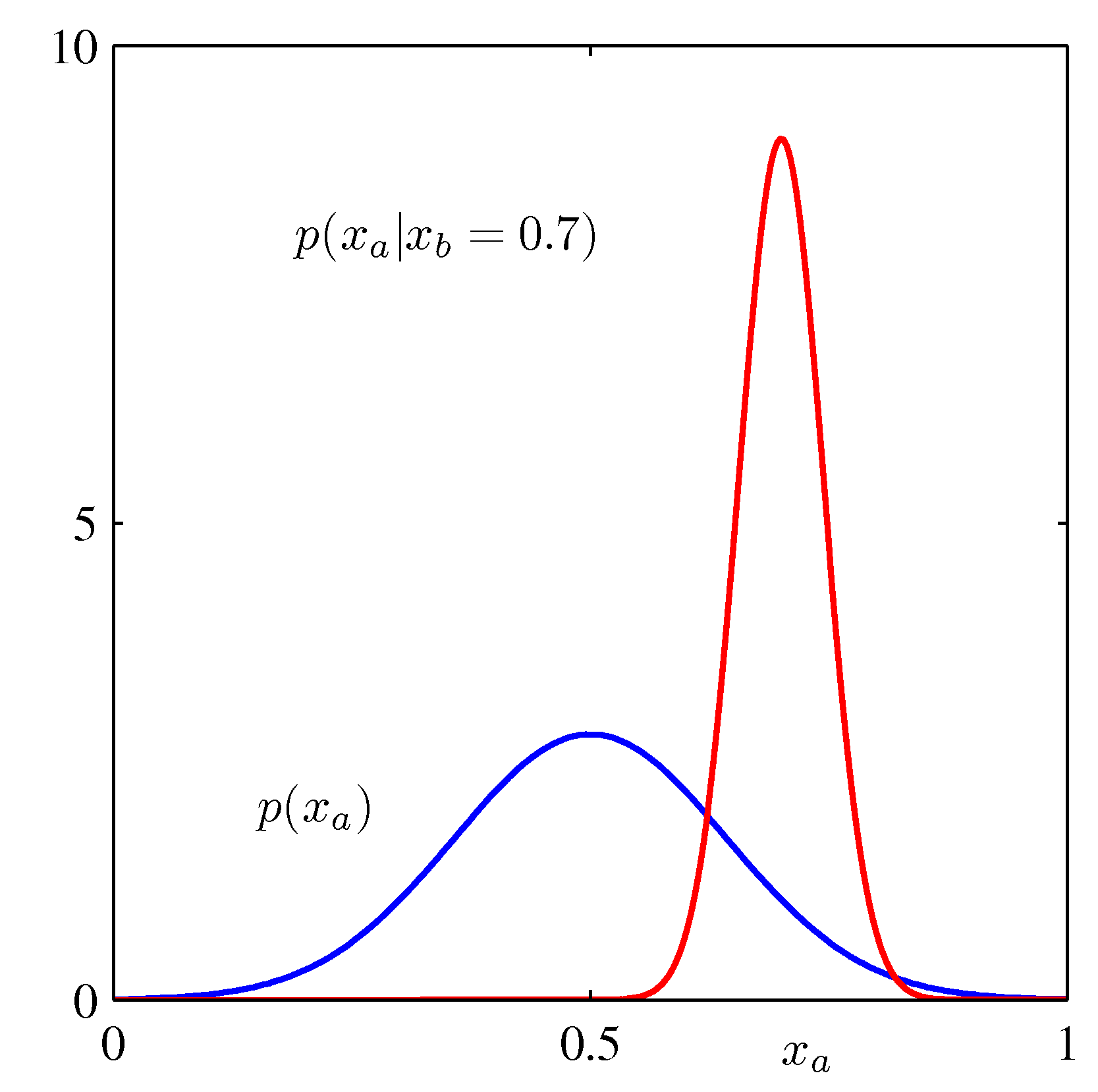
위의 그림은 $ p(x_a, x_b) $ 에 대한 분포를 그림으로 그린 것이다. (녹색)
여기서 푸른 선은 $ p(x_a) $ 를 나타낸다.
붉은 선은 $ p({x_a|x_b=0.7}) $ 일 때의 값이다.
모두 가우시안 분포의 모양을 따르고 있다는 것을 확인할 수 있다.

2.3.3. 가우시안 변수를 위한 베이즈 이론 (Bayes’ theorem for Gaussian variables)

지금까지 가우시안 분포 $ p({\bf x}) $ 에서 $ x=({\bf x}_a, {\bf x}_b) $ 로 나누어 $ p({\bf x}_a|{\bf x}_b) $ 와 $ p({\bf x}_a) $ 도 가우시안 분포가 된다는 것을 확인했다.
또 조건부 분포 $ p({\bf x}_a|{\bf x}_b) $ 의 평균 값이 $ {\bf x}_b $ 에 대한 선형 함수임을 확인했다.
이제 가우시안 주변 확률 분포인 $ p({\bf x}) $ 와 가우시안 조건부 분포 $ p({\bf y}|{\bf x}) $ 에 대해 살펴볼 것이다.
- 이 때 $ p({\bf y}|{\bf x}) $ 의 평균 값은 $ {\bf x} $ 에 대한 선형함수이고 분산값은 $ {\bf x} $ 에 독립적이다.
이는 가우시안 선형 모델 (linear Gaussian model) 의 한 예이다.
- 이와 관련된 내용은 8장에서 다시 다룰 것이다.

$p({\bf x}) = N({\bf x}\;|\;{\pmb \mu}, \Lambda^{-1}) \qquad{(2.99)}$ $p({\bf y}|{\bf x}) = N({\bf y}\;|\;{\bf A} {\bf x}+{\bf b} , L^{-1}) \qquad{(2.100)}$

위와 같은 식이 주어졌다고 생각하면 된다.
- $ p({\bf x}) $ 는 가우시안 주변 확률
- $ p({\bf y}|{\bf x}) $ 는 가우시안 조건부 확률
  - 평균 : $ {\bf x} $ 에 대해 선형 함수
  - 분산 : $ {\bf x} $ 와 독립적
  - 만약 $ {\bf x} $ 는 $ D $ 차원이고, $ {\bf y} $ 는 $ M $ 차원 데이터라면 행렬 $ {\bf A} $ 는 $ D \times M $ 행렬이 된다.
이번 절에서 하고자 하는 것은?
- 베이즈 이론를 활용하여,
- $ p({\bf z}) = p({\bf x})p({\bf y}|{\bf x}) $ 인 식을 $ p({\bf x}|{\bf y})p({\bf y}) $ 와 같은 식으로 전개함
- 곱의 법칙에 따라서 $ p({\bf z}) $ 즉, $ p({\bf x}, {\bf y}) $ 를 구할 수 있고,
- $ p({\bf y}) $ 와 $ p({\bf x}|{\bf y}) $ 도 구할 수 있다.
- 이게 왜 필요할까 싶지만 이후 장에서 가끔 사용된다.
  - 예를 들어 현재 분포를 $ p({\bf x}) $ 와 $ p({\bf y}|{\bf x}) $ 를 만족하도록 만들어놓고, 최종적으로 $ p({\bf y}) $ 등을 만들어낸다.
이후 과정은 증명 과정이다.
우선 $ {\bf x} $ 와 $ {\bf y} $ 의 결합 확률을 $ {\bf z} $ 로 정의하자.

${\bf z} = \dbinom{ {\bf x} }{ {\bf y} } \qquad{(2.101)}$

이제 결합 분포에 로그를 씌운다.

$\ln{p({\bf z})} = \ln p({\bf x}) + \ln p({\bf y})\\ = -\frac{1}{2}({\bf x}-{\pmb \mu})^T\Lambda({\bf x}-{\pmb \mu}) -\frac{1}{2}({\bf y}-{\bf A}{\bf x}-{\bf b})^T{L}({\bf y}-{\bf A}{\bf x}-{\bf b})+const \qquad{(2.102)}$

여기서 const 영역은 $ {\bf x} $ 나 $ {\bf y} $ 와는 상관없는 텀이다.
그 외의 텀은 $ {\bf z} $ 의 요소들에 대한 이차형식(quadratic)의 함수이다.
- 앞서 이런 형태의 식에 대한 가우시안 분포 여부를 확인했었다.
- 따라서 이 분포도 가우시안 분포가 된다는 것을 알 수 있다.
어쨌거나 위의 식을 모두 전개하여 이 중 이차항만을 추려보자.
- 알다시피 공분산을 구하기 위해서이다.

$-\frac{1}{2}{\bf x}^T(\Lambda + {\bf A}^T\Lambda{\bf A}){\bf x} - \frac{1}{2}{\bf y}^T{\bf L}{\bf y} + \frac{1}{2}{\bf x}^T{\bf A}{\bf L}{\bf y}\\ = -\frac{1}{2}\dbinom{ {\bf x} }{ {\bf y} }^T \left(\begin{array}{cc}\Lambda+{\bf A}^T{\bf L}{\bf A} & -{\bf A}^T{\bf L}\\-{\bf L}{\bf A} & {\bf L}\end{array} \right) \dbinom{ {\bf x} }{ {\bf y} } = -\frac{1}{2}{\bf z}^T{\bf R}{\bf z} \qquad{(2.103)}$

신기하게도 $ {\bf z} $ 에 대한 이차형식(quadratic) 형태의 식이 전개되었다.
따라서 $ R $ 은 정확도 행렬이 된다. (공분산의 역행렬)

${\bf R} = \left(\begin{array}{cc}\Lambda+{\bf A}^T{\bf L}{\bf A} & -{\bf A}^T{\bf L}\\-{\bf L}{\bf A} & {\bf L}\end{array}\right) \qquad{(2.104)}$

역행렬을 만드는 식을 이용하여 공분산도 구할 수 있다.

$cov[{\bf z}]={\bf R}^{-1} = \left(\begin{array}{cc}\Lambda^{-1} & \Lambda^{-1}{\bf A}^T \\ {\bf A}\Lambda^{-1} & {\bf L}^{-1}+{\bf A}\Lambda^{-1}{\bf A}^T \end{array}\right) \qquad{(2.105)}$

복잡해보이긴 해도 구할수 없는 식은 아니다.
이제 일차항을 묶어 얻어진 계수와, 앞서 구한 공분산을 이용하여 평균을 구할 수 있다.
일차항은 다음과 같다.

${\bf x}^T\Lambda{\pmb \mu} - {\bf x}^T{\bf A}^T{\bf L}{\bf b} + {\bf y}^T{\bf L}{\bf b} = \dbinom{ {\bf x} }{ {\bf y} }^T\dbinom{\Lambda{\pmb \mu}-{\bf A}^T{\bf L}{\bf b}}{ {\bf L}{\bf b} } \qquad{(2.106)}$

따라서 평균값은 다음과 같다.

$E[{\bf z}] = {\bf R}^{-1}\dbinom{ {\bf x} }{ {\bf y} }^T\dbinom{\Lambda{\pmb \mu}-{\bf A}^T{\bf L}{\bf b}}{ {\bf L}{\bf b} } \qquad{(2.107)}$

$ {\bf R}^{-1} $ 을 대입하여 전개해보자. 최종 식으로 다음을 얻을 수 있다.

$E[{\bf z}] = \dbinom{ {\pmb \mu} }{ {\bf A} {\pmb \mu} - {\bf b}} \qquad{(2.108)}$

각 요소의 평균이 결국 $ {\bf z} $ 의 평균이 된다.
- 직관적으로 매우 당연한 결과이지만 이를 얻어내기까지의 수식 계산이 쉽지 않네.
지금까지 결합 분포 $ p({\bf x}, {\bf y}) $ 를 살펴보았으므로 이제 주변 확률 분포(marginal distribution)를 살펴보도록 하자.
여기에서는 앞서 다루었던 결합 분포의 성질을 이용하게 된다.
얻은 결과는 다음과 같다. (식을 전개하기가 귀찮다.)

$E[{\bf y}] = {\bf A}{\pmb \mu} + {\bf b} \qquad{(2.109)}$ $cov[{\bf y}] = {\bf L}^T + {\bf A}\Lambda^{-1}{\bf A}^T \qquad{(2.110)}$

여기서 $ {\bf A}={\bf I} $ 인 경우 두 가우시안의 관계가 convolution 관계라고 한다.
- 여기서 convolution 은 두 개의 가우시안 함수가 서로 오버랩되는 영역을 나타내는 식이라고 생각하면 된다.
- 이렇게 오버랩되는 영역도 마찬가지로 가우시안 분포를 따르게 된다.
- 이 때 생성되는 분포의 평균는 각각의 분포의 평균의 합의 평균이 되고 분산은 각각의 분포의 분산의 합의 평균이 된다.
이제 조건 분포 $ p({\bf x}|{\bf y}) $ 에 대해 좀 알아보도록 하자.
이 때의 평균과 분산은 너무나도 쉽게 구해지는데, 왜냐하면 이미 앞에서 다 구했기 때문이다. (식 2.73, 2.15)

$\Sigma_{a|b}=\Lambda_{aa}^{-1}$ ${\pmb \mu}_{a|b}={\pmb \mu}_a - \Lambda_{aa}^{-1}\Lambda_{ab}({\bf x}_b-{\pmb \mu}_b)$

이걸 $ p({\bf x}|{\bf y}) $ 에 맞게 대입만 하면 된다.

$E[{\bf x}|{\bf y}] = (\Lambda+{\bf A}^T{\bf L}{\bf A})^{-1}\{ {\bf A}^T{\bf L}({\bf y}-{\bf b})+\Lambda{\pmb \mu}\} \qquad{(2.111)}$ $cov[{\bf x}|{\bf y}] = (\Lambda+{\bf A}^T{\bf L}{\bf A})^{-1} \qquad{(2.112)}$

Mareginal and Conditional Gaussians

이제 정리를 해보자.
다음과 같은 가우시안 확률 분포가 주어졌을 때,

$p({\bf x}) = N({\bf x}\;|\;{\pmb \mu}, \Lambda^{-1}) \qquad{(2.113)}$ $p({\bf y}|{\bf x}) = N({\bf y}\;|\;{\bf A}{\bf x}+{\bf b}, {\bf L}^{-1}) \qquad{(2.114)}$

주변 확률 분포와 조건부 확률 분포는 다음과 같다.

$p({\bf y}) = N({\bf y}\;|\;{\bf A}{\pmb \mu}+{\bf b}, {\bf L}^{-1}+{\bf A}\Lambda^{-1}{\bf A}^T) \qquad{(2.115)}$ $p({\bf x}|{\bf y}) = N({\bf x}\;|\;\Sigma\{ {\bf A}^T {\bf L}({\bf y}-{\bf b})+\Lambda{\pmb \mu}\}, \Sigma) \qquad{(2.116)}$

단, $ \Sigma $ 는 다음과 같다.

$\Sigma = (\Lambda + {\bf A}^T{\bf L}{\bf A})^{-1} \qquad{(2.117)}$

이런 복잡한 식을 도대체 어디다 써 먹을까하는 생각이 들 수 있지만, 이후에 나온다.
- 보통 $ p({\bf x}) $ 가 가우시안 분포로 주어지고 이 때 $ p({\bf y}|{\bf x}) $ 를 $ {\bf x} $ 에 대한 선형식을 가지는 평균값의 꼴로 만들기만 하면,
- 이 때의 $ p({\bf y}) $ 와 $ p({\bf x}|{\bf y}) $ 를 위의 식을 통해 만들어낼 수 있다.

2.3절의 분량이 너무 길어지는 관계로 이후 절은 Part.II 으로 넘긴다.

Chapter. 2

2.3.1. 조건부 가우시안 분포 (Conditional Gaussian distributions)

2.3.2. 주변 확률 가우시안 분포 (Marginal Gaussian distributions)

2.3.3. 가우시안 변수를 위한 베이즈 이론 (Bayes’ theorem for Gaussian variables)