목표 : 전방향(feed-forward) 네크워크에서 에러 함수 \( E({\bf w}) \) 의 그라디언트를 가장 효율적으로 구하는 식을 구하자.
- 이를 에러 역전파 알고리즘(backpropagation) 이라고 부른다.
- 혹은 줄여서 backprop 이라고 한다.
- ‘역전파’ 라는 용어보다는 원래 표현인 backprop 표현을 주로 사용하도록 하겠다.
- 사실 신경망에서는 backpropagation 이라는 용어가 좀 애매하게 사용되기도 한다.
- 예를 들어 MLP 자체를 backprop망 이라 부른다.
- 혹은 MLP 에서 sum-of-square 에러 함수를 최소화하기 위해 사용되는 그라디언트 방식을 backprop이라고도 한다.
- 여기서는 이런 혼동을 피하기 위해 학습 과정을 자세히 살펴보도록 한다.
- 일반적인 학습 과정은 에러 함수를 최소화하기 위한 반복 과정을 포함하고 있다.
- 반복 중에 가중치가 계속 갱신된다.
- 하나의 작업이 여러 번 반복되는 것으로 이해될 수 있는데, 이 때 하나의 작업은 크게 두 개의 단계로 나누어진다.
- 첫번째 단계는 \( {\bf w} \) 에 대한 에러 함수의 미분 값을 구하는 것이다.
- 이 때 backprop 은 그라디언트 값을 구하는 효율적인 도구를 의미한다.
- 이후에 언급되겠지만 그라디언트를 구하는 기법은 야코비안(jacobian), 헤시안(Hessian) 을 구하는 계산에서도 응용될 수 있다.
- 두번째 단계는 그라디언트를 이용해서 \( {\bf w} \) 의 업데이트 분량을 계산하는 과정이다.
- 이 때 그라디언트 감소(gradient descent) 기법이 가장 유명한 기법이고 기타 다른 기법도 존재한다.
- 첫번째 단계는 \( {\bf w} \) 에 대한 에러 함수의 미분 값을 구하는 것이다.
- 이 두 단계를 구분하는 것은 매우 중요하다.
5.3.1. 에러 함수의 미분 값을 평가하기 (Evaluation of error-function derivatives)
- backprop 알고리즘은 다음의 조건에서 쉽게 사용 가능하다.
- 임의의 feed-forward 신경망
- 임의의 미분 가능한 비선형 활성 함수
- 다양한 종류의 에러 함수
- 가장 먼저 간단한 모델을 이용하여 식을 전해할 것이다.
- 시그모이드 형태의 히든 레이어를 가지는 단일 레이어 모델 (용어가 이상한데 그냥 2-layer 모델이다.)
- 이 때 사용되는 에러 함수는 sum-of-square 모델
- 현실에서는 정말 다양한 에러 함수를 정의할 수 있다.
- 예를 들어 i.i.d 데이터를 이용한 MLE 함수를 사용할 수 있다.
- 이 때 에러 함수는 모든 관찰 데이터의 에러의 합으로 표현 가능하다.
- 로그 가능도 함수가 각 관찰 데이터의 로그 가능도 함수 값의 합인것 처럼 에러 함수로 이와 비슷하게 정의된다.
- 이제 이 함수의 \( \triangledown E({\bf w}) \) 에 대해 고민을 하도록 하자.
- 이런 방식을 배치(batch) 모드라고 한다. (에러를 모두 합해서 한번에 사용)
-
이후에 온라인 업데이트 방식도 살펴볼 것이다.
- 이제 \( y_k \) 에 대한 간단한 선형 모델을 살펴보자.
- 위의 식은 사실 신경망과는 아무런 관계가 없다. 3장에서 살펴본 선형 함수라고 생각하면 된다.
-
다만 출력 값 \( y_k \) 가 하나가 아니라 \( K \) 개이고 각각 독립적으로 계산된다.
- 이 때 sum-of-square 에러 함수는 다음과 같다.
- 하나의 샘플에 대해 출력값이 \( K \) 개이므로 이에 대한 에러의 합으로 표현된다.
-
이 때 \( y_{nk}=y_k({\bf x}_n, {\bf w}) \) 가 된다.
- 이를 \( {\bf w}_{ji} \) 에 대해 미분해보자.
- 갑자기 \( j \) 가 등장해서 이상할 수 있으나,
- 앞서 사용한 \( k \) 는 임의의 특정 \( k \) 를 의미하고
- \( j \) 는 말 그대로 임의의 출력 노드를 의미한다.
- 전체 \( {\bf w} \) 벡터에 대한 미분이 아니라 \( w_{ji} \) 에 대한 미분임에 주의할 것.
- 이건 4장에서 보던 식과 비슷한 형태이다.
- 이 식은 회귀, 이진 분류, 다변수 분류와 같은 목적에 상관이 없이 얻을 수 있는 일반화된 식이다.
- 일반적인 feed-forward 네트워크에서 입력 유닛에 대한 가중치 합은 다음과 같다.
- 이미 5.1절에서 bias 라로 불리우는 추가 유닛의 존재를 확인했다. 활성 함수에 이 값이 +1 로 고정 추가된다.
- 여기서 \( z_i \) 는 이전에 연결된 레이어의 유닛 출력값이거나 비선형 활성 함수를 통해 얻어진 결과 값이다.
- 하나 이상의 \( z_i \) 가 존재하고 이는 식 (5.48)에서 기술한 입력 값의 합을 입력으로 받고 \( j \) 번째의 값을 출력하게 된다.
- 전방 전파 (forward propagation)
- 학습 데이터가 입력되면 입력 벡터로 들어와서 히든 레이어의 활성 함수에 의해 계산된 값이 전파되어 최종 출력에 이르게 된다.
- 이러한 과정을 전방 전파라고 한다.
- 이제 에러 함수 \( E_n \) 을 파라미터 \( w_{ji} \) 로 미분한 식을 살펴보도록 하자.
- 최종 출력값은 입력 패턴 \( n \) 에 영향을 받는다.
- 하지만 여기서 식에 이걸 다 기입하면 복잡하니까 잠시 \( n \) 은 생략하고 보도록 하자.
- 최종 에러값은 두 번의 함수를 거쳐 출력되므로 이를 나누어서 고려할 수 있다.
- 식이 점점 복잡해지므로 간단한 표기법을 도입하도록 한다.
- \( \delta_j \) 를 종종 에러처럼 표현하곤 한다.
- 식 (5.48)을 편미분하여 다음과 같은 식을 얻을 수 있다.
- 미분값은 그냥 출력 값이 된다. 이제 식을 결합하자.
- \( w_{ji} \) 에 대한 미분값은 각 유닛마다 얻어지는 에러 \( \delta_j \) 에 출력값 \( z_i \) 를 곱하여 얻을 수 있다.
- 따라서 실제 미분 값을 구하기 위해서는 각 유닛마다 에러 \( \delta_j \) 만 계산하기만 하면 된다.
- 최종 출력단에서의 에러 값은 이미 구했었다.
- 4.3.6 절에서 언급했듯이 이를 정준 링크 함수(canonical link function)라고 생각하면 다음을 얻을 수 있다.
- 히든 유닛의 에러 값은 체인 법칙(chain rule) 을 이용하여 전개 가능하다.
- 이 식을 자세히 보면 히든 유닛의 \( \delta \) 값은 네트워크에서 전파된 쪽 노드의 \( \delta \) 값을 되받아(backward) 얻을 수 있다는 것을 알 수 있다.
- 이를 그림으로 나타내면 다음과 같다.
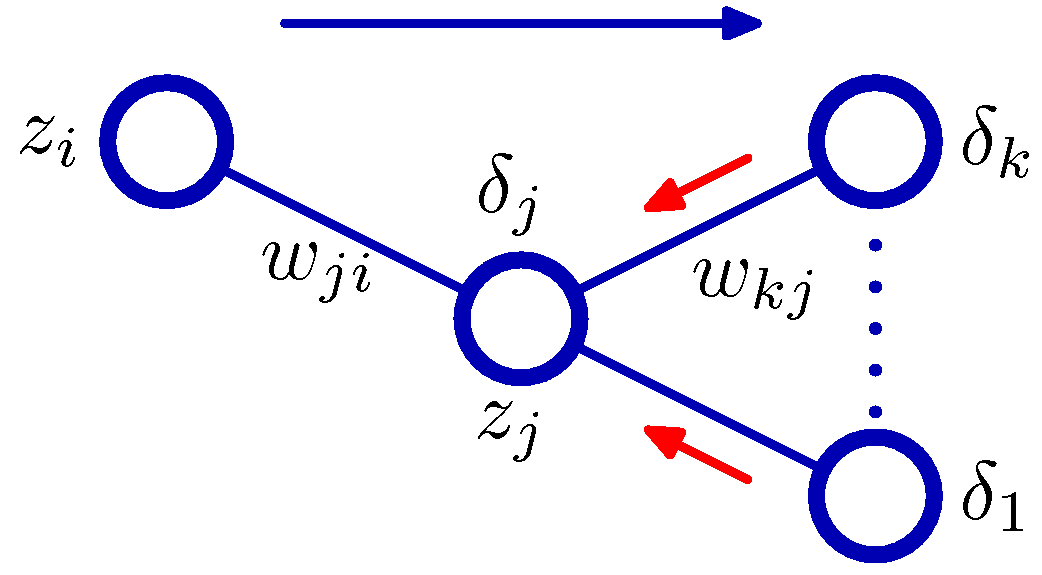
- 이를 backpropagation 이라고 부른다.
- Error Backpropagation
- 입력 벡터 \( {\bf x}_n \) 에대해 식 (5.48) 과 식 (5.49)을 이용한 전방향 전파를 진행한다.
- 출력 유닛에서 \( \delta_k \) 값을 구한다. 식 (5.54) 를 사용한다.
- 히든 유닛의 \( \delta_j \) 값을 구하기 위해 역전파를 진행한다. 식 (5.56)을 사용하면 된다.
- 식 (5.53)을 이용하여 미분 값을 구한다.
- 배치 모드(batch mode)에서는 에러 \( E \) 를 모든 테스트 샘플의 에러 합으로 사용하면 된다.
- 사실 위의 식은 활성 함수 \( h(\cdot) \) 이 모두 동일하다고 가정하고 작성한 식이다.
- 하지만 사실 각 유닛들이 서로 다른 활성 함수를 사용할 수도 있다.
- 이 경우 개별적인 활성 함수를 식에 대입하여 사용하면 된다.
5.3.2 간단한 예제 (A simple example)
- 앞서 살펴본 역전파 방식은 에러 함수, 활성함수, 그리고 네크워크 구성을 일반화한 형태의 식이다
- 이러한 알고리즘을 활용한 일반적인 응용을 살펴보기 위해서 여기서는 아주 간단한 형태의 예를 도입하도록 한다.
- 아주 간단하면서도 실제 사용 가능한 수준의 신경망 예제를 만들어 보자.
- 일단 그림 (5.1) 과 같이 2개의 레이어(layer)를 가지는 네트워크를 고려해보자.
- 이 때 에러 함수는 최소 제곱합(sum-of-square)을 사용하고 선형 활성 함수를 이용한다.
- 사용되는 활성 함수의 식은 다음과 같다.
- 이 때 에러 함수는 최소 제곱합(sum-of-square)을 사용하고 선형 활성 함수를 이용한다.
- \( \tanh(\cdot) \) 함수는 다음과 같다.
- 활성 함수를 미분한 식도 살펴보자.
- 기본적인 최소 제곱합 에러 함수는 다음과 같다.
-
출력값 \( y_k \) 는 출력 유닛 \( k \) 에서의 출력값이 된다. \( t_k \) 는 이에 대응되는 타겟 값을 의미한다.
-
이제 네트워크 구성을 위한 식들을 간단하게 정리해보자.
- 출력 유닛에서의 \( \delta \) 함수 값은 다음과 같다.
- 이제 역전파를 위한 히든 유닛에서의 \( \delta \) 값을 살펴보자.
- 이 식들을 조합하여 첫번째 레이어와 두번째 레이어의 가중치 값의 미분 값을 구하면 다음과 같다.
5.3.3 역전파 알고리즘의 효율 (Efficiency of backpropagation)
- 역전파에서 가장 중요한 것 중 하나로 계산의 효율성을 들 수 있다.
- 이 문제를 이해하기 위해서 실제 에러 함수를 미분하여 평가하는 작업이 얼마나 많은 컴퓨터 연산을 발생시키는지 확인해보도록 하자.
- 이 때 네트워크에서 구해야 하는 가중치 \( W \) 의 수를 함께 고려한다.
- 에러 함수를 평가하는 과정에서는 매우 많은 갯수의 파라미터 \( W \) 에 대해 \( O(W) \) 만큼의 연산이 필요하게 된다.
- 그리고 파라미터의 개수는 유닛의 수보다 크다. (물론 sparse 모델은 이렇지 않을수도 있겠지만 흔한 모델은 아니다.)
- 따라서 식 (5.48)에 의해 전방향 전파는 \( O(W) \) 의 계산 비용이 필요한다.
- 반면 역전파의 경우에는 미분을 위해 유한 차분(finite difference) 기법을 도입해다고 생각하고 이에 대한 비용을 근사적으로 예측해보자.
- 보통 \( e « 1 \) 이다. 정확도를 향상시키려면 \( e \) 는 매우 작은 값이어야 한다.
- (참고) finite difference method
- 유한 차분법은 \( f(x+b)-f(x+a) \) 형태의 수학 식을 의미한다.
- 그리고 이를 \( (b-a) \) 값으로 나누게 되면 difference quotient 를 얻는다.
- 이 때 \( |b-a| \) 가 0에 가까워지면 이를 미분 근사로 생각할 수 있다.
- 따라서 finite difference method 는 수치적 미분 방식을 계산하기 위한 도구이다.
- 수치적인 미분식을 사용하는 경우에는 역전파의 계산 비용이 \( O(W) \) 로는 불가능하다.
- 정확도를 높이기 위해 symmetrical central differences 를 사용할 수도 있다.
- 참고로 위의 식은 테일러 급수를 이용하여 얻어낸 식이다.
- 전개를 해 보면 마지막 차항이 \( O(e) \) 가 아닌 \( O(e^2) \) 으로 나오는지 그 이유를 알 수 있다.
- 따라서 전방 전파시에는 \( O(W) \) 이고 역전파에서는 \( O(W^2) \) 의 비용이 소요된다.
- 실제로 이러한 수학적 미분 방식을 통한 계산 식이 매우 중요한데, 다른 방식을 이용하여 연전파를 구한 값과 비교를 할 수 있는 대상으로 사용할 수 있기 때문이다.
- 따라서 다른 방식으로 얻어지는 결과가 올바른지를 비교해 볼 수 있는 방법으로 응용이 가능하다.
5.3.4 야코비안 행렬 (The Jacobian matrix)
- 지금까지 신경망에서의 전파, 역전파 방식에 대해 살펴보았다.
- 이 때 역전파 방식에서 에러 함수의 미분을 통한 갱신 방식을 사용하는 것도 확인하였다.
- 여기서 사용된 역전파 계산 방식은 이와 유사한 다른 미분 식에서도 응용 가능하다.
- 이 중에서 야코비안 행렬 (jacobian matrix)을 계산하는데에도 역전파 전개 방식을 도입할 수 있다.
- 이번 절은 좀 뜬금 없지만 야코비안 행렬 계산을 위한 역전파 기법을 살펴보는 절이라고 생각하면 된다.
- 이 행렬의 정의는 출력 값을 입력 값으로 미분한 식으로 표현된다.
- 야코비안 행렬은 백터를 출력하는 (즉, 출력 값이 하나의 실수 값이 아니라 벡터이다.) 1차 미분 행렬이다.
- 만약 출력 값이 하나의 경우에는 야코비안 행렬은 하나의 행(row) 만 가지게 된다.
- 이러한 경우는 우리가 알고 있는 일반 미분식이다.
- 따라서 아코비안 행렬이라고 하는 것은 출력 값이 여러 개인 함수에 대한 편미분을 일반화한 행렬이라고 생각하면 된다.
- 만약 출력 값이 하나의 경우에는 야코비안 행렬은 하나의 행(row) 만 가지게 된다.
- 야코비안 행렬은 독립된 모듈의 형태로 시스템을 구축할 때 유용하게 사용될 수 있다.
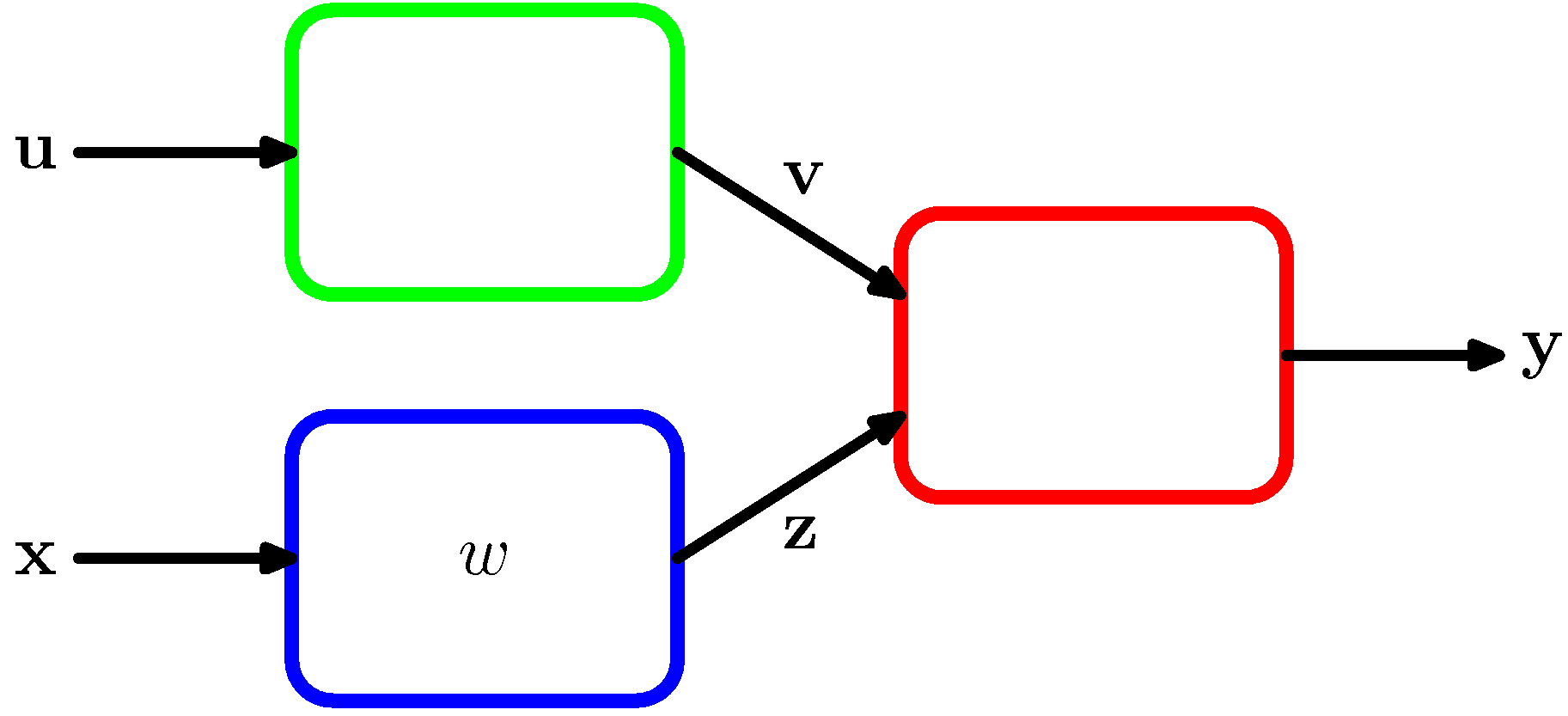
- 위의 그림에서 박스는 고정된 모듈을 의미한다.
- 여기서 \( E \) 에 대한 \( w \) 에 대한 값을 계산하기 위해 다음의 식을 사용한다.
- 이 중 가운데 텀이 야코비안 행렬이 된다.
- 아코비안 행렬은 입력에 대한 출력의 국지적인 민감도(local sensitivity)를 측정하는 용도로 사용 가능하다.
- 여기서 \( |\Delta x_i| \) 는 매우 작은 값이다.
- 일반적으로 학습된 신경망에서 입력과 출력 사이에 비선형 함수가 존재하기 때문에 \( J_{ki} \) 는 상수값이 되지 않는다.
- 따라서 실제 값은 입력 값에 영향을 받게 된다.
- 이 말은 입력 데이터가 들어올 때마다 야코비안 행렬도 다시 계산이 되어야 한다는 의미이다.
- 야코비안 행렬의 계산과 신경망의 역전파 방식은 매우 유사하게 전개될 수 있다.
- 크게 중요한 내용들도 아니니 식만 좀 살펴보자.
- 야코비안에서도 마찬가지로 수치 미분을 이용하여 실제 행렬이 정확히 구해졌는지 확인할 수 있다.