1. Feed-forward Network

• 회귀(regression)를 위한 선형 모델과 분류(classification)를 위한 선형 모델은 이미 3장, 4장에서 다 다루었다.
• 고정된 개수의 비선형 기저 함수를 사용하는 선형 결합 모델은 다음과 같이 기술될 수 있다.

• 여기서 함수 \( f(\cdot) \) 는 활성 함수(activation function)이다.
  • 회귀 문제에서는 활성 함수가 identity 함수. 즉, 입력 값을 그대로 반환하는 함수이고,
  • 분류 문제에서는 시그모이드( sigmoid )나 소프트맥스( softmax ) 같은 비선형 함수가 사용되었다.
• 기저 함수 \( \phi_j({\bf x}) \) 에 조정할 파라미터 계수 \( {w_j} \) 를 내적하는 식을 사용하는데,
  • 신경망의 경우 기저 함수는 그냥 \( \phi={\bf x} \) 함수를 사용하게 된다.
• 이제 가장 기본적인 형태의 신경망 모델을 살펴보자.

• 여기서 \( D \) 는 입력 벡터 \( {\bf x} \) 의 차원으로 \( {\bf x} = (x_1,…,x_D) \) 라고 생각하면 된다.
• \( j=1,…M \) 인 값으로 해당 레이어(layer)의 노드 개수로 생각하면 된다. 레이어는 첨자로 쓰여진 \( (1) \) 과 같은 형태로 나타내어진다.
  • 현재 레이어(layer)가 \( (1) \) 이므로 첫번째 레이어에 속한 노드의 개수는 총 \( M \) 개이다.
• \( w_{ji}^{(1)} \) 은 가중치 (weight) 라고 부르며, \( w_{j0} \) 는 바이어스 (bias) 라고 부른다.
• \( a_j \) 는 3장에서와 마찬가지로 활성자 (activations) 라고 부른다.
• 이 값들은 서로 다른 비선형의 활성 함수 (activation function) \( h(\cdot) \) 에 의해 변경되게 된다.

• 위의 식은 \( a_j \) 의 값을 비선형 활성 함수인 \( h(\cdot) \) 에 대입하여 \( z_j \) 를 얻는 결과를 식으로 정리한 것이다.
• 신경망에서는 위와 같은 작업을 처리하는 노드를 히든 유닛(hidden units)이라고 부른다..
• 보통 비선형 함수인 \( h(\cdot) \) 함수는 시그모이드(sigmoid) 함수나 하이퍼볼릭 탄젠트(tanh) 함수를 주로 사용하게 된다.
• 최종 출력 결과도 작성해보자.

• 여기서는 \( k=1,…K \) 이고 \( K \)는 출력할 필드의 개수가 된다.
• 레이어 번호를 보면 \( (2) \) 번 레이어 임을 알 수 있다.
• 마찬가지로 \( w_{k0}^{(2)} \) 은 바이어스이다.
• 여기에 활성 함수(activation function)를 적용하면 최종 출력값인 \( y_k \) 를 얻을 수 있다.
  • 이때 사용되는 활성 함수는 3장에서 사용된 함수와 비슷하다. (결국 sigmoid 또는 softmax를 사용한다.)
• 시그모이드를 활용한 식으로 전개를 해보자.

• 알다시피 위의 경우는 2-class 문제를 해결할 때 사용한다. K-class 문제에서는 softmax를 사용하면 된다..

• 이제 지금까지 설명했던 구조를 하나의 식으로 표현하자.

• 가장 중요한 기본 식이 이제서야 나왔다.
• 이렇게 해서 하나의 예제에 대해 최종적인 함수식을 얻게 되었다.
• 이 식을 구조화된 그림으로 표현하면 다음과 같다.

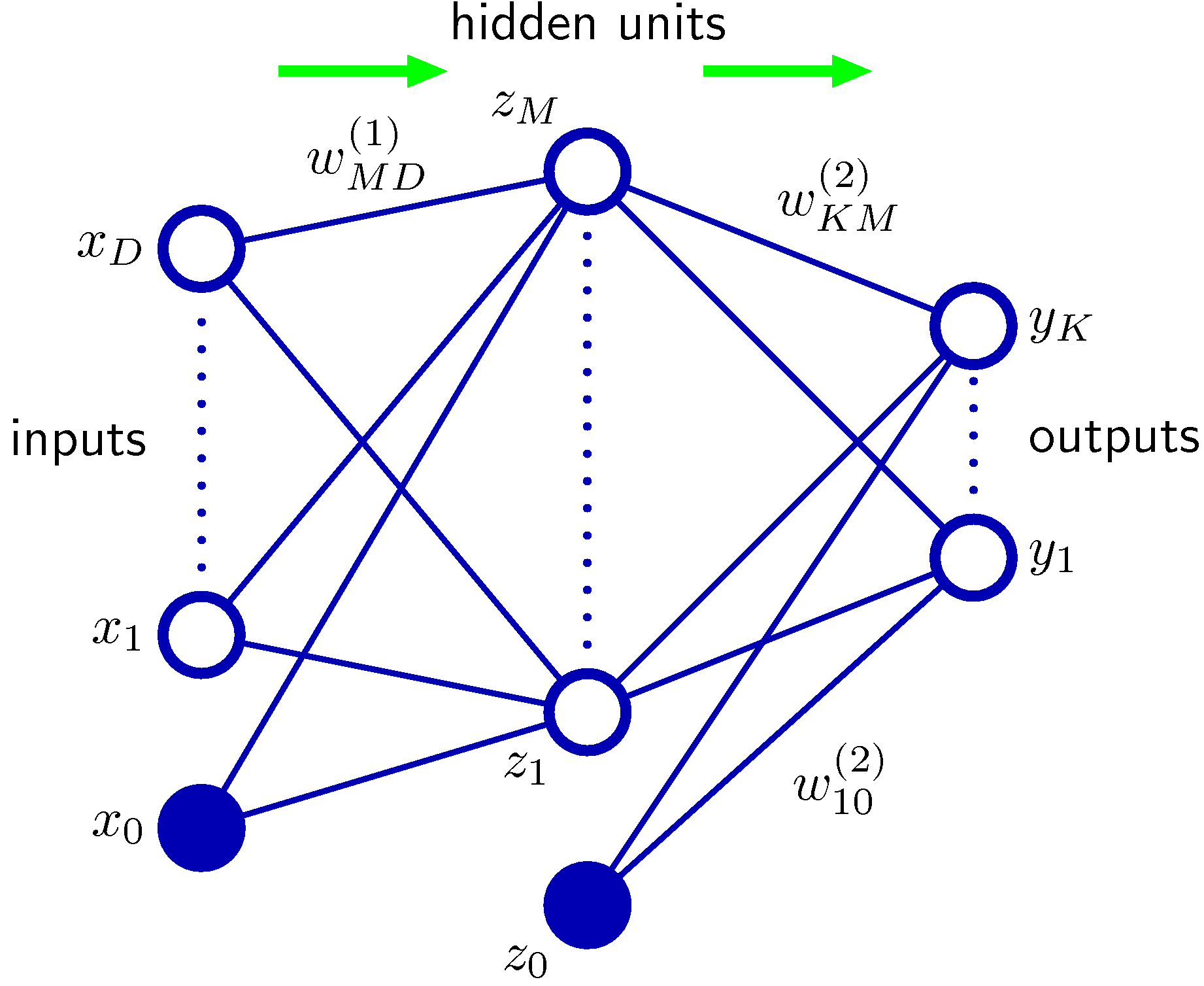
• 위의 그림이 지금까지 설명한 신경망을 도식화한 것으로 가장 기본적인 형태의 2-layer 신경망이다.
• 최종 출력되는 \( {\bf y} \) 는 위에 기술한 수식으로 계산할 수 있다.
• 신경망은 네트워크를 통해 forward 방향으로 정보를 전달하여 계산하는 방식을 취함
• 물론 위의 네트워크는 8장에서 소개되는 그래픽 모델은 아님. 이건 뒤에서 더 자세히 보기로 하고,
• 3.1 절에서 논의한 것처럼 바이어스는 \( x_0=1 \) 을 도입하여 좀 더 간단한 수식으로 정리할 수 있다.

• 마찬가지로 2번째 레이어에서도 이 식을 적용하면,

MLP (Multi-layer perceptrons)

• 4.1.7 절에 설명한 퍼셉트론(perceptron) 모델과 신경망 모델은 사실 동일하므로 멀티 레이어(layer)인 경우 이를 MLP 라고 부른다.
  • 신경망은 활성 함수로 시그모이드 스타일의 함수를 쓰고 퍼셉트론은 (불연속이고 비선형인) Step 함수를 사용한다는 차이가 있다.
• 만약 활성 함수에 비선형 함수가 아닌 선형 함수를 도입하면 어떻게 될까?
  • 활성 함수 자리에 선형 함수가 도입되면 최종적으로 \( y_k({\bf x}, {\bf w}) \) 함수는 비선형이 아니라 선형 함수가 된다.
  • 왜냐하면 선형 함수의 결합은 다시 선형 함수가 되기 때문.
  • 결국 히든유닛이 없는 함수와 동일한 상태가 된다.
  • 히든 유닛이 없는 신경망은 단일 퍼셉트론과 차이가 없고, 따라서 그냥 선형 분류기가 된다.
  • 따라서 MLP를 사용하려 했지만 퍼셉트론을 쓰는 것과 동일한 삽질을 하게 됨.
• 위의 2-layer 모델보다 좀 더 일반화된 모델 생성도 가능한가?
  • 2-layer 가 가능한 것을 보았으므로 중간 히든 유닛을 더 추가하여 N-layer 모델을 구성하는 것도 가능하다.
    • 하지만 당연히 연산해야 할 양도 많아지겠지.
  • 추가로, skip-layer 를 도입할 수도 있다.
    • 예를 들어 2-layer 모델을 사용하되, 일부 노드는 입력 변수에서 출력 변수로 바로 전달되는 엣지가 생성될 수도 있음.
    • 아래 그림을 참고하면 된다. (바이어스 노드는 생략)
  • sparse network
    • 레이어간 모든 연결이 존재하는 Dense 네트워크가 일반적이지만, 일부 노드만 연결되어 있는 모델도 있음.
    • 이런 모델을 Convolutional-NN 이라고 한다. (5.5.6절에 나온다.)
    • 하지만 특별한 언급이 없다면 신경망은 그냥 Dense 신경망이라 생각하면 된다.

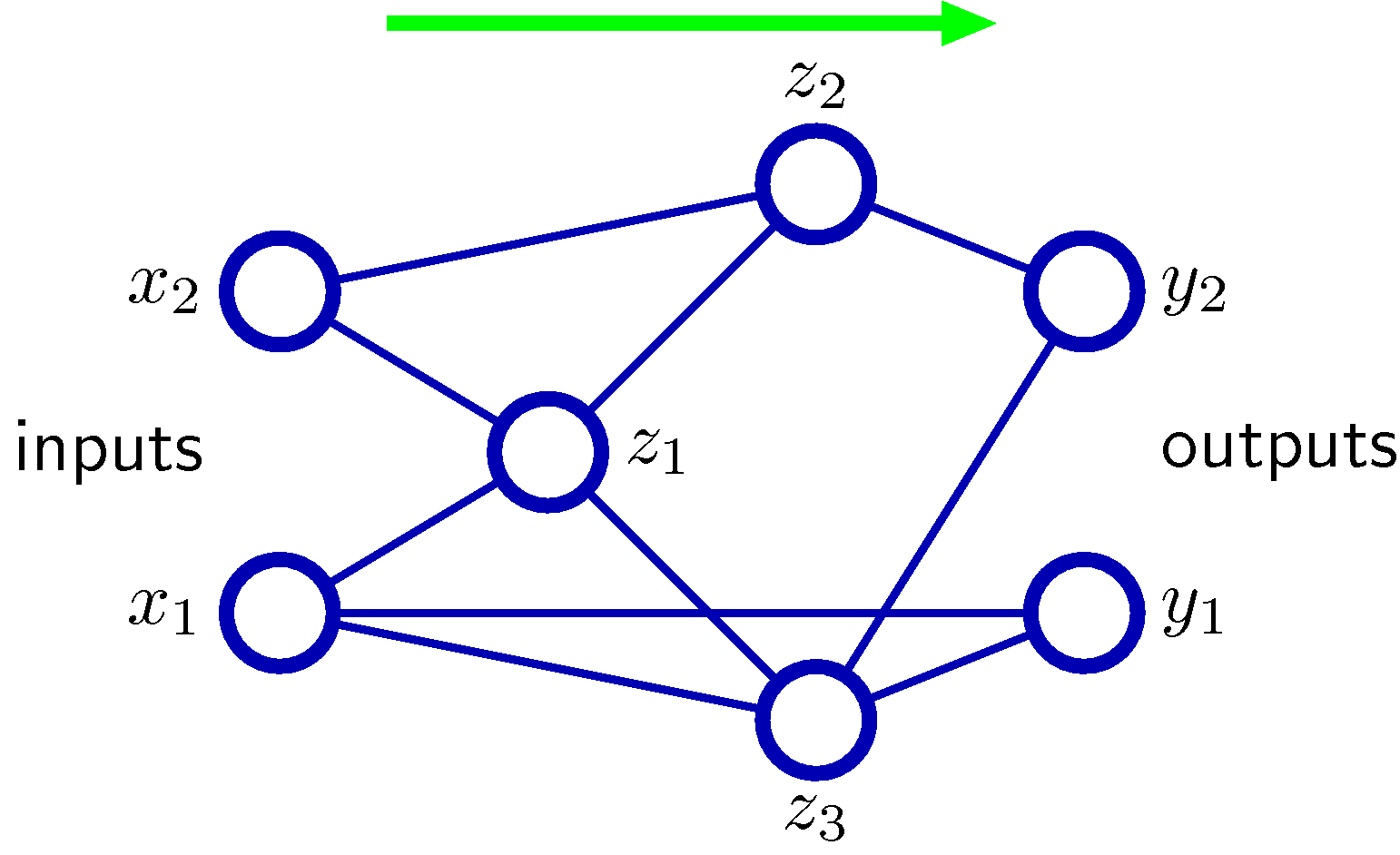
• skip-layer 또는 sparse-network 등의 신경망은 좀 더 일반화된 신경망이라 볼 수 있음.
  • 하지만 여기서도 feed-forward 라는 제한은 남아있으며, 이로 인해 출력값은 입력에 대한 결정(deterministic) 함수가 됨을 보장한다.
    • 그냥 최종 결과가 항상 도출될 수 있다는 것으로 간주하면 된다는 말이다.
  • 이를 일반화한 식을 기술해보자.

• 이는 한 노드로 들어오는 모든 노드들의 합을 표현한 식이다.

Universal Approximation

• 사실 feed-forward 네트워크를 활용한 근사법은 오랜 기간을 거쳐 광범위하게 연구되어 왔다.
• 신경망은 범용적인 근사법을 이미 제공함. (웬만한 경우에서도 다 사용해 볼 수 있다는 이야기다.)
• 예를 들어 2-layer 신경망일지라도,
  • 충분한 히든 유닛을 사용하기만 한다면 어떠한 연속 함수일지라도 근사해 낼 수 있음. (수학적으로 증명되어 있음.)
  • 임의의 활성 함수를 사용해도 근사할 수 있으나 물론 다 되는건 아님. 예를 들어 다항함수(polynomial)는 사용하면 안된다.
  • 물론 히든 유닛을 어마어마하게 넣게 되면 학습 시간이 너무 길어지거나, 현실적으로는 계산이 불가능해질 수 있음.
• 2-layer 신경망으로 근사한 함수의 결과는 다음과 같다.

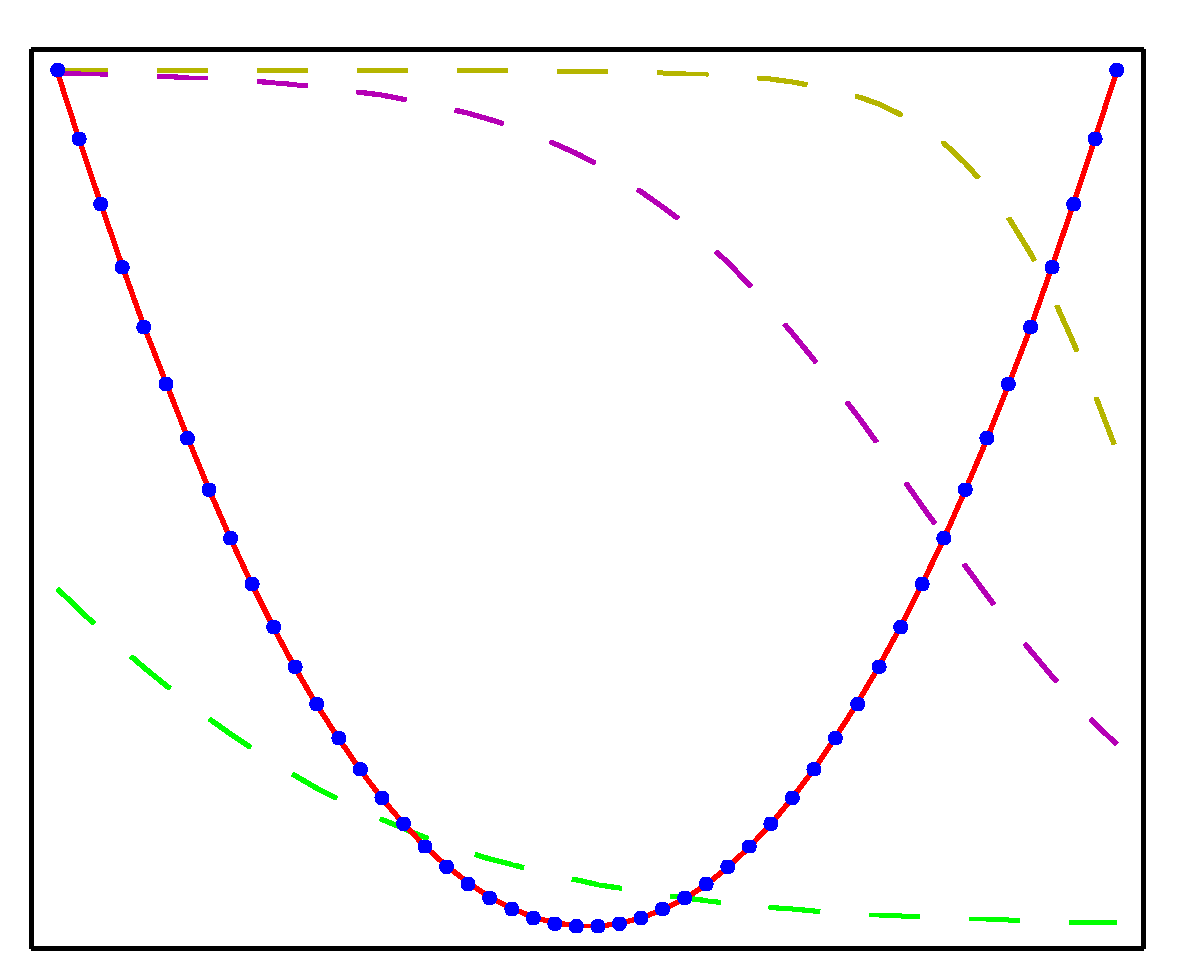
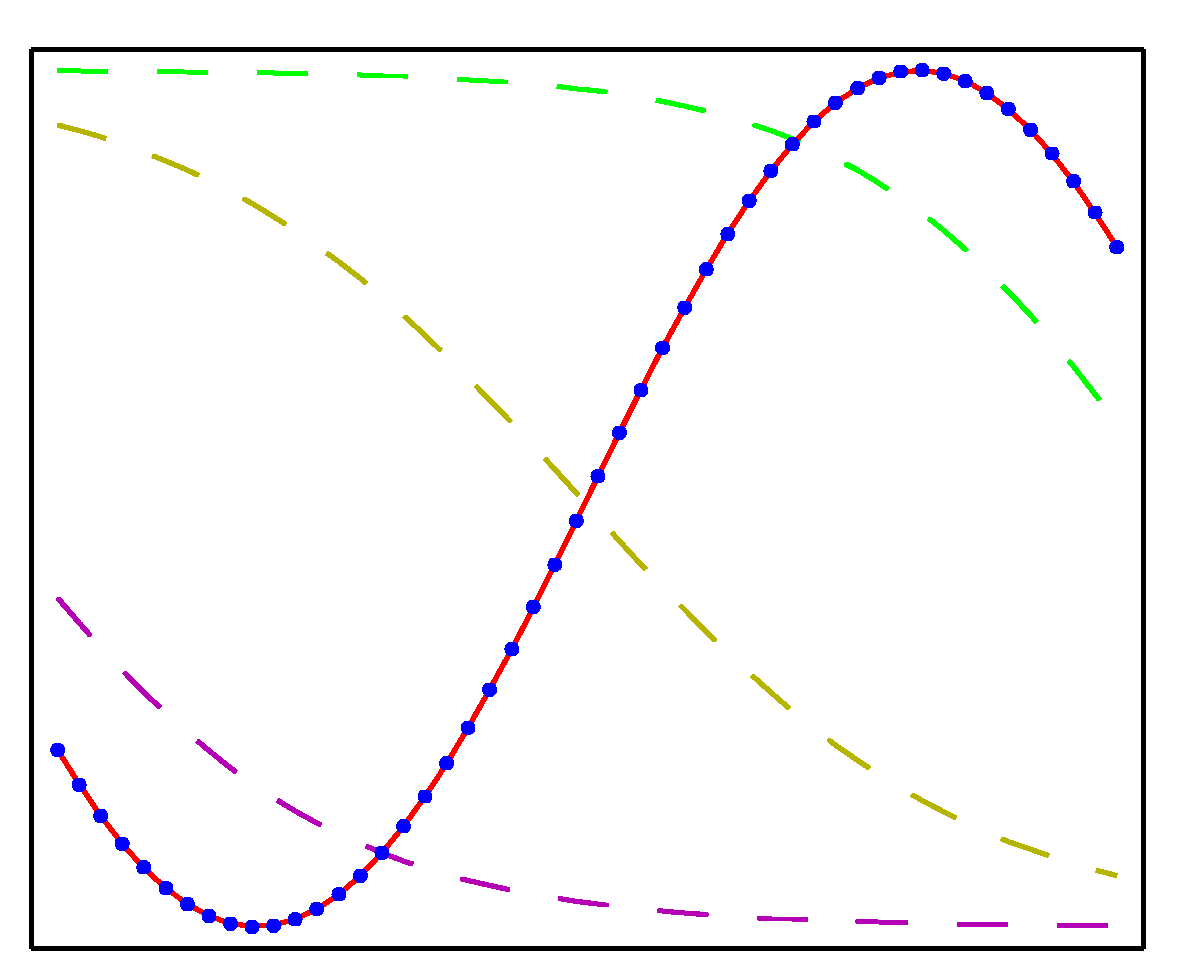
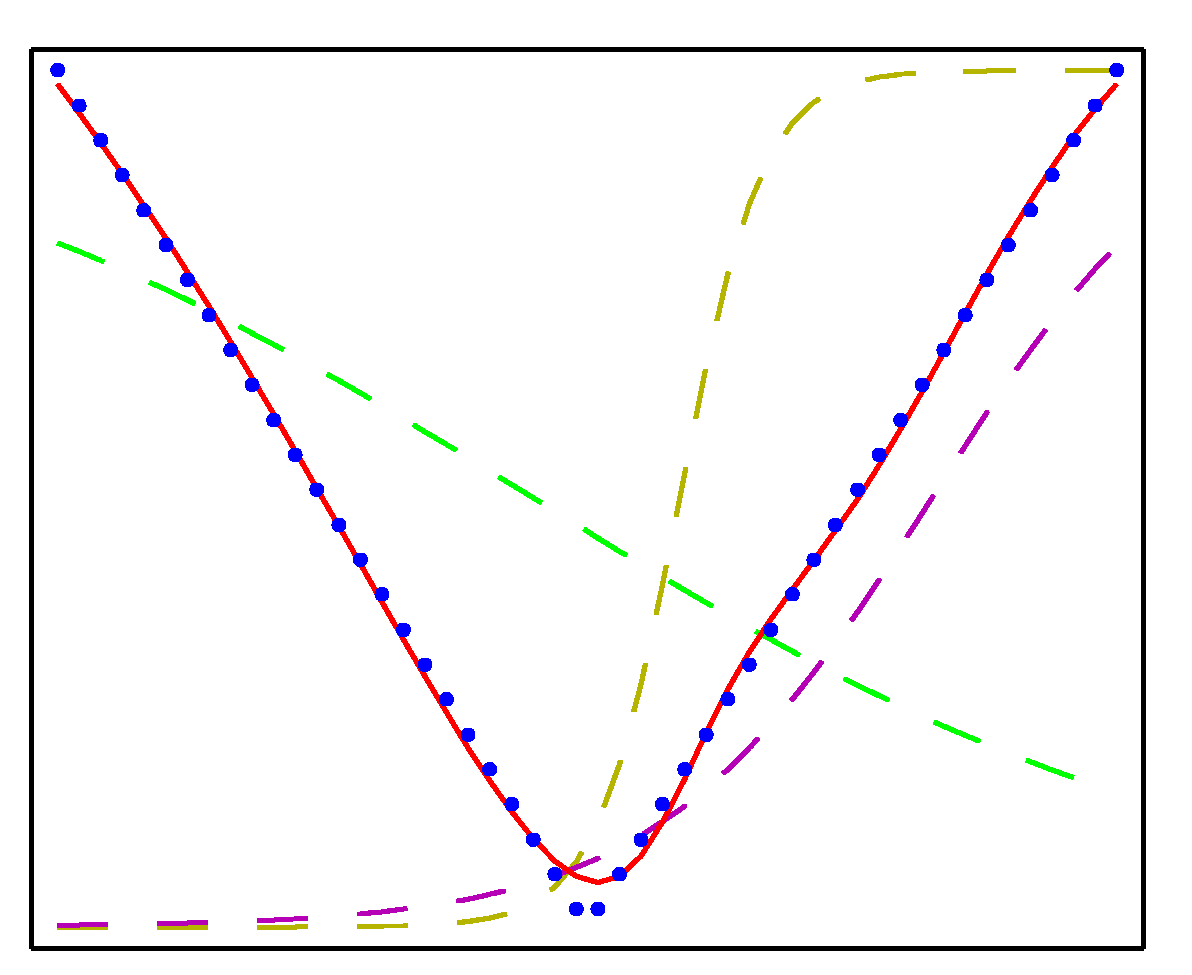
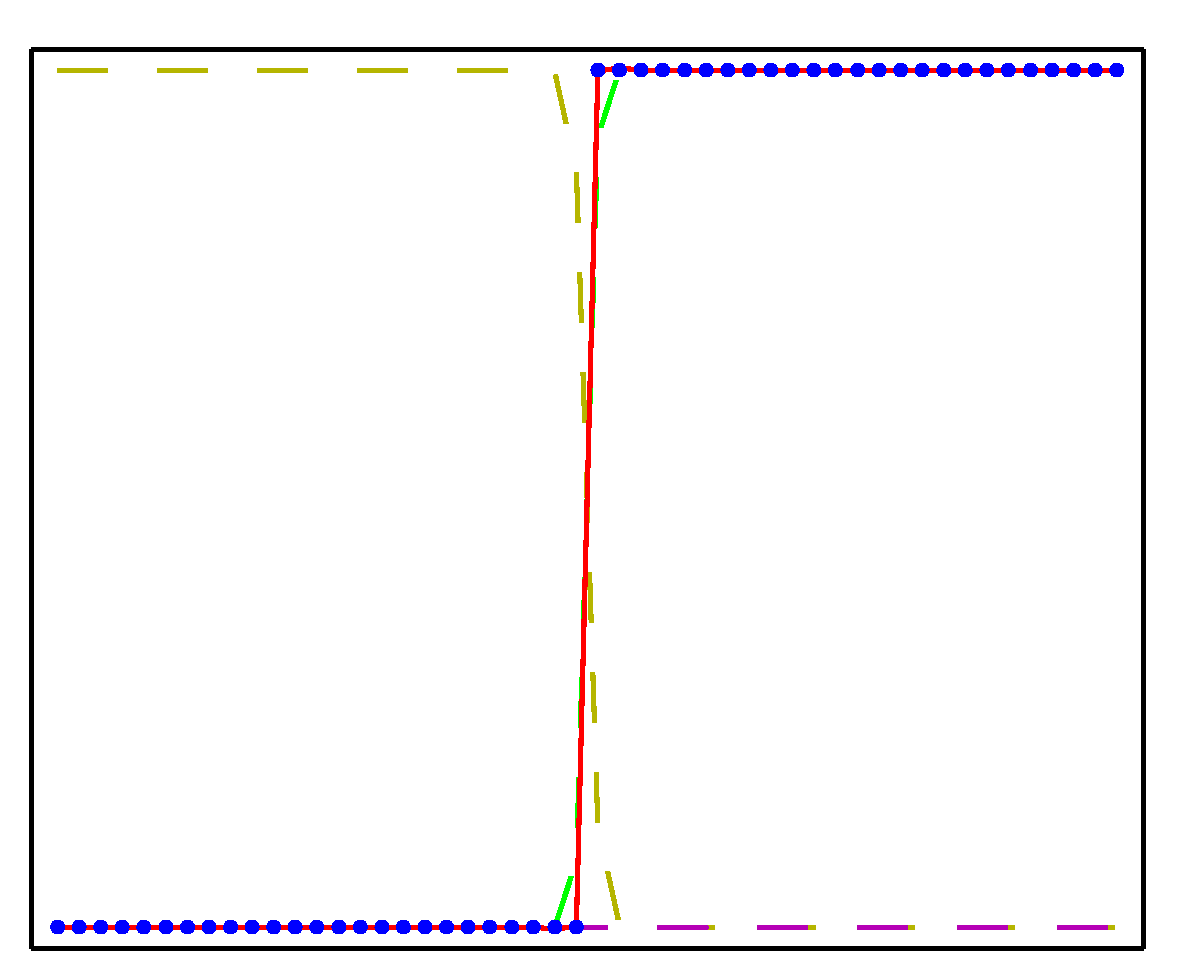
• 위의 그림에서 각 점들은 각각 (a) \( x^2 \) , (b) \( sin(x) \) , (c) \( |x| \) , (d) \( H(x) \) 로부터 생성된 점들이다. ( \)H \) 는 스텝함수)
  • 각각 50개의 샘플을 만들었으며, 히든 유닛으로 3개를 이용하여 결과를 만들어냈다.
  • 활성 함수는 \( tanh(\cdot) \) 를 사용하였다.
  • 근사한 식은 붉은색 선으로 실제 결과와 매우 유사함을 알 수 있다.
  • 물론 초기 \( {\bf w} \) 값을 어떻게 선정하느냐에 따라 결과가 많이 달라질 것이므로 어떻게 선정하느냐가 중요한데, 책에는 안 나와있다.

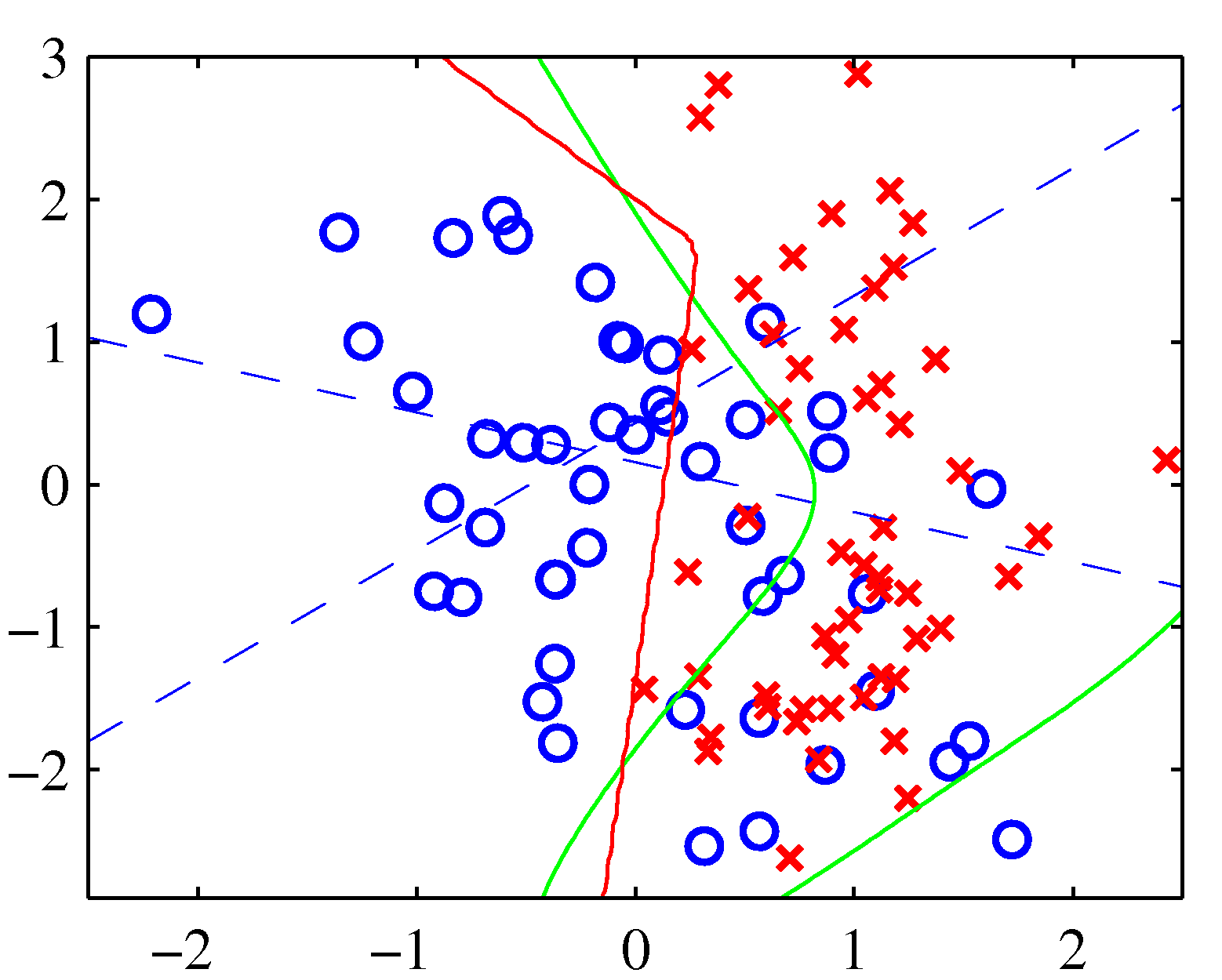
• 위의 그림은 2-layer 신경망을 간단하게 도식화한 그림이다.
  • 파란색 점선이 히든 레이어로 인해 구분되는 선형식을 의미한다. ( \)z=0.5 \) 일 때의 값이다.)
  • 붉은 색 선이 최종적으로 얻은 분류식이다.
  • 녹색 선이 실제 최적화된 분류선이 된다. (근데 이게 어떤 기준에 의해 선정되었는지는 모름.)

5.1.1. \( {\bf w} \) 공간의 대칭성 (Weight-space symmetries)

• 베이즈 모델과 비교하여 feed-forward 네트워크가 가지는 독특한 특성은,
  • 서로 다른 \( {\bf w} \) 에 대해서도 동일한 입력에 대해 동일한 출력 결과를 만들어낼 수 있다는 것이다.
  • 이러한 특성을 Symmetry 라고 하는데, 다음과 같은 Symmetry 가 있다.
• Sign-flip symmetry
  • 예를 들어 일반적인 2-layer 네트워크에서 히든 유닛에 대한 활성 함수가 \( \tanh \) 라고 할 때,
  • 수학적으로 \( \tanh(-a) = - \tanh(a) \) 가 성립하는 것을 이미 알고 있다. (odd function)
  • 따라서 어떤 히든 유닛 \( j \) 에 대해 연결되어 입력되는 \( w_{ji} \) 벡터의 부호를 바꾸면 출력 값은 기존 값에 부호만 바뀐 값이 된다.
  • 이 때 그 다음 레이어에서는 다시 \( w_{kj} \) 의 부호가 바뀌게 되면 이전과 동일한 결과를 얻게 된다. ( \)w_{kj} \cdot o_j \) 이므로)
  • 즉, 부호만 반대인 경우가 두 단계를 거치면 동일한 결과가 만들어지는 현상을 만들 수 있다.
  • 2-layer에서 히든 유닛이 \( M \) 개의 경우 이러한 경우를 총 \( 2^M \) 개 만들어 낼 수 있다. (조합)
  • 사실 \( \tanh(\cdot) \) 가 예를 들기 쉬워서 이야기한 것이지만 다른 활성 함수에서도 이런 현상을 만들어 낼 수 있다.
• Interchange symmetry
  • 같은 레이어 내 임의의 히든 유닛 2개에 대해 서로 위치를 바꾸게 되는 경우에도 최종 출력 값은 변함이 없다. (당연하다.)
  • 하지만 이런 경우 인덱스 번호는 바뀌게 되므로 \( {\bf w} \) 벡터 자체는 서로 다른 벡터로 취급할 수 있다.
  • 따라서 2-layer에서는 이런 경우를 총 \( M! \) 개 만들 수 있다.
• 종합하자면, 2-layer 환경에서는 간단하게 생각해봐도 동일한 결과를 만들어 낼 수 있는 \( {\bf w} \) 경우가 대략 \( M!\times 2^M \) 개나 된다.
• 다행인지 불행인지 \( {\bf w} \) 에 대한 symmetry 현상은 이 두 가지가 전부이다.
• 뭐, 결론은 동일한 결과를 가지는 \( {\bf w} \) 가 무궁무진 할 수 있으므로 잘 찾아야 한다는 것.
  • 전역 최소점을 찾을 수 없는 환경에서 동일한 에러 값을 가지는 \( {\bf w} \) 벡터가 다수 존재한다는 것은 구현자 입장에서 부담일 수 밖에 없다.