2. Network Training

지금까지 입력 벡터 $ {\bf x} $ 로부터 파라미터를 가지는 비선형 함수를 적용하여 출력 벡터 $ {\bf y} $ 를 만드는 신경망에 대해 살펴보았다.
앞서 최소 제곱법을 이용하여 다항식 커브 피팅 문제를 해결한 것처럼(1.1절) 여기서도 이런 형태로 에러 함수를 정의할 수 있다.

$E({\bf w}) = \dfrac{1}{2}\sum_{n=1}^{N}\|{\bf y}({\bf x}_n, {\bf w})-{\bf t}_n\|^2 \qquad{(5.11)}$

이제 이걸 확률 모델을 이용해서 식을 전개해보자.
- 이러한 확률적 해석은 네트워크 학습에 대한 일반적인 관점을 제공해주고,
- 풀려고하는 문제에 맞는 출력 함수와 에러 함수 선정 방식을 적절하게 설명할 수 있다.

회귀(Regression)

이제 신경망을 이용해서 3장에서 다루었던 회귀(regression) 문제를 풀어보도록 하자.
- 출력 값은 1차원의 실수 값으로 $ t $ 라고 표기했었다.
- 우리가 가정했던 사실은 $ t $ 가 $ x $ 에 종속적인 평균 값을 가지는 가우시안 분포를 따른다는 것이었다.
- 이를 수식으로 표현하면 다음과 같다.

$p(t|{\bf x}, {\bf w}) = N(t\;|\;y({\bf x}, {\bf w}), \beta^{-1}) \qquad{(5.12)}$

여기서 $ \beta^{-1} $ 은 가우시안 노이즈의 정확도(precision)를 의미한다. (분산의 역수이다.)
- 지금까지 다 봤던 내용들이므로 후딱 후딱 넘기도록 하자.
가능도 함수(likelihood)를 구하기 위해 식을 설정하도록 한다.
- 입력값 : $ {\bf X}=({\bf x}_1,…,{\bf x}_N) $ 이고 서로 독립적으로 발현된다. ( i.i.d )
- 출력값 : $ {\bf t}={t_1,…,t_N} $ 이고 1차원 실수 값

$p({\bf t}\;|\;{\bf X}, {\bf w}, {\bf \beta}) = \prod_{n=1}^{N}p(t_n\;|\;{\bf x}_n, {\bf w}, \beta)$

음의 로그항을 이용하여 식을 전개하면 다음과 같은 에러 함수를 얻을 수 있다.

$\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n, {\bf w})-t_n\}^2 - \frac{N}{2}\ln\beta + \frac{N}{2}\ln(2\pi) \qquad{(5.13)}$

여기서 사용될 $ y $ 함수는 앞서 설명했다. (식 5.7 참고)
- 즉 2-layer 모델을 기준으로 식을 전개해 보도록 하자.
이후에 이 식을 이용하여 베이지언 방식을 이용한 풀이법을 설명할 것이지만, 우선은 MLE 방식을 설명한다.
사실 신경망에서는 로그 가능도 함수를 최대화하는 문제로 처리하는 방식보다 에러 함수를 최소화하는 문제로 처리하는 것이 일반적이다.
물론 가능도 함수를 최대화하는 문제나 에러 함수를 최소화하는 문제나 모두 동일한 식을 만들어내는 것은 이전 장에서도 다 보았던 것들이다.
따라서 회귀 문제를 푸는데 있어 가능도 함수가 아닌 에러 함수를 정의하고, 정의된 에러 함수로부터 가장 적합한 $ {\bf w} $ 를 구하는 문제로 진행하도록 해보자.

$E({\bf w}) = \frac{1}{2}\sum_{n=1}^{N}\{y({\bf x}_n, {\bf w})-t_n\}^2 \qquad{(5.14)}$

원래 하던대로 MLE 를 구하면 된다.
- 다만 신경망에서는 $ y({\bf x}, {\bf w}) $ 가 비선형이기 때문에 $ E({\bf w}) $ 가 nonconvex 이다.
- 이 말은 미분을 해도 전역 최소점을 찾을 수 없다는 의미이다.
따라서 이를 구하는 문제는 에러 함수의 로컬 최소값(local minima) 형태로 구해지게 되는데 이건 5.2.1 절에서 설명하도록 하겠다.
우선 $ {\bf w}_{ML} $ 은 찾았다고 생각하고 $ \beta $ 를 구하는 식부터 좀 보자.
- 예전에 했던 방식대로 음로그 가능도 함수를 이용해서 구하면 된다.

$\dfrac{1}{\beta_{ML}} = \frac{1}{N}\sum_{n=1}^{N}\{y({\bf x}_n, {\bf w}_{ML})-t_n\}^2 \qquad{(5.15)}$

예전에 구한 식과 차이가 없다.
만약 $ t $ 의 결과가 단일 차원이 아니라 벡터가 되면 어떻게 될까?
- 이것도 예전과 마찬가지로 노이즈는 각 차원에 독립적이고 동일한 값을 가진다고 가정하고 식을 전개하면 된다.

$p({\bf t}|{\bf x}, {\bf w}) = N({\bf t}\;|y({\bf x}, {\bf w}), \beta^{-1}{\bf I}) \qquad{(5.16)}$

이 경우 최종 식도 거의 유사한 형태로 얻을 수 있게 된다.

$\dfrac{1}{\beta_{ML} } = \frac{1}{NK}\sum_{n=1}^{N}\|{\bf y}({\bf x}_n, {\bf w}_{ML})-{\bf t}_n\|^2 \qquad{(5.17)}$

여기서 $ K $ 는 타겟 값 벡터의 개수이다.
앞서 이야기한대로 회귀(regression) 문제에서 활성 함수는 identity 함수를 사용했으므로 $ y_k=a_k $ 가 성립한다.
- 즉, 회귀 문제는 함수 값 자체를 예측하는 문제이므로 활성 함수 $ f(\cdot)={\bf x} $ 였었다.
따라서 다음과 같은 식이 성립함을 알 수 있다.

$\dfrac{\partial E}{\partial a_k} = y_k-t_k \qquad{(5.18)}$

조금 뜬금없다 싶지만 이후에 Backpropergation 문제를 다룰 때 등장하므로 여기서 한번 눈에 익혀두면 좋다.

이진분류

이제 이진 분류의 문제를 살펴보도록 하자. (즉, classification 문제이다.)
앞 장에서 보았듯이 이진 분류 문제에서는 활성 함수로 시그모이드와 같은 함수들이 사용된다.

$y=\sigma\;(a)\equiv\dfrac{1}{1+\exp(-a)} \qquad{(5.19)}$

위의 식을 사용하면 $ 0\le y({\bf x}, {\bf w}) \le 1 $ 의 결과를 얻게 된다.
이진 문제이므로 $ p(C_1|{\bf x}) $ 와 $ p(C_2|{\bf x}) $ 를 표현해야 하는데 당연히 $ y $ 와 $ 1-y $ 로 사용한다.
이 식은 베르누이 프로세스와 동일하므로 다음과 같이 하나의 식으로 표현 가능하다.

$p(t|{\bf x}, {\bf w}) = y({\bf x}, {\bf w})^t\{1-y({\bf x}, {\bf w})\}^{1-t} \qquad{(5.20)}$

모든 관찰 데이터는 독립적으로 발생한다고 가정하므로 에러 함수를 최소 제곱법이 아닌 음의 로그 가능도 함수로 정의하면 된다.
이를 크로스 엔트로피 (cross-entropy) 라고 한다. 3장에서 소개한 내용이다.

$E({\bf w}) = - \sum_{n=1}^{N}\{t_n\ln{y_n} + (1-t_n)\ln(1-y_n)\} \qquad{(5.21)}$

분류 문제에서는 노이즈 정확도인 $ \beta $ 와 같은 요소는 없다.
왜냐하면 관찰 데이터에 이미 명확한 레이블(label) 타겟 값이 결정되어 제공되기 때문이다.
- 물론 레이블(lebel)이 잘못 표기된 데이터가 존재할 수도 있는 법이다.
- 뭐, 사실 이런 경우에도 쉽게 확장 가능하기는 하다. 더 이상 깊게 다루지는 않는다.
위의 수식에서는 cross-entropy 를 이용했는데, 사실 sum-of-squares 를 사용해도 상관은 없다고 한다.
- 다만 Simard 가 쓴 논문에 따르면 cross-entropy 가 학습 속도도 더 빠르고 일반화 성능도 더 좋다고 한다.
3장에서도 살펴보았지만 최종 출력 결과를 $ K $ 개의 이진 분류기를 이용해서 다분류기를 만들 수 있다.
- 이 경우는 최종 출력 결과가 각각의 시그모이드 활성 함수를 가진 $ K $ 개의 출력 노드로 생각할 수 있다.
이 때의 확률 모델은 다음과 같이 기술할 수 있다.

$p({\bf t}|{\bf x}, {\bf w}) = \prod_{k=1}^{K}y_k({\bf x}, {\bf w})^{t_k}[1-y_k({\bf x}, {\bf w})]^{1-t_k} \qquad{(5.22)}$

이제 cross-entropy 모델을 적용한다. 따라서 음로그 가능도 함수를 에러 함수로 정의한다.

$E({\bf w}) = - \sum_{n=1}^{N}\sum_{k=1}^{K} \{t_{nk}\ln{y_{nk} }+(1-t_{nk})\ln(1-y_{nk})\} \qquad{(5.23)}$

여기서 $ y_{nk} $ 는 $ y_{nk}=y_k({\bf x}_n, {\bf w}) $ 이다.
마찬가지로 이 함수를 출력값으로 미분한 식은 어떻게 될까?

$\dfrac{\partial E}{\partial a_k} = y_k-t_k$

오, 회귀 문제나 분류 문제나 에러 함수를 출력값으로 미분한 값은 동일한 결과가 나온다는 것을 알 수 있다.
마찬가지로 여기서도 간단하게 이런 사실만 알고 넘어가도록 하자. 뒤에서 다시 나온다.
신경망이 일반적인 선형 분류식과 다른점이 뭘까?
- 지금까지 살펴본 신경망에서 첫번째 레이어에 속한 가중치 $ {\bf w} $ 가 여러 출력값(말단)들 사이에서 다양하게 공유된다는 것을 알 수 있다.
  - 즉, 수식 내에서 보면 하나의 히든 노드가 최종 출력 값에 다양한 가중치를 통해 영향을 미치고 있음을 알 수 있다.
  - 선형 분류기의 경우 이러한 요소들이 모두 독립적으로 적용되고 있는 것과 마찬가지.
- 첫번째 레이어에서 이루어지는 작업은 사실 비선형 속성 선택(feature selection)을 의미하게 된다.
  - 따라서 좋은 자질을 가지고 있는 속성을 취하는 것이 된다.
- 서로 다른 출력에 대해 Feature가 공유되어 일반화 측면에 유리하다. (그런데 왜인지는 딱히 감이 오지를 않네.)

다중분류

이제 최종적으로 다중 분류식을 보자.
입력 데이터는 $ K $ 개의 서로 다른 클래스 중 하나에 속하게 된다.
이전에 다루었던 1-of-K 방식을 사용한다.
이를 이용한 일반화된 에러 함수는 다음과 같다.
- 즉 $ K $ 개의 출력 값에 대한 에러 값을 모두 합산하는 형태

$E({\bf w}) = - \sum_{n=1}^{N}\sum_{k=1}^{K}t_{nk}\ln y_k({\bf x}_n, {\bf w}) \qquad{(5.24)}$

이 때 $ y_k({\bf x}, {\bf w}) = p(t_k=1|{\bf x}) $ 이다.
사실 4장에서 다루었던 방식으로, 최종적으로 소프트맥스(soft-max) 함수를 얻게 된다.

$y_k({ {\bf x}, {\bf w} })=\dfrac{\exp(a_k({\bf x}, {\bf w}))}{\sum_j\exp(a_j({\bf x}, {\bf w}))} \qquad{(5.25)}$

이제 재미난 성질을 좀 보자. 위의 식에서 $ a_k $ 영역에 어떤 상수를 더해도 이 식은 항상 성립하게 되는데,

$\exp(a+b)=\exp(a)\exp(b)$

위와 같은 성질이 있기 때문이다.
- 따라서 위의 식에 대입하여 $ a_k $ 항에 특정 상수를 더하더라도 분자, 분모가 서로 약분되어 상수항은 사라지게 된다.
- 결국 $ a_k $ 에 어떤 상수를 더해도 최종 식 $ y_k $ 는 변하지 않기 때문에 에러 함수는 $ {\bf w} $ 공간에서 특정 방향으로는 상수가 된다.
  - 이게 무슨말이가 싶지만 다음을 기악해보자.
- 이를 막기위해 정칙화(regularaition)를 도입해야 한다. (당연히 뒤에 나온다.)
마지막으로 에러 함수를 $ a_k $ 로 미분한 값을 알아보자.

$\dfrac{\partial E}{\partial a_k} = y_k-t_k$

역시나 처음에 봤던 식이 나왔다.
- 이번 절이 주는 교훈은 아주 명확하다.
- 풀고 싶은 문제(즉, 회귀, 이진, 다중분류)에 따라 에러 함수를 다르게 정의하지만,
- $ a_k $ 에 대한 에러 함수의 미분 값은 $ y_k-t_k $ 로 모두 동일하다.
- 이후에 중요하게 사용되므로 꼭 기억하자.

5.2.1 모수 최적화 (Parameter optimization)

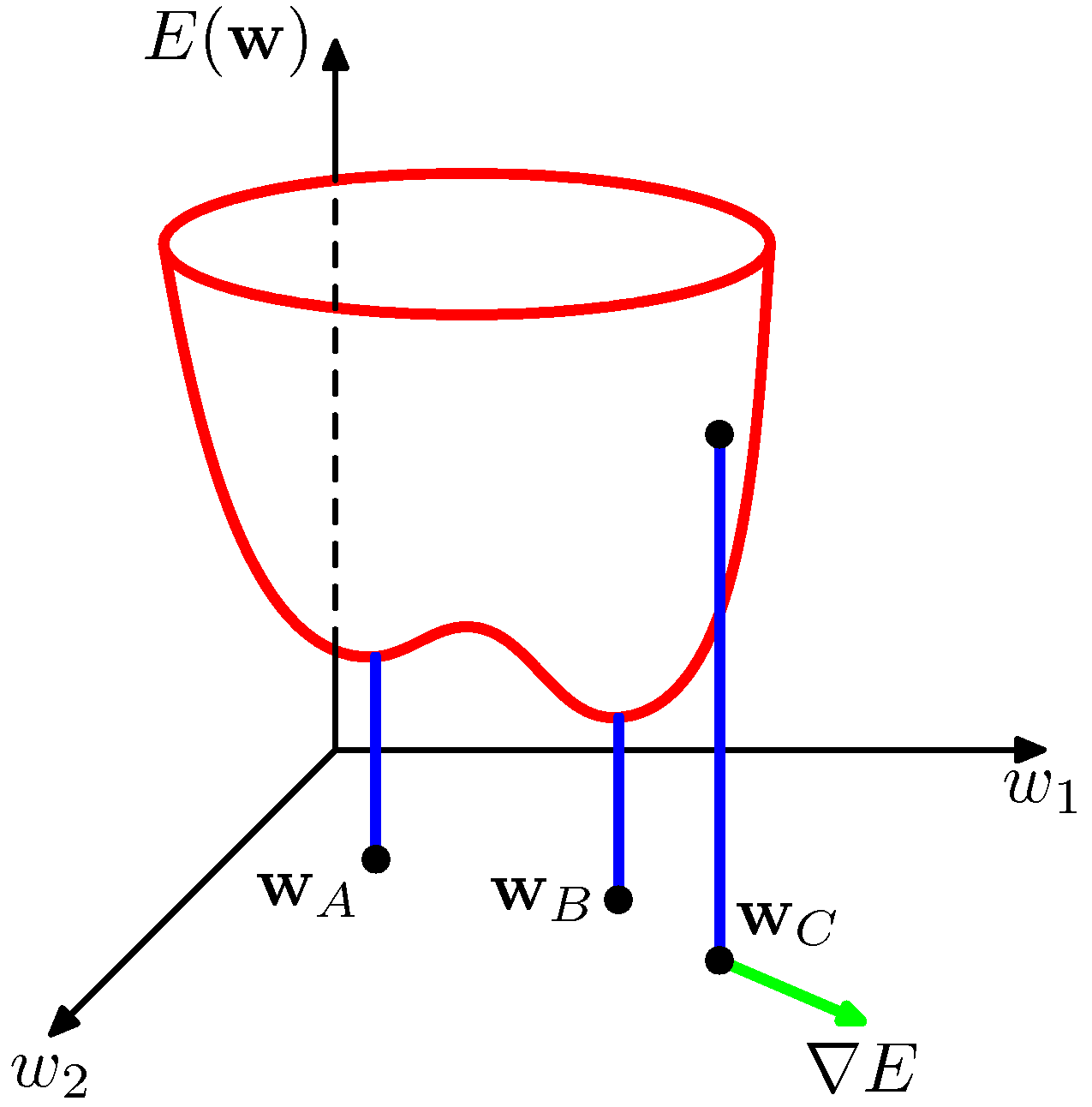
figure5.5

다음 단계로 어떻게 에러 함수 $ E({\bf w}) $ 를 최소화하는 벡터 $ {\bf w} $ 를 찾을 수 있는지 확인해보자.
위의 그림을 보면 임의의 한 점 $ {\bf w}_C $ 에서 미분한 벡터의 방향이 $ \nabla E $ 임을 알 수 있다.
- 임의의 한 점 $ {\bf w} $ 에서 약간 떨어진 곳을 $ {\bf w}+\delta{\bf w} $ 라고 하면,
- $ \delta E \simeq \delta{\bf w}^T\nabla E({\bf w}) $ 라고 할 수 있다.
- 에러 함수는 미분 가능하므로 최소값은 당연히 Gradient 가 없어지는 지점에서 나타나게 된다. ( $ \nabla E=0 $ )
- 그 외에는 $ -\nabla E({\bf w}) $ 방향으로 조금씩 이동하면 된다.

$\nabla E({\bf w})=0 \qquad{(5.26)}$

에러 함수는 비선형 함수에 종속되기 때문에 Gradient 값이 0이 되는 지점이 무척이나 많을 수 있다.
이런 지점을 지역 최소점(Local Minimum) 이라고 하고, 이 중 가장 작은 값을 가지는 지점을 전역 최소점(Global Minimum) 이라고 한다.
학습의 최종 목적은 전역 최소점(Global Minimum)을 찾는 것이지만 현실적으로 정확한 값을 찾기 어렵기 때문에 몇 개의 지역 최소점(Local Miminum)을 찾아 이 중 가장 작은 값을 가지는 지점을 정답으로 간주한다.
비선형 연속 함수의 최적화 문제에서 가중치를 구하기 위한 방법은 다음과 같다.
- (1) 초기값 $ {\bf w} $ 를 정하고,
- (2) 가중치 공간 내에서 특정 형태의 반복 식을 통해 찾고자 하는 위치를 계속 변경한다.
- (3) 목적함수에 좀 더 부합되는 $ {\bf w} $ 를 업데이트하고 이를 계속 반복함.

${\bf w}^{(\tau+1)}={\bf w}^{(\tau)}+\nabla{\bf w}^{(\tau)} \qquad{(5.27)}$

여기서 $ \tau $ 는 반복 스텝을 의미한다.
많은 경우에 Gradient 방식을 이용하여 값을 갱신하게 된다.
Gradient 방식의 중요성을 이해하기 위해 테일러 급수라를 이용한 에러 함수 근사 방법을 확인해 보는 것도 좋다.

5.2.2. 지역 이차형식 근사 (local quadratic approximation)

임의의 한 점에서의 함수를 근사하기 위한 여러 방법이 존재하는데,
- 이 중 테일러 급수를 이용한 함수 근사는 매우 유명함.
- 간단하게 테일러 급수를 이용한 함수 근사식을 확인해보자. 아래가 테일러 급수이다.

$f(x) \simeq f(a) + \dfrac{f'(a)}{1!}(x-a) + \dfrac{f''(a)}{2!}(x-a)^2 + \dfrac{f'''(a)}{3!}(x-a)^3 + \cdots$

물론 간단하게 표기할 수도 있다.

$\sum_{n=0}^{\infty}\dfrac{f^{(n)}(a)}{n!}(x-a)^n$

보시다시피 한 점 $ a $ 에서 함수 식을 근사하게 된다.
차수가 계속 증가할수록 한 점에서의 근사 값이 더 정확해지지만, 계산량이 너무 많아진다.
이제 이 식을 이용해서 에러 함수를 근사해보자.
- 물론 차수를 무한히 늘릴 수 없으므로 2차까지만 확장한다. (좀 심한 가정 아닌가?)

$E({\bf w}) \simeq E({\bf \widehat{w} }) + ({\bf w}-{\bf \widehat{w} })^T{\bf b} + \frac{1}{2}({\bf w}-{\bf \widehat{w} })^T{\bf H}({\bf w}-{\bf \widehat{w} }) \qquad{(5.28)}$

여기서 못 보던 값인 $ {\bf b} $ 와 $ {\bf H} $ 가 등장했다.
$ {\bf b} $ 는 $ {\bf \widehat{w} } $ 일 때의 $ E $ 의 Gradient 값이다. ${\bf b}\equiv\nabla \left.E\right|_{w=\hat{w} } \qquad{(5.29)}$
$ {\bf H} $ 는 헤시안(Hessian) 행렬이라고 부른다. ( $ {\bf H}=\nabla\nabla E $)

$({\bf H})_{ij}=\left.\dfrac{\partial E}{\partial w_i \partial w_j}\right|_{w={\hat{w}} } \qquad{(5.30)}$

이걸 최초의 식에 대입하며 풀면 다음의 식을 얻을 수 있다.

$\nabla E \simeq {\bf b} + {\bf H}({\bf w}-{\bf \widehat{w} }) \qquad{(5.31)}$

만약 $ {\bf w} $ 가 $ {\bf \widehat{w} } $ 에 충분히 가깝게 접근하면 위의 식은 꽤나 적절한 근사 식으로 생각할 수 있다.
자, 이제 특정 지점에서 이차 형식의 근사 식이 에러 함수를 최소화 하는 지역 최적점이라고 가정해보자.
그럼 $ \nabla E=0 $ 을 만족할 것이고 이 때의 $ {\bf w} $ 를 $ {\bf w}^* $ 라고 하면,

$E({\bf w})\simeq E({\bf w }^*) + \frac{1}{2}({\bf w}-{\bf w}^*)^T{\bf H}({\bf w}-{\bf w}^*) \qquad{(5.32)}$

이 때 헤시안 행렬 $ {\bf H} $ 는 $ {\bf w}^* $ 에 대해 얻어진 행렬이 된다.
이 함수가 기하학적으로 어떠한 모양을 가지게 되는지 분석하기 위해 헤시안 행렬에 대한 식을 잠시 전개해 보자.

${\bf H}{\bf u}_i=\lambda{\bf u}_i \qquad{(5.33)}$

헤시안 행렬은 대칭 행렬이다. (선형대수 책 참고)
- 따라서 대칭 행렬이 가지는 특징을 그대로 가지게 되는데 이는 고유 벡터와 많은 관련이 있다.
- 위의 식은 정방 대칭 행렬에서의 고유 벡터 식을 표현한 것이다.
- 여기서 $ {\bf u}_i $ 가 고유 벡터가 된다. 대칭 행렬에 대해 생성되는 고유 벡터끼리는 서로 직교(orthonormal)하므로,

${\bf u}_i^T{\bf u}_j=\delta_{ij} \qquad{(5.34)}$

위와 같은 형태로 기술할 수 있다.
- 근데 사실 위의 $ \delta $ 가 정확하게 뭘 의미하는지 모르겠다.
- $ i \neq j $ 인 경우 0, $ i = j $ 인 경우 1인 식을 의미하는 건가? (이거 같다.)
$ {\bf x}^T{\bf H}{\bf x} $ 와 같은 형태는 선형 대수 책에 많이도 나오는 형태이다.
여기서는 $ ({\bf w}-{\bf w}^*) $ 가 헤시안 행렬 좌, 우로 오는 것을 알 수 있다. 이 벡터는 기저 벡터로 표현이 가능한데,
- 고유 벡터가 orthonormal 하므로 고유 벡터를 기저 벡터로 사용 가능하다.

${\bf w}-{\bf w}^*=\sum_i \alpha_i{\bf u}_i \qquad{(5.35)}$

위의 식이 가능한 이유는 $ {\bf u}_i $ 가 단위 기저 벡터가 되기 때문에 표현 공간 내에서 임의의 한 벡터를 벡터를 기저 벡터의 선형 합으로 표현 가능하기 때문.
여기서 $ \alpha $ 는 일정한 크기의 상수이다.
이와 관련된 내용은 선형 대수 책을 참고하면 대부분의 교재에서 나오는 내용이다.
최종 식은 다음과 같이 기술할 수 있다.

$E({\bf w})=E({\bf w}^*) + \frac{1}{2}\sum_i\lambda_i\alpha_i^2 \qquad{(5.36)}$

헤시안 행렬 $ {\bf H} $ 이 양의 정부호 행렬(positive definite) 이 되기 위한 필요 충분 조건(i.f.f)은 다음과 같다.

${\bf v}^T{\bf H}{\bf v}>0, \;for\;all\;v\neq 0 \qquad{(5.37)}$

왜 헤시안 행렬이 양의 정부호 행렬이 되어야 하는 것일까?
- 양의 정부호 행렬이어야만 극소값을 가지게 된다.
- 그 외에는 새들 포인트가 되거나 극대값이 되어버림.
이 때 고유 벡터는 기저 벡터가 되기 때문에 고유 벡터로 임의의 벡터를 표현 가능하다.
따라서 임의의 벡터 $ {\bf v} $ 를 다음과 같이 표기 가능하다.

${\bf v}=\sum_{i}c_i{\bf u}_i \qquad{(5.38)}$

따라서 다음의 식을 얻게 된다.

${\bf v}^T{\bf H}{\bf v}=\sum_{i}c_i^2\lambda_i \qquad{(5.39)}$

그리고 $ {\bf H} $ 가 양의 정부호 행렬이 되기 위한 필요 충분조건으로 고유 값이 모두 양수( \)>0 \)) 여야 한다.
- 이건 양의 정부호 행렬의 필요 충분 조건이 된다.
새로운 좌표 축에서 고유 벡터를 이용해 에러 함수를 표현한 그림은 다음과 같다.

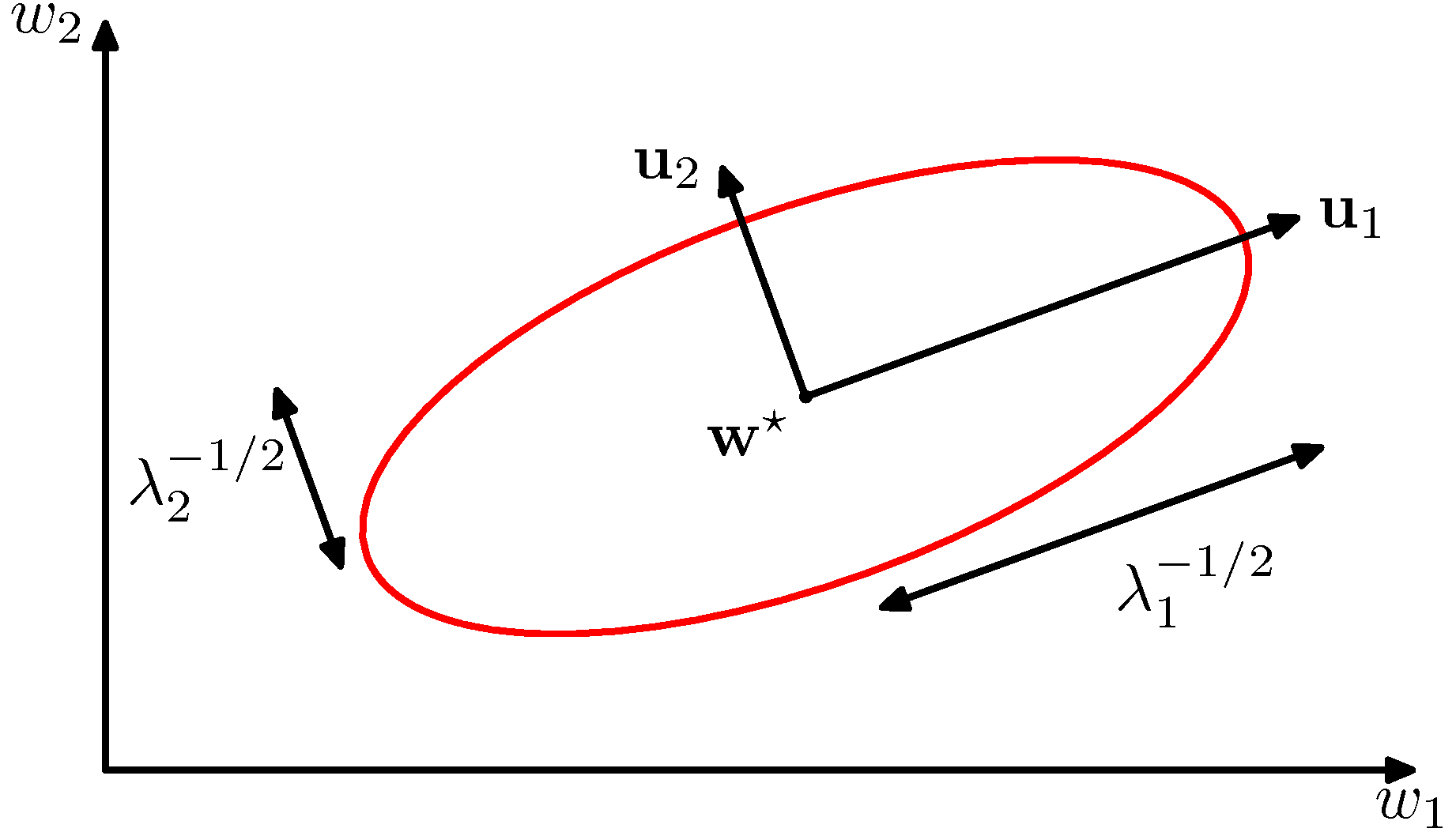
figure5.6

사실 이거 많이 본 그림이다.
양의 정부호 행렬을 가져야만 타원형의 결과를 얻을 수 있다.
에러 함수는 최소 값인 $ {\bf w}^* $ 을 중심으로 가지는 이차 형식의 함수로 정의될 수 있다. 이는 결국 타원이 된다.
붉은색 선은 동일한 에러 값을 가지는 위치이며, 타원체를 기준으로 고유 벡터로는 타원의 방향을, 고유값으로는 타원의 퍼짐을 알 수 있다.
$ {\bf w}^* $ 근처의 어떠한 값도 모두 $ E({\bf w}^*) $ 보다는 큰 값을 가지게 된다.
- $ \lambda $ 값이 양수이므로 양의 상수가 에러 값에 추가되게 된다.
- $ \lambda $ 는 아까 말했듯 타원을 만드려면 양수가 되어야 함.
어쨌거나 극소값을 가지기 위한 조건으로 1차식인 경우 아래 식을 만족해야 한다.

$\left.\dfrac{\partial^2 E}{\partial w^2}\right|_{w^*}>0 \qquad{(5.40)}$

이를 확장하여 $ D $ 차원의 경우에는 헤시안 행렬이 양의 정부호 행렬이 되어야 한다. (극소값을 가지기 위해)

5.2.3 그라디언트 정보 사용하기 (Use of gradient information)

우리는 이후에 역전파 알고리즘(backpropagation)을 사용하기 위해 에러 함수의 경사도(gradient)를 구하는 식을 사용하는 것을 보게 될 것이다.
경사도라는 말은 좀 어색하므로 앞으로는 그냥 그라디언트라고 표기할 것이다.
이후에 역전파 알고리즘으로 에러 함수의 그라디언트를 효율적으로 평가 가능하다. (뒤에서 보자.)
에러 함수를 이차 형식(quadratic)의 근사 식으로 표현한 식을 다시 한번 생각해보자.

$E({\bf w}) \simeq E({\bf \widehat{w} }) + ({\bf w}-{\bf \widehat{w} })^T{\bf b} + \frac{1}{2}({\bf w}-{\bf \widehat{w} })^T{\bf H}({\bf w}-{\bf \widehat{w} })$

여기서 얻어야할 요소들은 $ {\bf b} $ 와 $ {\bf H} $ 이고 이들은 총 $ W(W+3)/2 $ 개의 파라미터로 이루어져 있다.
- 헤시안 행렬은 대칭 행렬이므로 위와 같은 개수가 나온다.
여기서 $ W $ 는 벡터 $ {\bf w} $ 의 차수를 의미한다.
여기서 지역 최소점은 이 이차 형식의 최소점이 되고 따라서 이 때의 연산량은 $ O(W^2) $ 에 영향을 받게 된다. (이차식이기 때문)
- 에러 값을 구할 때 $ O(W^2) $ 만큼의 연산이 들어간다고 생각하면 된다.
- 따라서 함수를 평가하기 위해서 $ O(W^2) $ 만큼의 비용이 들고,
- 이러한 평가를 각각의 $ {\bf w} $ 요소에 대해 변경을 해보면서 수행해야 하므로 $ O(W) $ 의 비용이 든다.
- 따라서 전체 필요한 비용은 $ O(W^3) $ 이 된다.
하지만 그라디언트 정보를 사용하게 되면 어떻게 될까?
- $ W $ 개의 가중치에 대해 이미 $ \nabla E $ 값이 존재한다고 하면 그냥 $ O(W) $ 로 데이터를 갱신할 수 있다.
- 마찬가지로 backpropergation 알고리즘을 사용하게 되면 $ \nabla E $ 를 구하는데 $ O(W) $ 의 비용이 들어간다.
- 총 $ O(W^2) $ 으로 계산을 끝마칠 수 있다.

5.2.4 그라디언트 감소 최적화 (Gradient descent optimication)

Batch Method

가장 손쉬운 접근법은 가중치를 업데이트할 때 에러 함수의 그라디언트를 사용하는 것.

${\bf w}^{(\tau+1)} = {\bf w}^{(\tau)} - \eta \nabla E({\bf w}^{(\tau)}) \qquad{(5.41)}$

이 때 $ \eta > 0 $ 을 만족해야 하며 $ \eta $ 는 학습률(learning rate) 이라고 한다.
관찰 데이터를 한번에 사용해서 가중치를 갱신하는 방식을 batch 방식이라고 하며 가중치 갱신 작업이 진행되는 동안 에러 함수 값을 가장 작게 만드는 방향으로 가중치 벡터가 갱신되게 된다.
- 이를 gradient descent 또는 steepest descent 라고 부른다.
- 하지만 실제로 성능은 그리 좋지 못하다.
많은 경우 conjugate gradients 와 같은 방식이나 quasi-Newton 방법을 이용하여 batch 방식을 사용한다.
- 실제 이러한 방식이 더 좋은 성능을 내는 것으로 알려져 있다. (빠른 속도와 더 간단한 그라디언트 함수 사용)
앞서 설명한데로 에러 함수를 그라디언트 방식으로 접근하는 경우에 전역 최소점이 아닌 지역 최소점을 찾게 된다.
- 따라서 랜덤하게 초기값을 지정한 뒤에 가급적 여러 번 작업을 반복하여 가장 최소가 되는 지점을 선택하여 사용하면 된다.

On-line Method

배치 모드가 아닌 데이터를 하나씩 업데이트하는 방식도 있다.
이를 on-line 방식이라고 한다.
- 실제로 성능도 좋고 많은 데이터를 처리하기에 적합한 방식이다.
이제 각각의 독립된 관찰 데이터를 이용하여 에러 함수를 정의하여 보자.

$E({\bf w}) = \sum_{n=1}^{N}E_n({\bf w}) \qquad{(5.42)}$

on-line gradient descent 방식을 sequential gradient descent 또는 stochastic gradient descent 라고도 부른다.
가중치에 대한 갱신은 다음과 같은 방식을 사용한다.

${\bf w}^{(\tau+1)} = {\bf w}^{(\tau)} - \eta \nabla E_n({\bf w}^{(\tau)}) \qquad{(5.43)}$

입력 데이터를 순차적으로 입력하면서 반복을 수행할 수도 있고 임의로 데이터를 선택해가며 반복을 수행할 수도 있다.
일정 크기의 부분 집합 데이터를 기본 단위로 하여 처리하는 mini-batch 방식을 사용할 수도 있다.
온라인 업데이트 방식의 장점은 redundancy 에 있다.
- 만약 입력 데이터를 그대로 복사해서 2배의 크기로 만들어 학습을 한다고 해보자.
- 이럴 경우 배치 모드는 2배의 연산 비용이 들어간다.
- 하지만 온라인 업데이트 방식은 동일한 비용이 들어간다.
또 다른 장점은 지역 최소점을 탈출할 가능성에 있다.
- $ E_n({\bf w}) $ 의 stationary 지점은 $ \nabla E({\bf w}) $ 의 stationary 지점과 다르기 때문에 지역 최소점을 벗어날 수 있는 여지가 생긴다

Chapter. 5