- 앞서 로지스틱 회귀에 대한 베이지안 관점을 살펴보았다.
- 이제 3.3, 3.5절에서 다루었던 선형 회귀 분석에 대한 베이지안 방식보다 좀 더 복잡한 형태를 살펴보게 될 것이다.
- 이제부터 사후 분포가 가우시안 분포라는 가정은 버리도록 한다.
- 사후 분포가 가우시안이라고 가정한 것은 가능도 함수와 사전 확률이 모두 가우시안이라고 가정했기 때문
- 하지만 앞 절에서 살펴보았듯이 가능도 함수에 사용되는 클래스-조건부 밀도가 가우시안 분포라고 말하기 어렵다.
- 따라서 \( < \) “애매한 분포” \( \times \) “가우시안 분포” \( = \) 가우시안? \( > \) 에 대한 대답을 하기가 어려워진다.
- 이제 사후 분포를 근사하기 위한 방법 중 널리 알려진 라플라스 근사법(laplace approximation)에 대해 다루어보도록 하자.
- 물론 라플라스 함수가 사후분포만을 근사하기 위한 근사식은 아니고 임의의 함수를 특정 위치에서 정규 분포로 근사하는 기법이다.
- 우리는 다음 절에서 사후 분포를 라플라스 근사법을 이용해서 근사하는 것을 확인할 것이다. 그래서 미리 언급되는 것이다.
- 이제 우리의 목표는 연속된 입력 범위를 가진 입력 변수에 대한 가우시안 밀도 함수를 근사하는 작업이다.
- 즉, 우리가 얻게 되는 사후 확률 분포가 애매하기는 하지만 그 분포와 가장 비슷한 가우시안 분포를 찾고 이를 대신 사용한다는 것이다.
- 그러기 위해서는 어떤 확률 분포에 대한 근사 분포로서 가우시안 분포를 찾는 과정을 알야아 햔다. 이제부터 살펴볼 것이다.
- 입력 변수 \( z \) 에 대해 가우시안 출력 분포는 다음과 같이 정의하도록 한다.
- 일단 \( z \) 는 1차원 데이터라고 가정한다. 이후에 다차원 데이터 영역으로 확장하도록 한다.
- 여기서 \( Z \) 는 \( Z=\int f(z)dz \) 를 의미한다. (즉, 확률값을 만들기 위한 정규화 계수가 된다.)
- 우리는 \( Z \) 를 알지 못하는(unknown) 값이라고 간주한다.
- 하고자 하는 일은 명확한데, 주어진 입력 변수를 보고 이를 가장 잘 표현하는 정규 분포를 근사하는 것.
-
\( f(z) \) 는 사실 어떤 함수가 되어도 상관은 없다. 다만 이 함수에 가장 가까운 정규 분포를 찾을 것이다.
- 1단계 : \( p(z) \) 에 대한 최빈값(mode) 찾기
- \( p(z) \) 를 \( z \) 에 대해 미분하여 0 이 되는 지점 \( z_0 \) 를 찾는다.
- 2단계 : \( \ln f(z) \) 를 \( z \) 에 대한 2차식 형태로 근사한다.
- 가우시안 분포는 로그를 사용했을 경우 변수에 대한 2차식의 형태로 만들어진다.
- 바꾸어 말하면 \( \ln f(z) \) 를 \( z \) 에 대한 2차 함수로 근사할 수 있다면 이에 대한 확률 밀도를 가우시안 형태로 근사 가능하다는 것.
- 따라서 테일러 급수에서 2차 텀까지 근사 식을 적용해 보자.
- 갑자기 테일러 급수가 등장해서 당황할 수 있지만 특정 함수를 한 위치에서 근사하는 식으로 생각하면 된다.
- 물론 모든 함수식을 다 근사할 수 있는 것은 아니고 무한번 미분 가능한 \( f(z) \) 함수가 필요하다.
- 일단은 이렇게 가정하고 테일러 급수를 적용해보도록 하자.
- 이제 \( f(z) \) 에 대한 로그 함수를 테일러 급수로 근사하되, 이 식을 2차식이 되도록 만든다.
- 2차 식까지 적용을 했는데 1차 식(한 번 미분한 텀)은 수식에 없다.
- 왜냐하면 \( z=z_0 \) 인 경우 미분 값이 0인 지점이기 때문이다. 이 점을 중심으로 테일러 급수를 전개했다.
- 자, 이제 로그를 없애서 지수 함수의 꼴로 만들어 보자.
- 자 이제 예쁜 모양을 얻긴 했지만 정규 분포로 가기엔 조금 부족한 면이 있다.
- 이 식을 가급적 정규화 상수가 포함된 식으로 바꾸자. 새로운 함수 \( q \) 를 정의하고 위의 식을 우겨넣는다.
- 물론 이 경우에는 \( A>0 \) 인 경우만 가능하다.
- \( z_0 \) 를 최대값으로 생각했기 때문에 \( f(z) \) 의 함수에서 \( z_0 \) 의 위치에서의 2차 미분값은 당연히 음수가 나와야 한다.
- 따라서 이 식에 의해 \( A \) 는 양수가 나와야 한다. (부호가 반대이므로)
- 이게 라플라스 근사식(Laplace approximation)이 된다.
- 좀 더 자세한 사항은 아래 그림을 참고하자.
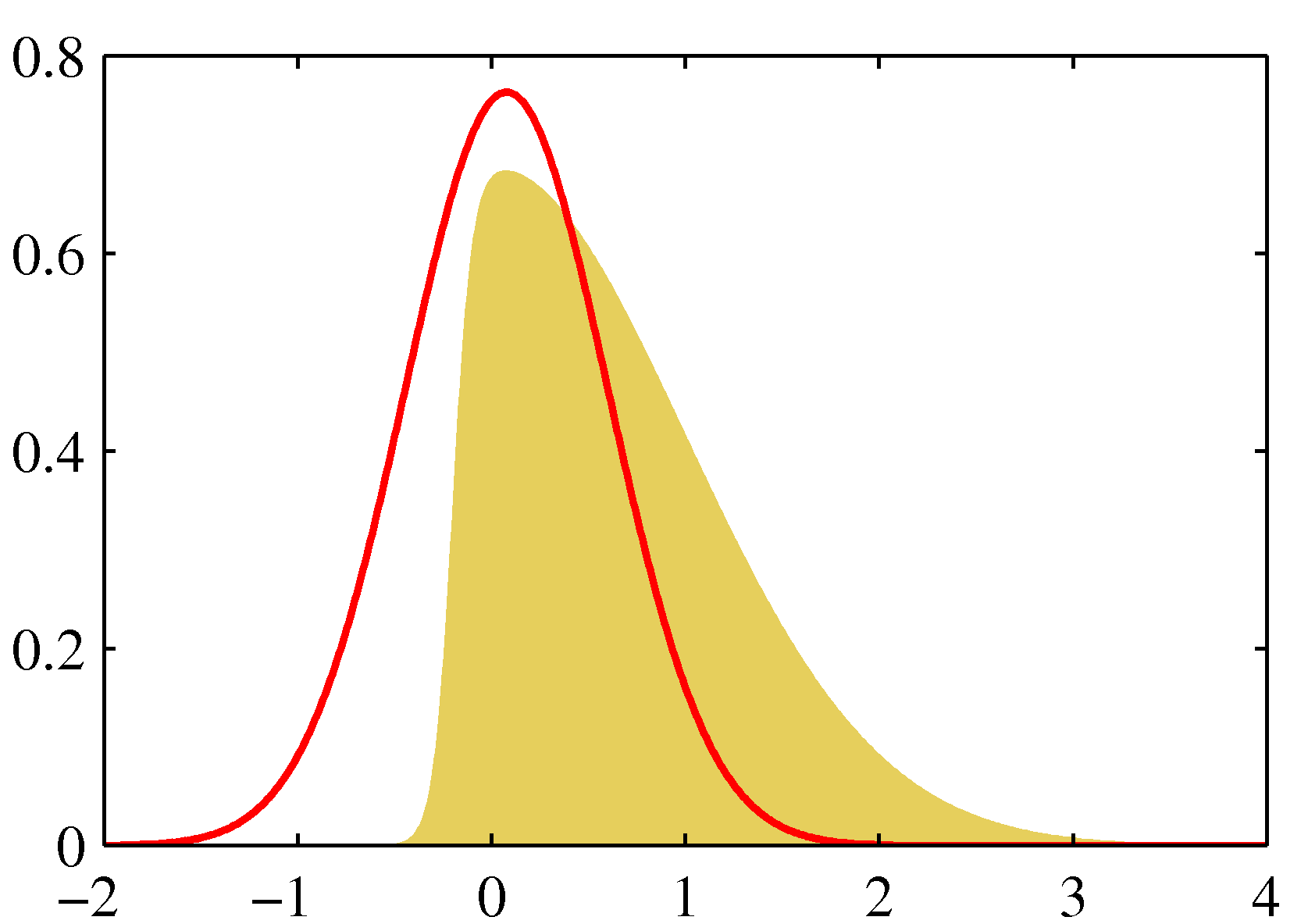
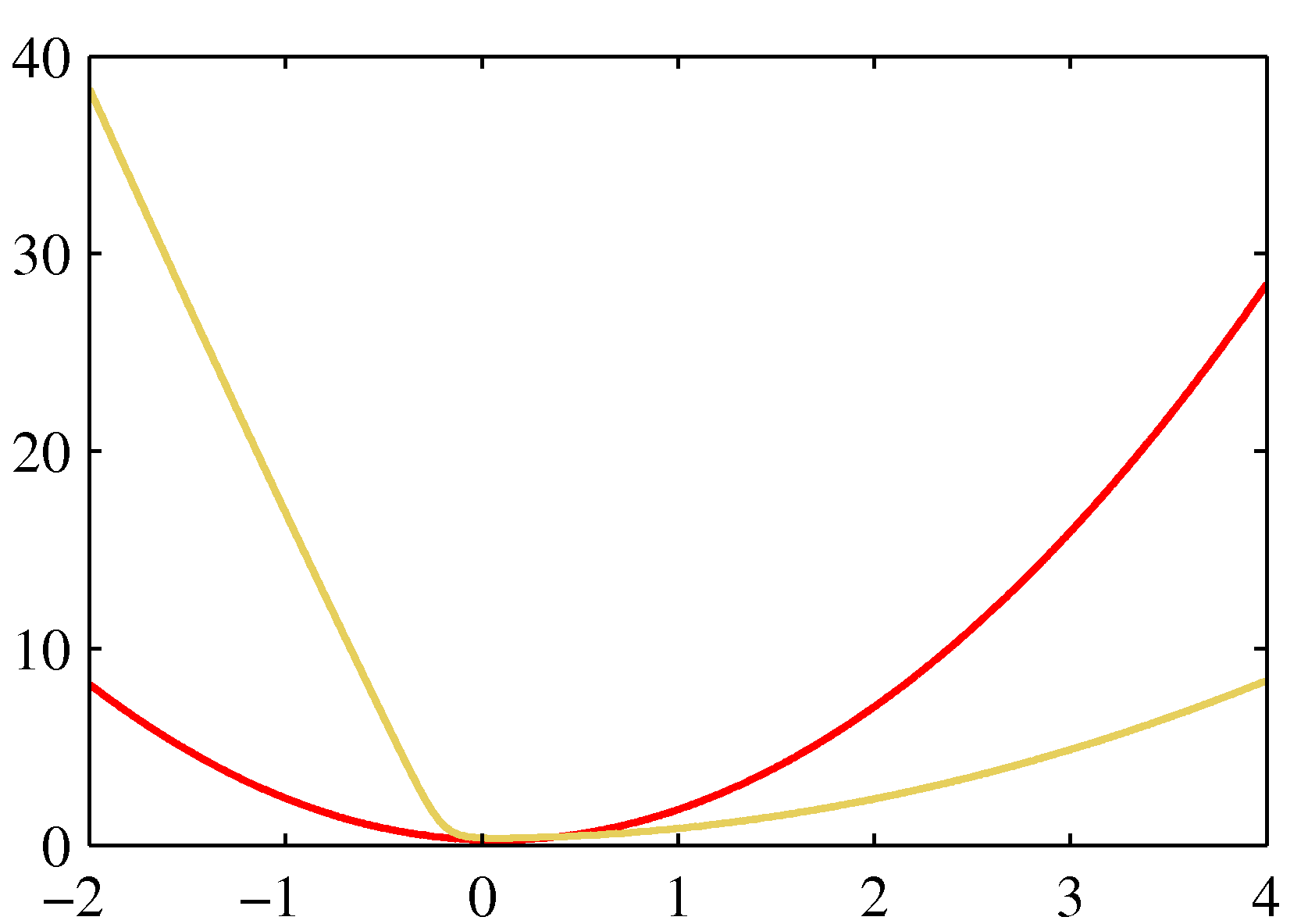
- 왼쪽을 보면 실제 \( p(z) \) 분포는 노란색 영역이고 이를 붉은 색의 정규 분포로 근사한 것이다.
- 오른쪽은 음 로그를 붙인 결과로 가장 작은 값이 같다는 것을 알 수 있다.
M 차원으로의 확장
- 이제 이 식을 다차원으로 확장을 해보자.
- 사실 앞서 설명한 것과 거의 같은 내용이고 \( z \) 를 \( M \) 차원의 벡터로 간주하고 확장하면 된다.
-
테일러 급수로 근사를 하기 때문에 1차에 대한 식 \( \nabla f({\bf z}) \) 가 식에서 제거된다.
- 여기서 \( {\bf A} \) 는 \( M\times M \) 크기를 가지는 헤시안(Hessian) 행렬이다.
- 1차원 식에서와 유사하게 다음과 같이 정의된다.
- 이제 로그를 없애보자.
- 마찬가지로 \( q({\bf z}) \) 를 정의하도록 한다.
- 당연히 다변량 정규 분포의 형태를 고려하여 확장한다.
- 마찬가지로 \( {\bf A} \) 는 양의 정부호 행렬 (positive definite) 성질을 가지고 있어야 한다.
- 참고로 헤시안 행렬에서 모두 양의 값, 모두 음의 값, 혹은 양/음이 섞여 있는 경우 모두 다른 성질을 가지게 된다.
- 이제 정리 좀 해보자.
- 라플라스 근사를 얻기 위해서는 우선 최빈값(mode) \( {\bf z}_0 \) 를 찾아야 한다.
- 실제로는 \( {\bf z}_0 \) 을 찾기 위해서 최적화 알고리즘 등을 사용하게 된다.
- 실제 분포가 단봉(unimodal) 형태가 아닌 다봉(multi-modal) 형태일 수 있다.
- 이 경우 어떤 봉우리를 선택하느냐에 따라 결과가 달라질 수 있다.
- \( {\bf z}_0 \) 를 찾은 후에는 헤시안 행렬을 구한다.
- 정규화 상수 \( Z \) 는 반드시 구할 필요는 없다.
- 근사식이 결정되면 원래 분포와 상관없이 적당한 정규화 계수가 구해진다.
- 데이터 샘플이 많을 수록 근사 값은 정확해진다.
- 중심 극한 정리(Central Limit theorem)에 의해 관측된 데이터가 많을 수록 모수의 분포가 가우시안 분포 형태에 가깝게 된다.
라플라스 근사의 문제점
- 가우시안 분포에 기반하고 있으므로 입력 범위가 반드시 실수형 변수여야 한다.
- 만약 다른 경우 변수의 범위를 변환해야 한다.
- 예를 들어 \( 0\le\tau<\infty \) 인 경우 \( \ln(\tau) \) 를 사용한다.
- 뭐 사실 이런건 중요한게 아니고, 가장 큰 문제점은,
- 근사식이 특정 값들에 의해서만 결정되므로 이 값 외에 다른 의미있는 전역 특성이 존재하는 경우 이를 알아내기 어렵다.
- 10장에서 좀 더 알아보게 될 것이다.
4.4.1 BIC 기법과 모델의 비교 (Model comparison and BIC)
- 앞서 살펴본 내용을 계속 확장하여 진행한다.
- 처음에 식을 세울 때 정규화 계수 \( Z \) 는 굳이 추론하지 않아도 된다고 했다.
- 하지만 모델 선택을 위해 \( p({\bf z}) \) 를 구해야 하는 상황이라면 이 식이 필요하다.
- 따라서 이 값을 유추해보자.
- 이 정규화 상수 \( Z \) 를 가지고 모델의 증거 영역(Evidence)을 추정하는데 사용할 수 있다.
- 모델 evidence 를 구하는 방식은 3장 5절에서 이미 다룬 내용이다.
- 아주 간단히만 정리하자면,
- 모델은 모수의 선택에 영향을 주고, 좀 더 좋은 모델을 선정할 때에는 \( p(D|M_i) \) 의 확률 값을 비교하여 더 좋은 모델을 선택하게 됨.
- 하나의 모델에 대한 식을 산정하면 \( M_i \) 는 우선 생략하고 이 때 필요한 모수들로 식을 전개해 봄.
- 모델 증거(model evidence)에 관련된 식은 다음과 같다.
-
이 때 \( \theta \) 는 모델에 종속적이며 우리는 \( p(D|\theta)p(\theta) \) 를 가우시안 형태로 근사함
-
이제 \( f({\bf z})=p(D|{\bf z})p({\bf z}) \) 라 하여 정규화 상수 \( Z \) 전개식에 대입하여 풀어본다.
- 그러면 \( Z=p(D) \) 가 된다.
- 여기에 로그를 취하면,
- 이 중에서 2번째 텀부터 마지막 텀까지는 Occam’s factor 라고 불린다.
- 여기서는 모델 비교를 위한 확률 값 \( p(D) \) 에 대한 패널티 텀으로 작용한다.
- \( \theta_{MAP} \) : \( \theta \) 에 대한 사후 확률의 최빈 값( mode. 즉 \( {\bf z}_0 \) )
- \( {\bf A} \) : 헤시안 행렬
- 식 (3.137) 을 보자.
- 첫번째 텀은 최적화된 파라미터를 통해 얻어지는 로그 가능도 함수이다.
- 그리고 나머지 텀들은 오컴의 팩터(Occam factor)라 불리우는 텀으로 모델 복잡도에 대한 패널티로 작용된다.
- 만약 사전 분포로 가우시안 분포를 선택하는 경우 헤시안 행렬은 full rank 가 된다.
- 따라서 우리는 다음의 식으로 이 식을 근사할 수 있다.
- 여기서 \( N \) 은 데이터의 수이고 \( M \) 은 파라미터 \( {\bf \theta} \) 의 수이다.
- 식에서 일부 추가적인 상수를 제외하였다.
- 이것을 BIC (Bayesian Information Criterion) 또는 Schwarz criterion (1978) 이라고 부른다.
-
챕터 1장에서 소개한 AIC 와 비교해보자면 BIC 는 모델 복잡도가 증가할수록 페널티가 더 커진다.
- 이러한 페널티 텀을 도입하는 것은 무척이나 쉽지만 실제로는 잘못된 결과를 도출하게 될 수도 있다.
- 일단 헤시안 함수가 full rank 되어있다는 가정은 파라미터를 결정하기 어려운 상황에서는 잘 맞지 않는 가정이다.
- 따라서 우리는 이 식을 다시 라플라스 근사를 통해 구하기도 한다. 이는 5.7절을 참고하도록 하자.