- 2-class 문제에서는 클래스 \( C_1 \) 로 분류되는 사후 확률 \( p(C_1|{\bf x}) \) 가 시그모이드(sigmoid) 함수로 제공되는 것을 확인하였다.
- 또 K-class 문제에서는 클래스 \( C_k \) 로 분류되는 사후 확률 \( p(C_k|{\bf x}) \) 가 소프트맥스(softmax) 함수로 제공되는 것을 확인하였다.
-
이를 해결하기 위해 실제 계산은 클래스-조건부 확률(class-conditional density) 값을 이용하였음을 확인하였다.
- 여기서는 다른 접근 방식을 취한다.
- MLE를 활용하여 직접적으로 파라미터를 결정하는 방법을 알아보자.
- 이를 위한 iterative reweighted least squares(IRLS) 알고리즘을 살펴볼 것이다.
- 앞절에서는 간접적인 파라미터 결정 방법으로 클래스-조건부 확률(class-conditional density)를 알아보았는데, 이는 Generative 모델 방식이다.
- 클래스-조건부 밀도와 사전 확률를 이용하여 사후 확률을 결정한다.
- 이번 절에서는 discriminative 학습의 형태를 제안하고 이를 통해 \( p(C_k|{\bf x}) \) 를 정의하여 MLE를 사용한다.
- 이런 방식의 장점은 구해야 할 모수(paramter)의 개수가 Generative 모델에 비해 적다
- 또한 Generative 모델에서 클래스-조건(class-conditional) 확률 분포를 잘못 선택하거나 실제 데이터의 분포를 잘 근사하지 못하는 경우 이를 사용하면 더 좋은 결과를 얻을 수 있다.
4.3.1 고정된 기저 함수들 (Fixed basis functions)
- 지금까지 입력 벡터 \( x \) 를 판별시 그대로 사용하는 형태의 분류 모델을 살펴보았다.
- 이제부터는 고정된 비선형 기저 함수(basis function)를 이용하여 입력 벡터를 \( \phi({\bf x}) \) 로 변환하는 형태를 사용할 것이다.
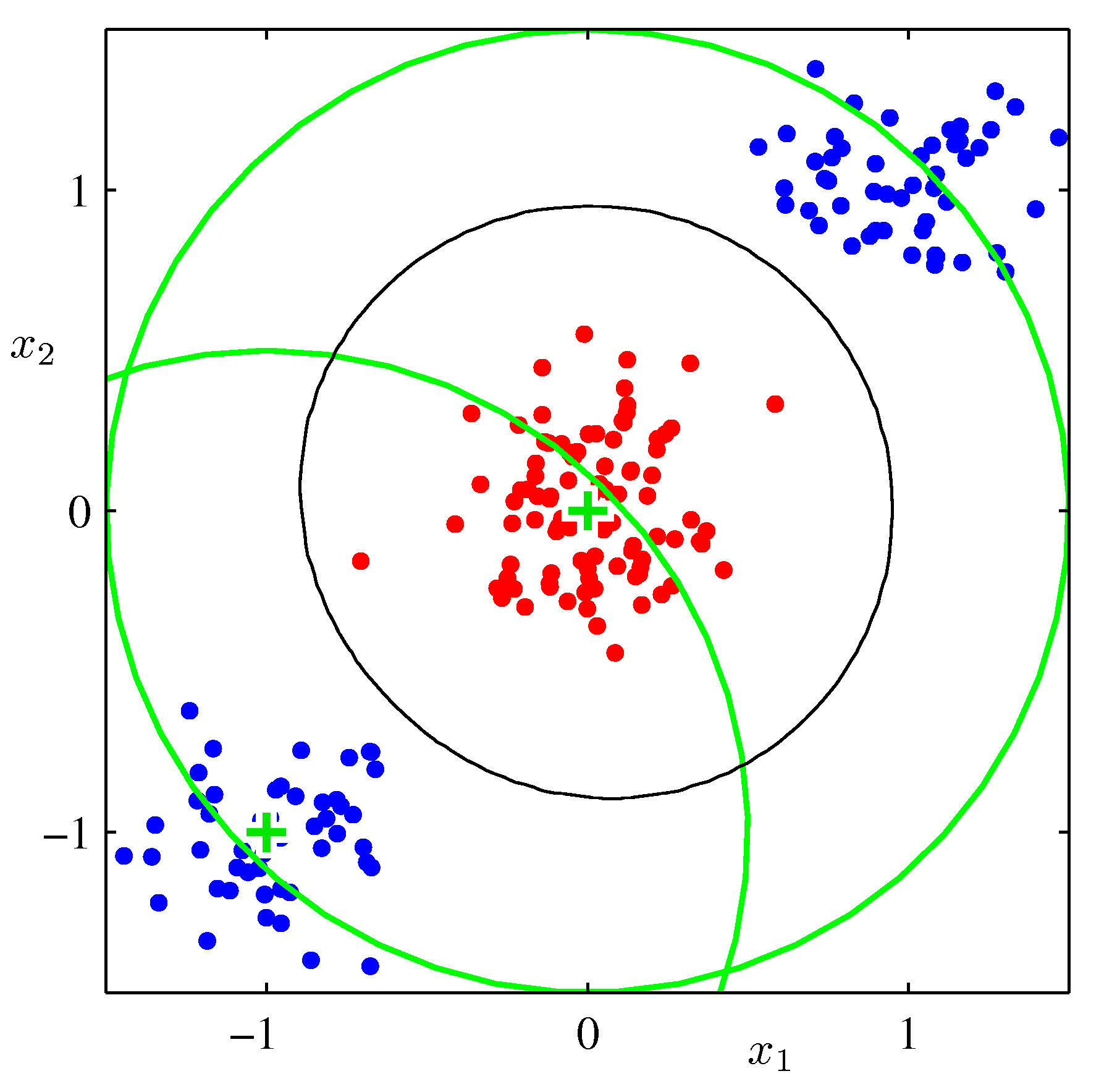
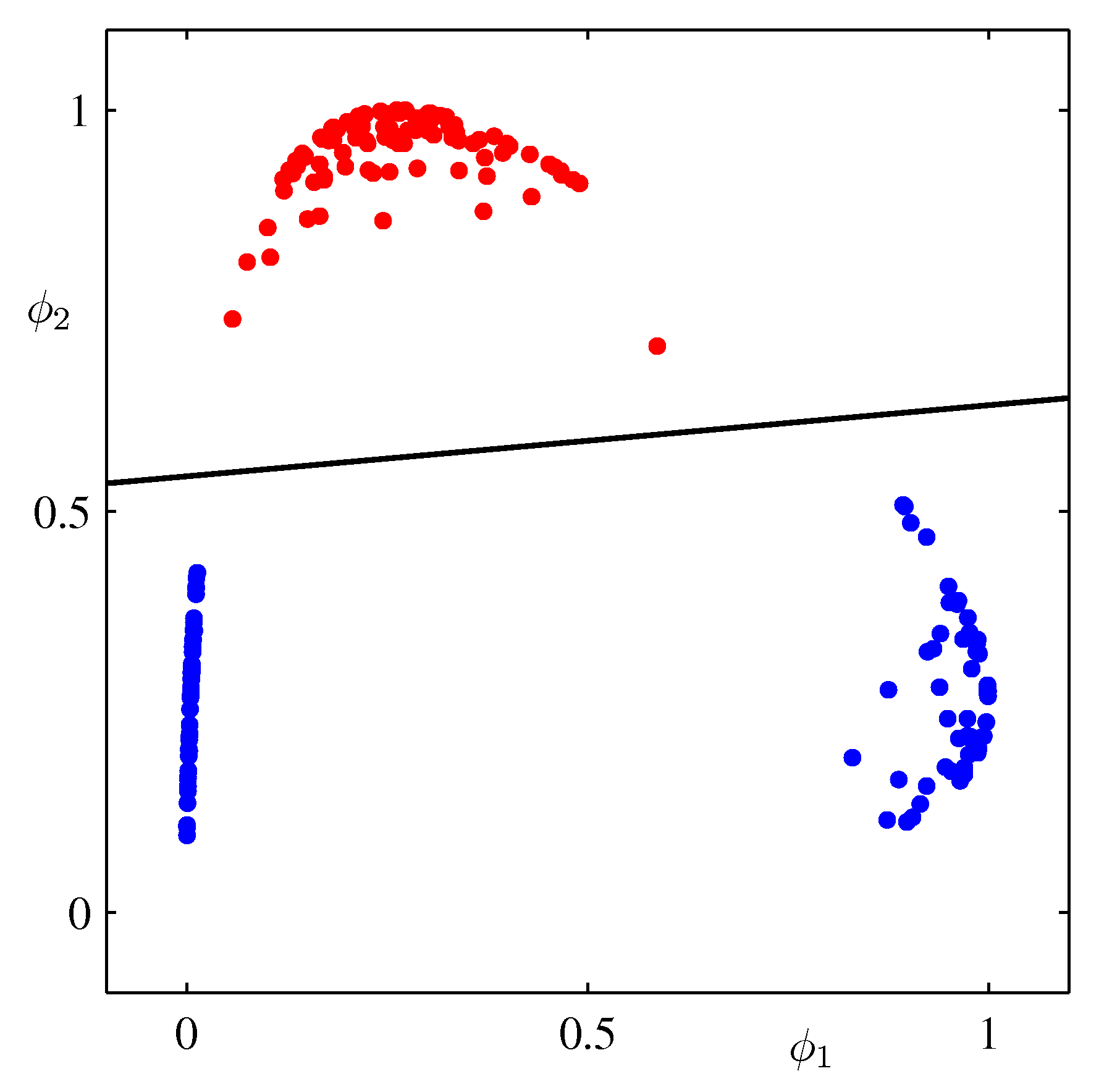
- 위의 그림은 비선형 기저 함수를 이용하여 변환된 데이터를 선형 판별하는 방법을 묘사하고 있다.
- 왼쪽 그림은 최초 원본 입력 \( (x_1, x_2) \) 에 대한 입력 공간을 나타내며, 샘플 데이터가 2개의 클래스로 구성되고 있음을 알 수 있다.
- 오른쪽은 최초의 입력 데이터가 \( (\phi_1({\bf x}), \phi_2(\bf x)) \) 로 변환된 뒤, 선형 판별식에 의해 클래스가 구별되고 있는 것을 보여주고 있다.
-
왼쪽에서 원형으로 되어 있는 검은색의 범위들은 오른쪽 공간으로 변환 후 선형으로 만들어지는 것을 확인할 수 있다.
- \( \phi({\bf x}) \) 공간에서 선형으로 분리되는 클래스들이 원래 공간 상에서도 선형 분류가 되어야 할 필요는 없다.
- 그리고 3장에서 살펴보았듯이 \( \phi_0({\bf x})=1 \) 을 추가로 정의하여 식에 넣는다.
-
이에 상응되는 \( w_0 \) 파라미터는 선형 회귀에서와 동일하게 Bias 역할을 수행하게 된다.
- 현실적으로 클래스-조건부 밀도(class-conditional density) \( p({\bf x}|C_k) \) 는 각각의 클래스 사이에서 중첩되기 쉽다.
- 따라서 각각의 값이 0 또는 1 과 같이 명확한 값으로 떨어지기보다는 이 사이의 어떤 값을 가지게 되는 경우가 많다.
- 1장에서 살펴보았듯 표준화된 결정 이론을 적용하여 사후 확률을 구하게 되는 경우, 이 값은 최적의 솔루션이 된다.
- 수식에 의해 에러를 최소화하게 된다.
- 그렇다고 \( \phi({\bf x}) \) 와 같은 기저 함수를 도입한다고 해서 이러한 중첩 현상이 해소되는 것도 아니다.
- 오히려 중첩의 정도를 증가시키거나, 원래 관찰 공간에서는 없었던 중첩들을 만들어내기도 한다.
- 그럼 왜 이런 기저 함수를 사용하는가?
- 기저 함수를 적절하게 선택하는 경우에 오히려 사후 확률 값을 더 쉽게 모델링 할 수 있기 때문.
- 마지막으로 고정된 형태의 기저 함수는 중요한 제약 사항을 가지고 있다.
- 이에 대한 자세한 내용들은 이후 장에서 계속 살펴볼 것이다. (기다리자)
- 하지만 이런 제약사항들에도 불구하고 실제 응용 단계에서는 많이 활용되고 있으니 일단은 좀 살펴보자.
4.3.2 로지스틱 회귀 (Logistic Regression)
- 이제 2-class 문제에서의 일반화된 선형 모델(generalized linear model)에 대해 알아보도록 하자.
- 4.2 절에서 분류 \( C_1 \) 에 대한 사후 확률 값은 로지스틱 회귀로 기술되는 것을 확인하였다.
- 이 식을 다시 기술하면 다음과 같다.
- 기존에는 \( x \) 데이터를 바로 사용하였으나 여기서는 \( \phi \) 함수를 통해 변환 후 사용하게 된다.
- 변환된 입력 공간에서는 로지스틱 시그모이드 방식과 동일하게 처리된다.
- 2-class 문제이므로 \( p(C_2|\phi)=1-p(C_1|\phi) \) 이다.
- 여기서 \( \sigma \) 는 로지스틱 시그모이드(logistic sigmoid) 라고 부른다.
- 사실 통계에서는 이를 로지스틱 회귀(logistic regression)라고 부르지만
여기서는 회귀가 아닌 분류를 강조하므로 그냥 sigmoid 라고 부른다.
- 사실 통계에서는 이를 로지스틱 회귀(logistic regression)라고 부르지만
- 기저 함수 \( \phi \) 가 M 차원을 공간을 가지게 된다면, 이 모델은 \( M \) 차원의 조정 가능한 모수를 가지게 된다.
- 이와 대조적으로 가우시안 클래스-조건부 밀도에서는 일반적으로 더 많은 모수를 요구하게 된다.
- 여기서는 만약 \( x \) 가 \( M \) 차원이라면 필요한 평균의 개수는 \( 2M \) 이 되고 공분산을 위해 \( M(M+1)/2 \) 개의 모수가 추가로 필요하다.
- 지금 다루고 있는 문제는 2-클래스 문제이다.
- 만약 사전 분포 \( p(C_1) \) 까지 고려하게 되면 총 \( M(M+5)/2+1 \) 개의 파라미터가 필요하게 된다.
- 즉, \( M \) 에 대해 이차 형식으로 추정해야 할 파라미터 개수가 증가한다.
- 여기서는 만약 \( x \) 가 \( M \) 차원이라면 필요한 평균의 개수는 \( 2M \) 이 되고 공분산을 위해 \( M(M+1)/2 \) 개의 모수가 추가로 필요하다.
- 이와 대조적으로 가우시안 클래스-조건부 밀도에서는 일반적으로 더 많은 모수를 요구하게 된다.
- 우리는 로지스틱 회귀 모델의 모수 값을 결정하기 위해 MLE를 사용할 것이다.
- 이를 위해서 로지스틱 회귀 모델의 미분값에 대해 간단히 살펴보고 넘어가도록 하자.
- 식 자체는 어렵지 않다. 간단하게 증명하면,
- 현재 2-class 문제를 다루고 있으므로 기저 함수를 포함한 가능도 함수(likelihood) 함수를 정의해보자.
- data set : \( {\phi_n, t_n} \)
- \( t_n \in {0, 1} \)
- \( \phi_n = \phi({\bf x}_n) \)
- \( y_n = y(\phi_n) = \sigma({\bf w}^T\phi_n) \)
- 모수를 추정하기 위해 이번에는 음수항의 로그 가능도 함수를 사용한다. (negative logarithm of likelihood)
- 이를 에러 함수로 정의한다.
- 이런 형태의 에러 함수는 cross-entropy error function 으로 알려져 있다.
- 특별한 것은 없고 가능도 함수에 음의 로그 값을 붙인 결과를 의미한다.
- 이제 \( {\bf w} \) 에 대해 미분하면,
- 이에 대한 증명은 연습문제 4.13을 참고할 것. (앞서 설명된 \( \frac{d\sigma}{da} \) 가 사용된다.)
- 간단히만 정리해둔다.
- 식(4.91)을 보면 로지스틱 시그모이드의 미분과 관련된 요소들은 식에 더 이상 남아있지 않고,
- 로그 가능도 함수의 기울기(gradient)를 위한 간단한 형태의 식이 된다.
- 사실 위의 식은 3장에 언급된 선형 회귀 모델의 \( \triangledown E(w) \) 와도 거의 같은 형태를 취하고 있다.
- 원한다면 한 번에 하나의 데이터를 추가하여 값을 업데이트하는 순차적인 모델을 만들어 낼 수 있다.
- \( n^{th} \) 에 대한 입력을 \( \triangledown E_n \) 로 놓으면 된다.
- 업데이트를 위한 식은 3장에서 언급한 것처럼 (식 3.22)를 사용하면 된다.
- MLE를 사용하는 방식이 오버 피팅을 만들어낼 수 있다는 것은 이미 알고 있을 것이다.
- 여기서도 마찬가지인데, 데이터 집합이 선형 분류가 가능한 경우 최대한 이를 분류하기 위해 과도한 피팅을 시도하기도 한다.
- 이런 경우 \( \sigma=0.5 \) 즉 \( {\bf w}^T\phi=0 \) 을 만족하기 위한 초평면을 찾는 문제가 되고,
- 좀 더 정확한 값을 찾기 위해 \( {\bf w} \) 의 값이 매우 커지는 현상이 발생한다.
- 이런 경우 로지스틱 시그모이드 값이 중간 영역에서 급격한 기울기를 가지게 되어 결국 스텝 함수와 동일한 형태로 만들어지게 된다.
- 이 경우에는 각각의 샘플 데이터가 특정 클래스로 분류될 확률이 모두 \( p(C_k|{\bf x})=1 \) 이 되어 버린다.
- 사후 확률이 이런 극단적인 값으로만 나오기 때문에 가능한 최적의 결정면을 여러 개 얻을 수 있다.
- 사실 이 중에 최적의 결정면이 존재함. 모델이 극단적이어서 이를 구분하지 못함
- 이에 대한 내용은 이후 그림 10.13 에서 설명함
4.3.3 IRLS (Iterative reweighted least squares)
- 이제 3장에서 소개한 선형 회귀 모델에서의 MLE를 잠시 떠올려보자.
- 우리는 가우시안 노이즈 모델을 선정하여 식을 모델링했고, 이 식은 닫힌 형태(closed-form)이므로 최적의 해를 구할 수 있었다.
- 이 식은 모수 벡터 \( {\bf w} \) 에 대해 2차식의 형태로 제공된다. 그래서 최소값이 1개이다.
- 로지스틱 회귀에서는 안타깝게도 더 이상 닫힌 형태의 식이 아니다.
- 시그모이드 식에 의해서 비 선형 모델이 된다..
- 하지만 2차식이 그리 중요한 요소는 아님
- 좀 더 정확하게 이야기하자면, 에러 함수는
Convex함수 이므로 Newton-Raphson 기법을 이용하여 최적화 가능하다. - 이를 통해 로그 가능도 함수에 대한 2차 근사식으로 사용 가능하다.
- Newton-Raphson 갱신 방식은 아래와 같이 주어진다.
- 여기서 \( {\bf H} \) 는 헤시안 행렬로 \( E({\bf w}) \) 함수에 대한 2차 미분값으로 정해진다.
- 이제 식(3.3) 과 식(3.12)를 이용하여 위의 식을 적용해 보도록 한다.
- 참고로 예전 식들은 다음과 같다.
- 따라서 이 함수의 그라디언트와 헤시안은 다음과 같다.
- 여기서 \( \Phi \) 는 \( N \times M \) 크기의 행렬이다. (이 때 \( n^{th} \) 열은 \( \phi_n^T \) 에 의해 주어진다.)
- Newton-Raphson 업데이트 식은 다음과 같이 된다.
- 이 식은 이미 앞서 보았던 최소 제곱법의 식이다.
- 이 경우에는 에러 함수가 이차형식(
quadratic) 꼴이므로 Newton-Raphson 식이 한번의 반복으로 값을 얻을 수 있도록 전개된다.
- 이 경우에는 에러 함수가 이차형식(
- 이제 Newton-Raphson 업데이트를 로지스틱 회귀에 적용해보기 위해
cross-entropy오차함수에 대입을 해보도록 하자. (식 4.90)
- 여기서 \( R \) 은 \( N \times N \) 인 대각 행렬이다.
- 이 식에 의해 Hessian 행렬은 더이상 상수(constant)가 아니다.
- \( R \) 로 인해 \( {\bf w} \) 값에 의존하게 되고, 에러 함수는 더 이상 이차형식이 아니게 된다.
- \( y_n \) 이 \( (0 \le y_n \le 1) \) 이라는 사실로 부터 (이는 시그모이드 함수의 출력 범위이다.) \( H \) 의 속성을 이해할 수 있다.
- 임의의 벡터 \( {\bf u} \) 에 대해 \( {\bf u}^T{\bf H}{\bf u}>0 \) 을 만족한다.
- 따라서 헤시안 행렬 \( {\bf H} \) 는 양의 정부호 행렬(positive definition)을 만족하게 되어 에러 함수는 \( {\bf w} \) 에 대해 이차형식의 함수가 된다.
- 최종적으로 하나의 최소값을 찾아 낼 수 있게 된다.
- 로지스틱 회귀 모델에서 Newton-Raphson 을 활용한 업데이트 모델은 다음과 같다.
- \( {\bf z} \) 는 \( N \) 차원의 벡터이다.
- 식 (4.99)를 자세히 보면 앞서 살펴보았던 최소 제곱법의 일반식(normal equation)과 같은 형태임을 알 수 있다.
- 여기서 norman equation 은 \( GD \) 방식이 아닌 미분을 통한 파라미터 찾기 형태의 식을 말한다.
- 하지만 \( R \) 이 상수가 아니라 파라미터 \( {\bf w} \) 에 영향을 받는 요소이므로 이를 반복 업데이트 방식으로 풀어야 한다.
- 이러한 연유로 이러한 식을 IRLS ( iterative reweighted least squares )라고 부른다.
- 이렇게 가중치가 부여된 최소 제곱 문제는 가중치 대각 행렬 \( {\bf R} \) 을 분산(variance) 값으로 생각할 수도 있는데,
- 왜냐하면 로지스틱 회귀 문제에서 \( t \) 의 평균과 분산 값이 다음으로 주어져있기 때문이다.
- 여기서는 \( t^2=t \) 를 사용하였다. (단, 이때 \( t\in{0,1} \) 이다.)
- 사실은 IRLS 는 변수 \( a={\bf w}^T\phi \) 에 대해 선형 문제를 가진다.
- 따라서 로지스틱 시그모이드 함수 지역 근사 기법을 사용한다.
4.3.4 다중 로지스틱 회귀 (Multiclass logistic regression)
- 다중 클래스 분류 문제를 다루는 Generative 모델에서는 선형 함수인 소프트맥스(softmax)가 사용된다고 이야기했다.
- 여기서 활성자(activations) \( a_k \) 는 다음과 같이 정의된다.
- 클래스 조건부 분포와 사전 분포를 분리하기 위해 MLE 를 사용하고 베이즈 이론을 이용하여 사후 분포를 얻는다.
- 이를 통해 암묵적으로 파라미터 \( {\bf w_k} \) 를 구하게 된다.
- 이를 위해 \( y_k \) 에 대한 미분 식이 필요하다.
- 여기서 \( I_{kj} \) 는 단위 행렬(identity matrix) 이다.
- 이제 MLE 를 구한다. 가장 쉬운 방법은 타겟 벡터 \( {\bf t}_n \) 에 대해 \( 1-of-K \) 코딩 스킴을 적용한다.
- 따라서 클래스 \( C_k \) 는 이진 벡터가 되어 \( k \) 에 해당되는 값은 1로 설정되고 나머지는 0으로 설정된다.
- 이 때의 가능도 함수는 다음과 같다.
- 이 때 \( y_{nk} = y_k(\phi_n) \) 이고 \( {\bf T} \) 는 \( N \times K \) 인 행렬이다.
- 여기에 음의 로그 값을 붙이면 다음과 같아진다.
- 이는 cross-entroy 라고 알려져있다.
- 정의된 에러함수 \( E \) 에 대한 미분값을 알아보도록 하자.
- 이 때 식 (4.106)을 사용하여 구하면 된다.
- 이 식을 구하기 위해 \( \sum_k t_{nk}=1 \) 을 사용하였다. (소프트맥스의 특징이다.)
-
이 식은 선형 모델과 로지스틱 회귀 모델에서 보았던 에러 함수와 동일한 기울기와 형태를 취하고 있는 것을 알 수 있다.
- 한번에 하나의 패턴에 적용하는 순차 알고리즘 공식을 사용할 수도 있다.
- 앞서 선형 회귀 모델에서 하나의 데이터 \( n \) 에 대해 가능도 함수를 벡터 \( {\bf w} \) 로 미분한 식 \( (y_n-t_n) \) 과 \( \Phi_n \) 를 곱한 식을 얻었었다.
- 유사하게 에러 함수 식(4.108)과 소프트맥스 활성화 함수의 결합을 같은 형태로 얻을 수 있다.
- 배치(batch) 형태의 알고리즘을 얻기 위해서는 앞서 살펴본 IRLS 알고리즘에 대응되는 형태의 Newton-Raphson 업데이트를 사용 가능하다.
- 이를 위해서는 \( j \) , \( k \) 내에 있는 \( M \times M \) 크기의 헤시안 행렬의 값을 계산해야 한다.
4.3.5 프로빗 회귀 (Probit regression)
- 지금가지 우리는 클래스-조건부 분포가 지수족 분포를 따를 때의 사후 분포를 로지스틱 회귀를 이용하여 구하는 것을 살펴보았다.
- 이 때 선형 함수에 로지스틱 혹은 소프트맥스 변환을 통해 사후 분포를 예측하였다.
- 그러나 클래스-조건부 분포로 선택할 수 있는 분포가 모두 간단한 사후 확률을 가지는 것은 아니다.
- 예를 들어 가우시안 혼합 분포를 사후 분포로 사용하는 경우 이런 모양을 얻을 수 없다.
- 따라서 여기서는 discriminative 확률 모델의 또 다른 형태를 살펴보도록 한다.
- 2개의 분류 분제를 가진 일반화된 선형 모델(generalized linear modle) 프레임워크를 고려한다.
- 이 때 \( a={\bf w}^T\phi \) 이고, 함수 \( f(\cdot) \) 는 활성 함수(activation function)가 된다.
- 여기서 링크(활성) 함수를 noisy threshold model 로 고려해볼 수 있다.
- 이 함수는 입력 \( \phi_n \) 을 \( a_n={\bf w}^T\phi_n \) 으로 평가한 다음 이를 다음처럼 해석할 수 있다.
- 여기서 \( \theta \) 는 고정된 값이 아니라 랜덤 변수로 취급한다.
- \( \theta \) 가 확률 밀도 \( p(\theta) \) 를 가진다면 활성 함수는 다음과 같이 기술할 수 있다.
- 이는 조건식에 의해 \( P(a\ge \theta) \) 를 나타내는 식이 되기 때문이다.
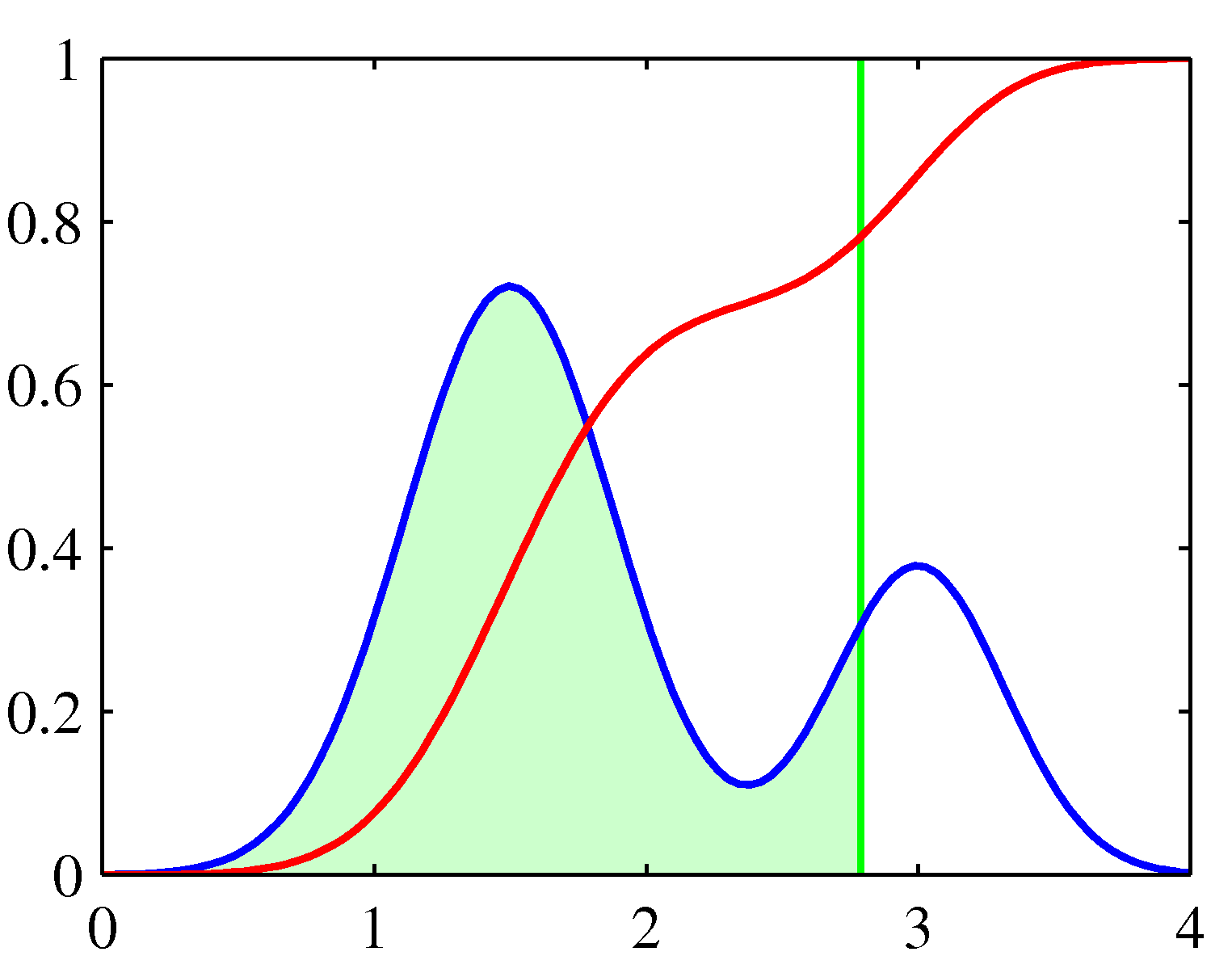
- 여기서 파란색 라인은 \( p(\theta) \) 로 두 개의 가우시안 함수의 혼합으로 이루어진 것을 알 수 있다.
- 붉은색 라인은 CDF 인 \( f(a) \) 로 대충 시그모이드 함수와 비슷하게 생겼다.
- \( x \) 축은 \( \theta \) 의 값으로 연두색 영역의 직선 위치가 바로 \( a \) 라고 생각하면 된다.
- 이제 \( p(\theta) \) 를 표준 정규 분포 (평균이 \( 0 \) 이고 분산이 단위 분산 \( 1 \) 인 가우시안 확률 분포)로 생각한다면 식을 다음과 같이 기술할 수 있다.
- 이 함수를 역 프로빗 함수(inverse probit function)라고 부른다.
- 시그모이드와 거의 유사한 형태의 값을 가진다. 그림 4.9를 참고하면 된다.
- 실제 구현체에서는 다음과 같은 식을 주로 사용한다.
- 이 함수는 보통 \( erf \) 함수 또는 에러 함수라고 부른다.
- 이 때 “에러 함수”의 의미가 기계 학습에서의 에러 함수를 의미하는 것이 아니니 유의할 것
- \( erf \) 함수를 이용하여 역 프로빗 함수를 전개하면 다음 식을 얻을 수 있다.
- 이 식을 프로빗 회귀 (probit regression)식이라고 부른다.
- MLE를 이용하여 모델의 파라미터 값을 결정할 수 있다.
- 이 때 프로빗 회귀는 로지스틱 회귀와 유사한 결과를 얻게 된다.
- 실제 4.5 절에서 프로빗 모델의 사용법을 확인할 것이다.
- 실제 문제에서는 고려해야 할 사항으로 outliers 가 있다.
- 입력 벡터 \( s \) 를 측정할 때 에러가 발생하거나 타겟 값 \( t \) 가 잘못 부여된 경우에 발생할 수 있다.
- 이런 데이터가 존재하는 경우 분류 결과를 심각하게 왜곡할 수 있음
- 로지스틱 모델과 프로빗 모델은 이러한 상황에서 다르게 동작하게 된다.
- 로지스틱 시그모이드의 경우 \( x\rightarrow\infty \) 이면 활성화 함수의 값이 \( \exp(-x) \) 와 같이 급격하게 줄어든다.
- 반면 프로빗 활성화 함수는 \( \exp(-x^2) \) 과 같이 줄어들기 때문에 outlier에 훨씬 민감함
- 하지만 로지스틱과 프로빗 모델 모두 데이터는 모두 정확하게 라벨링되어 있다고 가정하는 모델이다.
- 물론 잘못된 라벨의 영향도를 타겟 값 \( t \) 가 잘못된 값으로 할당될 확률 \( \epsilon \) 로 표현하여 모델 요소로 포함할 수 있다.
- 이 경우 타겟 값에 대한 확률 분포는 다음과 같이 기술할 수 있다.
4.3.6 정준 연결 함수 (Canonical link functions)
- 가우시안 노이즈 분포를 사용한 선형 회귀 모델에서 에러 함수는 음 로그 가능도 함수(negative log likelihood)를 사용한다. (식 3.12)
- 참고로 (식 3.12)는 다음과 같다.
- 위의 식에서 \( y_n = {\bf w}^T\Phi_n \) 이며 오차함수를 파라미터 \( {\bf w} \) 로 미분한 결과로 부터 식을 유도한다.
- 로지스틱 시그모이드 활성 함수 또는 softmax 활성 함수를 cross-entropy 오차 함수를 결합하는 식에서도 비슷한 것을 확인함
- 이제 이러한 식들을 exponential family 식으로 전개를 시켜보도록 하자.
- 이 때의 활성 함수를 정준 연결 함수 (canonical link function) 이라고 한다.
- 한국말로 번역한 것이 좀 이상하므로 그냥 영어로 표현해서 사용하는 것이 더 좋을듯 하다.
- 일단 타겟 변수의 확률 식을 표현해보자.
- 4.2.4절에서는 입력 데이터 \( {\bf x} \) 에 대해 exponential family 분포를 가정했지만 여기서는 타겟 값 \( t \) 에 대해 가정한다.
- 식 (2.226) 을 참고하도록 하자.
- 일반화된 선형 모델 ( generalized linear model , Nelder & Wedderburn (1972) ) 식은 다음과 같다.
- 여기서 함수 \( f( \dot ) \) 는 활성 함수 ( activation function )로 알려져있다.
- 그리고 이 때 \( f^{-1}( \dot ) \) 이 바로 연결 함수( link function )이다.
- 이제 식 (4.118) 의 log likelihood 함수를 \( \eta \) 의 함수로 표현해 본다.
- 모든 관찰값이 동일한 스케일(scale) 파라미터를 공유한다고 가정한다.
- 따라서 \( s \) 는 \( \eta \) 에 대해 독립적이다.
- 모델 파라미터 \( {\bf w} \) 에 대해 미분하면,
- 여기서 \( a_n = {\bf w}^T \phi_n \) 이고, \( y_n = f(a_n) \) 이다.
- \( f(\psi(y)) = y \) 이고 따라서 \( f’(\psi)\psi’(y) = 1 \) 이다.
- 또한 \( a=f^{-1}(y) \) 이므로 \( a=\phi \) 이고 결국 \( f’(a)\psi’(y) = 1 \) 이 된다.