2. Prob. Generative Models

교재 1.5.4 절에서 간단하게나마 Generative 모델을 이용한 분류 방식에 대해 다루긴 했었다.
우선 시작하기에 앞서 용어를 좀 정리하자.
- 이 교재에서는 용어를 좀 엄격하게 쓰는 편인데, 지겹지만 잘 구분해서 쓰자
- 사후 확률 (posterior) : $ p(C_k|{\bf x}) $
  - 임의의 데이터 $ x $ 가 주어졌을 때 이 데이터가 특정 클래스 $ C_k $ 에 속할 확률
  - $ x $ 는 샘플 하나를 의미하며 벡터로 표기된 이유는 여러 개의 feature를 가지기 때문임
- 클래스-조건부 밀도 (class-conditional density) : $ p({\bf x}|C_k) $
  - 가능도 함수(likelihood function)가 아니냐고 묻는 분이 계시는데, 아니다.
  - 특정 클래스에서 입력된 하나의 데이터 $ x $ 가 발현될 확률을 의미하며, 각각의 클래스별로 계산되기 때문에
    - 데이터를 클래스 단위로 나누어 놓고 나면 각 클래스에 대한 $ p({\bf x}) $ 를 의미하는 것과 마찬가지가 된다.
    - 보통 가능도 함수(likelihood) 등을 통해 얻어진 모수 값을 이용하여 분포의 모양을 선택한 뒤 $ x $ 의 확률 값을 구하게 된다.
      - $p({\bf x}|\theta_{ml}) $
- 가능도 함수 (likelihood) : $ p({\bf X}|C_k) = \prod p({\bf x}_i|C_k) $
  - 주어진 샘플 데이터가 실제 발현될 확률값을 주로 사용하며, 로그를 붙이는게 일반적이다.
  - 샘플 데이터는 i.i.d 를 가정하므로 보통은 확률 곱으로 표현 가능하다.
  - 특정 분포(distribution)를 사용하는 경우 주로 모수 추정에 사용된다.
  - 모수 추정이 완료되면 클래스-조건부 밀도 등의 식에서 이를 모수 값으로 사용한다.
클래스-조건부 밀도 $ p({\bf x}|C_k) $ 를 이용한 접근 방식에 대해 자세히 알아보도록 하자.
- Generative 모델은 사후 확률 $ p(C_k|{\bf x}) $ 를 직접 구하는 것이 아니라 간접적 사후 확률을 예측하는 모델이다.
- 따라서 사후 확률 대신 클래스-조건부 밀도와 사전 확률 등으로 사후 확률을 예측한다.
- 즉, 임의의 $ x $ 가 특정 클래스에 속할 확률 값을 확인하고 이 중 가장 큰 확률 값을 가지는 클래스로 $ x $ 가 속할 클래스를 결정할 수 있다.
- 가장 먼저 2-class 문제를 살펴보자. 다음은 $ x $ 가 클래스 $ C_1 $ 에 속할 확률을 모델링하는 식이다. (베이즈 룰)

$p(C_1|{\bf x}) = \dfrac{p({\bf x}|C_1)p(C_1)}{p({\bf x}|C_1)p(C_1)+p({\bf x}|C_2)p(C_2)}=\dfrac{1}{1+\exp(-a)} = \sigma\;(a) \qquad{(4.57)}$ $a=\ln{\dfrac{p({\bf x}|C_1)p(C_1)}{p({\bf x}|C_2)p(C_2)}} \qquad{(4.58)}$

$ \sigma\;(a) $ 는 로지스틱 시그모이드(logistic sigmoid) 함수이며, 다음과 같이 정의된다.

$\sigma\;(a)=\dfrac{1}{1+\exp(-a)} \qquad{(4.59)}$

수식이 왜 이렇게 전개되는지 궁금할수도 있는데, 생각보다 쉽다.

$\alpha = p({\bf x}|C_1)p(C_1)$ $\beta = p({\bf x}|C_2)p(C_2)$ $\dfrac{\alpha}{\alpha+\beta}=\dfrac{1}{\frac{\alpha+\beta}{\alpha}} = \dfrac{1}{1+\frac{\beta}{\alpha}}=\dfrac{1}{1+\exp({-\ln(\frac{\alpha}{\beta})})}$

시그모이드 함수를 그리면 다음과 같다.

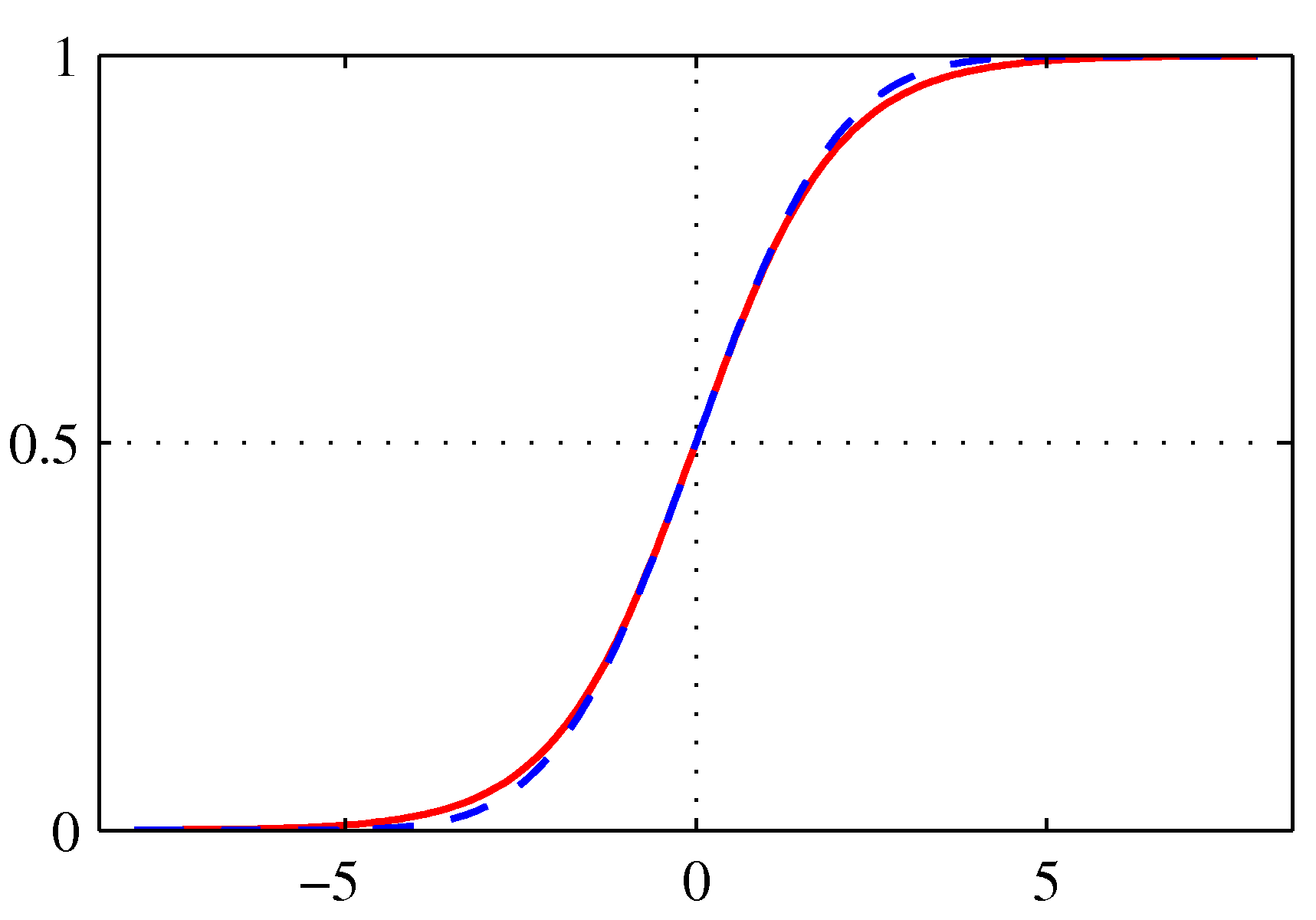
figure4.9

그림에서 보듯 sigmoid 라는 용어는 함수 식이 $ S $ 자 형태를 취하기 때문에 붙여진 이름이다.
- 이런 함수들을 가끔 squashing function 이라고도 부르는데,
- $ x $ 축 영역의 모든 값에 대응되는 함수 출력 값이 특정 범위에만 존재하기 때문이다. (여기서는 0 ~ 1 사이)
붉은 색 실선이 시그모이드(sigmoid) 함수이며, 청색 점선은 프로빗(probit) 함수로 이 함수는 이후에 설명된다.
- 프로빗 함수가 시그모이드 함수와 거의 유사한 특징이 있음을 보이기 위해 함께 표현한 것이다.
시그모이드 함수는 다음과 같은 특징이 있다.

$\sigma\;(-a) = 1 - \sigma\;(a) \qquad{(4.60)}$

시그모이드가 도입된 이유는,
- 시그모이드 자체가 특정 값으로 수렴되는 성질이 있으며 (0~1 사이의 값)
- 따라서 이 값을 확률 값으로 고려를 해도 되기 때문이다.
- 게다가 모든 점에서 연속이며 미분 가능하므로 수학적 전개에도 매우 편리하다.
다음으로 로지스틱 시그모이드의 역(inverse)은 다음과 같다.

$a=\ln\left(\dfrac{\sigma}{1-\sigma}\right) \qquad{(4.61)}$

이를 로짓(logit) 이라고 부른다.
2-class 문제에서는 $ \ln \frac{p(C_1|{\bf x})}{p(C_2|{\bf x})} $ . 즉 각각의 확률에 대한 비율(ratio)에 로그(log)를 붙인 것과 같다.
- 이를 로그 오즈(log odds) 라고 한다.
- 좀 더 자세히 설명하자면, 성공 확률 $ p $ 와 실패 확률 $ (1-p) $ 에 대한 odds 는 $ \frac{p}{(1-p)} $ 이므로 여기에 로그를 붙인 것과 같다.
- 로짓이라는 개념이 좀 뜬금없어 보이지만 이후 식에서도 자주 등장하므로 잊지는 말자.
$ p(C_1|x) $ 는 여기서 사후(posterior) 확률이 되는데 이를 로지스틱 회귀식을 이용해서 기술한다.
이 식을 가지고 좀 더 일반화하면 $ K>2 $ 인 경우에서도 식을 확장할 수 있다.
- 이를 일반 선형 모델(generalized linear model)이라고 한다.

$p(C_k|{\bf x}) = \dfrac{p({\bf x}|C_k)p(C_k)}{\sum_j{p({\bf x}|C_j)p(C_j)}}=\dfrac{\exp(a_k)}{\sum_j{\exp(a_j)}} \qquad{(4.62)}$

이를 normalized exponential 함수라고 부르며, 다중 클래스 분류에 사용되는 시그모이드 식이 된다.
- 이 때 $ a({\bf x}) $ 는 $ {\bf x} $ 에 대한 선형 함수로 처리 가능하다.
- 사실 맨 처음에 설명했던 2-class 모델도 위의 식으로 전개하면 동일한 식을 얻어낼 수 있다.
  - 위 식을 $ \exp(a_1)/(\exp(a_1)+\exp(a_2)) $ 로 놓고 전개하면 2-class 시그모이드가 나온다.
어쨌거나 여기서 $ a_k $ 는 다음과 같이 정의된다.

$a_k = \ln(p({\bf x}|C_k)p(C_k)) \qquad{(4.63)}$

normalized exponential 함수를 소프트 맥스 (softmax function) 함수라고 부른다.
이는 max 함수에 대한 평활화(smoothed) 버전이기 때문이다.
- 평활화의 의미를 현재 고려할 필요는 없고, 일단 모든 점에서 미분 가능한 식으로 변환된다고 생각하자.
- 만약 $ a_k \gg a_j $ 라면 $ p(C_k|{\bf x}) \simeq 1 $ 이고 $ p(C_j|{\bf x}) \simeq 0 $ 이 된다. (단, $ j \neq k $)
다음 절에서는 이러한 클래스 조건 밀도를 특정 분포로 가정해서 처리하는 과정을 살펴볼 것이다.
- 우선 연속적인 입력 값을 확인한 뒤에 이산적인 값을 처리하는 방법을 살펴보자.
짧은 요약
- 이번 절이 좀 두서없이 설명되는 것들이 많아 혼동되는 부분이 있는데, 간단한 사실만을 기억하면 된다.
  - 2-class 에서는 sigmoid 를 이용해서 분류.
  - K-class 에서는 softmax 를 이용해서 분류.

4.2.1 연속적인 입력값 (Continuous inputs)

일단 클래스-조건부 밀도(class-conditional density)가 가우시안 형태라고 가정하자.
또한 가장 간단한 구조를 고려하여 모든 클래스 사이의 공분산(covariance) 값은 모두 동일하다고 가정한다. (중요한 제약)
그러면 어떤 클래스가 주어졌을 때 해당 데이터가 나올 확률은 다음과 같다.

$p({\bf x}|C_k) = \dfrac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp\left\{-\dfrac{1}{2}({\bf x}-{\bf \mu}_k)^T\Sigma^{-1}({\bf x}-{\bf \mu}_k)\right\} \qquad{(4.64)}$

2-class 문제로 이를 고려해보자.
최초 조건부 확률 식에 판별식을 넣는다.

$p(C_1|{\bf x})=\sigma({\bf w}^T{\bf x}+w_0) \qquad{(4.65)}$

이 식은 위에서 $ \sigma(a) $ 로 정의되어 있었다. 마찬가지로 $ a=\ln\frac{p({\bf x}|C_1)p(C_1)}{p({\bf x}|C_2)p(C_2)} $ 였다.
가우시안 분포 식을 위에 넣고 대입한다.

${\bf w}^T{\bf x}+w_0 = \ln\frac{p({\bf x}|C_1)p(C_1)}{p({\bf x}|C_2)p(C_2)}$

이를 전개하면 다음의 식이 얻어진다.

${\bf w} = \Sigma^{-1}({\bf \mu_1}-{\bf \mu_2}) \qquad{(4.66)}$ $w_0 = -\frac{1}{2}{\bf \mu_1}^T\Sigma^{-1}{\bf \mu_1} + \frac{1}{2}{\bf \mu_2}^T\Sigma^{-1}{\bf \mu_2} + \ln{\frac{p(C_1)}{p(C_2)}} \qquad{(4.67)}$

$ x $ 에 대한 2차 텀이 모두 사라지면서 직선 식이 얻어진다.
- 이는 두 클래스 사이의 공분산이 동일하기 때문에 이차항의 계수가 부호만 다르고 크기가 일치하여 약분되기 때문이다.
- 자세한 전개 방식은 생략한다.
여기서 조금만 상상을 해보면, 같은 분산을 가지는 두개의 가우시안 분포가 만나는 지점은 당연히 직선의 형태일 것이라 생각해볼 수 있다.

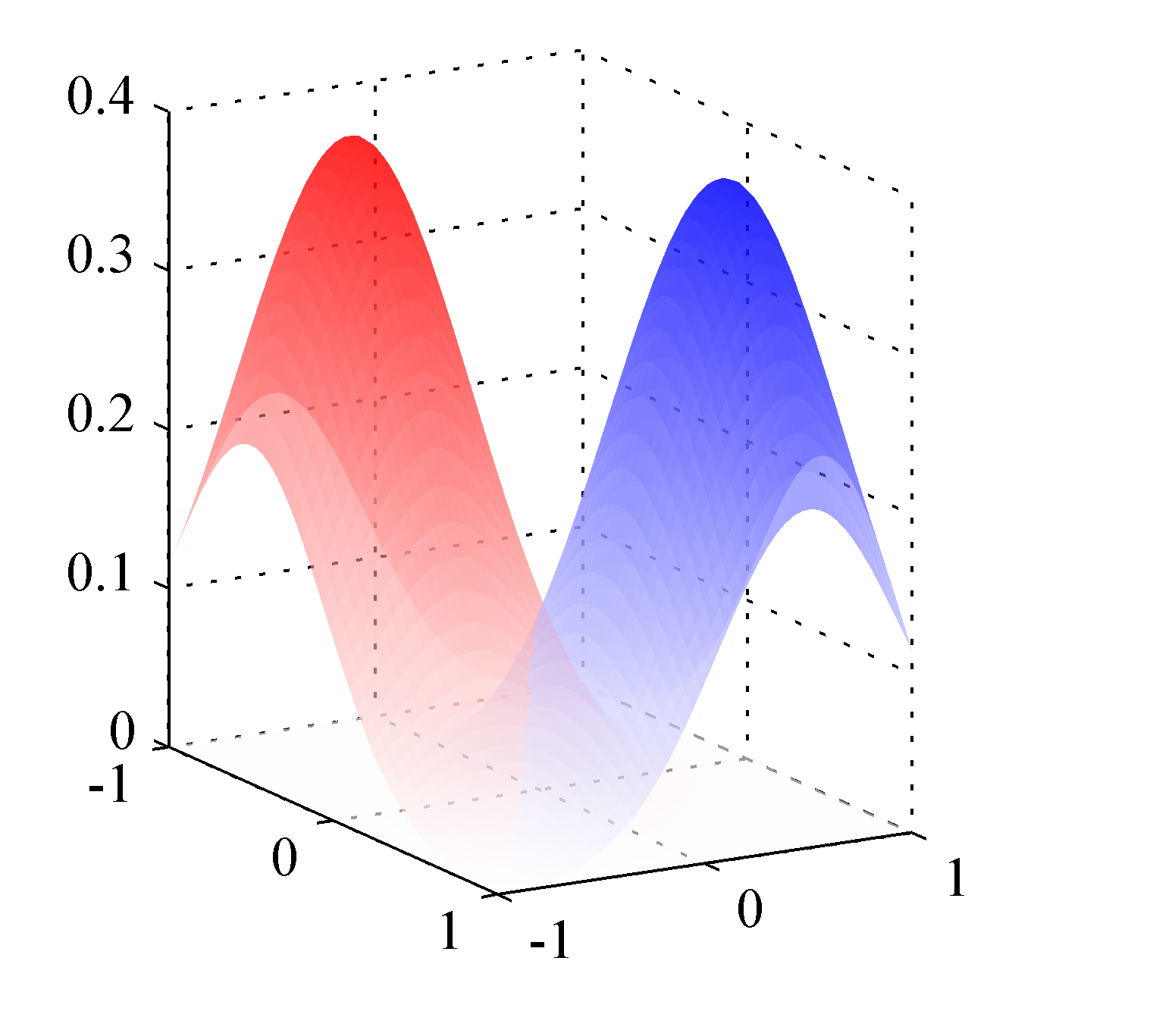
왼쪽 그림은 2-class 조건에서의 확률 밀도를 표현한 것이다.
- 공분산이 동일하므로 모양은 같다. (평균 위치만 틀림)
- 따라서 이를 분할하는 경계면은 당연히 직선이 된다.
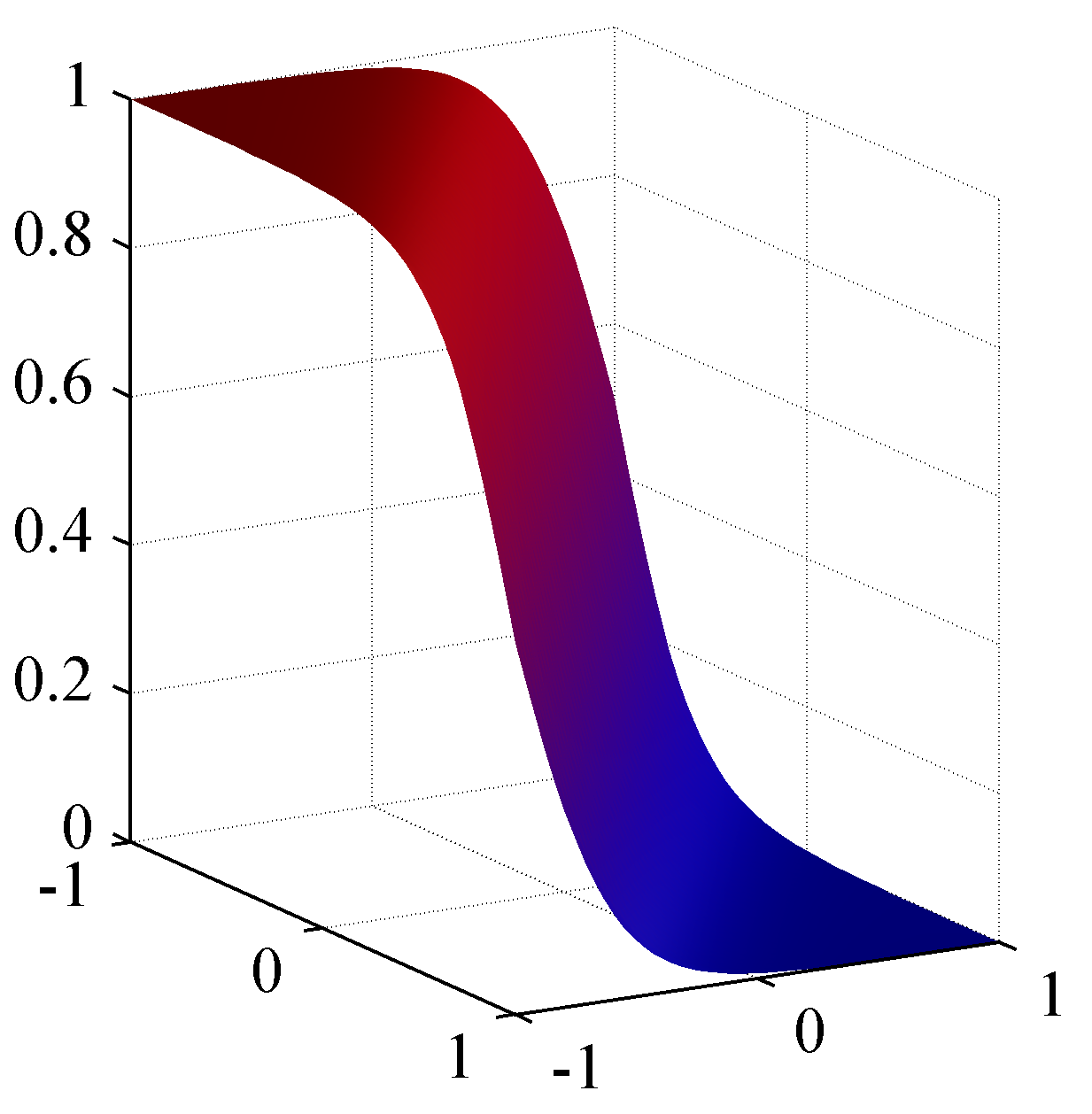
오른쪽은 $ x $ 에 대한 시그모이드 함수로 어떤 클래스에 속하는지에 대한 부분은 색깔로 확인할 수 있다
- 딱 중간 위치에서 클래스가 나누어지는 것을 알 수 있다 (2-클래스 문제이므로)
만약 이를 $ K $ 클래스 문제로 확장하면 어떻게 될까?
- 식 (4.62)와 식 (4.63)을 일반화시키면 $ K $ 클래스 문제도 풀어낼 수 있다.

${\bf w}_k = \Sigma^{-1}{\bf \mu}_k \qquad{(4.69)}$ $w_{k0} = -\frac{1}{2}{\bf \mu}_{k}^{T}\Sigma^{-1}{\bf \mu}_k + \ln p(C_k)\qquad{(4.70)}$

사실 우리는 식을 간단히 만들기 위해 각 클래스에서 사용되는 공분산이 동일하다고 가정했다.
그러나 만약 각각의 클래스들의 공분산이 다르다면 어떻게 될까?
- 이 경우 경계면을 구하는 수식에서 이차항이 사라지지 않고 남게 된다.
- 따라서 경계 면이 곡선이 될 수도 있다.

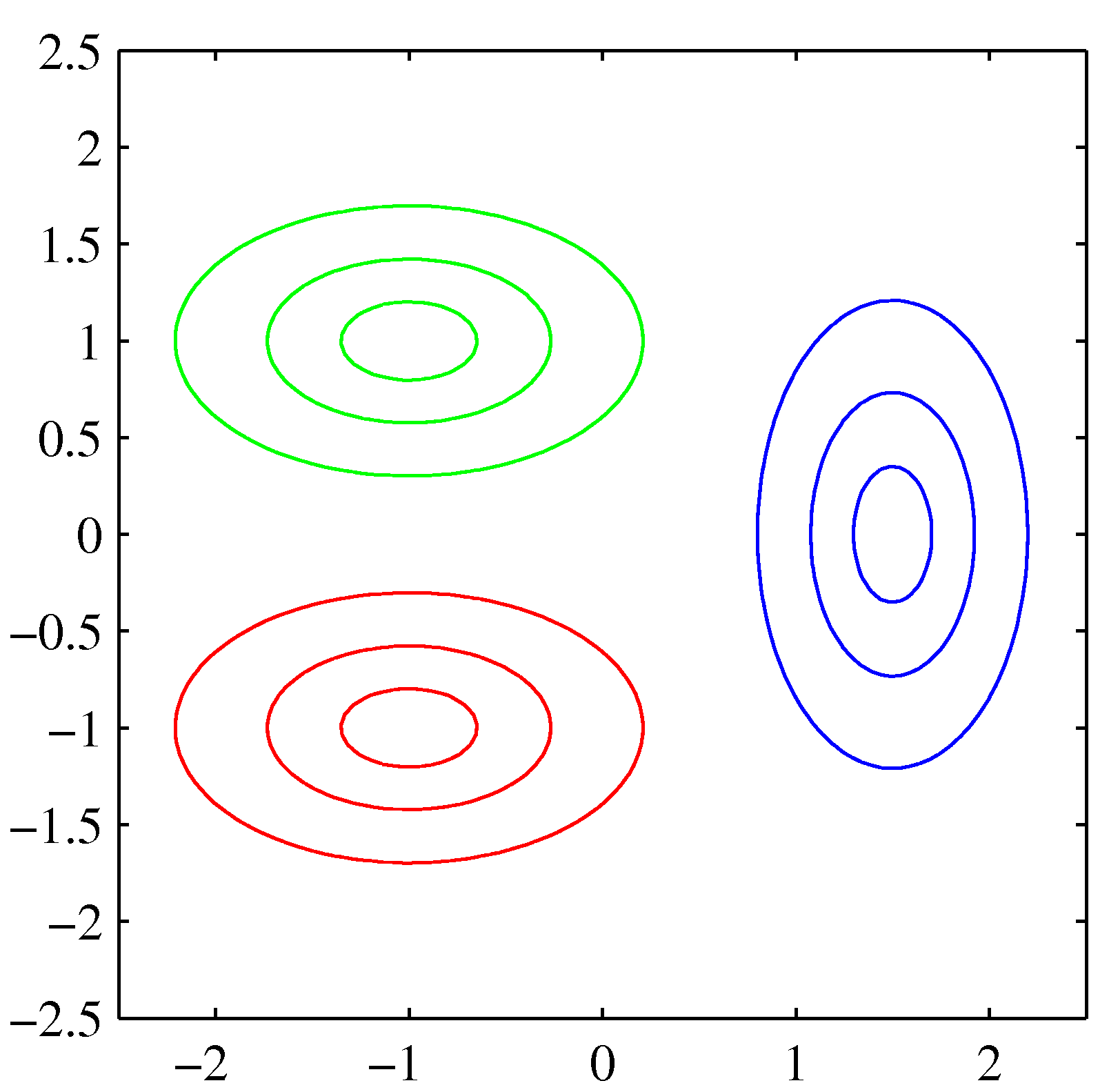
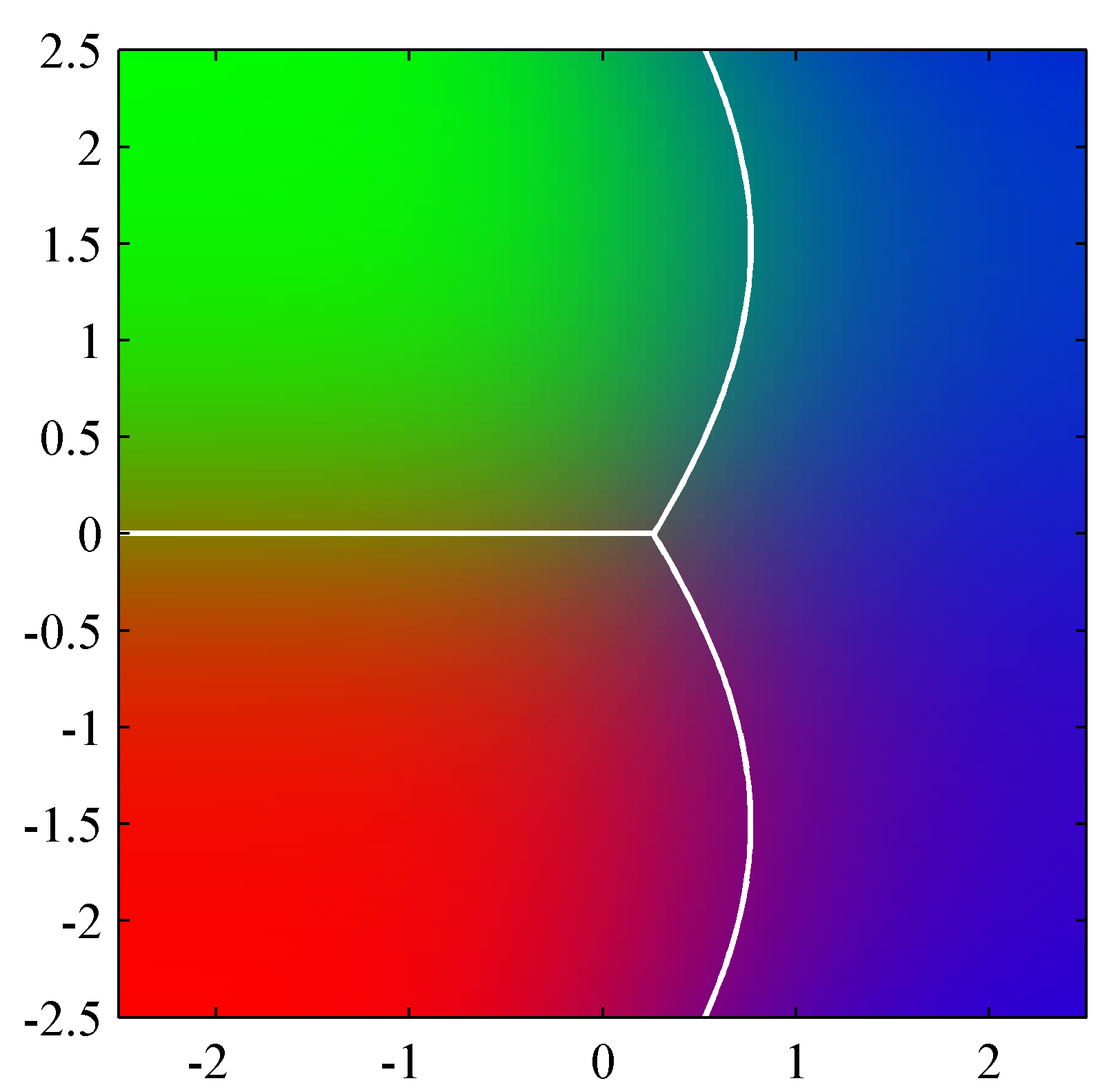
위의 그림을 보면 녹색과 적색의 클래스는 동일한 공분산을 가지므로 경계면이 직선이 됨을 알 수 있다.
그러나 청색 클래스 데이터는 다른 공분산을 가지고 있기 때문에 경계면이 곡선이 된다.
교재에서는 위의 그림 말고는 공분산이 다른 경우에 대한 자세한 설명이 나와있지 않다.
- 하지만 다른 패턴 인식 책에는 잘 나와 있는 경우가 많으니 참고할 것. (예로 Duda 패턴인식 2장)

4.2.2 최대 가능도(MLE) 풀이법 (Maximum likelihood solution)

지금까지 우리는 조건부 확률에 대한 모델로 $ p({\bf x}|C_k) $ 를 고려했었다.
자, 이제 MLE를 이용하여 모수를 추정하는 방법을 살펴보자.
더불어 이번 절에서는 사전(prior) 확률 $ p(C_k) $ 를 함께 고려하여 전개하도록 한다.
- 물론 착각하지 말아야 할 것은 모수(parameter)에 대한 사전 확률을 의미하는 것이 아니다.
- 즉, 베이지안 방식의 모수 추정을 사용한다는 의미는 아니라는 것이다.
- 여기서 말하는 사전 확률은 클래스에 대한 사전 확률을 의미한다. $ p(C_k) $
여기서도 마찬가지로 2-class 문제를 먼저 살펴보고, $ K>2 $ 인 경우로 확장하도록 한다.

2-class 문제인 경우

결합 확률로 문제를 정의해 보자.

$p({\bf x}_n, C_1) = p(C_1)p({\bf x}_n|C_1) = \pi N({\bf x}_n\;\mu_1, \Sigma)$ $p({\bf x}_n, C_2) = p(C_2)p({\bf x}_n|C_2) = (1-\pi) N({\bf x}_n\;\mu_2, \Sigma)$

여기서도 마찬가지로 공분산은 서로 같다고 가정한다.
실제 데이터는 $ ({\bf x}_n, t_n) $ 으로 $ t_n=1 $ 인 경우 $ C_1 $으로, $ t_n=0 $ 인 경우 $ C_2 $ 로 분류한다.
이제 가능도 함수(likelihood)를 정의해보자.

$p({\bf t}, {\bf X} \;| \pi, {\bf \mu}_1, {\bf \mu}_2, \Sigma) = \prod_{n=1}^N\left(\pi N({\bf x}_n\;|{\bf \mu}_1, \Sigma)\right)^{t_n}\left((1-\pi)N({\bf x}_n\;|{\bf \mu}_2, \Sigma)\right)^{1-t_n} \qquad{(4.71)}$

2-class 에서는 가능도 함수를 binomial 분포와 같은 식으로 정의할 수 있다.
여기서 $ {\bf t} $ 는 $ {\bf t} = (t_1,…,t_N)^T $ 로 정의된다.
$ \pi $ 구하기
- $ \pi $ 를 구하는 식은 별로 안 어렵다.
- 로그 가능도 함수를 $ \pi $ 에 대해 미분하여 관련된 항목만 모으면 다음과 같아진다.
- 이 값을 0으로 놓고 $ \pi $ 를 구하면 된다. (지금까지 많이 해왔던 작업이다.)

$\sum_{n=1}^{N}\left\{ t_n\ln\pi + (1-t_n)\ln(1-\pi) \right\} \qquad{(4.72)}$ $\pi = \dfrac{1}{N}\sum_{n=1}^{N}t_n = \dfrac{N_1}{N} = \dfrac{N_1}{N_1+N_2} \qquad{(4.73)}$

여기서 $ N_1 $ 은 $ C_1 $ 에 속하는 샘플의 수이고 $ N_2 $ 는 $ C_2 $ 에 속하는 샘플의 수이다.
$ \pi $ 는 정확히 $ C_1 $ 에 속하는 샘플의 비율을 의미하게 된다.
이 식은 K-class 문제로 쉽게 확장 가능하다. ( $ K>2 $)
- 이를 일반화하면 $ \pi_k = N_k / N $ 을 얻을 수 있다.
- 이에 대한 유도는 연습문제 4.9 에서 확인 가능하다.
$ {\bf \mu} $ 구하기
- 마찬가지로 로그 가능도 함수로부터 각각의 $ \mu $ 값으로 미분하여 값을 구한다.

$\sum_{n=1}^{N}t_n\ln N({\bf x}_n\;|{\bf \mu}_1, \Sigma) = -\dfrac{1}{2}\sum_{n=1}^{N}t_n({\bf x}_n-{\bf \mu}_1)^T\Sigma^{-1}({\bf x}_n-{\bf \mu}_1) + const \qquad{(4.74)}$

이 식을 0으로 놓고 $ {\bf \mu}_1 $ 에 대해 풀면 다음을 얻을 수 있다.

${\bf \mu}_1=\dfrac{1}{N_1}\sum_{n=1}^{N}t_n{\bf x}_n \qquad{(4.75)}$

마찬가지로 $ {\bf \mu}_2 $ 에 대해서도 동일한 해법으로 계산 가능하다.

${\bf \mu}_2=\dfrac{1}{N_2}\sum_{n=1}^{N}(1-t_n){\bf x}_n \qquad{(4.76)}$

$ \Sigma $ 구하기
- 마지막으로 $ \Sigma $ 를 구하는 과정을 살펴보자.
- 여기서도 동일하게 로그 가능도 함수로부터 공분산으로 미분하여 값을 구한다.
- 공분산을 구하는 식은 좀 복잡하기는 하다.

$-\dfrac{1}{2}\sum_{n=1}^{N}t_n\ln |\Sigma| -\dfrac{1}{2}\sum_{n=1}^{N}t_n({\bf x}_n-{\bf \mu}_1)^T\Sigma^{-1}({\bf x}_n-{\bf \mu}_1) -\dfrac{1}{2}\sum_{n=1}^{N}(1-t_n)\ln |\Sigma| -\dfrac{1}{2}\sum_{n=1}^{N}(1-t_n)({\bf x}_n-{\bf \mu}_1)^T\Sigma^{-1}({\bf x}_n-{\bf \mu}_1)\\\\ = -\dfrac{N}{2}\ln |\Sigma| - \dfrac{N}{2}Tr\left\{\Sigma^{-1}{\bf S}\right\} \qquad{(4.77)}$

여기서 $ {\bf S} $ 는 다음과 같다.

${\bf S}=\dfrac{N_1}{N}{\bf S}_1+\dfrac{N_2}{N}{\bf S}_2 \qquad{(4.78)}$ ${\bf S}_1 = \dfrac{1}{N_1}\sum_{n \in C_1} ({\bf x}_n-{\bf \mu}_1)({\bf x}_n-{\bf \mu}_1)^T \qquad{(4.79)}$ ${\bf S}_2 = \dfrac{1}{N_2}\sum_{n \in C_2} ({\bf x}_n-{\bf \mu}_2)({\bf x}_n-{\bf \mu}_2)^T \qquad{(4.80)}$

이는 교재 2.3.4 절에서 다루었던 가우시언 공분산 MLE 추정 과정과 거의 같다.

K-class 구하기 ( $ K>2 $)

$ \pi $ 구하기 : 간단하게 $ \pi $ 를 구하는 방법만을 살펴보자.
- 1-to-K 이진 타겟 값 $ {\bf t} $ 를 이용하여 가능도함수를 정의한다.

$p(\phi_n, {\bf t}_n\;|{\bf \pi}) = \prod_{n=1}^{N}\prod_{k=1}^{K}(p(\phi_n\;|C_k)\cdot\pi_k)^{t_{nk}}$ $\ln p(\phi_n, {\bf t}_n\;|{\bf \pi}) = \sum_{n=1}^N\sum_{k=1}^Kt_{nk}\left\{\ln p(\phi_n|C_k) + \ln\pi_k \right\}$

$ \sum_k\pi_k = 1 $ 을 활용하여 라그랑지안 승수를 도입한다.

$\ln p(\phi_n, {\bf t}_n\;|{\bf \pi}) + \lambda\left(\sum_{k=1}^K\pi_k-1\right)$

$ \pi_k $ 에 대해 미분하면 식을 얻을 수 있다.

$-\pi_k\lambda = \sum_{n=1}^Nt_{nk}=N_k$

양 번에 $ \sum_k $ 를 씌우면 $ \pi_k=\frac{N_k}{N} $ 를 얻을 수 있다.
그 외 K-class 환경 하에서 $ \mu $ 와 $ \Sigma $ 를 구하는 것은 별도의 연습 문제를 참고하기 바란다.
여기서는 간단하게 요약만 해 놓는다.
평균

${\bf \mu}_k = \dfrac{1}{N_k}\sum_{n=1}^N t_{nk}{\bf x}_n$

공분산

$\Sigma = \sum_{k=1}^K\dfrac{N_k}{N}{\bf S}_k$ ${\bf S}_k = \dfrac{1}{N_k}\sum_{n=1}^{N}t_{nk}(\phi_n-{\bf \mu}_k)(\phi_n-{\bf \mu}_k)^T$

위의 식은 마찬가지로 $ \Sigma $ 가 모든 클래스마다 동일하다는 가정 하에서 얻어진 식이다.

4.2.3 데이터가 이산 값일 때의 처리 (Discrete Features)

이제 입력 값이 연속적인 값이 아니라 이산적인 값이라고 생각해보자. ( $ x_i $)
문제를 단순화하기 위해 $ x_i $ 가 가질 수 있는 값은 $ x_i \in {0, 1} $ 뿐이다.
입력 데이터가 $ D $ 차원이라면 각 클래스별로 얻을 수 있는 확률 분포의 실제 $ x $ 의 이산적인 범위는 $ 2^D $ 개이다.
- 이 중 독립 변수는 $ 2^D-1 $ 이며 확률의 총 합이 1이기 때문에 변수 하나가 줄어들었다. (summation constraint)
여기서는 $ x $ 의 각 속성(feature)이 독립적이라고 가정하여 계산의 범위를 축소하도록 한다.
각 속성(feature)들이 모두 독립적이라는 가정을 Naive Bayes 가정이라고도 한다.
이제 샘플 하나의 클래스-조건부 확률 모델을 다음과 같이 기술할 수 있다.

$p({\bf x}|C_k) = \prod_{i=1}^{D}\mu_{ki}^{x_i}(1-\mu_{ki})^{1-x_i} \qquad{(4.81)}$

이 식을 K-class 문제에서의 $ a_k $ 함수에 대입하면

$a_k({\bf x})=\ln(p({\bf x}|C_k)p(C_k))$ $a_k({\bf x})=\sum_{i=1}^{D}\left\{x_i\ln \mu_{ki}+(1-x_i)\ln(1-\mu_{ki})\right\}+\ln p(C_k) \qquad{(4.82)}$

여기서도 $ a_k $ 함수는 $ x_k $ 에 대해 선형 함수이다. (feature가 독립적이라 가정했으므로)
2-class에서는 시그모이드를 도임하면 동일한 식을 얻을 수 있다.
여기는 $ x_i $ 의 값이 이진 값인 경우만 고려했다. 하지만 $ M>2 $ 이 상태를 가지는 $ x_i $ 에 대해서도 유사한 결과를 얻을 수 있다.

4.2.4 지수족 패밀리 (Exponential family)

지금까지 살펴본 내용에 따르면 지금까지 유도한 식들이 일정한 규칙을 따르고 있다는 것을 알 수 있는데,
- 사후 확률(posterior)의 경우 가우시안 분포든 이항 분포든 상관 없이 sigmoid 또는 softmax를 이용해서 모델링 할 수 있다.
- 당연히 2-class는 시그모이드(sigmoid), K-class ( $ K\ge2 $)는 소프트맥스(softmax)였다.
이걸 더 일반화시킬 수 없을까?
- 클래스-조건부 밀도(class-conditional density)가 지수족(exponential family) 분포를 따를 경우 가능하다.
- 교재 2.4 절에서 지수족 분포에 대해 설명을 이미 했다.
- 즉, 지수족 분포를 따를 경우의 확률 분포는 다음과 같은 일반식으로 기술 가능함을 이미 배웠다.

$p({\bf x}\;|\lambda_k) = h({\bf x})g(\lambda_k)\exp(\lambda_k^T u({\bf x})) \qquad{(4.83)}$

여기서는 $ u({\bf x})={\bf x} $ 로 제한한다.
- 이는 앞서 공분산 값을 클래스마다 동일하다고 가정했던 것과 같은 맥락의 제약 조건이다.
- 계산을 손쉽게 하기 위한 가정일 뿐이다.
다음으로 scale 파라미터 $ s $ 를 추가한다.
- 사실 모든 지수족 분포에는 고유의 파라미터가 있다.
- 이게 클래스별로 달라야 하는데 이게 바로 $ \lambda_k $ 이다.
- 하지만 우리는 모든 클래스가 동일한 스케일 파라미터를 공유한다고 가정했다.
  - 예를 들어 공분산이 모든 클래스마다 동일하다고 가정했던 것.
- 이런 제약 조건을 넣기 위해 임의의 공유 파라미터 $ s $ 를 추가한다.
파라미터를 추가하는 것은 2.4.3절의 (식 2.236)에서 이미 소개하였다.
이제 기본 식에 $ s $ 파라미터를 추가하자.

$p({\bf x}\;|\lambda_k, s) = \dfrac{1}{s}h\left(\dfrac{1}{s}{\bf x}\right)g\left(\lambda_k\right)\exp \left(\dfrac{1}{s}\lambda_k^T u({\bf x})\right) \qquad{(4.84)}$

기존의 $ \lambda $ 와는 별도로 조건절에 파라미터가 추가되었다.
2-class 에서 사용한 $ a_k $ 함수에 이를 대입하여 전개해보자.

$a({\bf x})=\dfrac{1}{s}(\lambda_1-\lambda_2)^T{\bf x}+\ln g(\lambda_1) - \ln g(\lambda_2) + \ln p(C_1) - \ln p(C_2) \qquad{(4.85)}$

이걸 K-class 에도 확장할 수 있는데 간단하게 식만 적어본다.

$a_k({\bf x}) = \dfrac{1}{s}\lambda_k^T{\bf x}+\ln g(\lambda_k) + \ln p(C_k) \qquad{(4.86)}$

가정에 의해 모두 선형 식임을 확인할 수 있다.

Chapter. 4