- 판별함수(discriminant function)는 입력 벡터 \( x \) 를 받아 \( K \) 클래스 중 하나의 클래스를 반환하는 함수이다.
- 이번 절에서는 선형 판별(linear discriminant)에 대해 알아보기로 한다.
- 처음에는 간단한 형태인 2-class 문제를 살펴보고 이후 \( K>2 \) 인 경우에 대해서도 살펴보도록 하자.
4.1.1 두개의 클래스 판별 (Two classes)
- 선형 판별식의 가장 간단한 형태는 다음과 같다.
- 여기서 \( w \) 는 가중치 벡터( weight vector )라고 부른다. 회귀(regression)와 마찬가지로 \( w_0 \) 는 바이어스(bias) 라고 부른다.
- 이 때 bias 에 음수 값을 취하면 이를 threshold 라고 부른다.
- 보통 2-class 문제에서는 \( y({\bf x}) \ge 0 \) 인 경우 이를 \( C_1 \) 으로 분류하고 아닌 경우 \( C_2 \) 로 분류한다.
- 따라서 이 때의 결정 경계면(boundary)은 \( y({\bf x})=0 \) 임을 알 수 있다.
- 이제 임의의 두 점 \( {\bf x}_A \) 와 \( {\bf x}_B \) 가 결정 경계면 위에 있다고 해보자.
- 이 때에는 \( y({\bf x}_A)=y({\bf x}_B)=0 \) 을 만족한다.
- 따라서 \( {\bf w^T}({\bf x}_A-{\bf x}_B)=0 \) 을 만족하게 되고, 여기서 \( w \) 는 결정 경계에 대해 수직( orthogonal )임을 알 수 있다.
- 또한 결정 경계에서 식을 전개하면 다음의 식을 얻을 수 있다.
- 자, 이제 \( D=2 \) 라고 할 때 그림을 좀 살펴보도록 하자.
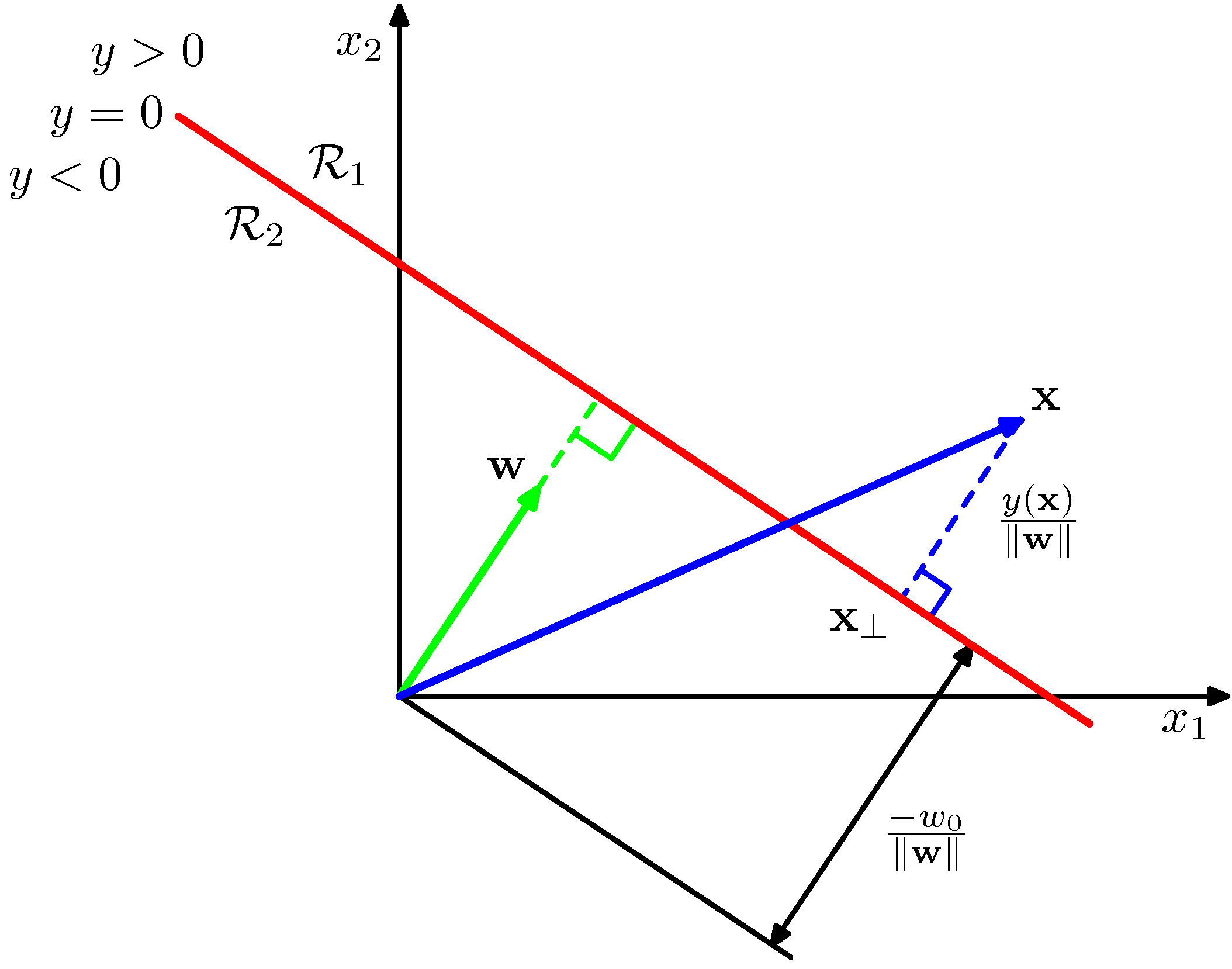
- 임의의 한 점 \( x \) 에 대해 결정 경계면에 수직으로 내린 지점을 \( x_\perp \) 라고 하자.
- 이 경우 다음과 같은 식이 성립한다.
- 3장에서와 비슷하게 \( x_0=1 \) 을 이용하면 식을 좀 간단하게 적을 수 있다.
- \( {\bf \tilde{w} }=(w_0, {\bf w}) \)
- \( {\bf \tilde{x} }=(x_0, {\bf x}) \)
- 이 경우에는 D+1 차원의 공간을 D 차원의 초평면(hyperplanes)으로 나눈다고 생각하는게 이해하기 더 쉽다.
4.1.2 여러 개의 클래스 판별 (Multiple classes)
- 이제 \( K>2 \) 인 상황을 생각해보자.
- 사실 K-class 문제는 2-class 문제를 여러 개 조합해서 해결할 수 있다.
- 만약 K-1 개의 2-class 분류기가 있다고 생각하면 K 개의 클래스를 분류 가능하다.
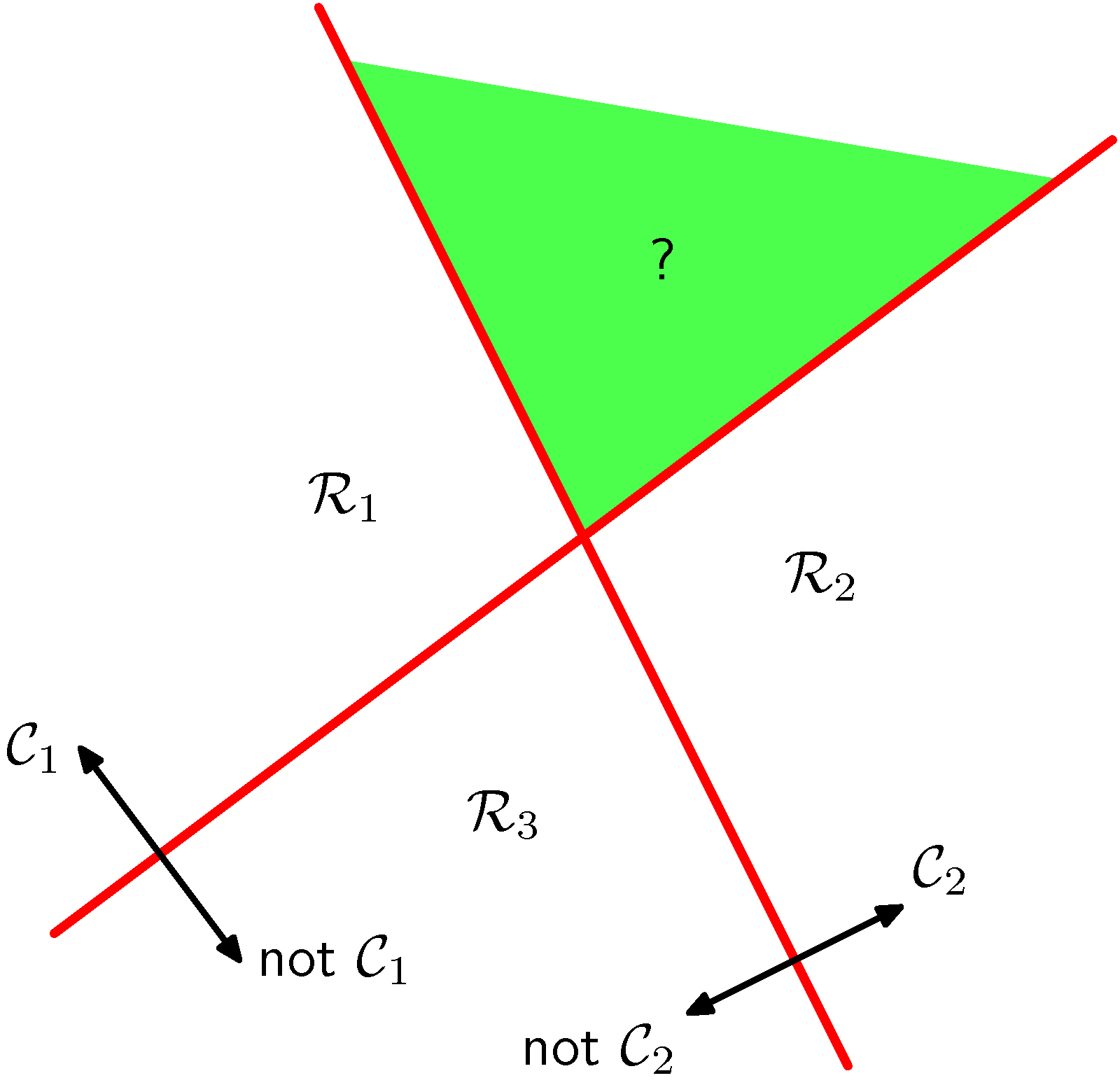
- 왼쪽 그림을 보면 3개의 클래스를 구별하기 위해 2개(즉, K-1개)의 2-class 분류기로 3개의 영역을 나누고 있다.
- 다만 이런 경우 녹색의 \( (?) \) 영역과 같이 판정이 불가능한 영역이 생겨난다.
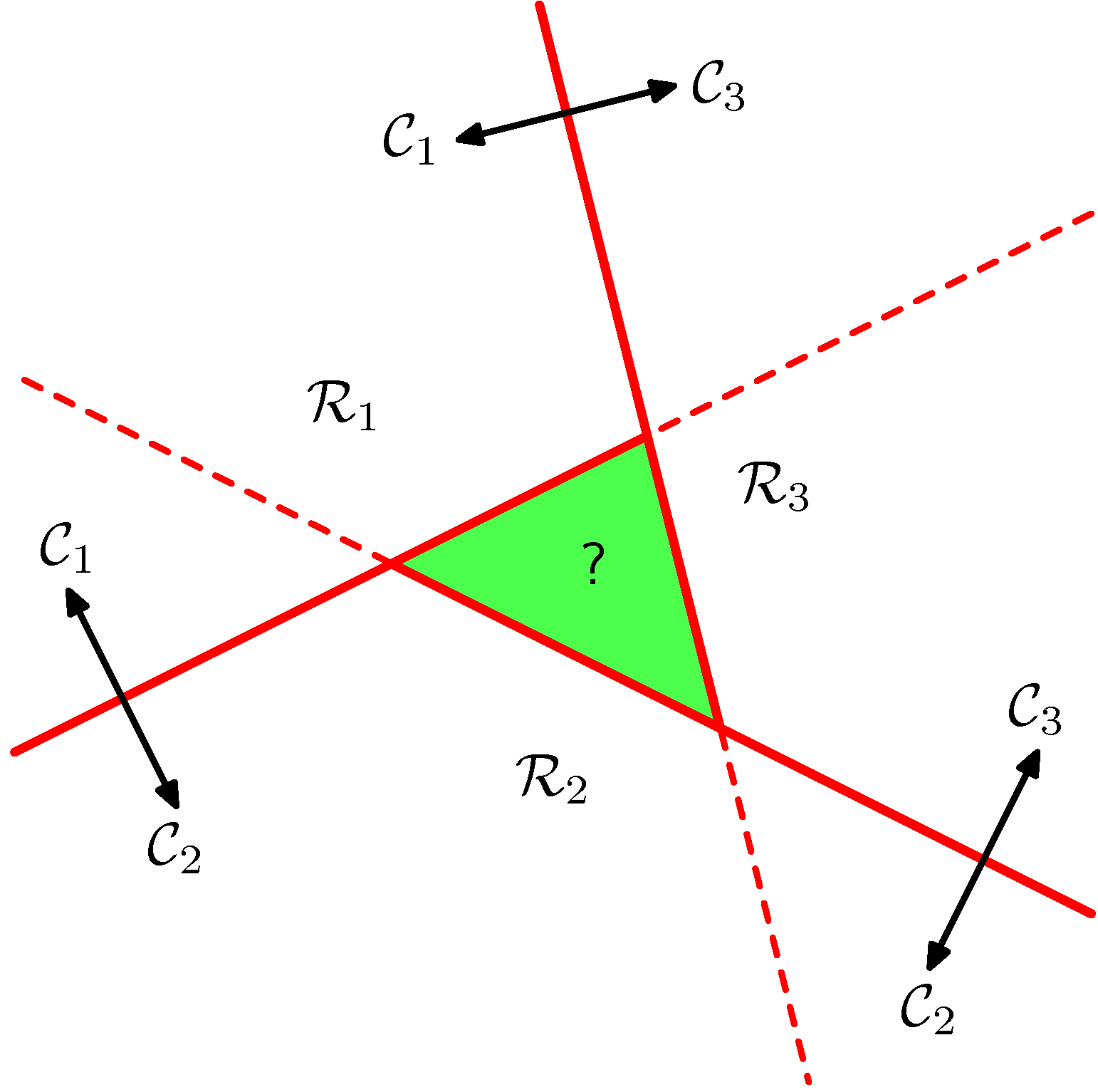
- 이와 유사하지만 좀 더 다른 방식으로 오른 쪽 그림과 같은 방법도 생각해 볼 수 있다.
- 즉, \( K(K-1)/2 \) 개 만큼의 분류기를 써서 K 클래스를 분류하는 것이다.
- 그러나 이 경우도 \( (?) \) 영역과 같이 분류가 애매한 영역이 생겨난다.
- 이런 문제를 해결하기 위해 다음과 같은 방식을 도입해보도록 한다.
- 위와 같은 판별식은 \( j{\neq}k \) 일 때 \( y_k({\bf x})>y_j({\bf x}) \) 를 만족하면 \( x \) 를 클래스 \( C_k \) 로 판별하게 된다.
- 따라서 두 클래스 간의 경계면은 \( y_k({\bf x})=y_j({\bf x})=0 \) 이 아니라 \( y_k({\bf x})=y_j({\bf x}) \) 에서 형성된다. 이 때 식을 전개하면,
- 이건 2-class 문제에서 사용하던 직선 식과 같은 형태이다.
- 두 판별식으로 인해 만들어지는 경계면이 직선 식이 된다. 혼동하면 안된다.
- 이런 판별식을 사용하는 경우 결정 구역은 단일 연결(singly connected)로 이루어지고 볼록(Convex)하다.
- 예를 들어 하나의 지역이 여러 선으로 이루어진 도형의 모양이라면, 모두 하나의 선으로 연결되어 있고,
- 내부의 어느 각 하나라도 180도를 넘지 않는다.
- 이를 증명하기 위해 다음과 같은 경우를 생각해보자.
- 임의의 점 \( {\bf x}_A \) 와 \( {\bf x}_B \) 는 같은 지역에 놓여있다.
- 이 두 점 사이에 위치한 임의의 한 점을 나타내기 위해서는 다음과 같은 식을 사용하면 된다.
- 만약 \( \lambda \) 가 \( 0 {\le} \lambda {\le} 1 \) 인 값이라면, 우리는 다음과 같이 식을 기술할 수 있다.
- 여기에서 \( {\bf x}_A \) 와 \( {\bf x}_B \) 모두 같은 영역 \( R_k \) 에 속하게 되므로 \( y_k({\bf x}_A)>y_j({\bf x}_A) \) 이고 \( y_k({\bf x}_B)>y_j({\bf x}_B) \) 이다.
- 또 \( y_k(\widehat{ {\bf x} }) \) 는 \( y_k({\bf x}_A) \) 와 \( y_k({\bf x}_B) \) 로만 구성된다.
- 위의 식 때문에 \( y_j(\widehat{ {\bf x} }) \) 는 \( y_k(\widehat{ {\bf x} }) \) 보다 클 수가 없다.
- 결국 모든 \( j{\neq}k \) 에서 \( y_k(\widehat{\bf x})>y_j(\widehat{\bf x}) \) 가 된다.
- 따라서 \( R_k \) 는 단일 연결(singly connected)로 되어 있고, 볼록(convex)하다. 아래 그림과 같다는 이야기.
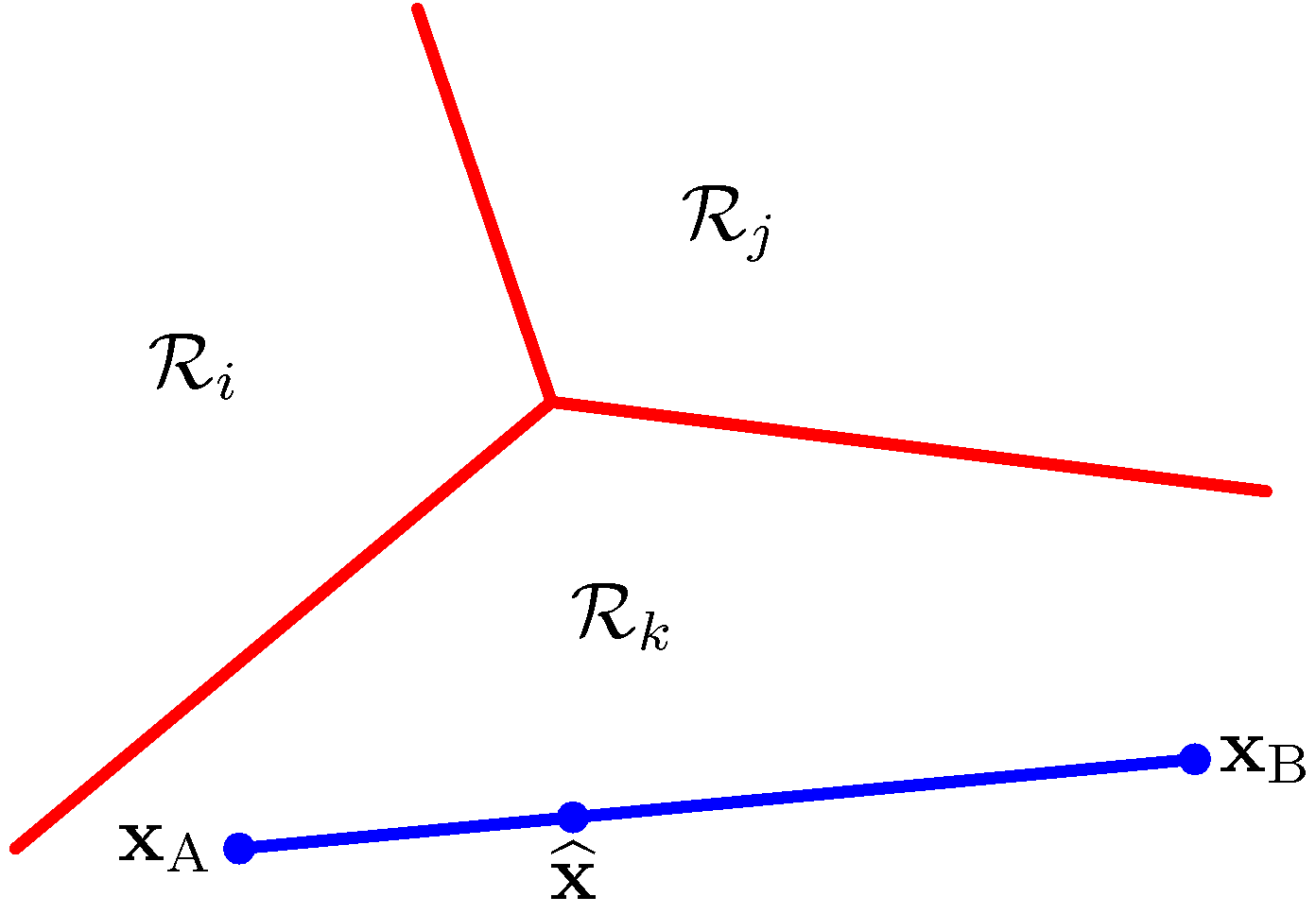
- 좀 더 자세한 내용은 다음 절을 참고하자.
- 앞으로 우리는 선형 판별(linear discriminant)을 위한 세가지 방법을 살펴볼 것이다.
- 최소 제곱법
- 피셔(Fisher)의 선형 분류기
- 퍼셉트론(perceptron) 알고리즘
4.1.3 최소제곱법을 이용한 분류 (Least squares for classification)
- 이미 3장에서 파라미터를 이용한 선형 함수 모델을 살펴보았다.
- 이 때 사용한 방식이 sum-of-squares 에러 함수 방법이다.
- 이 값을 최소화하는 방법으로 문제를 해결했다.
- 이걸 가지고서 K 클래스 분류 문제를 해결할 수 있을까?
- 최소 제곱법을 사용하면 조건부 기대값 \( E[{\bf t}|{\bf x}] \) 을 근사할 수 있음을 이미 배웠다. (1.5.5절)
- 앞서 언급했던 1-to-K 이진 코딩 형태의 타겟 벡터 \( {\bf t} \) 로 고려하면 이 때의 조건부 기대값은 사후(posterior) 확률값의 벡터가 된다.
- 하지만 이 값은 대부분 그리 정확하지 않는데다가 0~1 사이의 범위를 넘어가기도 한다. (왜 그런지는 조금 후에 나온다.)
- 이것은 모델이 별로 유연하지 않기 때문인데 그 이유를 간단히 살펴보도록 하자.
- \( C_k \) 클래스를 판별하는 판별식은 다음과 같다.
- 여기서 \( k=1,…,K \) 일 때, 이 식을 다시 기술해보자.
- \( \tilde{W} \) 는 행렬로써 \( k \) 개의 컬럼을 가지고 있으며, \( k^{th} \) 인 하나의 컬럼은 \( \tilde{w}_k=(w_{k0}, {\bf w}_k^T)^T \) 로 정의된다.
- 마찬가지로 \( \tilde{\bf x} \) 는 \( \tilde{\bf x}=(1, {\bf x}^T)^T \) 로 정의된다. (단, \( x_0=1 \) )
- 그리고 이와 같은 형태의 수식은 3.1 절에서 이미 다루어본 주제이다.
- 이제 새로운 입력 변수 \( x_{new} \) 가 주어지면 이에 대한 클래스는 \( y_k=\tilde{\bf w}_k^T\tilde{\bf x} \) 중 가장 큰 값을 가지는 \( y_k \) 의 \( k \) 클래스로 정해진다.
- 자, 우리는 이제 앞서 살펴보았던 방식과 동일하게 에러 함수값을 최소화하는 형태로 \( \tilde{W} \) 를 구하는 형식으로 식을 전개할 것이다.
- 3장에서는 입력 데이터는 \( { {\bf x}_n, {\bf t}_n} \) 의 형태로 주어졌었다.
이 때 \( n \) 번째 데이터의 타겟 값을 \( {\bf t}_n^T \) 라 하면, 모든 샘플에 대한 타겟 벡터를 \( \bf T \) 라고 정의할 수 있다. - 마찬가지로 \( n \) 번째의 입력 데이터를 \( \tilde{\bf x}_n^T \) 라 하면, 전제 샘플 데이터를 \( \tilde{\bf X} \) 로 정의할 수 있다.
- 이제 sum-of-squares 에러 함수는 다음과 같이 정의된다.
- \( Tr \) 은 행렬의 trace를 의미한다. 혹시 trace가 뭔지 모를 수도 있으니 잠시 적어놓는다. (대각선분의 합이다.)
- 그리고 여기서 trace를 도입한 것은, 단지 수식 표기가 쉽기 때문일 뿐 큰 의미는 없다.
- 에러 함수의 정의가 이상하다고 느껴질 수도 있다. : \( (\tilde{\bf X}\tilde{\bf W}-{\bf T}) \) 부분
- \( T \) 벡터는 0 또는 1의 값을 가지는 1-to-K 벡터가 N개인 벡터 (즉, \( {N}\times{K} \) 인 행렬)
- \( \tilde{\bf X}\tilde{\bf W} \) 는 실수 값을 가지는 벡터 (즉, \( {N}\times{M} \cdot {M}\times{K} = {N}\times{K} \) 인 행렬)
- 연산 결과 행렬의 크기는 같지만, 얻어지는 실제 값들의 범위가 다르다. (한쪽은 0~1 범위, 한쪽은 실수 범위)
- 그러나 조금만 생각해보면, \( W \) 벡터는 방향만 의미가 있고 값 자체는 스케일링이 가능하다는 것을 알 수 있다.
- 즉, 어차피 판별식으로만 사용되기 때문에 각각의 \( y \) 에 대해 적절한 크기로 스케일링되기만 하면 된다.
- 위와 같은 경우에는 알아서 \( W \) 값이 \( X \) 의 범위에 따라 적절한 범위의 값으로 만들어질 것이다.
-
따라서 위의 에러 함수를 사용하면 알아서 원하는 범위의 \( W \) 값들이 결정될 수 있다.
- 늘 하던대로 \( \tilde{\bf W} \) 에 대해 미분하고 식을 전개하면 다음과 같다.
- 여기서 \( \tilde{\bf X}^{\dagger} \) 는 \( \tilde{\bf X} \) 의 pseudo-inverse 행렬이다. (3장의 정의 참고)
- 이제 식을 정리하면 다음과 같다.
- 최소 제곱법을 이용한 방식에는 재미난 성질이 있는데, 주어진 트레이닝 데이터 집합의 타겟 값이 아래와 같은 선형 제약을 만족한다면,
- 어떤 \( x \) 에 대해 값을 예측하더라도 다음과 같은 선형 제약을 가지게 된다.
- 증명은 생략하기로 하자. 연습문제 4.2 풀이를 찾아보면 된다.
- 위의 식을 조금만 응용해봐도 \( y({\bf x}) \) 가 얻어질 범위를 예측해 볼 수 있는데,
- 1-of-K 코딩 방식을 사용하는 경우 어떤 \( x \) 에 대해서도 \( y(x) \) 의 모든 합은 1이 된다.
-
다만 각각의 값들이 반드시 \( (0, 1) \) 범위 내에 존재하는 것은 아니므로 (즉, 음수가 나오기도 한다) 이를 확률값이라고 생각할 수는 없다.
- 최소 제곱법은 닫힌 성질(close-form)을 만족하기 때문에 판별식으로 원하는 값을 반드시 찾아낼 수 있다.
- 그러나 문제는 (앞서도 확인한 내용이지만) 최소 제곱법의 경우 특이치(outlier)에 대해 너무 민감한 성질을 보인다는 것이다.
- 그래서 실제 응용에서는 최소 제곱법 보다는 좀 더 강건한(robustness) 모델을 선호하게 된다.
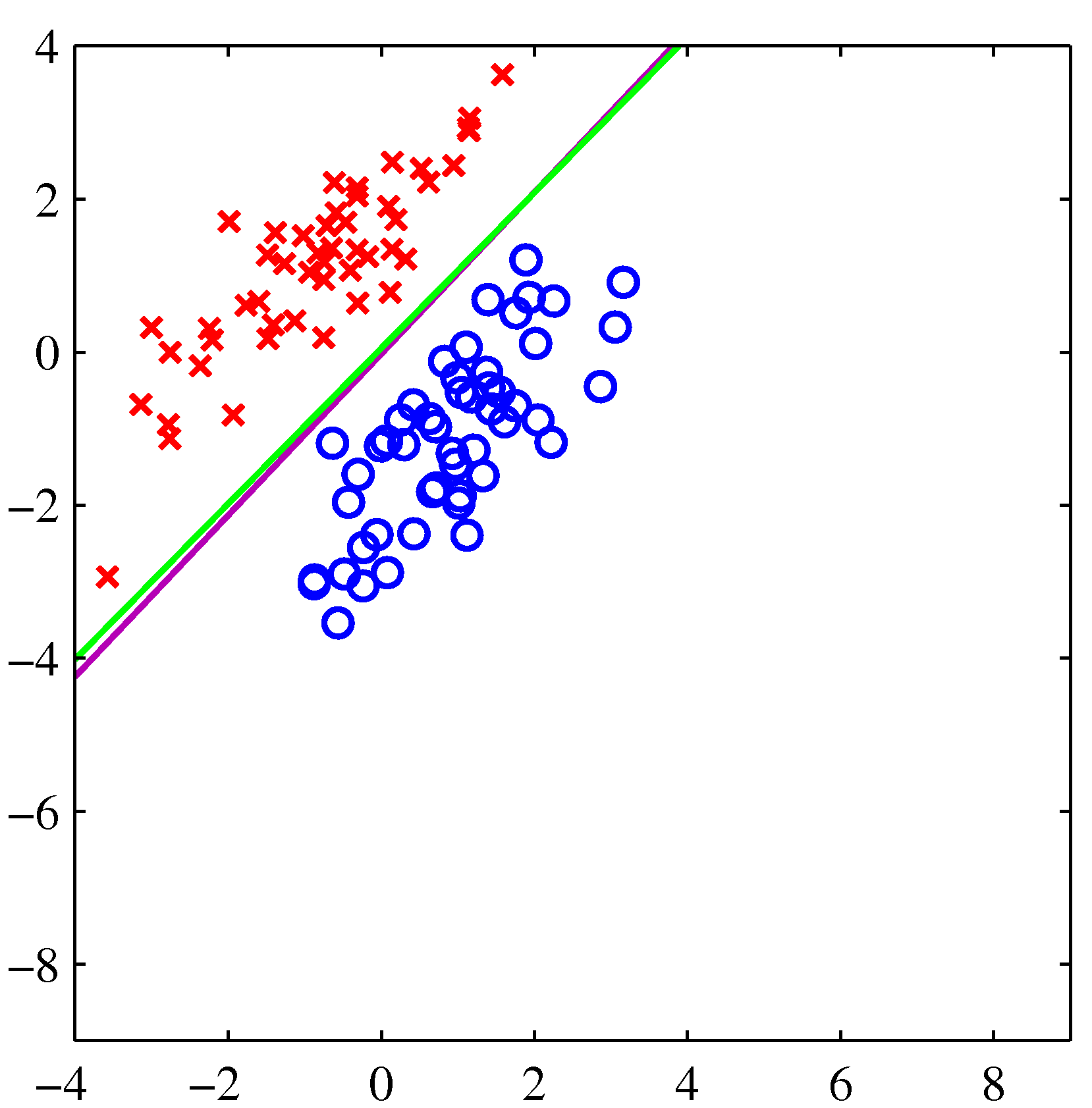
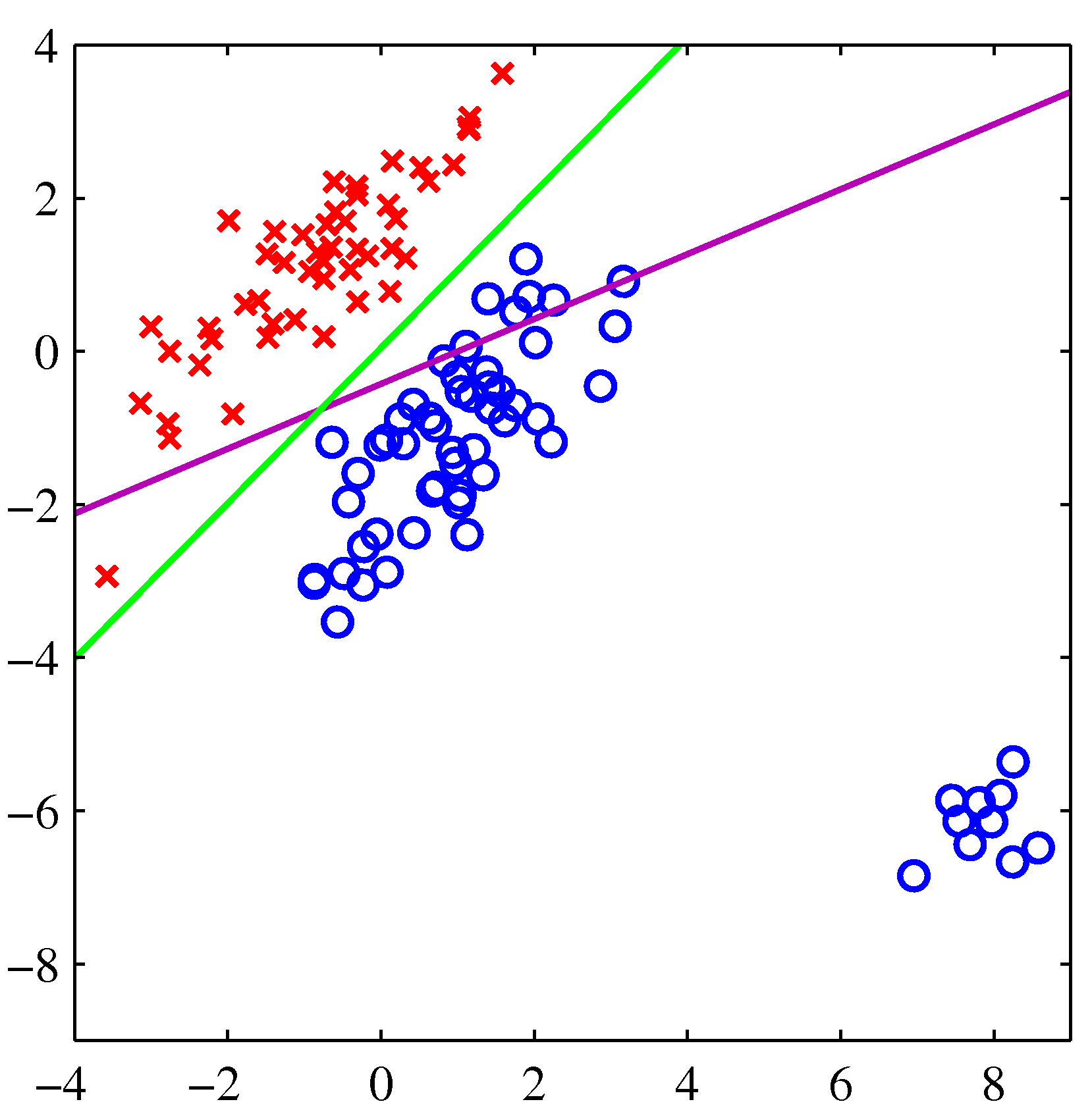
- 녹색 선은 로지스틱 회귀 분석, 보라색 선은 최소 제곱법을 사용한 것이다.
-
왼쪽의 경우는 둘 다 좋은 결과를 보여주고 있지만, 오른쪽처럼 특이값이 등장한 경우 최소 제곱법은 좀 문제가 있다는 것을 보여준다.
- 3차원 클래스 분류 문제도 좀 살펴보자.
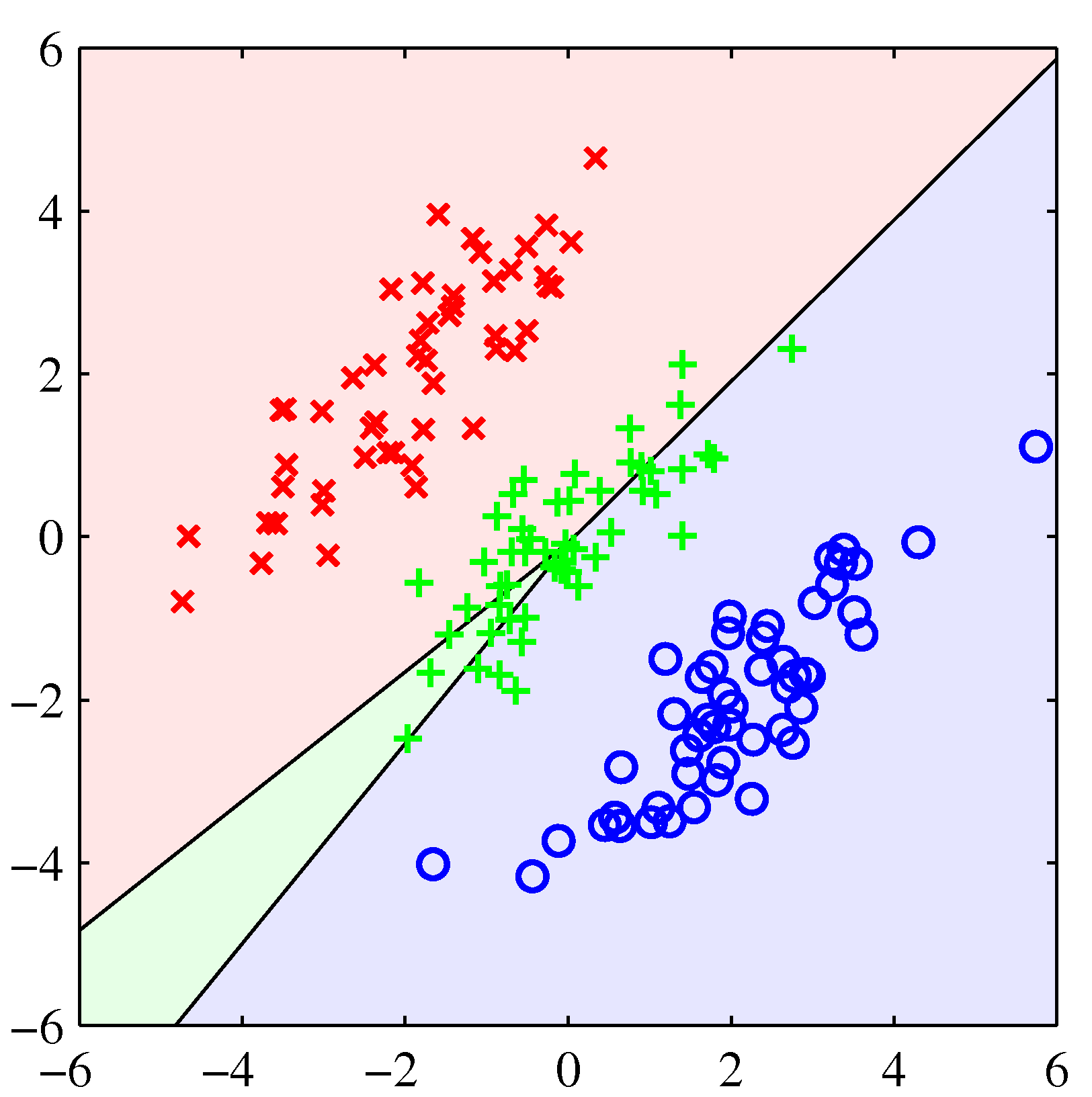
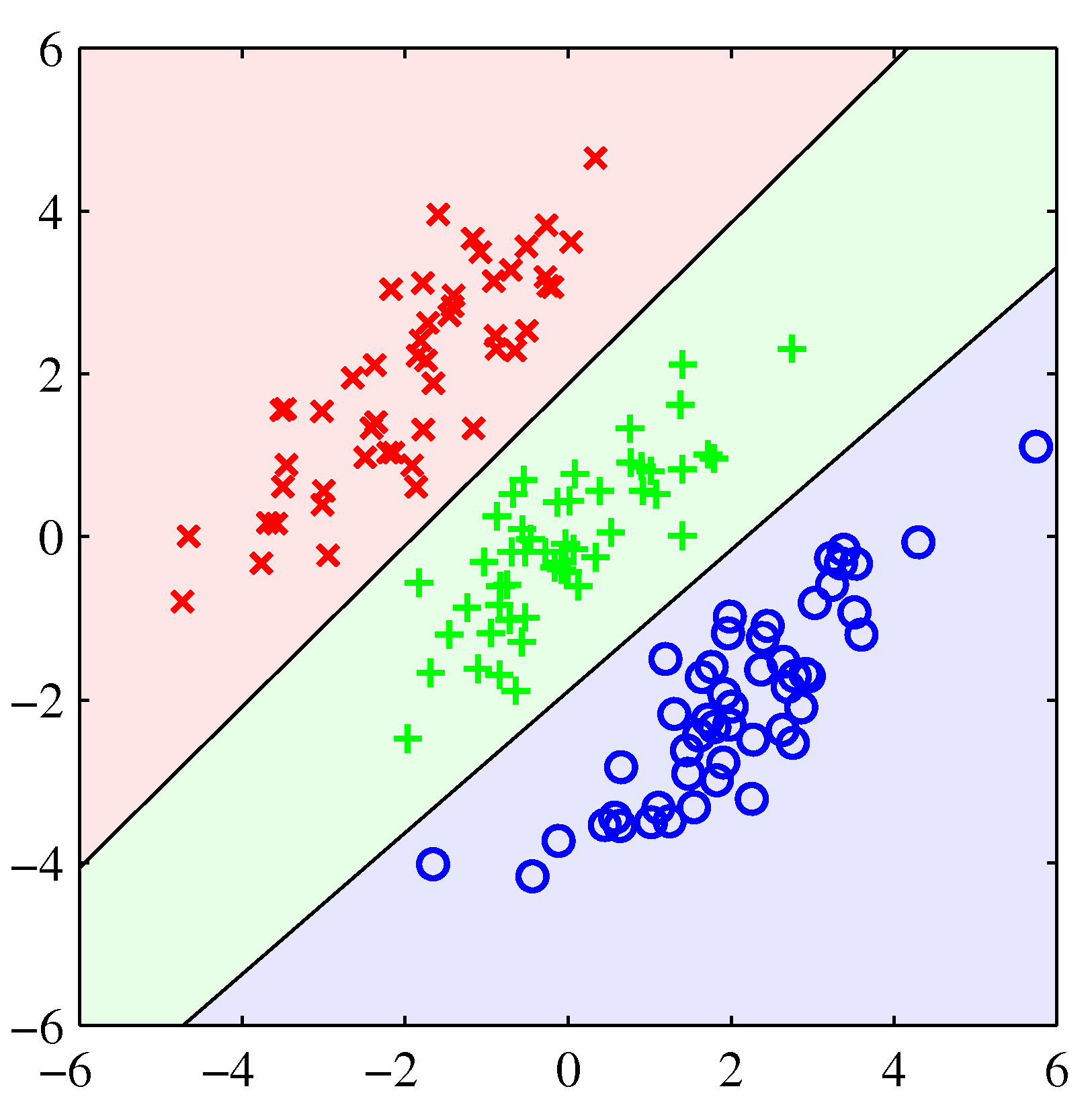
- 왼쪽이 최소 제곱법, 오른쪽이 로지스틱 회귀 분석법이다.
- 최소 제곱법이 이렇게 엉망인 결과를 내고 있다는 것이 사실 그리 놀랍지는 않다.
- 왜냐하면 우리는 타겟 벡터가 가우시안 조건부 분포를 가지고 있다는 가정을 하고 있기 때문이다.
- 3장에서 MLE를 다룰 때 사용했던 개념을 그대로 차용함.
- 이진(binary) 값 형태의 타겟 값을 가진 경우 이러한 가정이 잘 맞지 않는 것은 어찌보면 당연한 일
4.1.4 피셔의 선형 분류법 (Fisher’s linear discriminant)
- 현대 통계학의 아버지인 피셔가 자신있게 내어 놓은 선형 분류법
- 사실 기본 개념은 PCA 와 같다. 여기에 클래스 문제를 추가한 것과 크게 다른 것이 없음.
- 따라서 PCA를 이해한다면 피셔의 방식은 바로 이해를 할 수 있다.
-
일단은 2-클래스 문제로 접근을 시도해 보자.
- 일간 해야 할 일은 \( D \) 차원의 데이터를 하나의 차원으로 투영하는 과정이 필요하다.
- 이 때 벡터를 투영하는 식은 다음과 같다. (단, 여기서 \( {\bf w} \) 는 단위벡터로 생각하는게 쉽다.)
- 이 식은 임의의 한 벡터를 한 차원의 벡터 위의 한 점, 즉 스칼라 값으로 변환해준다.
- 혹시 벡터 투영(projection) 식이 위와 같아야 하는지 잘 모르겠다면 아래 식을 참고한다. (한 벡터를 단위 벡터에 투영한다.)
- 사실 반드시 단위 벡터일 필요는 없는데, 특정 상수를 곱하면 스케일링이 가능하기 때문이다.
- 이 때 \( y \) 에다가 threshold 를 두어 이 값을 비교해서 클래스를 판별하게 된다. (여기서 threshold 는 \( -w_0 \) 가 된다.)
- \( y\ge-w_0 \) 인 경우 \( C_1 \) 아닌 경우 \( C_2 \)
-
결국 대단할 것은 없고 단순한 선형 분류기를 만드는 것
- 높은 차원을 낮은 차원으로 축소하는 경우 당연히 정보 손실이 발생한다.
-
여기서는 가중치 벡터 \( {\bf w} \) 를 잘 선택해서 차원을 축소하더라도 정보 손실이 가장 적은 방향으로 모델을 구성한다. (사실 이게 PCA 원리)
- 모델의 구성
- D 차원의 데이터를 어떤 1차원의 축으로 투영(projection)하되
- 같은 클래스 내의 데이터끼리는 최대한 모여있고,
- 다른 클래스를 가지는 데이터 끼리는 최대한 떨어져있도록 할 수 있는
- 그런 1차원 벡터를 구해야 한다.
- 2-class 문제에서 각 클래스의 무게 중심, 즉 평균을 나타내는 벡터를 표기해보자.
- 일단은 위의 값을 가지고 두 클래스간의 거리가 최대화되도록 하는 식을 전개해볼 예정이다.
- 각 클래스의 평균 벡터가 1차원의 벡터로 투영된 후의 값은 다음과 같다. (투영 후에는 실수 값이 된다.)
-
이 때 두 평균 벡터가 투영된 후 두 점 사이의 거리를 보자.
- 앞서 언급했지만 각 클래스가 어떤 1차원 벡터로 투영 후 거리가 최대가 되는 문제는 위의 식처럼 각 클래스의 평균 벡터가 투영 후 최대의 거리를 가지는 문제로 생각하면 된다.
-
물론 위의 식에서는 나오지 않지만 거리 를 최대화 하는 문제이므로 \( m_2-m_1 \) 을 가장 크게 하는 값을 구하는 문제이다. - 식에 굳이 절댓값 기호를 붙이지 않는 이유는 \( w \) 벡터에 포함된 부호로 이를 만들어낼 수 있기 때문. 중요한 건 아니다.
- 우리는 위의 식에서 \( {\bf w} \) 를 찾아야 하는데, 그냥 식만 살펴보면 \( {\bf w} \) 값만 무한정 키우면 식의 값이 커지게 된다.
- 하지만 \( {\bf w} \) 는 단위 벡터로 고정을 해서 이런 애매한 상황을 없애버린다. : \( \sum_i{w_i^2}=1 \)
- 뭐 그냥 라그랑지앙 승수를 도입하기 위한 수순이라고 생각하면 된다.
- 이제 이 식을 라그랑지앙 승수(Lagrange multiplier)를 도입해서 최소값을 구하게 된다.
- 별거 없고 \( f={\bf w}^T({\bf m_2}-{\bf m_1})-\lambda(\sum{w^2}-1) \) 을 두고 미분하면 된다.
- 그럼 대충 \( {\bf w} \) 값은 \( ({\bf m_2}-{\bf m_1}) \) 에 비례상수를 곱한 식으로 만들면 된다는게 나온다. : \( {\bf w} \propto ({\bf m_2}-{\bf m_1}) \)
- 하지만!!! 안타깝게도 이것 만으로는 2% 부족하다.
- 그림을 보면서 좀 설명해보자.
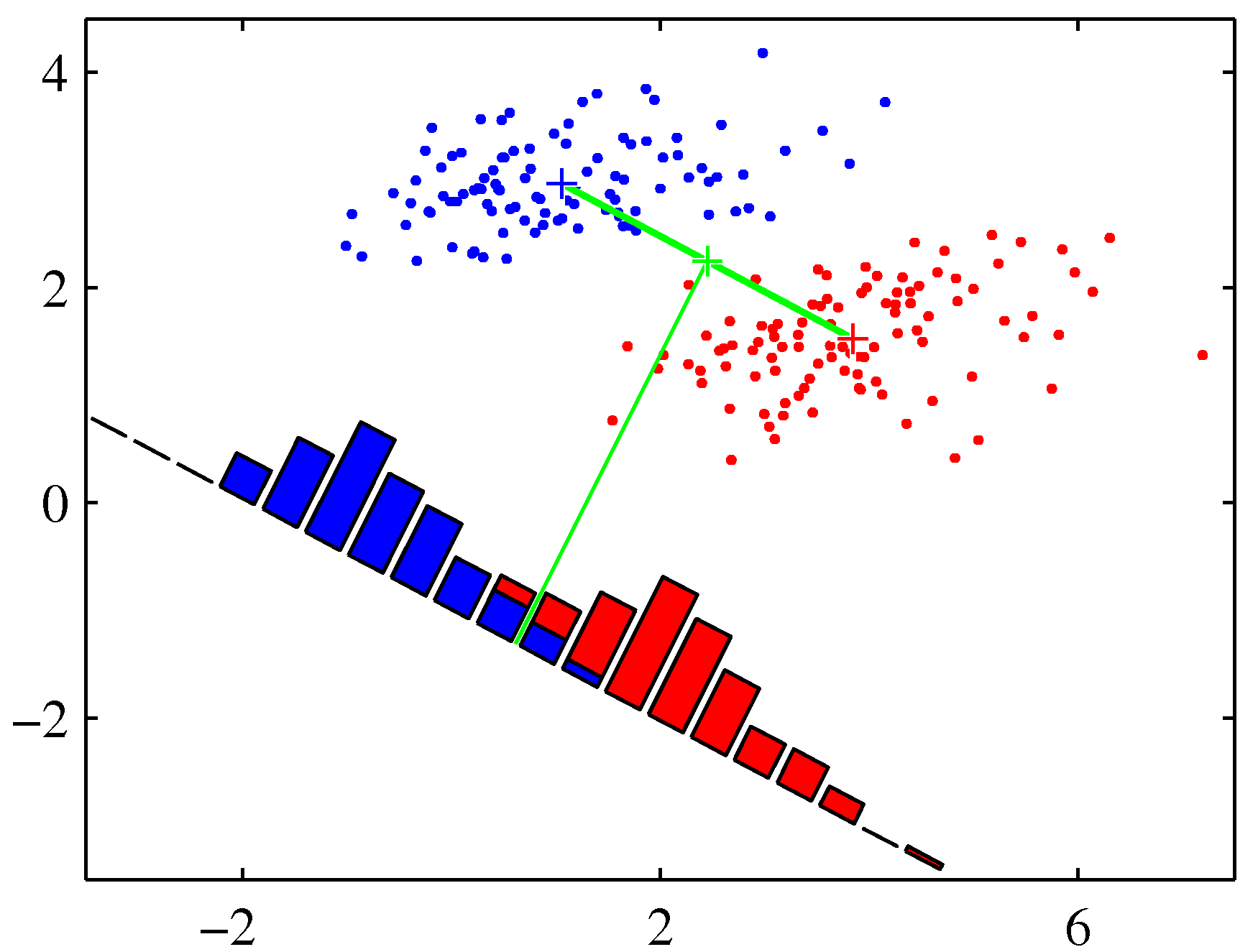
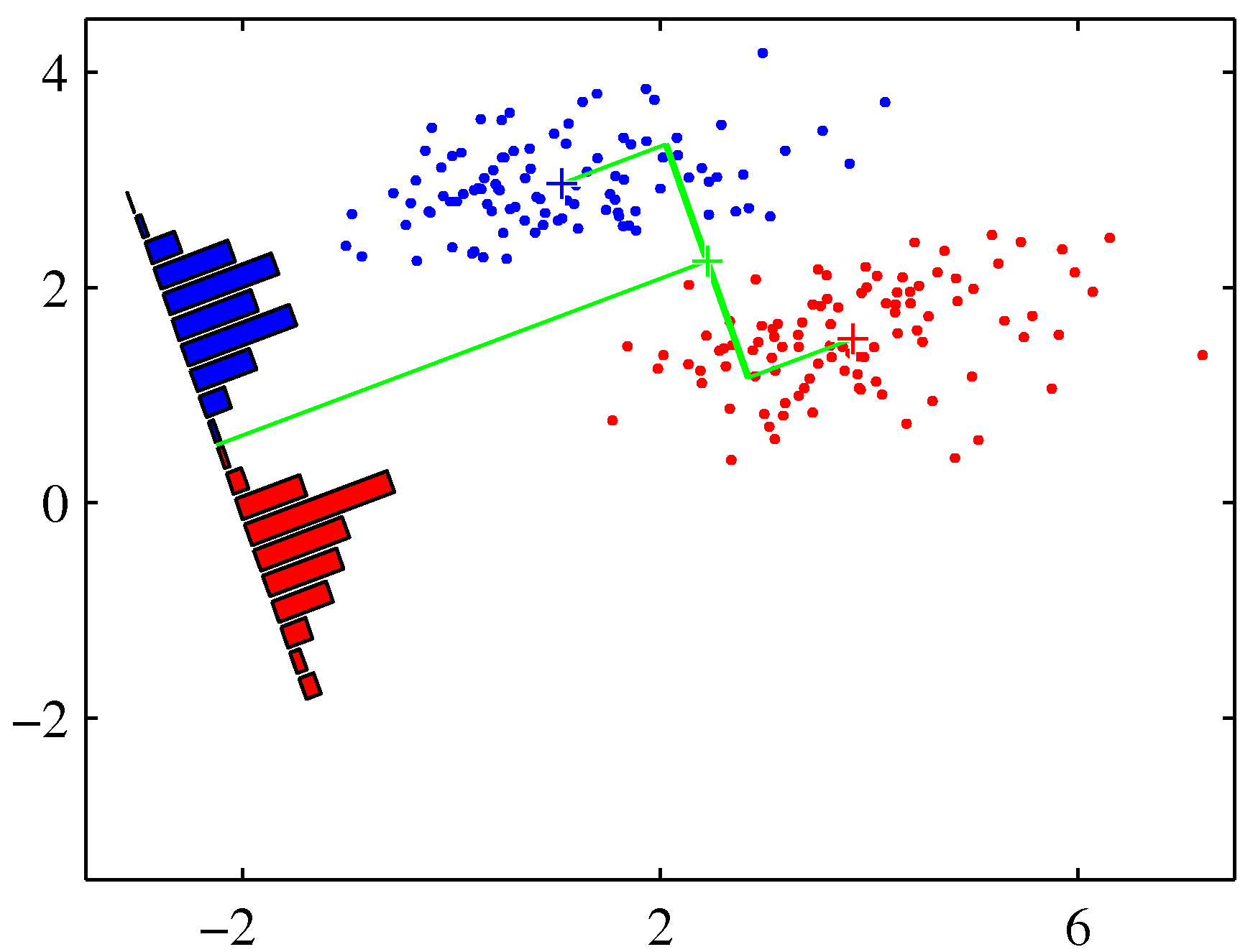
- \( {\bf w} \) 는 원래 판별 경계에 수직인 단위 벡터가 되고,
- 위의 수식에서는 각 클래스의 평균 사이의 거리에 위치한 직선이 \( {\bf w} \) 벡터를 만들어내는데 영향을 주게 된다.
- 그럼 딱 왼쪽의 그림이 구해지는데, 사실 우리는 직관적으로 왼쪽보다 오른쪽이 좋다는 것을 알 수 있다.
- 사실 오른쪽이 바로 Fisher 판별식. 바로 뒤에 나온다.
- 이런 현상는 하나의 클래스 내에서 각 차원의 상관 정도가 높아 공분산 행렬이 diagonal 형태가 되지 않을 때 주로 발생한다.
- 즉, 특정 차원 사이의 상관 관계가 높다.
- 이제 최종적으로 Fisher 의 방식을 확인해보자.
- 실제 아이디어는 앞서 언급했다. 클래스 사이의 거리는 최대화시키되 한 클래스 내의 데이터를 투영했을 때의 분산도가 최소화하는 벡터를 선택하는 것이다.
- 그러기 위해서는 동일 클래스 내의 데이터에 대해 투영 후 얻어진 결과에 대한 분산도를 정의해야 한다.
- 여기서 \( y_n \) 은 한 점에서의 투영 후 값을 의미하며 당연히 \( y_n={\bf w}^T{\bf x_n} \) 으로 정의된다.
- 따라서 위의 식은 투영 후 점들의 분산도를 의미하게 된다.
- 최종 피셔 판별식은 다음과 같이 정의할 수 있다.
- 이제 앞선 식들을 모두 대입해서 정리하면 다음과 같은 식을 얻게 된다.
- 여기서 \( {\bf S}_B \) 는 클래스 사이의 공분산 (bitween-class covariance)
- 그리고 \( {\bf S}_W \) 는 한 클래스 내부 데이터 사이의 공분산의 합 (within-class covariance)
- 이제 \( J({\bf w}) \) 를 \( {\bf w} \) 에 대해 미분하면 다음의 식을 얻게 된다.
- 최종 식으로 다음과 같은 식을 얻게 된다.
-
이것이 바로 피셔의 선형 판별식(Fisher’s linear discriminant)이다.
- 참고로 클래스 내의 분산이 등방성(isotropic)의 형태라면, \( {\bf S}_W \) 는 단위 행렬이 된다.
-
이 경우에는 앞서 설명한대로 평균의 중간 값을 지나는 직선 형태로 구할 수 있다.
- 가우시안 분포를 이용하여 분류에 대한 조건부 밀도 \( p(y|C_k) \) 로 모델링할 수도 있다.
- 이렇게 식을 구성한 뒤에 가우시안에서 필요한 모수(paramter)의 값을 추정함
- 투영된 결과를 클래스별로 가우시안 분포 모델을 찾아 최적의 임계값을 결정함
- 이 가정은 중심 극한 정리에서 비롯됨.
4.1.6 최소 제곱법과의 관계 (Relation to least squares)
- 선형 판별식을 이용한 최소 제곱법은 타겟 값에 최대한 가까운 값을 예측하는 것이 목표임
- 이와 대조적으로 Fisher 분류법은 출력 공간에 대해 최대한 떨어저 있는 모델을 설정함
- 2-class 문제에서 Fisher 의 방식은 최소 제곱법의 특수 케이스 중 하나로 생각할 수 있다.
- 이를 확인하기 위해 기존에 사용하던 이진(binary) 타겟 값이 아닌 다른 스킴(scheme)을 사용해보자.
- 여기서 \( N_1, N_2 \) 는 각 클래스에 속한 샘플 수가 된다. \( N \) 은 전체 샘플의 수이다.
- 이제 에러 함수를 다시 정의해 보자.
- \( {\bf w} \) 로 미분하고 이 식의 값을 0으로 두어 전개하자.
- 여기서 \( t_n \) 에 대해 우선 살펴보면,
- 다음으로 클래스 상관 없이 전체 평균값을 확인해보자.
- 이걸 최초 식에 대입하면 \( w_0 \) 에 대한 정보를 구할 수 있다.
- 이제 아래 식을 다시 정리해보자. (기본 식에 \( {\bf x}_n \) 을 곱한 식이다.)
- 이 식을 전개하면 다음을 얻을 수 있다.
- 최종적으로 다음 식을 얻게 된다.
- 이건 Fisher 판별식에서 보던 식과 동일하다.
- 게다가 Bias 값도 찾았는데 ( \)w_0=-{\bf w}^T{\bf m} \)) 이를 이용하면 다음과 같이 전개 가능하다.
- \( y({\bf x})={\bf w}^T({\bf x}-{\bf m})>0 \) 이면 \( C_1 \) 클래스로 분류. 아니면 \( C_2 \) 로 분류.
4.1.6 여러 클래스 범위에서의 피셔 판별식 (Fisher’s dicriminant for multiple classes)
- 이제 \( K \) 의 값이 2보다 큰 경우 (즉, 여러 개의 클래스가 존재) Fisher 판별식의 처리 방법에 대해 살펴보자.
- 설명에 앞서 한 가지 가정을 하고 시작한다. 분류하고자 하는 클래스 \( K \) 보다 차원 \( D \) 가 더 크다는 것이다.
- 이런 경우 기존 \( D \) 차원을 더 낮은 차원으로 변환하는 식을 아래와 같이 기술할 수 있다.
- 여기서 \( W \) 의 컬럼 개수는 \( D’ \) 로 정의한다. 당연히 \( D’ \) 의 값은 \( D \) 보다 작다.
- 이후 살펴보겠지만 실제 나누어야 할 클래스의 개수를 \( k=1,…,D’ \) 로 정의하게 된다.
- 즉, 분류해야 할 클래스만큼 차원을 낮추는데, 이 때 사용되는 \( W \) 는 클래스별로 정의하게 된다.
- within-class 공분산 행렬
- 앞서 살펴본 \( {\bf S}_W \) 를 K개의 클래스 버전으로 확장하면 된다.
- \( N_k \) 는 클래스 \( C_k \) 에 속한 샘플의 수이다.
- between-class 공분산 행렬
- 우선은 클래스 사이의 분산이 아닌 전체 데이터에 대한 공분산 행렬를 정의한다.
- \( N \) 은 전체 샘플 합계 : \( N=\sum_{k}N_k \)
- \( {\bf m} \) 은 전체 평균
- 이것을 다시 within-class variance 와 between-class variance 로 나눌 수 있다.
- 즉, \( S_T \) 로부터 \( S_W \) 를 제외한 나머지를 \( S_B \) 라고 정의한다.
- 이게 왜 이런 식이 나왔는지 궁금할 수도 있다. 개념적으로 잘 와닿지도 않고,
- 하지만 식을 전개해보면 위와 같은 성질이 있다는 것을 확인할 수 있음
- 자, 이제 이 식을 가지고 2-class 문제와 동일하게 에러 함수를 정의하여 이를 최소화하는 식으로 만들어야 한다.
- 우선 맨 첫 절에 설명했듯이 실제 입력 범위인 \( x \) 차원은 이후 \( D’ \) 차원으로 축소되므로 \( D’ \) 차원에서의 분산 값을 정의해보자.
- 이제 에러 함수를 정의해보자.
- 사실 여러 가지 선택지가 존재하는데 여기서는 그냥 간단하게 Fukunaga 가 제안한 모델을 살펴보자.
- 같은 클래스 내에서의 분산도는 작게, 다른 클래스 사이의 분산도는 크게
- 이 식을 전개하면 다음과 같은 최종 식을 얻게 된다.
- 이 때, \( J \) 를 최대화하는 \( w \) 를 구하는 문제이다.
- PCA를 다루어 보았다면 좀 더 쉽게 이해할 수 있는데, 사실 \( {\bf S}_W^{-1}{\bf S}_B \) 의 eigen 벡터에 의해 얻어지는 가중치를 구하는게 포인트.
4.1.7 퍼셉트론 알고리즘 (The perceptron algorithm)
- 신경망 등에서 사용되는 퍼셉트론 알고리즘
-
여기서는 아주 간단한 형태의 퍼셉트론만 확인한다.
- 2-Class
- 여기서는 기저 함수를 넣어 일반화된 식으로 표현한다.
- 여기서 \( f \) 는 활성 함수(activation fucntion)로 가장 간단한 형태는 아래와 같은 계단형 함수이다.
- 여기서 \( \phi_0({\bf x})=1 \) 이다.
- 앞서 살펴보았던 이진 분류 문제에서는 \( t \in {0, 1} \) 로 정의되었으나 여기서는 조금 다르다.
- \( t=+1 \) 인 경우 \( C_1 \) 으로, \( t=-1 \) 인 경우 \( C_2 \) 로 분류된다.
- 굳이 이런 식으로 정의하는 이유는 일반화된 식을 표기할 때 이렇게 정의해야 수식적으로 더 깔끔하게 떨어지기 때문이다.
- 퍼셉트론에서도 마찬가지로 \( {\bf w} \) 를 구하는 것이 주된 목표가 된다.
- 에러 함수를 정의하고 이를 최소화하는 방법을 강구하면 이를 구할 수 있을 것 같다.
- 에러 함수는 어떻게? 그냥 간단히 생각해보면 오분류된 샘플의 개수로 정의해보면 될 것 같다.
- 하지만 이건 좀 잘못된 생각.
- 어떤 \( {\bf w} \) 에 대해서도 이 값은 상수 값을 가지는데다가,
- 불연속적인 값을 가지게 되므로 미분이나 Gradient 와 같은 방식을 사용할 수 없다.
- 따라서 조금은 다른 방식으로 에러 함수를 정의하게 된다.
- \( \phi_n=\phi({\bf x}_n) \)
- \( M \) 은 오분류된 데이터 집합
- 만약 \( x_n \) 이 \( C_1 \) 에 속한다면 \( {\bf w}^T\phi({\bf x}_n)>0 \)
- 만약 \( x_n \) 이 \( C_2 \) 에 속한다면 \( {\bf w}^T\phi({\bf x}_n)<0 \)
- 여기에 \( t \in {+1, -1} \) 이므로 \( {\bf w}^T\phi({\bf x}_n)t_n \) 은 항상 양수 (양수X양수, 음수X음수)
- 이런 식으로 정의하면 오분류된 샘플이 없을 때 에러 함수 값이 0이 되고, 그 외에는 값이 커진다.
- 에러를 최소화 하는 방향으로 식을 전개해야 하므로 Gradient 방법으로 \( {\bf w} \) 를 만들자.
- \( \eta \) : 파라미터 학습 비율 (paramter learning rate)
-
\( \tau \) : 알고리즘 스텝 인덱스
- 사실 \( w \) 를 얻은 뒤 \( y({\bf x}, {\bf w}) \) 에 대입하는 경우 활성화 함수 \( f \) 에 의해 \( w \) 자체의 크기 비율은 중요하지 않게 된다.
- 따라서 위의 수식에서는 \( \eta \) 의 값을 그냥 1로 놓고 사용해도 문제는 없다.
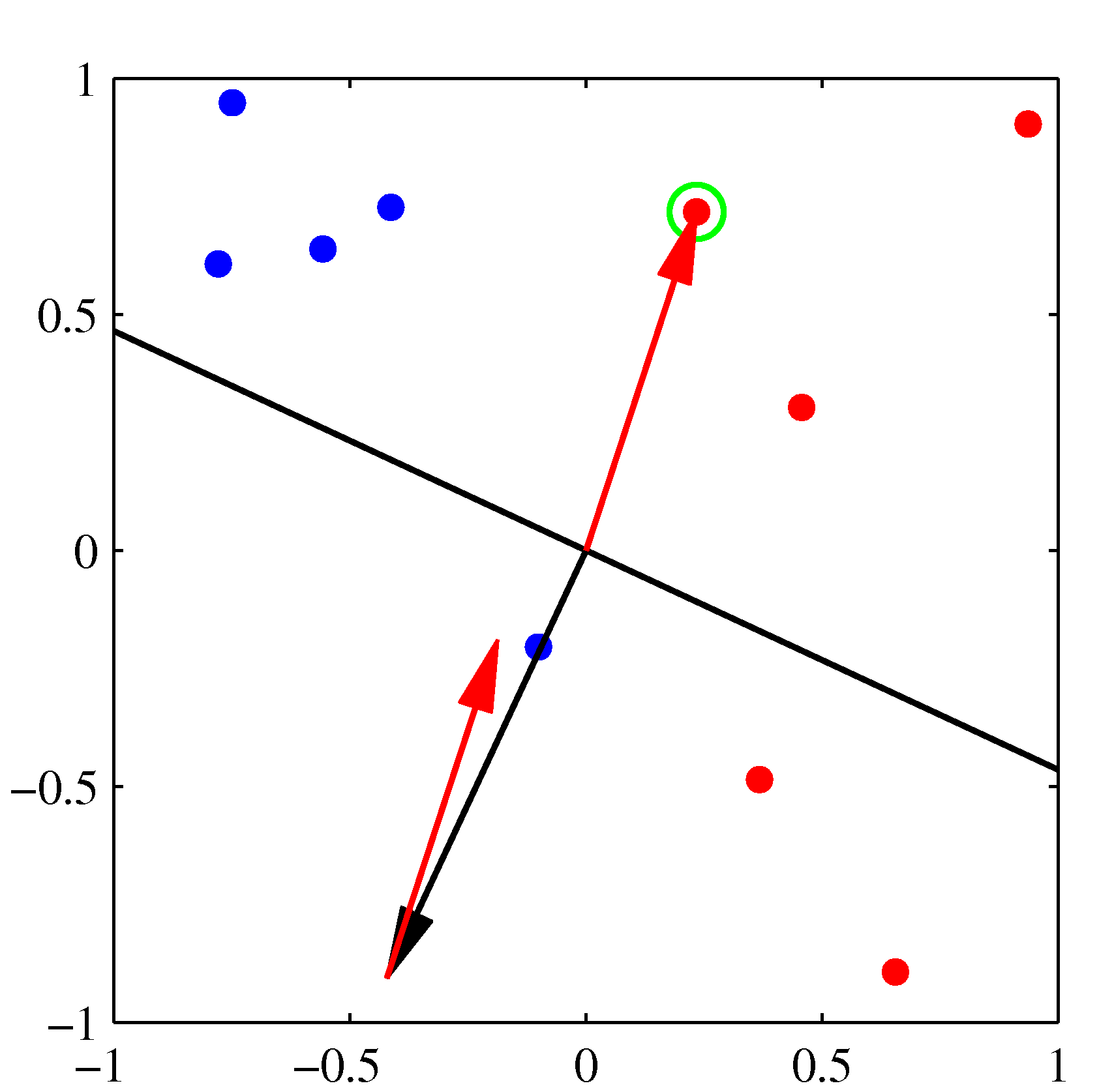
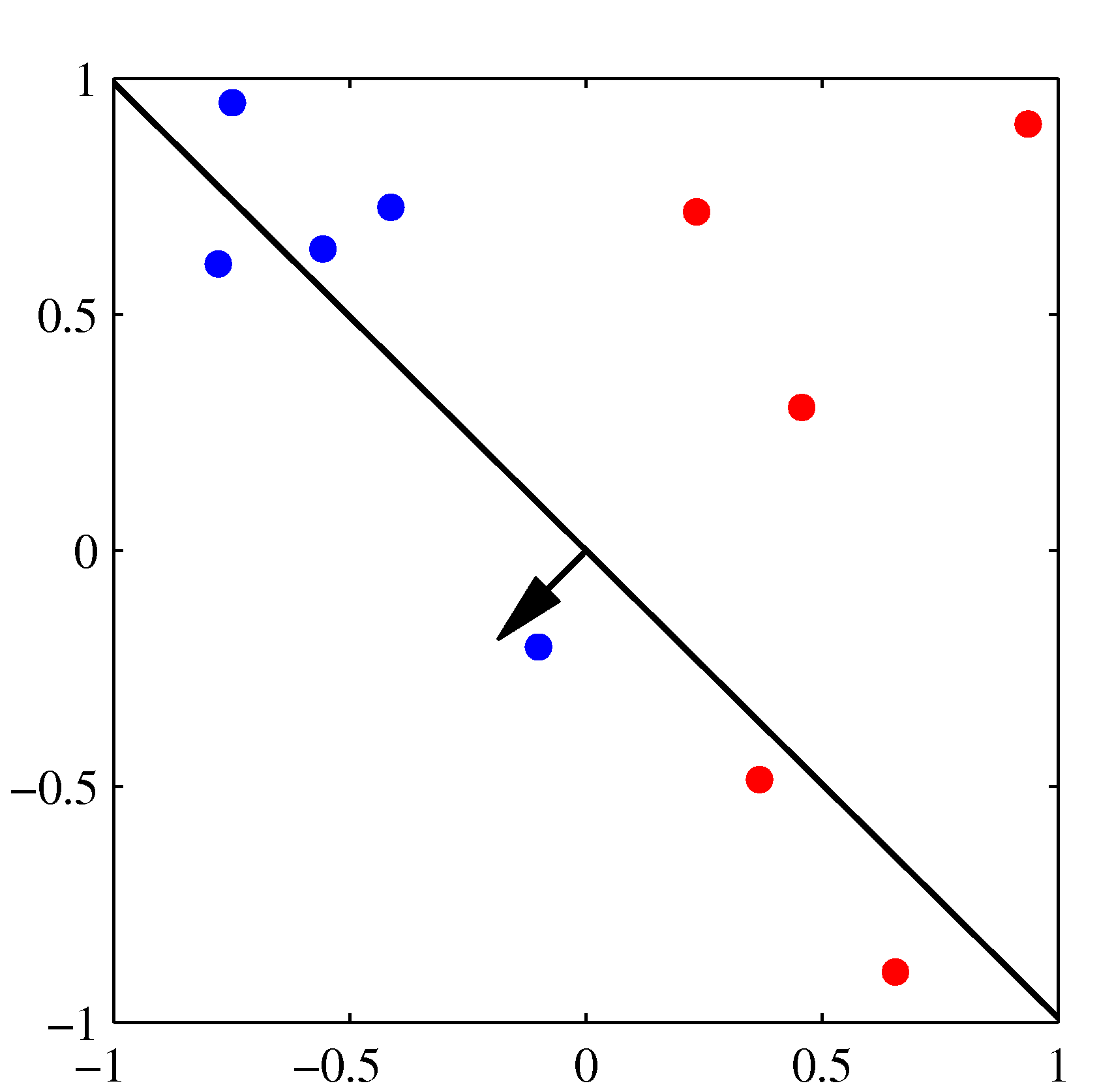
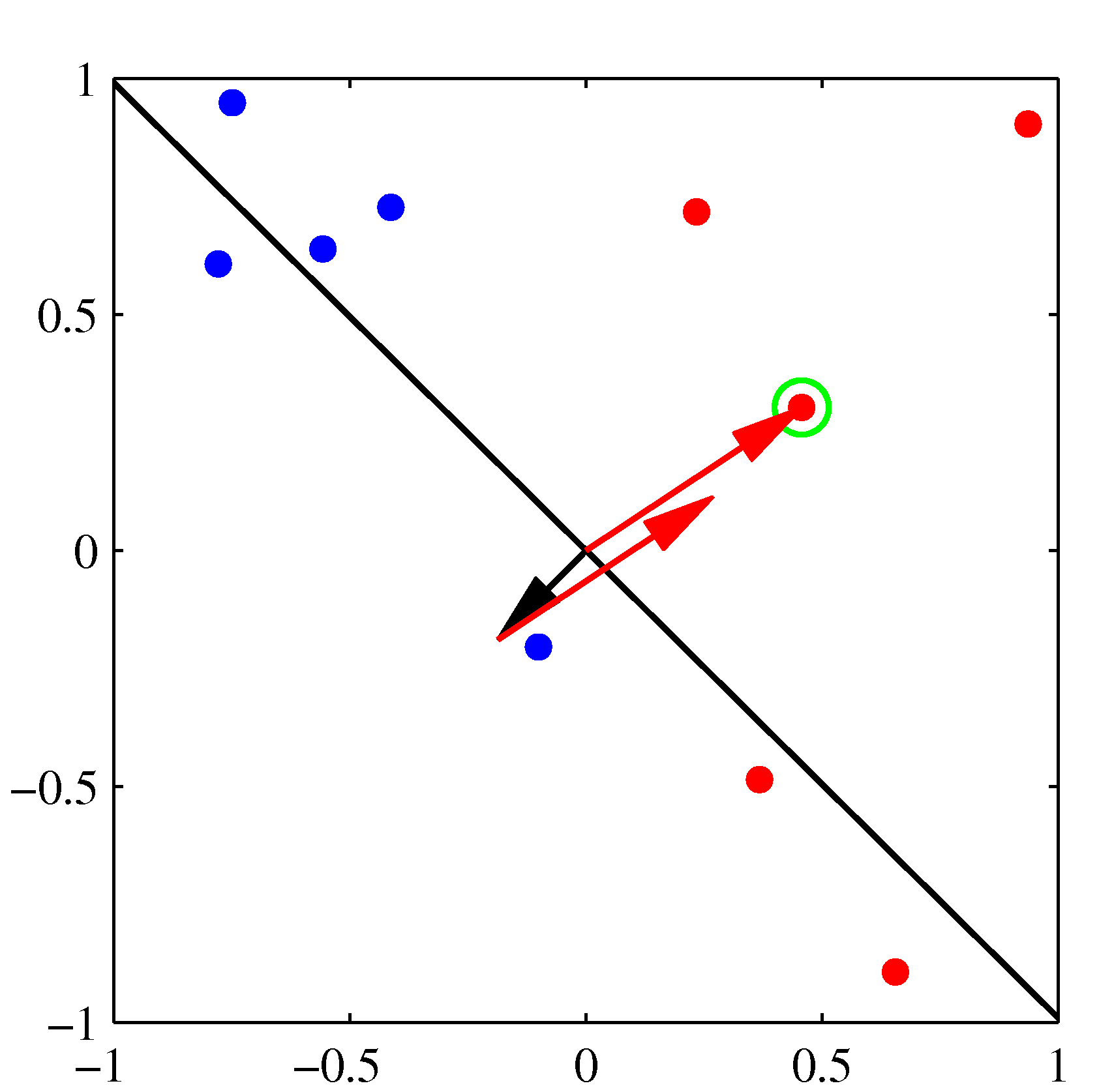
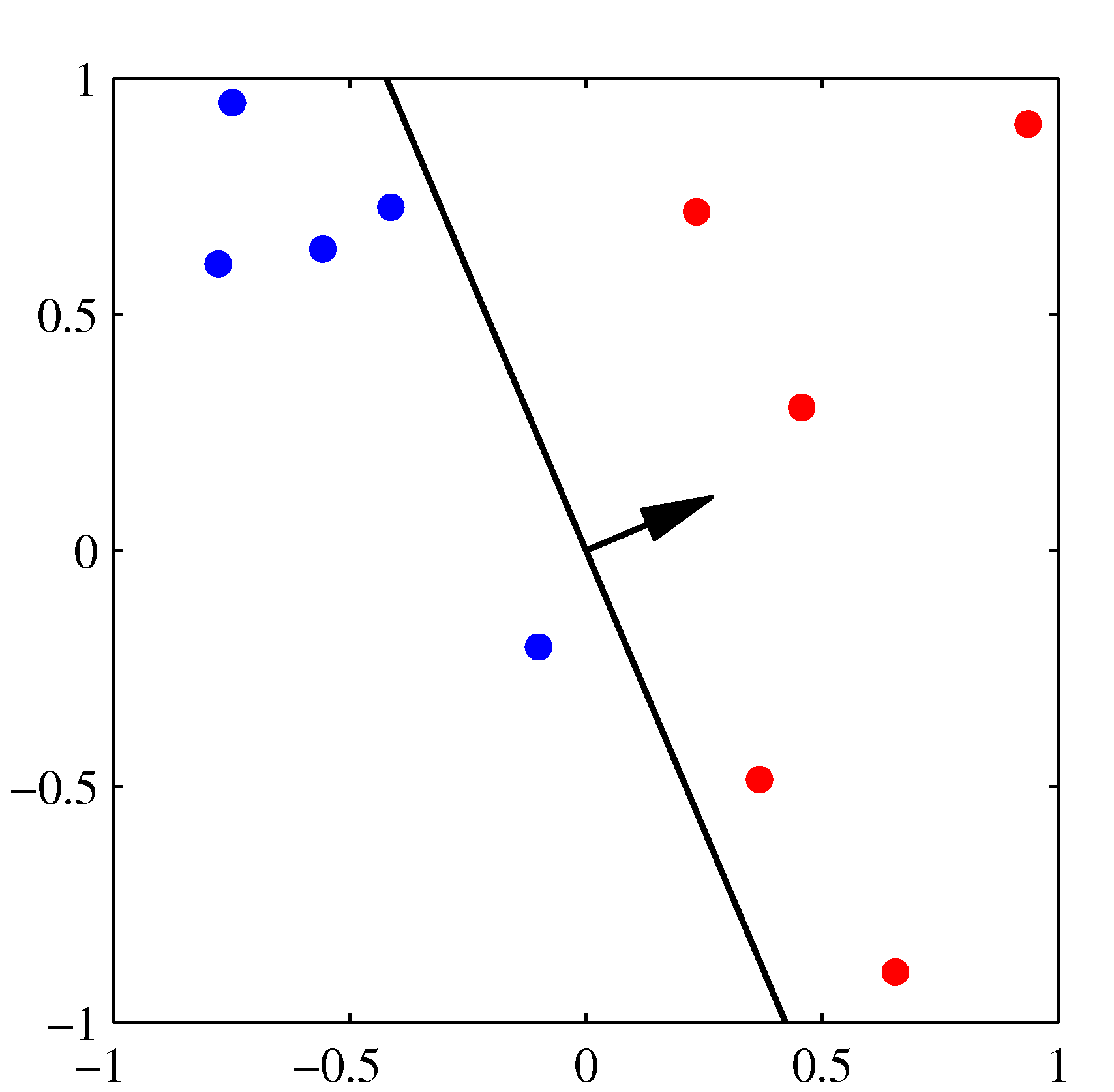
- 위의 그림은 퍼셉트론의 동작 방식을 잘 설명하고 있다.
- 각 축은 \( x \) 의 결과가 아니라 \( \phi(x) \) 를 통해 얻어진 축이라고 생각하면 된다. : 2차원이므로 \( (\phi_1, \phi_2) \)
- 왼쪽 상단이 최초 임의의 \( w \) 값에 의해 생성된 판별 경계(검은색 선)로, 이를 시작으로 오분류된 데이터를 가지고 보정된다.
- 최초 오분류된(녹색 점의 샘플) 데이터에 의해 검은색의 \( {\bf w} \) 벡터가 붉은 색 방향 만큼 보정된다.
-
순차적으로 진행되면서 최종 결정 경계가 완성된다.
- 퍼셉트론 알고리즘에서 개별적으로 업데이트되면서 에러가 점점 줄어든다는 것을 알 수 있는데, 이는 다음의 식으로 확인 가능하다.
- 이 때 \( \eta=1 \) 이다.
- 물론 이런 가중치 벡터의 변경은 이전 단계에서 잘 분류되던 패턴을 다시 오분류로 만들어낼 수도 있다.
-
따라서 퍼셉트론 학습 규칙은 매번에 전체 오차 수가 감소된다는 보장을 할 수는 없다.
- 퍼셉트론 수렴 법칙 (Perceptron convergence theorem)
- 정확한 해법이 있다는 조건에서는 퍼셉트론 방식은 유한 번 반복시 정확한 해법을 찾을 수 있음
- 이 때의 조건은 학습 데이터 집합이 선형으로 분리 가능하든 것
- 하지만 실제 수렴하기까지 요구되는 단계의 수는 알기 어렵다.
- 이게 수렴된 상태인지, 아니면 선형 분리가 불가능한 상태인지, 아니면 현재 수렴 속도가 매우 더딘것인지 알기가 어렵다.
- 실제 데이터가 수렴 가능한 조건일지라도 여러 해법이 존재함
- 파라미터 초기값에 의존하는 알고리즘
- 데이터 순서에 의존하는 알고리즘
- 게다가 데이터 집합 자체가 선형 분리되지 않는다면 퍼셉트론은 결코 수렵되지 않는다.
- 퍼셉트론은 출력 값이 확률 값이 아니다.
- 쉽게 다차원( \)K>2 \) ) 화 시킬 수 없다.
- 중요한 제약 중 하나는 고정된(fixed) 기저 함수의 선형 결합을 기반으로 한다는 것
- 이후에 이와 관련된 사항을 더 살펴보게 될 것이다.