7. Example

초간단 예제를 통해 앞서 배운 내용들을 정리해보자.
동일한 문제에 대해 약간씩 문제 정의를 바꾸어가며 배운 내용을 확인해보는 시간.
그냥 넘기지 말고 간단하게나마 살펴보도록 하자.
- 특히나 MDP 설명 부분에는 처음 언급하는 개념도 등장하니 꼭 보도록 하자. (즉, $Q$ 함수)

MP (Markov Process) (a.k.a MC)

MP 문제도 사실 MDP 에 속하는 문제라고 생각할 수 있다.
- 즉, 어떤 상태에서 선택할 액션이 모두 한개이고 보상도 동일한 MDP 라고 고려할 수 있다.
따라서 가장 먼저 MP 문제를 놓고 MDP 식으로 전개를 해 보도록 하자.
여기서 예제로 제시하는 문제는 어떤 학생(agent)의 행동을 나타내는 MP 이다.

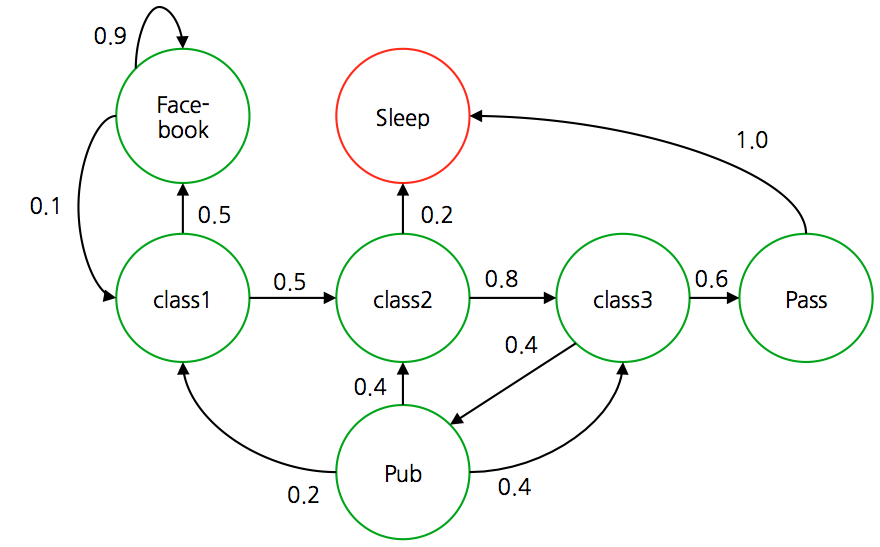
figure7.1

전체 상태는 위와 같이 정의되어 있고 실제 전이 확률도 함께 표기되어 있다.
Episode
- Markov 모델을 따라 생성된 시퀀스 결과를 에피소드(episode)라고 정의한다.
- 에피소드의 정확한 의미는 Simulated Model 에서 다시 언급되므로 일단은 이 정도로만 이해하고 넘어가자.
- 아주 간단하게 말하자면, 초기 시작 상태가 주어지고 종료 시점까지의 상태 전이를 저장한다.

$Episode = \{ S_1, S_2, ..., S_N\}$

위의 학생 마코프 모델에서 몇 개의 에피소드를 간추려 보면 다음과 같다.
- ${EP}_1 = (C1, C2, C3, Pass, Sleep)$
- ${EP}_2 = (C1, FB, FB, C1, C2, Sleep)$
- ${EP}_3 = (C1, C2, C3, Pub, C2, C3, Pass, Sleep)$
- ${EP}_4 = (C1, FB, FB, C1, C2, C3, Pub, C1, FB, FB, FB, C1, C2, C3, Pub, C2, Sleep)$
보면 알겠지만 시작 상태는 $C1$ 이고 종료 터미널은 $Sleep$ 상태이다.
- 즉, 현재 환경은 $H$ 가 특정 값(=횟수)으로 정해진 환경이 아니라 터미널 노드가 존재하는 환경이다.
이 때의 전이 확률 테이블은 다음과 같다.

figure7.2

MP 는 이 정도만 살펴보고 넘어가도록 하자.
- 문제가 너무 쉬워서 더 다룰게 없다.
배운바와 같이 MP 의 경우 상태( $X$ ) 와 전이 확률 ( $P$ ) 만 있으면 적당히 응용 가능하다.
- 예를 들면 특정 Ep 가 발생할 확률을 구한다던지 등.

MRP (Markov Reward Process)

이제 MP 모델에 보상(reward)이 정의된 모델을 기술해 보자.
- 이 모델이 정확히 DP 모델인 것은 아니다. 전이 확률이 있기 때문이다.
- 하지만 액션(action)이 정의되어 있지 않으므로 일반적인 MDP 모델은 아니다.
- 보상이 주어진 MP를 MRP 라고 한다. 근데 이 용어는 중요한 것은 아니니 신경쓰지 말자.
물론 이 모델은 MDP 모델에 포함된 모델이라고 생각하면 된다. (각 상태에서 취할 수 있는 액션이 하나인 MDP)
- 따라서 각 상태가 모두 알려져있다. 이 때의 보상 값이 다음과 같이 정의되어 있다고 하자.

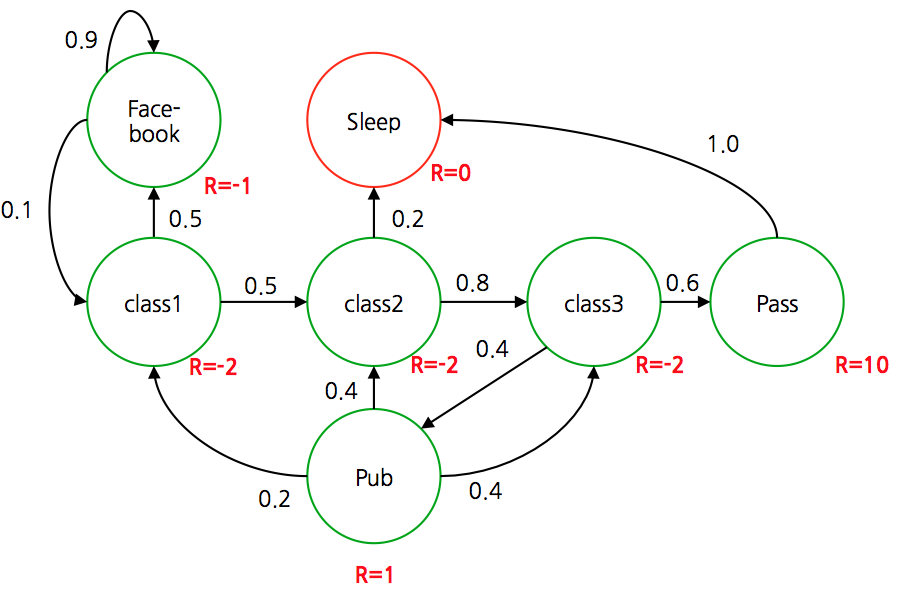
figure7.3

이때 사용되는 보상의 정의는 “학생의 만족도” 정도로 고려하면 될 듯 하다.
- 물론 과목을 모두 수강(pass)하는 것이 술집에 가는 만족도보다 10배 이상이 되는지는 의문이긴 하다.
이렇게 정의를 하면 각 상태에서의 value 함수 $V$ 의 값을 계산할 수 있다.
따라서 여기서는 다음과 같은 조건으로 계산을 진행해보자.
- 초기 상태 : $X_1 = C1$
- $\gamma = \frac{1}{2}$
- $G_H(x) = R_2 + \gamma R_3 + … + \gamma^{H-2}R_{H}$
- 이 때의 임의의 Ep 에 대해 함수 $V$ 의 결과를 살펴보자.
  - 물론 사용된 Ep 는 앞서 살펴본 MP 에서의 Ep 와 동일하게 사용해보았다.

$\begin{array}{ccccc}C1,C2,C3,Pass,Sleep & \rightarrow & G(C_1) = -2 - 2\times\frac{1}{2}-2\times\frac{1}{4} + 10\times\frac{1}{8} & = & -2.25\\ C1,FB,FB,C1,C2,Sleep & \rightarrow & G(C_1) = -2 - 1\times\frac{1}{2}-1\times\frac{1}{4} - 2\times\frac{1}{8} - 2\times\frac{1}{16} & = & -3.125\\ C1, C2, C3, Pub, C2, C3, Pass, Sleep & \rightarrow & G(C_1) = -2 - 2\times\frac{1}{2} - 2\times\frac{1}{4} + 1\times\frac{1}{8} - 2\times\frac{1}{16}... & = & -3.41\\ \end{array}$

$V$ 대신 $G$ 를 사용하여 값 함수를 표현하였다. ( $G$ 는 Gain 을 의미한다.)
- 왜냐하면 위의 경우에는 특정한 샘플에 대한 $V$ 값을 계산한 것이므로 하나의 예에 대한 $V$ 값을 표기하기 위해 $G$ 를 사용한 것이다.
- 따라서 실제 $V$ 는 이 $G$ 값에 대한 기대값, 즉 $V = E[G]$ 를 사용해야 한다.
- 좀더 정확히 표현하자면,

$V(s) = E[G_t|S_{t} = s]$

MRP는 MDP 와는 다르게 특정 상태에서 액션을 고른다거나 하는 작업은 없기 때문에,
- 그냥 특정 상태에 대한 $V$ 값을 얻어내는 정도의 작업을 고려할 수 있다.
하지만 여기서 좀 주의 깊게 살펴볼 내용이 있는데 바로 discount factor $\gamma$ 에 관한 것이다.
- MRP를 통해 discount factor 가 가지는 의미(?)를 확인해보는 시간을 갖자.

만약 $\gamma$ 를 $\gamma=0$ 으로 하여 각각의 상태에 대해 $V$ 값을 구하면 다음과 같다.

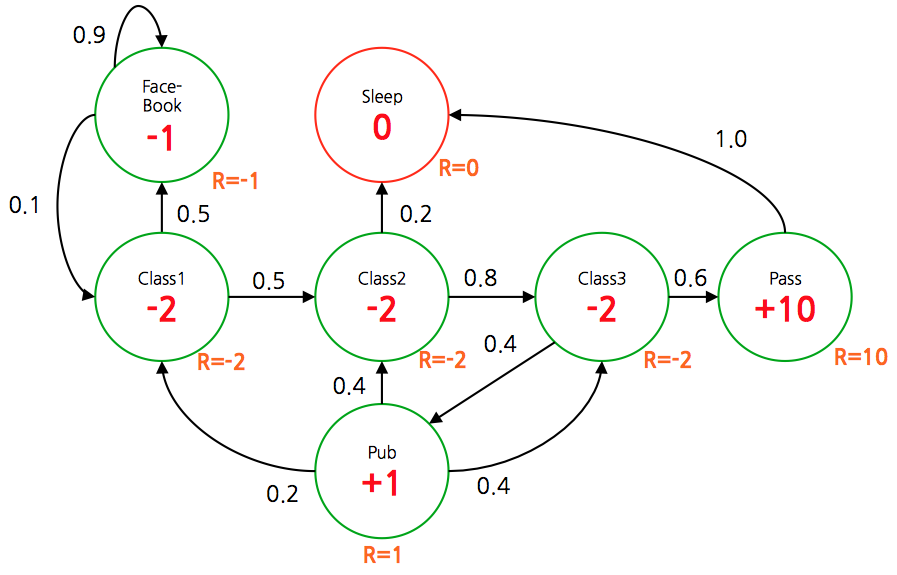
figure7.4

붉은 색의 값이 각 상태에서의 $V$ 값이 된다. (즉, $G$ 의 기대값)
- 이 때 discount factor $\gamma$ 가 $\gamma=0$ 이라면 해당 상태에서의 보상(reward)값이 그대로 $V$ 함수의 결과가 된다는 것을 알 수 있다.

다음으로 $\gamma$ 를 $\gamma=0.9$ 로 놓고 계산해보자.

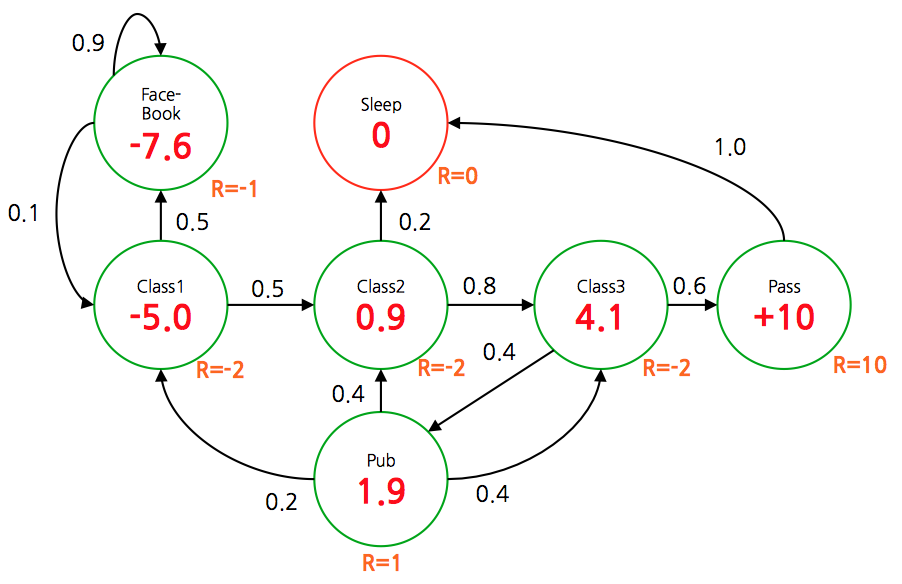
figure7.5

$\gamma$ 값이 1에 가까울수록 최종 보상이 크게 되는 쪽의 상태들의 $V$ 값이 더 커진다는 것을 확인할 수 있다.
간단하게 요약하자면,
- $\gamma$ 가 작을수록 현재 상태에서 주어지는 보상에 더 관심을 가지게 되고,
- $\gamma$ 가 커질수록 보상이 커지는 상태 쪽으로 이동이 용이하도록 $V$ 값이 변하게 된다는 것이다.

MDP

이제 이 문제를 MDP 문제로 좀 바꾸어 보자.
MDP로 문제를 전환하기 위해서는 당연히 액션(action)이 정의되어야 한다.

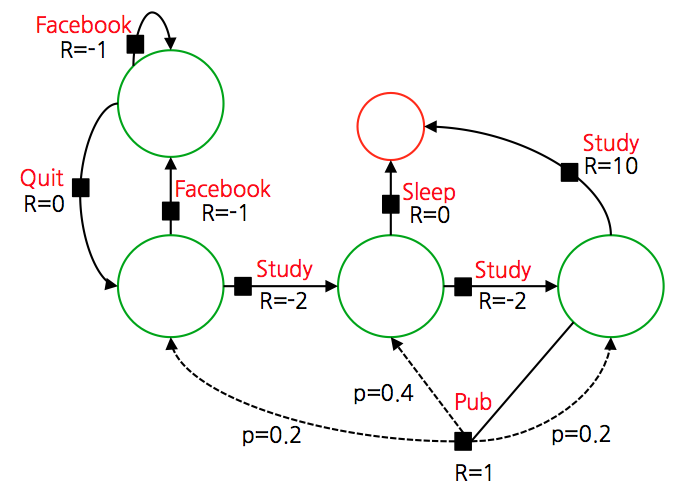
figure7.6

검은 색 블록이 추가되었는데 이게 액션을 의미한다.
- 너무 많은 액션이 추가되면 계산이 복잡해지기 때문에 역시나 최대한 단순화된 버전으로 변경한다.
- 액션별로 전이 확률을 나누어야 하는데 보통의 경우 이런 케이스를 최대한 줄이고 하나 정도만 이런 경우를 추가한다.
  - 아래 그림을 보면 Pub 케이스에서 이를 확인할 수 있다.
  - 이를 위해 Pub 를 상태(state) 에서 액션(action)으로 기존과 다르게 정의했다.
앞서 정의한 policy $\pi$ 는 다음과 같다.

$\pi(a|s) = P[A_t=a|S_t = s]$

policy 가 의미하는 것은 무엇일까?
- policy 는 에이전트(agent)의 전체 행동을 정의하는 행위이다.
- MDP 에서 사용되는 policy 는 현재 상태가 무엇인가에 달려있다. (마코프 속성과 같다.)
- 많이 사용되는 policy 모델은 stationary policy 이다. (time-independent 모델)
MDP 에서 사용되는 전이 확률과 보상 함수를 정의해보자.

$P^{\pi}_{s, s'} = \sum_{a \in A} \pi(a|s)P_{ss'}^{\;a}$ $R_s^{\pi} = \sum_{a \in A}\pi(a|s)R_s^{\;a}$

앞에서 언급되지 않았지만 Value function $V$ 는 사실 2종류로 나눌 수 있다. ( VI, PI 를 말하는게 아니다.)
- state-value function
- action-value function
이중 state-value function 는 지금까지 살펴본 방식이고 action-value function 은 아직 살펴보지 않은 방식이다.
state-value function
- 이건 지금까지 알아보았던 $V$ 함수이다.

$V^{\pi}(s) = E_{\pi}[G_t|S_t=s]$

action-value function
- 자 이제 새로운 value 함수가 등장한다.

$Q^{\pi}(s, a) = E_{\pi}[G_t|S_t=s, A_t = a]$

드디어 $Q$ 라는 이름의 함수가 등장하기 시작했다.
- 이후 $RL$ 에서는 $V$ 보다 $Q$ 를 더 많이 보게 될 것이다.
기존의 $V$ 는 상태 $s$ 에 종속된 함수였다. 따라서 $V(s)$ 와 같은 형태로 표현되었다.
하지만 $Q$ 함수는 이제 두 개의 변수에 의해 제어된다. 바로 $s$ 와 $a$ 이다. 따라서 $Q(s, a)$ 로 표기된다.
앞서 언급한 내용이지만 deterministic policy 를 취하는 경우 특정 상태 $s$ 에서의 액션 $a$ 는 정해진 값으로 제공되는 반면,
stochastic policy 의 경우 특정 상태 $s$ 에 대해 취해지는 액션 $a$ 는 확률 함수에 의해 결정되는 모델이다.
$Q$ 함수는 여기서 stochasitic 모델과 관련이 있는데, 특정 액션을 취하고 난 뒤의 V 값을 Q 로 여기면 된다고 생각하면 쉽다.
- 따라서 $Q$ 함수는 다음과 같이 정의할 수 있다.

$V^{\pi}(s) = \sum_{a \in A} \pi(a|s)Q^{\pi}(s, a)$

쉽게 이야기하자면, 어차피 $\pi(a|s)$ 가 확률 함수로 주어지기 때문에 함수 $V(s)$ 는 $Q(s, a)$ 에서 $a$ 에 대한 기대값을 의미하게 된다.
식을 보면 $V$ 함수를 $Q$ 의 함수식으로 표현하고 있는데, 관점을 다르게 하여 다음과 같은 식으로 기술할 수도 있다.

$Q^{\pi}(s, a) = R^{a}_s = \gamma \sum_{s' \in S}p_{ss'}^a V^{\pi}(s')$

이 식을 통합하여 식을 전개하면 다음과 같다.

$V^{\pi}(s) = \sum_{a \in A}\pi(a|s)\left(R^a_s + \gamma\sum_{s' \in S} p_{ss'}^{a} V^{\pi}(s')\right)$

앞서 보던 식과 동일한데, 상태 $s$ 에서 선택되는 액션이 확률 함수로 주어진다는 차이 말고는 없다.
- 이 차이는 꽤나 중요한데, 이후에 각 상태에서 선택되는 액션의 확률 값을 조절하는 모델을 살펴보게 될 것이다.
이제 앞서 MDP 를 푸는 방식에 맞추어 $V$ 값을 계산 보도록 하자. 한 스텝을 진행하면 다음과 같다.

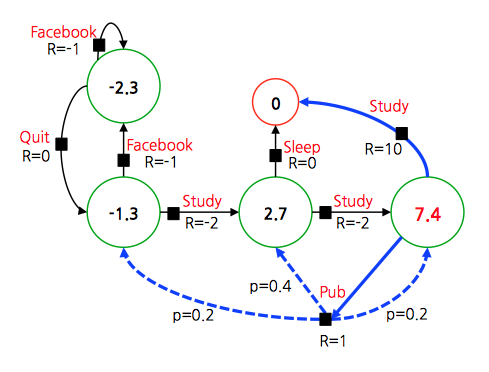
figure7.7

$7.4 = 0.5 \times (1 + 0.2 \times -1.3 + 0.4 \times 2.7 + 0.4 \times 7.4) + 0.5 \times 10$

종료 상태가 존재하므로 $\gamma = 1$ 로 하여 $V^*$ 를 구하면 다음과 같다.

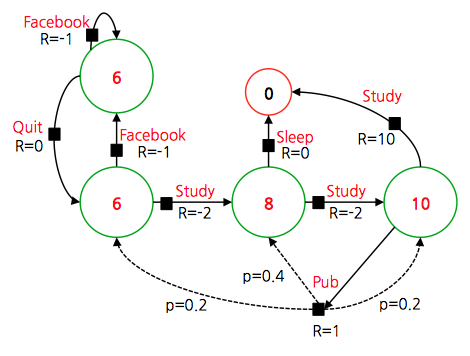
figure7.8

위 모델은 액션이 확률 함수로 주어지는 모델이므로 기대값을 이용하여 최종 policy 를 정하게 된다.
- 앞서 살펴본대로 먼저 $Q$ 값을 얻어 계산해도 된다.

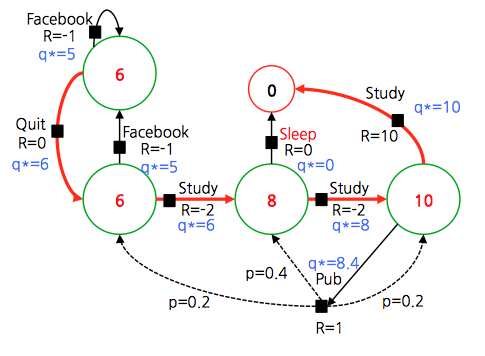
figure7.9

최종 policy $\pi$ 를 얻을 수 있다.

Extensions to MDPs

앞서 Infinite Horizon MDP 모델을 살펴보았다.
- 하지만 여기서는 예제는 생략하도록 하자.
사실 MDP 를 확장한 모델이 꽤 많다.
- Infinite MDP
- Continuous MDP
- Partially Observable MDP (POMDP)
- Undiscounted MDP
- Average Reward MDP
전부 다룰 수는 없으니 이름만이라도 보고 넘어가자.