4. Markov Decision Process (MDP)

• 드디어 Markov Decision Process (이하 MDP)까지 도착했다.
  • 역사를 좀 살펴보자면 MDP 는 1950년대 Bellman 과 Howard 에 의해 시작되었다.
  • 꽤 오랜 역사를 자랑하고 있지만 실제 \(AI\) 영역에서 활발히 사용된 것은 1990년대 이후이다.
• 일단 앞서 설명한 개념들을 계속 확장해 보도록 하자.

확률 프로세스의 확장

• 지금까지 배운 모델에다가 새로운 개념인 액션(action)을 추가해 보도록 하자.
• 이제 각 상태(state)에서 다른 상태(state)로의 이동시, 발생하는 작업 행위를 액션(action) 이라고 정의한다.
• 그리고 이 때 어떤 상태에 있느냐에 따라 취할 수 있는 액션이 다를 수 있다.
• 상태 \(x\) 에서 취할 수 있는 액션을 \(A(x)\)라 하면 \(A(x) \in A\)이다.
  • 하지만 혼동을 하지는 말자. 액션 자체가 상태에 종속적인 개념은 아니다.
  • 특정 상태에서만 사용 가능한 한정된 액션이 정의되어 있고, 이러한 액션을 모두 묶어놓은 전체 액션 집합을 정의할 수 있다.
• 그리고 앞서 정의한 전이 확률 함수에 액션에 대한 속성이 포함되게 된다.

• 이는 상태 \(x\)에서 상태 \(y\)로 액션 \(a\)를 취한 뒤 다른 상태로 이동할 확률을 의미한다.
  • 이 때 \(x, y \in X\)이고 \(a \in A(x)\)이다.
• 그리고 이 말은 어떤 액션을 취하는가에 따라 전이 확률이 달라질 수 있다는 말이다.

• 이번 절의 가장 중요한 내용이 바로 이것이다. 사실 이 액션의 존재 유무가 MP 와 MDP를 구분하는 핵심 요소이다.
  • MP (Markov Process) : \(p(s’|s)\)
    • 상태의 이동 제약 조건에 이전 상태만 영향을 받는다.
  • MDP (Markov Decision Process) : \(p(s’|s, a)\)
    • 상태의 이동 제약 조건에 이전 상태와 행해진 액션에 영향을 받는다.
• 그리고 이 액션을 취함으로써 얻어지는 보상(reward)을 정의하자.

• 즉, 어떤 상태 \(x\) 에서 액션 \(a\) 를 취했을 때 얻어지는 보상을 \(R(x, a)\) 로 기술한다.
• 이 값을 다음과 같이 표기하기도 한다. (즉, 보상은 실수 값이어야 한다.)

• 표기법이 좀 낮설수도 있는데,
  • 상태 \(X\)와 이 상태에서 취할 수 있는 액션 \(A(x)\)에 대해 정의된 보상 값이 있다는 이야기다.
  • 모든 상태에 대해 가용한 액션마다 보상이 정의되어 있다는 말씀.

Policy

• MDP 에서 가장 자주 등장하는 정책(policy) 이라는 표현이 이제서야 등장한다.
• 그런데 이건 거의 고유명사처럼 쓰이고 있어서 그냥 한글로 정책 이라고 이야기하기가 너무 촌스럽다.
  • 그냥 영어로 읽어야 한다. 그래야 다른 사람한테 무시당하지 않는다.
    • 게다가 폴리시 가 아니라 팔러시 로 발음하는 듯. 유식하게 보이기 위해 꼭 이렇게 발음하자.
  • 그래서 이후에도 policy 라고 표기한다. 그리고 표기 문자로 \(\pi\) 를 사용한다. (de facto ??)
• 그렇다면 policy \(\pi\) 란 무엇인가?
  • “스텝(step) 시퀀스에서 각각의 상태(state)들과, 그 상태들에 매핑(mapping)된 액션(action)의 집합이다.”
  • 위의 정의를 대충 이해하지 말고 정말 곰곰히 생각해보어야 한다.

• 말이 참 애매하다. 돌이켜보면 학생 시절에도 policy 를 이해하지 못하고 수업을 마친 학생이 반 이상은 되는 듯 하다.
• 그냥 간단히 생각하여 policy \(\pi\)를 어떤 특정한 함수, 또는 하나의 자료구조 덩어리라고 생각하자.
  • 그냥 우리가 흔히 알고 있는 Map 자료 구조를 생각하자. (‘key’, ‘value’ 쌍으로 이루어진 그거 맞다.)
  • 이 때 Key 는 상태(state)가 되고 Val 은 특정한 액션(action)이 된다.
    • 쉽게 생각하여 모든 상태 \(s\)에 대해 특정한 액션 하나가 모든 \(s\) 마다 정의된 Map 자료 구조를 상상하면 된다.
  • 단, 내부적으로 상태 변수 \(t\) 가 존재한다. (여기서 \(t\) 는 스텝을 의미한다.)
  • 따라서 \(t\) 값이 무엇이냐에 따라 해당 Key 에 대한 Val 값이 달라질 수 있다.
  • 최종적으로 스텝 \(t\)마다 \([state, action]\)형태의 Map 집합으로 이루어진 자료구조를 상상할 수 있다.
    • \( \pi = { \{ map_{0-step}[s,a], map_{1-step}[s,a], …, map_{t-step}[s,a]} \} \)
• 이제 \(\pi_0(x)\)라 함은 0번째 스텝(step)에서 임의의 상태 \(x\)에서 사용되는 액션 \(A(x)\)를 의미하게 된다.
  • 이때 상태 \(x\)는 임의의 상태를 지칭하는 랜덤 변수로 생각해도 된다.
• 그런데 사실 이것은 좀 대충 정의한 개념이다.
  • 어떤 경우에는 \(\pi\)가 상태(state)들에 매핑된 고정된 액션(action) \(a\)를 의미하는 것이 아니라,
  • 상태에 매핑된 ‘액션에 대한 확률 함수(probability function)’로 정의할 수도 있다.
  • 즉, 앞서 \([s,a]\)에서 \(a\)가 특정 값이 아닌 \(p(a|s)\)확률 함수를 가지는 랜덤 변수로 취급될 수 있다는 말이다.
    • 따라서 특정 상태 \(x\) 에 대한 출력 값은 실수가 아닌 액션에 대한 확률 함수가 반환되게 된다.
    • 그리고 이 말이 이해가 안된다면 확률 함수를 잘 이해하고 있지 못하는 것이다.

• 상세한 내용은 아래 내용을 참고하도록 하자.

• 결론적으로 policy \(\pi\)를 크게 두 가지로 나누어 생각할 수 있다.
  • Determinitic policy
  • Stochastic policy

Deterministic policy

• 결정적 policy 상황에서는 policy 를 다음과 같이 정의할 수 있다.

• 위의 표기법은 생각보다 중요하다.
  • 임의의 \(\pi\)를 하나의 함수로 생각하여 특정 \(\pi\)를 따르는 시퀀스에서 특정 시점 \(t\)에 대해 상태 \(x\)를 대입하면 그 때에 사용될 정확한 액션을 얻을 수 있다.
  • 만약 policy \(\pi\)가 모든 \(t\)에 대한 내용을 포함하고 있는 경우 식에서 \(t\)를 생략해도 상관 없다.
    • 위의 식이 이를 나타낸다.

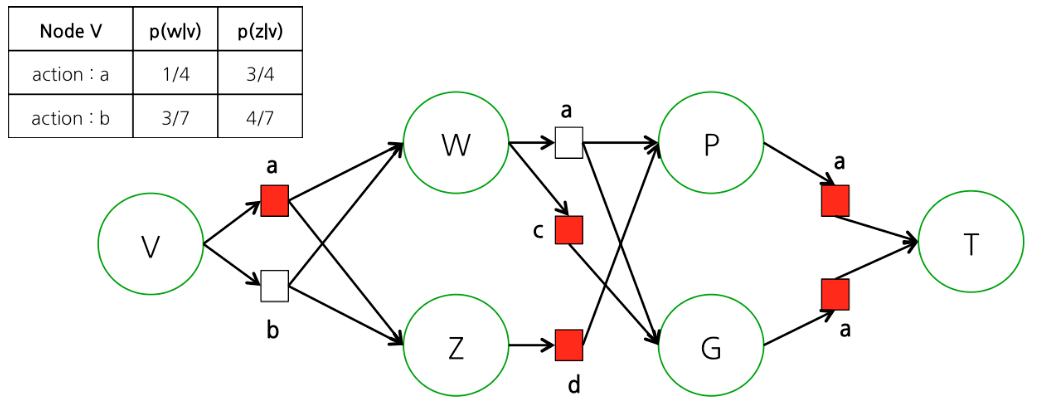
• 위 그림을 나타내는 policy \(\pi\) 하나를 정의해보자.

• 즉, 특정 스텝 \(t=0\) 에서 사용될 액션이 무조건 정해져있고 이에 따른 경로가 선택되어 진다.
  • 위의 그림에서 표를 보면 \(t=0\) 인 상황에서 상태 \(V\)에서의 액션 정보가 정의되어 있다.
  • \(t=0\) 인 상황 하에 상태 \(V\)에서 사용 가능한 모든 액션 집합은 \(\{a, b\}\)이다.
  • 하지만 주어진 policy \(\pi_{sample}\)에서는 \(t=0\) 스텝이고 상태 \(V\)인 경우 액션 \({ a}\)를 선택하도록 기술되어 있다.
  • 그런데 왜 \(\pi_0(W)\) 같은 것은 정의가 되어 있지 않을까?
    • 사실 \(t=0\)에 대해 모든 상태에 대해 사용될 액션이 \(\pi\)에 다 정의되어 있어야 한다.
      • 즉, 임의의 스탭 \(t\) 에서 모든 상태 \(x\) 에 대한 액션 값이 정의되어 있어야 한다는 의미이다.
    • 하지만 해당 시점 (즉, 여기서는 \(t=0\) 일 때 절대 도달할 수 없는 상태이다. 따라서 이 경우에는 생략이 가능하다.
      • 그냥 해당 내용은 실제로는 발생할 수 없어 딱히 필요하지 않기 때문에 생략이 되어 있다고 생각하면 된다.

Stochastic policy

• stochastic policy 모델에서는 \(\pi\)를 사용하는 형태가 조금 다르다.
  • deterministic policy 에서는 \(\pi\)자체를 함수 식처럼 사용하게 되는데, 여기서는 추가로 이 식을 조건 확률식처럼 표기하게 된다.
  • 즉, 액션도 확률적으로 취하게 된다. 이로 인해 \(\pi\) 는 조건부 확률 함수가 된다.

• 또는 다음과 같이 표기하기도 한다. (좀 혼동스럽더라도 이해하자)
  • 출력 결과로 액션에 대한 확률 함수가 반환된다고 생각하면 쉽다.

• 이 모델은 특정 상태에서 선택될 액션이 확률 함수로 주어진다.
  • 따라서 deterministic policy 모델에 비해 좀 더 복잡한 형태를 취한다.

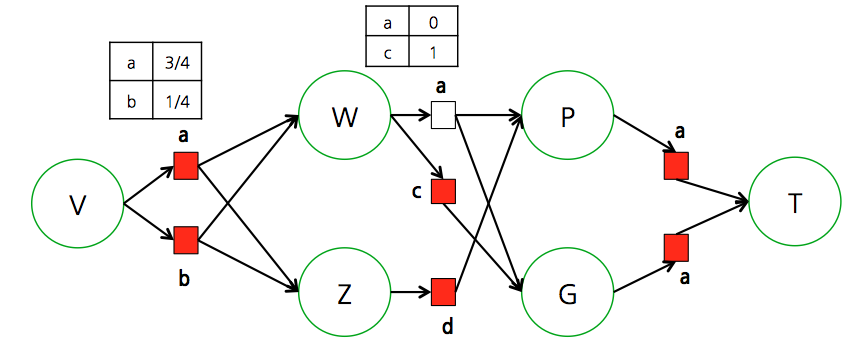
• 사실 주어지는 문제 혹은 도메인에 따라 어떤 모델을 사용할지 결정되는 경우가 많다.
• 하지만 일단 여기에서는 deterministic policy 모델만을 염두해 두고 정리를 진행하도록 한다.
  • 액션에 확률 함수를 도입하는 것은 사실 그리 어려운 일은 아니지만 공부하는 중에는 혼동될 수 있으므로 잠시 잊자.

MDP

• 이제 \(X_t^{\pi}\)를 정의하자. \(X_t^{\pi}\)는 랜덤 변수로 상태 \(X\)가 특정 스텝 \(t\)에서 policy \(\pi\)를 따르는, 상태 \(X\)대한 랜덤 변수로 취급된다.
  • 말이 되게 어렵지만 기존에 살펴보았던 SP 모델에 대해 어떤 policy \(\pi\) 가 주어진 상태의 모델이라고 생각하면 된다.
  • 이런 경우 어떠한 상황에서라도 선택할 수 있는 액션을 (\(\pi\) 를 통해) 얻어올 수 있게 된다.
• 우리가 관심있어 하는 것은 비용(Reward)이다. 사전 정의된 policy \(\pi\)를 가진 프로세스에서 \(H\)스텝(step) 이후에 발생된 비용을 계산하면 어떻게 될까?
  • 물론 여기에는 discount factor 도 적용되어 있다.

• 뭔가 복잡해 보이는 식이지만 말로 풀어쓰면 쉽다.
  • 어떤 policy \(\pi\)를 따르는 프로세스에서 각 단계의 상태에서의 액션을 수행 뒤 얻어지는 보상의 총합을 계산하자는 말이다.
• 그리고 앞서 상태 사이의 전이 확률도 \(p(y|x, a)\)와 같은 형태로 표현했었는데 아래와 같은 표기법으로 다시 작성할 수도 있다.

• 사실 이 표기 방식을 반드시 외울 필요는 없는데, 실제 사람들마다 표기법이 중구난방이기 때문.

• 앞절에서 policy 가 뭔지를 살펴보았다.
• 사실 policy 는 순차적으로 어떤 상태를 방문하여 특정 액션을 선택하는 방식처럼 보이기도 한다.

• 위와 같이 실제 프로세스가 진행되어 얻어진 시퀀스를 History 라고 한다.
  • 지금은 중요하지 않지만 그냥 용어만 기억하자.
  • 참고로 한번의 시퀀스를 모두 끝내면 이를 한 개의 에피소드(episode)로 취급한다.
  • 생각보다 자주 등장하는 용어라서 잊어버리면 안된다.

Value Function (V)

• 이제 어떤 임의의 policy 를 선택하여 프로세스를 진행한 뒤 얻어지는 총 보상(or 비용)을 \(V\)라는 함수로 정의하도록 하자.
  • 이 식은 매우 중요하다. 왜냐하면 이제부터 \(\pi\)와 더불어 계속해서 언급이 될 식이기 때문이다.
  • 이 함수를 value 함수라고 한다
• 약간 스포를 하자면 이 함수가 등장함으로써 DP 가 모델에 녹아들게 되는 것이다.
  • DP의 경우 각 상태에 대해 특정 값들을 저장하는 형태를 취함으로써 space-complexity 와 time-complexity 를 교환하는 효과를 가졌었다.
  • 여기서도 마찬가지로 Value 함수가 이러한 정보를 담는 매개체로 사용되게 된다.
  • 결국 각 상태(state)에 대해 어떤 값들을 저장하게 될 것이라는 것을 짐작해 볼 수 있다.
• 일단 첫번째 step을 시작으로 \(H\)까지의 step이 진행되는 것을 생각해보자.
  • 즉 터미널 상태가 존재하거나 step \(t\)의 최대 값이 고정된 형태.
  • 일단은 터미널 상태는 존재하지 않고 \(H\)가 고정된 숫자 값이라 고려하자.
  • 그리고 각 step에서의 액션은 이미 정해져있고 이를 따르는 프로세스를 쭉 진행한다고 하자.
  • 하지만 policy \(\pi\)에 의해 진행된 상태 전이는 사실 반복할 때마다 다를 수 있다.
    • 왜냐하면 동일한 액션을 선택하여도 다음 상태에 대한 전이가 확률 함수로 표현되기 때문.
    • 즉, \(t=k\)인 상황에서 상태 \(s\)로부터 특정 액션 \(a\)를 여러 번 수행할 때 \(t=k+1\)의 상태 \(s’\) 가 항상 동일하게 얻어진다고는 말할 수 없다.
    • policy 자체는 특정 상태에 따른 액션만을 정의한 것이지, 액션을 통해 얻어지는 다음 상태는 확률적으로 얻어지게 되는 것이다. (중요)
  • 어쨌거나 특정한 policy \(\pi\)를 따르는 경우 얻어질 수 있는 보상(reward)를 표현해보자.
    • 대략적으로 이런 형태의 식이 될 것이다.

• \(utility\)는 아직 정해진 함수는 아니다. 좀 고려해야 할 사항이 있기 때문이다. 일단 임의의 함수라고 생각하자.
  • 너무 고민되면 일단 \(utility\)함수 자체가 존재하지 않는다고 생각해도 된다.
• 어쨌거나 우리가 최종적으로 원하는 것은 이 식을 이용하여 최적의 상황을 만들어내는 것.
  • 우리가 원하는 최적의 상황이라는 것은 보상을 최대화 시키는 것이다.
  • 그리고 이러한 보상을 최대화하기 위해 우리가 조정해야 하는 것은 특정 상태에서 사용할 액션들을 조합하는 것.
    • 즉, 가장 그럴듯한 policy \(\pi\) 를 만들어내는 것.
  • 모든 \(\pi\)와 모든 \(h\)에 대해 \(V_h^* \ge V_h^{\pi}\)를 만족하는 policy 를 \(\pi^*\)라 정의하자.
    • 즉, 이런 액션 순서를 따르면 무조건 최대의 보상이 나올 수 있다고 생각하고 이 때의 policy 를 \(\pi^*\)라고 기술한다는 것이다.
  • 물론 최적의 \(\pi^*\)는 하나 이상일 수 있다. (즉, 동일한 최대의 보상을 여러 policy 로부터 만들어 낼수도 있음.)
  • 그리고 이러한 \(\pi^*\)를 정의된 함수 \(V\)로부터 얻을 수 있어야 한다.

\(Utility\) 함수 정하기.

• 만약 \(utility\) 함수를 그냥 다음과 같이 정의하면 어떻게 될까?

• 눈치가 빠른 사람이라면 알겠지만 당연히 문제가 있으니까 처음부터 이렇게 기술을 하지는 않았을 것이다.
  • 이렇게 함수를 정의하면 동일한 policy 에 대해 여러번 작업을 반복하여 수행하는 경우 누적된 최종 보상 값이 달라질 수 있다.
    • 앞서 이야기했지만 \(\pi\)만으로 특정 상태에서 다음 상태로 이동하는 것을 모델에서 고정시킬 수는 없다.
    • 즉, 거시적인 관점에서 함수의 입력 값으로 동일한 상태 집합 \(X\)과 고정된 policy \(\pi\)를 넣어도 출력 결과가(보상 총합) 매번 달라질 수 있다는 것이다.
    • 이런 함수(문제)를 잘 정의되지 않은 함수 (not a well-defined function) 라고 한다. (수학 용어다.)
• 그리고 사실 잘 정의된 함수 (well-defined function) 를 어떻게든 구해서 사용한다고 하더라도 문제가 있는데,
  • 어떠한 경우에도 \(V_h^* \ge V_h^{\pi}\)항상 만족하는 \(\pi^*\)가 실제로 존재하지 않을 수 있다.
  • 즉, 수학적으로 언제나 최대 보상값을 보장하는 근이 없을 가능성도 있다는 의미라고 대충 생각해두자.
  • 아 머리아파. 어쨌거나 실제 수학적으로도 이와 관련된 내용이 증명되어 있거나 증명해야 한다는 이야기다.
• 그래서 여기서는 차선책인 ELAU (Expected Linear Additive Utility) 라는 utility 함수를 도입한다.
  • 괜히 어려운 용어가 나와서 두렵기는 하지만 별거 없고 그냥 보상의 기대값(expectation value)을 평가 함수로 사용한다.
    • 표준어로 기댓값이지만 조금 낮설은 감이 있으니 그냥 기대값이라 쓰자.

• 기대값(평균)을 사용하는 경우 적당히 좋은 policy 를 얻을 수 있다는 것이 증명되어 있다. (즉, 차선책이다.)
  • 이에대한 증명 식이 존재하는데 봐도 이해가 안되고 있으니 그냥 넘어가도록 하자.
    • 뭐 대충 식을 보면 임의의 에러 \(\epsilon\)을 정의하고 이 에러보다 작은 에러를 포함하는 좋은 policy 를 얻을 수 있음을 증명한다.
  • well-defined function 여부도 중요한데 이것도 그냥 그러려니 하자.
    • 사실 상황에 따라 기대값을 도입하는 것 외에도 추가 조건이 더 필요한 경우가 있다.
    • 이후에 필요한 경우 이러한 추가 조건을 별도로 기술하게 될 것이다.
      • 예를 들어 특정 문제에서는 discount factor \(\gamma\)가 \(0 \lt \gamma \le 1\)을 만족해야 한다는 등.
• 물론 여기서는 \(\gamma\)를 \(1\)보다 큰 값을 사용할 수도 있다. 각각의 경우를 다음과 같이 생각할수도 있다.
  • \(0 \le \gamma \lt 1\): 매 순간의 보상에 더 관심을 둔다.
  • \(\gamma \gt 1\): 더 먼 시점의 보상에 관심을 둔다.
  • \(\gamma = 1\): 동일한 보상 비율을 가지므로 시간에 독립적이다.
  • 물론 대부분의 경우 \(1\)또는 \(1\)보다 작은 실수 값을 사용한다.
  • 이로 인해 문제가 어떻게 달라지는지는 이후 관련 예제들을 살펴보면 쉽게 이해할 수 있을 것이다.
• 실제 MDP에서 사용되는 value 함수는 다음과 같다.

• 식을 보면 알겠지만 초기 시작 상태 위치가 주어져있다. ( \(X_0^{\pi}=x\) )

• 사실 엄밀히 말하면 위에서 정의한 \(V_H\)함수도 항상 well-defined function 인 것은 아니다.

  • 오실로스코프처럼 계속 동일한 값을 반복하는 환경이 존재할 수도 있다.
    • 주어진 상황에 따라 위의 식이 완전하지 않는 경우도 있다는 것이다.
  • 앞서 언급했지만 이런 경우에는 추가적인 조건이 더 필요하다고 한다.
  • 몇 가지 조건을 추가하여 완전한 식을 가지는 모델 중 유명한 모델은 다음과 같은 것이 있다.
    • finite-horizon MDP
    • infinite-horizon MDP with descount-factor
    • stochastic shortest-path MDP
  • 문제 정의시에 well-defined function 을 만족하기 위한 추가 조건들이 기술될 것이다.
    • 물론 뒤에서 다루게 될 내용들이다.

MDP Concept

• MDP는 RL에 속하는 모델로 주어진 환경을 완벽하게 기술할 수 있는 환경에서 사용하는 모델이다.
  • 즉, 모든 환경(상태 등등)을 관찰 가능한 모델이다.
  • 주어진 환경에 대한 전지적 시점을 가지고 있는 모델이다.
  • 물론 주어진 실세계의 문제들이 이러한 조건은 만족시키지 못하는 경우가 많다.
    • 따라서 이들은 기본 MDP 에 추가적인 제약들을 가진 MDP 라는 관점으로 접근 가능하다.
    • 이런 추가적인 제약들을 어느 정도 해결하면 결국 단순한 MDP 문제가 된다.
• 따라서 사실 모든 RL 문제를 MDP 형태로 표현이 가능하다.
  • 이에 대한 내용은 이후에 살펴보도록 하자.

Optimal Principle

• 바로 다음으로 넘어가기 전에 보상 함수 \(V\)를 적절히 전개하여 재귀 가능한 식으로 구성하는 것을 살펴보고 넘어가자.
• 그리고 이를 이용하여 어떻게 보상(reward) 함수 \(V\)의 값을 가장 크게 만드는 \(\pi^*\)를 찾을 수 있는지도 살펴보도록 하자.
• 일단 \(H\)스텝을 가지고 특정한 policy \(\pi\)를 따르는 경우의 보상 함수를 정의해보자.

• 여기서 \(p(X_0^{\pi}=x, X_1^{\pi}=y)\)는 \(p_{xy}^{\pi_0(x)}\)로 표기할 수 있다.
• 앞쪽의 식을 정리하면,

• 이 때 \(V_{H-1}^{\pi}(y)\)를 위의 식에서 확인 가능하다.

• 이를 최종 식에 대입하면 다음과 같다.

• 일전에 보았던 비용 함수 전개식에 확률 함수가 추가로 도입된 것을 이해할 수 있을 것이다.
• 이제 아래 식이 가장 중요한 식이다. 최종 식은 다음과 같다.

• 이후에는 이 식으로부터 보상을 가장 크게 하는 \(\pi^*\)값을 찾을 것이다.
• 이 식을 나타내면 다음과 같다.