6. Infinite-Horizon Discounted Reward MDP (IHDR-MDP)

지금까지 유한 크기의 $H$ 스텝을 가지는 finite-horizon MDP 에 대해 살펴보았다.
이제 infinite-horizon with discount factor 모델을 살펴볼 시간이다.
- 이건 FH-MDP와는 좀 다르게 부르는 용어가 참 다양하다.
- 여기서는 그냥 제목대로 IHDR-MDP라고 사용하겠다. 하지만 통일된 용어가 아니다.
- $H=\infty$ 인 모델 정도로 생각하면 된다.
잠시 이전에 사용한 보상 함수(value function)를 살펴보자.

$V_H^{\pi}(x) = E\left[\sum_{t=0}^{H-1}\gamma^{t} R(X_t^{\pi}, \pi_t(X_t), X_{t+1}^{\pi}) \;\left|\right.\; X_0^{\pi}=x\right]$

여기서 $\gamma=1$ 이고 $R$ 함수가 양의 상수 값이라고 가정한다면,
이 조건에서의 $H=\infty$ 에 대한 $V_H$ 는 다음과 같다.

$V_{H=\infty}^{\pi} = \infty$

따라서 $H=\infty$ 인 상황에서는 더 이상 문제 해결을 할 수 없는 상태가 된다.
그렇기 때문에 $H=\infty$ 인 상황에서는 무조건 다음 조건이 추가로 필요하게 된다.

$0 \le \gamma \lt 1$

그리고 당연히 보상값 $R$ 도 마찬가지로 $\infty$ 가 되어서는 안된다.

IHDR-MDP

infinite horizon discounted reward MDP 는 $\gamma$ 값 제한 외에도 추가적으로 한가지 조건이 더 필요하다.
바로 policy $\pi$ 가 stationary 하다는 것이다.
- 이 의미는 스텝 $t$ 에 상관없이 특정 상태에서의 액션 선택이 동일하다는 것이다.
- 이렇게 해야지만 IHDR-MDP에서 well-defined function 이 된다. (증명은 역시나 생략하자.)
이제 이전과 마찬가지로 IHDR-MDP 모델을 정의하여 보자.

$IHDR\;MDP\;(X, A, R, P, \gamma)$

각 의미는 다음과 같다.
- $X$ : (유한) 상태 집합
- $A$ : (유한) 액션 $A(x)$ 의 집합
- $R$ : 보상(reward) 함수 ( $X \times A(x) \rightarrow \mathbb{R}$ ) ( w/ stationary )
- $P$ : 확률 전이 테이블 ( w/ stationary )
- $\gamma$ : discount factor ( $0 \le \gamma \lt 1$ )
이 때 사용되는 value 함수 또한 finite-horizon 과 거의 동일하다.

$V^{\pi}(x) = E\left[\sum_{t=0}^{\infty}{\gamma}^{t}R(X_t^{\pi}, \pi(X_t^{\pi}), X_{t+1}^{\pi})\left|\right. X_0^{\pi}=x\right]$ $V^{*}(x)=\max_{\pi}V^{\pi}(x)\qquad(\forall x\in X)$

식을 잘보면 FH-MDP 에서 보이던 스텝 $H$ 표기가 사라졌다. 대신 보상의 합을 $\infty$ 까지 진행한다.
- 물론 실제 계산을 할 때에는 $\infty$ 하게 반복하지는 않는다.
- 당연하겠지만 $\gamma$ 에 의해 특정 값으로 수렴하게 된다.
  - 이런 스타일의 식들이 대부분 그러하지만 값이 특정 범위 내로 수렴하면 종료한다.
- 하지만 중요한 것은 $\gamma$ 가 단지 $V^{\pi}$ 함수의 수렴성을 위한 요소로만 사용되는 것은 아니라는 것을 기억하자.
  - 왜 이런 이야기를 하는지는 뒤에 다시 언급한다.
이제 IHDR-MDP의 value 함수에 대한 Bellman 의 최적화 식을 정의하자.

$V^*(x) = \max_{a\in A(x)}\left(\bar{R}(x, a) + \gamma\sum_{y\in X}p_{xy}^a V^*(y)\right)$

이 때 $V^*(x)$ 는 단일 값(unique value) 을 가진다는 것이 보장된다.
그리고 그 때의 policy $\pi$ 를 $\pi^*$ 라고 정의한다.
- 물론 이 값이 유일 해는 아니다. 앞서 이야기한 바대로 하나의 $V$ 값에 대해 동일한 값을 가지는 $\pi$는 여러 개가 만들어질 수 있다.
증명은 당연히 생략하자.
- 값의 수렴성을 기준으로 식을 세우게 되는데 그냥 간단히 생각해도 $\gamma$ 로 인해 값은 수렴하게 되어 있다.

VI (Value Iteration) vs. PI (Policy Iteration)

지금까지 2 종류의 MDP 문제를 살펴보았다. (FH-MDP, IHDR-MDP)
- 실제로는 MDP 관련해서 이보다 훨씬 많은 모델이 존재한다. 그래도 주로 많이 사용하는 모델은 IHDR-MDP 이다.
최적의 보상 함수가 무엇인가를 살펴보았는데 이제 실제 현실에서 주로 사용되는 계산 방식을 다룰 것이다.
결국 목적은 $\pi$ 를 얻는 것인데, 최적의 policy $\pi$ 를 구하는 방법은 두 가지가 있다.
- VI (value iteration) 과 PI (policy iteration) 방식이 존재한다.

VI : Value Iteration

VI 라고 부르는 방식은 지금까지 우리가 보아왔던 방식이다. (더 설명할게 있을까?)
- 아래 처리 방식을 살펴보도록 하자.
- DP 를 풀던 방식과 비슷하다.
- 다만 $V$ 값을 수렴시까지 진행하고 수렴 후 역으로 각 상태에서 최적의 액션을 선택하게 된다.
- 아래 식은 일단 $H$ 스텝을 가진 VI 로 기술되어 있다. 이를 $\infty$ 형태로 바꾸는 것은 아주 간단하다.

start with $V_0^*(x) = 0$ for all $x$
for $i=1$ to $H$
- given $V_i^*$ , calculate for all states $x \in X$
- $V_{i+1}^*(x) \leftarrow \max_{a}\left(\bar{R}(x, a) + \gamma\sum_{x’\in X}p_{xx’}^a V^*(x’)\right)$

$H$ 를 높은 값으로 놓고 반복하면서 $V$ 의 값이 모든 상태에 대해 수렴하는 경우 종료한다.
이 때 수렴 여부는 값의 차이를 적당히 지정하여 사용하면 된다.

PI : Policy Iteration

보통 PI 로 부르는데 이는 VI 방식과는 좀 다른 방식으로 진행한다.
- 임의의 $\pi$ 를 하나 지정하여 기존의 $V$ 함수를 수렴할 때까지 수행한다.
- 그 다음 일부 액션을 변경하여 $V(x)$ 가 더 커지는 액션임을 확인하면 이 액션을 새로운 $\pi$ 에 포함시킨다.
PI 는 다음과 같은 방식으로 진행된다.
- Step 1 : policy evaluation
  - 임의로 어떤 고정된 policy $\pi$ 를 정하고 이에 대해 보상 함수가 수렴될 때까지 계산한다.
- Step 2 : policy improvement
  - 앞 단계에서 결정된 $\pi$ 를 기본으로 사용하되 반복하여 몇가지 새로운 액션을 골라 최종 $V$ 를 다시 계산한다.
  - 이 결과가 기존의 $V$ 값보다 큰 경우 선택된 액션을 추가한 새로운 policy $\pi$ 를 업데이트한다.
- policy $\pi$ 가 수렴될 때까지 위 두 단계를 반복한다.
상대적으로 VI 비해 좀 무식한 방법이라는 느낌도 들지만 특정 조건에서는 훨씬 더 빠르게 수렴한다.
- 상태나 액션의 개수가 너무 많아 $VI$ 비용이 높은 경우 $PI$ 가 훨씬 유리하다.
혹은 상태(state)가 매운 큰 환경에서 더 잘 동작하기 한다.
주로 stationary policy 인 상황에서 사용된다.
- non stantionary policy 에서는 반복 횟수가 기하급수적으로 증가하게 된다.

Iterate until values converge

$V_{i+1}^{\pi_k}(x) \leftarrow \bar{R}(x, \pi_k) + \gamma\sum_{x'\in X}p_{xx'}^{\pi_k} V^{\pi_k}(x')$

Policy improvement

$\pi_{k+1}(x) = {\arg\max}_{a}\left(\bar{R}(x, a) + \gamma\sum_{x'\in X}p_{xx'}^{a}V^{\pi_k}(x')\right)$

그런데 정말 이런 방식으로 해도 최적의 policy $\pi^*$ 를 구할 수 있을까?
- 다행히 VI 방식과 동일한 $\pi^*$ 를 구할 수 있음이 증명되어 있다.
- 이 증명도 생략한다.
  - 물론 이론적인 증명일 뿐 현실적으로는 $VI$ 와 $PI$ 가 다른 결과를 낼 수도 있다.
  - 즉, 높은 연산량을 요구하는 경우 둘 다 근사값을 사용할 수 밖에 없다.

[Example] Simple IHDR-MDP

FH-MDP 와 마찬가지로 여기서도 예제를 좀 살펴보자.
- 예제를 확인해보면 보다 쉽게 이해할 수 있을 것이다.
- stationary 모델이므로 $t$ 는 고려할 필요가 없다.

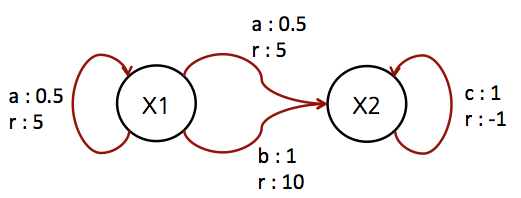
figure6.1

$A = \{ a, b, c \}$
$X = \{ x_1, x_2 \}$
$A(x_1) = \{ a, b \}$
$A(x_2) = \{ c \}$

Direct Method (일명 손계산)

VI , PI 이런거 다 떠나서 이렇게 간단한 모델인 경우에는 infinite-horizon MDP 일지라도 손으로 반복적으로 최적 값을 계산 가능하다.
- 이 문제가 중요한 이유는 단순한 모델에서는 아래 방식을 일반화시켜 수식을 만들어 낼수도 있다.
- 하지만 바쁜 우리는 간단하게 예제로만 살펴보고 넘어가도록 하자.
이제 손계산으로 정답을 먼저 확인해보도록 하자.

$V^*(x_1) = max_a\left(\bar{R}(x_1, a) + \gamma\sum_y p_{xy}^a V^*(y)\right) = max_a\left(\bar{R}(x_1, a) + \frac{\gamma}{2}V^*(x_2) + \frac{\gamma}{2}V^*(x_1) \;,\; \bar{R}(x, b) + \gamma V^*(x_2)\right)\\ = max_a\left(5+ \frac{\gamma}{2}(V^*(x_1)+V^*(x_2)) \;,\;10 + \gamma V^*(x_2)\right)$ $V^*(x_2) = -1 + rV^*(x_2)$

$V^*(x_2)$ 는 정리하면,

$V^*(x_2) = \frac{-1}{1-\gamma}$

$V^*(x_2)$ 를 $V^*(x_1)$ 에 대입 가능하다.

$V^*(x_1) = max_a\left(5+ \frac{\gamma}{2}V^*(x_1) - \frac{\gamma}{2}\times\frac{1}{1-\gamma} \;,\;10 - \frac{\gamma}{1-\gamma}\right)$

식을 살펴보면 결국 $\gamma$ 가 최적 조건에 영향을 준다는 것을 알 수 있다. (이제 중요한 사실이다.)
일단 $\gamma=\frac{1}{2}$ 로 하여 문제를 풀어보자.

$V^*(x_2) = -2$ $V^*(x_1) = \max_a\left(5 + \frac{1}{4}V^*(x_1) - 0.5 \;,\; 10 - 1\right) = max_a\left(4.5 + 0.25V^*(x_1), 9\right)$

이 때 좌측의 값을 전개하여 정리하면 값이 $6$ 이 되므로 $9$ 보다 작다.
따라서 $x_1$ 에서의 최종 선택은 $b$ 액션이어야 한다.

Value Iteration

여기서도 일단 $\gamma = 0.5$ 로 놓고 시작하자.

$V_{n+1}(x_1) = max_a \left(5 + \frac{\gamma}{2}V_n(x_1) + \frac{\gamma}{2}V_n(x_2)\;,\;10+\gamma V_n(x_2) \right)$ $V_{n+1}(x_2) = -1 + \gamma V_n(x_2)$

초기화 과정 (일단 임의 값을 지정해보자.)

$V_0(x_1) = V_0(x_2) = -10$

반복 진행 (iteration)

$V_1(x_2) = -1 + 0.5(-10) = -6$ $V_1(x_1) = max_a\left(5+0.25\times(-10) + 0.25\times(-10)\;,\;10+0.5\times(-10)\right)=5$ $V_2(x_2) = -1 + 0.5(-6) = -4$ $V_2(x_1) = max_a\left(5+0.25\times(5) + 0.25\times(-6) \;,\; 10 + 0.5\times(-6)\right)=7$ $V_3(x_2) = -1 + 0.5\times(-4) = -3$ $V_3(x_1) = max_a\left(5+0.25\times(7) + 0.25\times(-3) \;,\; 10+-.5(-3\right)=8.5$

위의 과정을 반복하면 결국 $x_1$ 에서 액션 $b$ 를 선택하게 된다.
- 그리고 그 때의 값도 손으로 계산한 $9$ 와 비슷해진다.
- 위의 식에서도 $8.5 \simeq 9$ 이다.

Policy Iteration

여기서는 일부러 초기값을 다르게 지정해 보도록 하자. (이렇게 시작해도 나중에 계산이 들어맞는지 확인하기 위해)

$\gamma = 0.95$

일단 처음에는 임의의 policy $\pi$ 를 지정해야 한다.

$\pi_0(x_1) = b$ $\pi_0(x_2) = c$

반복 진행 (iteration)

$V^{\pi_0}(x_1) = 10 + 0.95 V^{\pi_0}(x_2)$ $V^{\pi_0}(x_2) = -1 + 0.95 V^{\pi_0}(x_2)$

이제 $V^{\pi_0}$ 가 수렴될 때까지 VI 를 진행한다.

$V^{\pi_0}(x_1) = -9$ $V^{\pi_0}(x_2) = -20$

policy improve

$\pi_1(x_1) = \max \left( 5 + 0.475V^{\pi_0}(x_1) + 0.475V^{\pi_0}(x_2)\;,\;10+0.95V^{\pi_0}(x_2)\right) = \max\left(-0.8775\;,\;-9\right)$ $\pi_1(x_2) = \pi_0(x_2)$

최종적으로 다음과 같은 액션이 선택된다.

$\pi_1(x_1) = a$ $\pi_1(x_2) = c$

얻어진 결과가 $\pi_0 \neq \pi_1$ 이므로, 다시 위의 과정을 반복한다.

$V^{\pi_1}(x_1) = 5 + 0.475V^{\pi_1}(x_1)+0.475V^{\pi_1}(x_2)$ $V^{\pi_1}(x_2) = 10 + 0.95 V^{\pi_1}(x_2)$

수렴된 값은 다음과 같다.

$V^{\pi_1}(x_1) = -8.571$ $V^{\pi_1}(x_2) = -20$

따라서 다음 policy $\pi$ 가 결정된다.

$\pi_2(x_1) = a$ $\pi_2(x_2) = c$

이제 $\pi_1 = \pi_2$ 이므로 이를 최종 policy $\pi^*$ 로 놓고 종료한다.