2. Dynamic Programming (DP)
- Dynamic Programming(이하 DP)은 우리말로 동적 프로그래밍(DP)이라고 한다.
- RL에서는 기본적으로 확률 동적 프로그래밍 (Probabilistic Dynamic Programming) 기법을 사용하게 된다.
- 즉, 기본적인 DP 모델에 확률 이론이 포함된다는 이야기이다.
- 따라서 여기서는 먼저 간단하게 동적 프로그래밍(DP)이 뭔지 확인해보고 넘어가도록 하자.
- 물론 동적 프로그래밍을 이해하기 위해서는 먼저 결정적 프로그래밍(deterministic programming) 방식을 무엇인지 이해하고 있어야 한다.
- 여기서는 이런것까지 언급할 시간이 없다. 바로 동적 프로그래밍이 뭔지만 보고 넘어가도록 하자.
- 물론 학교 다닐때 다 배운 내용이기도 하다. (예를 들어 BFS , DFS 등이 대표적인(가장 쉬운) 결정적 프로그래밍 기법.)
- 최단거리 같은거 많이 구해보았을 것이다.
동적 프로그래밍의 기초
- 최적화 기법 중 하나로 재귀(recursion)를 이용하여 최적화 솔루션을 얻어내는 방식을 사용한다.
- 동적 프로그래밍으로 풀 수 있는 가장 유명한 문제로 배낭 문제(Knapsack problem)를 들 수 있다.
- 이것만 살펴보면 DP를 쉽게 이해할 수 있다.
0-1 Knapsack problem
- 문제 정의
- 배낭이 하나 있다고 하자. 이 때 배낭에 담을 수 있는 부피 용량은 \(W\) 이다. (단, \(W>0\) 이다.)
- 배낭에 담을 수 있는 아이템(item)도 \(n\) 개를 가지고 있다. 최대한 효율적으로 아이템을 배낭에 담아야 한다.
- 이 때 아이템(item) \(i\) 는 2개의 속성 값을 가지고 있다.
- \(w_i\) : 아이템의 용량
- \(v_i\) : 아이템의 중요도 (즉, 가중치)
- 물론 용량이 클수록 중요도가 커진다거나 하는 것은 아니다.
- 목표 : 최대한 중요한 아이템을 선별하여 배낭에 담도록 하자. (중요하다는 의미는 전체 가중치 합이 가장 크도록 만든다는 의미다.)
- 단, 각각의 아이템은 쪼갤 수 없다. 오로지 배낭에 담을지 말지만 결정 가능하다.
- \(n\) 개의 아이템을 \(T={1,2,…n}\) 이라고 하면
- \((\sum_{i \in T} w_i) \le W\) 의 제약 하에,
- \(\max(\sum_{i \in T}v_i)\) 를 만족하는 \(T\) 의 부분집합을 구해야 한다.
- 단순하게 생각하여 조합 가능한 \(T\) 의 부분집합 갯수를 고려하면 모두 \(2^n\) 개의 부분 집합이 나온다.
- 이를 동적 프로그래밍을 이용하여 풀어보고, 이후에 확률론을 접목시킨 확률 동적 프로그래밍이 무엇인지 살펴볼 것이다.
- 아래에서 바로 확인하겠지만 동적 프로그래밍이란 결국 주어진 문제를 더 작은 단위의 문제로 나누고 (D&C),
- 중간 계산 과정을 잠시 어딘가에 저장해 두었다가 사용을 하는 최적화 풀이 알고리즘이다.
- 결국 공간(space)과 시간(time)을 트레이드 오프하는 알고리즘이 된다.
Step 1.
- 문제를 더 작은 단위의 문제들로 나눈다.
- 일단 목표 달성을 위한 평가 배열 \(V[(0…n),(0…W)]\) 를 정의한다. ( \(1 \le i \le n\) 이고 \(0 \le w \le W\) 이다.)
- 단순히 목적 함수를 쉽게 나타내기 위한 수단이므로 너무 어렵게 고민하지는 말자.
- \(V[i,w]\) 를 정의해보자.
- \(V\) 는 실수 값을 저장하는 2차원 배열이라고 생각하면 된다.
- 각각의 공간에는 어떤 값을 저장할 것인데,
- 집합 \({1,2,…,i}\) 의 어떤 부분 집합에 대해서 \(V[i,w]\) 는 이 부분집합으로 만들어 낼 수 있는 \(v\) 값 중 최대값을 저장할 것이다.
- 이 때 이 부분 집합으로 구성 가능한 부피의 최대 값이 \(w\) 이다.
- 예를 들어 \(V[2, 20]\) 이라는 의미는 1번, 2번 아이템만을 이용하여 총 부피 20 이내의 모든 부피에 대해 가능한 최대 이득을 저장하게 된다.
- 반드시 1번, 2번을 다 사용한다는 의미는 아니고 이들의 부분집합을 사용하면 된다.
- (표기법이 좀 허술해도 이해해달라. 10년전 자료를 정리해서 그렇다.)
- 따라서 문제 정의에 따라 \(V[n,W]\) 를 구하는게 우리의 목표가 된다.
- 즉, \(n\) 아이템의 부분 집합 중 용량 \(W\) 에 가장 근접하는 부분 집합의 최대 \(v\) 값을 단순하게 \(V[n,W]\) 로 표현할 수 있다는 것이다.
- 왜 이딴 식으로 정의를 했는지는 문제 풀이를 보면 알 수가 있다.
Step 2.
- 작게 나누어진 문제들의 풀이들을 재귀적인 방식으로 정의하도록 하자.
- 다음과 같이 우선 초기 조건을 정의한다.
- 이제 이 외의 경우들을 재귀 함수를 통해 정의해보도록 하자.
- 곰곰히 생각해보면 어렵지않다. 잘 생각해보면 모든 경우를 수를 순차적으로 고려하는 방식이라 생각해도 된다.
- 다만 이를 계산할 때 각각의 경우에 따라 이미 계산했던 내용들을다시 계산해야 하는 수고로움이 발생한다.
- 이 때 이전에 계산한 결과들을 별도의 \(V\) 테이블에 저장을 하여 두고 나중에 이 값이 필요하게 되면 이를 재사용한다는 개념이다.
- 아래 그림을 보면 \(i=0\) 인 상태에서부터 \(i=n\) 인 상태까지 모든 가능한 결과를 테이블 \(V\) 에 저장하게 된다.
- 임의의 \(i\) 위치에서는 이전의 결과 값을 이용하여 현재 상태에서의 최적 값을 찾고 이 때의 이전 값의 위치를 저장하게 되는 것이다.
- 작업은 보통 bottom-up 방식의 계산으로 풀이를 진행한다.
- 실제 예제를 보자.
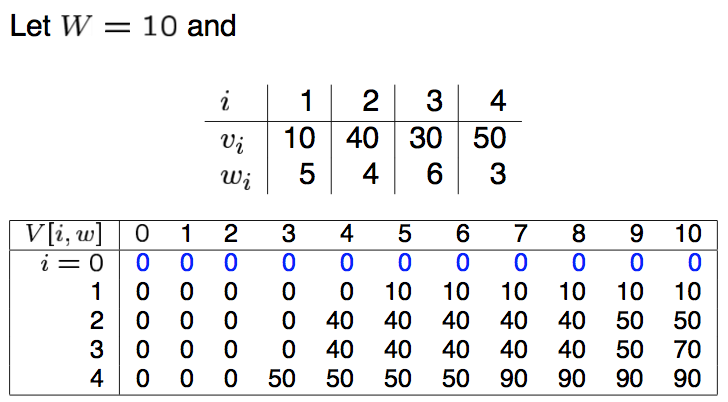
- 구체적인 예를 통해 확인하는게 가장 쉽다.
- 현재 아이템은 총 4개이고 \(i\)로 표현한다. 각각의 무게와 가치가 기술되어 있다.
- 특정 아이템을 나타낼 때에는 \(i_1\) 등으로 표현하도록 하겠다.
- 표를 보면 row 는 \(V\) 의 정의 중 첫번째 파라미터 \(i\) 를 의미한다. col 은 \(V\) 정의 중 두번째 파라미터 \(w\) 를 의미한다.
- 1 단계
- \(i=1\) 인 경우는 아이템 \(i_1\) 만을 사용하여 가방을 채운다는 것을 의미한다.
- 아이템 \(i_1\) 은 무게 \(w_1\) 가 \(5\) 이므로 가방의 무게 \(0\) 부터 \(4\)를 만족하는 가장 좋은 방법은 아이템 \(i_1\)을 선택하지 않는것.
- 2 단계
- 이제 row \(i=2\) 인 상황을 보자.
- 이 경우에는 아이템 \(i_1\) 과 \(i_2\) 를 최대한 이용해서 value 값을 최대로 만드는 경우를 채울 것이다.
- 그런데 이미 이전 row 인 \(i=1\) 에서 아이템 \(i_1\) 을 이용하여 값을 만들어 놓았기 때문에,
- 여기에 아이템 \(i_2\) 를 넣고 빼고 하면서 value 를 최대로 많드는 경우를 계산하면 된다.
- 3단계
- row \(i=3\) 인 경우도 2단계와 동일하다.
- 오로지 \(i=2\) 인 값으로 부터 아이템 \(i_3\) 을 넣고 빼어가면서 최대 이득을 발생하는 경우의 값을 채우기만 하면 된다.
- 예를 들어 \(i=3, w=10\) 인 경우의 최대 값을 만들어보자.
- 이 때 아이템 \(i_3\) 의 무게는 \(6\) 이다.
- 필요한 계산은 오로지 \(i_3\)을 사용했을 때의 경우와 안했을 때의 경우의 최대값을 비교해보면 된다.
- 먼저 사용하지 않을 경우 그냥 row \(i=2\) 에서 \(w=10\) 인 값을 읽어오면 된다. 바로 \(50\) 되겠다. ( \(i=2, w=10\) )
- 다음으로 사용할 경우 현재 아이템의 무게가 \(6\) 이라고 했으므로 이전 단계에서 \(10-6\), 즉 무게가 \(4\) 이하의 경우 중 가장 큰 \(w\) 값을 읽어온다.
- 이 경우를 보면 \( (i=2, w=4) \) 일때의 \(v\) 는 값이 \(40\) 이다. 아이템 \(i_3\) 의 \(v\) 는 \(30\) 이므로 이를 더한다. \(70\) 이 된다.
- 이제 \(50\) 과 \(70\) 을 비교하면 당연히 \(70\) 이 크다. 즉 아이템 \(i_3\) 을 넣는것이 \(i=3, w=10\) 인 경우에서는 가장 효율적인 셈.
- 이후의 과정은 이를 반복하는 것이다.
- 이제 최종 결과 값으로 \(V[4, 10]=90\) 를 찾을 수 있다.
- 그리고 위의 표에서는 보이지 않지만 내부적으로 어떤 아이템이 선택되었는지를 계산 중에 저장해놓을 수 있다.
- 그러면 실제 사용된 아이템도 쉽게 얻을 수 있다.
- 이 정도로 동적 프로그램을 살짝 맛고보만 넘어간다.
- 일단은 Tree 형태의 탐색 방식을 가지고 있다는 정도만 보면 된다.
- 이런 식으로 프로그래밍을 한번이라도 해봤던 사람이라면 쉽게 이해할 수 있을 것이다.
- 여기서 중요한 포인트는 문제를 재귀적인 형태로 해결하고 있다는 것.
- 마찬가지로 MDP에서도 문제를 재귀적인 형태로 변경하여 문제 풀이를 진행하게 된다.
- 그리고 모든 상태에 대해 최적의 결과를 모두 어딘가에 ‘저장’ 하고 있다는 사실도 잊지 말자.
RL 과의 연관성
- DP 는 계산 복잡도가 높을 뿐이지 그냥 일반적인 알고리즘일 뿐이다.
- 이런 이유로 최적값을 얻을 수 있는 모델이다.
- MP 와는 다르게 능동적인 모델이라 할 수 있는데 사용자가 암묵적으로 상태 전이를 선택할 수 있다.
- 물론 최대 보상을 가지는 deterministic한 상태 전이를 선택하게 되기 때문에 MDP 등과는 차이가 있다.
- 이후에는 MP 모델을 바탕으로 DP 구조를 적용한 모델들을 살펴보게 될 것이다.

