- Reinforcement Learning (이하 RL) 을 살펴보기 전에 반드시 먼저 이해해야 하는 모델은 바로 MDP (Markov Decision Process) 이다.
- 하지만 MDP를 이해하기 위해서는 먼저 MP (Markov Process) 모델부터 알아야한다.
- 당연히 MDP에 비해 좀 더 간단한 모델이고 MDP의 기본 베이스가 되는 모델이다.
- 여기서는 아주 간단하게 MP 모델이 무엇인지 정도만 이해하고 넘어가도록 한다.
- 시작하기 전에 MP 문제를 마코프 체인 (Markov Chain, MC)이라고 부르기도 한다.
- 마코프 체인(이하 MC)은 이산 확률 프로세스(discrete stochastic process)이다.
- 참고로 연속(continuous) 확률 프로세스를 다루는 MC가 있긴 하다. 하지만 여기서는 다루지 않는다.
- 여기서 확률 프로세스란 확률 분포를 가진 랜덤 변수(random variable)가 일정한 시간 간격(time interval)으로 값을 발생시키는 것을 모델링하는 것을 의미한다.
- 이러한 모델 중 현재의 상태가 오로지 이전 상태에만 영향을 받는 확률 프로세스를 MP 라고 한다.
- 즉, MC 로 이루어진 프로세스를 MP 라고 한다는 것이다. 그냥 동일한 용어라고 생각하자.
- MP 모델은 딱 두 가지 속성으로 표현 가능하다.
- \( X \) : (유한한) 상태 공간(state space)의 집합.
- \( P \) : 전이 확률 (transition probabilty). 모든 상태(state) \( X \) 사이의 전이 확률을 의미한다.
- 이를 아래와 같이 표기한다.
- 별로 어렵게 생각할 필요는 없고 주어진 문제를 위의 두 가지 요소로만 기술한다고 생각하면 된다.
- 따라서 이 두가지 표현할 수 없는 문제는 당연히 MP로 해결할 수 없다.
- 일단 MP로 처리 가능한 문제에 대해서만 집중하도록 하자.
- 스텝 (step)
- 각 상태의 전이는 이산 시간(discrete time)에 이루어지며, 상태 집합 \(X\) 에 속하는 어떤 임의의 상태에 머무를 때의 시간을 스텝(step)이라고 정의한다.
- 만약 현재 스텝을 \(n\) 이라 하면, 이 다음 스텝은 \(n+1\) 라고 기술할 수 있다.
- 이 때의 상태 전이 확률 값을 간단하게 기술해보자.
- \(p_{ij}\) 는 상태 \(i\) 에서 \(j\) 로 전이될 확률 값을 의미한다.
- \(X_n\) 은 스텝 \(n\) 에서 머물러있는 상태(state)를 의미하며 정확히는 해당 상태(state)에 대한 랜덤 변수 (즉, r.v.)를 의미한다.
- 중요한 것은 상태 \(i\) 를 방문했을 때, 그 이전에 어떤 상태에 방문했는지 상관 없이 상태 \(i\) 에서의 다음 상태 \(j\) 로의 전이 확률 값은 언제나 동일하다.
- 이것은 MPd의 기본 속성이며 모델을 단순하게 만들어준다.
- 또한 이를 무기억성 속성이라고도 한다.
- 수식으로 표현하면 다음과 같다.
- 이러한 특성(다음 상태의 확률이 오로지 전 상태에만 영향을 받는 특성)을 마코프 속성(Markovian Property)이라고 부른다.
- 추가적으로 전이 확률의 조건은 다음과 같다.
- 이것은 전이 함수가 확률 함수이기 때문에 당연히 만족해야 하는 식이다.
- 이제 MP를 그래프로 표현하는 방법을 살펴보도록 하자.
- 일반적으로 상태(state) \(X\) 는 원(circle)으로 표기하고,
- 전이 확률 \(P\) 는 상태 사이의 화살표로 표현하게 된다.
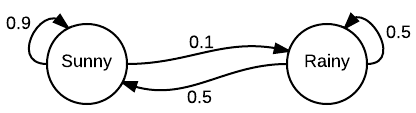
- 이제 스텝 \(n\) 인 상황에서 현재까지 발생한 사건이 발현될 가능성을 확률 값으로 표현해보자.
- 현재 상태에서의 확률 함수는 다음과 같이 나타낼 수 있다.
- 시작 시점부터 현재 상태까지 진행된 결과에 대한 확률값을 표현하고 있다.
- 이를 베이즈 룰을 이용하여 전개한다. 별로 어려운 내용은 없다.
- 다음으로 임의의 상태 \(i\) 에서 출발하여 다른 상태 \(j\) 로의 n-step 전이 확률을 나타내보자.
- 여기서는 상태 \(i\) 로부터 정확히 \(n\) 회 이동을 하여 상태 j 에 도달하는 경우를 나타낸다. 이때의 함수를 \(r\) 로 표기한다.
- 위와 같이 \(r\) 함수에 대해 재귀적으로 표현 가능하고 다시 확률 함수로도 전환 가능하다.
- 위 식에서 \(p^{(2)}\) 에 기술된 지수값 \((2)\) 는 제곱을 의미하는 것이 아니라 총 2-step 임을 나타내는 요약식이다.
- 즉, 2 단계를 거쳐 \(i\) 에서 \(j\) 까지 이동하는 확률 값을 의미하게 된다.
- 이제 이 표현 방법을 일반화하여 아래와 같이 기술할 수 있다.
- 물론 이 식은 RL과 직접적인 관계가 있는 것은 아니지만 개념을 잡기위해 눈여겨두자.
- 사실 마코프 모델은 이걸로 끝이 아니다.
- 워낙 자주사용되는 모델인만큼 관련 자료를 찾아보는 것도 좋을 듯 하다.
- 다음의 용어가 가지는 의미를 한번 정도는 확인해보도록 하자.
- irreducible markov chain
- recurrent markov chain
- aperiodic markov chain
- ergodic
- stationary distribution
- 물론 다음에 나올 내용들은 위 용어들의 의미를 몰라도 전혀 문제가 없다.
RL과의 연관성
- 지금까지 설명한 MP 모델은 MDP 모델의 근간이 되는 모델이다.
- 따라서 이산적 time 스텝을 가지는 모델을 계속 살펴볼 것이다.
- 마찬가지로 무기억성 속성 또한 계속 유지되는 모델을 사용할 것이다.
- MP 는 수동적인 모델이다.
- 이게 무슨 말인고 하니 MP(X, P) 환경 하에서는 사용자가 개입할 여지가 별로 없다.
- Time step 이 진행되는 동안 알아서 상태가 전이되어 진다.
- 따라서 이 모델에서는 사용자가 변경할 수 있는 요소는 전혀 없다.
- 다만 관심있게 볼 만한 요소들이 몇 가지 있는데 다음과 같은 예제가 있다.
- n-step 이후 특정 상태 s 에 대해 agent 가 머무를 확률 값.
- 특정 seq 에 대한 발현 확률.
- 이에 반해 이후에 살펴볼 모델은 사용자가 Action을 제어함으로써 전체 작업에 직접적인 개입을 하게 된다.
