1. Variational Inference

변분법은 18세기 오일러와 라그랑주의 변분 이론에서 출발했다.
- 우리는 “함수” (function) 라는 개념을 아주 익숙하게 사용하고 있다.
  - 일반적으로 함수는 입력으로 실수를 사용하고, 이 값과 매핑(mapping)된 실수를 반환하는 블랙 박스로 생각할 수 있다.
  - 이 때 함수를 미분한다는 것은 입력 값을 아주 조금 변경했을 때의 출력 값의 변화를 측정하는 것과 같다.
- 마찬가지로 “범함수” (functional) 라는 개념이 있다.
  - 범함수는 함수를 입력으로 받아 실수를 반환하는 함수이다.
  - 미분의 개념을 확장하여 입력 함수를 아주 조금 변경했을 때의 출력 값의 변화를 동일한 방식으로 해결할 수 있다.
  - 이러한 개념을 잘 이해할 수 있는 예로 엔트로피 함수 $ H[p] $ 를 들 수 있다.
    - 엔트로피 함수는 확률 분포 $ p $ 를 입력받아 이 때의 정보값을 반환해 준다.

$H[p] = - \int p(x)\ln p(x)dx \qquad{(10.1)}$

이제 범함수의 미분을 어떻게 할 수 있는지 알아보자.
- 마찬가지로 입력으로 들어가는 함수가 극미하게 변경될 때 출력 값의 변화를 미분으로 정의 가능하다.
- 이와 관련된 표준화된 풀이 방법을 Appendix.D 에 기술해 놓았으니 한 번 살펴보기 바란다.
  - 근데 막상 읽어보면 그리 도움이 되지는 않는듯.
- 많은 최적화 문제들이 변분 방식을 사용하면 쉽게 해결 가능하다.
- 이 방법은 입력 가능한 여러 함수들 중에 결과를 가장 최대화하거나 최소화하는 함수를 결정할 수 있도록 한다.
결국 범함수를 최대화 혹은 최소화하는 함수 값을 찾는 문제로 귀결됨.
- 사실 이번 장에서 다루는 문제들은 범함수의 최대/최소 문제를 다루고 있다고는 하지만,
- 사용되는 수식에서 이러한 방식이 잘 드러나지는 않고 있다.
- 왜냐하면 실제 수식을 전개하는 방식은 거의 비슷한 형태로 이루어지다보니까, 여기서는 변분법의 결과에만 주목한다.
- 따라서 변분적 특성들은 그냥 $ KL $ 의 개념에 흡수되어 표현되고 있음.
변분법은 실제로는 근사 기법은 아니다.
- 하지만 찾아야 하는 함수의 형태를 제한하기 때문에 결국은 근사화된 식이 얻어지게 된다.
- 찾아야 하는 함수의 형태를 다음과 같이 제한함
  - 이차 함수 (quadratic)
  - 혹은 고정된 기저 함수의 선형 결합으로 구성된 함수
  - 혹은 인수 분해 가정의 형태 (factorization assumption)
- 이게 무슨 소리인고 하니 $ q $ 함수를 특정한 형태의 제약 사항을 추가하여 우리가 구하기 쉬운 확률 분포로만 고려한다는 것임
- 이러한 제약 조건이 자연스레 근사 분포를 만들어내게 되는 이유가 된다.
이제 이러한 변분 방식이 어떻게 추론 문제에 적용될 수 있는지를 확인해보도록 하자.
- 우선 주어진 모델이 베이지언 모델을 따른다고 가정하다.
- 이런 경우 모든 파라미터는 랜덤 변수로 주어지게 된다.
- 결국 사전 분포를 필요로 하게 된다.
- 마찬가지로 잠재 변수도 함께 주어지게 된다.
- 주어진 환경을 정리해 보자.
  - $ {\bf Z} $ : 잠재 변수와 사용되는 모든 파라미터 집합
  - $ {\bf X} $ : 관찰 변수
  - 이 때 입력 데이터는 $ N $ 개이고 서로 독립적이다.
  - 따라서 $ {\bf X} = { {\bf x}_1,…,{\bf x}_n} $ 이고 $ {\bf Z} = { {\bf z}_1,…,{\bf z}_n} $
로그 주변 확률 $ \ln p({\bf X}) $ 는 EM 알고리즘과 마찬가지로 다음과 같은 형태로 분해 가능하다.
- 앞서 EM 알고리즘에서 살펴본 전개 방식과 거의 동일하기 때문에 전개는 생략하도록 하자.

$\ln p({\bf X}) = L(q) + KL(q\|p) \qquad{(10.2)}$

이 때 각각의 텀에 대한 정의는 다음과 같다.

$L(q) = \int q({\bf Z}) \ln \left\{\frac{p({\bf X}, {\bf Z})}{q({\bf Z})}\right\}d{\bf Z} \qquad{(10.3)}$ $KL(q\|p) = - \int q({\bf Z}) \ln \left\{\frac{p({\bf Z}|{\bf X})}{q({\bf Z})}\right\}d{\bf Z} \qquad{(10.4)}$

식은 EM 과 거의 동일하게 보이지만 파라미터 $ \theta $ 가 모두 $ {\bf Z} $ 로 흡수되었다.
파라미터 $ \theta $ 는 고정된 값이 아니라 랜덤 변수로 적용됨
추가로 잠재 변수는 연속형 변수로 처리되어 합산 식이 적분 식으로 대체하였다.
EM 알고리즘에서는 $ q $ 함수를 $ p({\bf Z}|{\bf X}) $ 인 사후 분포로 대체하여 $ L $ 함수를 최대화하는 과정으로 식을 전개하였다.
- 즉, $ L(q) $ 를 최대화하는 과정. 동시에 $ KL $ 이 최소화된다.
- $ q = p({\bf Z}|{\bf X}) $ 로 하여 $ KL $ 으로 0으로 만들어 $ L $ 을 최대화시킴
여기서는 사후 분포 $ p({\bf Z}|{\bf X}) $ 를 구하기 어려운 모델을 다루게 된다.
- 따라서 $ q $ 함수를 사후 분포로 놓는 것이 아니라,
- 분포 $ q $ 를 제한적인 계열의 분포로 고려하고 이를 이용하여 $ KL $ 값을 최소화하는 파라미터를 구하는 것
- 추가로 이러한 선택에 있어 오버피팅 문제가 없어야 한다.

이제 근사할 분포의 계열을 제한하는 모델을 살펴보도록 하자
- 모수를 사용하는 분포 (parametric distribution)로 $ q $ 함수를 제한한다.
- 이러면 $ q({\bf Z}|{\bf w}) $ 로 생각할 수 있다. 이 경우 $ {\bf w} $ 에 의해 분포의 모양이 결정된다.
- 결국 범함수 $ L(q) $ 는 $ {\bf w} $ 에 대한 함수라고 생각될 수 있음
- $ {\bf w} $ 를 최적화하는 과정을 통해 근사 분포를 만들어낸다.

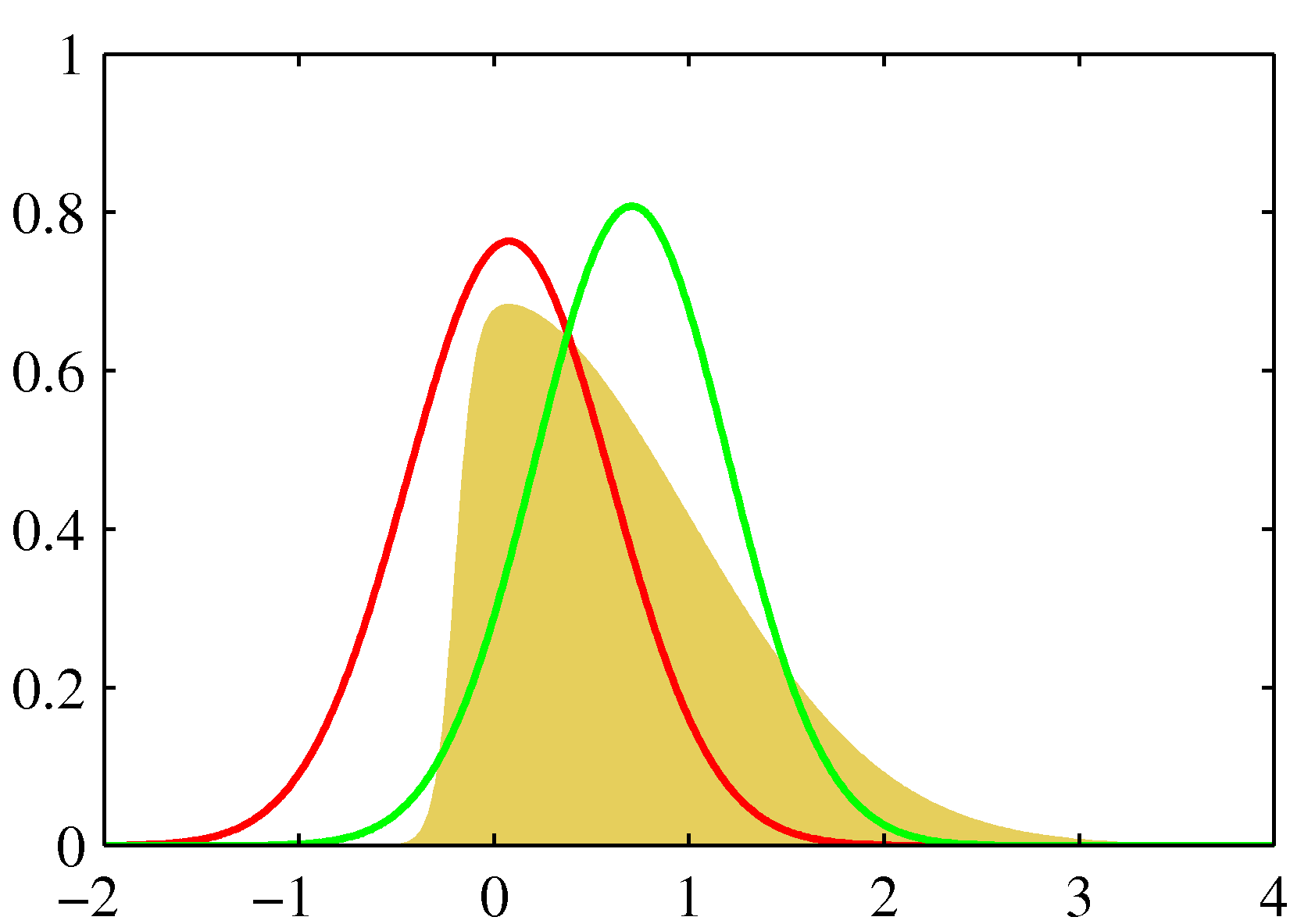
위의 그림은 $ q $ 함수의 계열을 제한하여 근사를 수행한 결과를 표기한 것이다.
- 왼쪽 그림에서 우선 노란색 영역은 근사를 해야 할 원본 분포이다. 여기서는 $ p({\bf Z}|{\bf X}) $ 가 된다.
  - 그리고 이 함수는 intractible 속성을 가진다.
  - $ p(z) \propto \exp(-z^2/2)\sigma(20z + 4) $
  - $ \sigma(z) = (1 + e^{-z})^{-1} $
- 또한 붉은 색 선은 라플라스 근사, 녹색 선은 변분 근사식이다.
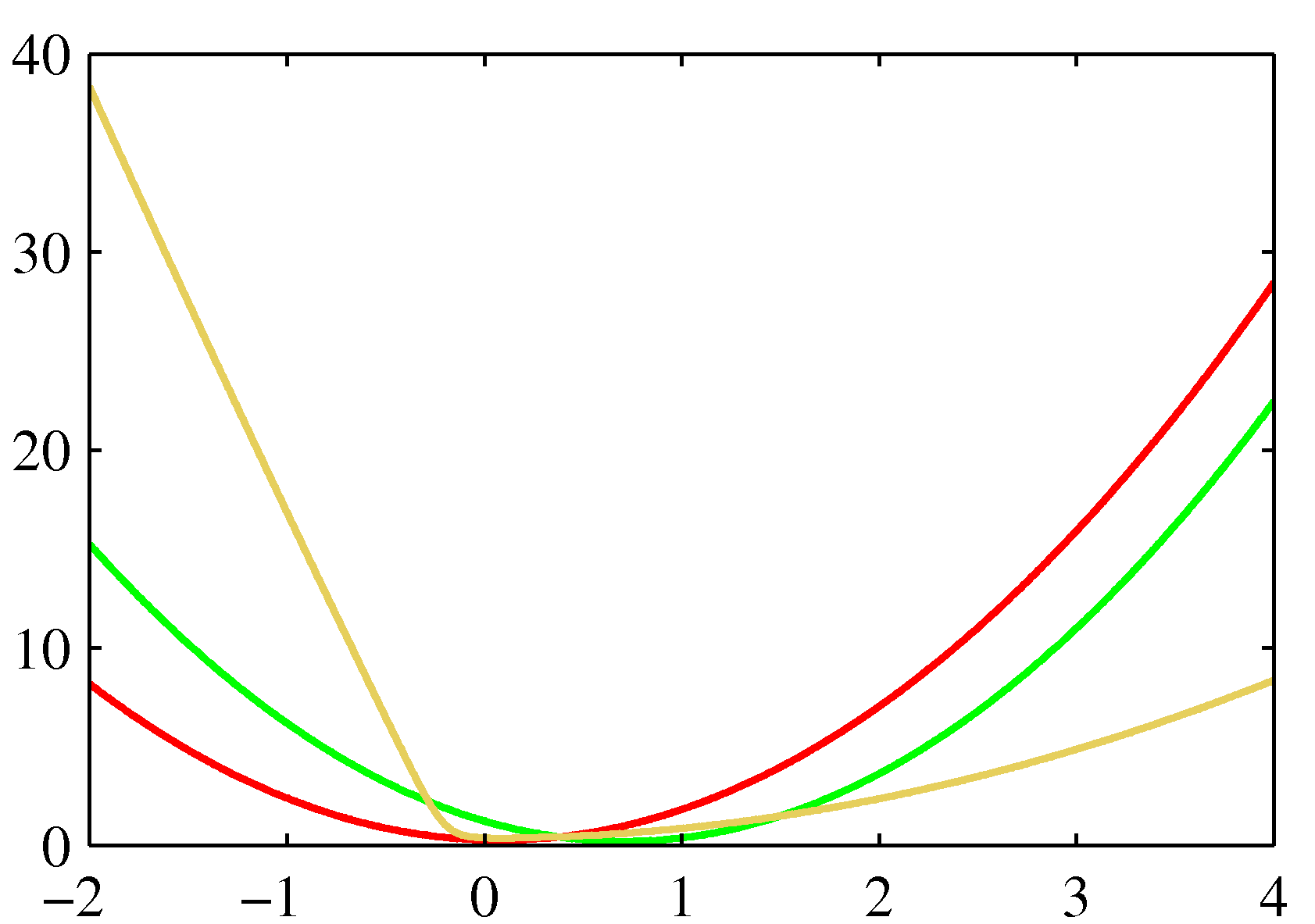
- 오른 쪽 그림은 음의 로그 함수를 취한 값이다.
- 결국 $ KL $ 값을 최소로 만드는 식을 구하게 된다.

10.1.1. 인수분해된 분포의 사용 (Factorized distributions)

이제 분포 $ q({\bf Z}) $ 의 종류를 제한하는 또 다른 방법을 살펴보도록 하자.
우선 우리는 잠재 변수 $ {\bf Z} $ 가 그룹 (disjoint group) $ {\bf Z}_i $ 로 나누어진다고 가정한다.
- 이 때 $ i=1,…M $ 이다.
- 반드시 모든 요소로 하나 하나 나눌 필요는 없다. 적당한 기준에 따라 나누어지면 된다.
- 이와 관련된 내용은 뒤에 더 나온다.
이런 경우 우리는 기존의 $ q({\bf Z}) $ 함수를 다음과 같이 기술할 수 있다.

$q({\bf Z}) = \prod_i^M q_i({\bf Z}_i)$

여기서는 이러한 가정 외에 추가적인 가정은 더 이상 없다는 것이 중요한 포인트.
추가로 각각의 $ q_i({\bf Z}_i) $ 에 대해서는 추가적인 제약을 가질 필요가 없다.
이렇게 factorized form 형태를 가지는 변분 추론 방식을 물리학에서는 평균장 이론(mean field theory)이라고 부른다.
[참고] 평균장 이론
- 물리학에서 개발된 근사 프레임워크로 자기 모순 없는 장 이론(self-consistent field theory)라고도 함
- 다수의 상호작용이 있는 복잡한(many-body) 문제를 단순한 하나의 상호작용(one-body)의 단순 모델로 표현하는 방법
- 각각의 요소에 대한 상호작용을 이해하고 계산하기 어려우니, 평균 상호 작용으로 취급하는 것
- 예) 모든 자석이 같은 방향을 향하면, 모든 자기장이 합쳐져 큰 자석이 됨
- 자석 전체를 설명하려면 각각의 작은 원자 자석들을 두개씩 골라서 문제를 풀어야 함 : 너무 많음
- 자석이 보고 있는 방향은 주변 자석이 보고 있는 방향의 평균적인 방향에 해당한다고 보는 것 : 평균장 근사
- 멀리 떨어진 자석들 사이의 연결 관계를 보지 않겠다는 것으로 문제를 간단하게 만들게 됨
이와 같은 가정을 가지고 $ L(q) $ 를 가장 크게 하는 $ q $ 함수를 찾는 것이 우리의 목표가 된다

$L(q) = \int \prod_i q_i \times\left\{\ln p({\bf X}, {\bf Z}) - \sum_i \ln q_i\right\}d{\bf Z}\\ = \int q_j \prod_{i \neq j}q_i(\ln p({\bf X}, {\bf Z})-\ln q_j)d{\bf Z}-\int q_j\prod_{i \neq j}q_i\sum_{i \neq j}\ln q_i d{\bf Z}\\ = \int q_j \left\{ \int \ln p({\bf X}, {\bf Z})\prod_{i \neq j} q_i d{\bf Z}_i \right\} d{\bf Z}_j - \int q_j \ln q_j d{\bf Z}_j + const\\ = \int q_j \ln \tilde{p}({\bf X}, {\bf Z}_j)d{\bf Z}_j - \int q_j \ln q_j d{\bf Z}_j + const$

여기서 $ \tilde{p}({\bf X}, {\bf Z}_j) $ 는 다음과 같다.

$\ln \tilde{p}({\bf X}, {\bf Z}_j) = E_{i \neq j}[\ln p({\bf X}, {\bf Z})] + const$

사실 수식의 표현 방식이 썩 맘에 들지는 않는다.
- 좀 꼼꼼히 살펴보면서 식이 어떻게 전개되는지 살펴보자.
- 중요한 부분은 $ L(q) $ 함수가 임의의 특정 $ q_j $ 에 관련있는 텀과 관련없는 텀으로 분리할 수 있다는 것
$ E_{i \neq j}[\ln p({\bf X}, {\bf Z})] $ 는 $ i \neq j $ 인 모든 $ {\bf z}_i $ 에 대해 $ q $ 분포의 평균 값을 구한것이다.

$E_{i \neq j}[\ln p({\bf X}, {\bf Z})] = \int \ln p({\bf X}, {\bf Z})\prod_{i \neq j} q_i d{\bf Z}_i$

위의 식이 중요하다. 실제 계산이 되는 식이므로 잊지 않도록 한다.

이제 $ L $ 함수를 가장 크게 만드는 $ q $ 함수를 구하는 식을 만들어보자.
앞서 $ KL $ 값을 최소로 하기 위해서는 $ q=p({\bf Z}|{\bf X}) $ 를 만족해야 한다고 했다.
- 하지만 여기서는 $ p({\bf Z}|{\bf X}) $ 를 구할 수 없으므로 $ L(q) $ 를 최대화하는 문제로 생각을 해야 한다.
- 식 전개를 하지는 않지만 $ L(q) $ 함수를 다음과 같이 전개 가능하다.

$L(q) = -KL(q_j\|\tilde{p}({\bf X}, {\bf Z})) + const$

마찬가지로 $ L(q) $ 를 최대화하기 위해서는 위의 식을 기초로 하여 다음과 같은 조건을 만족하게 식을 만들면 된다.

$\ln q_j^*({\bf Z}_j) = E_{i \neq j}[\ln p({\bf X}, {\bf Z})] + const$

이 식이 변분 방식을 사용하기 위한 가장 기본적인 식이 된다.
로그를 없앤 식을 보도록 하자.

$q_j^*({\bf Z}) = \frac{\exp(E_{i \neq j}[\ln p({\bf X}, {\bf Z})])}{\int \exp(E_{i \neq j}[\ln p({\bf X}, {\bf Z})])d{\bf Z}_j}$

로그를 지수화시키고 정규화시킨 결과이다.
- 실제 로그를 붙인 상태로 사용하는 경우가 더 편할 경우도 있다.
- 손쉽게 로그 상태로 변환 가능하며 정규화 상수도 쉽게 구할 수 있다.

10.1.2. 인수분해 근사식의 속성 (Properties of factorized approximations)

변분 추론 방식은 실제 사후 분포를 인수분해된 형태로 구하는 형태를 사용한다.
인수 분해된 분포로 원래 분포를 근사하게 된다.

Example : 가우시안으로 인수 분해된 근사 추론 방법

인수분해한 가우시안 분포를 이용하여 사후 분포를 근사하는 방식을 살펴보도록 한다.
두개의 연관 변수 $ z_1, z_2 $ 에 대한 가우시안 분포 $ p({\bf z}) = N({\bf z} | \mu, \Lambda^{-1}) $를 가정하자.
이 때의 평균과 정확도는 다음과 같다고 하자.

${\bf \mu} = \dbinom{ {\bf \mu}_1 }{ {\bf \mu}_2},\;\; \Lambda = \left(\begin{array}{cc}\Lambda_{11} & \Lambda_{12}\\ \Lambda_{21} & \Lambda_{22}\end{array}\right) \qquad{(10.10)}$

이 때 $ \Lambda_{21} = \Lambda_{12} $ 이다. (대칭성에 의해)
이제 $ q({\bf z}) = q_1(z_1)q_2(z_2) $ 형태로 인수분해된 가우시안을 사용하여 위 분포를 근사할 것이다.
최적화 값인 $ q_1^{*} $ 를 찾기 위해 식(10.9) 를 사용한다.
우측 전개식에서는 $ z_1 $ 에 종속적인 텀(term)만을 유지하도록 한다.
즉, $ z_2 $ 와 관련된 텀(term)은 모두 상수(const) 영역으로 분리해 낼 수 있다.

$\ln q_1^{*}(z_1) = E_{z_2}[ \ln p({\bf z})] + {const} \\\\ = E_{z_2}\left[ -\frac{1}{2}(z_1 - \mu_1)^2 \Lambda_{11} - (z_1-\mu_1)\Lambda_{12}(z_2-\mu_2) \right] + {const} \\\\ = -\frac{1}{2}z_1^{2}\Lambda_{11} + z_1\mu_1\Lambda_{11} - z_1\Lambda_{12}(E[z_2] - \mu_2) + {const} \qquad{(10.11)}$

이 식의 우변 쪽을 잘 살펴보면 $ z_1 $ 에 대한 이차함수(quadratic) 임을 알 수 있다.
$ \ln(\cdot) $ 을 취했을 때 이차 함수의 형태가 도출된 것을 보면 원래의 $ q_1^{*}(z_1) $ 은 가우시안 분포라고 생각할 수 있음.
이는 처음부터 $ q_1(z_1) $ 이 가우시안 분포라고 가정한 것이 아님에도 이러한 결과를 얻게되는 것임.
모든 가능한 분포 $ q_1(z_1) $ 로부터 시작하여 KL 의 변분 최적화 결과를 통해 이러한 식이 유도되었음.
식(10.9) 에서 사용된 const 값은 계산할 필요가 없다.
- 필요하면 마지막에 값을 얻어낼 수 있는 정규화 상수이기 때문.
이제 완전 제곱식을 이용하여 가우시안 분포의 평균과 정확도를 계산할 수 있음.
- $ ax^2 + bx + c = 0 \rightarrow (x + b/2a)^2 = const $ 와 같은 식을 사용함.

$q_1^{*}(z_1) = N(z_1|m_1, \Lambda_{11}^{-1}) \qquad{(10.12)}$ $m_1 = \mu_1 - \Lambda_{11}^{-1}\Lambda_{12}(E[z_2]-\mu_2) \qquad{(10.13)}$

동일하게 $ q_2^{*}(z_2) $ 에 대해 식을 얻을 수 있음.

$q_2^{*}(z_2) = N(z_2|m_2, \Lambda_{22}^{-1}) \qquad{(10.14)}$ $m_2 = \mu_2 - \Lambda_{22}^{-1}\Lambda_{12}(E[z_1]-\mu_1) \qquad{(10.15)}$

위의 식을 보면 두 식이 서로 연결되어 있는 식임을 알 수 있음.
- 즉, $ q_1^{*}(z_1) $ 가 $ q_2^{*}(z_2) $ 의 기대값에 의존한다. (반대도 성립)
- 따라서 이에 대한 풀이는 어떤 수렴 기준을 만족할 때까지 차례로 변수를 업데이트하는 구조를 취하게 된다.
- 이를 계속 반복하여 문제를 해결한다.
위에서 언급한 예제는 이런 방식 외에 닫힌 형태의 (closed-form) 솔루션이 존재하는 단순한 문제임.
- 즉, $ E(z_1)=m_1 $ 이고 $ E(z_2) = m_2 $ 이므로
- $ E(z_1)=\mu_1 $ 과 $ E(z_2)=\mu_2 $ 를 구하면 $ m_1 = \mu_1 $ 과 $ m_2 = \mu_2 $ 를 만족함을 알 수 있음.
- 특이점이 존재하지 않는 유일한 솔루션을 제공함.
- 이 식은 임의의 다차원의 가우시안 분포로 확장이 가능하다.

$ KL(p\|q) $ 의 최소화

지금까지 본 변분 추론 방식은 $ KL(q\|p) $ 를 최소화하는 방식을 사용한 것이다.
- 이를 이용하여 $ q_j^{*}(z_j) $ 를 구했다.
이와 대조적으로 $ KL(p\|q) $ 를 최소화하는 방식을 사용할 수 있다.
- 사실 이 방식이 이후에 다룰 Expectation Propagation 방식이다.
다시 처음으로 돌아가 $ q({\bf z}) $ 가 인수 분해된 근사 분포라 가정한 상태에서,
- $ KL(p\|q) $ 의 최소화 문제를 살펴보자.
참고로 1장에서 다루었던 KL 은 다음과 같았다. (식 1.113)

$KL(p\|q) = -\int p(x) \ln q(x) dx - \left( -\int p(x) \ln p(x) dx \right) = - \int p(x) \ln \left\{ \frac{ q(x) }{ p(x) } \right\} dx$

이제 이 식을 다시 정리해보자.

$KL(p\|q) = -\int p({\bf Z}) \left[ \sum_{i=1}^{M} \ln q_i({\bf Z}_i) \right]d{\bf Z} + {const} \qquad{(10.16)}$

이 때 위 식의 const 영역은 $ - \int p({\bf Z}) \ln \frac{1}{p({\bf Z})} d{\bf Z} $ 이다.
이 값은 $ p({\bf Z}) $ 에 대한 엔트로피 값으로 $ q({\bf Z}) $ 와는 무관한 값이 된다.
이제 각 요소 $q_j({\bf Z}_j) $ 에 대해 다음과 같은 최적화 식을 만들어 낼 수 있다.

$q_j^{*}({\bf Z}_j) = \int p({\bf Z})\prod_{i \neq j} d{\bf Z}_i = p({\bf Z}_j) \qquad{(10.17)}$

$ q_j({\bf Z}_j) $ 는 확률 함수여야 하므로 적분 값이 1이어야 한다.
이를 통해 Lagrange multiplier를 적용 가능하다.

Chapter. 10

1. Variational Inference

10.1.1. 인수분해된 분포의 사용 (Factorized distributions)

10.1.2. 인수분해 근사식의 속성 (Properties of factorized approximations)

Example : 가우시안으로 인수 분해된 근사 추론 방법

\( KL(p\|q) \) 의 최소화