3. An Alternative View of EM

이번 절에서는 EM 알고리즘에서 사용되는 잠재 변수(latent variable)의 핵심적인 역할에 대해 살펴볼 것이다.
- 잠시 기억을 떠올려보면 입력 샘플 $ {\bf x}_n^T $ 에 대응되는 $ {\bf z}_n^T $ 가 존재하는 것으로 처리하였다.
EM 알고리즘의 최종 목적은 데이터 $ {\bf X} $ 가 주어졌을 때 잠재 변수를 통해 MLE 를 구하는 것이다.
- 물론 잠재 변수 $ {\bf Z} $ 에 대해 사전에 알려져있는 정보는 없다.
- 이후 잠재 변수와 입력 변수에 대한 조건부 분포 형태로 문제를 풀게 된다.
EM 알고리즘에 대해 잠시 생각해보는 시간을 갖도록 하자.
- 우리는 지금까지 SGD (Stocastic gradient descent) 등의 함수 최적화 방식을 배웠었다.
- 그럼에도 불구하고 EM 이라는 방식을 사용하는 이유는 뭘까?
  - 현실적으로는 SGD 연산보다 EM 방식이 이해하기도 쉽고 구현하기도 쉽다. 그래서 많이 쓴다.
  - 물론 성능이 더 좋다고는 말할 수 없음.
- 그럼 다른 방법 대신 무조건 EM 을 쓰면 되는것 아닌가?
- 모든 경우에 EM 을 적용할 수 있는 것은 아니고 일정한 조건이 필요함
  - 조건에 부합되는 모델에서는 당연히 그냥 사용하면 되고,
  - 조건에 부합되지 않는 경우에는 모델 자체를 해당 조건으로 변환을 하여 조건을 만족하게 한 뒤에 식을 추스려야지만 EM 을 사용할 수 있다.
- 그럼 EM 을 사용할 수 있는 조건이란?
  - 일단 잠재 변수가 존재해야 한다. (EM 자체가 잠재 변수가 있는 경우를 해결하기 위한 모델이다.)
  - 잠재 변수가 관찰되지 않았을 경우에는 모델의 파라미터 추정이 불가능한 상태를 가진다.
  - 하지만 잠재 변수가 관찰된 후에는 모델의 파라미터 추정이 가능해진다.
  - 혼합 분포가 EM 을 적용하기 좋은 예인데,
    - 잠재 변수의 역할이 혼합 분포 내의 한 분포를 선택하는 것을 나타내는 랜덤 변수인 경우 쉽게 적용 가능하다.
    - 이것은 지난 절에서 살펴본 내용이다.

잠재 변수가 주어진 모델의 MLE 를 이해하여 보자.

$\ln p({\bf X}|{\bf \theta}) = \ln \left\{ \sum_{\bf Z} p({\bf X}, {\bf Z}|{\bf \theta}) \right\} \qquad{(9.29)}$

간단한 합의 공식(sum rule)을 이용한 식이다.
- 위의 식은 합의 공식으로 표현되어 있지만 $ {\bf Z} $ 가 연속 변수인 경우 적분으로 표현할 수 있다.
여기서 중요한 점은,
- 잠재 변수가 로그(log) 함수 안에서 합으로 표현되고 있다는 것이다.
  - 결합 확률 분포 $ p({\bf X}, {\bf Z} | {\bf \theta}) $ 가 지수족 분포를 따른다고 할지라도,
    - 이에 대한 주변 확률 분포 $ p({\bf X} | {\bf \theta}) $ 는 지수족 분포가 아닐 수 있다.
    - 가우시안 함수를 합한 식에 로그를 취한 함수는 간단한 이차 형식(quadratic)의 함수가 아니다.
  - 이는 결국 복잡한 형태의 MLE 풀이를 가지게 된다.
앞서서 complete 와 incomplete 의 개념을 배웠었다.
- Complete Data : $ { {\bf X}, {\bf Z} } $
  - 모든 관찰 데이터에 대해 잠재 변수 $ {\bf Z} $ 가 주어진 모델
  - 이 때의 로그 가능도 함수는 $ \ln p({\bf X}, {\bf Z} | {\bf \theta}) $ 가 된다.
  - 각각에 대해 가능도 함수를 구하게 되므로 어렵지 않다.
- Incomplete Data : $ { {\bf X}} $
  - 모든 관찰 데이터에 대해서만 주어지고 잠재 변수는 주어지지 않는다.
  - 결국 가능한 모든 잠재 변수의 값에 대한 분포를 고려해야 한다.
  - 로그 가능도 함수는 $ \ln p({\bf X} | {\bf \theta}) = \ln { \sum_Z p( {\bf X}, {\bf Z} | {\bf \theta} ) } $ 로 주어진다.
  - 로그 함수 내에 합(sum) 에 대한 수식이 존재하기 때문에 최대화 시키는 지점을 찾기가 어렵다.

이제 EM 을 이용하여 로그 가능도 함수를 계산하는 방법을 살펴보도록 하자.
- 앞서 이야기한대로 로그 가능도 함수가 계산 가능한 경우는 오로지 잠재 변수 $ {\bf Z} $ 가 관찰된 경우 밖에 없다.
- 하지만 일반적으로 이러한 잠재 변수의 실제 값은 얻을 수 없다. (즉, 오로지 얻을 수 있는 데이터는 incomplete 데이터)
- 따라서 이 경우 MLE를 풀기 위해서는 샘플을 통해 이 잠재 변수를 추정하여 값이 제공된다고 생각하는 수 밖에 없다.
- 그래서 Expectation of Log-likelihood 가 등장한다.
- 별거 없고, 로그 가능도 함수에서 잠재 변수의 값을 정확히 알기 어려우므로 그냥 평균(기대) 값을 식으로 표현한 것.
  - 즉, 가능도 함수에 $ E[\ln p({\bf X}, {\bf Z} | {\bf \theta})] $ 를 사용하게 된다.
  - 물론 가능도 함수 대신 이 수식을 사용하는 것이 타당한지에 대한 의문이 들 수 있는데, 왜 가능한지는 다음 절에 나온다.
  - 여기서는 아무런 설명 없이 바로 그냥 식이 제공되기 때문에 의아해할 수도 있지만 우선은 그런가보다 하고 진행하도록 하자.
- 예전에도 이와 비슷한 상황을 좀 보긴 했는데 손실 함수를 최소화하는 방식도 이와 유사한 방식이다.
  - 물론 기억은 잘 나지 않을 것이다.
이렇게 정의한 가능도 함수의 기대값을 좀 전개해보자.

$E_Z[\ln p({\bf X}, {\bf Z}|\theta)] = \sum_{\bf Z} p({\bf Z}|{\bf X}, {\bf \theta})\ln p({\bf X}, {\bf Z}|{\bf \theta})$

참고로 함수에 대한 기대값을 구하는 식은 다음과 같다. $E[f]=\sum_x p(x)f(x)$
이제 기대값을 최대로 만드는 파라미터 값을 추론할 것이다.
이 때 EM 을 사용하게 되는데 앞서 살펴본 방식과 동일한 형태로 위의 값을 최대화하는 과정으로 만들어 낼 수 있기 때문

E-Step

우선 주어진 파라미터는 고정되어 있다고 하고 이를 $ {\bf \theta}^{old} $ 라고 하자.
여기서 잠재 변수 $ {\bf Z} $ 의 확률 값 $ p({\bf Z}|{\bf X}, {\bf \theta}^{old}) $ 를 얻어야 한다.
이렇게 얻어진 확률 값을 이용하여 complete-data 가능도 함수의 값을 구할 것이다.
- 즉, 가능한 $ {\bf Z} $ 의 확률 값을 추론한 뒤 이를 이용하여 각각의 파라미터 값을 추론하는 MLE 과정을 진행할 것이다.
잠재 변수의 기대값이 예측되었을 때, 이제 일반 파라미터 $ \theta $ 를 가지고 complete-data 가능도 함수의 기대값을 서술해보자.

$Q({\bf \theta}, {\bf \theta}^{old}) = \sum_{\bf Z} p({\bf Z}|{\bf X}, {\bf \theta}^{old}) \ln p({\bf X}, {\bf Z}|{\bf \theta}) \qquad{(9.30)}$

수식이 크게 차이가 있는 것은 아니지만, $ {\bf Z} $ 를 추론할 때에는 사전에 결정된 파라미터를 사용한다는 것을 알 수 있다.
이후에는 그냥 $ \theta $ 에 대한 함수가 된다.
따라서 이 함수 값을 최대화하는 방법은 이제 별로 어렵지 않다.

M-Step

여기서는 예측된 $ {\bf Z} $ 의 기대값을 이용해서 이를 최대화하는 파라미터를 구하는 단계가 된다.

${\bf \theta}^{new} = \arg\max_{\theta} Q({\bf \theta}, {\bf \theta}^{old}) \qquad{(9.31)}$

사실 기존에 정리한 EM 방식과 동일하다. 정리해보자.

EM 알고리즘 일반화

관찰데이터 $ {\bf X} $ 와 잠재 변수 $ {\bf Z} $ 가 파라미터 $ {\bf \theta} $ 에 의해 주어졌을 때,
결합 분포는 $ p({\bf X}, {\bf Z}|{\bf \theta}) $ 와 같이 표현 가능하다.
이 때 $ p({\bf X}|{\bf \theta}) $ 값을 가장 크게 만드는 파라미터 $ {\bf \theta} $ 값을 얻고 싶다. (MLE를 이용)
- Init Step : (임의의) 파라미터 $ {\bf \theta}^{old} $ 의 값을 설정한다.
- E-Step : $ p({\bf Z}|{\bf X}, {\bf \theta}^{old}) $ 값을 추론한다.
- M-Step : $ {\bf \theta}^{new} $ 값을 추론한다. 이 때,
  - $ {\bf \theta}^{new} = \arg\max_{\bf \theta} Q({\bf \theta}, {\bf \theta}^{old}) \qquad{(9.32)} $
  - $ Q({\bf \theta}, {\bf \theta}^{old}) = \sum_{\bf Z}p({\bf Z}|{\bf X}, {\bf \theta}^{old})\ln p({\bf X}, {\bf Z}|{\bf \theta}) \qquad{(9.33)} $
- 새롭게 구해진 파라미터의 값들이 수렴 상태인지 확인한다.
  - 수렴되지 않았다면 아래 작업 후 Step-2 로 돌아간다.
  - 수렴되었을 경우 종료한다.
    - $ {\bf \theta}^{old} \leftarrow {\bf \theta}^{new} \qquad{(9.34)} $

참고로 위의 수식에서도 $ Singularity $ 문제는 여전히 발생할 수 있는데, 다음 식을 도입하여 이를 제거할 수 있다. (MAP 방식)

$Q({\bf \theta}, {\bf \theta}^{old})+\ln p({\bf \theta})$

Missing Variables

지금까지 이산 잠재 변수가 존재할 때의 MLE 처리를 수행하는 EM 알고리즘을 살펴보았음.
사실 이 방식은 입력 데이터에서 관찰되지 못한 데이터(un-observed variables)가 존재하는 경우에도 적용 가능한 방법임
- 가능한 모든 변수에 대한 결합 분포를 만든 다음 주변화 작업을 통해 해당 변수를 남기게 하면 된다.

9.3.1. 가우시안 혼합분포 다시 보기 (Gaussian mixtures revisited)

잠재 변수를 이용하여 GMM 을 다시 해석해보도록 한다.
- 물론 자세한 내용은 이미 앞절에서 다루었으므로 여기서는 일반화 식으로의 전개만을 다루도록 한다.

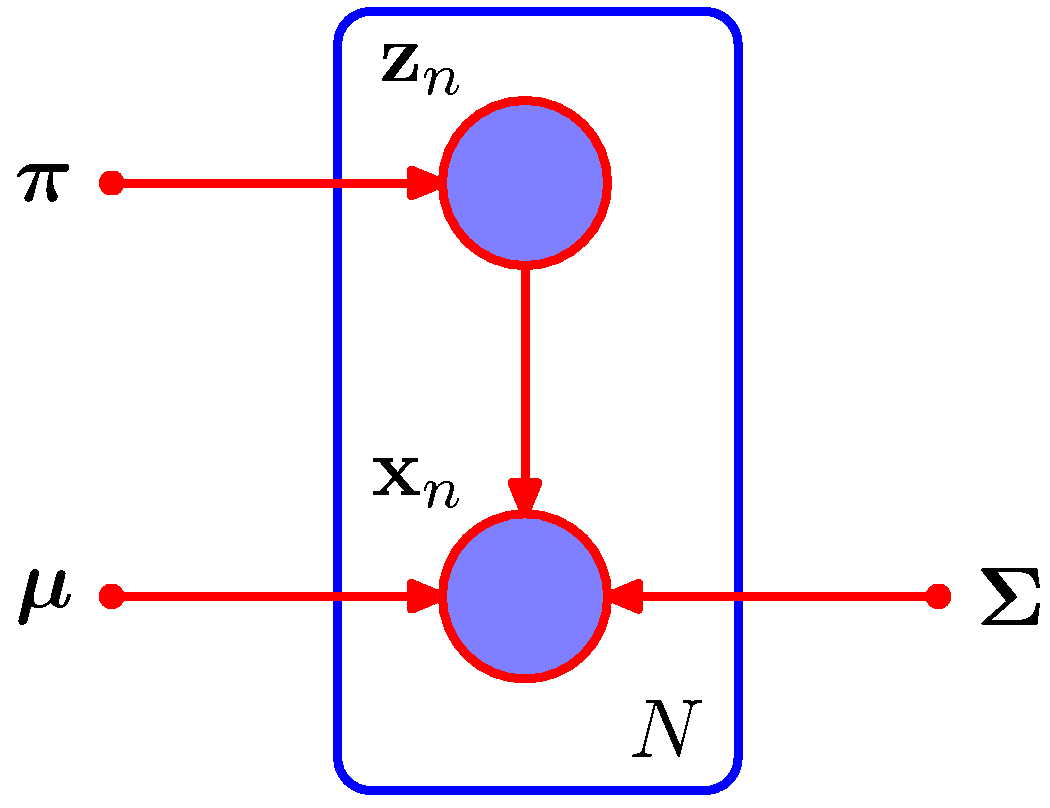
figure9.9

위의 그림은 complete-data 에 대해 GMM 모델을 표기한 것이다.
- 잠재 변수도 관찰되었으므로 음영으로 처리되어 있다.
이제 complete 데이터에 대한 가능도 함수와 로그 가능도 함수를 살펴보자.

$p({\bf X}, {\bf Z}|{\bf \mu}, \Sigma, {\bf \pi}) = \prod_{n=1}^N\prod_{k=1}^K \pi_k^{z_{nk}} N({\bf x}_n|{\bf \mu}_k, \Sigma_k)^{z_{nk}} \qquad{(9.35)}$ $\ln p({\bf X}, {\bf Z}|{\bf \mu}, \Sigma, {\bf \pi}) = \sum_{n=1}^N\sum_{k=1}^K z_{nk}\{\ln\pi_k + \ln N({\bf x}_n|{\bf \mu}_k, \Sigma_k)\} \qquad{(9.36)}$

이 식은 incomplete 데이터에 대한 로그 가능도 함수보다 쉽게 계산되는 꼴이다.
- incomplete 와 다르게 $ \ln(\cdot) $ 함수가 가우시안 분포에 바로 적용 가능함.
- 이것으로부터 파라미터의 MLE 값은 쉽게 계산 가능한데, 각각의 파라미터에 대해 convex 형태의 식이기 때문이다.
- 물론 $ {\bf z}_k $ 은 $ {\bf z}_k \in {0,1} $ 이므로 식 전개에 영향을 주지 못하고, 하나의 가우시안 함수에 대해 처리하는 것처럼 동작하게 된다.
- 따라서 각각의 $ k $ 에 대해 MLE 를 구하게 되면 다음과 같은 결과를 얻을 수 있음을 알 수 있다.

$\pi_k = \frac{1}{N}\sum_{n=1}^N z_{nk} \qquad{(9.37)}$

이제 incomlete 데이터를 살펴보도록 하자. 이에 대한 로그 가능도 함수는 다음과 같다.

$\ln p({\bf X}|{\bf \mu}, \Sigma, {\bf \pi}) = \sum_{n=1}^N \ln \left\{\sum_{k=1}^K \pi_k N({\bf x}_n|{\bf \mu}_k, \Sigma_k)\right\}$

앞서 살펴본 바와 같이 complete 데이터는 는 닫힌 형태(closed form)의 식이므로 MLE 처리가 가능.
하지만 incomplete 데이터는 로그 식 내에 합의 식이 존재하므로 이게 안된다.
따라서 EM 에서 보았던 로그 가능 함수의 평균 값을 정의하여 최대화하는 방식으로 전개해야 한다.
기존에 살펴보았듯이 결국 잠재 변수의 사후 분포를 통해 $ {\bf Z} $ 를 먼저 추론해야 하는 것.
우선 $ {\bf Z} $ 에 대한 사후 분포를 구하는 식을 기술해 보자.

$p({\bf Z}|{\bf X}, {\bf \mu}, \Sigma, {\bf \pi}) \propto \prod_{n=1}^{N}\prod_{k=1}^{K}[\pi_k N({\bf x}_n|{\bf \mu}_k, \Sigma_k)]^{z_{nk}} \qquad{(9.38)}$

물론 위의 식은 다음 식으로 부터 얻어진 것이다.
- $ p({\bf z})=\prod_{k=1}^{K} \pi^{z_k} $
- $ p({\bf x}|{\bf z}) = \prod_{k=1}^{K} N({\bf x}|{\bf \mu}_k, \Sigma_k)^{z_k} $
우선 결론부터 보고 나서 식을 확인하도록 하자.
$ E $ 단계에서 필요한 $ {\bf Z} $ 의 사후 확률 분포를 구하고 나면 로그 가능도 함수의 평균 값을 고려해야 한다.

$E_{\bf Z}[\ln p({\bf X}, {\bf Z}|{\bf \mu}, \Sigma, {\bf \pi})] = \sum_{n=1}^N \sum_{k=1}^K \gamma(z_{nk})\{\ln\pi_k+\ln N({\bf x}_n|{\bf \mu_k}, \Sigma_k)\}$

위의 식은 앞서 complete 데이터라고 가정한 뒤 얻어진 가능도 함수의 식과 거의 동일하다.
- 단지 $ z_{nk} $ 식이 $ \gamma(z_{nk}) $ 로 변경되었을 뿐이다.
교재에는 식이 어떻게 전개되었는지 설명이 없다.
식 전개를 먼저 좀 보자. 우선 수식 전개에 필요한 식 몇개를 기술한 다음 실제 식을 전개한다.

$E[X+Y] = E[X]+E[Y]$ $p({\bf x}_n|{\bf z}_n) = \prod_{k=1}^K N({\bf x}_n|{\bf \mu}_k, \Sigma_k)^{z_nk}$

이제 식을 전개한다.

$E_{\bf Z}[\ln p({\bf X}, {\bf Z}|\theta)] = E_{\bf Z}[\sum_n\ln p({\bf x}_n, {\bf z}_n|\theta)] = \sum_n E_{\bf Z}[\ln p({\bf x}_n, {\bf z}_n|\theta)]\\\\ = \sum_{n=1}^N E_{\bf Z}[\ln (p({\bf z}_n) p({\bf x}_n|{\bf z}_n, \theta))] = \sum_{n=1}^N E_{\bf Z}[\ln[\prod_{k=1}^K (\pi_k N({\bf x}_n|{\bf \mu}_k, \Sigma_k))^{z_{nk}}]]\\\\ =\sum_{n=1}^N \sum_{k=1}^K E_{z}[(z_{nk})\ln(\pi_k N({\bf x}|{\bf \mu}_k, \Sigma_k))] = \sum_{n=1}^N \sum_{k=1}^K E_{z}[z_{nk}] \ln(\pi_k N({\bf x}_n|{\bf \mu}_k, \Sigma_k))\\\\ =\sum_{n=1}^N \sum_{k=1}^K \gamma(z_{nk})\{\ln\pi_k+\ln N({\bf x}_n|{\bf \mu_k}, \Sigma_k)\}$

$ E[z_{nk}]=\gamma(z_{nk}) $ 는 다음으로 확인 가능하다.

$E[z_{nk}] = \frac{\sum_{ {\bf z}_n} z_{nk}\prod_{k'}[\pi_{k'} N({\bf x}_n|{\bf \mu}_{k'}, \Sigma_{k'})]^{z_{nk'}}}{\sum_{ {\bf z}_n} \prod_j [\pi_j N({\bf x}_n|{\bf \mu}_j, \Sigma_j)]^{z_{nj}}}\\\\ = \frac{\pi_k N({\bf x}_n|{\bf \mu}_k, \Sigma_k)}{\sum_{j=1}^K \pi_j N({\bf x}_n|{\bf \mu}_j, \Sigma_j)} = \gamma(z_{nk})$

이제 얻어진 식으로부터 MLE 를 수행해서 파라미터를 얻는 식을 만들어낸다.
- 뭐, 당연하게도 앞에서 구한 결과와 동일한 식을 얻게 된다.

${\bf \mu}_k = \frac{1}{N_k}\sum_{n=1}^N\gamma(z_{nk}){\bf x}_n$ $\Sigma_k = \frac{1}{N_k}\sum_{n=1}^N \gamma(z_{nk})({\bf x}_n-{\bf \mu}_k)({\bf x}_n-{\bf \mu}_k)^T$ $\pi_k = \frac{N_k}{N}$

9.3.2. K-means 와의 관계 (Relation to K-means)

가우시안 분포를 위한 EM 알고리즘과 K-means 알고리즘은 매우 유사하다.
앞서 살펴보았듯이 K-means 는 경성(hard) 클러스터 방식
- 하나의 샘플이 오로지 하나의 클러스터에만 속하는 구조
EM 은 사후 분포에 대해서 연성(soft) 클러스터 방식을 제공하였다.
- 즉, 각각의 클러스터에 대해 샘플이 속할 확률 값을 표현
또한 K-means 는 각 클러스터에 대해 분산도를 고려하지 않았다.
- 오로지 평균과의 거리로만 고려된다.
- 유클리디안 거리 측정 방식이기 때문
사실 K-means 알고리즘은 $ GMM $ 알고리즘의 특별한 경우를 나타낸다.
- 만약 각각의 가우시안 컴포넌트의 분산 값이 서로 동일하고 독립적이라고 하자. ( $ e{\bf I} $ )
- 이 경우 $ {\bf x} $ 에 대한 확률 분포는 다음과 같게 된다.

$p({\bf x}|{\bf \mu}_k, \Sigma_k) = \frac{1}{(2\pi e)^{M/2}}\exp\left\{-\frac{1}{2e}\|{\bf x}-{\bf \mu}_k\|^2\right\}$

여기서 $ K $ 개의 가우시안 분포를 고려한다면,
responsibility 함수는 다음과 같게 된다.

$\gamma(z_{nk}) = \frac{\pi_k \exp\{-\|{\bf x}_n-{\bf \mu}_k\|^2/2e\}}{\sum_j \pi_j \exp\{-\|{\bf x}_n-{\bf \mu}_j\|^2/2e\}}$

이제 분산 $ e\rightarrow0 $ 이라고 하자.
- 결국 평균만 의미가 있고, 분산 값은 의미가 없어지게 된다.
responsibility 함수는 결국 binary indicator 가 된다.
이제 로그 가능도 함수의 기대값을 살펴보자.

$E_{\bf Z}[\ln p({\bf X}, {\bf Z}|{\bf \mu}, \Sigma, {\bf \pi})] \rightarrow -\frac{1}{2}\sum_{n=1}^N\sum_{k=1}^K r_{nk}\|{\bf x}_n-{\bf \mu}_k\|^2+const$

이 식은 기존의 K-means 에서 정의한 distortion measure (식 9-1)와 계수를 빼고 동일하다.

9.3.3. 베르누의 혼합 분포 (Mixtures of Bernoulli distributions)

지금까지 살펴본 분포에서는 $ {\bf x} $ 가 모두 연속 변수였다.
이제 이산 분포인 베르누이 분포에 대한 혼합 분포를 살펴보도록 하자.
사실 이게 $ HMM $ 알고리즘을 배우는데 초석이 되는 부분이다.
이제 $ D $ 차원의 이항 변수가 있다고 하자. ( $ i=1,…,D $ )
이제 이를 베르누이 분포로 나타내면 다음과 같다.

$p({\bf x}|{\bf \mu}) = \prod_{i=1}^D \mu_i^{x_i}(1-\mu_i)^{(1-x_i)}$

단, $ {\bf x}=(x_1,…,x_D)^T $ 이고 $ {\bf \mu} = (\mu_1,…,\mu_D)^T $ 이다.
이 때의 평균과 공분산을 살펴보자.

$E[{\bf x}] = {\bf \mu}$ $cov[{\bf x}] = diag(\mu_i(1-\mu_i))$

이제 여기서 $ K $ 개의 베르누이 분포가 사용된다고 생각해보자.
이러면 혼한 분포는 다음과 같은 형태가 될 것이다.

$p({\bf x}|{\bf \mu}, {\bf \pi}) = \sum_{k=1}^K \pi_k p({\bf x}|{\bf \mu}_k)$

이 때 $ {\bf \mu} = ({\bf \mu}_1,…,{\bf \mu}_K) $ 이고 $ {\bf \pi} = (\pi_1,…,\pi_K) $ 이다.
물론 각 $ k $ 에 대한 $ {\bf x} $ 에 대한 분포도 다음과 같다.

$p({\bf x}|{\bf \mu}_k) = \prod_{i=1}^D \mu_{ki}^{x_i}(1-{\bf \mu}_{ki})^{(1-x_i)}$

이 때의 평균과 분산은 다음과 같아진다.

$E[{\bf x}] = \sum_{k=1}^K \pi_k{\bf \mu}_k$ $cov[{\bf x}] = \sum_{k=1}^K \pi_k \{\Sigma_k+{\bf \mu}_k{\bf \mu}_k^T\}-E[{\bf x}]E[{\bf x}]^T$ $\Sigma_k = diag\{\mu_{ki}(1-\mu_{ki})\}$

단일 베르누이 분포에서는 분산이 $ diag $ 였지만 혼합 분포는 더 이상 $ diag $ 가 아니다.
계속해서 로그 가능도 함수를 살펴보자.

$\ln p({\bf X}|{\bf \mu}, {\bf \pi}) = \sum_{n=1}^N \ln \left\{\sum_{k=1}^K \pi_k p({\bf x}_n|{\bf \mu}_k)\right\}$

역시나 로그 안에 합(sum)에 관한 식이 들어있다. 이런 경우 닫힌 형태(closed form)가 아님을 이미 확인했다.
따라서 이 경우에도 EM 알고리즘을 도입해야 한다.

마찬가지로 이제 잠재 변수 $ {\bf z} $ 를 도입해야 한다.
- 가우시안 혼합 분포에서 사용한 것과 마찬가지로 $ K $ 개의 상태를 나타내는 1-to-K 형태의 이산 변수이다.
- $ {\bf z}=({\bf z}_1,…,{\bf z}_K)^T $
잠재 변수가 주어졌을 때의 조건부 분포는 간단하게 기술할 수 있다.

$p({\bf x}|{\bf z}, {\bf \mu})=\prod_{k=1}^K p({\bf x}|{\bf \mu}_k)^{z_k}$

잠재 변수의 사전 확률 분포는 다음과 같다.

$p({\bf z}|{\bf \pi}) = \prod_{k=1}^K \pi_k^{z_k}$

이제 EM 알고리즘을 사용하기 위해 로그 가능도 함수 식을 만들어야 한다.

$\ln p({\bf X}, {\bf Z}|{\bf \mu}, {\bf \pi})=\sum_{n=1}^N\sum_{k=1}^K z_{nk}\left\{ \ln\pi_k + \sum_{i=1}^D[x_{ni}\ln\mu_{ki}+(1-x_{ni})\ln(1-\mu_{ki})]\right\}$

이것에 대한 기대값을 계산한다.

$E_{\bf Z}[\ln p({\bf X}, {\bf Z}|{\bf \mu}, {\bf \pi})] = \sum_{n=1}^N\sum_{k=1}^K \gamma(z_{nk})\left\{\ln\pi_k + \sum_{i=1}^D[x_{ni}\ln\mu_{ki}+(1-x_{ni})\ln(1-\mu_{ki})]\right\}$

$ \gamma(z_{nk})=E[z_{nk}] $ 이다. E-Step 에서 계산된다.

$\gamma(z_{nk})=E[z_{nk}] = \frac{\sum_{ {\bf z}_n} z_{nk}\prod_{k'}[\pi_{k'} p({\bf x}_n|{\bf \mu}_{k'})]^{z_{nk'}}}{\sum_{ {\bf z}_n} \prod_j [\pi_{j} p({\bf x}_n|{\bf \mu}_j)]^{z_{nj}}} = \frac{\pi_k p({\bf x}_n|{\bf \mu}_k)}{\sum_{j=1}^K \pi_j p({\bf x}_n|{\bf \mu}_j)}$

로그 가능도 함수의 기대값 수식 내에서 responsibility 함수가 사용되는 영역은 다음밖에 없다.

$N_k = \sum_{n=1}^N \gamma(z_{nk})$ $\bar{\bf x}_k = \frac{1}{N_k}\sum_{n=1}^N \gamma(z_{nk}){\bf x}_n$

M-Step 에서는 파라미터에 대한 추정을 한다.
- 증명은 생략한다. 간단하게 기술해보자.

${\bf \mu}_k = \bar{\bf x}_k$ $\pi_k = \frac{N_k}{N}$

교재에는 나오지 않지만 다항 분포(multinomial distribution)에 대해서도 동일한 방식으로 식 전개가 가능하다.

베르누이 혼합 분포의 예제

figure9.10a

위의 예제는 숫자 인식을 위한 데이터로 5개의 데이터가 주어졌다.
쉽게 알 수 있듯 2,3,4 와 같은 값을 결정해야 한다.
EM 알고리즘을 이용하여 이를 분류해보자. $ K=3 $ 을 가정하고 전개하자.
총 600개의 데이터를 이용한다. (물론 숫자는 2,3,4 뿐이다.)
초기 $ \pi_k=1/K $ 로 시작한다.
이미지 벡터는 0과 1로 값으로 gray-scale 을 표현한다.
- 이 둘을 구분짓는 확률 값은 0.5로 정의한다.
EM 을 수행하기 위해서는 해당 필드에 대한 확률의 기대(평균) 값이 필요하다.
- (0.25, 0.75) 사이의 범위에서 랜덤하게 하나를 선택하여 시작하도록 하자.
공액 사전 분포로는 베타 분포(beta)를 사용하였다.

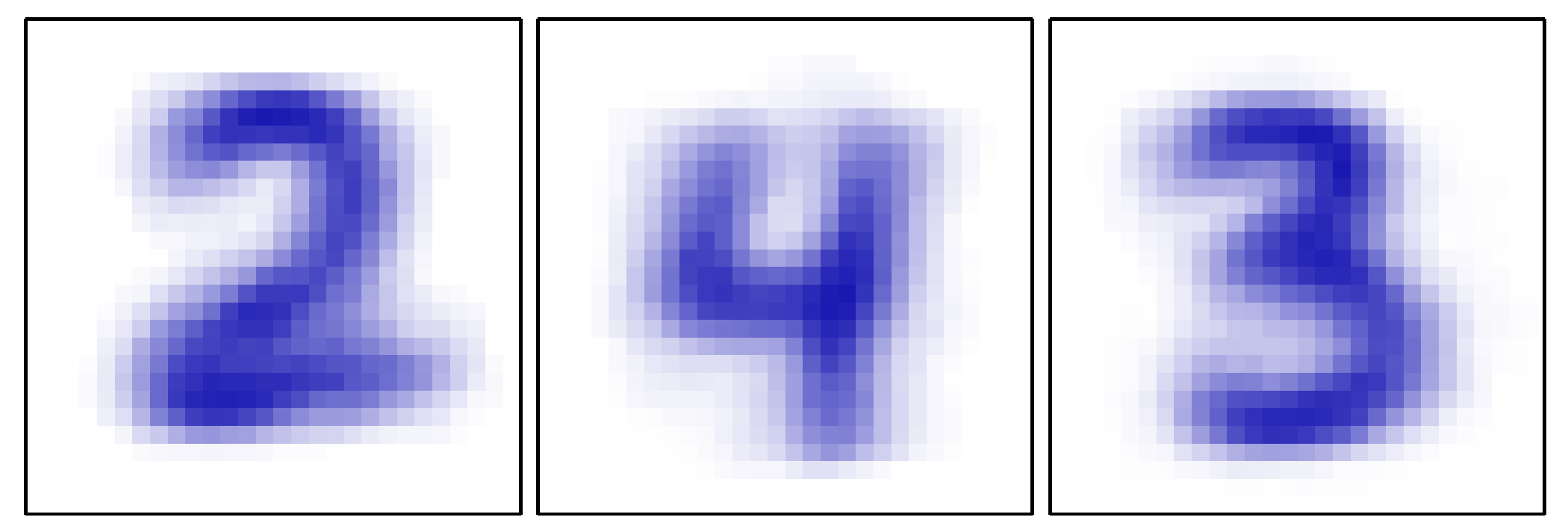
figure9.10b

위의 그림은 3개의 클러스터로 나누어진 후에 각각의 평균값으로 그림을 표현한 것이다.
- 대충 들어맞는 느낌이 있다.

figure9.10c

위의 경우는 $ K=1 $ 인 경우이다.
- 이 때에는 전체 샘플에 대한 평균 값으로 처리되게 된다.
- 따라서 위의 이미지는 샘플 이미지의 평균 이미지

9.3.4. 베이지안 선형 회귀 EM (EM for Bayesian linear regression)

이번 절은 꽤나 독특한데 앞서 살펴보았던 GMM 처럼 혼합 모델이 아닌 모델에 대한 EM 적용을 다루고 있다.
- 결국 이러한 기법이 결국 다음 절의 EM 알고리즘의 일반화 과정까지 이어지게 된다.
마지막 EM 에제로 앞장에서 다루었던 베이지안 선형 회귀(Bayesian linear regression) 를 다루어보자.
- 생각이 나지 않는다면 3.5.2 절을 참고하도록 하자.
여기에는 하이퍼-파라미터(초모수) $ \alpha $ 와 $ \beta $ 가 사용된다.
- 우리는 EM 알고리즘을 이용하여 이 초모수를 예측하게 될 것이다.
잠시 기억을 떠올려보자.
- 보통 초모수의 값은 사용자가 임의대로 지정하게 되는데,
- 주어진 샘플을 이용하여 가장 적절한 초모수 값을 선택하는 방법도 가능하다.
  - 즉, 예측 모델(predictive model)의 형태로, 주어진 데이터를 통해 초모수를 지정하고 새로운 데이터를 추정하는 문제.
  - 3.5.2절이 이와 관련된 내용이었다.
- 이를 위해 evidence 함수 $ p({\bf t}|\alpha, \beta) $ 를 최대화하는 $ \alpha $ 와 $ \beta $ 를 수식으로 찾아내는 과정이 있었다.
- 이 때 실제 파라미터 $ {\bf w} $ 가 없는 이유는 주변화(marginalize) 되었기 때문.
- 이거 어디서 많이 보던 스타일이었다. (즉, EM 알고리즘과 동일한 형태이다.)
- 이제부터 최적의 $ \alpha $ 와 $ \beta $ 를 구하기 위한 EM 기법을 살펴보도록 하자.
  - 이제 우리가 모수로 사용했던 $ {\bf w} $ 가 잠재 변수 $ {\bf Z} $ 역할을 수행하고 초모수 $ \alpha $ , $ \beta $ 가 파라미터로 사용된다.
E-Step 에서는 $ {\bf w} $ 에 대한 사후 분포를 구하게 되고, (이 때 $ \alpha $ 와 $ \beta $ 는 고정)
M-Step에서는 로그 가능도 함수의 기대값을 최대화하는 $ \alpha $ 와 $ \beta $ 값을 구하게 된다.
이제 가장 먼저 로그 가능도 함수를 설계해야 한다. ( $ E[\ln p({\bf t}, {\bf w}| \alpha, \beta)] $ )

$\ln p({\bf t}, {\bf w}| \alpha, \beta) = \ln p({\bf t}|{\bf w}, \beta)+\ln p({\bf w}|\alpha)$

이 때 $ p({\bf t}|{\bf w}, \beta) $ 와 $ p({\bf w}|\alpha) $ 는 (식3.10)과 (식3.52) 에 기술되어 있다.

$p({\bf t}|{\bf X}, {\bf w}, \beta) = \prod_{n=1}^N N(t_n|{\bf w}^T\phi({\bf x}_n), \beta^{-1})$ $p({\bf w}|\alpha) = N({\bf w}|0, \alpha^{-1}{\bf I})$

이제 최종적으로 로그 가능도 함수의 기대값을 기술하자.

$E[\ln p({\bf t}, {\bf w}|\alpha, \beta)] = \frac{M}{2}\ln\left(\frac{\alpha}{2\pi}\right) - \frac{\alpha}{2}E[{\bf w}^T{\bf w}]+\frac{N}{2}\ln\left(\frac{\beta}{2\pi}\right) - \frac{\beta}{2}\sum_{n=1}^N E[(t_n-{\bf w}^T\phi_n)^2]$

이를 미분하여 식을 만들면 된다. M-Step 에서 초모수의 값을 보정하게 된다.

$\alpha = \frac{M}{E[{\bf w}^T{\bf w}]}=\frac{M}{m_N^T m_N+Tr(S_N)}$

이건 3장에서 얻어진 식과는 조금 다르다.
- 하지만 이 식도 결국 $ M\times M $ 행렬의 역행렬 연산과 관련이 있기 때문에 반복에 따른 비용은 비슷하다.
수식을 편하게 전개하기 위해 3.5.2절에서 했던 것처럼 quantity $ \gamma $ 를 정의한다.

$\gamma = M-\alpha\sum_{i=1}^M\frac{1}{\lambda_i+\alpha} = M - \alpha Tr(S_N)$

사실 이 식은 (식3.92)에서 사용했던 방식으로 해도 얻을 수 있다.

$a{\bf m}_N^T{\bf m}_N = \gamma = M- \alpha Tr(S_N)$

이후 $ \beta $ 를 전개하면 3.5.2절에서 보았던 것과 동일한 결과를 얻는다.

EM을 이용하여 베이지언 선형 회귀의 초모수 값 결정하기

E-Step
- responsibilities 계산 : 잠재변수 $ {\bf w} $ 의 값을 결정한다.
- $ p({\bf w} | {\bf t}, \alpha, \beta) = N({\bf w} | {\bf m}, S) $
- $ m=\beta S\Phi^T{\bf t} $
- $ S^{-1}=\alpha{\bf I}+\beta\Phi^T\Phi $
M-Step
- $ \alpha^{-1} = \frac{1}{M}({\bf m}^T{\bf m}+Tr(S)) $
- $ \beta^{-1} = \frac{1}{N}\sum_{n=1}^N {t_n-{\bf m}^T\phi({\bf x}_n)}^2 $
RVM(Relevance vector machine) 회귀는 교재에 간단히 언급되나 생략함.

Chapter. 9

9.3.1. 가우시안 혼합분포 다시 보기 (Gaussian mixtures revisited)

9.3.2. K-means 와의 관계 (Relation to K-means)

9.3.3. 베르누의 혼합 분포 (Mixtures of Bernoulli distributions)

9.3.4. 베이지안 선형 회귀 EM (EM for Bayesian linear regression)