3. Markov Random Fields

• 지금까지 우리는 방향성 그래프 모델을 살펴보았다.
• 이제부터는 방향성 그래프만큼 유명한 비방향성 그래프 모델을 살펴볼 것이다.
• 가장 대표적인 모델로 Markov Random Field 라는 모델을 살펴볼 것이다.
  • 흔히 Markov network 또는 비방향성 그래프라고 알려져있다.
• 일단 바로 시작하지 말고 교재에 나오지 않는 간단한 내용들을 먼저 확인해보고 가자.
  • 왜 이런 내용을 먼저 설명하지 않고 시작하는지 모르겠다.
• factor
  • 일단 시작하기 전에 factor 라는 개념부터 이해하고 있어야 한다.
  • 정의부터 살펴보자.
    • \(\{X_1, … X_k\}\) : 랜덤변수의 집합
    • factor \(\psi(X_1, … X_k)\) : 랜덤변수의 집합을 파라미터로 받는 함수(혹은 테이블)이라고 볼 수 있다.
    • \(\psi : f(X_1, … X_k) \rightarrow R\) 로 생각하면 쉽다.
  • factor 의 예
    • 결합 분포(joint distribution) : 랜덤변수 값의 조합에 대한 확률값의 함수. \(P(A, B, C)\)
    • 조건부 확률 분포(conditional probability distribution) : \(P(A, B | C)\)
    • 보면 알겠지만 앞서 살펴보았던 조건부 확률조차 모두 factor의 예임을 알 수 있다.
  • factor 와 관련된 주요 용어 및 기능들
    • general factors
      • 확률의 개념에 해당하지 않는 녀석들.
      • 일반적인 함수라고 생각하면 된다. Markov random field 에서 등장한다.
    • factor product
    • factor marginalization
    • factor reduction
• undirected graphical model (a.k.a. Markov random field, Markov network)
  • 노드들의 집합, 링크들의 집합으로 구성된다.
  • 노드(node) : 변수 or 변수들의 그룹.
  • 링크(link) : 노드들의 pair 를 연결. undirected (즉, 화살표 없음).
• Pairwise Markov Networks
  • 비방향성 그래프
  • 노드(node) : 랜덤변수(r.v.) \(X_1, … X_n\)
  • factor : \(\phi_{ij}(X_i, X_j)\) 는 \(X_i - X_j\) 를 잇는 각 링크와 연관된다.
  • 이 요인을 potential function 이라고도 한다.
• factor product
  • factor 의 곱을 의미하며 확률 함수처럼 정규화되어 있지는 않다. (합이 1이라는 정규화)
  • \(\tilde{P}(A, B, C, D) = \phi_1(A,B) \times \phi_2(B, C) \times \phi_3(C, D) \times \phi_4(A,D) \)
  • 즉 실제 값이 \(0.0\) ~ \(1.0\) 사이의 값도 아니고, 다 더해도 \(1\)이 아니다.
  • 이를 확률로 해석할 수 있을려면, 정규화 과정을 거쳐야 한다.
• \(P(A, B, C, D) = \frac{1} {Z} \tilde{P}(A, B, C, D)\)
  • 위 예제에서 확률분포 \(P(A,B)\) 와 factor \(\phi_1 (A,B)\) 를 같은 개념으로 보면 안된다.
• 모든 분포를 Pairwise Markov Network 으로 표현될 수 있는 건 아니다.
  • 랜덤 변수 \(\{X_1, … X_n\}\), 각 랜덤변수 \(X_i\)는 \(d\)가지 값을 가질 수 있을 때,
  • fully connected pairwise Markov network가 가질 수 있는 파라미터 수(테이블 엔트리의 수) :
    • \(O(n^2d^2) \;«\; O(d^n)\)

8.3.1 Conditional independence properties

• 방향성 그래프에서는 노드의 조건부 독립(conditional independence) 속성 여부를 d-separation 을 통해 확인하였다.
• 이 과정은 두 노드와 관련된 집합이 차단(blocked)되어 있는지를 확인하는 방식인데 실제 사용하기엔 복잡하다.
  • head-to-head 등을 확인하기가 까다롭다.
• 이와는 반대로 비방향성 그래프 모델은 노드간 조건부 독립 여부를 확인하기 쉽다.
  • 간단하게 그래프 분할을 통해 확인이 가능하다.
• 조건부 독립성 테스트.

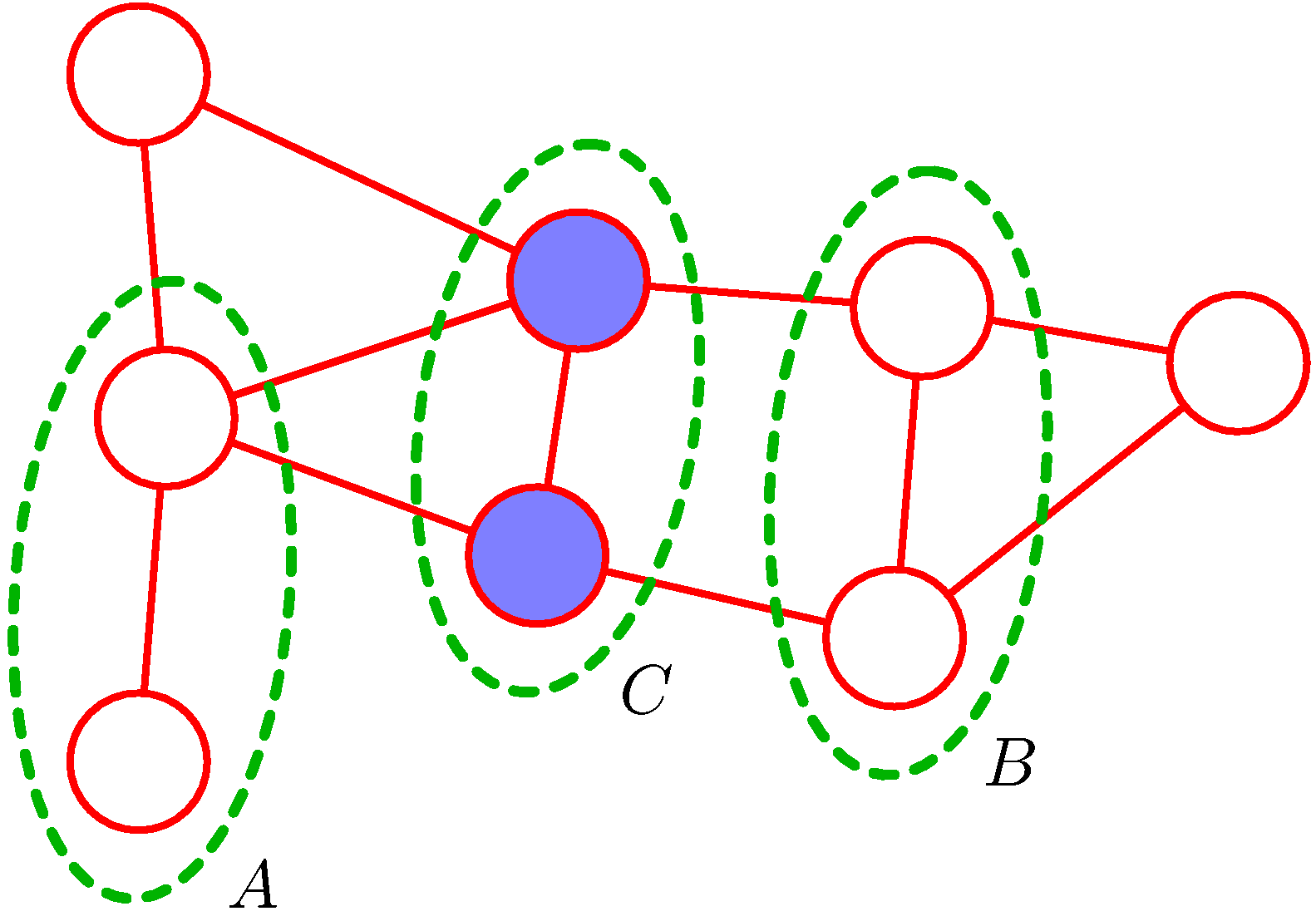
• 비방향성 그래프에서 노드 집합 A, B, C 의 조건부 독립 속성 판별하기.
• 그림만 봐도 한눈에 무얼 하려고 하는 것인지 쉽게 알 수 있다.
• 그림에서는 아래와 같은 조건이 만족된다.

• 이제 어떻게 이를 확인할 수 있는지 살펴보도록 하자.
• 방법 1 : 차단(block) 여부로 판정
  • 집합 \(A\)의 노드들과 집합 B의 노드들을 연결하는 모든 경로를 고려한다.
  • 경로가 집합 \(C\)의 하나 혹은 여러 개의 노드를 통과한다면, 경로가 차단된 것(blocked).
  • 모든 경로가 차단된 상태이면, 조건부 독립 속성을 만족한다 (그림 8.27).
  • 하나라도 차단되지 않은 경로가 있으면, 조건부 독립이 반드시 성립된다고 볼 수 없다.
  • 엄밀히 말하면, 적어도 그래프에 상응하는 분포 중에 어떤 것들이 해당 조건부 독립 관계를 만족하지 않는다는 뜻.
  • 이는 d-separation creterion 과 같은 방식.
  • 다만 explaining away 현상은 없어, 방향성 그래프(directed graph)보다 테스트가 간단하다.
• 방법 2 : 집합 \(C\)의 모든 노드를 삭제해 보기
  • 집합 \(C\) 에 속한 모든 노드와, 해당 노드에 연결되어 있는 모든 링크를 삭제한다고 상상해보자.
  • \(A\) 에 속한 노드와 B에 속한 노드를 연결하는 경로가 하나도 남아있지 않으면, 조건부 독립 속성을 만족하는 것.
  • 이런 경우 \(C\)가 주어진 상태에서 \(A\)와 \(B\)가 분리된다(separate)라고 한다.

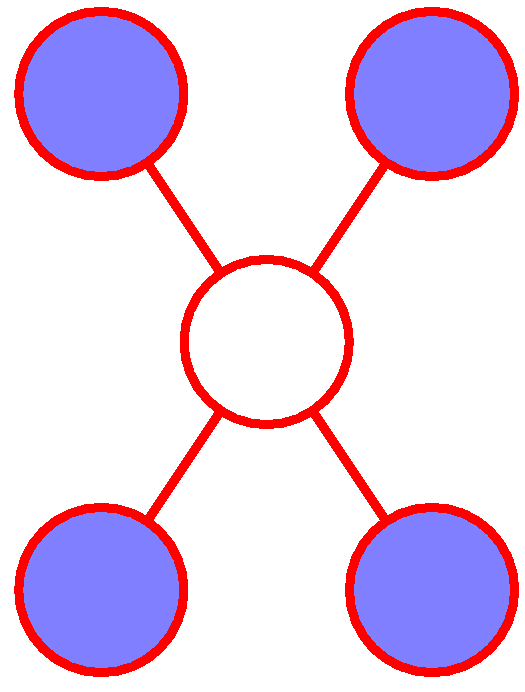
• 비방향성에서는 조건부 독립을 확인하는 것이 무척 쉽다.
• 그림에서 중앙의 노드는 이웃 노드를 조건으로 하는 모든 노드들에 대해 조건부 독립이다.

8.3.2 Factorization properties

• 조건부 독립 테스트에 부합하는 비방향성 그래프의 인수분해 규칙(factorization rule)을 찾아본다.
• 인수분해 과정에서, 결합 분포 p(x)를 그래프에 국한된(local to the graph) 변수 집합에 대한 함수의 곱으로 표현해야 한다.

• 지역성(locality)의 개념을 적절히 표현할 방법이 필요하다 (clique).

• Markov network에서의 인수분해(factorization)
  • \(I(P)\) : P가 만족하는 모든 조건부 독립 속성의 집합
  • \(I(P) = { (X \perp\!\!\!\perp Y | Z) : P \models (X \perp\!\!\!\perp Y | Z)}\)
• Gibbs distributon ( \(\Psi\) ) :
  • general factor \(\psi_i(D_i)\)의 조합을 모아놓은 것. \(\Psi = { \psi_i(D_i) }\)
  • 분포를 factor 곱으로 표현한 형태이다.
  • Gibbs distribution이 주어져 있으면, 이로부터 Markov network 을 유도하여 만들어낼 수 있다.
  • 아래 그래프를 유도하는 Gibbs distribution의 예
    • \(\{\psi_1(x_1, x_2, x_3), \psi_2(x_2, x_3, x_4)\}\)
    • \(\{\psi_1(x_1, x_2), \psi_2(x_2, x_3), \psi_3(x_3, x_4), \psi_4(x_1, x_3), \psi_5(x_2, x_4)\}\)
    • \(\{\psi_1(x_1, x_2, x_3), \psi_2(x_3, x_4), \psi_3(x_2, x_4)\}\)

• Gibbs distribution \(\Psi\) 로부터 그래프 \(G\)를 유도할 수 있고,
• \(\Psi\) 집합에 있는 모든 원소에 대한 normalized product \(P_{\Psi}\) 가 분포 P 와 같을 때
  • 분포 \(P\)가 그래프 \(G\)로 인수분해(factorization) 된다고 한다.

조건부 독립 속성

• 두 노드 \(x_i\), \(x_j\)를 직접 연결하는 링크가 없는 경우를 생각해 보자.
• 이 변수들은 그래프의 모든 다른 노드들이 주어진 상태에서 조건부 독립이어야 한다.
• 두 노드 사이를 직접 연결하는 경로(direct path)가 없고,
• 다른 경로들이 통과하게되는 노드들은 관측된(observed) 노드(즉, 이 경로들은 차단되어 있음(blocked))
• 이 때, 조건부 독립 속성은 다음과 같이 표현된다.

• 단 \(\textbf{x}_{ \backslash {i,j} }\) : 변수 집합 x에서 \(x_i\), \(x_j\) 를 뺀 나머지.

Clique

• 식(8.38)의 형태를 보아하니, 결합 분포 \(p(x_i, x_j)\)를 인수분해 하였을 때, \(x_i\), \(x_j\) 는 같은 요인(factor)에 나타날 수 없다.
• 이로부터 clique 이라는 개념이 등장하게 된다.
• clique
  • 그래프 노드들의 부분집합
  • 이 부분집합의 노드들은 fully connected 상태여야 한다. -즉, 모든 노드의 pair 사이에 링크가 존재해야 한다.
  • maxlmal clique : 더 이상 노드를 추가하게 되면 clique 이 깨지게 되는 경우.
• 그림을 보면서 확인해보자.

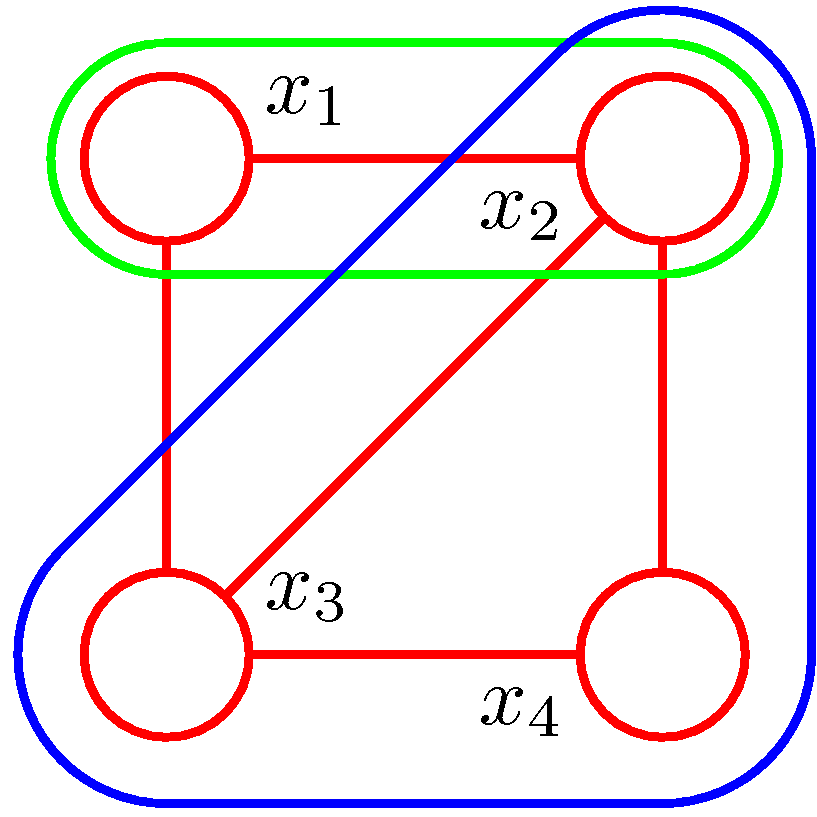
• 2개의 노드로 구성된 clique : \(\{x_1, x_2\}, \{x_2, x_3\}, \{x_3, x_4 \}, \{x_4, x_2 \}, \{x_1, x_3 \}\)
• maximal clique : \(\{ x_1, x_2, x_3 \}, \{ x_2, x_3, x_4 \}\)

• 여기서 \(\{ x_1, x_2, x_3, x_4 \}\) 는 clique가 아님 (\(x_1 - x_4\) 가 없으니까)

• 결합 분포의 분해(decomposition)
  • 결합 분포를 분해하면, 각 요인(factor)들은 clique에 속한 변수들의 함수.
  • maxlimal clique 들의 함수들을 사용하여 결합분포를 분해할 수 있다.
  • subset인 clique의 factor들은 정의해봤자 redundant하다.
  • 이미 maxlimal clique 의 factor에 포함되어 있음.
• clique 에 속한 변수 집합들의 결합 분포

• \(\textbf{x}_C \): clique \(C\)에 속해있는 변수 집합
• maximal clique에 대한 potential function \(\psi_C(\textbf{x}_C)\) 의 곱으로 표현된다.
• \(Z\) : 정규화 상수. partition function 이라고도 한다.

• \(p(\textbf{x}) \geq 0\) 임을 보장하기 위해, \(\psi_C(\textbf{x}_C) \geq 0 \) 인 경우만을 고려한다.

potential function의 해석

• 딱히 어떤 형태의 함수를 선택해야 한다는 제약이 없다
• 특정 확률적 해석이 없다(조건부 분포, 주변 확률 분포 등으로 굳이 해석되지 않아도 된다).
• 방향성 그래프에서는 각 요인이 변수들의 조건부 분포(확률)였던 것과 대비된다.
• 정규화 제약이 없어 potential function 형태를 유연하게 선택할 수 있다.
  • 이 말은 응용 애플리케이션에 따라 적절한 potential function을 선택해야 한다는 말.
• 방향성 그래프로부터 비방향성 그래프를 만들어내는 경우엔, potential function 이 조건부 확률 형태로 해석될 수도 있다.

정규화 상수(partition function)

• 비방향성 그래프의 주된 한계점은, 정규화 상수가 존재한다는 것이다.
• \(K\) 개의 상태(state)를 가진 M개의 이산 노드 모델에서 정규화 텀의 계산
• \(K^M\) 개의 상태에 대해 합을 계산해야 한다.
• 최악의 경우 계산량이 모델 크기에 exponential하게 증가.
• partition function이 필요한 경우도 있지만, 그렇지 않은 경우도 있다.
  • 필요한 경우
    • parameter learning.
  • 필요하지 않은 경우
    • 지역 조건부 분포(local conditional distributions)을 구할 때 : 두 주변 확률의 비율(ratio)로 계산할 수 있다. 계산과정에서 정규화 상수가 없어짐.
    • 지역 주변 확률(local marginal probabilities)을 구할 때 :
      • 정규화 안된 결합 분포(unnormalized joint distribution)를 사용하여 계산
      • 마지막에 명시적으로 정규화.

조건부 독립과 비방향성 그래프의 인수분해의 관계

• \(\psi_C(\textbf{x}_C) > 0\)(strictly positive) 으로 제한한다.

(그림 8.25) 그래프 모델을 필터로 활용하는 컨셉. 모든 가능한 분포의 집합이 고정된 변수 집합에 대해 정의되어 있고, 변수들은 특정 비방향성 그래프의 각 노드에 해당될 경우, \(\mathcal{UI}\) : 조건부 독립 특성을 만족하는 분포들의 집합 \(\mathcal{UF}\) : 그래프의 maxlimal clique 들에 대해, 식(8.39)의 형태로 인수분해되는 분포들의 집합 으로 정의했을 때, \(\mathcal{UI}\), \(\mathcal{UF}\)는 같다고 한다 Hammersley-Clifford theorem \(I(G) \subseteq I(P)\) 이면, P는 G로 인수분해 된다. Bolzmann distribution : potential function이 strictly positive 하다고 제한했기 때문에, exponential 형태로 표현하면 편하다. \(\psi_C(\textbf{x}_C) = \exp {-E(\textbf{x}_C) } \,\,\,\, (8.41)\) \(E(\textbf{x}_C)\) : 에너지 함수(energy function) 총 에너지 : 결합 분포 : potential들의 곱 -> 총 에너지 : 모든 maximal clique들의 에너지를 합하면 된다. 8.3.3 Illustration: Image de-noising 예제: binary image에서 노이즈 제거 관측된 노이즈 포함된 이미지: 이진 픽셀값의 배열로 표현. \(y_i \in {-1, +1 }\) i= 1,…, D 노이즈 없는 원본 이미지: \(x_i \in {-1, +1 }\) i= 1,…, D 노이즈 : 어떤 작은 확률로 랜덤하게 해당 픽셀의 부호를 뒤집는 것으로 표현한다. 목표 : 주어진 노이즈 낀 이미지를 복구하여 원본인 노이즈 없는 이미지를 얻는 것.

Markov random field model 사전 지식 노이즈 확률이 작으므로, \(x_i\)와 \(y_i\) 사이에 강한 상관관계가 존재. 원본 이미지의 인접한 픽셀 \(x_i\), \(x_j\) 사이에도 강한 상관관계가 존재. 이를 종합하면, 다음과 같이 비방향성 그래프를 사용하여 표현할 수 있다.

그래프는 두 가지 타입의 clique 으로 이루어져 있다( $ { x_i, y_i }, { x_i, x_j }$ ). 각 clique 에서 원소간의 관련성을 에너지 함수로 표현할 수 있다. \({ x_i, y_i }\) 의 에너지 함수 : \(-\eta x_i y_i\) (\(\eta\)는 0보다 큰 상수) \(x_i\), \(y_i\) 가 같은 부호이면 작은 에너지를 부여(더 높은 확률). \(x_i\), \(y_i\) 가 다른 부호이면 큰 에너지를 부여. \({ x_i, x_j }\) 의 에너지 함수 : \(-\beta x_i x_j\) (\(\beta\)는 0보다 큰 상수) \(x_i\), \(x_j\) 가 같은 부호이면 작은 에너지를 부여(더 높은 확률). \(x_i\), \(x_j\) 가 다른 부호이면 큰 에너지를 부여. 모델 전체(maximal clique)의 에너지 함수 : 부분집합의 에너지들을 더한다. \(E(\textbf{x}, \textbf{y}) = h \sum_i x_i - \beta \sum_{{i, j }} x_i x_j - \eta \sum_i x_i y_i \,\,\,\, (8.42)\) \(hx_i\) : bias 역할. 픽셀값의 부호가 어떤 한 쪽을 더 선호하도록 하는 효과(0이면 두 상태를 동등하게 취급). 결합 분포 : \(p(\textbf{x}, \textbf{y}) = \frac{1} {Z} \exp { -E(\textbf{x}, \textbf{y}) } \,\,\,\,(8.43)\) 조건부 분포 \(p(\textbf{x} | \textbf{y})\) : 노이즈 낀 이미지이 픽셀값으로 y 를 고정. 참고 : 이징 모델(Ising Model) 위의 에너지 함수는 이징 모델의 한 형태로 해석될 수 있다. (통계 물리학에서 다루는 모델인 듯.. 자세히 다루진 않겠다.) 일정 간격으로 입자들이 고정되어 있다. 각 입자는 이산 변수 \(\sigma_k \in { -1, +1 } \)로 표현된다. 입자들은 서로 가장 근접해 있는 입자들과만 상호작용을 한다. 주기적 경계 조건(1번째 입자와 N+1 번째 입자는 같다) 도입. 이 때, 에너지는 다음과 같은 헤밀토니안 함수로 주어진다. \(H(\sigma) = - \sum_{ {i,j}} J_{ij} \sigma_i \sigma_j -\mu \sum_{j} h_j\sigma_j \) 이미지 복구 과정 - 순차적 방법 목표 : 확률을 (가능하면) 최대화 하는 이미지 x 를 찾기(에너지는 최소화). 방법 : iterated conditional modes : 간단한 iterative scheme ICM : coordinate-wise gradient ascent \({x_i}\) 초기화: \(x_i = y_i\) 한번에 노드 하나씩 꺼내서(\(x_j\)), 노드의 두 가지 가능한 상태(\(x_j = +1\), \(x_j = -1\)) 에 대해 전체 에너지를 계산한다. 이 때 다른 노드들은 모두 고정. 간단한 지역적 계산법이라 효율적. 전체 에너지가 더 낮은 쪽으로 \(x_j\) 값을 설정한다. \(x_j\)가 그대로이면, 확률도 그대로. \(x_j\)가 바뀌면, 확률이 더 높아진다. 위 과정을 다른 위치에 대해서도 반복한다. 적절한 stopping criterion이 만족되면 멈춘다. local maximum 과 global maximum 순차적 방법으로 계산했을 때, 모든 위치에 대해 적어도 한번씩 방문하여 순차적 업데이트를 수행했고, 변수들이 더 이상 변하지 않는 지점에 이르면, 확률의 local maximum 값으로 수렴한 것(global maximum이라는 보장은 없다). 나중에 좀더 효율적인 알고리즘을 소개하는데, graph cuts 기반 알고리즘의 경우 global maximum 찾는 것을 보장한다. 8.3.4 Relation to directed graphs 방향성 그래프를 비방향성 그래프로 전환하기 비방항성 그래프의 clique potential 들을 방향성 그래프의 조건부 분포 식으로부터 도출할 수 있으면 된다. 이를 위해, 조건부 분포 각각이 적어도 한 clique의 멤버가 되는 형태로 만들어야 한다. 이런 전환 과정은 각종 추론(inference) 테크닉에서도 중요한 역할을 한다(예 : junction tree algorithm). 예제1: 각 노드당 부모 노드가 하나씩만 존재하는 경우

각 노드당 부모 노드가 하나씩만 존재하는 경우엔, 간단히 방향성 링크를 비방향성 링크로 바꾸기만 하면 된다. 방향성 그래프에서 표현하는 결합 분포 : 조건부 확률의 곱 \(p(\textbf{x}) = p(x_1)p(x_2|x_1)p(x_3|x_2) … p(x_N|x_{N-1}) \,\,\,\, (8.44)\) 비방향성 그래프 표현으로 변환했을 때의 결합 분포(8.39 기반) \(p(\textbf{x}) = \frac{1} {Z} \psi_{1,2}(x_1, x_2) \psi_{3,4}(x_3, x_4) …\psi_{N-1,N}(x_{N-1}, x_N) \,\,\,\, (8.45)\) \(\begin{align} \psi_{1,2}(x_1, x_2) & = p(x_1)p(x_2|x_1) \ \psi_{2,3}(x_2, x_3) & = p(x_3|x_2) \ \vdots \ \psi_{N-1,N}(x_{N-1}, x_N) & = p(x_N|x_{N-1}) \end{align}\) 주변 확률 p(x_1) 을 첫번째 potential function에 넣어 흡수. partition function Z=1. 예제2: 부모 노드가 하나 이상인 경우

부모 노드가 하나 이상인 경우(즉 ‘head-to-head’ 경로가 존재하는 경우)엔, 단순히 방향성 링크를 비방향성 링크로 바꾸는 것만으로는 충분하지 않다. 방향성 그래프에서 표현하는 결합 분포: \(p(\textbf{x}) = p(x_1)p(x_2)p(x_3)p(x_4 | x_1, x_2, x_3) \,\,\,\, (8.46)\) 비방향성 그래프로의 변환 식 (8.46)을 보면, 요인 \(p(x_4 | x_1, x_2, x_3)\) : 네 개의 변수에 대한 식이다. 조건부 분포를 한 clique potential 로 흡수하기 위해선, 이 네 변수가 모두 단일 clique에 포함되어야 한다. 이를 위해 노드 \(x_4\) 의 부모 노드 사이에 링크를 추가한다. moralization(부모끼리 결혼시키기?;). 이 과정으로 화살표를 모두 없앤 결과물을 moral graph 라고 한다. 예제의 moral graph fully connected 방향성 그래프였을 때엔 조건부 독립이었지만, 비방향성 그래프로 바꾸었을 때는 더이상 조건부 독립이 아니다. 일반화 그래프의 각 노드에 대해, 모든 부모 노드의 pair 사이에 비방향성 링크를 추가한다. 원래 링크에 있던 화살표를 제거하여 moral graph를 만든다. moral graph의 모든 clique potential을 1로 초기화 한다. 원래 방향성 그래프의 조건부 분포 요인을 곱해서 clique potential을 구성한다. moralization의 결과, 모든 변수를 담고 있는 maximal clique가 적어도 하나 존재하게 된다. 모든 경우 partition function Z=1. 조건부 독립 방향성 -> 비방향성 그래프 전환 과정에서, 그래프의 일부 조건부 독립 특성이 소실될 수도 있다(예제2). 무조건 fully connected 그래프로 변환해도 되긴 하지만, 모든 조건부 독립 특성을 제거하게 된다(vacuous). 최소한의 링크를 추가해서 되도록 독립 특성을 유지하도록 구성하는 게 좋다. D map 방향성 그래프 / 비방향성 그래프에서 표현되는 조건부 독립 특성이 서로 다르다. 이 문제를 그래프를 filter로 보는 관점(그림 8.25)에 기반하여 살펴보면, (주어진 변수들에 대해 모든 가능한 분포의 집합) -> (그래프) -> (그래프에 표현된 조건부 독립 특성이 반영되어 있는 분포만 걸러져 나옴) 분포 P가 만족하는 모든 조건부 독립 구문들이 그래프 G에 반영되어 있을 때, G는 P의 D map(Dependency map) 이다. \(I(P) \subseteq I(G)\) 예 : 링크가 하나도 없는 completely disconnected graph I map 여러 그래프 중, 특정 분포의 조건부 독립 특성을 가지고 있는 그래프만을 걸러낼 수 있다. (filter 로 작용할 그래프를 선택하는 관점). 그래프 G에 함축되어 있는 모든 조건부 독립 구문들을 분포 P가 만족하는 경우, G는 P의 I map(Independence map) 이다. \(I(G) \subseteq I(P)\) 분포 P가 그래프 G로 인수분해 될 때, G는 P의 I map이다. 예 : fully connected graph 불필요한 링크가 없는 I map을 Minimal I-map 이라고 한다. perfect map 그래프 G가 D map이면서 I map 인 경우, 분포 P에 대한 perfect map 이라고 한다. \(I(G) = I(P)\)

위 그림과 같이, 비방향성 그래프 / 방향성 그래프가 표현할 수 있는 perfect map의 범주에는 차이가 있다. 예제 1 : 비방향성 그래프 형태의 perfect map이 존재하지 않는 분포 분포(P)가 만족하는 조건부 독립 특성: \(A \perp!!!\perp B \,|\, \emptyset\) \(A \perp!!!!!\not\perp B \,|\, C\)

위의 방향성 그래프는 분포 P의 perfect map이다. 그러나, 비방향성 그래프로는 분포 P의 perfect map을 만들 수 없다. 예제 2 : 방향성 그래프 형태의 perfect map이 존재하지 않는 분포 분포(P)가 만족하는 조건부 독립 특성: \(A \perp!!!!!\not\perp B \,|\, \emptyset\) \(C \perp!!!\perp D \,|\, A \cup B\) \(A \perp!!!\perp B \,|\, C \cup D\)

위의 비방향성 그래프는 분포 P의 perfect map이다. 그러나, 방향성 그래프로는 분포 P의 perfect map을 만들 수 없다. chain graph 그래프 프레임웍을 확장하여 방향성 링크와 비방향성 링크를 모두 포함하게 만든 형태를 chain graph 라고 한다. 정리 Markov random field(Markov network) : 비방향성 그래프 모델 pairwise Markov network 조건부 독립 속성 판별 Markov blanket 인수분해 결합 분포를 요인의 곱으로 표현. 정규화 상수(partition function). 조건부 독립 특성과 인수분해의 관계. 비방향성 그래프와 방향성 그래프의 관계 Bayesian network <-> Markov network 변환 과정에서 조건부 독립 속성이 유실될 수 있다. D map, I map, perfect map Bayesian network와 Markov network의 표현력.