1. Bayesian Networks

• 방향성(directed) 그래프가 가지는 장점을 이해하기 위해 우선 세 개의 변수 \( a \) , \( b \) , \( c \) 에 대한 결합 확률 \( p(a,b,c) \) 를 고려해보자.
• 이 문제를 그래프로 표현하는데 별도의 정보들은 필요가 없다.
  • 하나의 랜덤 변수를 노드로 표현하고 이들의 관계를 엣지로 표현한다.
  • 이 변수들이 연속 변수인지 이산 변수인지는 상관이 없다.
• 더불어 그래프 모델이 가지는 장점은 특정 그래프가 분포들의 확률적 상태들을 나타낼 수 있다는 것이다.
• 확률곱 법칙을 이용하여 결합 확률 분포를 다음과 같이 전개할 수 있다.

• 두번째 텀을 계속해서 확률 곱 법칙으로 전개해 보자.

• 이러한 분해는 어떠한 결합 확률 분포에서도 만들어 낼 수 있다.

• 이를 그래프로 나타내면 다음과 같다.

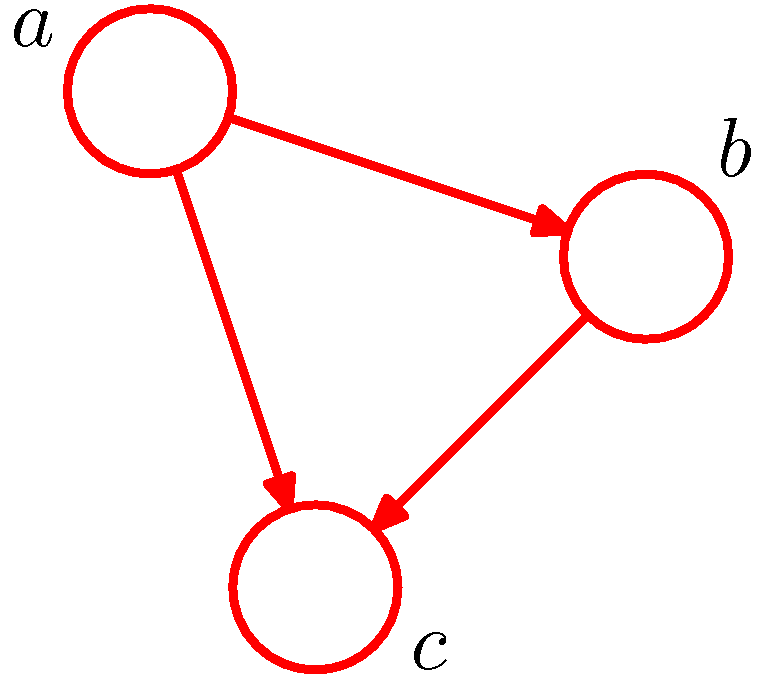
• 그림만 봐도 \( a \) , \( b \) , \( c \) 사이의 결합 확률 분포가 어떻게 구성되어 있는지를 손쉽게 확인할 수 있다.
• 그림에 대해 조금 간단하게 설명하자면,
  • 조건부 확률 분포(conditional distribution) 를 방향성 링크로 표현하고 있다.
  • \( p(c|a,b) \) 와 같은 조건부 확률식은 \( a \) 와 \( b \) 노드에서 \( c \) 노드로의 화살표로 표기되고 있다.
  • \( p(a) \) 자체는 링크로 표현되는 것이 아니라 노드로 표현되고 있다.
  • \( a \) 에서 \( b \) 방향으로 화살표가 가고 있다. 이런 경우 \( a \) 는 \( b \) 의 부모( parent ) 노드라고 한다.
  • 반대로 \( b \) 는 \( a \) 의 자식( child ) 노드라고 한다.
• 한가지 재미있는 사실은 식의 왼쪽 항은 각 랜덤 변수가 대칭인데 반해 오른쪽 항은 그렇지 못하다는 것이다.
  • 사실 반드시 위와 같은 분해만 만들어낼 수 있는 것은 아니고 랜덤 변수의 순서를 달리해서 식을 만들어 낼 수도 있다.
  • 이건 이후에 또 살펴볼 것이다.
• 이제 식을 좀 더 일반화시켜 보자.
• \( K \) 개의 변수를 가지는 결합 확률 분포가 \( p(x_1, …,x_K) \) 로 주어졌을 때, 다음과 같은 식이 성립한다.

• 오른쪽 항과 같은 그래프를 fully connected 그래프라고 하는데 임의의 두 쌍의 노드가 서로 연결되어 있기 때문이다.
• 지금까지 완전히 일반화된 결합 확률 분포를 다루고 있기 때문에 어떤 분포를 사용하던지 상관없이 이러한 분해를 사용할 수 있다.

• 이제 일부 링크가 없는 형태를 좀 살펴보도록 하자.

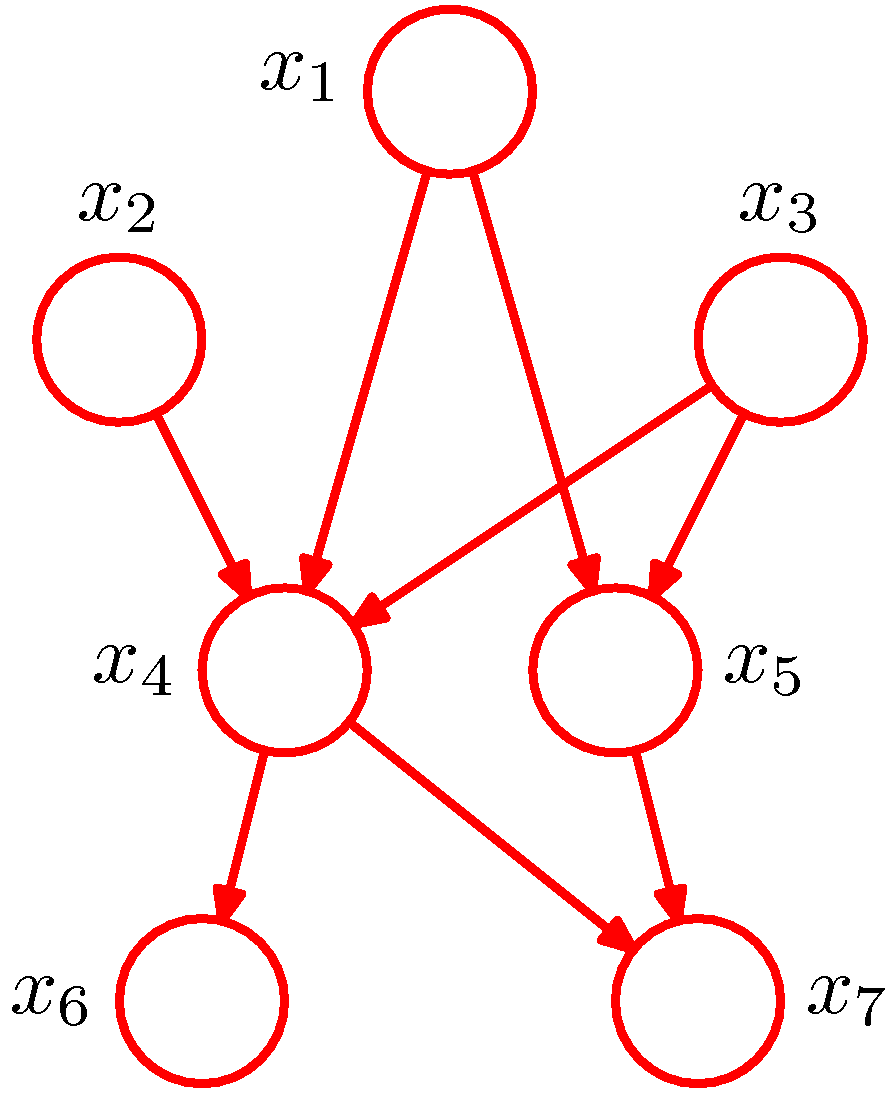
• 이 그래프는 fully connected 된 그래프는 아니다.
  • 예를 들어 \( x_1 \) 에서 \( x_2 \) 로, \( x_3 \) 에서 \( x_7 \) 로 가는 링크가 존재하지 않는다.
  • fully connected 모델은 사용자가 사전 지식이 없는 경우 만들어질 수 있는 모든 관계에 대한 도식을 나타낸 모델이다.
  • 반면 위의 그림처럼 사용자의 개입을 통해 상황에 따라 노드의 관계를 위와 같이 새롭게 구성할 수도 있다.
  • 결국 그래프 <표기>가 아닌 그래프 <모델>인 이유는 사용자가 정의한 모델을 그래프화된 형태로 표현하고 있기 때문.
    • 추가적으로 그래프 자체가 포함하고 있는 가정에 의해서도 모델 속성이 달라지기도 한다.
• 이런 형태로 주어진 그래프에서 결합 확률 \( p(x_1, …,x_K) \) 을 나타낼 수 있을까?
  • \( x_1 \) ~ \( x_7 \) 을 모두 포함하는 확률을 고려하면 된다.
  • 하지만 fully connected 가 아니므로 연결이 없는 확률식은 고려할 필요가 없다. 결국,

• 이것을 일반화한 식은 다음과 같다.

• 여기서 \( pa_k \) 는 \( x_k \) 의 부모 노드의 집합을 의미한다.
• 이 식의 핵심은 방향성 그래프 모델을 위한 결합 확률을 인수분해(factorization)하는 것이다.
• 하나의 노드가 하나의 변수에 매칭되고 있으므로 어떤 변수들의 연관 집합과 그래프의 노드로 표현되는 벡터화된 변수들을 동일하게 취급할 수 있다.

• 식의 좌변에 해당하는 확률은 항상 올바르게 정규화되는데 각각의 조건부 분포가 정규화되어 있기 때문이다.

• 방향성 그래프의 중요한 제약은 이러한 방향성 링크들이 사이클(cycle)을 형성하지 않는다는 것이다.
  • 이걸 다른말로 하면 닫힌 연결(closed path)이 없다는 것이다.
  • 이런 그래프를 DAG(directed acyclic graph)라고 부른다.
  • 이것은 임의의 한 점에서 링크를 따라 노드의 벡터를 구성할 때 한번 방문한 노드를 다시 방문하지 않는다는 의미이다.
• 결국 기존에 사용하던 모델들을 그래프 모델로 전환하여 표현하게 된다고 생각하면 된다.
  • 확률 이론을 이용한 기존의 모델들이 모두 베이지안 그래프 모델로 변환 가능한 것은 아니다.
  • 따라서 다른 그래프 모델, 즉 MRF 와 같은 그래프 모델이 존재하며 상황에 따라 선택할 수 있는 그래프 모델이 달라질 수 있다.

8.1.1. 예제 : 다항 회귀 (Example : Polynomial regression)

• 이제 방향성 그래프를 이용해서 확률 분포를 도식화하는 과정을 살펴보도록 한다.
• 1장에서 설명한 다항 회귀의 예제를 그래프 모델로 표현하도록 한다.
• 예제
  • 다항식의 결정 계수는 \( {\bf w} \) 로 주어지고 타겟 변수는 1차원 데이터로 전체 데이터는 \( {\bf t} = (t_1,…t_N)^T \) 로 주어진다.
  • 입력 데이터는 \( {\bf x}=(x_1,…,x_N)^T \) 이고 노이즈(noise) 는 정규 분포를 따른다. 이 때의 분산값은 \( \sigma^2 \) 이다.
  • 이제 결합 분포를 그래프 모델에 맞도록 기술해보자.

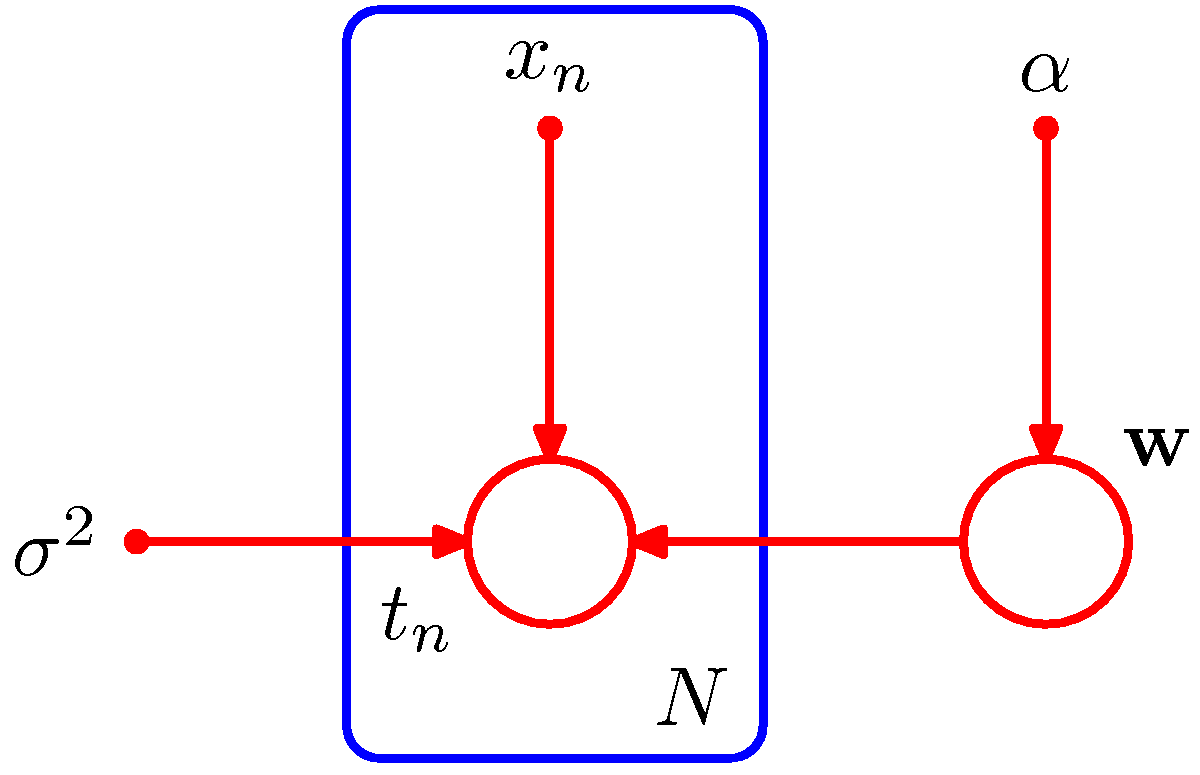
• 이에 대한 그래프 모델의 표현은 다음과 같다.

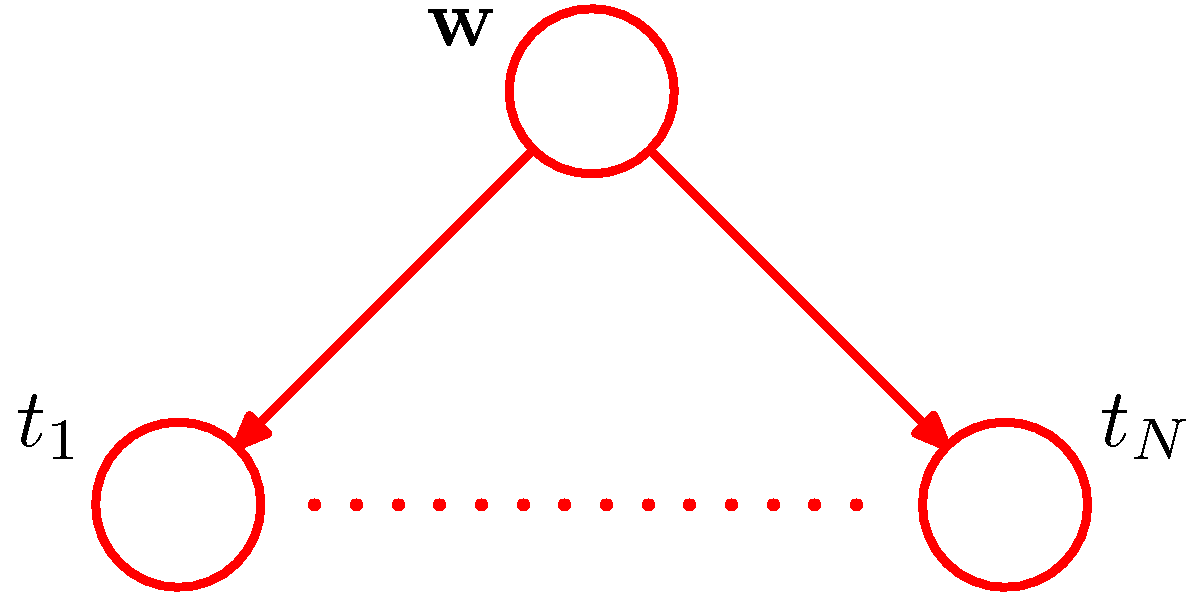
• 좀 더 복잡한 모델은 이후에 더 살펴볼 것이다.
• 그림을 보면 알 수 있듯 \( t_1,,,t_n \) 을 그래프로 표현하는게 그리 깔끔하지는 못하다.
  • 따라서 이를 더 손쉽고 간단하게 표기할 수 있는 방법을 알아보도록 한다.
  • 보통 하나의 그룹으로 표현되는 노드들을 박스 형태로 표기한다. 이를 plate 라고 한다.
  • 여기서는 \( t_n \) 에 속한 모든 \( N \) 개의 노드들을 하나의 박스로 표현 가능하다.

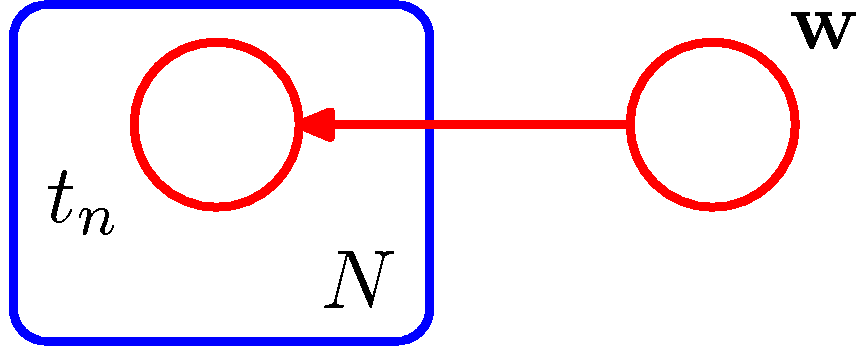
• 가끔씩은 모델의 파라미터와 관련된 확률 변수(stocastic variable)를 함께 표기하기도 한다.
• 따라서 앞에서 나왔던 식을 다음과 같이 기술할 수도 있다.

• 위의 식은 \( {\bf x} \) 와 \( \alpha \) , \( \sigma^2 \) 를 명시적으로 표기하고 있다.
  • 베이지안 추론 방식에서 사용되었던 추가 모수들이 등장했다.
  • 이 모수들도 마찬가지로 값을 얻어내거나 임의로 지정을 해야 하는 값이긴 하다.
  • 하지만 이 변수들은 랜덤 변수가 아니라 이미 값들이 결정되어 있는 변수로 취급받아야 한다.
  • 왜냐하면 이 값을 결정한 뒤에야 주 모수들의 값을 최종적으로 결정할 수 있기 때문이다.
• 따라서 그래프 표현에서는 이러한 변수들을 작은 원(small circle)의 형태로 표기한다.

• 기계 학습에서는 보통 관찰되는 데이터 값을 랜덤 변수로 취급한다.
  • 다항 커브 피팅 문제에서는 \( t_n \) 가 관찰되는 데이터 값이다.
  • 그래프 모델에서는 이를 observed variable 이라고 한다.
  • 반대로 주어진 관찰 데이터로부터 얻어지지 않는 랜덤 변수를 latent variable 이라고 한다.
  • 그림에서는 \( t_n \) 노드는 관찰된 변수(observed variable) 이지만 \( {\bf w} \) 는 은닉 변수(latent varible)가 된다.
    • 이러한 변수를 hidden variable 이라고도 한다.
    • 9장과 12장에서 이와 관련된 내용을 좀 더 심도있게 다루게 될 것이다.

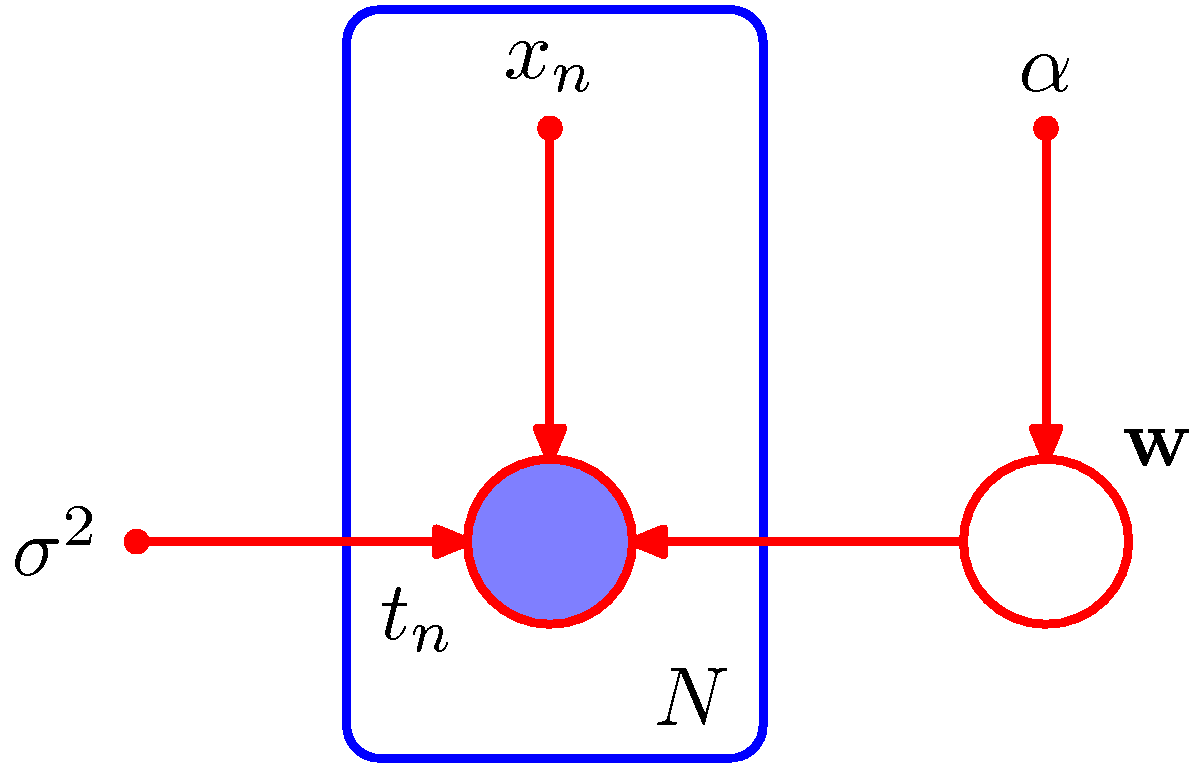
• 위의 그림에서 \( t_n \) 이 관찰된 변수이고, \( {\bf w} \) 가 은닉 변수이다.
  • 관찰되는 변수에 대해서는 음영(shade) 을 넣는다.

• 1.2.5 절에서는 위의 식에서 파라미터의 사후 분포를 구하는 식을 사용하였다. $p({\bf w}|{\bf t}) \propto p({\bf w})\prod_{n=1}^{N}p(t_n|{\bf w}) \qquad{(8.7)}$

• 위의 식에서는 값이 결정된 파라미터( determinstic paramter )는 마찬가지로 간단한 표기를 위해 생략되어 있다.
• \( {\bf w} \) 와 같은 파라미터는 중요한 성질을 가지는 파라미터인데, 새로운 입력 데이터에 대한 결과를 예측하는데 직접적으로 영향을 미치는 파라미터이기 때문이다.
• 새로운 입력 데이터를 \( \widehat{x} \) 라고 하자. 그리고 이에 대응되어 예측으로 나오게 될 타겟 값은 \( \widehat{t} \) 라고 하자.
• 이런 경우를 그래프 모델로 표현한 그림은 다음과 같다. (즉, 앞장에서 다루었던 예측(predictive) 분포 모델)

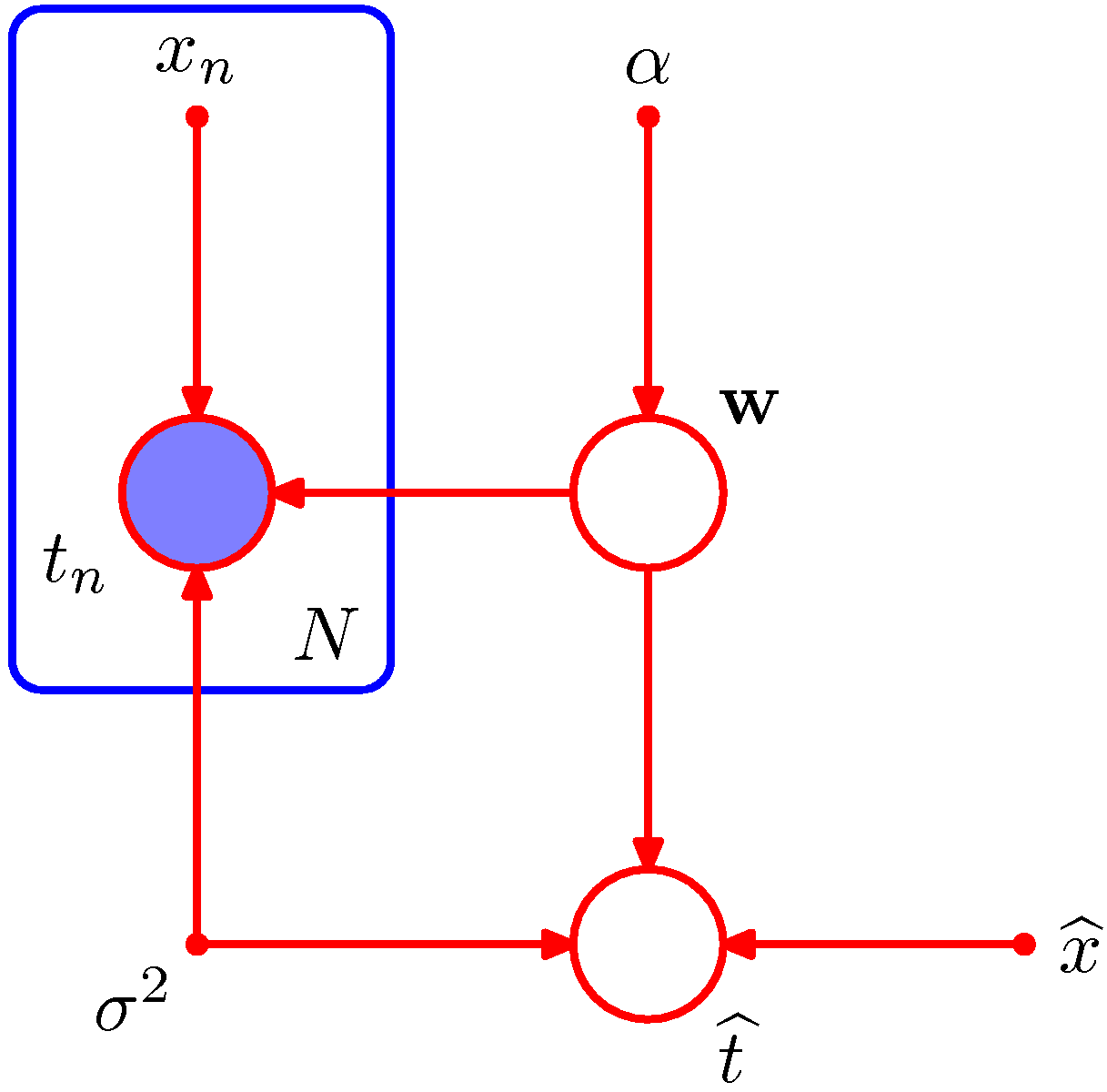
• 이 그래프 모델은 deterministic variable 까지 함께 표현되어 있다.
• 이걸 수식으로 옮기면 다음과 같다.

• 실제적인 계산 방법은 3장을 참고하도록 한다.
  • 하여튼 복잡한 모델을 손쉽게 그래프로 표현할 수 있다는 것이 중요하다.

8.1.2. 생성 모델 (Generative Model)

• 어떤 확률 분포로부터 임의의 샘플들을 만들어 내고 싶은 경우가 있다.
  • 이와 관련된 내용은 샘플링(Sampling) 기법을 소개하는 11장에서 다루고 있다.

• 여기서는 그 중 그래프 모델과 관련이 있는 ancestral sampling 이라는 유용한 기법에 대해서 알아보도록 하자.

• \( p({\bf x})=\prod p(x_k|pa_k) \) 에 대응되는 \( K \) 개의 변수로 이루어진 결합 확률 분포 \( p(x_1,…,x_K) \) 를 생각해보자.

• 모델에 대한 그래프가 주어졌을 때, 각각의 노드에 번호를 붙인다.
  • 이 때 자식 노드는 부모 노드보다 더 큰 번호를 부여한다.
• 우리의 최종 목표는 결합 확률로부터 샘플 \( \widehat{x}_1,…,\widehat{x}_K \) 를 도출하는 것이다.
• ancestral sampling 기법은 가장 작은 노드 번호부터 시작하여 그래프의 아래 노드로 이동하는 형태를 취한다.

Ancestral Sampling

• 가장 먼저 \( p({\bf x}_1) \) 분포로 부터 샘플 하나를 생성한다. 이를 \( \widehat{x}_1 \) 이라고 하자.
• 이제 노드 번호 순서대로 방문하면서 샘플을 생성한다.
• \( n \) 번째 노드에서 샘플을 생성할 때 \( p(x_n|pa_n) \) 분포를 이용하여 생성한다.
• 부모 노드에 해당하는 노드에 대한 샘플을 이미 주어지기 때문에 (부모 노드의 번호가 더 낮다.) 조건부 확률로 부터 샘플을 구할 수 있다.
  • 즉, 부모 노드는 고정된 실제 값을 가지게 된다.
• 마지막 \( x_K \) 의 샘플을 생성하고 나면 결합 확률로 부터 하나의 샘플( \( x_1,…,x_K \) )을 얻게 된다. 목적 달성!!
• 특정 분포로부터 실제 샘플을 얻는 방법은 11장에 언급하기로 한다.
• 주변 확률 분포로 샘플링하기.
  • 전체 분포로부터 샘플링 한 뒤에 불필요한 값은 버린다.
  • 예를 들어 \( p({\bf x}_2, {\bf x}_4) \) 와 같은 결합 분포에서 샘플링하기 원한다면,
  • 그냥 전체 샘플링을 한 뒤 \( \widehat{x}_2 \) 와 \( \widehat{x}_4 \) 만 취하여 사용하면 된다.
• 실제로 노드에 번호 붙이기 작업을 할 때.
  • 높은 번호를 가지는 변수 : 그래프의 종점에 대응되며 보통 관찰 데이터가 온다.
  • 낮은 번호를 가지는 변수 : 은닉 변수에 대응된다.
  • 은닉 변수의 역할?
    • 관찰되는 데이터가 복잡한 확률 분포로부터 생성될 때 좀 더 간단한 형태를 취하는 조건부 분포를 이용하여 데이터를 표현할 때 쓴다.
    • 이 때 사용되는 조건부 분포는 보통 지수족 (exponential family) 분포 등을 사용한다.

인과 모델 (Causal Model)

• 모델(model)은 관찰된 데이터가 어떤 과정을 거쳤는지를 표현할 수 있다.
  • 즉, 이 관찰 데이터가 왜 발생하였는지를 모델을 통해 설명할 수 있다.
  • 모델 자체의 정학성 여부는 논외로 하고 주어진 데이터를 모델의 인과적 과정으로 표현 가능하다고 생각하면 된다.
• 물체 인식 예제
  • 관찰된 데이터는 물체를 찍은 부분 이미지
  • 은닉 변수로는 해당 물체의 위치(position)와 방향(orientation)
  • 물체에 대한 사후 확률 예측
    • 가능한 모든 위치와 방향을 적분하면 구할 수 있다.
• 그래프 모델은 데이터가 발생하게된 인과 과정을 포함할 수 있음.

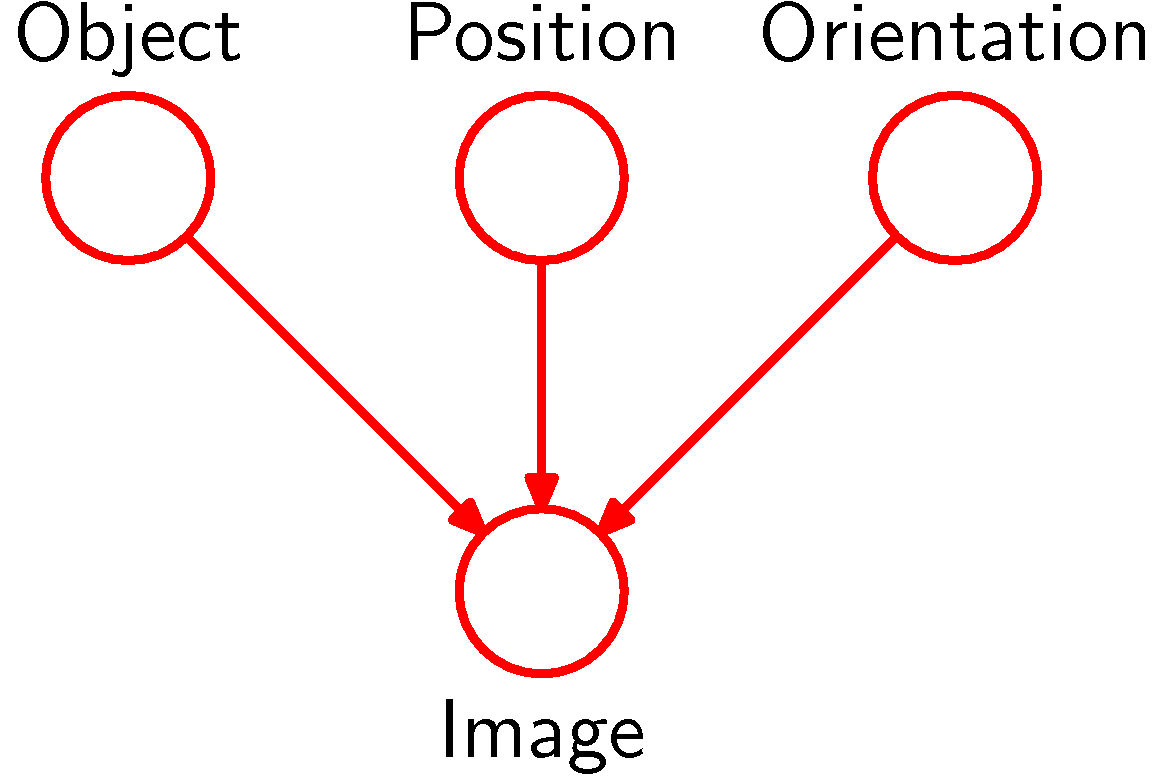
• 이러한 이유로 그래프 모델을 생성 모델, 즉, generative model 이라고 부른다.
  • 데이터를 생성할 수 있는 인과 모델을 generative 모델이라고 한다.
  • ancestrial sampling 과 같은 방식을 이용해서 데이터를 생성할 수 있다.
    • 마치 관찰된 데이터인 것처럼 데이터를 생성 가능하다.
    • 물론 이는 실제의 발현 데이터는 아니고 모델의 확률 분포에 의해 생성된 가상의 데이터
• 이와는 대조적으로 앞서 살펴보았던 다항 회귀(polynomial regression) 모델은 generative 모델이 아니다.

• 위의 그림처럼 그래프 모델의 도식으로 표현이 가능한데 왜 generative 모델이 아닐까?
  • 입력 데이터와 연관된 확률 분포가 없다.
  • 따라서 임의의 입력 데이터를 생성할 수가 없다.
  • 만약 \( p({\bf x}) \) 가 주어졌다면 만들 수 있다. (이런 경우 큰 원으로 표현되어야 한다.)
    • 이를 추가하기만 하면 된다고 생각할 수 있지만, 이를 고려했다가는 문제 자체가 너무 복잡해진다.

8.1.3 이산 변수 (Discrete Variable)

• 지금까지 우리는 지수족 분포에 속하는 중요한 분포들에 대해 다루어 보았다.
• 그리고 많은 경우 이러한 분포를 이용해서 문제를 해결하는 경우들도 살펴보았다.
• 사실 이러한 분포가 매우 간단한 상황에서만 통용 가능한 경우를 보았었지만, 복잡한 모델을 이렇게 간단한 분포를 이용해서 구성하는 방법도 매우 효용성이 높다.
• 그래프 모델에서는 부모-자식 노드 사이가 공액(conjugate) 관계에 있는 경우 몇 가지 장점을 가지게 된다.
• 우리는 두 가지 예제를 통해 이를 확인해 보도록 한다.
  • 부모-자식 관계인 노드가 이산 변수(discrete variables)일 때
  • 부모-자식 관계인 노드가 가우시안 변수(Gaussian variables)일 때
• 딱 봐도 명목형 데이터와 실수형 데이터를 입력 데이터로 가지는 경우를 대표한다고 생각해볼 수 있다.

이산 변수 (discrete variables)

• 확률 분포 \( p({\bf x}|{\bf \mu}) \) 가 이산(discrete) 변수 \( {\bf x} \) 인 확률 분포이고, 총 \( K \) 개의 상태를 가지고 있다고 하자.
  • 예를 들어 \( K=6 \) 이고 \( x_3=1 \) 인 데이터를 표형하는 방법은 \( {\bf x} = (0,0,1,0,0,0)^T \) 이다.
  • 그리고 \( \sum_{k=1}^{K}x_k=1 \) 이다.
• 모수 \( \mu_k \) 에 의해 발생되는 \( x_k=1 \) 의 확률은 다음과 같을 것이다.

• 이미 오래전에 살펴보았던 다항분포에 관한 식이다.
  • 그리고 여기에서는 \( K-1 \) 개의 독립 변수로 구성됨. (즉, \( K-1 \) 개의 모수가 필요하다.)
  • 왜냐하면 합이 1이라는 제약 조건 때문에 \( K-1 \) 개가 결정되면 자연스레 하나의 변수의 값이 결정됨.
• 이제 2개의 샘플이 얻어지는 상황의 확률 분포식을 생각해보자.
  • \( x_{1k}=1 \) 과 \( x_{2l}=1 \) 가 \( \mu_{kl} \) 로 부터 얻어질 확률식이다.

• 위의 식은 각각의 사건을 독립 사건으로 보고 다항 분포 두개의 식을 곱하는 식이 아니라,
  • 모든 발생 가능성을 염두해 두고 식을 전개한 식이다. ( \( =p({\bf x}_2|{\bf x}_1)p({\bf x}_1) \) )
  • 따라서 \( \sum_k\sum_l\mu_{kl}=1 \) 을 만족한다.
• 이 때에는 총 \( K^2-1 \) 개의 독립 변수가 존재한다.
  • \( (K-1)+K(K-1)=K^2-1 \) 을 얻는다.
• 이걸 좀 일반화시키면, \( M \) 개의 변수를 사용할 때 총 \( K^M-1 \) 개의 모수가 필요하다는 이야기.
• 이 관계를 도식화하면 다음과 같다.

• 하지만 만약 \( {\bf x}_1 \) 과 \( {\bf x}_2 \) 가 서로 독립적이라면 어떻게 될까?

• 위의 그림이 서로 독립적인 관계일 때의 그래프 모델을 표현한 것이다. ( \( =p({\bf x}_1)p({\bf x}_2) \) )
  • 이 경우 단지 \( 2(K-1) \) 개 만큼의 모수가 필요하다.
• 이런 경우 만약 \( K \) 개의 상태를 가진 \( M \) 개의 독립된 이산 변수가 존재한다면 요구되는 파라미터 수는 \( M(K-1) \) 이 될 것이다.

소결론

• Fully connected 모델은 복잡도가 높다.
• \( M \) 개의 이산 변수 \( {\bf x}_1,…,{\bf x}_M \) 이 주어진 경우에
• fully connected 모델이라면 \( K^M-1 \) 개의 모수가 필요하고

• link 가 하나도 없는 모델에서는 \( M(K-1) \) 개의 모수가 필요하다.

• 중간 정도의 연결성을 가지는 모델은 없는것인가?
  • fully connected 는 너무 과하고,
  • 좀 더 적은 파라미터를 가지되 일반화시키기 무리 없을 정도 수준의 모델이 있었으면 좋겠다.
    • 예) Chain of Nodes

• 특이 케이스 : Chain of Nodes

• 노드가 일렬로 연결되어 있다.
• 주변 확률 분포 \( p({\bf x}_1) \) 은 \( K-1 \) 개의 모수가 필요함.
• 조건부 분포 \( p({\bf x}_i|{\bf x}_{i-1}) \) 는 \( M-1 \) 개가 존재하고 각각 \( K(K-1) \) 개의 모수가 존재

• 필요한 모든 모수의 수는 \( (K-1)+(M-1)K(K-1) \) 이다. (어쨌거나 \( O(K^2) \) 크기.)

• 대안점
  • 위와 같은 형태의 모델에서 또 다른 대안으로 모수를 공유하는 방법이 있다.
  • 이게 무슨 말인고 하니 모수의 개수를 줄이기 위해 각각의 노드에 대한 모수를 동일한 모수로 사용한다는 것
  • 위의 식에서 조건부 분포 \( p({\bf x}_i|{\bf x}_{i-1}) \) 의 모수를 공유하여 사용하면 된다. (즉, \( K(K-1) \) 개가 필요함)
  • 최종적으로 \( (K-1)+K(K-1) \) 이 되어 \( K^2-1 \) 개의 모수가 요구된다.
  • 현실적으로 이런 케이스는 각각의 \( x_i \) 데이터들이 동일한 성질을 지니는 랜덤 변수 집합인 경우에나 가능함
    • 예를 들어 이미지 벡터에서 하나의 랜덤 변수는 픽셀 값
• 베이지언 방식
  • 위의 식을 베이지안 모델로 확장하여 디리슈레 분포를 사용하는 형태를 추가할 수 있다.
  • 이 경우 각각의 노드에 대해 사전 분포에 대한 모수가 추가로 요구된다.

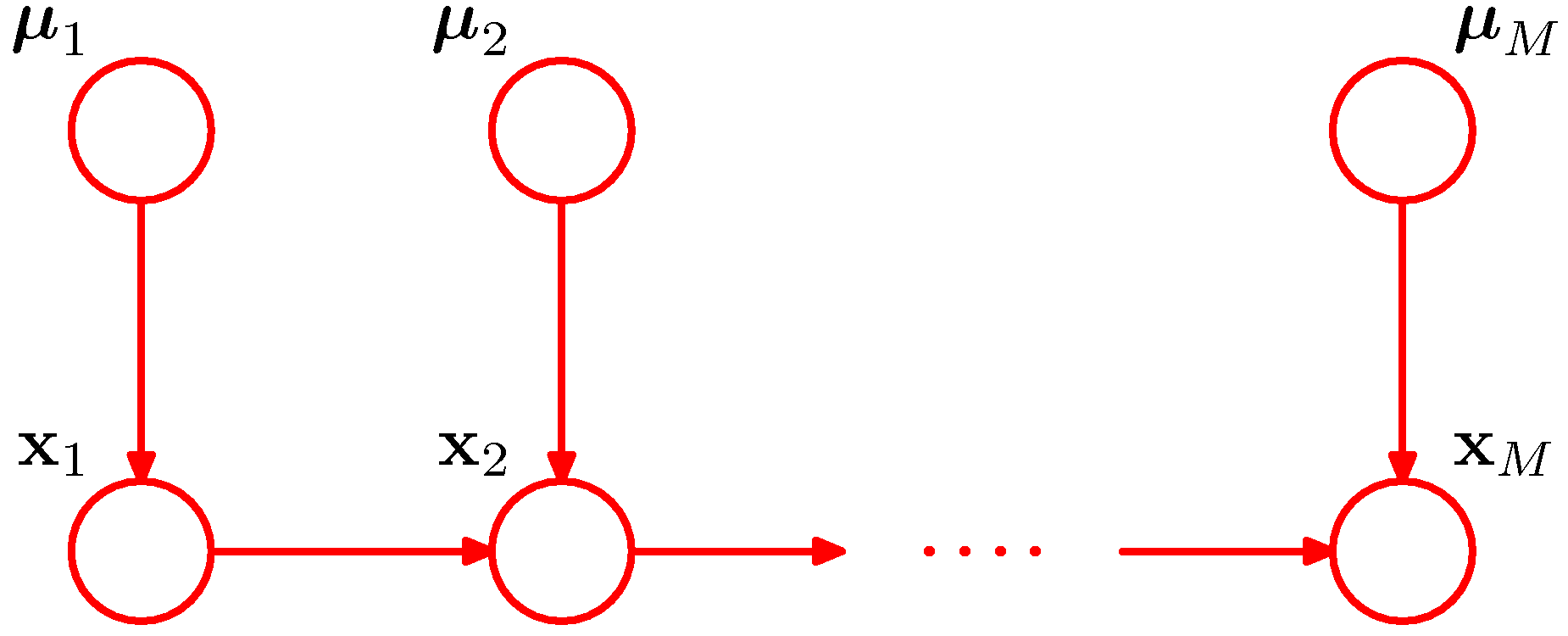
• 물론 이 때 사용되는 사전 분포의 모수는 모든 \( x_n \) 에 대해 동일한 값이 적용될 수 있다.
• 이를 표현하면 다음과 같다.

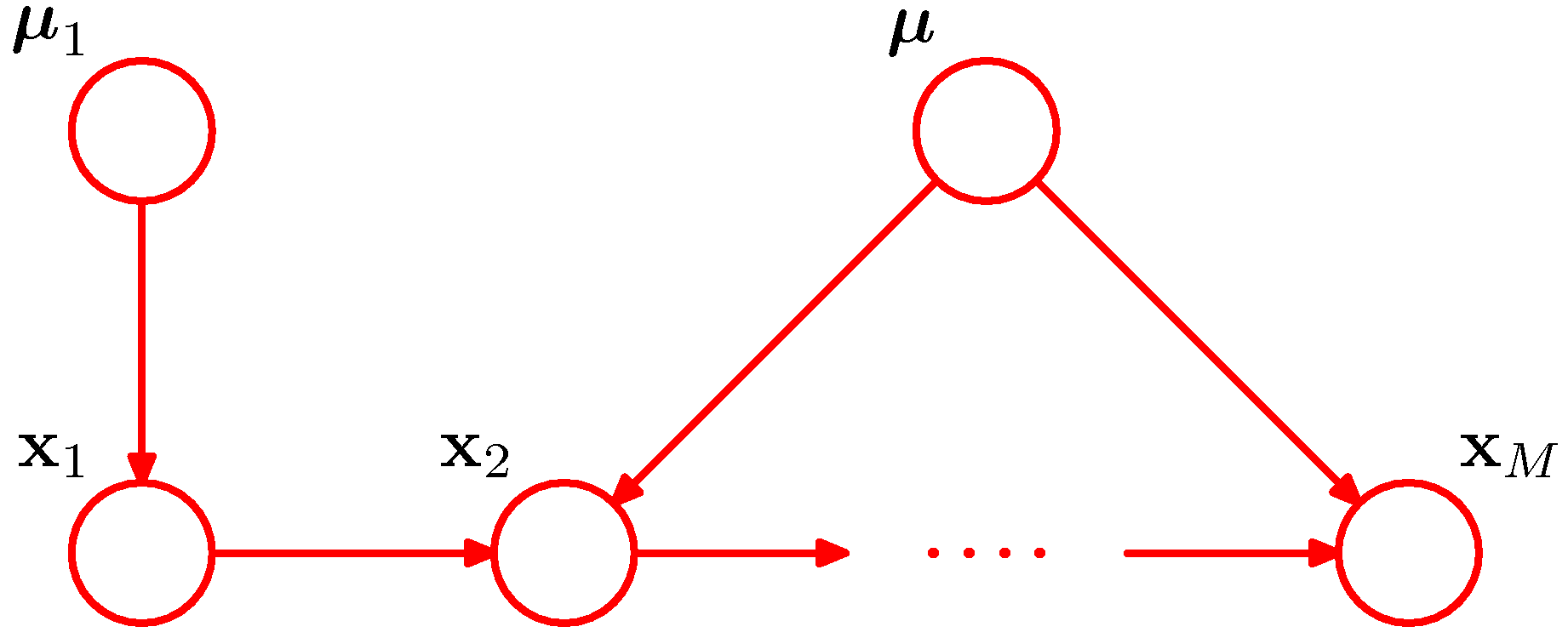
• 위의 그림은 조건부 분포 \( p({\bf x}_i|{\bf x}_{i-1}) \) 에만 동일한 사전 분포 모수를 추가한 그림이다.
• 우릭가 앞서 공액 사전 분포를 이용하여 재귀적인 업데이트 방식을 다루었듯이 여기서도 동일한 효과를 만들어 낼 수 있다.

• 지금까지 논의된 이야기들은 결국 지수적으로 증가하는 모델의 모수 개수를 줄이기 위한 방법들을 이야기하고 있는 것임
• 이산 변수를 기본으로 하는 모델의 파라미터가 지수적으로 증가하는 것을 막기 위한 또 다른 방법은 파라미터화된 조건부 확률 분포(parameterized models for conditional distribution)를 사용하는 것이다.

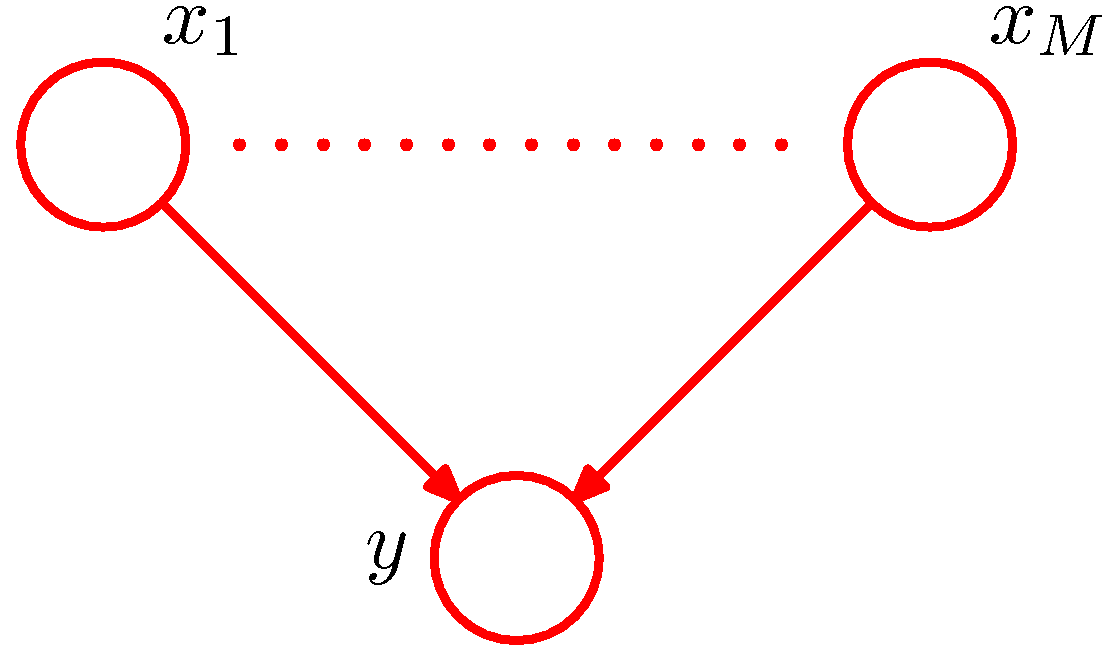
• 위의 그림은 간단한 예를 살펴보기 위한 것으로 입력 데이터는 binary 결과만을 가진다고 가정하자.
• 이렇게 작성하는 경우 \( M \) 은 \( y \) 에 대해 모든 부모의 노드 개수가 된다.
• 이 때 \( y \) 에 대한 확률 분포는 \( p(y|x_1,…x_M) \) 이 되고 총 필요한 모수의 수는 \( 2^M \) 개이다.
• 이제 어떤 결합 분포 \( p({\bf x}) \) 에 대한 확률 값을 \( p({\bf y}) \) 로 대응해 생각해 볼 수 있다.
• 여기에 로지스틱 회귀 식을 적용해보자.

• 여기서 \( \sigma(a)=(1+exp(-a))^{-1} \) 로 로지스틱 회귀라고 한다.
• \( {\bf x}=(x_0, x_1,…,x_M)^T \) 인 벡터로 총 \( (M+1) \) 의 차원을 가진다.
• \( {\bf w} \) 또한 \( {\bf w}=(w_0,…,w_M) \) 인 벡터로 마찬가지로 \( (M+1) \) 개의 차원을 가진다.
• 어쨌거나 아무리 복잡해봤자 이 수식은 \( M \) 에 대해 선형식의 복잡도를 가진다.
• 이런 방식은 앞서 다변량 가우시안 식에서 공분산 값을 제한하는 형태로 가정하여 모델 파라미터 수를 줄이는 효과와 유사하다고 하겠다.

8.1.4. 선형 가우시안 모델 (Linear-Gaussian models)

• 우리가 이번 절에서 진행할 내용은 다음과 같다.
  • 랜덤 변수들의 조합을 가우시안 선형 모델로 표현해보기.
    • 하나의 랜덤 변수를 가우시안 분포라고 가정한다.
    • 조건부 분포 또한 가우시안 분포가 되지만 \( p({\bf x}|{\bf y}) \) 의 식에서 \( y \) 또한 가우시안 분포로 부터 생성되는 데이터이기 때문에 해석이 어려움.
    • 이 때 조건부 분포(conditional distribution)의 평균은 부모 노드의 가우시안 분포의 평균에 대한 선형 함수로 해석.
      • 사실 이산 분포를 사용하는 모델(즉, 다항분포의 예)에서는 부모노드의 값의 결과에 따른 모든 가능한 집합으로부터 각각의 확률 분포를 만들면 되었었다.
        • 이를 CPD (conditional probablistic distribution)라고 부른다.
        • 이산 데이터의 경우 테이블 형식으로 전체 확률 표가 나온다고 해서 CPT (conditional probabilistic table) 라고도 한다.
      • 하지만 여기서는 이런 모델이 아니라 실제 가우시안 모델을 조건부 분포로 다루고 있는 모델을 만들어야 한다.
      • 그런데 이게 이미 2장에서 언급되어 있음. 2.3.3 절을 참고하기 바람
  • 일반적인 가우시안 모델과 공분산이 diagonal 형태의 가우시안 모델을 비교해보기
• 연속 랜덤 변수의 그래프 표현
  • 노드 \( i \) 가 하나의 연속 랜덤 변수 \( x_i \) 를 나타낼 때 만약 \( D \) 개의 변수를 그래프로 표현한다면,
  • 하나의 노드 \( i \) 와 이 노드의 부모 노드 \( pa_i \) 를 가지는 확률 분포를 다음과 같이 표현한다.
    • 이 내용은 2.3.3 절에 나온 조건부 가우시안 확률 분포를 참고하도록 하자.
    • 조건부 확률 분포를 부모 노드의 조건부 확률 분포의 결과 값에 대한 선형 결합으로 표현한다.
    • 따라서 기존 가우시안 분포에서는 사용하지 않던 모수 \( w_{ij} \) 가 추가되었다.

• 여기서 분산은 \( v_i \) 이고 \( w_{ij} \) 와 \( b_i \) 는 평균에 의해 주어지는 값이라 볼 수 있다.
• 결합 분포에 로그를 취한 식을 살펴보도록 하자.

• 여기서 \( {\bf x} = (x_1,…,x_D)^T \) 이고 “ \( const \) “ 영역은 \( {\bf x} \) 와는 무관한 텀이다.
• 이 식은 \( {\bf x} \) 에 대해 이차형식(quadratic) 함수인데 이를 통해 이 \( p({\bf x}) \) 확률 또한 가우시안 분포임을 알 수 있다.
• 결합 분포 \( p({\bf x}) \) 가 가우시안 분포임을 알았으니 이에 대한 평균과 공분산을 구해보도록 하자.
  • 평균과 분산 값은 조건부 분포를 재귀적인 수식으로 전개하면 얻을 수 있다.
  • 각각의 변수 \( x_i \) 는 다음과 같은 식으로 표현 가능하다.

• 이거 어디서 많이 보던 식이다.
  • 회귀(regression) 문제를 위와 같은 문제로 해석하여 해결한다.
• 여기서 \( \epsilon_i \) 는 평균이 0이고 분산이 1인 가우시안 랜덤 변수이다.
  • 따라서 \( E[\epsilon_i]=0 \) 을 만족하며 \( E[\epsilon_i\epsilon_j]={\bf I}_{ij} \) 를 만족한다.
• 이 때의 \( x_i \) 의 평균은 다음과 같이 얻을 수 있다.

• 우리가 찾고자 하는 평균 값은 \( E[{\bf x}] \) 의 값이며 이는 \( E[{\bf x}] = (E[x_i],…,E[x_D])^T \) 와 같다.
  • 실제 이 값을 계산하려면,
  • ancestral model 에서 살펴보았듯이 낮은 번호를 가지는 노드의 평균 값을 구하면서 반복적으로 계산하면 된다.
• 공분산도 동일한 방식으로 구할 수 있다.

Example

• 이제 모수의 개수와 관련된 내용을 살펴보기 위해 3개의 예제를 살펴볼 것이다.
  • case 1 : No links
  • case 2 : Fully connected
  • case 3 : Intermediate level of complexity (Chain of Nodes)
• 첫번째
  • 그래프 내에 아무런 link 도 존재하지 않는경우
  • 이 때에는 독립된 \( D \) 개의 노드만 존재하게 되고 따라서 \( w_{ij} \) 와 같은 파라미터는 필요하지 않다. (link가 없으므로)
  • 따라서 이 때 필요한 파라미터는 단지 \( D \) 개의 \( b_i \) 파라미터와 \( D \) 개의 \( v_i \) 파라밑터 뿐이다.
  • 결합 분포 \( p({\bf x}) \) 에 대해 평균 값은 \( (b_1,…b_D)^T \) 로 주어진다.
  • 결합 분포 \( p({\bf x}) \) 에 대해 공분산 값은 \( diag(v_1,…v_D) \) 로 주어진다.
  • 총 \( 2D \) 개의 파라미터가 필요하다.
  • 그냥 \( D \) 개의 독립적인 단변량 가우시안 분포로 고려된다.
• 두번째
  • Fully Connected 그래프인 경우
  • 이 때 임의의 한 노드는 자신보다 작은 노드 번호를 가지는 모든 노드를 부모 노드로 가지게 된다.
  • \( w_ij \) 의 경우 \( i \) 번째 줄에 해당하는 데이터는 \( i-1 \) 개가 존재한다. 따라서 lower triangler 행렬이 된다.
  • \( w_ij \) 의 파라미터 수는 \( D(D-1)/2 \) 가 된다. ( \( D \times D \) 행렬의 경우)
  • 결국 전체 파라미터의 수는 \( D(D+1)/2 \) 가 됨을 알 수 있다.
• 세번째
  • Graph with intermediate complexity 인 경우
  • 좀 더 간단하게 살펴보기 위해 아래의 그림으로 가정한다.

• 앞서 살펴보았던 재귀 식을 이용해서 \( p({\bf x}) \) 의 평균과 공분산을 구해보자.

• 마지막으로,
• 위의 수식은 하나의 노드가 일차원의 데이터라고 가정한 일차원 가우시안 모델을 가정한 것이다.
• 하지만 하나의 노드가 다차원 가우시안 모델이라고 생각하면 어떻게 될까?
• 어려울 것 같아 보이지만 앞 장에서도 다변량 가우시안 분포를 다루었으니 그리 어렵지 않다.

• 물론 \( {\bf W}_{ij} \) 는 정방 행렬이 아닐 수도 있는데 \( {\bf x}_i \) 와 \( {\bf x}_j \) 가 서로 다른 차수를 가질 수도 있기 때문이다.