2. Conditional Independence

여러 개의 변수를 다루고 있는 확률 문제에서 중요한 요소 중 하나는 조건부 독립(conditional independence) 문제.
세 개의 변수 $ a $ , $ b $ , $ c $ 가 있다.
- 이 때 $ b $ 와 $ c $ 가 주어졌을 때 $ a $ 에 대 조건부 확률을 계산해보자.
- 만약 $ a $ 가 $ b $ 에 독립적이라면 다음과 같은 식이 성립한다.

$p(a|b,c)=p(a|c) \qquad{(8.20)}$

이런 경우를 “$ c $ 가 주어졌을 때 $ a $ 는 $ b $ 에 대해 조건부 독립” 이라고 표현한다.
이런 상황에서 $ c $ 가 주어진 상태의 $ a $ 와 $ b $ 결합 분포는 다음과 같다.

$p(a,b|c) = p(a|b,c)p(b|c)=p(a|c)p(b|c) \qquad{(8.21)}$

이를 조건부 독립(conditional independence)이라고 하고 다음과 같이 표기한다.

$a\perp\!\!\!\!\!\perp b\;|\;c \qquad{(8.22)}$

확률 변수의 조건부 독립 여부는 매우 중요한 속성인데,
- 사용되는 모델을 단순화시킬 수 있고,
- 학습에 필요한 연산량을 낮출 수 있다.
따라서 여러 변수의 결합 확률(joint probability)을 얻어야 하는 경우,
- product rule 과 sum rule 을 이용하여 조건부 확률 분포로 전환한 다음,
- 각각의 조건부 확률로부터 독립 여부를 확인하여 모델을 단순화하는 과정을 진행할 수 있다.
- 물론 시간이 너무 많이 든다.
이럴 때 사용하라고 만든 프레임워크가 바로 d-separation 이다.
- 여기서 d 는 directed 를 의미한다.

8.2.1. 3개의 그래프 예제 (Three example graphs)

이제부터 3개의 노드를 가진 아주 간단한 방향성 그래프 모델을 이용하여 설명을 할 것이다.
준비한 예제는 총 3개이며 이를 이용하여 조건부 독립에 대해 고찰하는 시간을 가질 것이다.
동시에 이를 통해 d-separaton 이 가지고 있는 의미를 이해해 보도록 하자.

Example.1) Diverging Connections

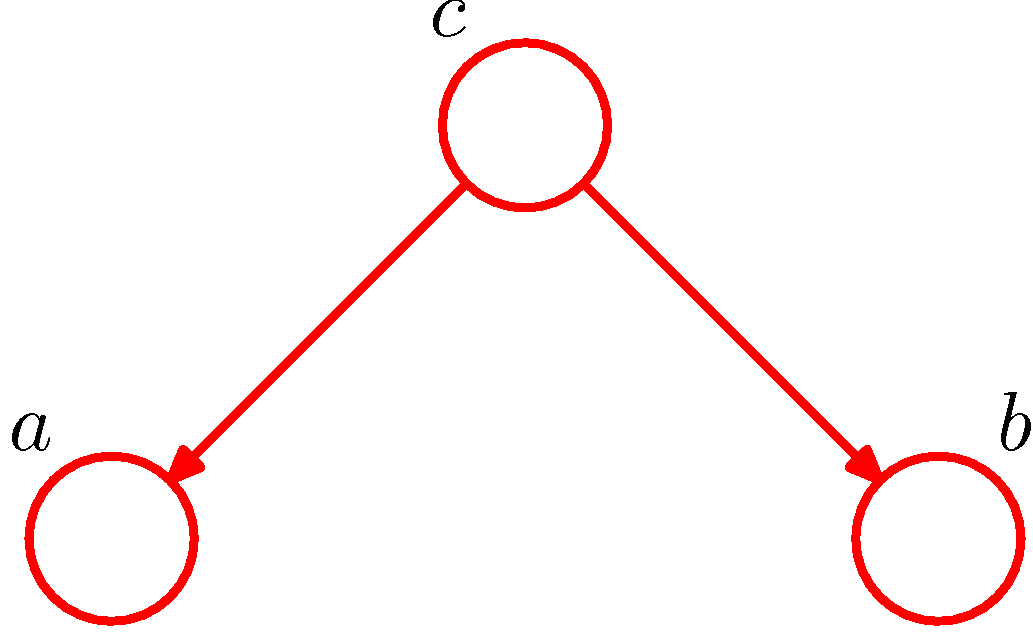
figure8.15

첫번째 예제는 위와 같은 그래프로 여기에서 결합 확률 분포를 찾아내도록 한다.

$p(a,b,c)=p(a|c)p(b|c)p(c) \qquad{(8.23)}$

어떠한 데이터도 관찰되지 않은 상황에서 $ a $ 와 $ b $ 사이의 독립성은 $ c $ 를 주변화하여 확인할 수 있다.

$p(a,b)=\sum_c p(a|c)p(b|c)p(c)\neq p(a)p(b) \qquad{(8.24)}$

이 식은 $ p(a)p(b) $ 와 같이 분해되지 않는다. 결국 아래와 같이 기술할 수 있다.

$a \not\!\!{\perp\!\!\!\!\!\!\perp}\; b\;|\;0 \qquad{(8.25)}$

여기서 $ 0 $ 은 공집합을 의미한다.
중간 심볼은 두 변수의 관계가 조건부 독립적이지 않다는 의미이다.
물론 특수한 조건에 따라 $ a $ 와 $ b $ 사이에 조건부 독립이 성립할 수도 있다.
- 하지만 일반화된 식으로 표현하자면 모든 경우에 성립하는 것이 아니므로 위와 같이 표기한다.
이제 변수 $ c $ 의 상태에 주목하자.

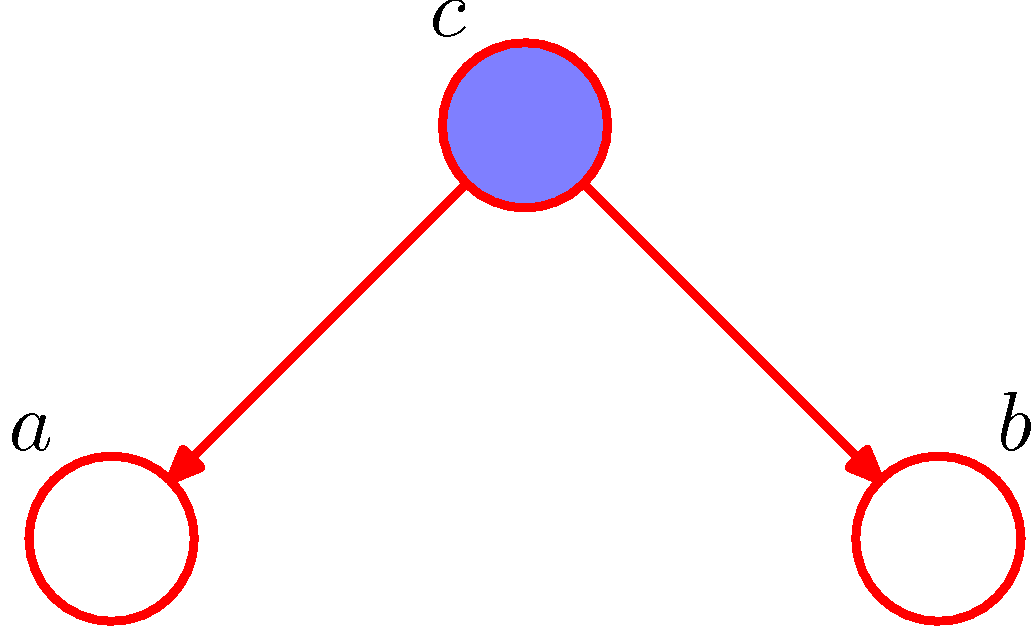
figure8.16

관찰 데이터 $ c $ 가 주어졌을 때 $ a $ 와 $ b $ 의 결합 확률은 다음과 같다.

$p(a,b|c)=\frac{p(a,b,c)}{p(c)}=p(a|c)p(b|c)$

$ c $ 가 주어진 경우는 조건부 독립이 성립함을 알 수 있다.
이로부터 다음의 식이 성립한다.

$a\perp\!\!\!\!\!\perp b\;|\;c$

위와 같은 그래프에서 노드 $ c $ 와 같은 경로를 가진 경우 tail-to-tail 이라고 한다.
- 노드가 두개의 화살표 꼬리 부분에 연결되어 있기 때문에
- 노드 $ c $ 를 관찰하게 되면 $ a $ 와 $ b $ 까지의 경로를 차단(block)하게 되어 $ a $ 와 $ b $ 가 서로 조건부 독립이 된다.
  - 즉, 차단되면 서로 독립적이 된다.

Example.2) Serial Connections

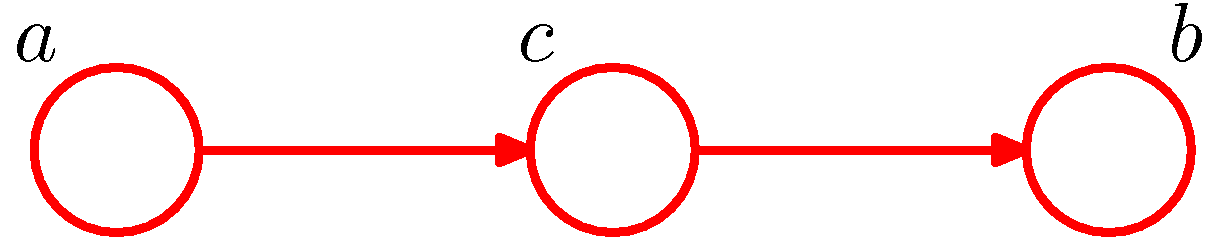
figure8.17

이번엔 위와 같은 모델이 주어진 상황이다. 결합 확률을 보자.

$p(a,b,c)=p(a)p(c|a)p(b|c) \qquad{(8.26)}$

관찰된 데이터가 주어지지 않은 상태에서 $ a $ 와 $ b $ 의 독립 여부를 확인해본다.

$p(a,b)=p(a)\sum_c p(c|a)p(b|c)=p(a)p(b|a) \neq p(a)p(b)$

이로부터 다음의 식이 성립한다.

$a \not\!\!\!{\perp\!\!\!\perp}b\;|\;0 \qquad{(8.27)}$

이제 첫번째 예제와 마찬가지로 $ c $ 가 주어졌을 때의 모델을 확인해보자.

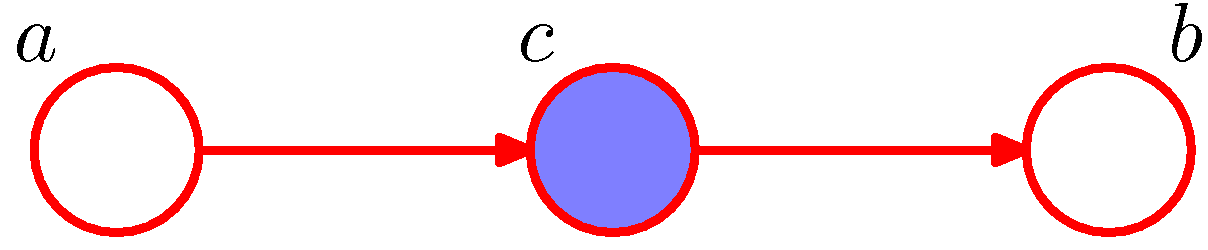
figure8.18

$p(a,b|c) = \frac{p(a,b,c)}{p(c)} = \frac{p(a)p(c|a)p(b|c)}{p(c)}=p(a|c)p(b|c)$

역시나 다음의 식이 성립함을 알 수 있다.

$a\perp\!\!\!\perp b\;|\;c$

위와 같은 그래프에서 $ c $ 를 head-to-tail 이라고 부른다.
- 하나의 화살표는 화살표의 머리가, 하나의 화살표는 화살표의 꼬리가 오기 때문이다.
- 예제 1과 마찬가지로 노드 $ c $ 를 관찰하고 나면 $ a $ 와 $ b $ 까지의 경로가 차단(block)되어 $ a $ 와 $ b $ 는 조건부 독립이 성립함.

Example.3) Converging Connections

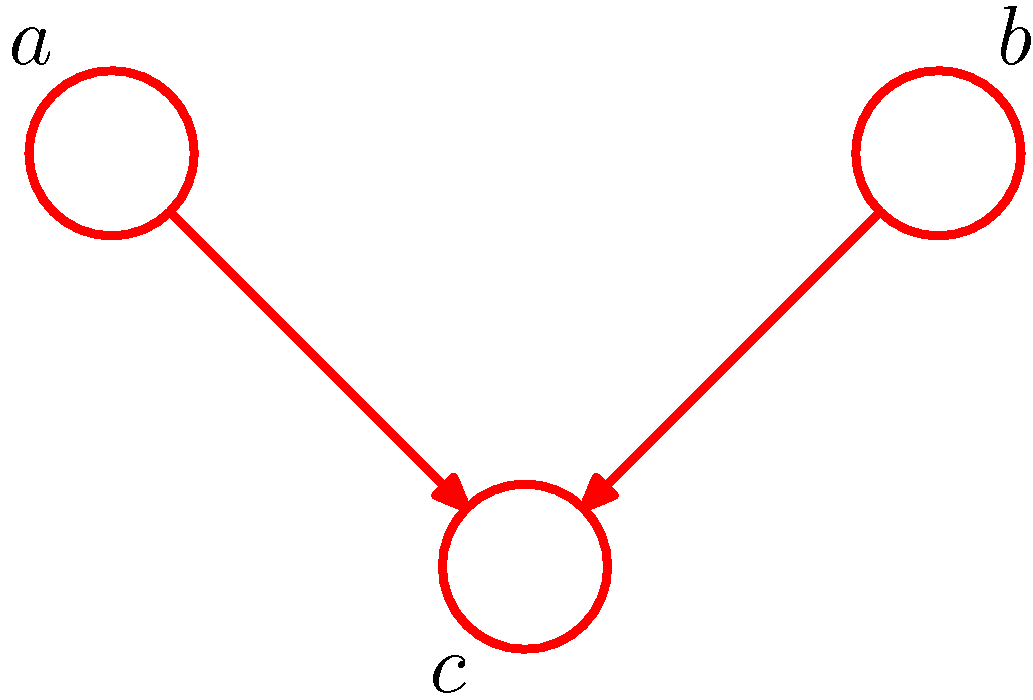
figure8.19

미리 좀 이야기하자면 위와 같은 그래프 모델은 앞선 예제와는 조금 다른 양상을 보인다.
우선 결합 분포는 다음과 같다.

$p(a,b,c) = p(a)p(b)p(c|a,b) \qquad{(8.28)}$

관찰된 변수가 없다고 하면 이 식을 $ c $ 에 대해 주변화(marginalize) 할 수 있다.

$p(a,b) = p(a)p(b)$

따라서 $ a $ 와 $ b $ 는 다음의 관계가 성립한다. (즉, 항상 독립적임)

$a\perp\!\!\!\perp b\;|\;0 \qquad{(8.29)}$

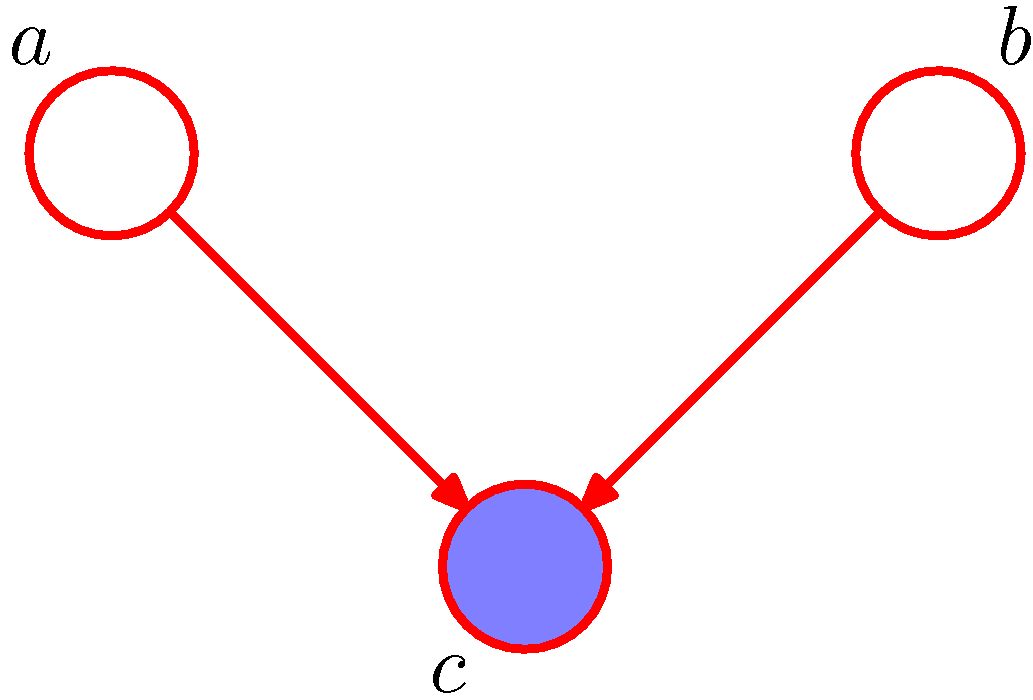
figure8.20

이제 $ c $ 가 관찰된 후의 식을 전개해 보자.

$p(a,b|c) = \frac{p(a,b,c)}{p(c)}=\frac{p(a)p(b)p(c|a,b)}{p(c)} \neq p(a|c)p(b|c)$

앞선 예제와는 다른 결과를 얻는다. 즉,

$a \not\!\!\!{\perp\!\!\!\perp}b\;|\;c$

이제 좀 명확해지는데 예제 3의 경우는 예제 1과 2의 정 반대의 현상을 만들어 낸다.
- 이 때 $ c $ 와 같은 노드를 head-to-head 라고 한다.
- 노드 $ c $ 가 관찰되지 않은 경우에는 경로가 차단(block)되고 $ a $ 와 $ b $ 는 서로 독립적이 된다.
- 반대로 노드 $ c $ 가 관찰되는 경우 경로가 차단 해제(unblock)되고 $ a $ 와 $ b $ 는 $ c $ 에 의해 종속적인 관계가 된다.
- 이건 그냥 생각을 해봐도 어느 정도 직관을 얻을 수 있는데, 결과가 주어지게 되면 무조건 원인이 들어맞아야 된다.
  - 존 코너를 살리려고 카일 리스가 왔다면, 언젠가는 반드시 카일 리스를 과거로 보내야 하겠지. (뭔 소리래.)
- 참, 용어에 주의해야 하는데 예제 3의 경우는 노드가 관찰되면 unblock, 관찰되지 않으면 block이다.
  - 즉, block은 관찰의 여부가 아닌 독립의 여부를 나타내게 된다. block 되면 노드를 기준으로 독립적이 된다.
예제 3과 관련해서 중요한 사항이 하나 더 있다.
- 노드 $ x $ 에서 노드 $ y $ 로의 경로가 존재한다면, 노드 $ y $ 는 노드 $ x $ 의 자손( descendant )이라고 부른다.
- 이 때 $ x $ 와 $ y $ 경로의 노드 중 head-to-head 노드가 존재한다고 할 때
  - 이 노드가 관찰(observed)되거나
  - 혹은 이 노드의 어떤 자손 노드가 관찰되면,
  - 이 노드는 unblock 상태가 된다. (즉, 차단되지 않고 독립성이 사라진다.)

Explaining away

예제 3과 같은 경우로 인해 발생되는 애매한 상황들을 제대로 이해하기 위해 좀 더 시간을 써 보도록 하자.
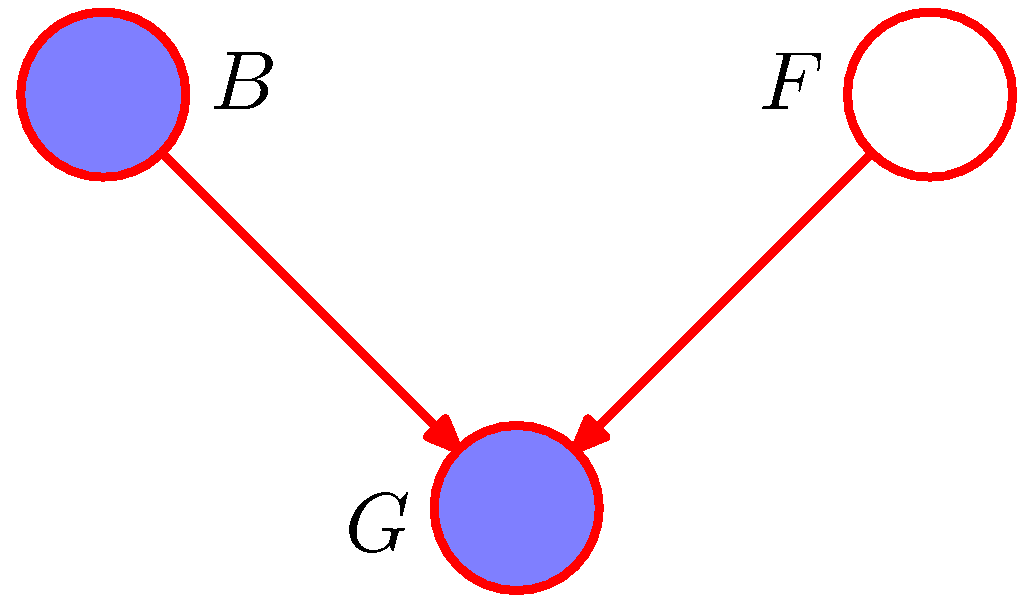
- 3개의 노드로 이루어진 아래와 같은 상황을 고려해 보자.

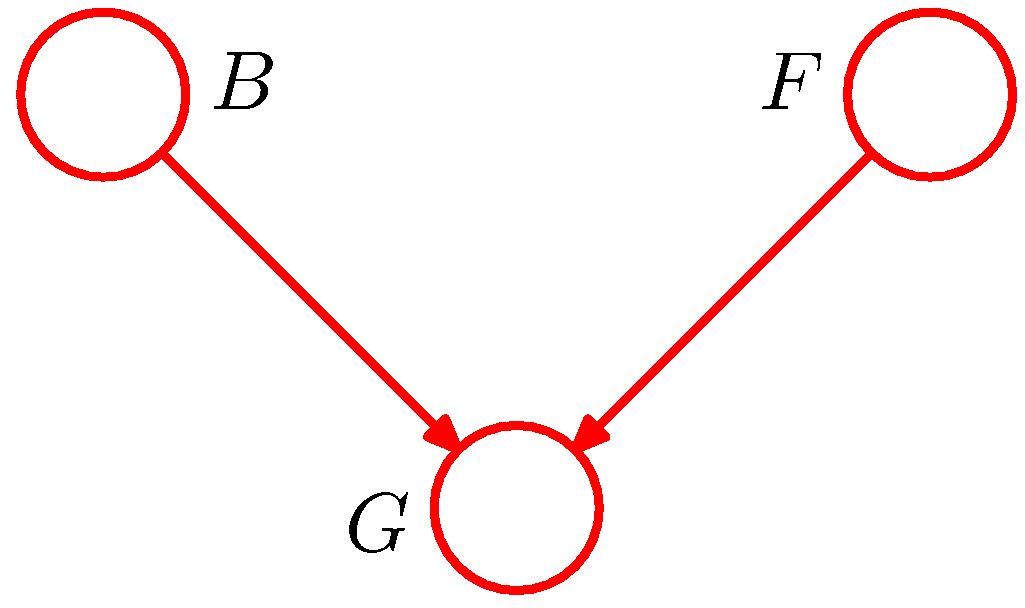
figure8.21a

이 예제는 자동차 연료 시스템의 그래프 구조이다.
- 각 노드는 이진(binary) 값을 가지는 노드로 구성되어 있다.
- 각 노드의 의미는 다음과 같다.
  - (B) 배터리의 상태 : 충전(B=1) or 방전(B=0)
  - (F) 연료 탱크의 상태 : full(F=1) or empty(F=0)
  - (G) 전기연료 게이지의 상태 : full(G=1) or empty(G=0)
배터리의 충전 상태와 연료 탱크가 채워진 상태는 각각 다음의 사전 확률을 가진다.

$p(B=1) = 0.9$ $p(F=1) = 0.9$

이제 연료 탱크과 배터리가 주어졌을 때 게이지가 Full 인 상태의 확률 값을 계산해본다.

$p(G=1|B=1, F=1)=0.8$ $p(G=1|B=1, F=0)=0.2$ $p(G=1|B=0, F=1)=0.2$ $p(G=1|B=0, F=0)=0.1$

확률의 합의 1이라는 사실에 의해 $ p(B=0)=0.1 $ , $ p(F=0)=0.1 $ 을 만족한다.
이제 몇 가지 상황을 주고 이에 대한 확률값을 확인해 볼 것이다.

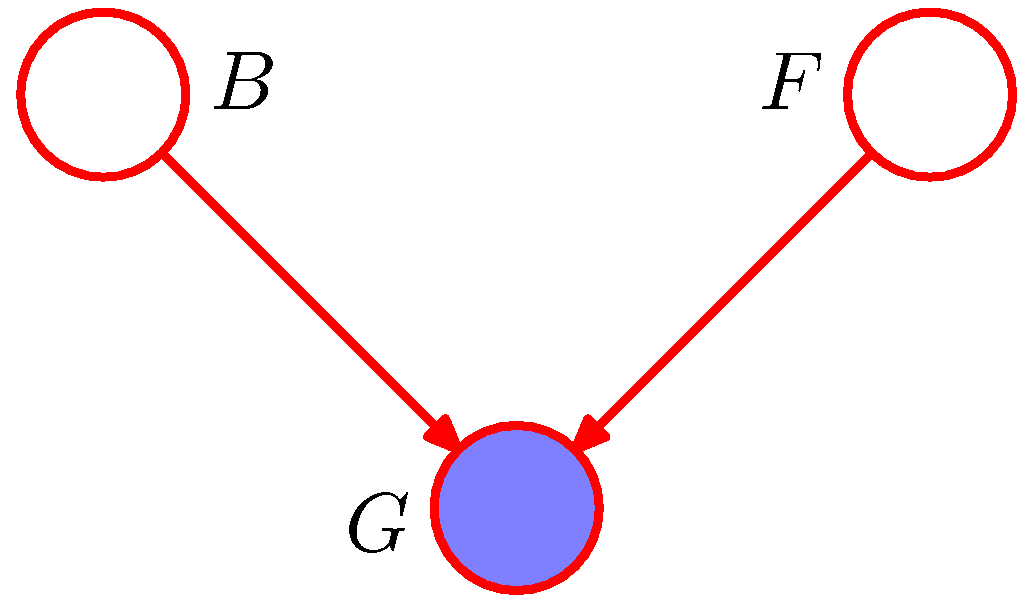
이제 $ G $ 가 관측 되었다고 가정하자. ( $ G=0 $ 인 상태로 가정한다.)
우선 이 때의 확률 값을 계산해보자. $ p(B,F,G) $ 에 대한 주변 확률 분포로 계산하면 된다.

$p(G=0)=\sum_{B\in\{0,1\} }\sum_{F\in\{0,1\} } p(G=0|B, F)p(B)p(F) = 0.315 \qquad{(8.30)}$

비슷하게 계속 계산이 가능하다.

$p(G=0|F=0) = \sum_{B\in\{0,1\} }p(G=0|B,F=0)p(B)=0.81 \qquad{(8.31)}$

최종적으로 다음의 결과를 얻는다.

$p(F=0|G=0) = \dfrac{p(G=0|F=0)p(F=0)}{p(G=0)}\simeq 0.257 \qquad{(8.32)}$

이 결과가 의미하는 바는 $ p(F=0|G=0) > p(F=0) $ 이다.
- 만약 $ G=0 $ 가 관찰되는 경우 $ F=0 $ 이 될 확률은 관찰되지 않았을 경우보다 더 큰 확률( $ 0.257>0.1 $ ) 값을 가지게 된다.
- 앞서 설명한 3-example 예제의 내용과 잘 부합한다.
- 게이지가 비워진 것이 관찰되는 사건은 탱크가 실제 비었을 가능성을 더 크게 만든다.
이제 $ B=0 $ 인 상태가 추가로 관찰되었다고 해보자.

$p(F=0|G=0, B=0) = \dfrac{p(G=0|B=0,F=0)p(F=0)}{\sum_{F\in\{0,1\} }p(G=0|B=0,F)P(F)}\simeq0.111$

배터리가 추가로 $ B=0 $ 을 관찰한 결과 확률 값은 0.25에서 0.111로 더 낮아졌다.
그럼에도 불구하고 사전 확률 $ p(F=0)=0.1 $ 보다 더 높은 확률 값이다.
- 연료 게이지 $ G=0 $ 인 관찰 결과는 여전히 빈 연료 탱크 가능성에 대한 evidence 를 제공하기 때문이다.

explain away

이와 같은 현상을 explain away 라고 한다.
자식 노드에 대해 알려진 사실이 없는 경우 부모 노드의 evidence가 (즉, 관찰된 부모노드의 확률값이) 다른 부모 노드에 영향을 못 미친다.
그러나 자식 노드가 관찰되면 부모 노드의 evidence 가 다른 부모 노드의 관찰 확률값에 영향을 주게 된다.

8.2.2. D-Sepration

앞서 배운 내용들을 확장하여 d-separation 이라 불리우는 방향성 그래프의 속성을 살펴볼 것이다.
방향 그래프 모델에 비-교차 부분 노드 집합 $ A $ , $ B $ , $ C $ 가 있다고 해보자. (하나의 노드가 아니라 부분 집합이다.)
이제 각 서브 집합의 조건부 독립 $ A\perp\!\!\!\perp B\;|\;C $ 를 확인할 것이다.
따라서 $ A $ 노드 집합에서 $ B $ 노드 집합 까지의 가능한 모든 경로를 대상으로 다음 조건을 확인해야 한다.
- 대상 경로 내에 다음 조건 중 하나에 해당하는 노드를 포함하고 있는 경우 이 경로는 차단(block)됨
  - (1). $ A $ 와 $ B $ 경로의 화살표가 head-to-tail 또는 tail-to-tail 이고 사이의 노드 중 일부가 C 노드 집합에 있을 경우
  - (2). $ A $ 와 $ B $ 경로의 화살표가 head-to-head 이고 사이의 노드 중 일부가 C 노드 집합에 없을 경우
- $ A $ 에서 $ B $ 까지의 모든 경로가 차단되면 $ A $ 와 $ B $ 는 $ C $ 에 의해 D-separated 되었다고 이야기한다.
- 이 경우 그래프 내의 모든 변수들에 대해 $ A\perp\!\!\!\perp B\;|\;C $ 가 성립한다고 말할 수 있다.
다음 그림을 통해 D-sepatation에 대해 이해를 해보도록 하자.

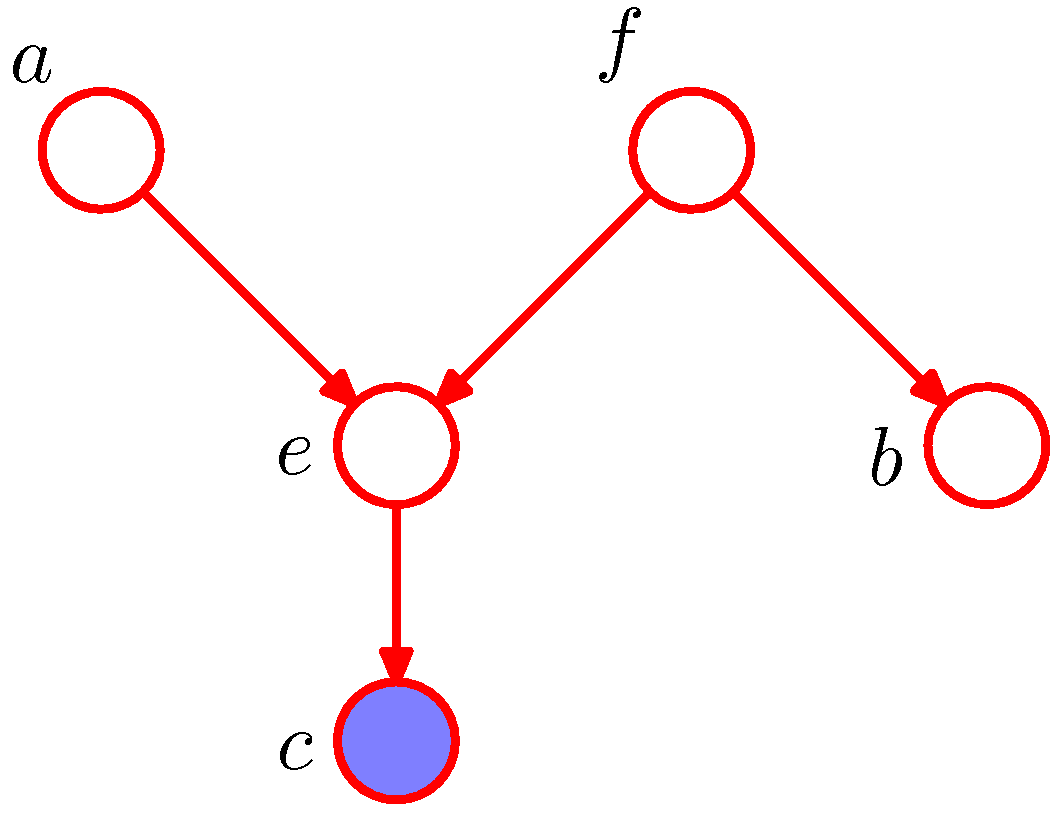
첫번째 그림을 보자.
- $ a $ 에서 $ b $ 로의 경로는 노드 $ f $ 에 의해 차단되지 않는다.
  - 이 경로는 tail-to-tail 이고 관찰되지 않았기 때문.
- 또한 $ e $ 로 인해 경로가 차단되지 않는다.
  - $ e $ 는 head-to-head 이고 관찰되지 않았지만 $ c $ 가 관찰되었기 때문에 더 이상 독립이 성립하지 않는다.
- 따라서 $ a\perp\!\!\!\perp b\;|\;c $ 가 성립하지 않는다.
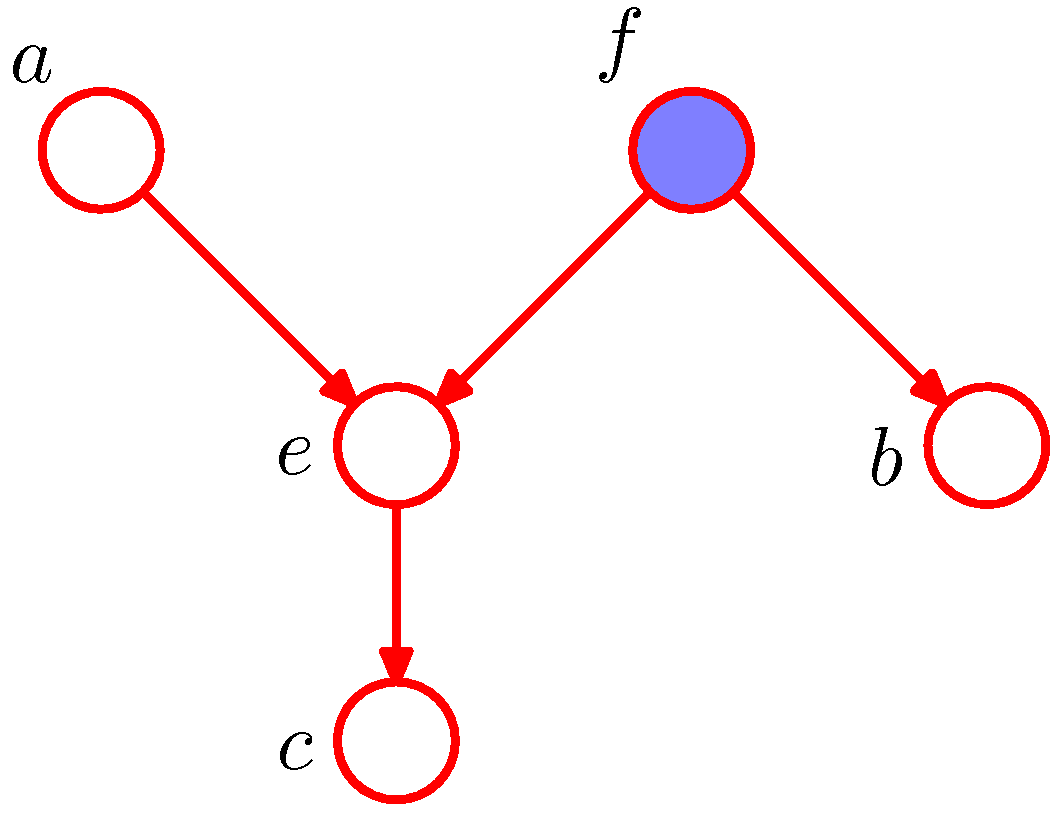
다음으로 두번째 그림을 보면,
- $ a $ 에서 $ b $ 로의 경로는 $ f $ 에 의해 차단된다. ( $ f $ 가 관찰되었기 때문에)
  - 따라서 $ a\perp!\!\!\\perp b\;|\;f $ 가 성립함.
- 마찬가지로 $ e $ 에 의해서도 차단된다.
  - $ e $ 는 head-to-head 이고 $ e $ 와 $ e $ 의 자식노드 $ c $ 모두 관찰되지 않았기 때문.
- 따라서 $ a\perp\!\!\!\perp b\;|\;c $ 가 성립한다.

잠깐 앞서 살펴보았던 그림 8.5 에 대해 생각을 해보자.

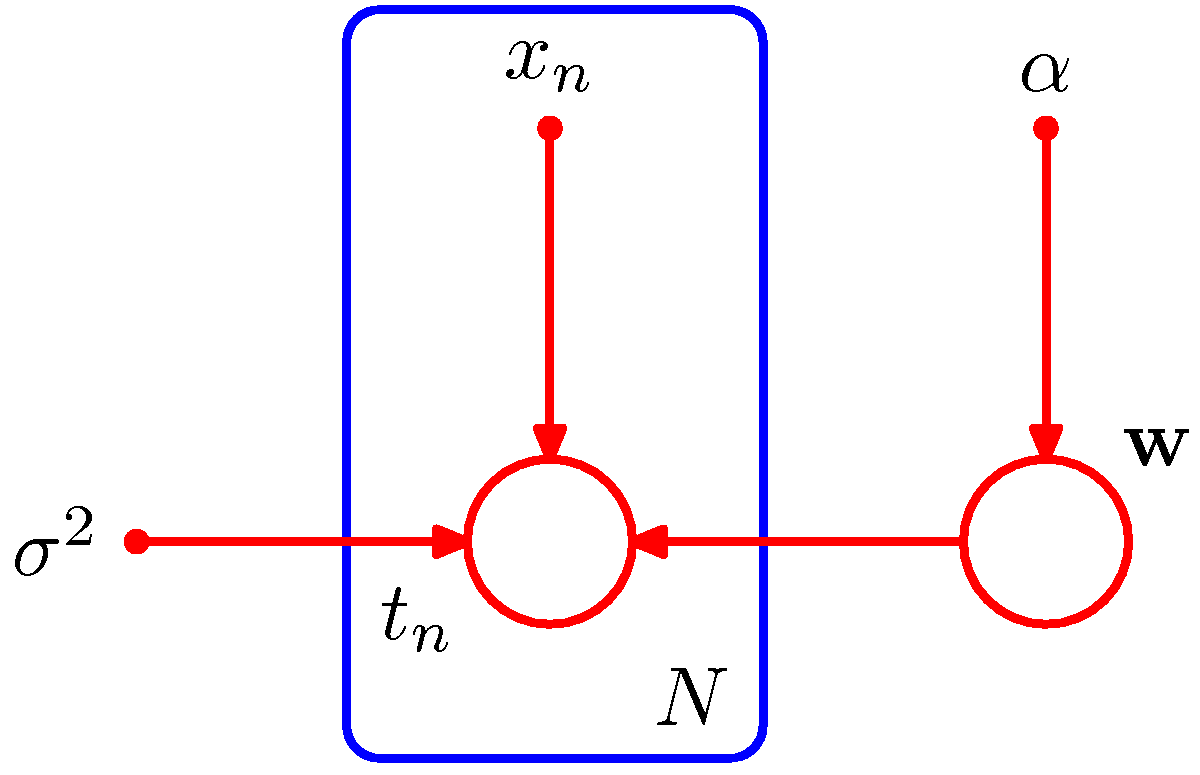
figure8.5

여기서 사용된 작은 원 값인 $ \alpha $ 와 $ \sigma^2 $ 은 사실 이미 관찰된 노드처럼 행동한다.
- 물론 일반적인 관찰 노드와는 차이가 있는데 해당 노드와 관련된 주변 확률(marginal distribution)을 구할 수 없다.
- 또한 이러한 노드는 부모 노드가 없다.
따라서 이 노드를 통하는 모든 경로는 항상 tail-to-tail 이고 차단되어 있다고 생각하면 된다.
결국 이러한 노드는 D-separation 을 구할 때 아무런 역할을 하지 못함. 따라서 그냥 무시하면 된다.
이제 독립적(i.i.d)으로 발현된 샘플이라는 개념을 D-sepation을 이용하여 확인해 보도록 하자.
- 여기서 다루는 모델은 1.2.4 절에서 다루었던 예제이다.

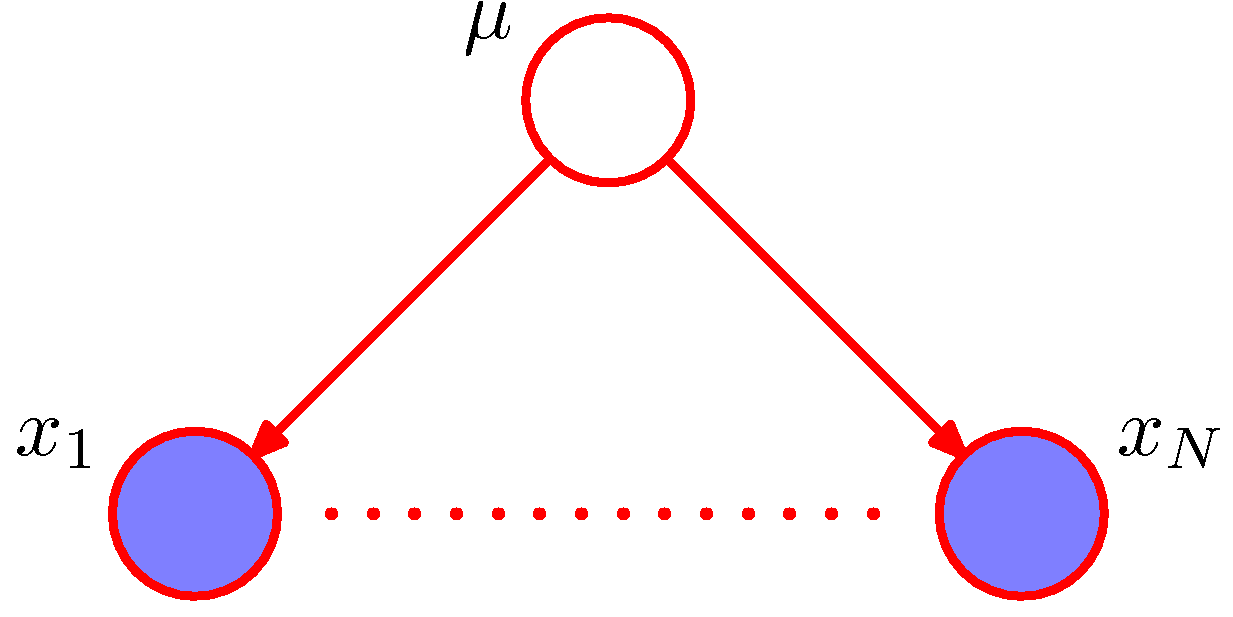
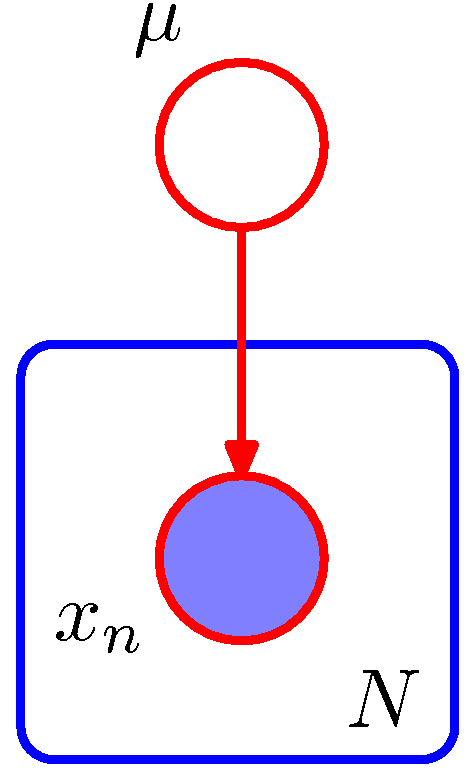
단병량 가우시안 분포에서 평균 $ \mu $ 에 대한 사후(posterior) 분포를 구하는 문제
- 결합 분포는 사전 분포 $ p(\mu) $ 와 조건부 분포 $ p(x_n|\mu) $ 를 이용하여 정의됨
- $ D={x_1, …, x_N} $ 을 이용하여 모수 $ \mu $ 를 추론하는게 목표. 즉, $ p(\mu|D) $ 를 구한다.
- 모든 샘플이 독립적으로 발현되었다고 가정하고 아래의 식으로 전개하게 된다.

$p(D|\mu) = \prod_{n=1}^N p(x_n|\mu) \qquad{(8.34)}$

이제 D-separation 을 이용하여 임의의 $ x_i $ 로부터 다른 임의 노드 $ x_{j \neq i} $ 로의 경로의 독립성을 살펴보자.
- 이 때 임의의 두 노드에 대해 모두 고유한 경로가 존재하고 이는 관찰 노드 $ \mu $ 에 대해 모두 tail-to-tail 관게임.
- 따라서 모든 경로는 차단(block)되고 이로 인해 데이터 $ D $ 는 주어진 $ \mu $ 에 대해 독립임. (뭐, 이런 뻔한 이야기를…)
하지만 이제 $ \mu $ 에 대해 적분을 해야 한다고 생각해보자. ( $ p(D, \mu) $ 에 대한 주변 확률이다.)

$p(D) = \int_{-\infty}^{\infty} p(D|\mu)p(\mu)d\mu \neq \prod_{n=1}^N p(x_n) \qquad{(8.35)}$

이 경우 $ \mu $ 는 관찰되지 않는 변수로 잠재 변수(latent variable)가 되고 관찰 값은 더이상 독립적이지 않게 된다.
- $ p(D|\mu) $ 와 $ p(D) $ 의 관계를 생각해보자. 이후 9장, 10장에서도 이러한 개념이 계속 등장한다.
- complete data 와 incomplete data 부분을 참고하도록 한다.

이제 또 다른 예제를 살펴볼 차례이다. 그림 8.7 을 다시 한번 보도록 한다.

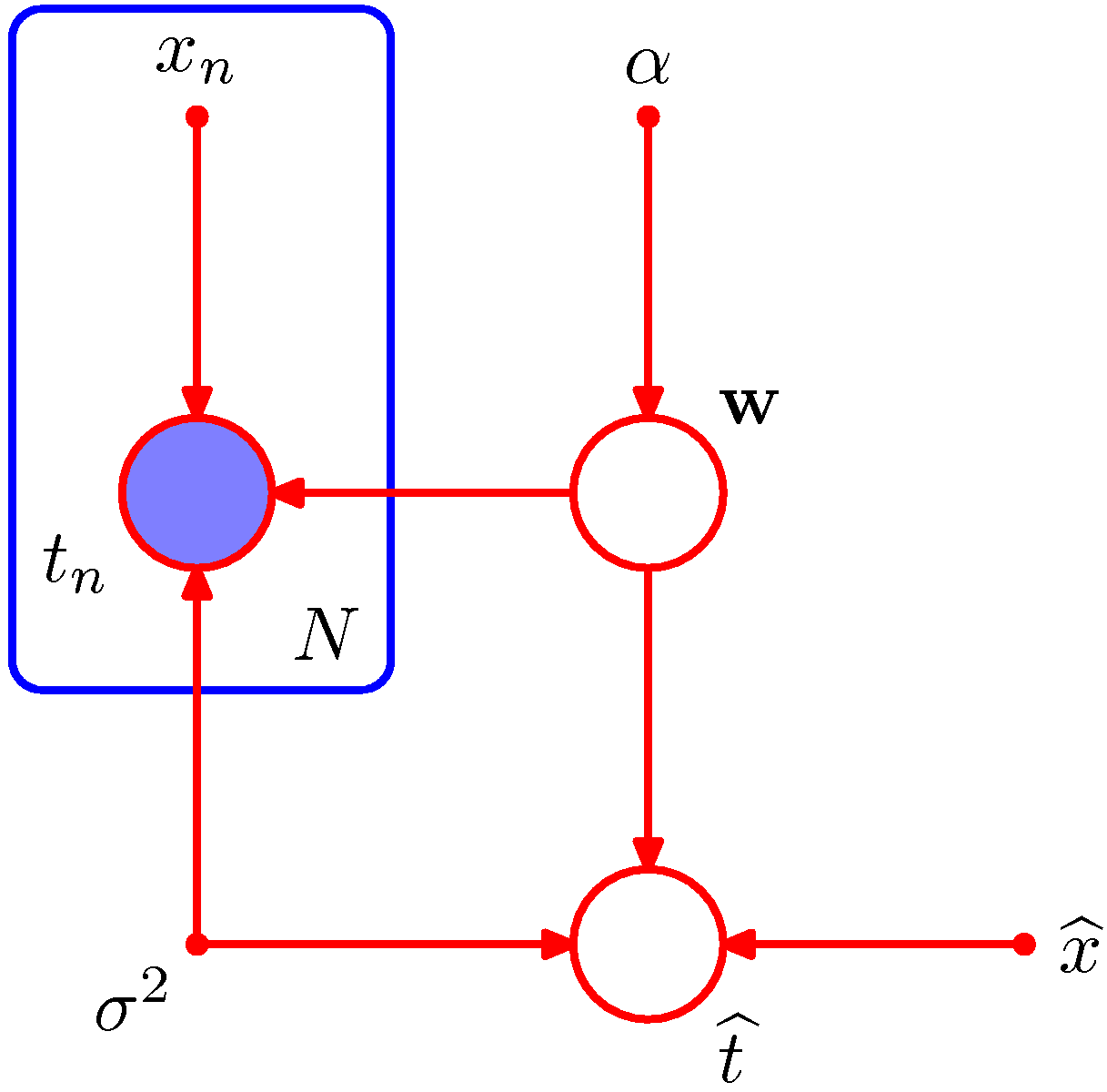
figure8.7

예측 분포 모델을 나타낸다.
위의 그림에서 다항식의 계수 $ {\bf w} $ 를 조건으로 하는 $ \widehat{t} $ 는 학습 데이터 $ {t_1,…t_N} $ 에 대해 독립적이다.

$\widehat{t} \perp\!\!\!\perp t_n\;|\;{\bf w} \qquad{(8.36)}$

따라서 파라미터 $ {\bf w} $ 를 구하기 위해 학습 데이터 $ t_n $ 을 사용한 다음,
학습 데이터는 버리고 얻어진 $ {\bf w} $ 를 이용하여 새로운 $ \widehat{t} $ 의 값을 만들어낼 수 있다.

그래프 모델과 관련있는 모델로 나이브 베이즈(Naive Baayes) 모델을 들 수 있다.
- 이 모델은 간단한 형태의 모델을 지향하기 때문에 조건부 독립성을 가정한다.
- D 차원의 벡터 $ {\bf x} = {x_1,…,x_D}^T $ 로 구성된 관찰 변수를 사용한다.
- K 차원의 이진 벡터 $ {\bf z} $ 로 분류된 값을 표현한다. (1-of-K 코딩 스킴을 사용한다.)
- 다항 분포 파라미터 $ {\bf \mu} $ 는 $ p({\bf z}|{\bf \mu}) $ 를 이용하여 $ z $ 를 생성
- $ {\bf z} $ 는 $ p({\bf x}|{\bf z}) $ 를 이용하여 $ {\bf x} $ 를 생성함.
- 이 때 다항 분포를 이용하게 되므로 $ {\bf \mu} $ 는 디리슈레 분포를 사용 가능하다.

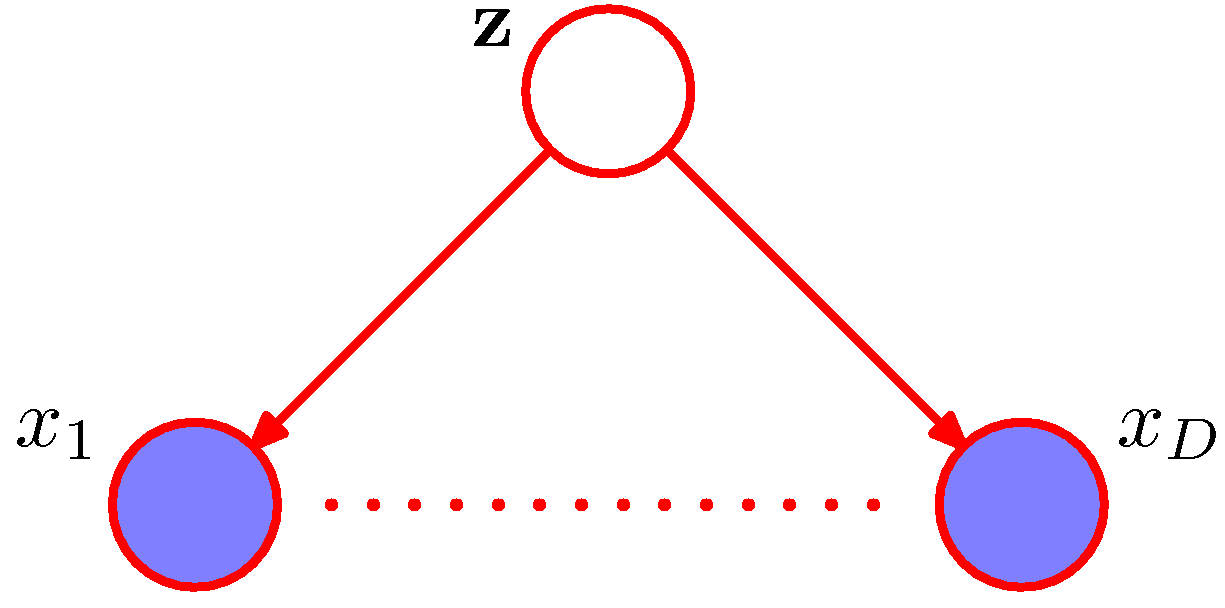
figure8.24

위의 그림은 나이브 베이즈를 그래프로 표기한 것이다.
- 변수 $ {\bf z} $ 는 학습 데이터 $ {\bf x}_i $ 와 $ {\bf x}_j $ 를 차단(block)한다. (단, $ i \neq j $ 이다.)
- 왜냐하면 해당 경로들이 노드 $ {\bf z} $ 에 대해 tail-to-tail 관계이기 때문ㅇ
- 따라서 변수 $ {\bf x}_i $ 와 $ {\bf x}_j $ 는 $ {\bf z} $ 가 주어진 경우 조건부 독립임을 알 수 있다.
- 그러나 $ {\bf z} $ 가 주변화되어 사라지면 $ {\bf x}_i $ 와 $ {\bf x}_j $ 의 경로가 더 이상 차단되지 않는다.
  - 이 경우 $ p({\bf x}) $ 가 $ {\bf x} $ 의 구성요소로 인수 분해 되지 않는다.
  - 앞서 언급했던 내용이다.
나이브 베이즈 모델에 있어서 가장 중요한 가정은,
- 분류를 위한 변수 $ {\bf z} $ 를 조건으로 할 때 입력 변수 $ {\bf x}_1,…,{\bf x}_D $ 들이 서로 독립적이라는 것.
타겟 결과가 기록된 학습 데이터가 주어지면 MLE 를 사용하여 이를 나이브 베이즈 모델에 적용 가능하다.
- 베이즈 이론을 이용하면 손쉽게 역확률을 구해낼 수 있기 때문
만약 변수 $ {\bf z}_k $ 가 주어졌을 때의 각 클래스 $ K $ 별로 얻어지는 데이터의 확률 분포가 가우시안 분포라고 가정하면,
- 나이브 베이즈 모델은 이 때 사용되는 가우시안 모델의 공분산이 Diagonal 이라는 것을 함축하게 된다.
  - 그 결과 타원형 등고선을 가지게 된다.
- 2장에서 다룬 내용이니 상기하기 바란다.
나이브 베이즈의 장점
- 나이브 베이즈 모델은 입력 공간의 차원이 높을 때 매우 유리하다.
- 또 이산 변수가 연속변수를 모두 포함하는 입력 데이터에서도 사용 가능하다.
  - 적절한 모델을 이용하여 각각을 개별적으로 표현하는 것도 가능하기 때문이다.
- 이러한 모델에서 조건부 독립 가정은 꽤나 강력한 무기가 된다.

Directed Factorization

우리는 앞서 DAG의 부분집합들을 이용하여 결합 확률 분포를 어떠한 조건부 확률 분포의 곱의 형태로 분해하는 과정을 살펴보았다.
- d-separation 을 이용하여 조건부 독립적인 상태들의 집합들로 표현 가능하다.
이를 좀 더 명확하게 하기 위해서 이제부터 그래프들을 하나의 필터(filter)처럼 취급하는 작업을 진행할 것이다.

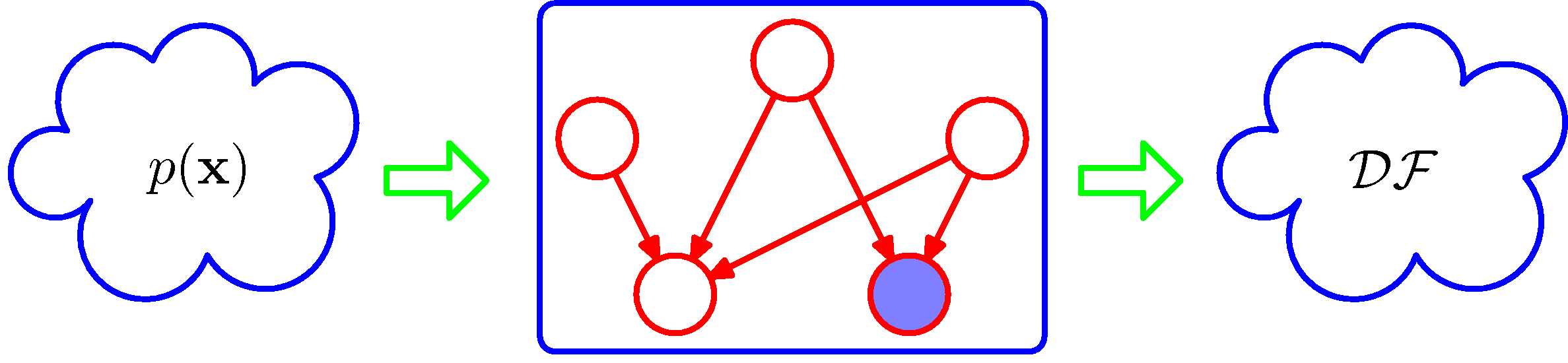
figure8.25

해당 그래프를 통과 가능한 모든 $ p({\bf x}) $ 의 부분 집합을 DF라고 한다.
그래프는 D-separation 기법을 적용해서 얻어진 모든 조건부 독립 속성들로 구성된 요소들의 집합이라 생각할 수 있다.
- 따라서 이러한 조건부 독립 속성을 만족하는 분포만 통과가 가능하다.
사실 어떠한 종류의 분포일지라도 사용이 가능하다.
- 이산 분포인지 연속 분포인지는 상관 없다.
- 그래프레 포함된 독립 속성 외에 추가적인 독립 속성을 가진 분포도 사용될 수 있다.

Markov Blanket

D 개의 노드를 가진 방향 그래프로 표현된 결합 분포 $ p({\bf x}_1,…,{\bf x}_D) $ 를 고려하자.
변수 $ {\bf x}_i $ 의 조건부 분포를 고려하는데 모든 남은 변수 $ {\bf x}_{j \neq i} $ 가 조건이 된다고 생각해보자.
이러한 경우 인수 분해 속성을 이용하여 이 조건 분포를 다음과 같은 분포로 표현 가능하다.

$p({\bf x}_i|{\bf x}_{j \neq i}) = \frac{p({\bf x}_1,...,{\bf x}_D)}{\int p({\bf x}_1,...{\bf x}_D)d{\bf x}_i} = \frac{\prod_k p({\bf x}_k|pa_k)}{\int \prod_k p({\bf x}_k|pa_k) d{\bf x}_i}$

추가적인 정리가 가능한데 변수 $ {\bf x}_i $ 에 대해 함수적 종속성이 없는 요소 $ p({\bf x}_k|pa_k) $ 는 $ {\bf x}_i $ 의 적분식 밖으로 빠진다.
- 결국 분모와 분자에서 사라지게 된다.
따라서 남은 조건을 고려하면 다음과 같다.
- 노드 $ {\bf x}_i $ 자신인 조건부 분포 $ p({\bf x}_i|pa_i) $
- $ {\bf x}_i \in pa_k $ 인 노드 $ {\bf x}_k $ 를 위한 조건부 분포 $ p({\bf x}_k|pa_k), ({\bf x}_i \in pa_k) $
이걸 $ {\bf x}_i $ 중심으로 도식화하면 다음과 같다.

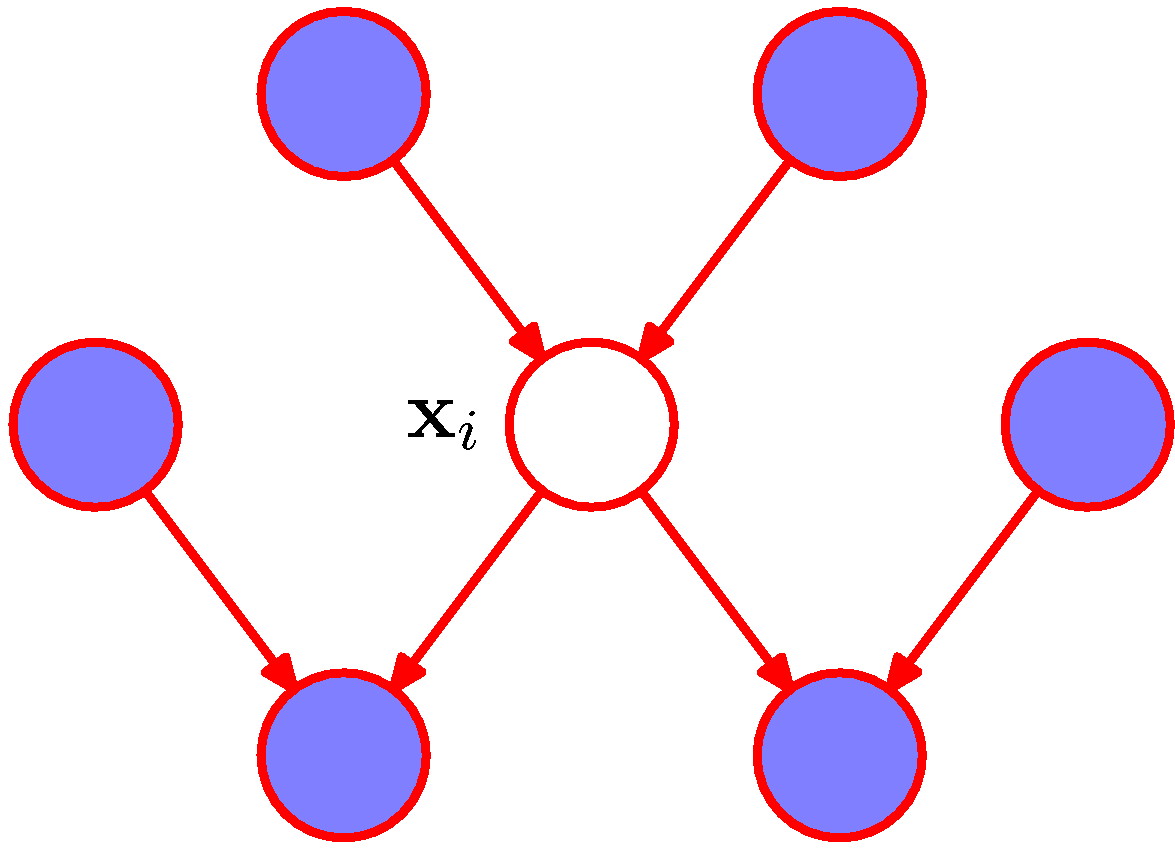
figure8.26

하나의 노드를 중심으로 해당 노드의 부모 노드, 자식 노드, 자식 노드에 연결된 자식의 부모 노드 집합을 Markov blanket 이라고 한다.
- 또는 Markov boundary 라고도 한다.
한 노드는 그 노드의 Markov blanket 이 모두 주어지면 네트워크와 조건부 독립성이 성립됨. (d-separation)

Chapter. 8

8.2.1. 3개의 그래프 예제 (Three example graphs)

8.2.2. D-Sepration