- 패턴 인식 분야에 있어 불확실성(uncertainty)은 가장 중요한 개념 중 하나.
- 이번 장에서 간단하게 확률 이론을 살펴본 뒤에 이를 결정 이론(decision theory)과 엮는 과정을 살펴볼 것이다.
- 불확실성(uncertainty)이 발생하는 이유
- 충분하지 못한 데이터로 인해.
- 관찰된 데이터에 포함된 노이즈(noise)로 인해.
- Probability Theory
- 불확실성을 정확하고 정량적으로 표현할 수 있는 수학적인 프레임워크를 제공.
- Decision Theory
- 불완전하고 모호한 정보로부터 최적에 예측안을 마련할 수 있다.
- 간단한 예제를 통해 우선 확률 이론에 대해 살펴보도록 하자. (사과와 오렌지 예제)
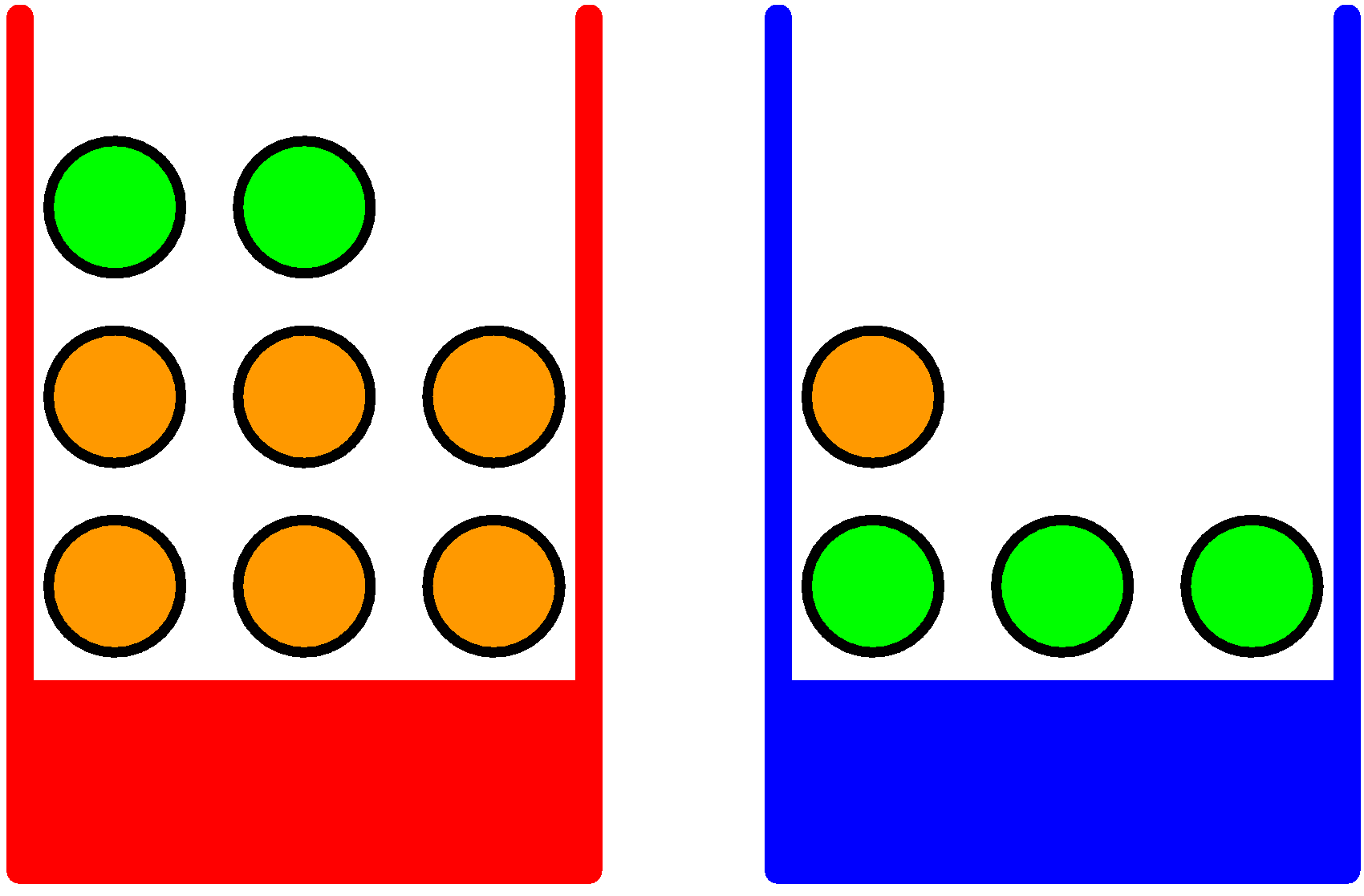
- 주어진 환경
- 두 개의 박스가 주어지고 하나는 빨간색 박스, 하나는 파란색 박스가 존재.
- 빨간색 박스에는 2개의 사과와 6개의 오렌지.
- 파란색 박스에는 3개의 사과와 1개의 오렌지.
- 우리는 임의로(랜덤) 하나의 박스를 선택해 하나의 과일을 꺼낸다.
- 이 때 “오렌지가 나왔는데 이 오렌지가 파란 박스에서 나왔을 확률은?” 같은 질문에 대답할 수 있어야 한다.
- 빈도론에 입각해서 각각의 확률 값들을 정량화 할 수 있다.
- 이번 절에 언급되는 내용은 너무 간단한 내용이라 자세하게는 설명하지 않는다.
- 확률식에 중요한 법칙 중 합의 법칙(sum rule), 곱의 법칙(product rule)에 대해 알아보자.
- 아주 간단한 법칙이지만 매우 중요하다.
- sum rule
- product rule
- 간단하게 이와 관련된 수식을 정리해본다.
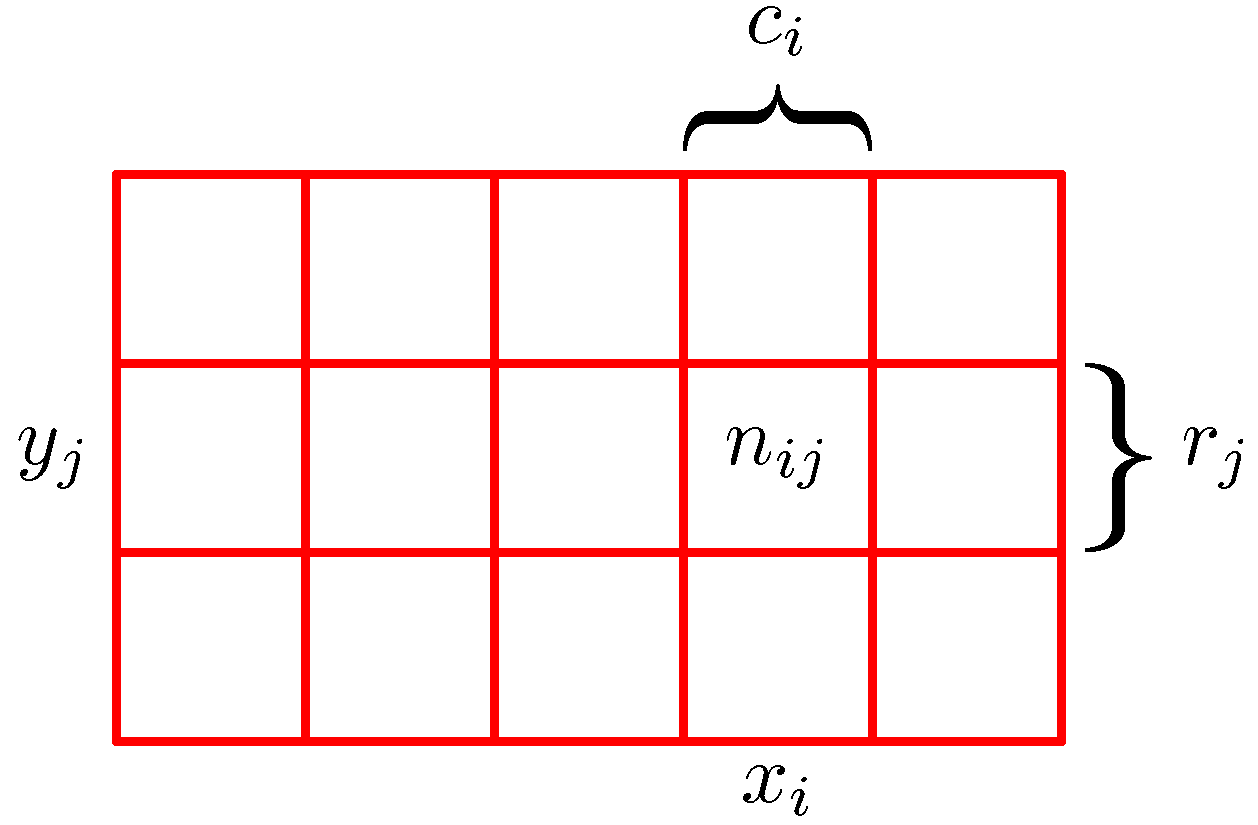
- 이 때 \(c_i=\sum_{j}{n_{ij}} \) 이다. 이로부터 합의 법칙을 유도할 수 있다.
- 곱의 법칙도 간단하다.
확률의 법칙
- sum rule
- product rule
- 다음으로 이를 이용하여 베이즈 정리를 기술한다.
- 너무 유명한 식이다. 더 이상의 설명은 생략한다. (잘 모르겠다면 다른 확률 교재를 참고하자.)
- 여기서 \( P(X) \) 는 확률 합을 1로 만들기 위한 정규화 상수가 된다.
- 이것을 그대로 사과와 오렌지 예제에 적용하면 다음과 같다.
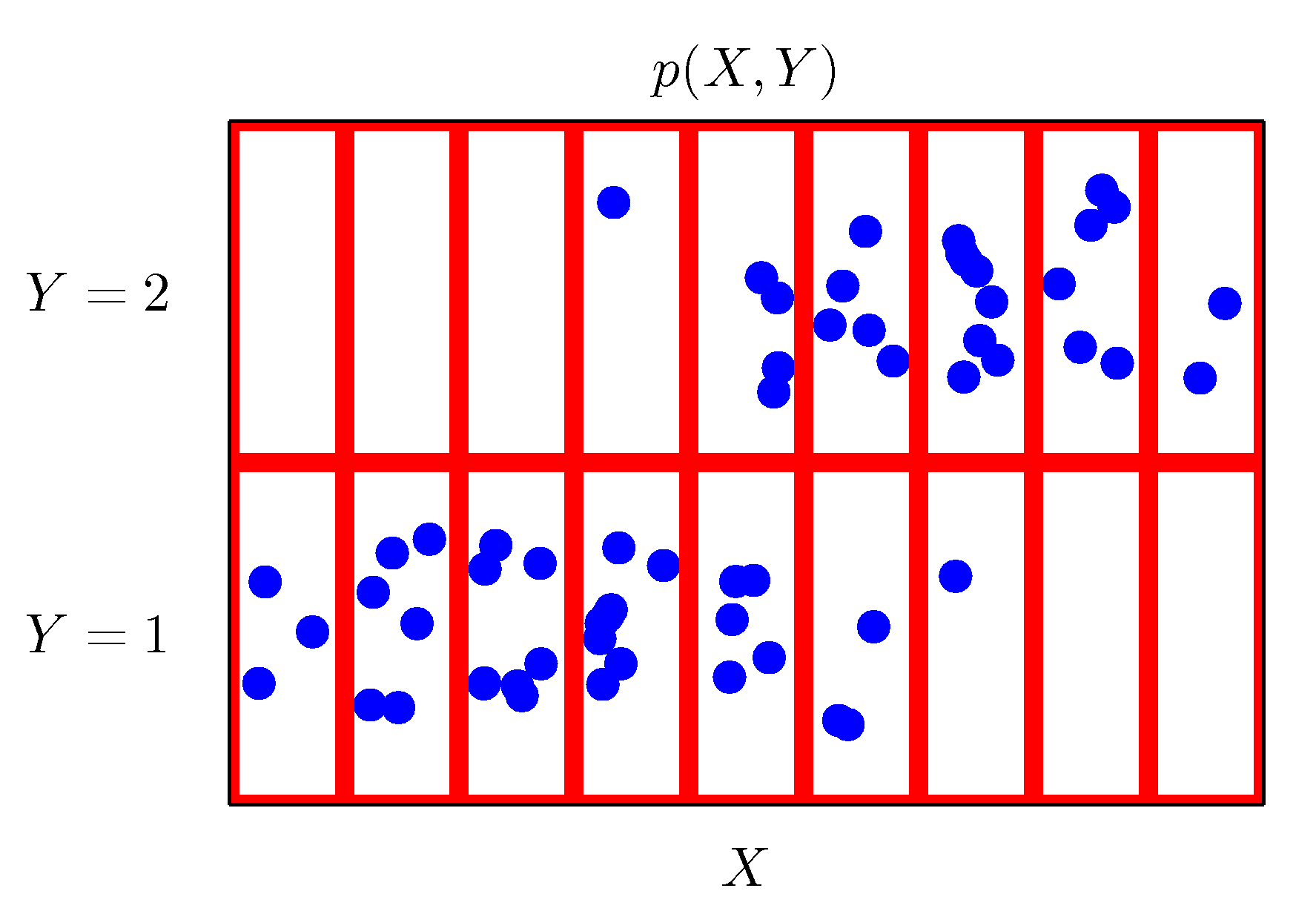
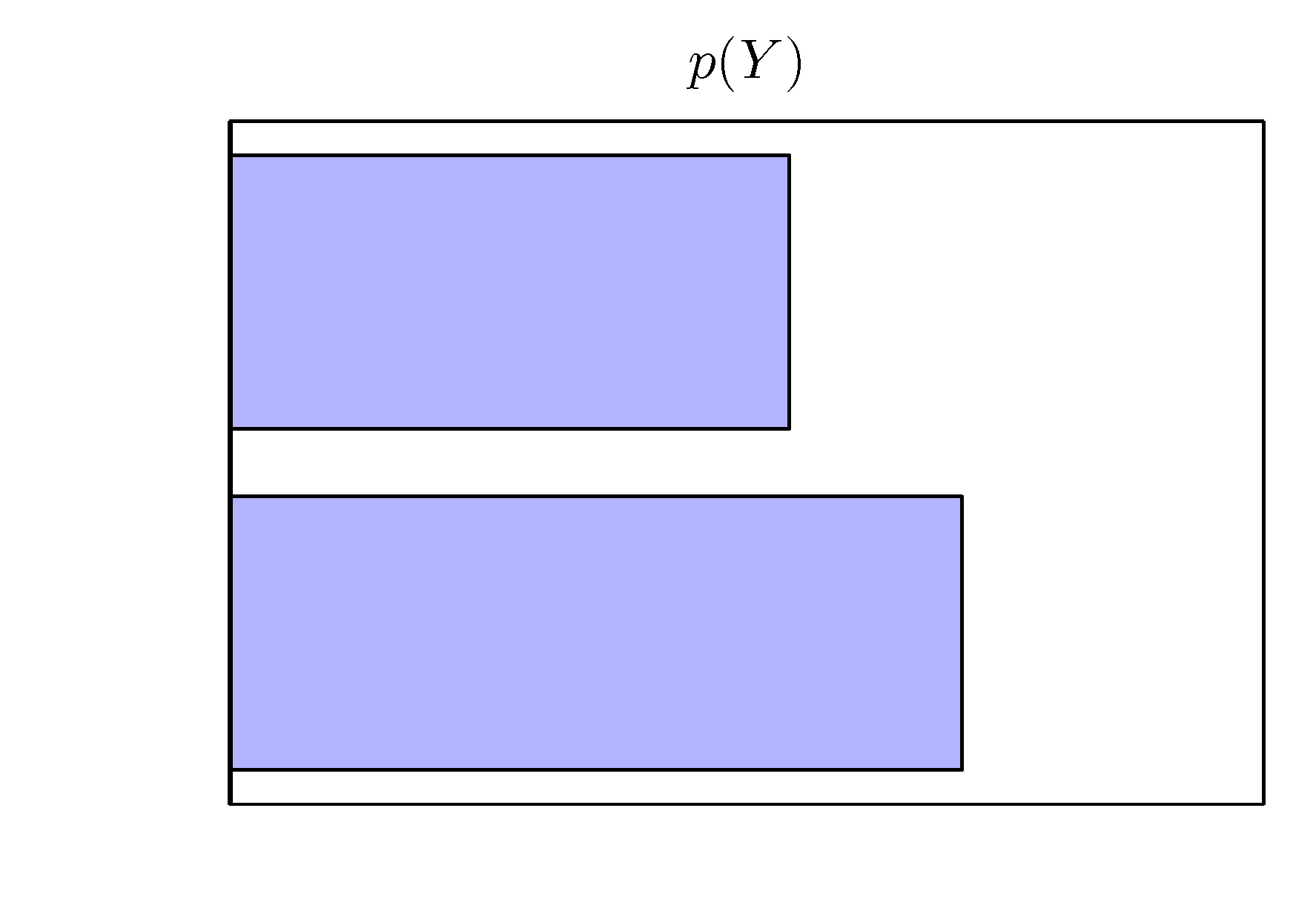
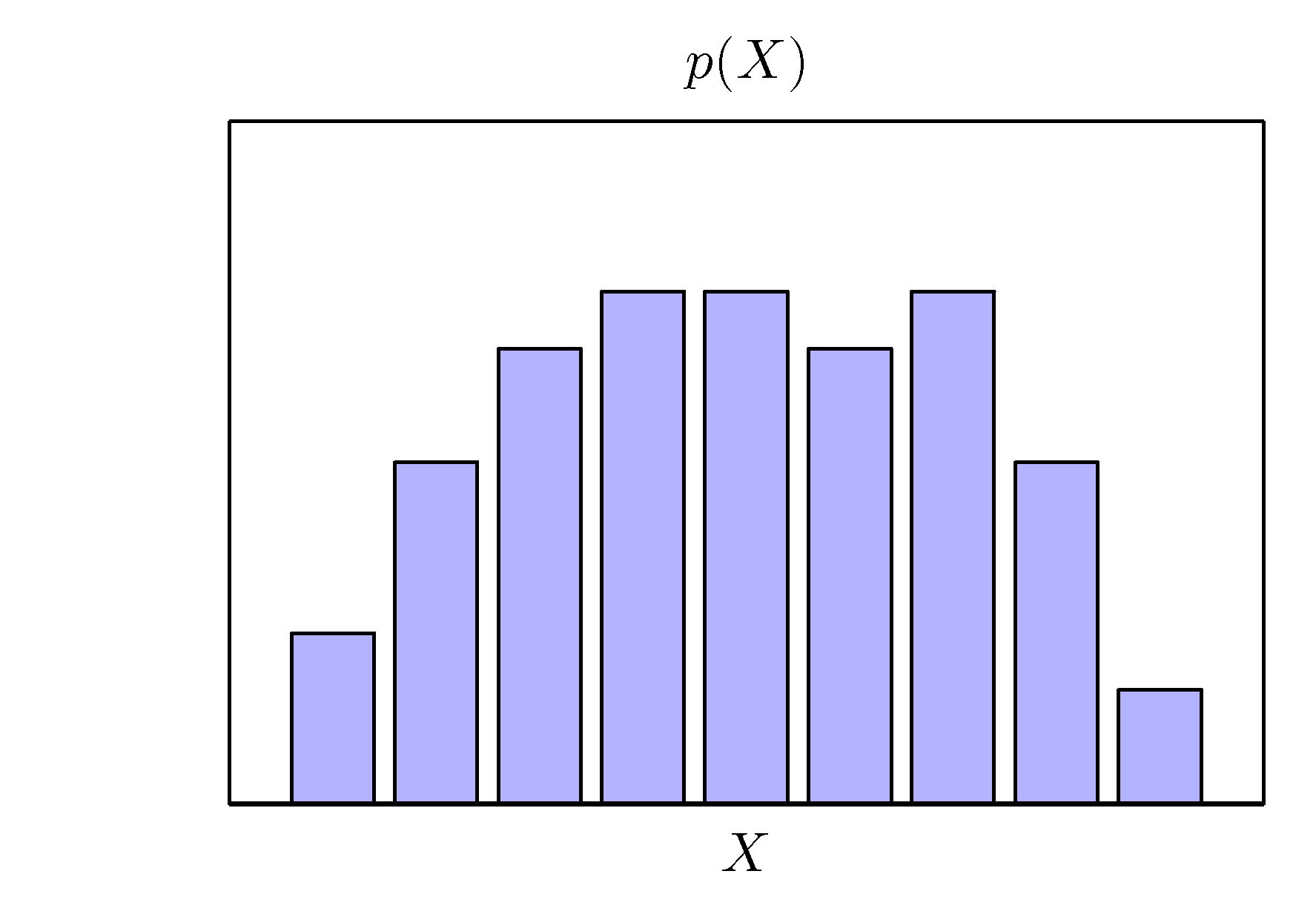
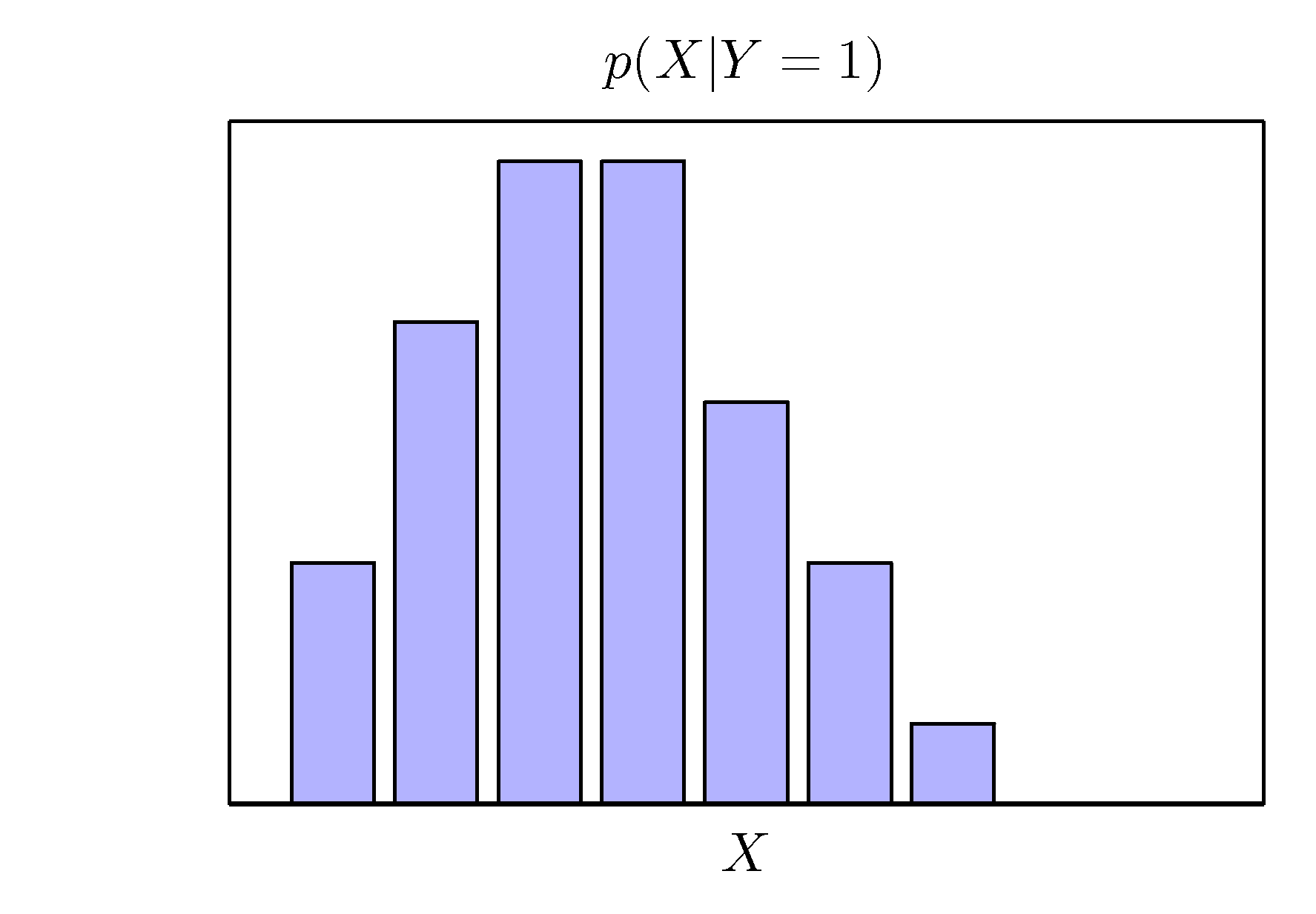
1.2.1. 확률 밀도 (Probabilty densities)
- 지금까지 이산(discrete)적인 사건에 대한 확률 식을 살펴보았다.
- 이번 절에서는 연속적인 입력 값에 대한 확률 식을 고려해 보도록 한다.
- 실수인 범위의 입력값에 대해서는 확률값을 모두 나열하기 어렵다.
- 예를 들어 몸무게 60kg와 60.0001kg 사이에도 많은 실수 값이 존재한다.
- 이런 경우 각각의 실수 값에 개별적인 확률값을 부여하기는 불가능하다.
- 따라서 확률 값을 구간(range)으로 표현한다. : \( R(x, x+\delta{x}) \)
- 여기서 \( \delta{x} \) 가 0에 수렴한다면, 값은 \( p(x) \) 가 된다.
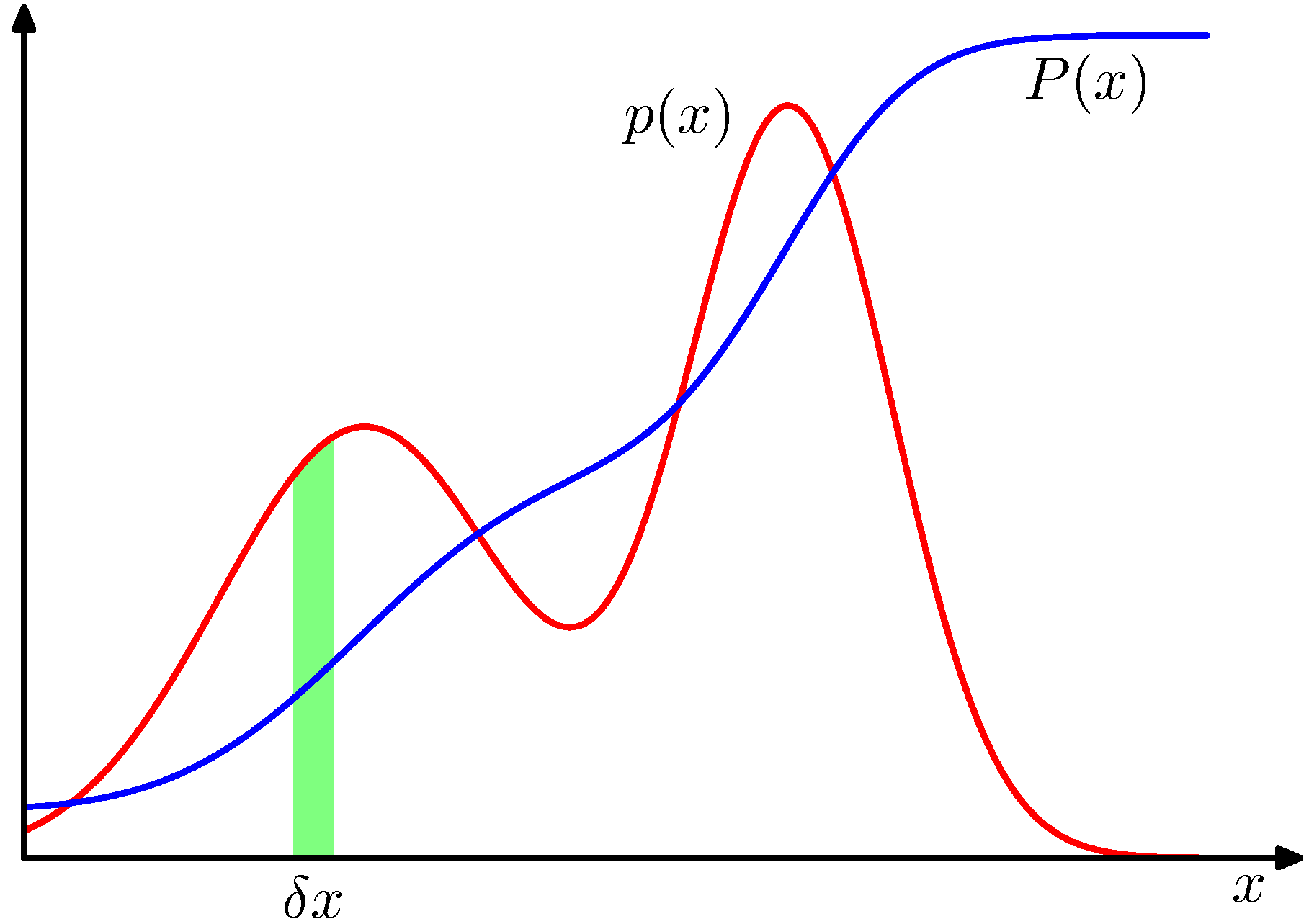
- 여기서 \( P(x) \) 는 확률의 누적식(즉, CDF)이 되고 \( p(x) \) 는 확률 밀도(probability density)가 된다.
- 확률 밀도는 다음과 같은 성질이 있다.
-
이 교재는 PDF 에 대한 설명이 자세히 나오지는 않는다. 대략적인 것은 이해하고 있으리라 생각한다.
- 입력되는 변수가 비선형인 값으로 변경되는 경우가 있을 수 있다. (예를 들면 \( y \rightarrow x^2 \) 과 같은 식)
- 이 경우 확률식도 함께 변환되어야 되는데 다음과 같은 성질을 만족한다.
- 결국 다음과 같이 사용 가능하다.
- \( x \) 에 대해 확률 함수 \(p(x)\) 가 주어졌을 때 구간 \( (-\infty, z) \) 에 대한 확률 값을 누적 분포 함수 (cumulative distribution function)라고 한다.
- 그림 1.12 를 보면 이해하기 쉽다. \( P(x) \) 를 미분하면 \( p(x) \)를 얻을 수 있다.
- 확률 함수는 벡터(vector) 변수에서도 동일하게 적용할 수 있다.
- 예를 들어 어떤 연속 변수 \(x\) 가 \( \{ x_1, …, x_D \} \) 로 구성된다면,
- 확률 함수는 \( p({\bf x}) = p(x_1,…,x_D) \) 로 고려될 수 있다.
- 마찬가지로 다음의 제약 조건이 성립한다.
- 연속 확률 밀도(PDF)에서도 sum rule, product rule 은 모두 적용 가능하다. (증명은 생략.)
- 착각해서는 안되는 부분은 실제 확률 값과 밀도 함수의 반환 값은 서로 다른 성질이다.
- 연속적인 확률 밀도에서 \( p(x) \) 를 통해 얻어진 실수 값은 실제 확률 값이 아니라 확률 함수의 반환 값이다.
- 따라서 아래 식은 연속 확률 함수에 대한 sum, product rule 을 의미한다.
- 이후에도 혼동이 되지 않으려면 PMF 와 PDF 의 차이를 명확하게 이해하여야 한다.
- 간단히 정리하자면 PMF 의 값은 그 자체로 확률 값이지만 PDF 의 경우 그 자체로 확률 값이 아니라 구간 적분해야 확률값이 된다.
1.2.2. 평균과 공분산 (Expactations and covariances)
- 확률식에서 주어진 데이터에 대한 무게 중심을 구하는 것은 매우 중요한데, 주로 평균이 사용된다.
- 여기서는 함수 결과에 대한 평균 값을 설명한다. (각각 이산, 연속 확률 함수이다.)
- 연속 함수에 대한 평균값을 근사하는 방법이 있는데, 최대한 많은 샘플을 생성해서 샘플을 통해 평균을 구하는 방법이 있다.
- 이 때 \( N \rightarrow \infty \) 이면 이 근사 값은 실제 값과 거의 같아지게 된다.
- 그리고 위와 같은 식이 쓸데없이 자꾸 언급되는 이유는 이후에 연속 확률 함수에 대한 샘플링 기법을 소개하기 위함이다.
- 이것도 뒤에 자세히 나오니 그냥 간단하게 확인만 하고 넘어가자.
- 간혹 여러 개의 변수를 사용하는 함수에 대해 평균 값을 표기할 경우가 있다.
- 이 때에는 평균에 사용하는 주변수를 함께 기술한다.
-
위의 경우에는 \( E_x[f(x,y)] \) 자체가 \( y \) 에 대한 함수처럼 사용될 수 있다.
-
조건부 평균(기대값)도 마찬가지로 정의할 수 있다.
- 이에 대한 분산은 다음과 같다.
- 이 식은 다음과 같이 전개되기도 한다.
- 지금까지 함수 \( f \) 에 대해서 전개했지만 이를 변수 \( x \) 로 놓고 처리해도 식이 성립한다. ( \( f(x)=x \) )
- 2개의 랜덤변수 \( x \) 와 \( y \) 에 대해 공분산(covariance)은 다음과 같이 정의된다.
- 위의 식에서 \( x \) 와 \( y \) 는 벡터로 확장 가능하다. (이 책은 벡터를 볼드체로 표현한다.)
1.2.3. 베이지언 확률 (Bayesian probabilities)
- 지금까지 확률을 고려하는데 있어 임의적으로 발생하는 사건에 대한 빈도를 바탕으로 식을 전개해 왔다.
- 이런 방식을 빈도론자(Frequentist) 방식이라고 한다.
- 이제 이와는 대조적인, 베이지언(Bayesian) 방식에 대해 알아보도록 하자
- 간단하게 이야기하자면 베이지언 관점에서는 모든 것이 불확실하다. (물론 이를 정량화한다.)
- 베이지언은 확률을 빈도의 개념이 아니라 믿음의 정도로 해석하는 관점이다.
- 빈도론적인 입장에서는 실제 데이터가 존재해야 불확실성을 정량화할 수 있다. (빈도를 통해 모델링 하므로)
- 하지만 베이지언 입장에서는 확률이라는 개념이 믿음의 정도를 나타내므로 사건이 발생하지 않은 경우에도 확률을 부여할 수 있다.
- 따라서 베이지안 방식에서는 좀 더 불확실한 경우에도 모델링이 가능하다.
- 예를 들어 ‘북극 얼음이 이번 세기에 녹아 없어질 확률’ (실제로는 아직까지 일어난 사건이 아님)을 서술할 수 있다.
- 사전 확률 모델을 작성하고 일부 측량 정보를 통해 사후 확률을 보정하는 방식을 취한다.
- 이게 약간 뜬구름 잡는 이야기같지만, 원해서 그리 된 것은 아니고 교재에서 설명한 예제가 너무 개떡 같아서 그렇다.
- 어차피 이후에 자세히 설명되므로 일단은 두 종류의 확률 추론 방식이 있다고만 알아두자.
- 이 중 빈도론은 고전적 확률 추정이고 (그래봤자 20세기 초) 베이지언 방식은 그나마 최근 경향이다.
- 엄밀히 말하면 베이지안 방식은 아주 오래전부터 언급되었으나 최근에 다시 주목받고 있음.
- 베이지언 방식이 무엇인지 아주 간단하게만 살펴보고 가자.
- 베이지언 관점은 확률의 개념을 빈도가 아닌 믿음의 정도로 고려하는 것이다.
- 물론 맹신적인 믿음은 아니고 (‘내가 이번주엔 로또에 당첨될꺼야!’) 전문가의 기준으로 확률적 모순이 없는 확률값을 제공해야 한다.
- 개념은 이렇지만 실제 사용시에는 일정한 사용 패턴을 가지게 되므로 (에를 들어 사전 분포를 도입한다거나) 그냥 익숙해지면 된다.
- 앞서 살펴본 Curve Fitting 문제에서는 모수 \( w \)가 알려지지 않은 고정된 값으로 여겨졌다. (unknown but fixed)
- 하지만 베이지안 방식은 모든 값이 확률 값이므로 이를 하나의 확률 변수로 고려하게 된다.
- 이제 베이즈 법칙을 이용하여 \( w \)에 대한 불확실성을 기술할 수 있다.
- 이 식은 관찰되는 데이터가 존재하기 이전에 이미 \( p({\bf w}) \) 를 통해 \( w \) 의 불확실한 정도를 수식에 반영하고 있다.
- 이는 모수(parameter)에 대한 사전(prior) 확률 분포를 의미한다.
- 실제 데이터를 통해 예측된 \( w \) 의 확률(likelihood)를 조합하여 실제 \( w \) 의 사후 확률(posterior)를 기술하고 있다.
- 최종적으로 다음과 같은 식을 만들어낼 수 있다.
- 분모로 포함되는 \( p(D) \) 의 경우 확률식에 대한 정규화 요소로 다음과 같이 정의된다.
- 위의 식 또한 무시하면 안되는데, 모델 선택(model selection)과 관련 깊은 수식이다.
- 1장에서는 대충 감만 익히고 2장에서 더 자세히 살펴보자.
- 애초에 1장에서 아무런 배경설명 없이 베이지안 추론을 설명하는 것 자체가 무리인듯 싶다.
-
그냥 마무리하기는 아쉬우니 빈도론자(Frequentist)와 베이지언(Bayesian)의 가능도 함수에 대한 입장 차를 좀 살펴보자.
- Likelihood in Frequentist
- \( {\bf w} \) 는 알려지지 않은 고정된 파라미터 값이다. (그리고 이를 추정하게 된다.)
- Maximum Likelihood 가 대표적인 추정자(estimator)로 보통 \( p(D | {\bf w}_{ML}) \) 를 최대로 만드는 \( {\bf w}_{ML} \) 를 구한다.
- 앞서 가정한 바와 같이 \( {\bf w}_{ML} \) 은 고정된 값이지만 알려져있지 않기 때문에 데이터로부터 추정해야 한다.
- 기계 학습 분야에서는 주로 log-likelihood 를 사용한다. (참고로 \( \log(\cdot) \) 함수는 단조 증가함수임)
- 통계적으로 정확도를 평가하기 위한 방법으로 Boostrap 기법(Sampling with Replacement 방식) 등을 활용하기도 한다.
- (가장 유명한) Cross Validation 기법이 여기에 속한다.
- Likelihood in Bayesian
- 파라미터 \( {\bf w} \) 를 랜덤변수로 간주하여 확률 분포로 사용한다. 이 때 \( D \) 는 물론 고정된다.
- 따라서 \( {\bf w} \) 는 고정된 값으로 얻어지는 것이 아니라 확률 함수 등으로 얻어지게 된다.
- 물론 실제 사용시에는 얻어진 확률 함수의 평균(mean)이나 최빈값(mode) 값을 대신 고정된(fixed) 값으로 사용할 수도 있다.
- MAP 등을 생각하면 쉽다.
- \( {\bf w} \) 가 확률 분포이므로 사전(prior) 지식을 자연스럽게 포함할 수 있다.
- MLE 에서는 동전을 3번 던져 앞면이 모두 나온 경우 파라미터 \( \theta \)의 값이 그냥 1이 된다.
- 하지만 베이지언 방식에서는 사전 확률로 인해 이 값이 보정된다.
- 따라서 빈도론자 방식보다 덜 극단적인 결과를 얻는다.
- 파라미터에 대한 사전(prior) 분포를 어떻게 정해야 하는지에 대한 논쟁이 있는데 이후에 더 자세히 살펴볼 것이다.
- 파라미터 \( {\bf w} \) 를 랜덤변수로 간주하여 확률 분포로 사용한다. 이 때 \( D \) 는 물론 고정된다.
- 이 교재는 베이지언 방식을 중점적으로 다루고 있다. 물론 빈도론자의 방식도 필요하면 다룬다.
- Bishop 아저씨는 베이지언 덕후이다.
- 아직까지 베이지언 방식이 널리 활용되지 못하고 있는데, 사후 확률을 구할 때 사용되는 주변 확률 분포를 구하기가 까다롭기 때문이다.
- MCMC(Markov Chain Monte Carlo, 11장) 등과 같은 Sampling 기법의 등장으로 최근에 많은 기술적 진보를 이루었다.
- 또 최근에는 이에 대한 대안으로 Variation Bayes, Expectation Propagation 등이 등장했다. (10장)
- 이후에 자세히 살펴볼 것이다.
- 하지만 별도의 교재를 통해 간단한 개념을 미리 파악하는 것이 좋다.
- 왜냐하면 이 교재에서는 기초적인 지식을 설명하지 않는 경우가 많기 때문.
1.2.4. 가우시안 분포 (Gaussian distribution)
- 2장에서 여러가지 확률 분포를 살펴보겠지만 우선 가우시안 분포에 대해서는 간단하게 확인하고 넘어가자.
- 근데 2장에서 가우시안 분포를 다시 자세히 설명하게 된다.
- 마찬가지로 1장은 개념 정도만 확인하고 2장에서 다시 살펴보면 된다.
- 도입부에 뜬금없이 가우시안 분포를 하나의 절로 할애한 것을 보면 앞으로 얼마나 자주 등장할지 예측할 수 있다. (암담하다.)
- 가우시안 확률 분포는 다음과 같읕 식으로 표현할 수 있다.
- 이 확률 분포는 2개의 파라미터(모수, parameter)가 존재한다.
- \( \mu \) : 평균(mean)
- \( \sigma \) : 표준편차(standard deviation)
- 또한 표준 편차 제곱(즉, 분산)의 역수 \( \beta=1/\sigma^2 \) 를 정확도(precision)라고 정의한다.
- 보통 수식 전개상 분산보다는 정확도를 기준으로 계산하는 것이 더 편리한 경우가 많기 때문.
- 이 교재에서도 수식을 전개할 때 정확도를 더 많이 사용한다.
- 하지만 어차피 분산과 같은 개념으로 여겨지게 된다.
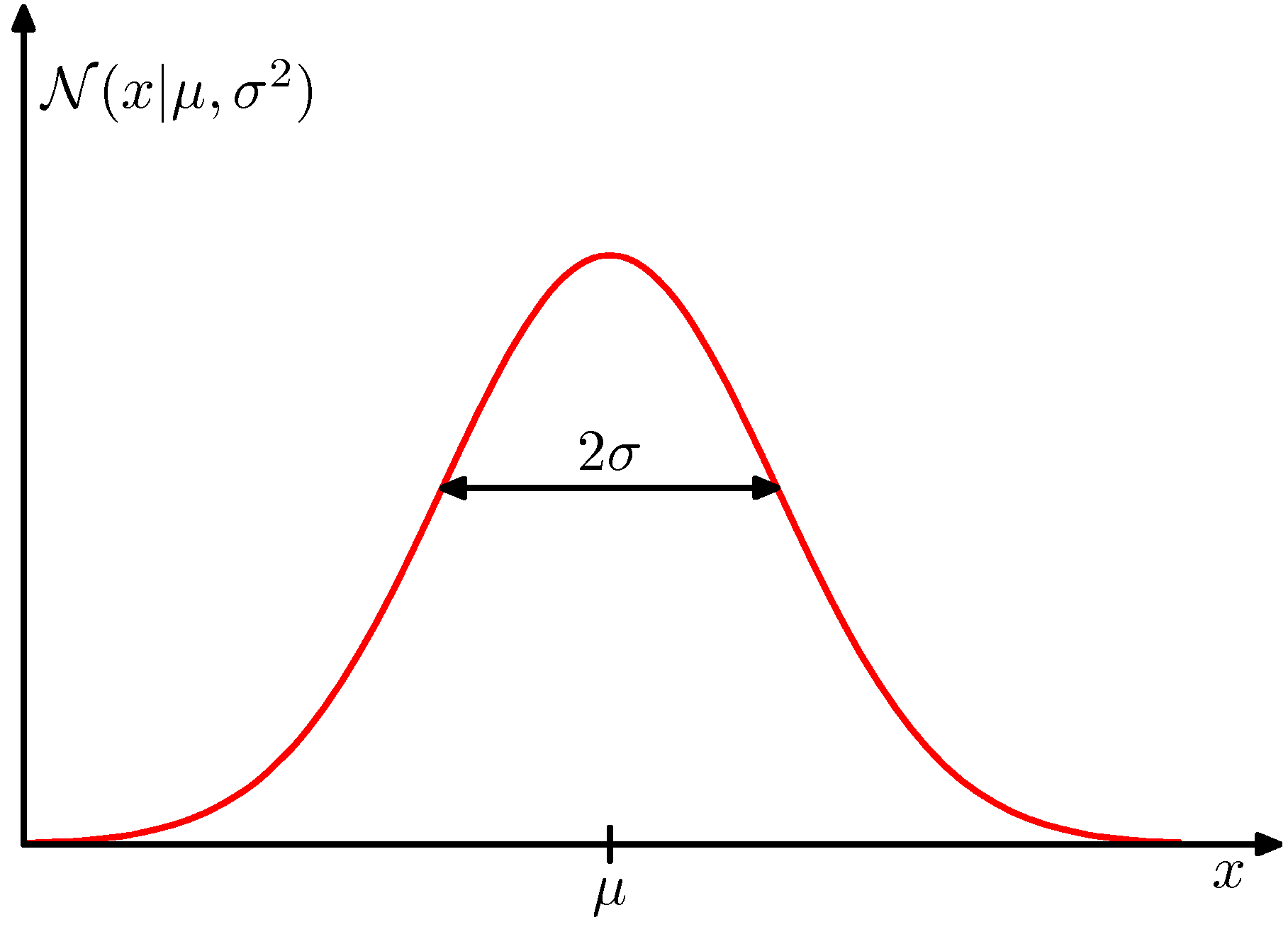
- 가우시안 분포를 정규 분포라고 부른다. 이 분포는 다음과 같은 성질이 있다.
- 앞서 설명한 것은 \( x \) 가 1차원(단변량)인 경우이고 이를 \( D \) 차원으로 확장 가능하다.
- 사실 이것이 가우시안 분포의 진정한 장점이다.
- 이를 다변량(multinomial) 가우시안 분포라고 부른다. 식은 다음과 같다.
- \( \Sigma \) 행렬은 \( D \times D \)크기의 정방행렬로, 공분산(covariance)이라 부른다.
- 이제 하나의 관찰 데이터 집합 \( {\bf x}=(x_1,…,x_N)^T \) 이 주어졌다고 해보자.
- 이 데이터 집합 하나가 관찰될 수 있는 확률은 과연 어떻게 될까?
- 각각의 데이터가 발현되는 가능성은 서로 독립적이므로( 즉, i.i.d ) 이 확률값들은 모두 독립 사건으로 처리할 수 있다.
- 즉, 각 사건이 독립적이기 때문에 확률의 곱으로써 표현이 된다.
- 하나의 데이터는 동일한 분포로부터 발현되었을 것이므로 이 확률을 다음과 같이 표기할 수 있다.
- 이것을 그림으로 나타내면 다음과 같다.
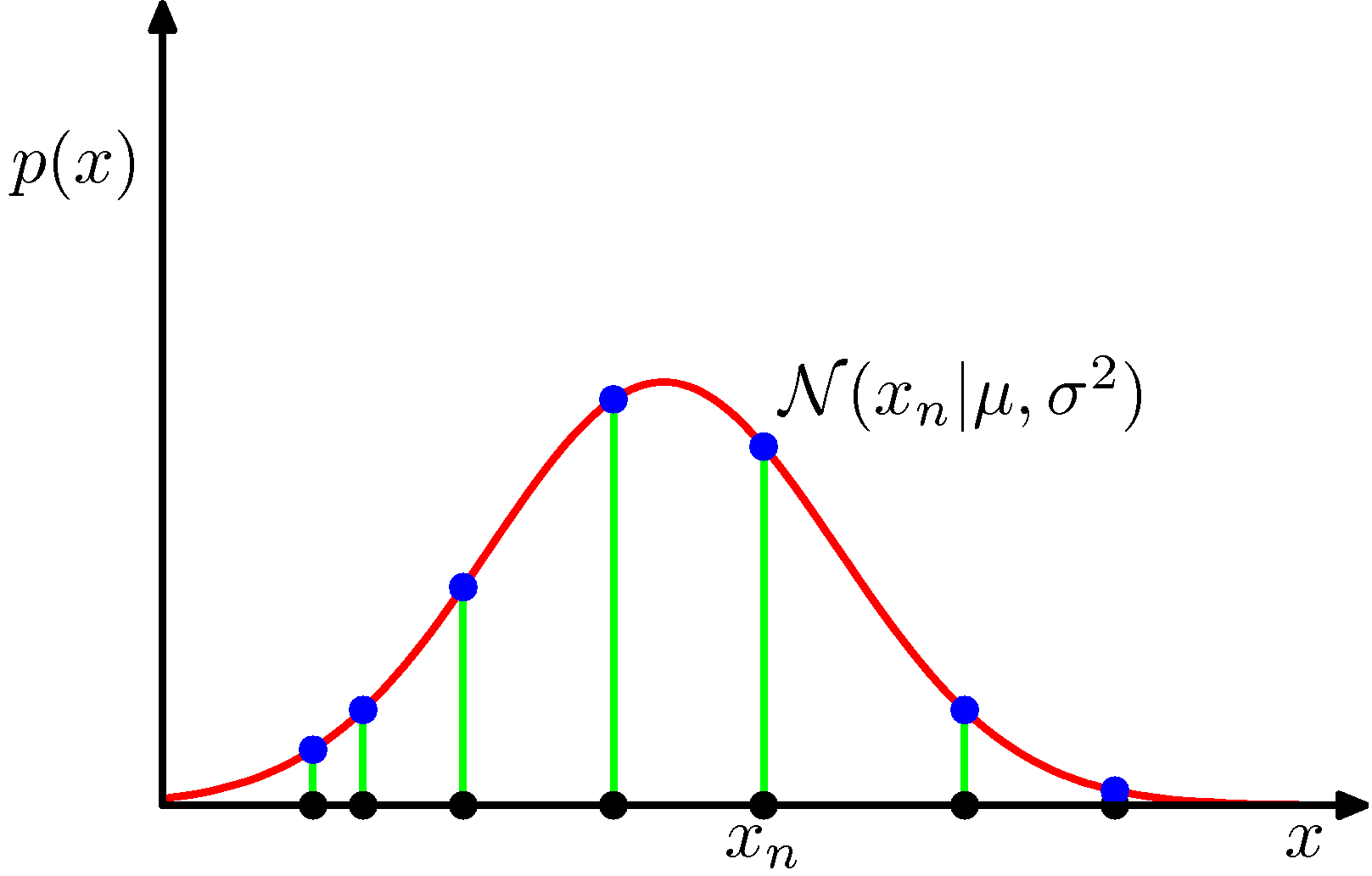
- 그럼 어떤 관찰 데이터가 하나의 가우시안 분포를 따른다고 생각해보자.
- 우리가 얻는 것은 관찰 데이터 집합이고 이를 이용하여 원래의 가우시안 분포를 결정하는 문제가 보통 우리에게 주어지는 문제들이다.
- 쉽게 말해 주어진 샘플이 어떻게 생겨먹은 가우시안 분포에서 나왔는지를 맟추어보라는 이야기이다.
- 이 경우 해를 구하는 것은 매우 간단한데 그냥 특정 가우시안의 평균과 분산 값만 결정하면 된다.
- 즉, 이제 우리는 \( p({\bf x}\;|\;\mu, \sigma^2) \) 를 이용하여 이러한 관찰 결과를 만들어낼 만하다고 생각할 수 있는 가장 타당한 \( \mu \) 와 \( \sigma \) 를 찾기만 하면 된다.
- 이를 바로 파라미터 추정이라고 부른다.
- 주어진 데이터를 이용하여 선택한 모델에 대한 파라미터, 즉 모수를 결정하는 문제.
- 계산을 편하게 하기 위해 \( \log \) 를 붙여 식을 전개한다. (단조증가)
- 이 함수의 값을 최대로 만드는 파라미터의 값은 다음과 같다. (모수가 2개이므로 편미분을 이용하면 된다.)
- 가능도 함수를 가장 크게 만드는 모수 값을 추정하므로 이를 MLE (Maximum likelihood estimation)라고 한다.
- 많은 교재에서 이를 그냥 ML 로 표기하는 경우가 많다.
- 그러나 ML 이 Machine Learning 이란 단어로도 많이 사용되어 혼동된다.
- 따라서 여기서는 ML 대신 MLE 만을 사용한다. (물론 변수 등의 첨자로 사용될 때에는 ML로 표기하기도 한다.)
- MLE 를 통해 얻어진 결과는 각각 샘플에 대한 평균과 분산 값이다.
- 물론 이 정도는 쉽게 이해하고 있을 것이라 생각한다.
- 이후에 MLE 접근 방식의 한계점에 대해서 다루어질 예정이다.
- 사실 위의 결과에서 분산 값은 bias 되어 있다.
- MLE 에서 보여지는 오버피팅의 한 예이다.
- 이 값들의 평균 값은 다음과 같다. (결국 실제 평균이 된다.)
- 분산 값의 평균은 다음과 같다.
- 위의 식으로부터 얻어진 아래의 분산 값은 unbias되어 있음을 알 수 있다.
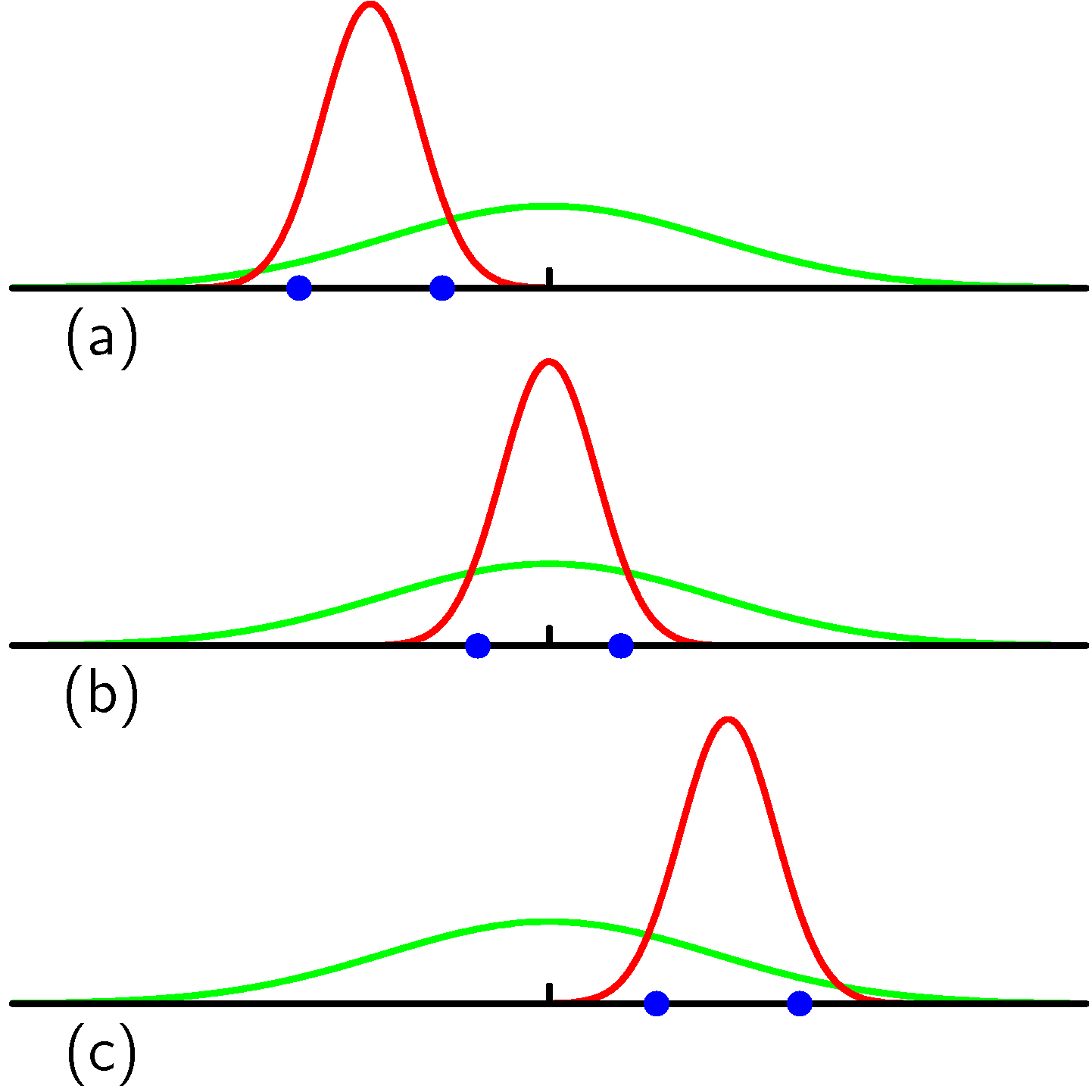
- 위의 그림은 파라미터의 bias, unbias 개념을 이해하고자 제시된 그림이다.
- 세개의 샘플 그룹에 대해 각각의 평균 값을 평균하면 실제 평균값에 가까워진다. (녹색이 실제 모집단의 정규 분포)
- 하지만 분산의 경우에는 세 개의 그룹의 분산 값을 평균해봐도 실제 분산 값에 가까워지지 않는다.
- 이것이 bias, unbias에 대한 내용이다.
- 모수 추정 집합의 평균 값이 실제 모수 값과 같아지면 unbias, 아니면 bias 이다.
- 관련된 내용은 이후에도 나오니까 지금은 대략적인 분위기만 살펴보고 넘어가자.
1.2.5. 다시보는 커브 피팅 (Curve fitting re-visited)
- 앞서 우리는 다항식을 이용하여 커브 피팅 방법을 처리하는 방법을 살펴보았다. (Error 함수를 이용)
- 이제 이 문제를 확률적인 관점에서 해석해보도록 하자.
- 이를 통해 에러 함수(error function)와 정칙화(regularization)에 대한 통찰을 얻을 수 있을 것이다.
- 또한 이를 확장하여 베이지안 관점에서의 해석법을 다루게 될 것이다.
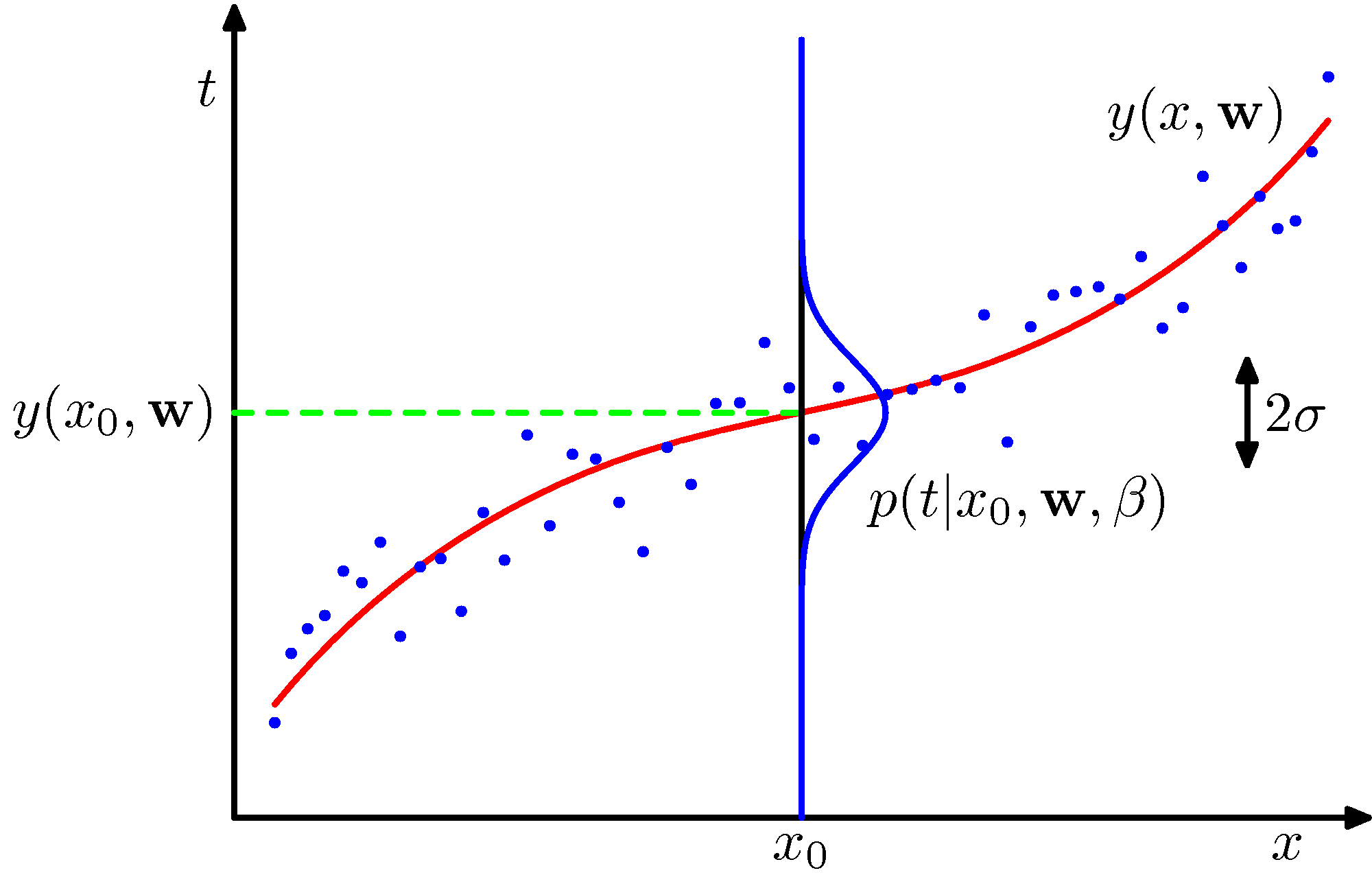
- 커브 피팅 문제의 최종 목표는 임의로 제공된 \( x \) 에 대해 이 때의 \( t \) 값을 예측하여 제공하는 것이다.
- 입력 데이터 \( {\bf x}=(x_1,…,x_N)^T \) 에 대응되는 타겟 값은 \( {\bf t}=(t_1,…,t_N)^T \) 이다.
- 우리는 주어진 환경을 다음과 같이 모델링할 수 있다. (그림을 참고하여 확인하자)
- 앞절에서 다루던 모델과는 약간 다르게 보일 것인데, 노이즈를 가우시안 분포로 고려하고 있다.
- 식의 차이를 잘 살펴보도록 하자. ( 식에 사용된 \( \beta \) 를 눈여겨 봐야 한다.)
- 여기서 \( \beta \) 는 노이즈의 정확도(precision)로써 실제 분포의 분산 값의 역수이다.
- 사실 이해를 하자면 간단한데, 한 점이 주어질 때 이를 나타낼 수 있는 근사식과 정규분포 형태의 노이즈 함수를 조합한 형태의 모델이다.
- 따라서 근사식을 현재 축의 중심에 두고 정규 분포의 형태를 가지는 노이즈 함수를 도입한다.
- 보통 가우시안 분포의 평균(mean) 파라미터에 상수(const)만을 사용하는 것이 일반적인 형태이나 이렇게 함수가 올 수도 있다.
- 평균이 들어올 자리에 \( y \) 함수가 들어앉아 있다.
- 처음 보는 형태라고 해서 당황할 필요는 없다.
- 이후에 다루겠지만 선형 가우시안 분포에서는 꽤나 익숙한 형태의 모델이다.
- 가우시안 조건부 분포에서도 많이 활용된다.
- 보통 가우시안 분포의 평균(mean) 파라미터에 상수(const)만을 사용하는 것이 일반적인 형태이나 이렇게 함수가 올 수도 있다.
- 이렇게 정의한 뒤 근사식만 결정되고 나면, 나머지 실제 값들과의 오차율은 에러 함수에 사용된다.
-
그림을 보면서 곰곰히 따져보면 그리 어려운 내용은 아니다.
- 자, 이제 실제 샘플 데이터를 이용하여 해당 데이터가 존재할 확률을 정의해보자.
- Generative 모델이므로 분포를 통한 파라미터 추론이 그 시작이 될 것이다.
- 가능도 함수를 정의하여 보자.
- 즉, 실제 얻어진 샘플의 결과와 이에 영향을 미치는 모수들의 관계를 확률식으로 표현한다.
- 로그를 취하고 이 가능도 함수 값을 최대로 만드는 파라미터 값을 추정한다.
- 이것으로부터 MLE 를 이용해 얻어지는 \( {\bf w} \) 를 \( {\bf w}_{ML} \) 로 표기한다.
- 여기서 마지막 2개의 텀(term)은 사실 \( {\bf w} \) 를 구하는 것과 아무런 관련이 없다.
- 따라서 첫번째 항의 \( \beta \) 를 잠시 1로 두고 보면( \( \beta=1 \) ) 기존의 에러 함수와 차이가 없다는 것을 이해할 것이다.
- 결국 sum-of-squares error function 이다.
- 다시 MLE 를 이용하여 \( \beta \) 값도 손쉽게 얻을 수 있다. (즉, 이번에는 식을 \( \beta \) 로만 미분한다.)
- 이렇게 얻어진 \( {\bf w} \) 와 \( \beta \) 값을 이용하여 새로운 데이터 \( x_{new} \) 의 타겟 값을 예측해 볼 수도 있다.
- 이런 확률 모델을 predictive 분포라고 부른다.
- 사실 여기서 베이지언 관점으로 식을 확장하여 파라미터 자체에 대한 확률 분포를 추가로 고려해볼 수도 있다.
- 즉, 사용되는 파라미터가 하나의 고정된 값이 아니라 랜덤 변수라고 가정한다.
- 뒤에서 자세히 다루겠지만 일단 \( {\bf w} \) 에 대한 사전(prior) 분포를 기술해보자.
- 여기서 \( \alpha \) 는 분포의 정확도(precision)가 된다.
- \( {\bf w} \) 는 그냥 가우시안 분포를 따른다고 가정한다는 것을 알 수 있다. (이 때의 사전 분포의 평균 값은 0으로 가정.)
- \( M+1 \) 은 벡터 \( {\bf w} \) 의 개수로 다항식 예제에서는 최대 \( M^{th} \) 의 차수를 가지는 다항식이 만들어진다.
- \( \alpha \) 와 같은 변수를 초모수(hyper-parameter) 즉, 하이퍼 파라미터 라고도 부른다.
- 베이즈 룰을 이용하여 식을 다음과 같이 분해 가능하다.
- 이 식에 가우시안 분포를 이용해서 전개를 하면 다음을 얻을 수 있다.
- 결국 앞서 다루었던 정칙화 에러 함수(regularized sum-of-squares error function) 와 식이 동일하다. (1.1절)
- 위의 식에서 \( \lambda \) 만 \( \lambda=\alpha/\beta \) 로 치환하면 된다.
- 이번 절에서는 베이지언 방식의 세부적인 전개 방식은 다루고 있지 않다.
- 어렵다고 느껴지면 3장에서 보도록 하자.
- 베이지언 방식을 사용하면 앞서 사용한 정칙화(regulrazation) 효과를 동일하게 가지게 되는 식이 유도된다는 것만 확인하고 가자.
1.2.6. 베이지언 커브 피팅 (bayesian curve fitting)
- 앞서서 잠깐 \( p({\bf w} | \alpha) \) 에 대한 논의를 했었다. 이게 사실 베이지언 방식이다.
- 완전한 베이지안(fully Bayesian) 접근법에서는 실제 가능한 모든 \( {\bf w} \) 에 대한 값을 반영해야 한다.
- 즉, \( {\bf w} \) 를 고정된 값이 아닌 랜덤변수로 고려한다.
- 이후에도 언급되겠지만 변수를 알려지지 않은 고정된 값으로 취급하는가, 랜덤 변수로 취급하는가에 따라 식이 달라지는 경우가 많다.
- 고정된 값인 경우 이를 임의의 값으로 결정하기만 하면 그냥 평범한 상수(const) 값이 되어버리지만,
- 랜덤 변수로 취급하는 경우에는 특정한 값으로 취급하기보단 하나의 확률 값으로 취급하기 때문에
- 보통은 확률 함수로써 변수를 표현하게 된다.
- 따라서 주변(marginalization) 확률 분포를 통한 베이지안 방식을 도입하여 이를 해결한다.
- 모수(parameter)에서는 모든 가능한 범위를 확률함수로 표현한다.
- 즉, 하나의 모수가 어떤 분포를 따른다고 가정하고 (랜덤변수이므로) 이에 대한 모수, 즉 모수의 모수를 고려해야 한다.
- 모수의 모수를 초모수(hyper-parameter)라고 한다.
- 여기서 잠깐? 모수에 대한 모수, 즉 초모수가 존재한다니?
- 그러면 초모수(hyper-parameter)의 모수(parameter)는 초초모수(hyper-hyper-parameter)인가?
- 농담같지만 실제 존재하는 개념이다.
- recursive 라는 말이 괜히 있는게 아니다.
- 하지만 여기서는 논의를 간단하게 하기 위해 초모수 \( \alpha \) 와 \( \beta \) 값을 알려지지 않은 고정된 값으로 취급하여 모델을 전개한다.
- 즉, 모델에 직접적으로 영향을 주고 있는 모수는 랜덤 변수로 고려하여 어떤 분포로 표현하지만,
- 이렇게 고려된 모수의 분포에 대한 모수(즉, 초모수)는 고정된 (하지만 알지 못하는) 값으로 취급한다는 것이다.
- 초모수는 MLE 에서의 모수의 역할이라고 생각하면 쉽다.
- 따라서 우리가 MLE 로 모수를 추정할 때 사용했던 그런 방식으로 초모수 값을 추정할 것이다.
- 기존 커브 피팅 문제에서는 \( {\bf x} \) 와 이 때의 타겟 \( {\bf t} \) 벡터를 이용하여 모델을 구성하고 새로운 데이터 \( x \) 에 대해 \( t \) 를 예측하는 방식을 취했다.
- 그러나 베이지언 방식에서는 기존의 데이터를 통해 새로운 데이터를 예측하는 모델을 하나의 수식으로 정리 가능하다.
- 이를 예측 분포(predictive distribution)라고 부른다.
- 기존의 샘플 데이터는 벡터 \( ({\bf x}, {\bf t}) \) 로 표기하고 예측할 데이터는 \( (x, t) \) 가 된다.
- 베이지언 방식에서는 자주 등장하는 형태이므로 유심히 살펴보기 바란다.
- 이 방식이 좋은 점은 특정한 \( {\bf w} \) 값을 고정하는 것이 아니라 \( {\bf w} \) 에 대한 모든 가능성이 확률 함수를 통해 모델에 이미 다 반영이 되어 있다는 것.
- MLE 에서도 없는 개념은 아니지만 베이지언 방식에서는 대놓고 이런 방식을 선호한다. (업데이트 모델)
- 3장에서 사후 분포 결과를 다시 사전 분포로 놓고 반복하는 예측 모델을 보게 될 것이다.
- 여기서 적분식 내에서 두번 째 텀을 파라미터에 대한 사후분포(posterior)라고 하고 이를 구하는 방식으로 전개된다.
- 유사하게, 이런 예측 분포도 하나의 가우시안 분포로 고려할 수 있는데 이렇게 해서 얻어지는 분포를 다음과 같이 표기할 수 있다.
- 일단은 식을 한번 살펴보는 정도로 마무리하면 된다. 3장에서 이에 대한 자세한(지겹도록!) 설명을 하게 될 것이다.
- 이런 식을 통해 sinusoidal 예제를 어떻게 해결하는지 간단하게 그림으로 확인해보자.
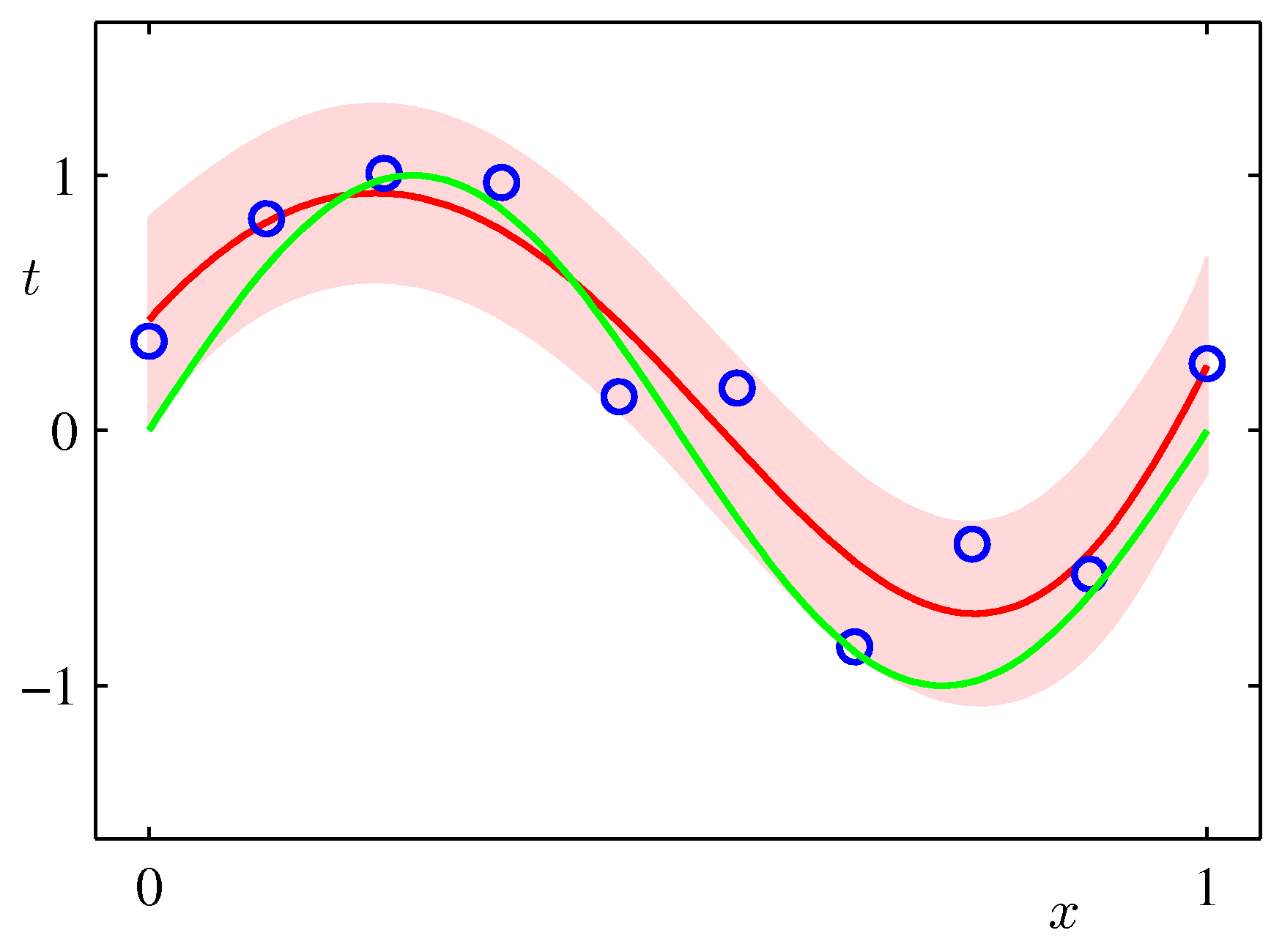
- 이 그림은 기저함수를 다항식(polynomial)으로 선택하여 만든 모델로, \( M=9 \) 이고 \( \alpha \) 는 0.005, \( \beta \) 는 11.1 이 사용되었다.
- 녹색 선이 원래 \( \sin(2\pi{x}) \) 곡선이고 빨간 선이 모델을 통해 만들어진 근사식이다.
- 연한 붉은 색의 밴드가 평균 값 주변의 분산( \( \pm{1} \) )을 나타내고 있다.