목표 : 실수 범위의 입력 변수 \( x \) 를 관찰한 후 이 관찰 값을 바탕으로 실수 범위의 타겟(target) \( t \) 의 값을 예측하고 싶다.
- 예제로 사용할 모델을 가정하는 것으로부터 시작한다.
- 타겟(target) \( t \) 가 함수 \( \sin(2\pi x) \) 로부터 발현되는 실수 값이라고 가정하자.
- 이 때 발현된 값은 노이즈(noise)를 포함하고 있다.
- 여기서 발생되는 노이즈(noise)는 주어진 문제가 본질적으로 확률에 의한 프로세스이기 때문이거나,
- 혹은 관찰되지 못한 다른 원인으로 인해 관측 값에 포함되게 된다.
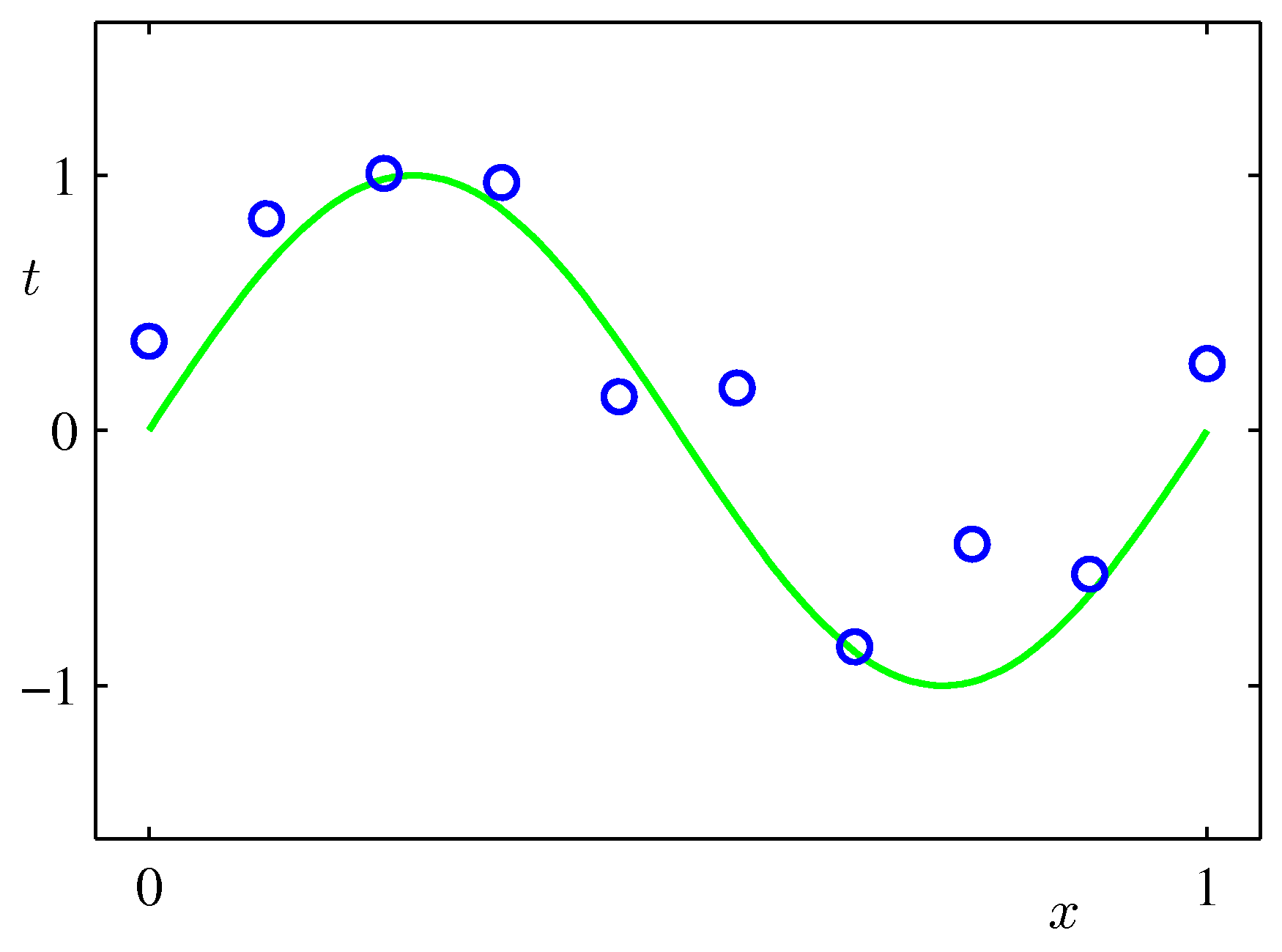
- 그림에서 녹색 선이 \( \sin(2\pi x) \) 함수.
- 이 함수에 가우시안 랜덤 분포에 의해 발생한 샘플이 파란색 원으로 표현되어 있다.
- 이 샘플들은 모두 노이즈가 포함된 상태로 발현되었다.
- 이해를 돕기위해 아마도 샘플은 일정한 구간 단위로 추출된 것으로 보인다.
- 노이즈를 포함한 관찰 데이터를 이용하여 최초 샘플 생성 함수인 \( \sin(2\pi x) \) 를 정확히 얻어내기란 쉬운 일이 아니다.
- 우리는 다음의 2가지 이론을 이용하여 이를 고찰하도록 한다.
- Probability Theory : 불확실성을 정량화시켜 표현할 수 있는 수학적인 프레임워크를 제공한다.
- Decision Theory : 확률적 표현을 바탕으로 적절한 기준에 따라 최적의 예측을 수행할 수 있는 방법론을 제공한다.
- 우리가 해야 할 일을 좀 더 구체적으로 명시해 보자.
- 학습 데이터를 이용하여 모델을 근사한 후 임의의 입력 데이터 \( \widehat{x} \) 에 대해 예측 결과 \( \widehat{t} \) 를 제공해 주어야 한다.
- 우리는 다음과 같은 식으로 모델을 선택하도록 한다.
- 이는 다항식(polynomial) 모델이다. 갑자기 다항식 모델이 등장한 이유는 ?
- 모델링을 해야 할 함수를 아직 알지 못하는 함수라고 가정하면 이를 근사할 수 있는 근사 식이 필요하다.
- 일반적으로 테일러 급수나 퓨리에 변환 식 등으로 함수 근사를 많이 한다.
- 여기서는 테일러 급수 형태의 근사식 추정을 수행하는 것이라 생각하면 된다.
- 테일러 급수 방식의 한 가지 예로 다항 함수를 도입한다.
- 보통 특정 위치에서의 함수를 근사하기 위한 수단으로 테일러 급수를 많이 사용한다.
- 일반적인 테일러 급수는 차수인 \( M \) 값을 늘릴수록 특정 위치(지점)에서 더 잘 맞는 근사식을 만들어 낼 수 있다.
- 하지만 우리가 하고자 하는 목적과는 약간 다를 수 있는데,
- 우리는 최대한 모델을 일반화하여 강건한 모델을 만들어 내는게 목적이다.
- 이게 무슨 말인고 하니 주어진 샘플 데이터에만 적합한 모델을 만들어내는 것이 아니라,
- 모델 구성 후 제공되는 임의의 데이터에 대해서도 그럴듯한 타겟 값을 내어주는 모델이 필요하다.
- 어쨌거나 모델을 다항식으로 사용하겠다고 마음 먹고 나면,
- 이제 문제는 고정된 \( M \) 값 내에서 가장 적합한 \( {\bf w} \) 를 구하는 문제로 전환된다.
- 원래 \( M \) 값이 고정된다는 가정은 할 필요가 없는 것이나 여기서는 일단 이렇게 시작한다.
- 식을 근사하기 위해 최적의 계수 \( {\bf w} \) 를 구하는 방법을 알아보자.
- 보통 이런 문제를 풀 때에는 에러 함수(error function)를 도입하여 문제를 해결한다.
- 모델로부터 도출된 \( y(x,{\bf w}) \) 함수와 실제 타겟 값 \( t \) 의 차이를 최소로 하는 방식을 통해 \( {\bf w} \) 값을 결정할 수 있다.
- 그리고 이 때 에러 함수는 보통 제곱합(sum-of-squares) 에러 함수를 사용한다.
- 변위의 합을 에러함수로 사용하는 것이 아니라 변위 제곱의 합을 사용하는 이유는?
- \( y \) 함수가
convex를 만족하는 경우 에러 함수도convex를 만족하는 함수가 되고 미분 가능하게 되어, - 에러 함수를 \( {\bf w} \) 에 대해 단순 미분하면 최소화 문제에서 유일한 해를 가지게 된다.
convex에 대한 개념은 뒤에도 언급하니 일단은 2차 방정식과 같은 함수라고 생각하도록 하자.- 2차 방정식의 그래프에서는 최소값 또는 최대값이 단 1개만 존재한다.
- \( y \) 함수가
- 또한 식에 \( \frac{1}{2} \) 과 같은 상수 계수가 포함된 이유는 이후의 수식 계산 전개를 편하게 하기 위해서이다.
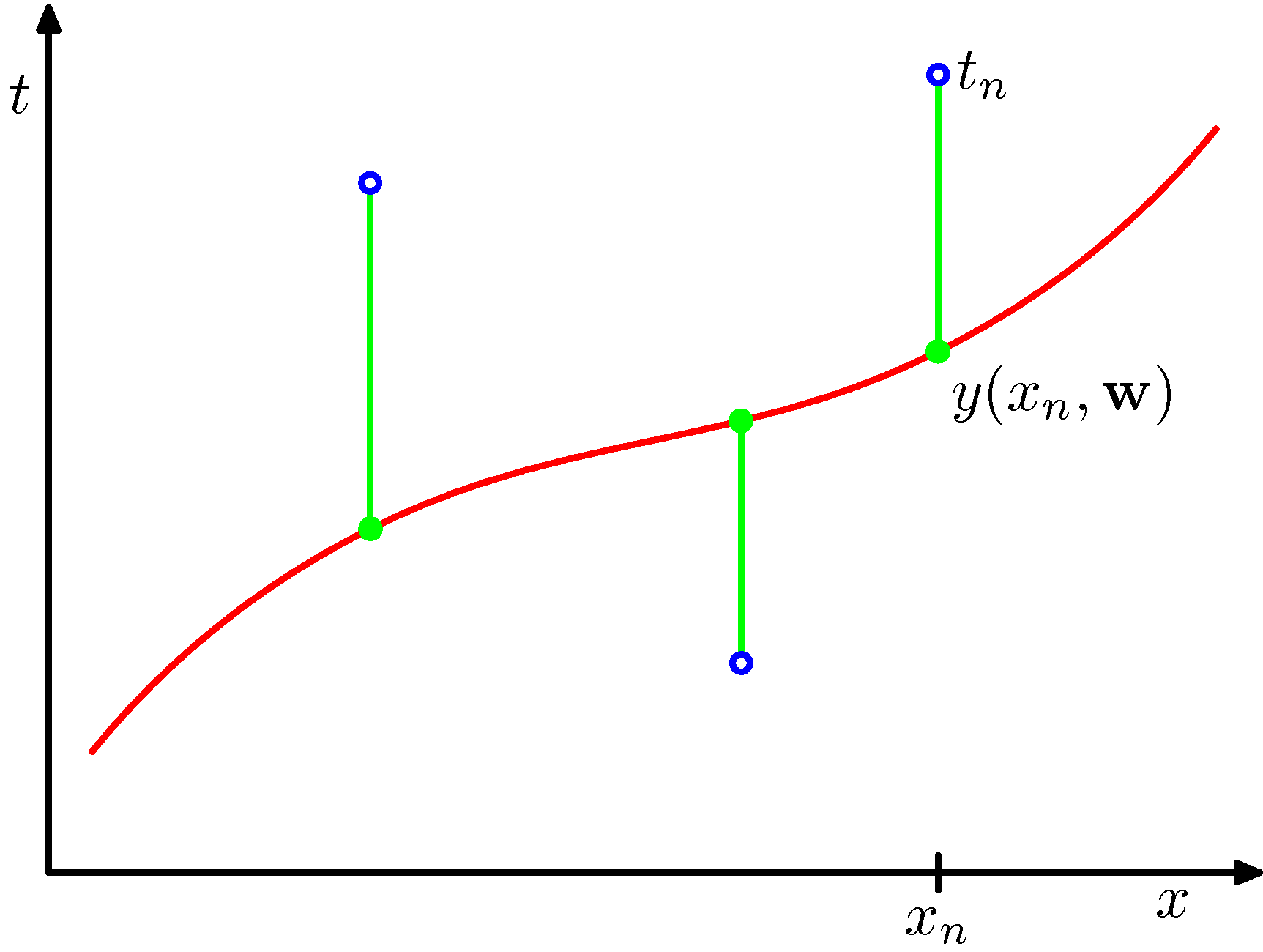
- 이제 우리는 함수 근사 문제를 \( E({\bf w}) \) 값을 최소로 만드는 \( {\bf w} \) 를 구하는 문제로 생각하면 된다.
- 정의된 에러 함수가 \( {\bf w} \) 에 대해 이차형식(
quadratic)의 함수 꼴이므로 이를 최소화 하는 값은 유일 해를 가지게 됨을 보장 받는다.quadratic이라는 용어는 선형 대수에서 자주 사용되는 용어이다.- 간단하게만 생각하면 차수가 2차식으로만 이루어진 다항식을 의미한다.
- 이것도 뒤에서 좀 더 자세히 언급될 것이다.
- 유일 해를 가질 때의 \( {\bf w} \) 값을 \( {\bf w}^* \) 라고 하자.
- 따라서 이 때 얻어지는 함수 값은 \( y(x, {\bf w}^*) \) 가 된다.
- 원래 \( y \) 함수는 \( x \) 와 \( {\bf w} \) 에 대한 함수이지만 학습 데이터를 이용하여 \( {\bf w} \) 를 특정 값 \( {\bf w}^* \) 로 고정할 수 있다면,
- \( y \) 함수는 결국 단일 변수 \( x \) 에 대해서만 처리되는 어떤 함수라고 생각할 수 있게 된다.
- 잘 모르겠어도 걱정하지 말자. 앞으로 계속 이에 대한 논의를 이어나갈 것이다.
- 다음으로 다항 함수( polynomial )의 \( x \) 의 차수 \( M \) 의 개수에 대해 생각해보자.
- 만약 \( M \) 값을 처음부터 고정하지 않고 직접 결정할 수 있다고 하면 어떤 값을 선택하는게 좋을지 고민해야 한다.
- 이 문제는 model comparison 또는 model selection 으로 불리는 중요한 개념이다.
- 다항식의 차수가 달라지면 예측한 모델의 함수식이 완전히 달라지게 된다.
- 결국 \( M \) 의 개수가 다르면 서로 다른 모델이라고 생각하면 된다.
- 주어진 데이터에 가장 적합한 모델을 선정하는 것도 중요한 관심 대상이 된다는 의미이다.
- 2장에 좀 더 자세히 언급하므로 여기서는 개념만 잡고 넘어가도록 한다.
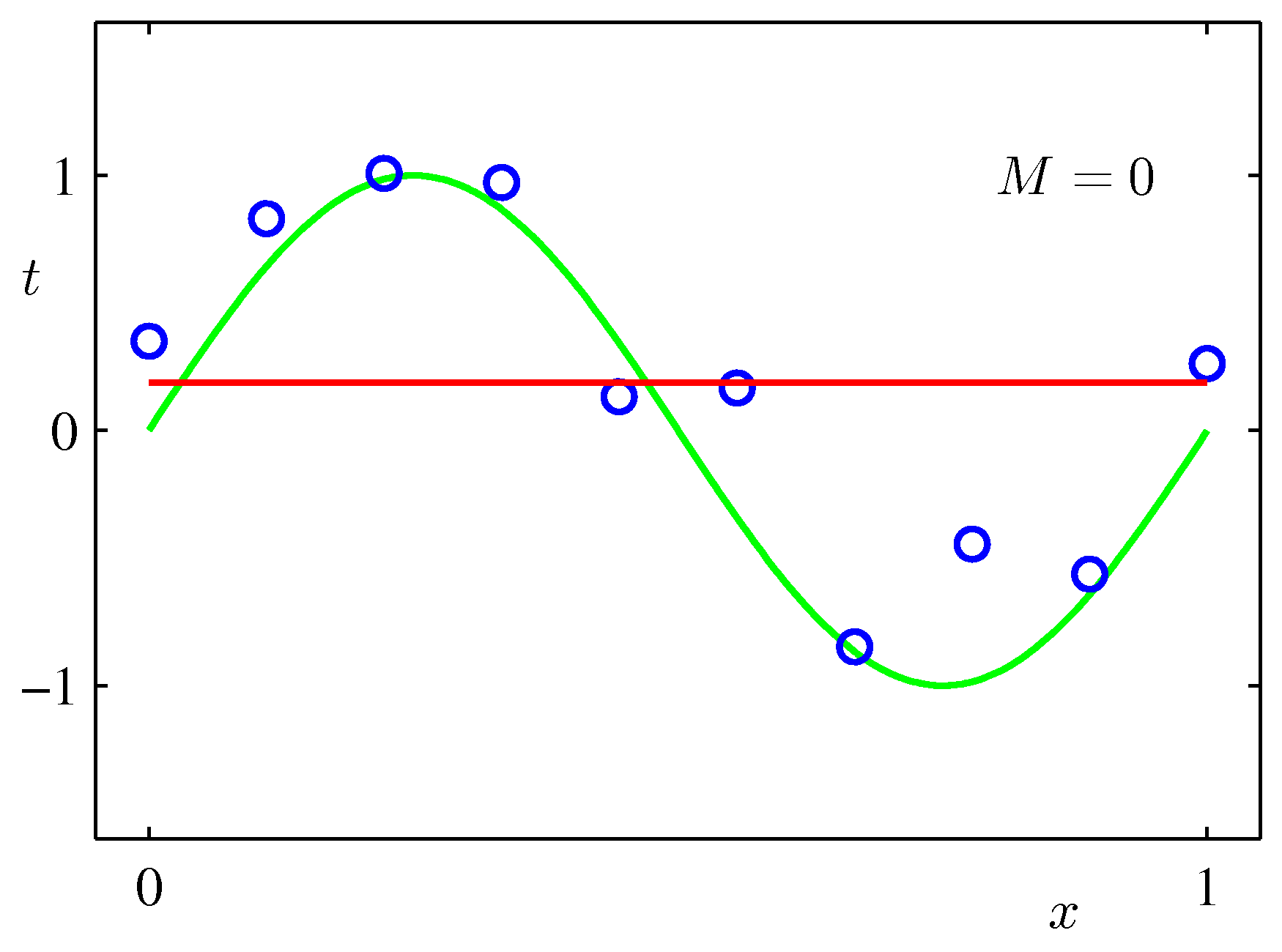
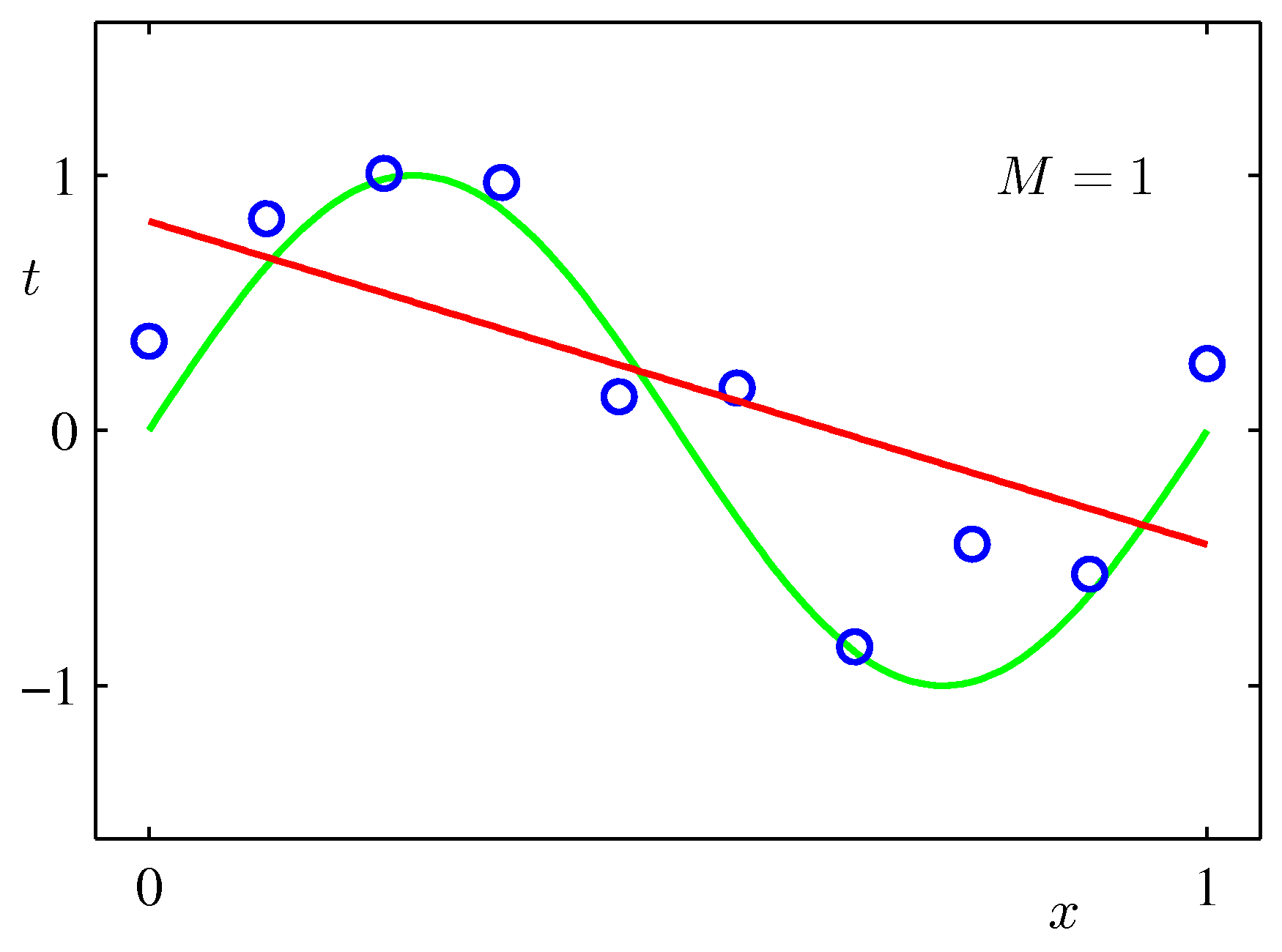
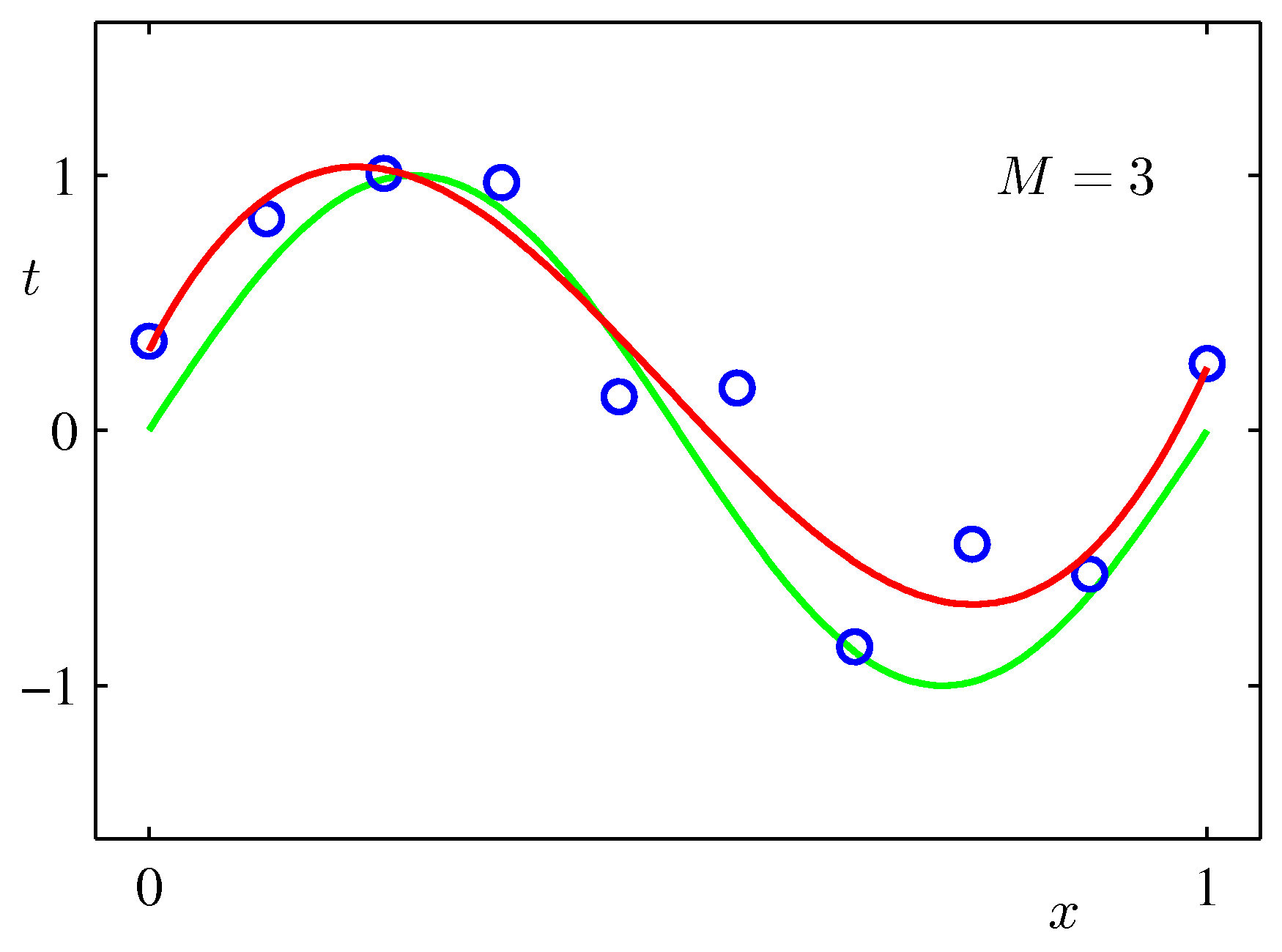
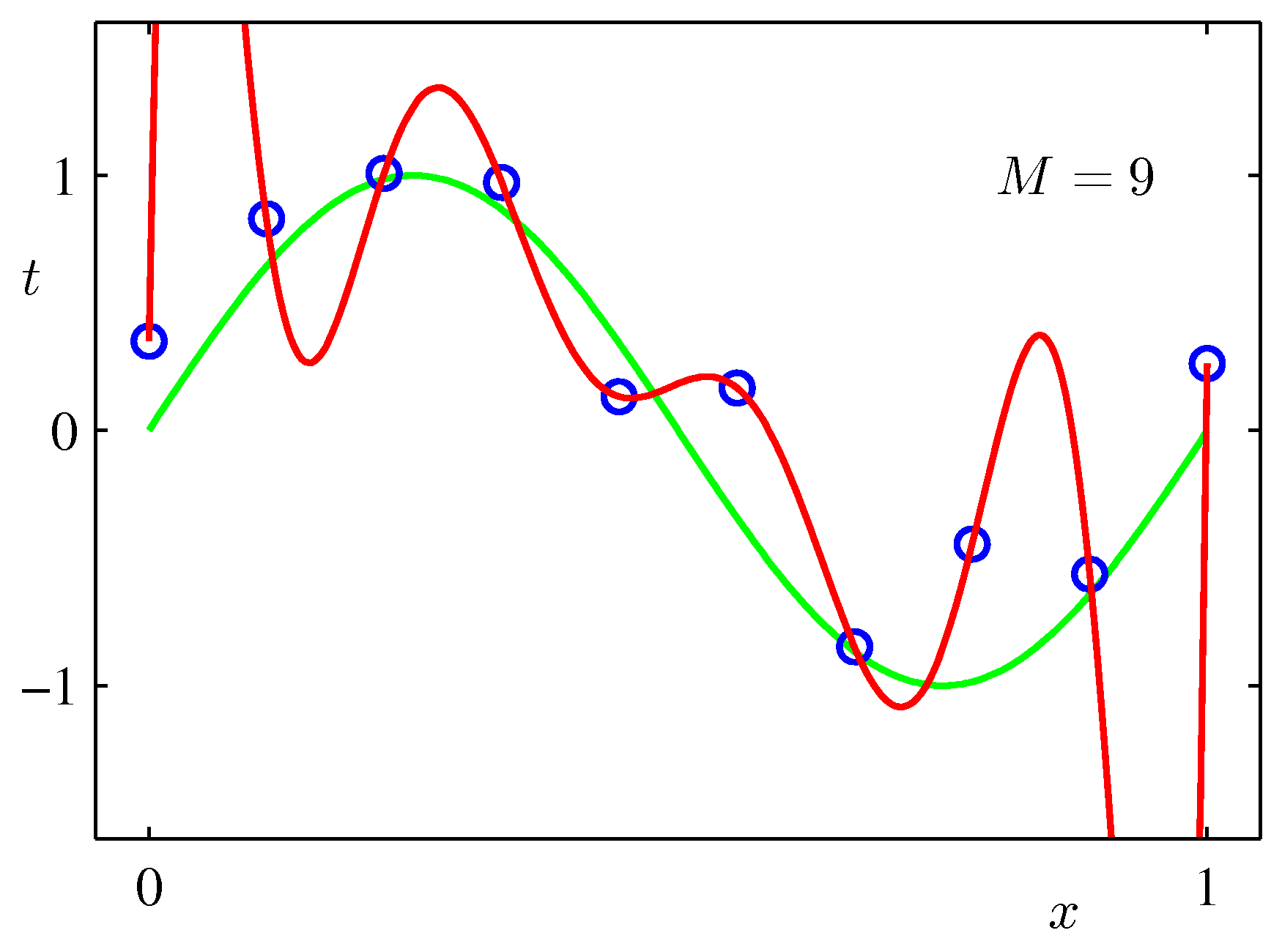
- 그림에서 확인할 수 있듯 \( M \) 값이 너무 작으면 언더피팅(under-fitting), 너무 높으면 오버피팅(over-fitting) 현상이 발생한다.
- \( M \) 이 1인 경우에는 그냥 직선의 방정식이 되어 단순한 직선 회귀식이 된다.
- \( M \) 이 너무 큰 경우는 노이즈에 대한 학습 결과도 모델 자체에 포함되어 주어진 데이터에 과도하게 적합되어진 결과를 얻게 된다.
- 그림을 보자. 현재는 M의 값이 3 정도에서 가장 좋은 결과를 얻은 것으로 보여진다.
- 혹자는 현재 주어진 데이터에 가장 적합한 결과를 갖는 \( M=9 \) 인 모델이 더 좋은 것이 아닌가 반문할 수도 있다.
- 그러나 우리의 최종 목적은 새로운 데이터 \( x \) 가 입력되는 경우에 가장 적합한 결과를 제공하는 일반화 모델을 작성하는 것이다.
- 따라서 노이즈 정보는 최대한 배제한 모델을 구성해야 한다.
- 이제 각 모델에 대한 평가를 해보자.
- 각 모델 별로 에러 값의 정도를 수치화하기 위해 \( RMS \) 에러를 정의하도록 하자.
- 문제 정의 자체가 에러 \( E \) 를 최소화하는 모델을 작성하였으므로 \( RMS \) 값이 작을수록 더 적합한 모델임을 알 수 있다.
- 여기서 \( RMS \) 값을 샘플 크기인 \( N \) 으로 나누는 이유는?
- 서로 다른 데이터 크기를 가지는 경우에 발생하는 스케일 문제를 보정하기 위한 정규화(normalization) 요소이다.
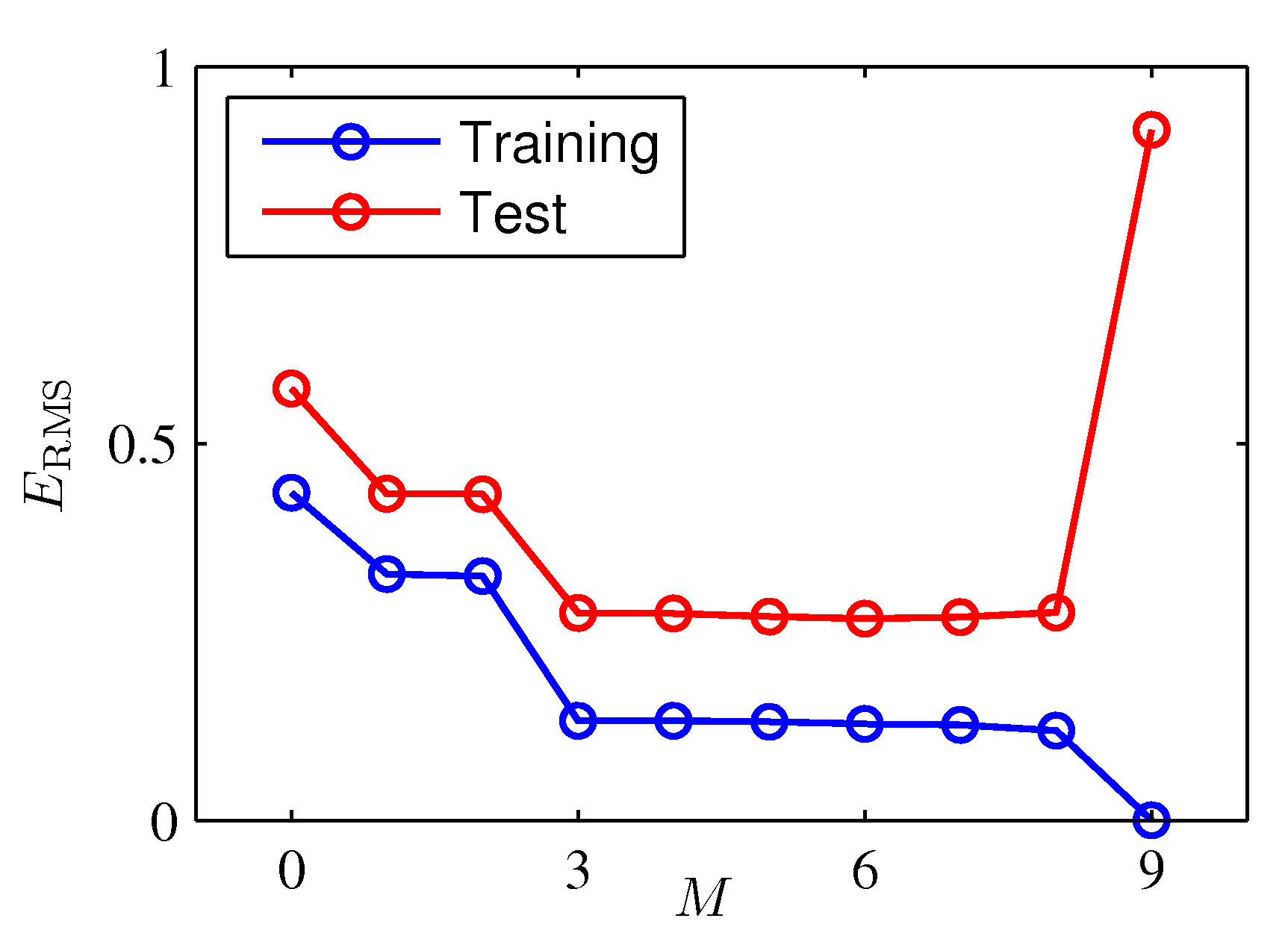
- 각각의 \( M \) 에 대해 \( RMS \) 의 값을 확인해보면 학습 데이터와 테스트 데이터의 차이를 쉽게 확인할 수 있다.
- \( M \) 이 \( 9 \)인 값부터 테스트 데이터의 에러 값이 급격하게 커지는 것을 확인할 수 있다.
- 물론 학습 데이터의 \( RMS \) 는 계속 작아진다.
- 바로 이 지점이 오버피팅를 발생시키는 지점이다.
- 이 때 \( y(x, {\bf w}^*) \) 함수가 요동을 치는 형태를 확인할 수 있다. ( \( M=9 \) 일 때의 그림 참고)
- 우리는 이로부터 약간의 직관을 얻을 수 있다.
- 다항 함수로부터 얻어진 \( {\bf w} \) 의 값을 확인해보면 \( M \) 이 \( 9 \) 인 상태에서 각각의 \( {\bf w} \) 값들이 매우 크거나 매우 작은 것을 알 수 있다.
- 이는 최대한 발현된 데이터 주변으로 모델 함수를 최대한 가깝게 이동시키기 위해 각각의 \( {\bf w} \) 값을 극단적으로 보정하려고 했기 때문이다.
- 항상 그런 것은 아니지만 오버피팅될 때의 모수 값들은 서로 편차가 커지게 되는 현상을 보인다.
- 다음으로 데이터의 크기에 따른 모델의 결과에 대해 고찰해보자.
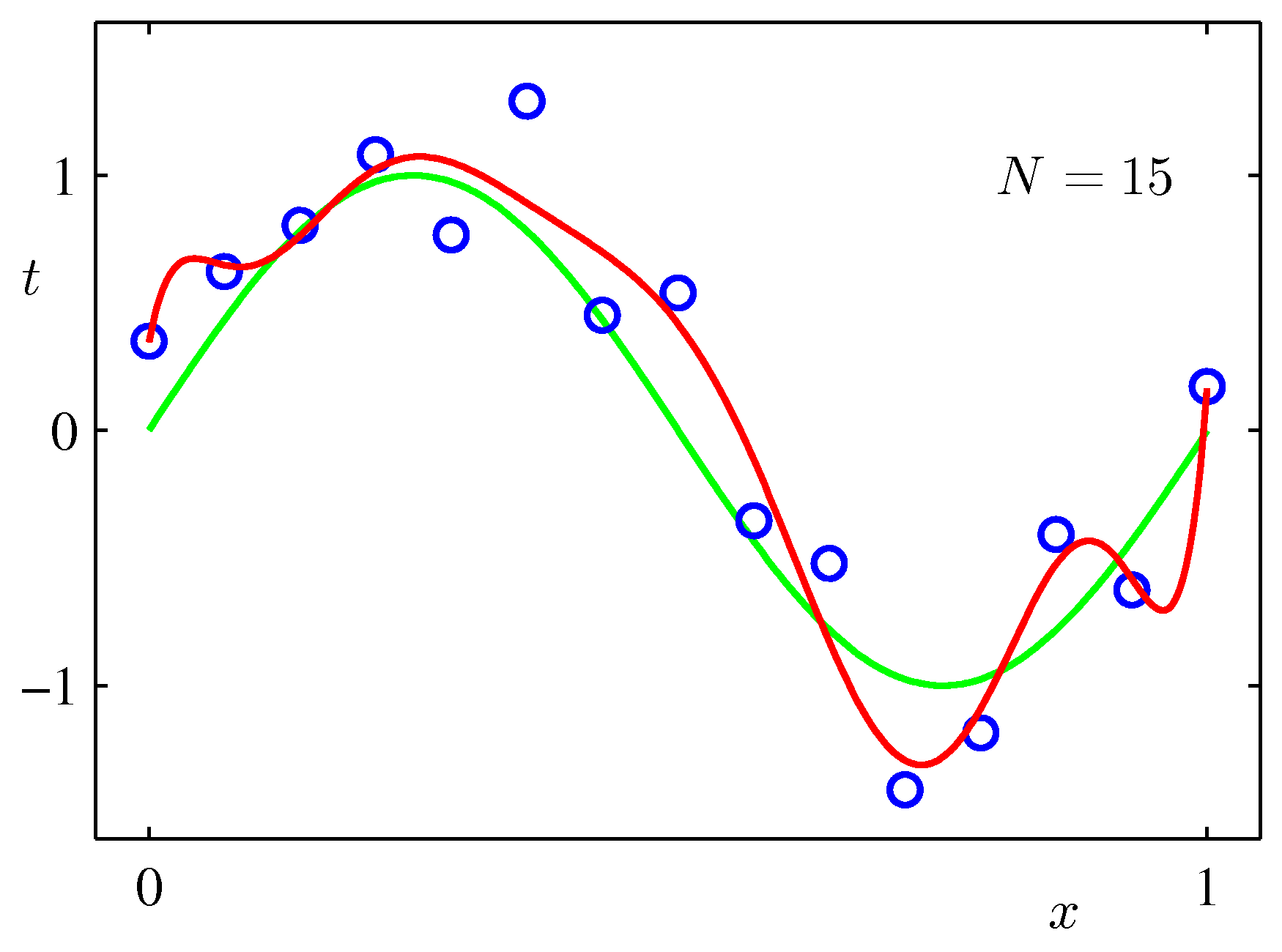
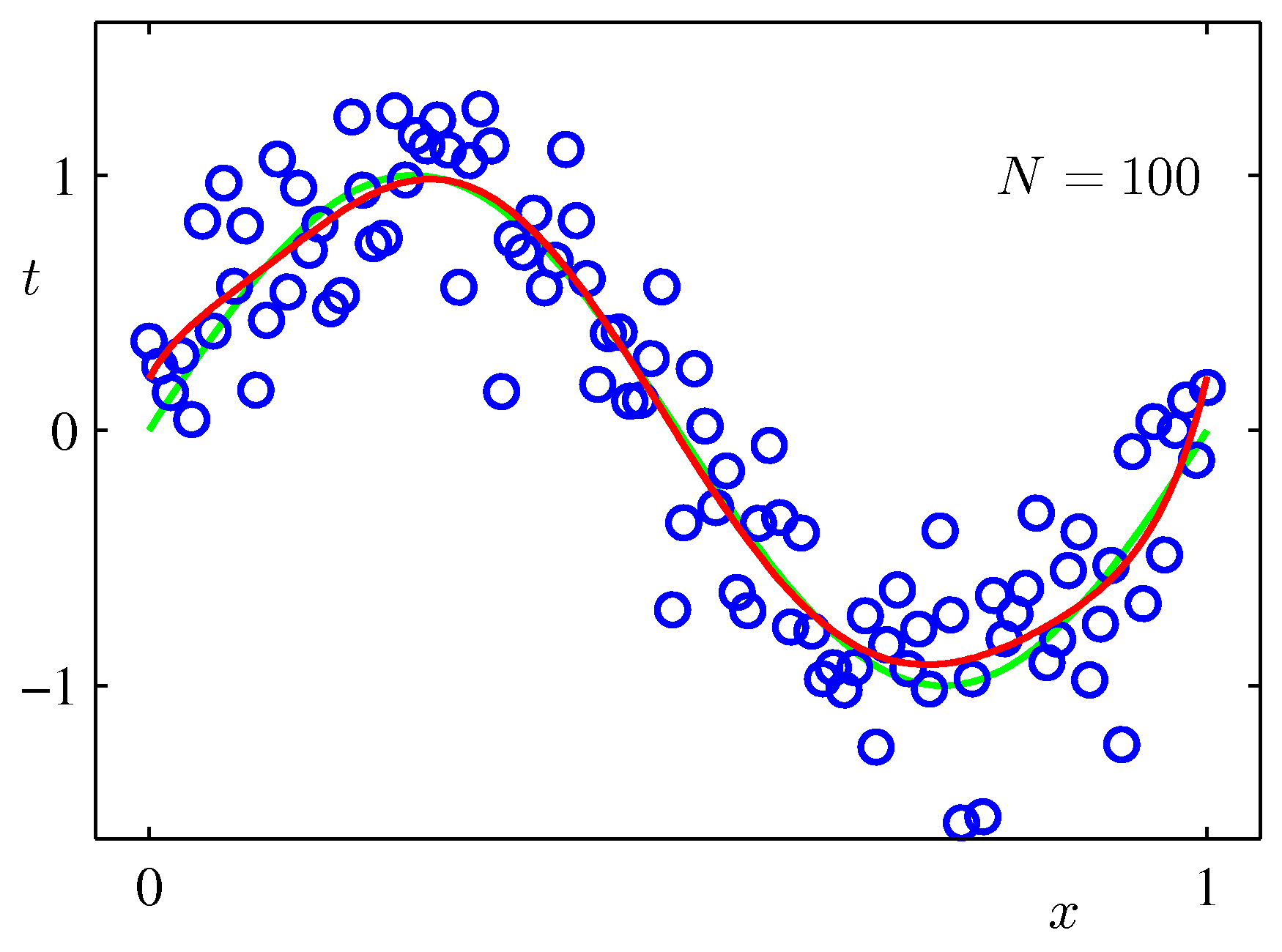
- 위 그림에서 사용한 \( M \) 의 값은 둘 다 9로 동일하다. ( \(M=9 \) )
- 그러나 왼쪽은 샘플 크기가 15개이고, 오른쪽은 샘플 크기가 100개인 데이터이다.
- 앞서 살펴보았듯, 적은 수의 샘플을 사용하는 경우 \( M=9 \) 정도에서는 오버피팅 현상이 발생했다. (왼쪽)
- 하지만 데이터 크기가 큰 오른쪽은 \( M=9 \) 임에도 불구하고 이런 현상이 없다.
- 우선 대략적으로 이해하자면, 관찰 데이터의 크기(개수)가 클수록 오버피팅 현상을 막을 수 있다.
- 휴리스틱 관점에서는 모델 파라미터의 개수는 샘플 크기의 1/5, 1/10 정도보다 작게 설정하는 것이 좋다.
- 물론 모델의 복잡도는 해결하고자 하는 문제에 맞게 결정하는 것이 합리적이다.
- 오버피팅(over-fitting) 현상은 피할 수 없는 운명의 데스티니.
- 앞으로 살펴볼 MLE(Maximum likelihood estimation)를 통해 이 문제를 좀 더 살펴볼 것이다.
- 또한 베이지안 접근 방식을 통해 이 문제를 해결하는 것도 살펴볼 것이다.
- 추가로 베이지안 접근 방식을 통해 효율적으로(effective) 모델 파라미터 개수를 결정하는 것도 확인할 것이다.
- 하지만 지금 당장은 기본부터 좀 배우고 진행하자.
- 주어진 데이터는 별로 없는데, 가급적 높은 차수의 파라미터를 가진 모델을 만들어낼 방법은 없을까?
- 약간의 테크닉을 통해 모델의 복잡도는 올리고 오버피팅은 가급적 막아내는 기법을 적용해 볼 수 있다.
- 바로 정칙화(regularization) 기법이다.
- 앞선 문제에서 보았듯, 오버피팅이 발생할 때 특정 \( {\bf w} \) 값이 매우 커지거나 매우 작아지는 현상을 확인할 수 있었다.
- 물론 이러한 현상은 회귀(regression) 문제 등에서 나타내는 현상이다.
- 하지만 모든 모델에서 오버피팅으로 인해 \( {\bf w} \) 값이 매우 커지거나 작아지는 것은 아니다.
- 이런 내용들은 일단 나중에 생각하기로 하고 우선 지금 당장은 주어진 문제에만 집중하도록 하자.
- 따라서 \( {\bf w} \) 가 취할 수 있는 값의 범위를 제한하여 가급적 큰 범위의 값을 가지는 \( {\bf w} \) 가 등장하지 못하도록 막는 것이다.
- 이를 수식화하여 에러 함수에 도입하면 다음과 같이 기술할 수 있다. (왜 이런 형태의 식이 등장하였는지는 나중에 계속 나온다.)
- 물론 이러한 현상은 회귀(regression) 문제 등에서 나타내는 현상이다.
- 여기서 \( \|{\bf w}\|^2\;{\equiv}\;{\bf w}^T{\bf w}\;{\equiv}\;w_0^2+w_1^2+…+w_M^2 \) 이다.
- 계수 \( \lambda \) 는 매우 중요한 요소로서 정칙화 텀(regularization term) 또는 정칙화 계수(regularization coefficient)라 부른다.
- \( \|{\bf w}\|^2 \) 는 정칙자(regularizer)라고 한다. 이 때 \( w_0 \) 는 생략되기도 한다.
- 정칙 기능이 추가되었더라도 식 자체는 \( w \) 에 대해 닫힌 구조(closed form)라는 것은 변함이 없다.
- 닫힌 구조라는 말에 너무 부담을 가질 필요는 없고, 그냥 여전히 명확한 해를 구할 수 있는 식이라는 정도로만 이해하면 된다.
- 위와 같은 형태의 정칙화는 Ridge 정칙화라고 부른다.
- \( {\bf w} \) 에 대해 정칙화 요소가
quadratic형태이다. - 이 외에도 Lasso 등 다양한 변종이 있다.
- 3장에서 다시 언급되므로 그 때 자세히 보도록 하자.
- 사실 기계학습 영역에서는 오래 전부터 weight decay 로 알려진 이러한 접근법이 존재했다.
- \( {\bf w} \) 에 대해 정칙화 요소가
- 정칙화 계수에 대해 조금 더 자세히 살펴보자.
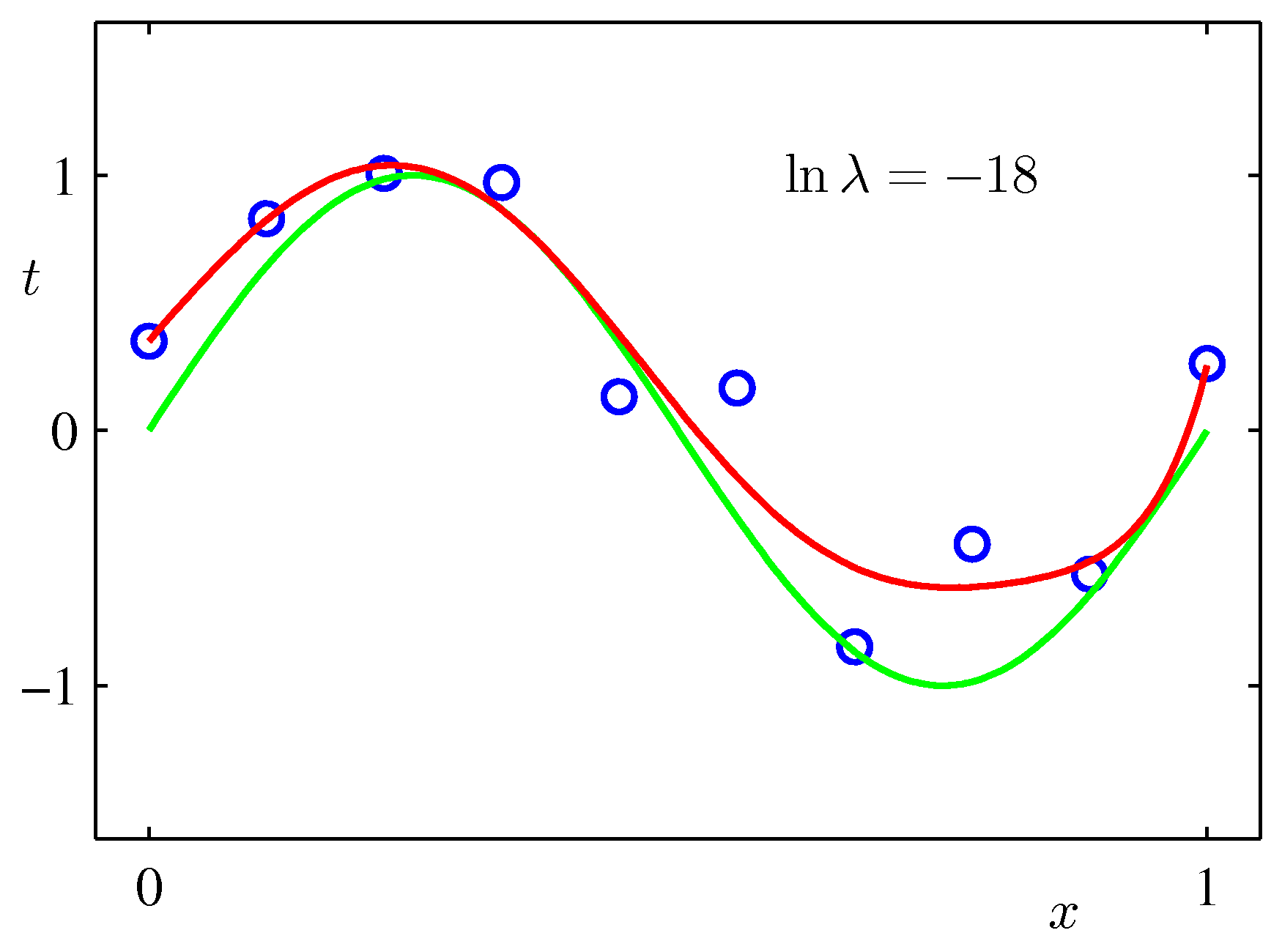
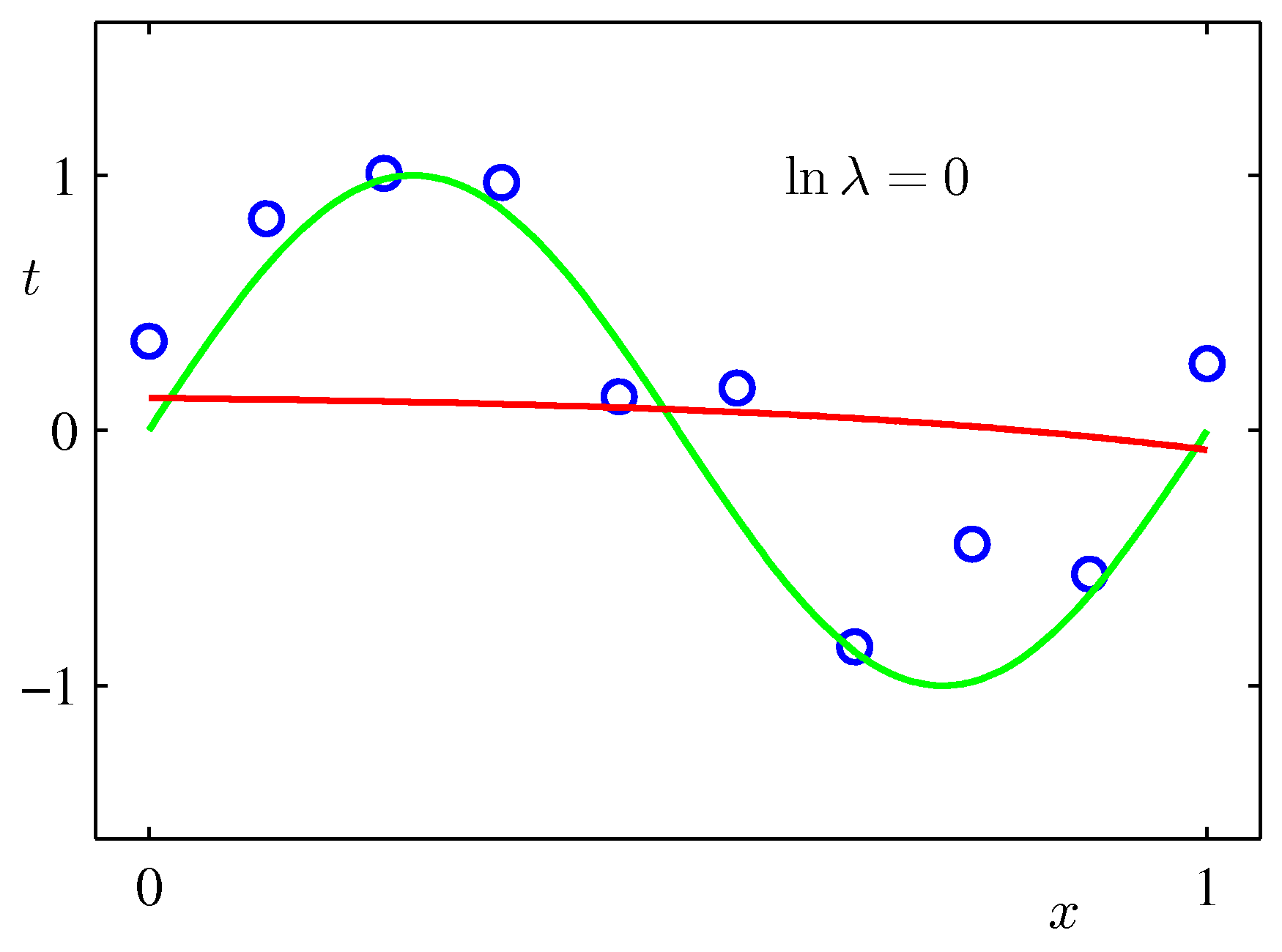
- 그림을 통해 \( M=9 \) 이고 동일한 크기의 샘플 데이터가 적용된 결과에 정칙화 요소를 반영하여 \( \lambda \) 를 추가하면 어떤 현상이 생기는지 확인해보자.
- \( \ln{\lambda}=-18 \) 인 경우 오버피팅이 없어지고 원래 근사하고자 했던 식 \( \sin(2{\pi}x) \) 와 매우 근접한 식을 얻을 수 있다.
- 그러나 \( \ln{\lambda}=0 \) 을 보면 알 수 있듯, 지나치게 큰 \( \lambda \) 값은 다시 언더피팅(under-fitting) 현상을 만들어낸다.
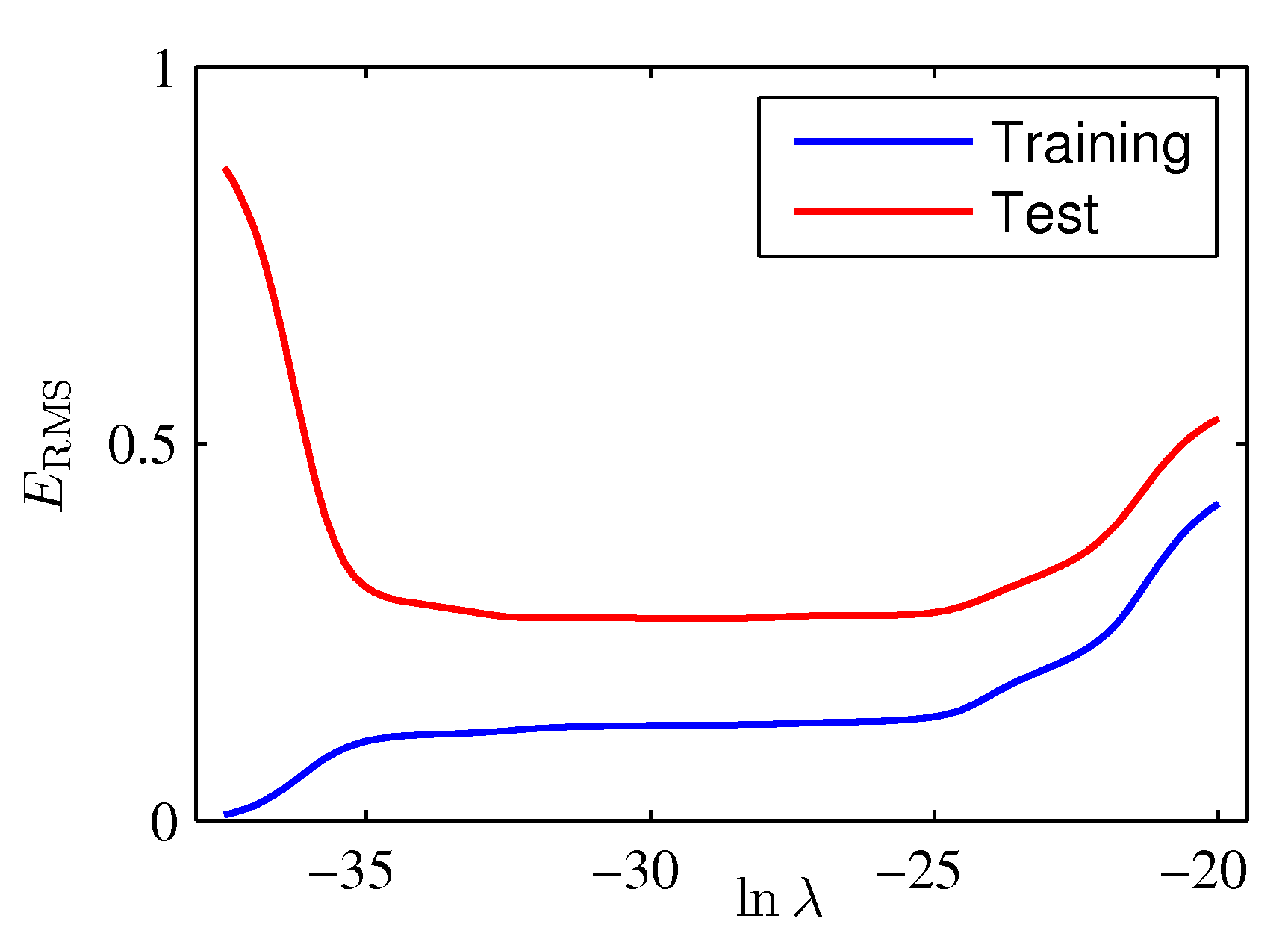
- 이제 정칙화 계수를 추가한 상태에서의 \( RMS \) 결과를 다시 한번 살펴보자.
- 앞선 결과와 다르게 학습 데이터와 테스트 데이터 모두에서 좋은 성능을 보임을 확인할 수 있다.