4. The EM Algorithm in General

$ EM $ : Expectation Maximization Algorithm

EM 알고리즘은 잠재 변수(latent variable)를 가지고 있는 확률 모델에서 MLE 를 구하는 일반화된 기법이다.
이번 절에서는 EM 알고리즘을 아주 일반적인 관점에서 해석하고,
이것이 변분 추론(variational inference)의 한 방식임을 설명할 것이다.
잠재 변수 $ {\bf Z} $ 를 가진 모델의 관찰 데이터 $ {\bf X} $ 가 주어졌을 때, 이에 대한 결합 법칙은 다음과 같이 기술할 수 있다.

$p({\bf X}|{\bf \theta}) = \sum_{\bf Z}p({\bf X}, {\bf Z}|{\bf \theta})$

여기서 $ {\bf Z} $ 는 이산 변수(discrete variable)로 가정한다.
- 물론 이론적으로는 $ {\bf Z} $ 는 실수 변수로도 계산 가능하다. (혹은 이산 변수와 실수 변수가 혼합된 형태)
- 이 경우 합의 식은 적분 식으로 교체되어야 한다.
알다시피 $ p({\bf X}|{\bf \theta}) $ 를 바로 구하기는 어렵다.
- 하지만 complete-data 가능도 함수 $ p({\bf X}, {\bf Z}|{\bf \theta}) $ 는 쉽게 계산 가능하다.

이제 잠재 변수 $ {\bf Z} $ 에 대한 함수로 $ q({\bf Z}) $ 를 제안한다.
- 이 함수는 어쨌거나 $ {\bf Z} $ 에 대한 함수이다. (그리고 이 함수는 확률 함수)
- 이제 다음의 식을 만족하는 어떤 $ q({\bf Z}) $ 가 존재한다고 생각해보자.

$\ln p({\bf X}|{\bf \theta}) = L(q, {\bf \theta}) + KL(q\|p)$

참으로 뜬금없는 식이 나왔다. 각 텀에 대한 정의는 다음과 같다.

$L(q, {\bf \theta}) = \sum_{\bf Z}q({\bf Z})\ln \left\{\frac{p({\bf X}, {\bf Z}|{\bf \theta})}{q({\bf Z})}\right\}$ $KL(q\|p) = -\sum_{\bf Z} q({\bf Z}) \ln \left\{\frac{p({\bf Z}|{\bf X}, {\bf \theta})}{q({\bf Z})}\right\}$

여기서 함수 $ L(\cdot) $ 은 $ q $ 에 대해 범함수( functional ) 이다.
- 범함수란 함수를 입력으로 받아 실수를 반환하는 함수
- 당연히 $ q $ 가 입력으로 들어가는 함수가 된다.
- 하지만 파라미터 $ \theta $ 에 대해서는 그냥 함수 (즉, 실수를 입력받아 실수를 반환.)
일단 이 식이 왜 도입되었는지 먼저 살펴보도록 하자.

일단 먼저 알아야 하는 식을 기술한다. (사실 이 식들은 모두 이미 1장에서 언급되어 있다.)
Jensen’s Inequality (옌슨 부등식)
- 만약 $ f(x) $ 가 convex 를 만족한다면 다음이 항상 성립한다.
  - 증명은 생략한다. 1장에 이미 증명을 해 놓고 있다.

$E[f(x)] \ge f(E[x])$

Gibb’s Inequality (깁스 부등식)
- 함수 $ q $ 와 $ p $ 에 대해 $ KL[p\|q] \ge 0 $ 을 항상 만족한다.
  - (참고) 만약 $ p=q $ 이면 $ KL[p\|q] = 0 $
  - (참고) 만약 $ p \neq q $ 이면 $ KL[p\|q] \gt 0 $
- (증명) $ KL[p\|q] = \sum_i p_i \ln{\frac{p_i}{q_i}} = - \sum_i p_i \ln{\frac{q_i}{p_i}}\ge -\ln[\sum_i p_i\frac{q_i}{p_i}]=-\ln[\sum_i q_i]=0 $
앞서 이야기한대로 우리가 EM 알고리즘을 통해 계산하고자 하는 확률값은 $ p({\bf X}|{\bf \theta}) $ 의 값이다.

$\ln p({\bf X}|{\bf \theta})=\ln\sum_{\bf Z} p({\bf X}, {\bf Z}|{\bf \theta})$

여기까지는 많이 보던 식이므로 그리 어려운 것이 없을 것이다.
이제 새로운 함수 $ q $ 를 도입한다. 이는 $ Z $ 에 대한 함수이다.

$\ln\sum_{\bf Z} p({\bf X}, {\bf Z}|{\bf \theta}) = \ln\sum_{\bf Z} q({\bf Z})\frac{p({\bf X}, {\bf Z}|{\bf \theta})}{q({\bf Z})} \ge \sum_{\bf Z} q({\bf Z})\ln\left\{\frac{p({\bf X}, {\bf Z}|{\bf \theta})}{q({\bf Z})}\right\} = L(q,{\bf \theta})$

결국 $ L(q,{\bf \theta}) $ 는 로그 가능도 함수의 Lower bound 함수가 된다.
- 왜 이런 해석이 가능한지는 뒤에서 좀 더 보도록 하고 식을 계속 만들어보자.
어쨌거나 $ L $ 함수가 로그 가능도 함수의 한 속성이라는 것을 알았다.
이제 로그 가능도 함수에서 $ L $ 함수를 빼는 식을 알아보기로 하자.

$\ln p({\bf X}|{\bf \theta})-L(q,{\bf \theta}) = \ln p({\bf X}|{\bf \theta}) - \sum_{\bf Z}q({\bf Z})\ln\left\{\frac{p({\bf X}, {\bf Z} | \theta )}{q({\bf Z})}\right\}\\\\ = \ln p({\bf X}|{\bf \theta}) - \sum_{\bf Z}q({\bf Z})\ln\left\{\frac{p({\bf Z}|{\bf X}, {\bf \theta})p({\bf X}|{\bf \theta})}{q({\bf Z})}\right\}\\\\ = \ln p({\bf X}|{\bf \theta}) - \sum_{\bf Z}q({\bf Z})\ln\left\{\frac{p({\bf Z}|{\bf X}, {\bf \theta})}{q({\bf Z})}\right\} - \ln p({\bf X}|{\bf \theta})\sum_{\bf Z}q({\bf Z})\\\\ = - \sum_{\bf Z}q({\bf Z})\ln\left\{\frac{p({\bf Z}|{\bf X}, {\bf \theta})}{q({\bf Z})}\right\} = KL[q({\bf Z})\|p({\bf Z}|{\bf X}, {\bf \theta})]=KL[q\|p]$

결국 최종 식으로 다음과 같은 결과를 얻게 된다.

$\ln p({\bf X}|{\bf \theta}) = L(q, {\bf \theta}) + KL(q\|p)$

그리고 $ KL $ 은 정의에 의해 $ p=q $ 인 경우에만 0이고 그 외에는 양수를 가지게 된다.
- 따라서 $ L $ 함수가 로그 가능도 함수의 lower bound 가 된다.
- 이를 다음과 같은 그림으로 표현 가능하다.

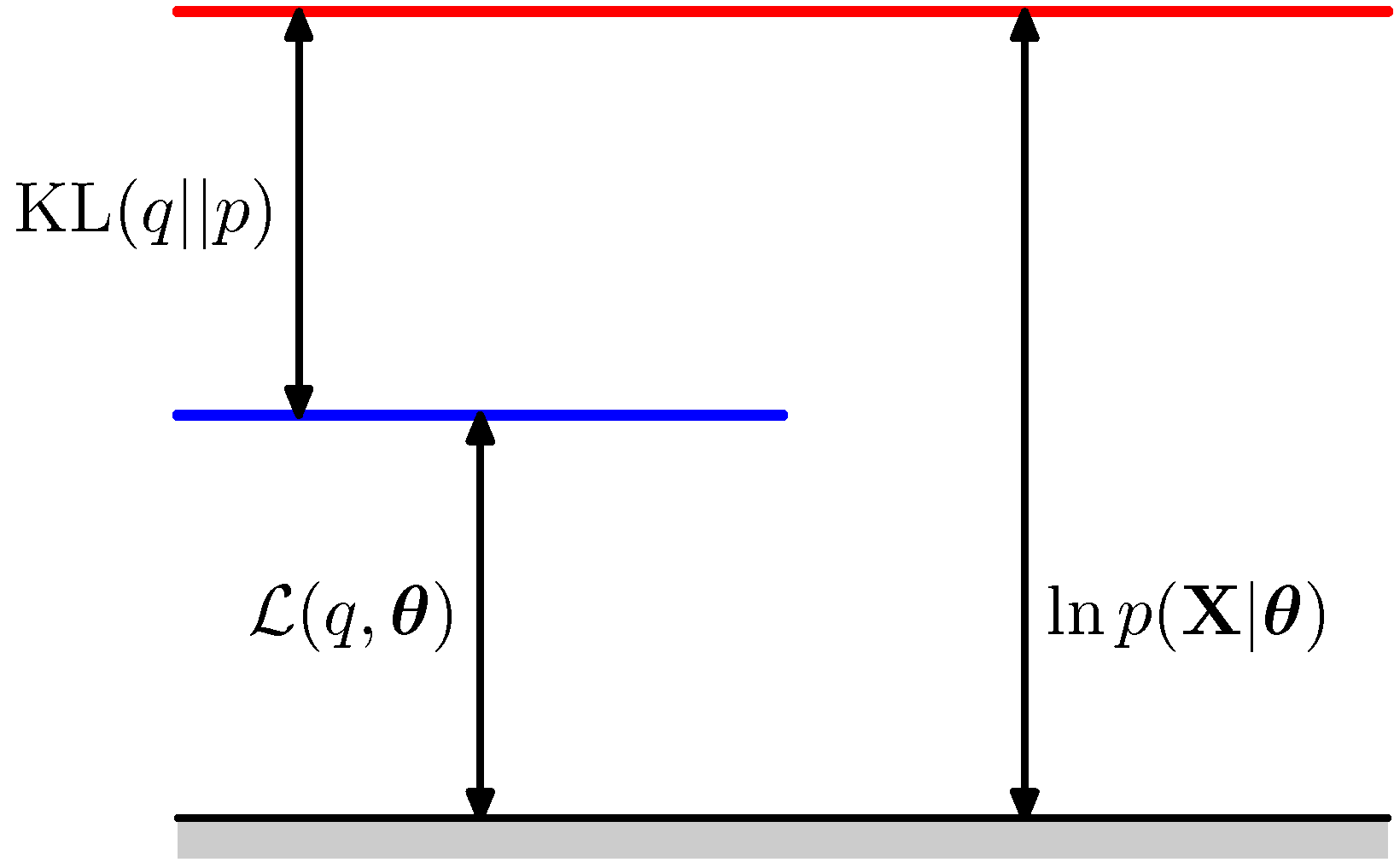
figure9.11

중요한 점은 $ L $ 함수와 $ KL $ 모두에 함수 $ q $ 가 관여하고 있다는 사실이다.
- 따라서 이 두함수는 $ q $ 에 대해 상보적인 관계를 가지게 된다.
- 결국 $ KL $ 을 최소화하는 $ q $ 를 선택하면 이 $ q $ 가 $ L $ 을 최대화하게 된다.
- 우리는 임의의 $ q $ 함수를 적절하게 선택하여 $ L $ 함수는 최대한 크게 하는 것으로 만들고 싶은 것이다.
  - 그래서 최종적으로 $ L $ 함수가 로그 가능도 함수와 같아지기를 원함
- $ KL $ 를 최소화하는 방법은 의외로 간단한데 $ p=q $ 이기만 하면 해당 값이 0이 된다.
  - 결국 $ q({\bf Z}) = p({\bf Z}|{\bf X}, {\bf \theta}) $ 로 계산하면 된다.
EM 알고리즘은 2단계의 과정을 반복적으로 수행하면서 MLE 를 구하는 방법이다.
그리고 위에서 제시된 식은 2개의 텀으로 나누어져 있는데, 이를 EM 각각의 Step 과 연결지어 생각할 수 있다.
다시 한번 EM 단계를 살펴보면서 위의 식을 어떻게 적용할 수 있는지 고민해보도록 하자.

E-Step

앞서 살펴보았듯 이 단계에서는 파라미터 $ \theta $ 를 특정 값으로 고정하게 된다. ( $ \theta^{old} $ )
그리고 이 값을 활용하여 responsibility 즉 $ {\bf Z} $ 의 사후 분포를 계산하는 과정이 필요했다.
이 과정을 $ L $ 함수를 통해 생각하자면 이 단계에서는 $ L $ 함수의 두 파라미터 $ q $ 와 $ \theta $ 중 $ \theta $ 는 고정된 값으로 생각하면 된다.
- 따라서 E-Step에서는 $ L(q, \theta^{old}) $ 의 값을 최대화하는 $ q $ 함수를 선택하는 단계가 된다.
- 뭐 사실 $ q $ 함수를 선택하고 말고 할 필요도 없이 그냥 $ q({\bf Z}) = p({\bf Z}|{\bf X}, {\bf \theta^{old}}) $ 를 구하게 된다.
이를 그림으로 도식화하면 다음과 같다.

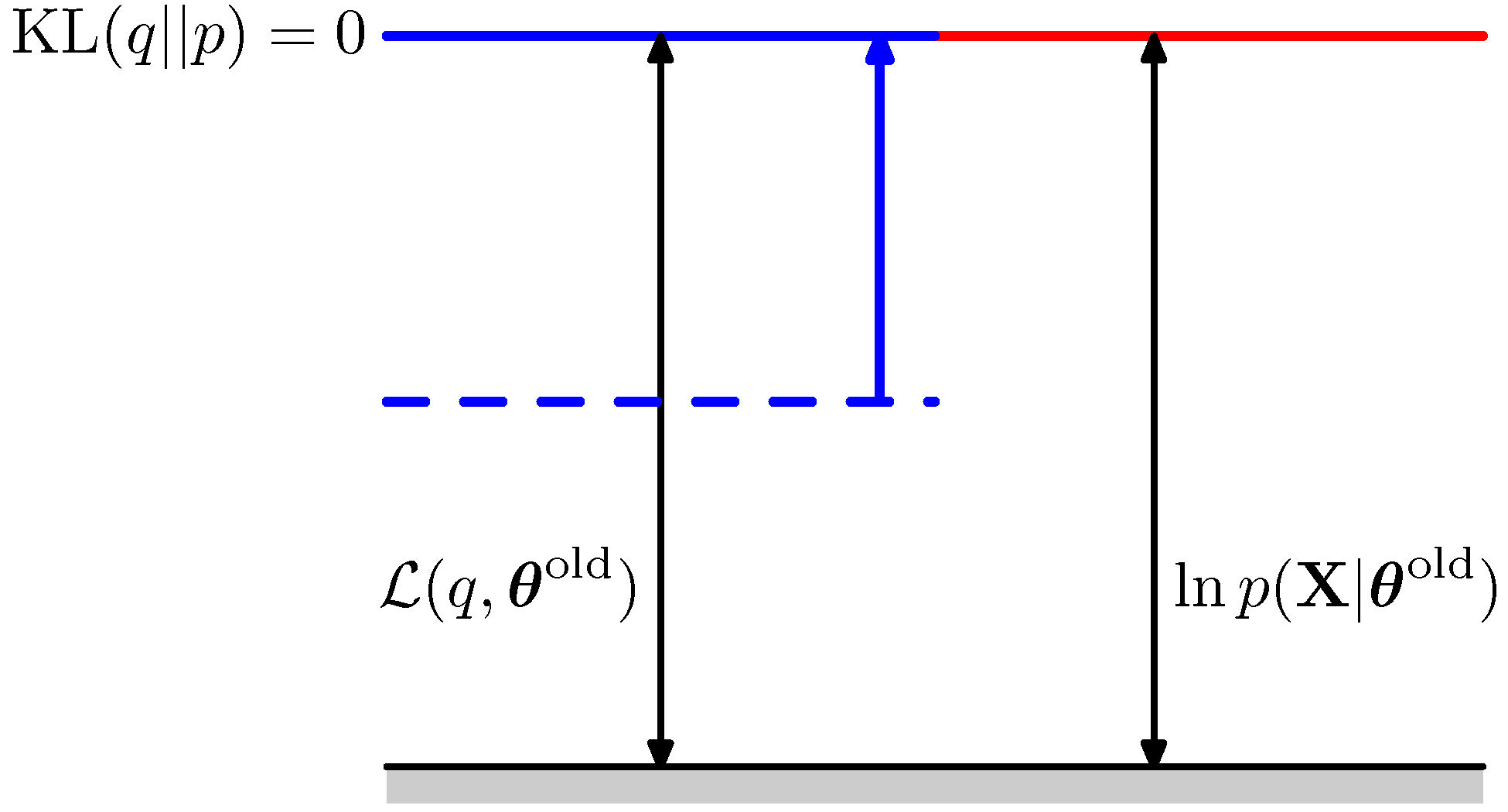
figure9.12

M-Step

M-Step은 잠재 변수 $ {\bf Z} $ 를 고정시킨 다음 새로운 파라미터 $ \theta^{new} $ 를 MLE를 이용하여 추론하는 단계이다.
이 과정을 $ L $ 함수를 통해 이를 고려하면 이제 $ q({\bf Z}) $ 를 고정시킨 상태에서 새로운 파라미터를 추론하게 된다.
물론 최대화 하는 함수는 여기서도 $ L $ 함수가 된다. ( $ L(q^{fixed}, \theta) $ 로 이는 $ \theta $ 에 대한 함수이다.)
- 이를 확인해보기 위해 $ L $ 함수를 간단하게 전개해 보도록 하자.

$q({\bf Z}) = p({\bf Z}|{\bf X}, \theta^{old})$ $L(q, \theta) = \sum_{\bf Z} p({\bf Z}|{\bf X}, \theta^{old})\ln p({\bf X}, {\bf Z}|\theta) - \sum_{\bf Z} p({\bf Z}|{\bf X}, \theta^{old})\ln p({\bf Z}|{\bf X}, \theta^{old}) = Q(\theta, \theta^{old}) + const$

이거 매우 중요한 수식임
그리고 두번 째 텀을 그냥 $ const $ 라고 표현했는데 사실 $ H(p) $ 인 범함수이다.
- $ const $ 로 표기할 수 있는 이유는 $ \theta $ 에 대해서는 그냥 상수이기 때문.
그런데 갑자기 $ Q $ 함수가 튀어나왔다. 특별한 것은 아니고 그냥 수식이 길어서 새롭게 정의한 함수임.
- 물론 $ Q $ 를 자세히 보면 $ \ln p({\bf X}, {\bf Z}|\theta) $ 에 대한 기대값임을 알 수 있음.
- 그래서 앞 절에서 로그 가능도 함수 대신에 이 값을 사용한 것이었음.
어쨌거나 M-Step에서도 $ L $ 함수를 최대화 하는 문제이고,
- 이 함수를 최대화 하는 파라미터를 구하면 전체 로그 가능도 함수의 최대 값이 증가하고 마찬가지로 $ L $ 함수의 값도 증가할 수 있다.
이를 그림으로 도식화하면 다음과 같다.

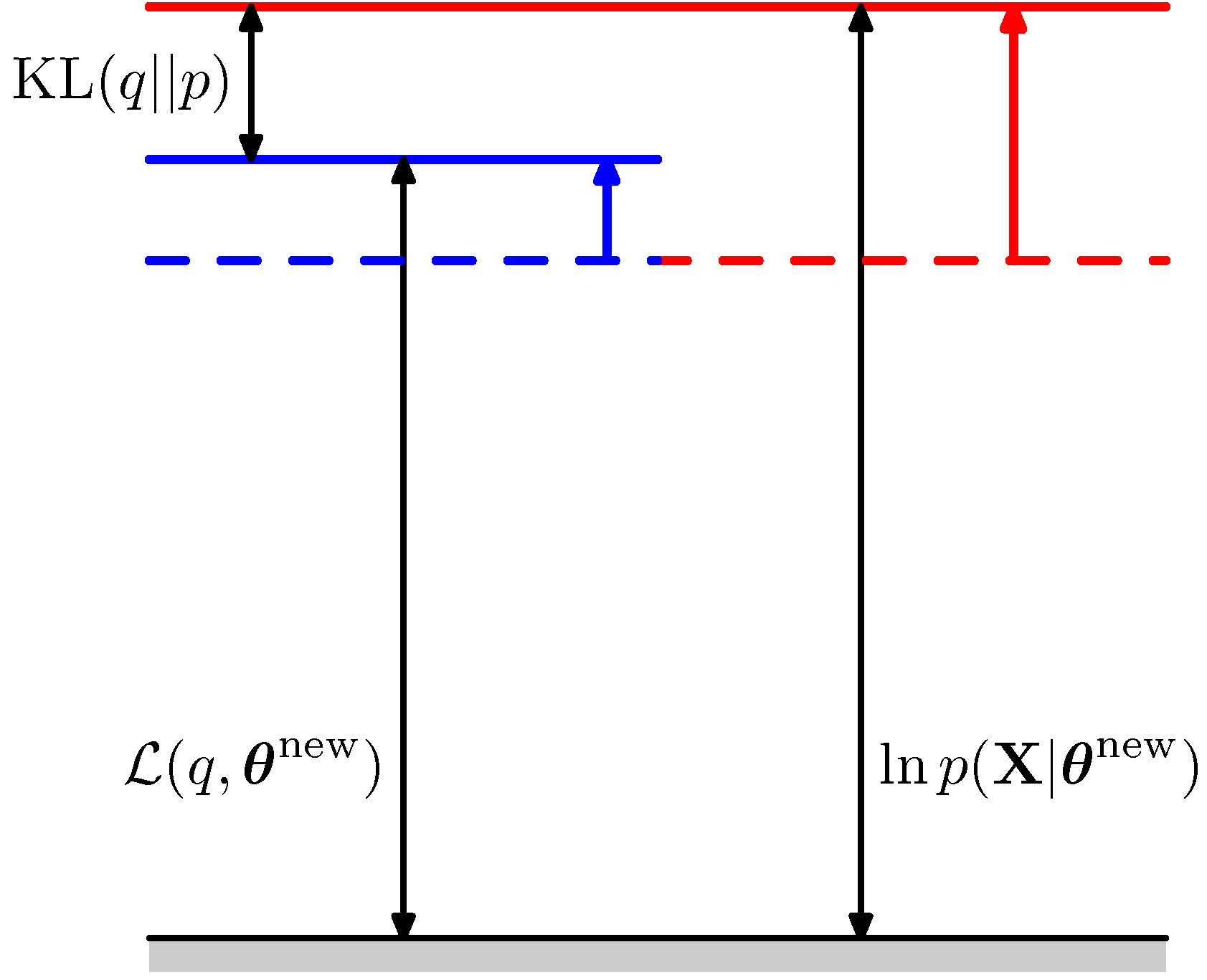
figure9.13

이제 정리하자.
- EM 알고리즘은 반복적인 과정을 통해 MLE를 구하는 알고리즘이다.
- $ q $ 함수를 도입하여 일반화된 EM 알고리즘을 도출해 볼 수 있음

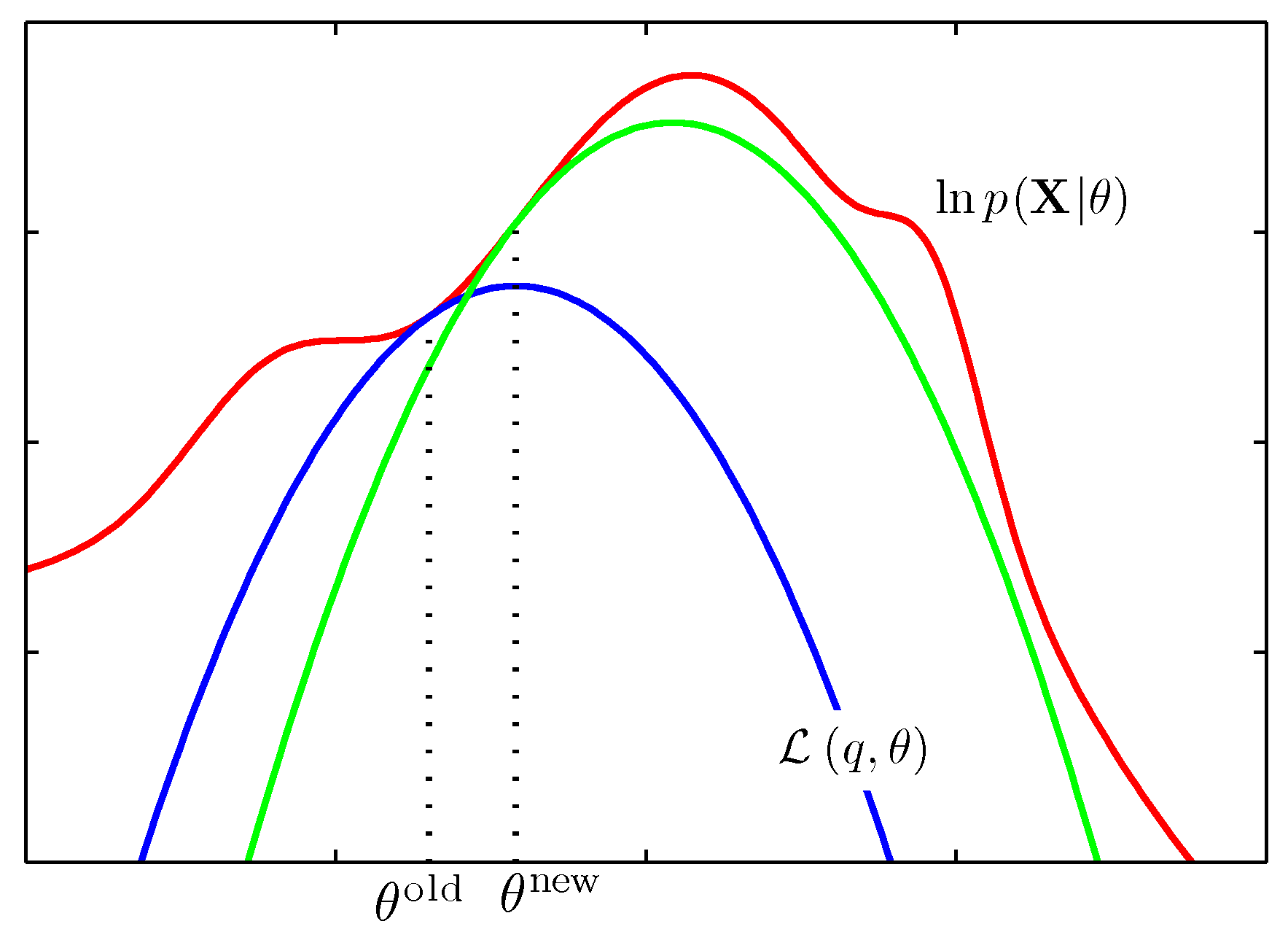
figure9.14

위의 그림이 이번 절의 모든 것을 요약하는 그림이다.
- 우선 임의의 파라미터 $ \theta^{old} $ 로부터 EM 알고리즘이 시작됨
- 해당 지점에서 로그 가능도 함수와 최대한 근사한 $ L $ 함수를 만들게 된다.
  - 이 때 $ L $ 함수는 $ \theta $ 에 대해 concave 함수이으로 위와 같은 그림이 된다. (파란색)
  - 이 단계가 E-Step에서 이루어진다.
- 얻어진 $ L $ 함수를 최대화하는 새로운 파라미터 값을 선정하게 된다.
  - 위의 그림에서는 $ \theta^{new} $ 이다.
  - 이를 이용하여 새로운 $ L $ 함수를 얻음. (초록색)
  - 이 단계가 M-Step 단계이다.
- 수렴 조건을 만족할 때까지 반복하게 된다.

만약 데이터 $ {\bf X} $ 가 모두 독립적이고 이에 대응되는 잠재 변수 $ {\bf Z} $ 가 서로 독립적이라고 가정한다면
- E-Step 에서 사용될 $ {\bf Z} $ 에 관한 함수를 다음과 같이 기술할 수도 있다.

$p({\bf Z}|{\bf X}, \theta) = \frac{p({\bf X}, {\bf Z}|\theta)}{\sum_{\bf Z}p({\bf X}, {\bf Z}|\theta)} = \frac{\prod_{n=1}^N p({\bf x}_n, {\bf z}_n|\theta)}{\sum_{\bf Z}\prod_{n=1}^N p({\bf x}_n, {\bf z}_n|\theta)}=\prod_{n=1}^N p({\bf z}_n|{\bf x}_n, \theta)$

결국 $ {\bf Z} $ 의 사후 분포는 각각의 데이터들의 요소 $ {\bf z}_n $ 에 대응되는 확률 값의 곱으로 표현된다.
- 이게 GMM 에서 각각의 데이터에 대해 $ {\bf z}_n $ 의 responsibility 값을 곱하는 것과 같은 것임.
EM 알고리즘에 $ p(\theta) $ 를 추가로 적용할 수 있다. (즉, 베이지안 모델)

$\ln p(\theta|{\bf x}) = \ln p(\theta, {\bf x}) - \ln p({\bf x})$

이를 풀이하면 다음과 같다.

$\ln p(\theta|{\bf X}) = L(q, \theta) + KL(q\|p) + \ln p(\theta) - \ln p({\bf X}) \ge L(q, \theta) + \ln p(\theta) - p({\bf X})$

여기서 $ p({\bf X}) $ 는 상수 값이 되고 식 자체가 크게 달라지는 것이 없다.
최대화를 진행하는 과정에서 이를 적용해보면,
- 새롭게 추가된 영역이 $ p(\theta) $ 이므로 $ q $ 함수를 선택하는 것은 기존의 EM 알고리즘과 달라질 것이 없다.
- 왜냐하면 $ q $ 함수는 오로지 $ L $ 함수와 $ KL $ 함수에서만 등장하기 때문
- M-Step 에서는 달라지게 되는데 실제 추정해야 할 로그 가능도 함수 값이 달라지기 때문
- 하지만 실제 식 적용에는 큰 변화가 없고 예전에 살펴보았던 MAP 과 같은 효과를 지니게 된다.

EM 알고리즘은 잠재 변수가 주어진 경우 MLE를 쉽게 적용할 수 있게 해주는 알고리즘임을 이미 확인했다.
그럼에도 불구하고 복잡한 모델이 주어졌을 때, E단계와 M단계가 아주 처리하기 힘든 경우도 존재한다.
이를 위해 2가지 확장 EM 버전이 존재한다.
GEM (generalized EM)
- M-Step 은 E-Step 과 상관없이 별도의 방식으로 구현 가능하다.
- E-Step 에서 얻어진 $ L $ 함수에 대해 이 함수 값을 최대로 하는 파라미터를 꼭 구할 필요는 없다.
- 그냥 단순하게 값이 커지는 방향으로 파라미터 값을 변경하기만 하면 된다. (SGD 방식)
- 따라서 단순하게 $ L $ 함수의 값이 더 커지는 방향으로의 파라미터를 선택하는 방법
  - 비선형 방식의 최적화 기법인 conjugate gradient 알고리즘 같은게 있다고 함
  - 또다른 GEM 구현 방식으로 ECM (expectation conditional maximization) 이 있음
    - 파라미터를 최대화 할 때 한번에 최대값으로 이동하는 것이 아니라,
    - 파라미터를 그룹화하여 그룹 단위로 최대화 과정을 수행하는 것
    - 자세히 언급되지 않았으므로 이 정도로만 생각하면 될 것 같다.
Incrimental EM
- 데이터 자체가 분산화되어 있어서 배치(batch) 방식의 업데이트가 불가능한 경우에 사용한다.
- 데이터를 스트리밍 방식으로 처리 가능함
- E-Step 단계가 여러 개의 데이터를 다루는 것이 아니라 하나의 데이터를 다루는 것처럼 수정됨
- E-Step, M-Step 모두 데이터 크기와 무관하게 고정된 계산량이 필요함
  - 왜냐하면 한 번 데이터를 거치면 완료되는 것이 아니라 데이터 입력에 의해 반복되면서 변경되기 때문
  - 실제로는 배치 버전보다 더 빠르게 수렴된다고 한다.

${\bf \mu}_k^{new} = {\bf \mu}_k^{old} + \left(\frac{\gamma^{new}(z_{mk})-\gamma^{old}(z_{mk})}{N_k^{new}}\right)({\bf x}_n-{\bf \mu}_k^{old})$ $N_k^{new} = N_k^{old} + \gamma^{new}(z_{mk}) - \gamma^{old}(z_{mk})$

Chapter. 9