- 앞서 2.3.9 절에서 이미 GMM 즉, 가우시안 혼합 모델을 살펴보았다.
- 잠시 언급해보자면 여러 개의 가우시안 분포를 선형 결합한 형태였다.
- 이번 절에서는 가우시안 혼합 분포를 이산 잠재 변수(discrete latent variable)를 도입하여 풀어갈 예정이다.
- 이러한 방법은 혼합 분포를 좀 더 명확하게 이해하는데 도움을 준다.
- 그리고 EM 알고리즘을 왜 사용해야 하는지도 이해하게 될 것이다.
- 이제 예전에 살펴보았던 식을 상기해보자.
- 이제 \( K \) 차원을 가지는 이진 랜덤 변수 (binary random variable) \( z \) 변수를 도입한다.
- 이전에도 보았던 1-to-K 코딩 스킴 형태의 변수다.
- 마찬가지로 잠재(latent) 변수의 형태로 식을 전개할 것이다.
- \( K \) 개의 요소 중 1개의 값만 1이고 나머지는 0인 값이다.
- 따라서 \( z_k \in {0,1} \) 이고 \( \sum_k z_k=1 \) 이다.
- 이제 잠재변수와의 결합 분포를 고려해보자.
- 식에 의해 \( p({\bf x}, {\bf z}) = p({\bf z})p({\bf x}|{\bf z}) \) 이다.
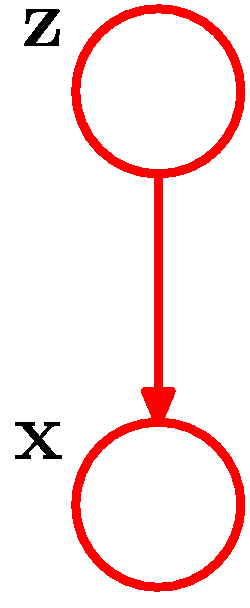
- 이제 \( z_k \) 의 주변 분포를 혼합계수(mixing coefficients) \( \pi_k \) 를 사용하여 정의할 수 있다.
- 파라미터 \( \pi_k \) 는 다음과 같은 성질을 만족해야 한다.
- 이제 \( {\bf z} \) 가 1-of-K 코딩 스킴을 사용하기 때문에 이에 대한 확률 식을 다음과 같이 사용할 수 있다.
- 이와 유사하게 이제 \( x \) 에 대한 조건부 확률을 표현해보자. \( x \) 는 \( z_k \) 가 주어졌을 때 가우시안 분포를 따른다.
- 어려운 내용은 아니다. 특정 클러스터에 해당하는 가우시안 분포를 조건부 분포로 표현한 것이다.
- 이를 일반화시키면 다음과 같아진다.
- 이제 \( {\bf x} \) 에 대한 주변 확률을 계산할 수 있다.
- 결국 예전에 봤던 식이 나오게 된다.
- 명시적으로 잠재 변수 \( {\bf z} \) 를 도입하며 \( {\bf x} \) 에 대한 주변 확률 분포를 구하는 식을 살펴보았다.
- 사실 이전에 보아왔던 것과 동일한 결과를 가진다는 것 외에는 별로 얻은 소득은 없어 보인다.
- 하지만 이제 우리는 명시적으로 잠재 변수를 도입하여 결합 확률 분포 \( p({\bf x}, {\bf z}) \) 를 사용하였다는게 중요하다.
-
주변 확률 \( p({\bf x}) \) 대신에 조건부 확률을 통해 작업을 진행할 수 있다. 이로써 \( EM \) 알고리즘도 함께 사용가능하게 되는 것이다.
- 이제 \( {\bf x} \) 가 주어졌을 때의 조건부 확률을 정의해보자.
- 우리는 \( \pi_k \) 가 \( z_k=1 \) 일 때의 사전 확률 값이라는 것을 알고 있다.
- 이제 \( \gamma(z_k) \) 는 관찰 데이터 \( {\bf x} \) 가 주어졌을 때의 사후 확률 값이 된다.
- 이후에 살펴볼 것이지만 \( \gamma(z_k) \) 를 성분 \( k \) 에 대한 responsibility 라고도 한다.
- 가우시안 혼합 모델을 이용하여 샘플을 생성하는 방법에 대해 살펴보도록 하자. (실제적인 내용은 11장에 나온다.)
- 이 작업을 수행하기 위해서는 우선 \( p({\bf z}) \) 분포로부터 \( {\bf z} \) 값을 생성해야 한다.
- 이 때의 값을 \( \widehat{\bf z} \) 라고 하자.
- 이제 \( \widehat{\bf z} \) 가 주어진 상태에서의 \( {\bf x} \) 값을 조건부 분포 \( p({\bf x}|\widehat{\bf z}) \) 에서 샘플을 생성한다.
- 이러한 샘플링 방식을 ancestral sampling 이라고 한다. 앞 장에서 이미 다루었던 내용이다.
- 우리는 \( p({\bf x}, {\bf z}) \) 로부터 샘플을 그려낼 수 있다.
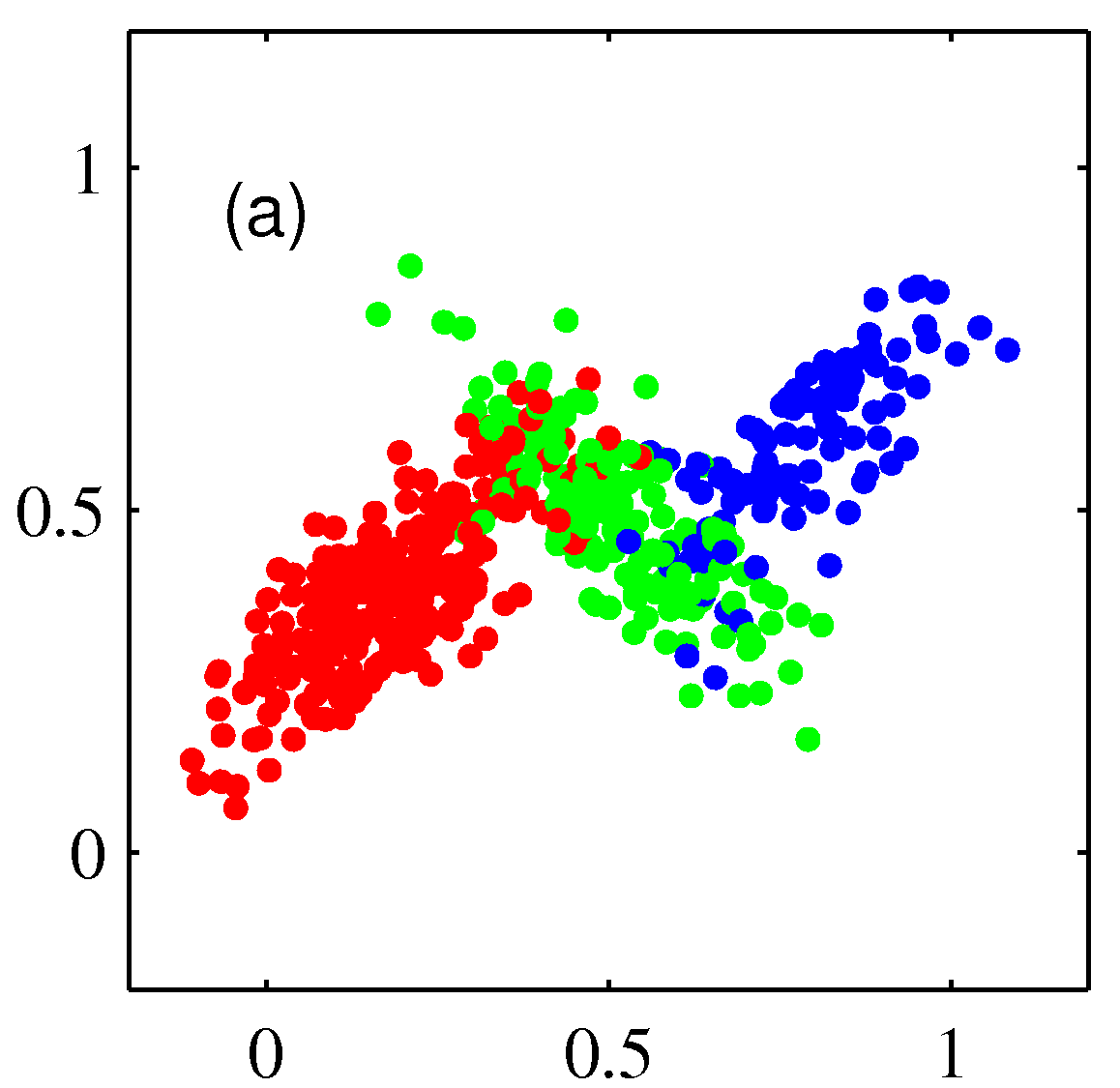
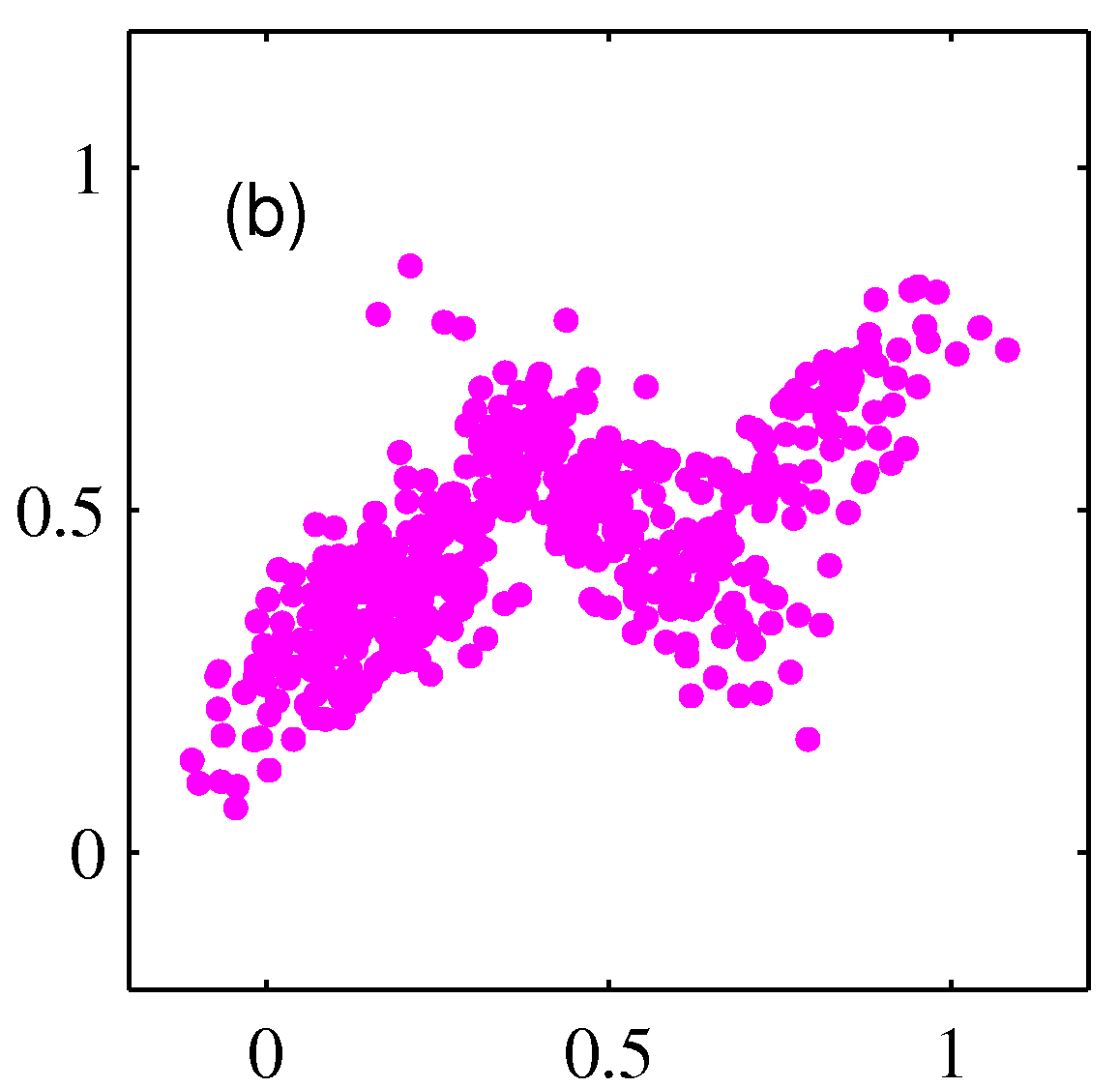
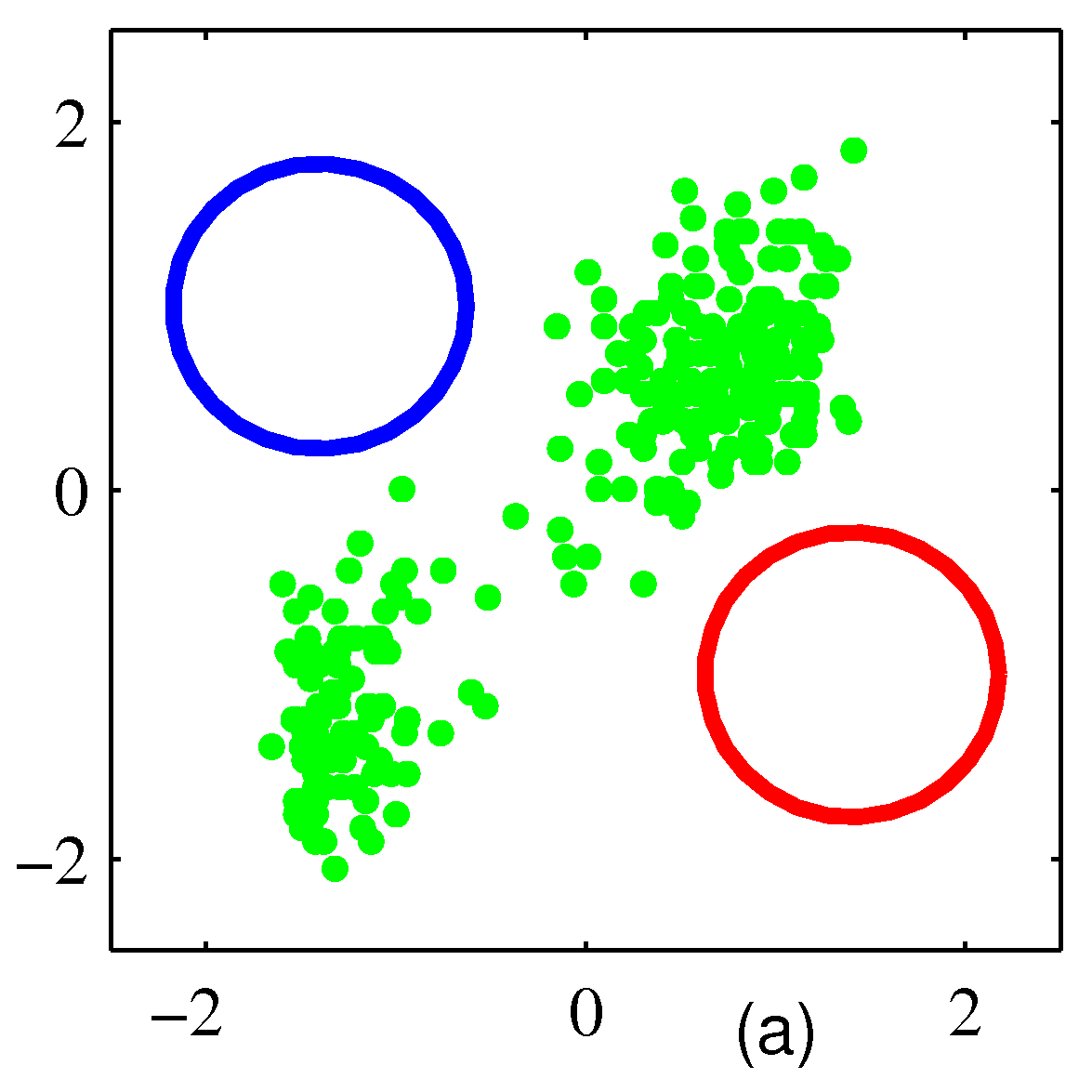
- 위 그림은 3개의 가우시안 혼합 분포로부터 500개의 샘플을 생성한 후의 그림이다.
- \( (a) \) 는 결합 분포 \( p({\bf z})p({\bf x}|{\bf z}) \) 로부터 각각의 \( z_k \) 에 대해 생성된 샘플을 다른 색으로 표현하고 있다.
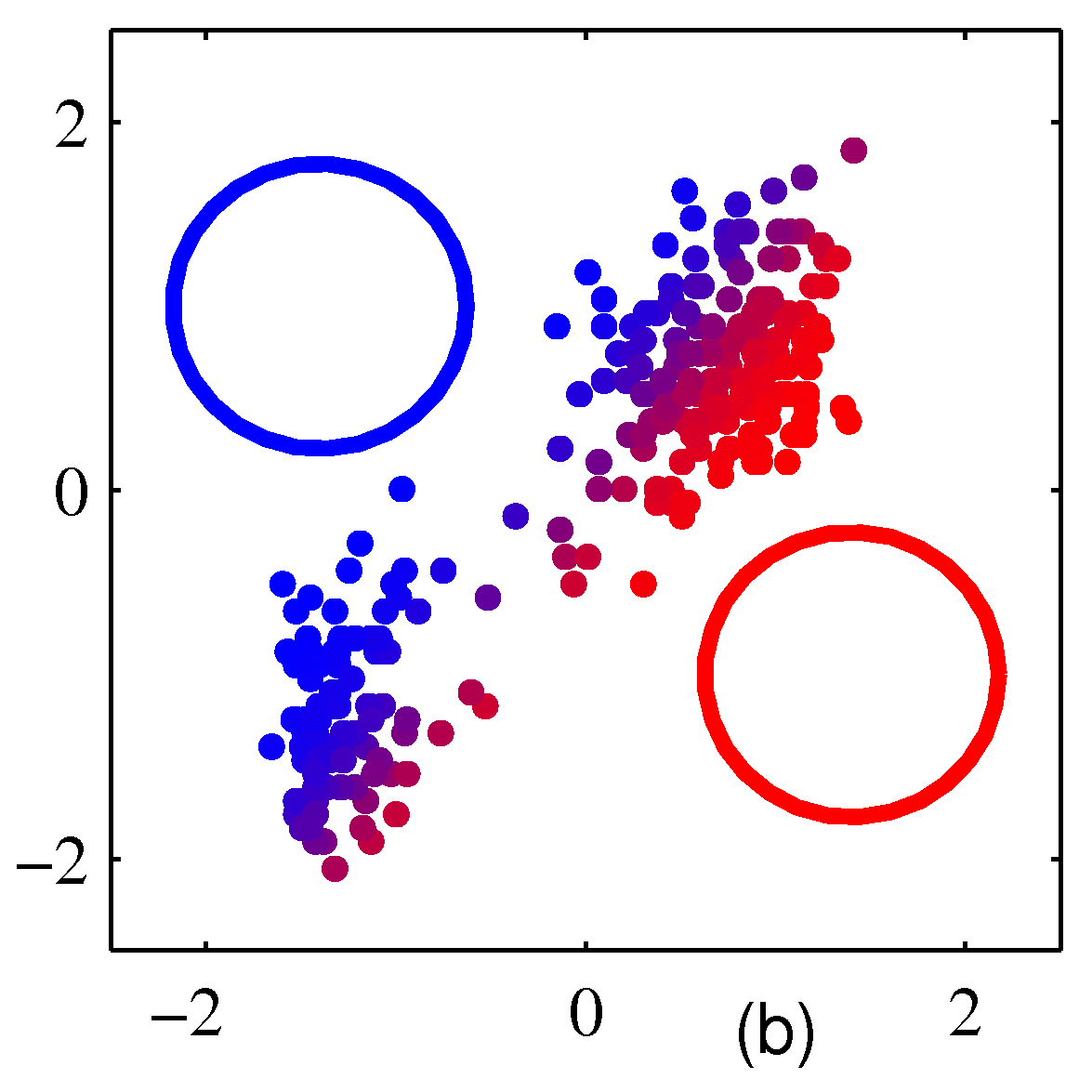
- \( (b) \) 는 생성된 데이터의 타겟 레이블을 삭제한 후의 결과이고,
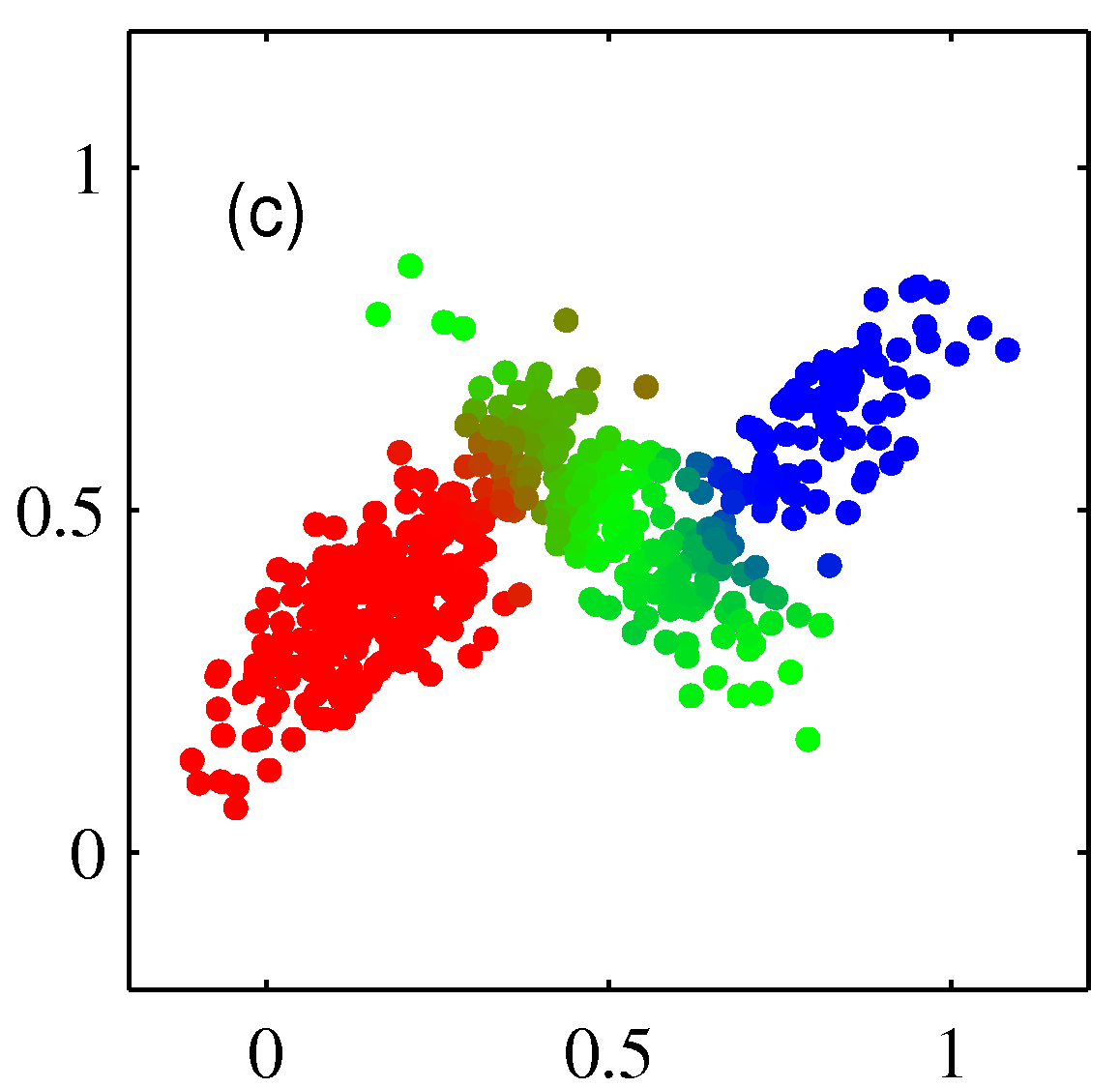
- \( (c) \) 는 \( \gamma(z_k) \) 에 따라 색을 달리하여 표현한 것이다.
- 하지만 위의 그림을 자세히보면 \( (a) \) 와는 색상이 좀 다른 것을 알 수 있는데,
- 실제 결과를 경성 혼합(soft mixture) 방식으로 표현했기 때문이다.
- 즉, \( \gamma(z_k) \) 의 값에 따라 각각의 색을 적당히 혼합했다.
- 예를 들어 \( \gamma(z_1)=1 \) 인 경우 완전히 붉은색으로 표기되지만,
- \( \gamma(z_2)=0.5 \) , \( \gamma(z_3)=0.5 \) 와 같은 결과를 얻은 경우 녹색과 파란색을 반반씩 섞게 된다.
- 참고로 \( (a) \) 와 같은 결과를 complete 하다고 표현하고 (b)와 같은 경우 incomplete 하다고 표현한다.
9.2.1. 최대 가능도 (Maximum likelihood)
- 관찰 데이터가 \( { {\bf x}_1,…,{\bf x}_N} \) 으로 주어졌다고 가정하자.
- 이를 이용하여 가장 적합한 혼합 가우시안 분포를 결정하는 문제를 확인해 볼 차례이다.
- 이 때의 입력 데이터는 \( N\times D \) 의 크기를 가지며, ( \( N \) 은 샘플의 개수, \( D \) 는 한 샘플의 차원)
- 따라서 입력 데이터를 행렬 \( X \) 로 표현할 수 있다 . 이런 경우에 한 줄의 해당하는 샘플은 \( {\bf x}_n^T \) 가 된다.
- 이제 이 샘플에 대응하는 잠재 변수 \( Z \) 를 고려해보자.
- 이 변수는 \( N\times K \) 크기의 행렬이 될 것이다. 이 때 한 샘플에 대응하는 잠재 변수는 \( {\bf z}_n^T \) 가 된다.
- 모든 데이터가 독립이라고 가정하면, 우리는 이를 그래프 모델로 쉽게 표현 가능하다.
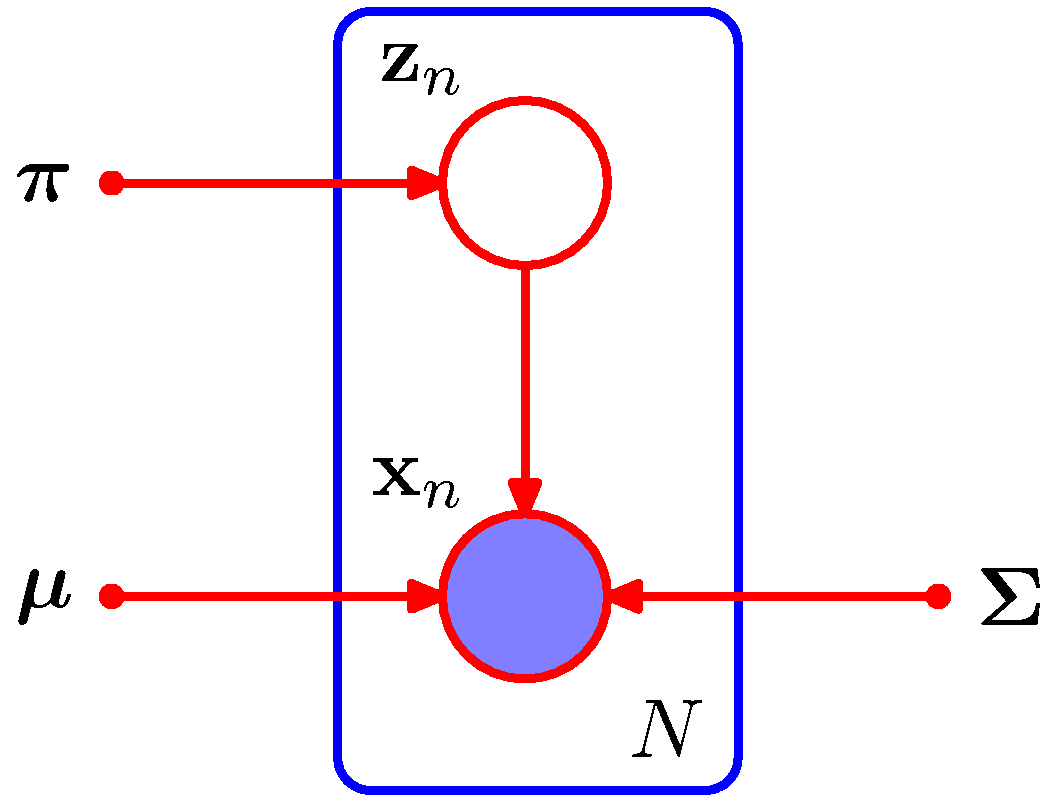
- 이제 로그 가능도 함수(likelihood function)를 기술해보자.
- MLE를 통해 이 함수를 최대화하는 파라미터를 찾는 과정을 살펴보기 전에 중요한 2가지 이슈에 대해 논의해보자.
- 특이점(singularities) 문제 (problem of singularities)
- 혼합의 식별 문제 (Identifiability of mixtures)
특이점 문제 (Problem of singularities)
- 공분산이 \( \Sigma_k=\sigma_k^2{\bf I} \) 인 간단한 모델을 생각해보자.
- 이 때 \( j \) 번째 분포만을 고려한다면 이 분포의 평균은 \( \mu_j \) 일 것이다.
- 그런데 이 때 오로지 단 1개의 샘플만이 이 컴포넌트에 속하게 된다고 생각해보자.
- 이런 경우 \( \mu_j={\bf x}_n \) 이 된다.
- 이러면 가능도 함수의 결과는 다음과 같이 된다.
- 이 때 \( j \) 번째 컴포넌트가 \( \sigma_j\rightarrow0 \) 인 성질을 가진다고 해보자.
- 즉, \( j \) 번째 컴포넌트의 확률 분포는 거의 하나의 값( \( \mu_j \) )으로 수렴되는 상태. (평균 값에서 높은 피크를 가진다)
- 이런 경우 가능도 함수의 결과 값도 무한대 값으로 수렴하게 된다.
- 가능도 함수는 각각의 분포의 곱으로 표현되기 때문에 가능도 함수 또한 무한대가 된다.
- 사실 이러한 형태의 가능도 함수는 우량조건(well-posed) 문제가 아님을 알 수 있는데,
- 이러한 특이점 문제가 언제나 발생을 하고,
- 가우시안 컴포넌트 중 하나가 특정 데이터 점으로 쏠리기만 해도 이러한 문제는 발생할 수 밖에 없다.
- 참고로 우량 조건의 문제란 명확한 해를 구할 수 있는 문제를 의미한다.
- 그런데 이 문제는 1개의 가우시안 모델을 사용하는 가능도 함수의 경우에도 동일하게 발생할 수 있는 문제가 아닌가?
- 결론부터 말하자면 하나의 가우시안 분포만을 사용하는 가능도 함수의 경우에는 이런 문제가 발생하지 않는데,
- 하나의 위치로 거의 수렴하는 단일 가우시안 모델은 (즉, \( \sigma\rightarrow0 \) 인 모델) 평균 값 외에는 밀도 값이 0이 된다.
- 따라서 가능도 함수에서 어떤 한 샘플이 평균 값과 같더라도 다른 샘플들이 0 값을 가지게 되므로 최종 곱은 0이 된다.
- 가능도 함수는 각 샘플에 대한 확률 분포의 곱으로 표기됨을 잊지 말자.
- 그리고 꽤 많은 수의 0의 곱과 무한대의 곱의 경우 0으로 수렴하는 속도가 더 빠르기 때문에 0이라고 생각할 수 있다.
- 물론 샘플이 한개밖에 없다면 발생할수 있겠지만 보통 하나의 가우시안 모델에서 샘플 한개만 주어진다고는 생각하기 어렵다.
- 반면 혼합 분포에서는 \( N \) 개의 샘플이 주어진다고 해도 한개의 샘플만 하나의 분포에 속하는 일이 발생 가능하다.
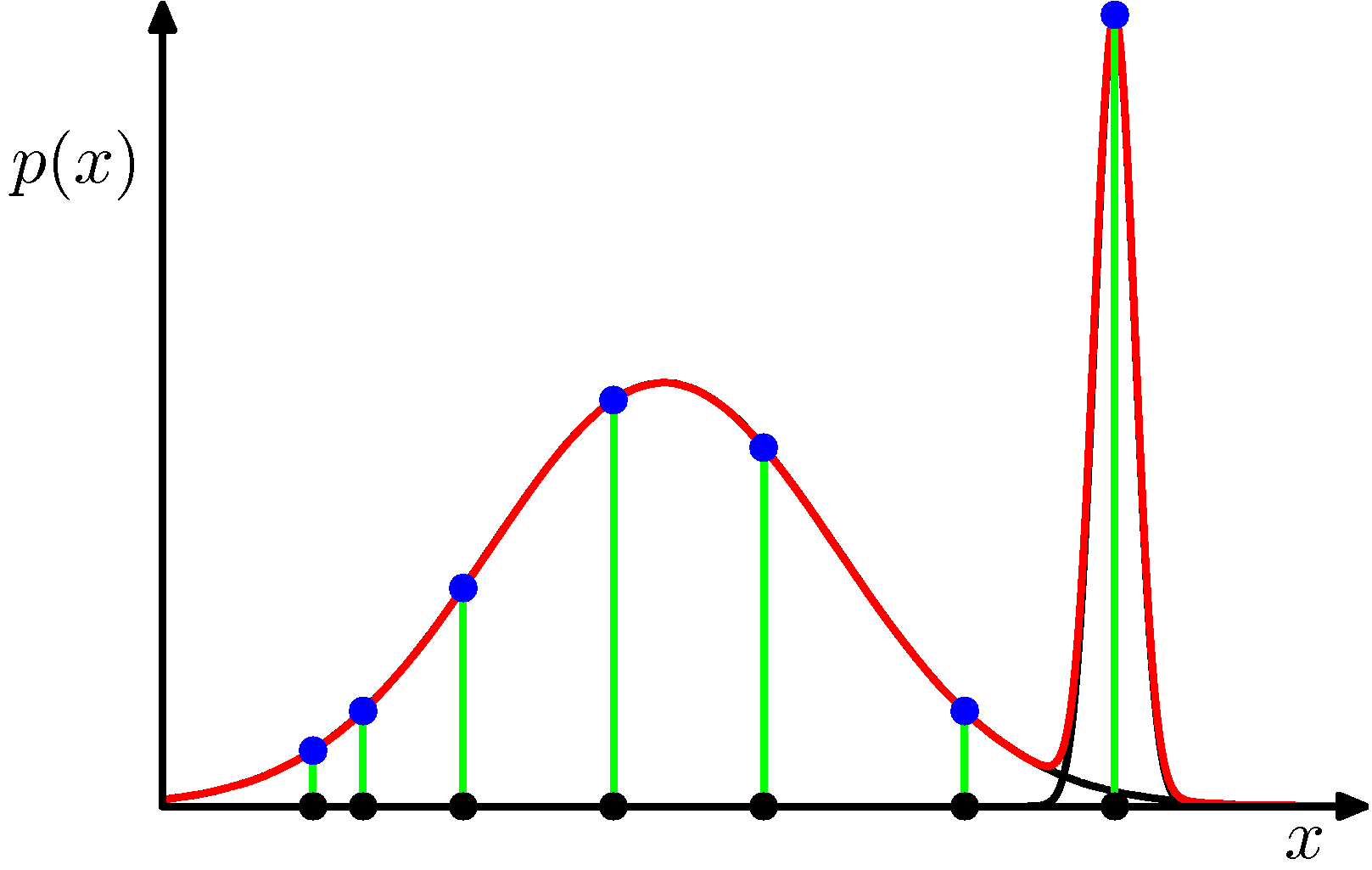
- 위의 그림을 보면 현재 2개의 가우시안 분포가 혼합된 형태이므로, 각각의 샘플들의 가능도 함수 값은 임의의 실수값을 가지게 된다.
- 하지만 마지막에 피크를 보면 해당 분포는 한 점을 중심으로 높은 피크를 그리는 형태이다.
-
최종적으로 모든 샘플의 가능도 함수 값을 곱해야 하는데 마지막 값으로 인해 발산한다.
- 사실 MLE 방식은 오버 피팅 문제가 존재하는데 이러한 특이점 문제도 오버 피팅 문제의 또 다른 예이다.
- 따라서 베이지안 방식에서도 이러한 문제는 발생하지 않는다.
- 이런 문제를 피하는 방법은 여러 가지가 있는데 휴리스틱한 방법으로는,
- 발현된 샘플이 평균 값과 일치하는 경우에 평균 값을 재설정하거나 공분산 값을 조절한다.
식별 문제 (Problem of Identifiability)
- 보통의 경우 \( p({\bf x}|\theta) \) 를 구하는데 있어서 \( \theta \neq \theta’ \) 인 경우 서로 다른 분포를 가지게 된다.
- 하지만 K 개의 컴포넌트를 사용하는 혼합 분포의 경우 MLE 결과를 동일하게 만들어내는 솔루션을 \( K! \) 개 만들 수 있다.
- 이유는 파라미터를 \( K \) 컴포넌트에 할당할 수 있는 방법이 총 \( K! \) 개 이기 때문.
- 따라서 임의의 한 샘플에 대해 동일한 혼합 분포 결과를 만들어낼 수 있는 샘플 수는 \( K!-1 \) 가 된다.
- 이러한 문제를 식별성 문제라고 한다.
- 이후 연속 잠재 변수를 다룰 때 좀 더 살펴보기로 하자.
9.2.2. 가우시안 혼합 분포를 EM으로 처리하기 (EM for Gaussian mixtures)
- 잠재 변수를 포함한 모델에서 MLE를 수행하기 위한 좋은 수단은 EM 알고리즘이다.
- 우리는 이후 일반화한 EM 알고리즘에 대해 살펴보고 이를 변분 방식의 프레임워크로 확장할 것이다.
- 그 시작으로 우선은 GMM 모델을 이용하여 EM 알고리즘을 적용하는 문제를 다룬다.
- 하지만 EM 알고리즘은 이렇게 제한적인 환경에서만 사용하는 모델은 아니고 다른 형태의 모델에서도 얼마든지 응용 가능하다.
- 가장 먼저 GMM 의 가능도 함수를 이용하여 식을 전개해 보도록 한다.
- 로그 가능도 함수 \( \ln p({\bf X} | \pi, {\bf \mu}, \Sigma) \) 를 미분하여 이 값이 0이 되는 때의 평균 값을 추정하도록 한다.
- 양변에 \( \Sigma_k \) 를 곱하고 전개하면 (물론 이 때 \( \Sigma_k \) 는 nonsingular 즉, 역행렬이 존재한다고 가정한다.)
- 우리는 \( N_k \) 를 클러스터 \( k \) 에 대한 effective number 라고 고려할 수 있다.
- 수식을 자세히 살펴보면 사실 \( k \) 번째 가우시안 분포의 평균 값인 \( {\bf \mu}_k \) 는 전체 샘플 데이터에 대한 평균 값을 취하고 있다는 것을 알 수 있다.
- 그럼에도 불구하고 하나의 클러스터에 국한된 평균 값으로 고려할 수 있는 이유는,
- 사후 분포 \( \gamma(z_{nk}) \) 에 의해 데이터 하나가 \( k \) 번째 가우시안 분포에만 영향을 미치는 정도를 계산할 수 있기 때문이다.
- 마찬가지로 로그 가능도 함수를 \( \Sigma_k \) 에 대해 미분하여 이 값을 0으로 놓고 풀면,
- 위의 결과를 살펴보면 기존의 1개의 가우시안 모델을 사용했을 때의 결과와 비슷한 형태에, 추가로 각 컴포넌트 별 가중치가 곱해진 형태로 식이 얻어진다.
- 이제 로그 가능도 함수를 혼합 계수 \( \pi_k \) 에 대해 미분하여 풀면 되는데, 혼합 계수는 추가적인 제약이 존재한다.
- 따라서 로그 가능도 함수에 이러한 제약을 추가하여 라그랑지안 승수 방식으로 처리한다.
- 양변에 \( \pi_k \) 를 곱하면 \( \gamma(z_{nk}) \) 가 나오게 된다. 이를 전개하면
- 결국 \( k \) 번째 혼합 계수는 responsibility 를 평균한 값이 된다.
- 이렇게 얻어진 평균과 분산, 혼합 계수는 자명한 (closed-form) 해를 가지지 못하는데 모두 \( \gamma(z_{nk}) \) 에 영향을 받기 때문.
- 따라서 이를 풀기 위해서는 다른 방식의 접근이 필요하게 된다. (iterative 방식의 도입)
EM 알고리즘의 적용과정
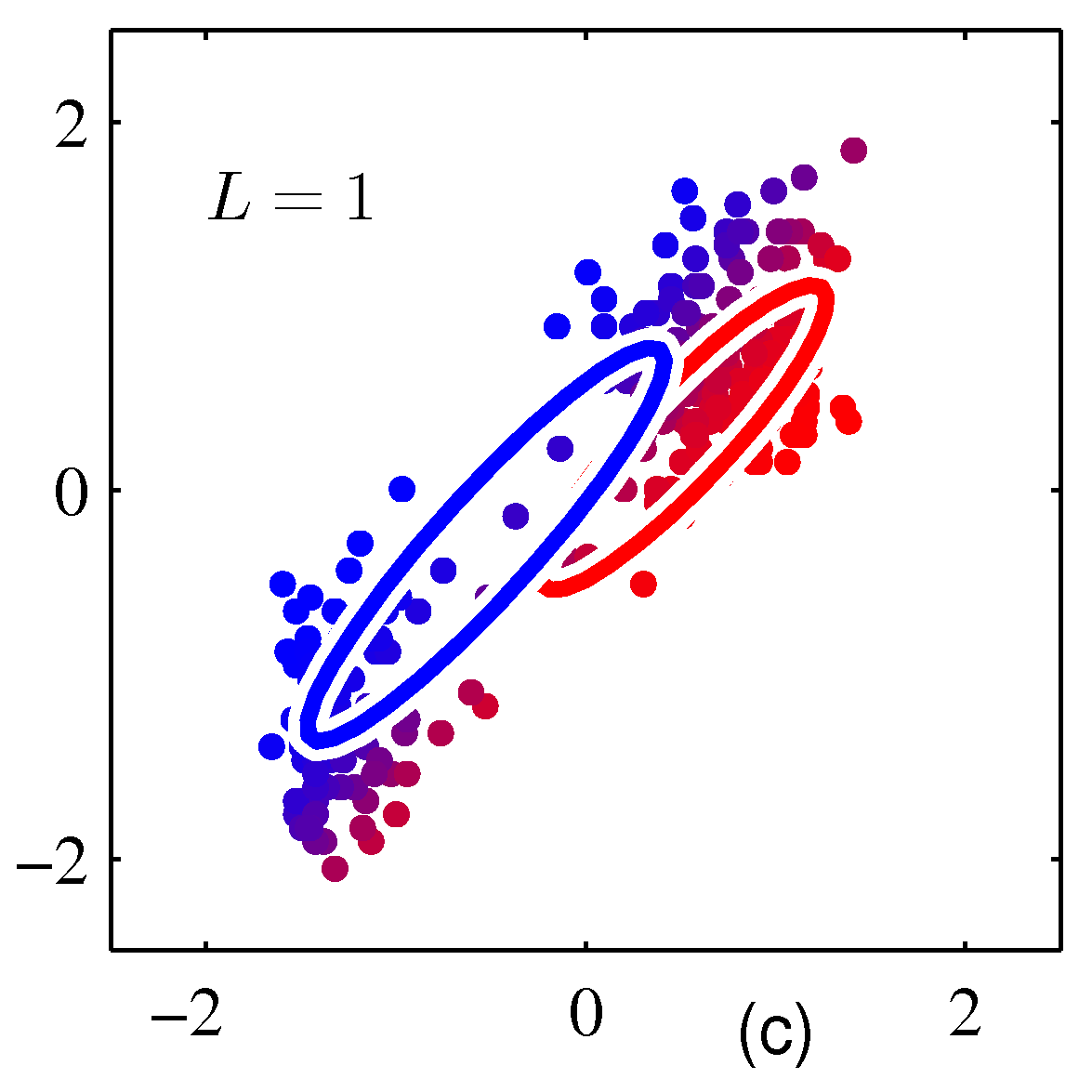
- EM 알고리즘은 반복적인(iterative) 방법을 이용하여 값을 추정하게 되는데 GMM 에서는 이를 다음과 같이 처리한다.
- Init-Step
- 그림 \( (a) \) 와 같이 임의의 값으로 평균과, 분산을 초기화한다.
- E-Step
- 현재 파라미터의 값을 사용하여 사후 확률 \( \gamma(z_{nk}) \) (responsibilities) 를 구한다.
- 그림 \( (b) \) 에 해당.
- M-Step
- E-Step 에서 계산한 사후 확률 값을 이용하여 MLE를 통한 평균, 분산, 혼합 계수의 값을 다시 추정한다.
- 그림 \( (c) \) 에 해당
- iterative
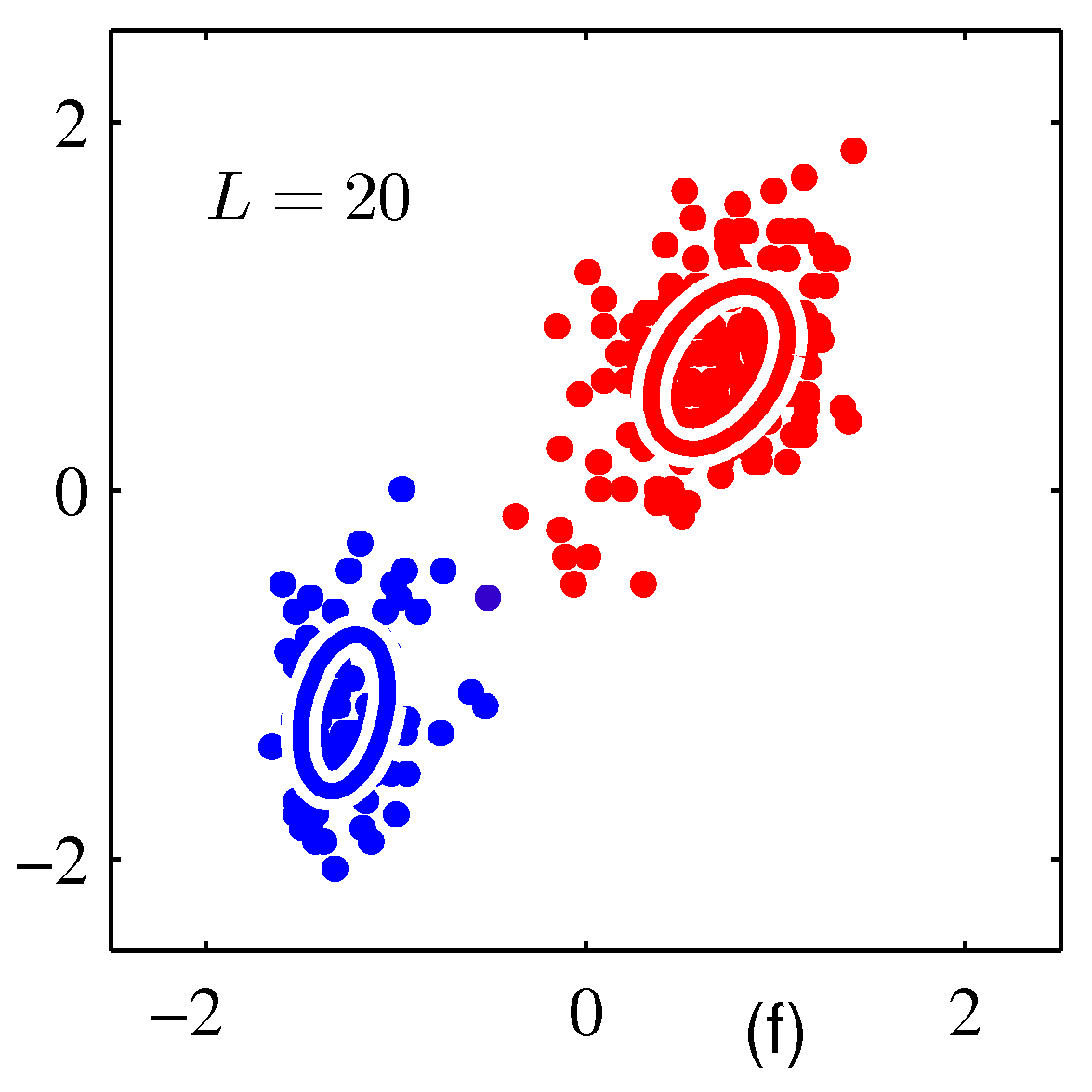
- 수렴 조건이 만족할 때까지 E-Step 과 M-Step 을 계속 반복
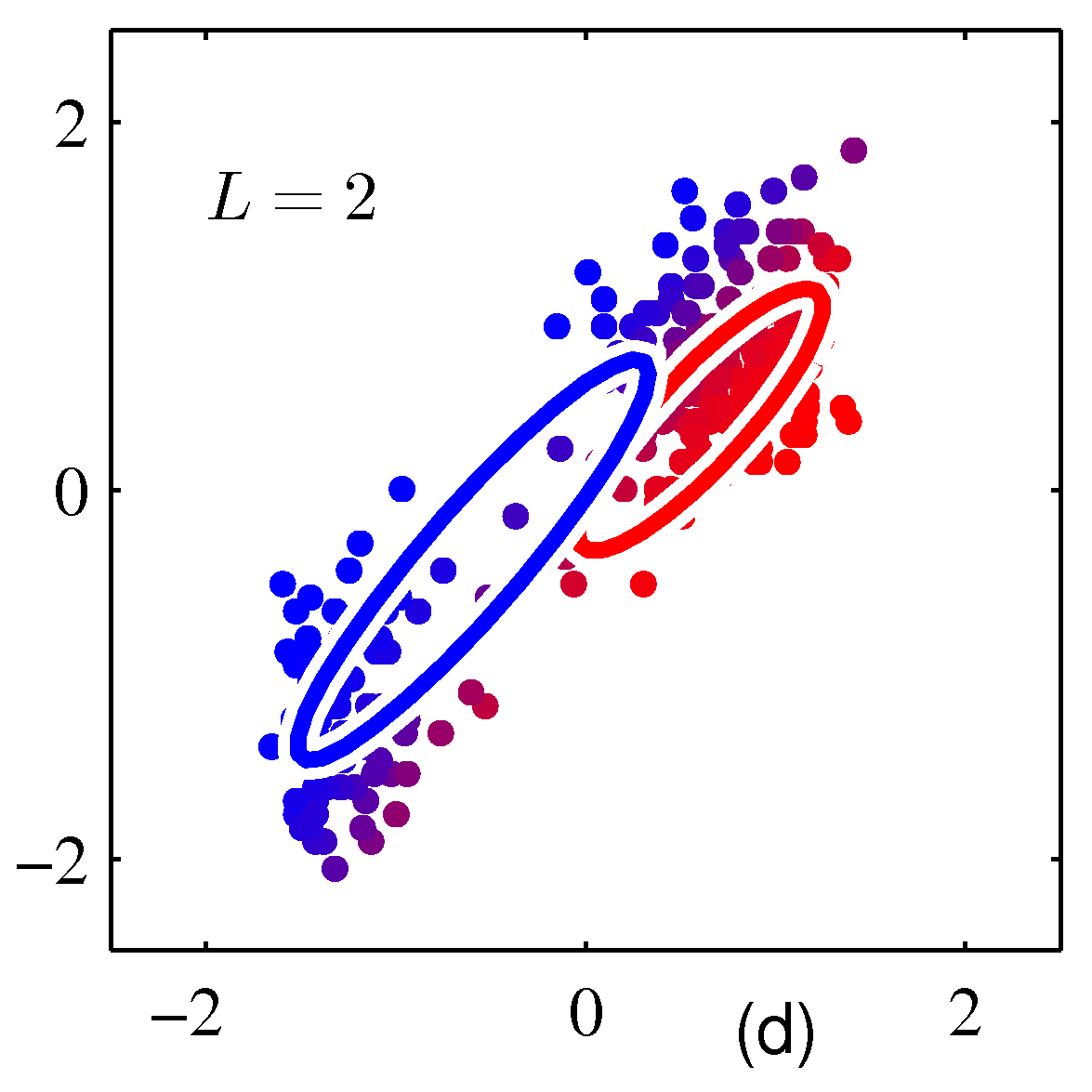
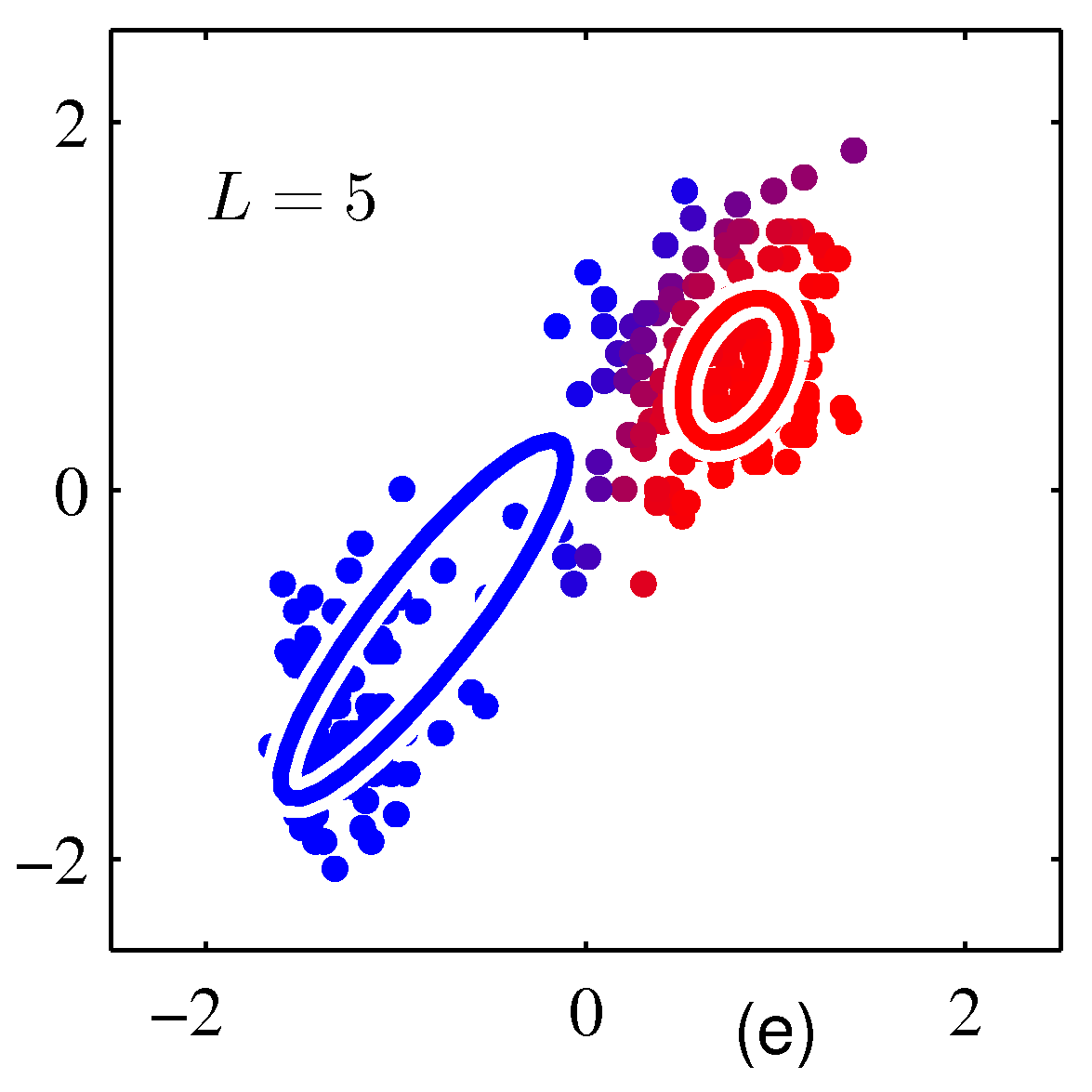
- 그림 \( (d), (e), (f) \) 에 해당.
- Init-Step
- 보통 EM 알고리즘이 K-means 알고리즘에 비해 반복 횟수가 많다.
- 따라서 보통의 경우 EM 알고리즘을 수행하기 전에 K-means 알고리즘을 돌려 적절한 초기값을 설정한 뒤에 다시 수행하는 경우가 많다.
- 앞서 설명한 대로 혼합 모델에서는 특이점 문제가 발생하지 않도록 주의를 기울여야 한다.
- 가우시안 분포에 한 점만 쏠리지 않도록 해야 한다.
- EM 알고리즘은 전역 최적해(global solution)를 보장하지 않는다. 따라서 지역 최적해(local solution) 만을 얻을 수 있다.
가우시안 혼합 모델의 EM 적용 정리
-
가우시안 혼합 모델(GMM)이 주어진 경우 다음과 같은 순서로 수행.
- 초기화 단계
- 평균 \( {\bf \mu}_k \) , 공분산 \( \Sigma_k \), 그리고 혼합 계수 \( \pi_k \) 를 적당한 값으로 초기화한다.
- E 단계
- 주어진 파라미터 값들을 이용하여 responsibility 값을 계산한다.
- M 단계
- 주어진 responsibility 값을 이용하여 파라미터를 추정한다.
- 가능도 함수 평가
- 파라미터 혹은 가능도 함수의 값이 수렴했는지 살펴본다. 수렴하지 않은 경우 E 단계로 돌아가서 반복.