- 우리는 이제부터 다차원 입력 데이터에 대해 해당 데이터가 어떤 그룹에 속하게 될지를 결정짓는 클러스터링 문제를 다루게 될 것이다.
- 이 때의 데이터 집합 \( ({\bf x}_1,…,{\bf x}_N) \) 을 고려하자.
- 이 데이터는 총 \( N \) 개의 데이터로 \( D \) 개의 차원을 가지며 \( K \) 개의 클러스터로 나눌 예정이다.
- 최종 목표는 모든 샘플 데이터를 \( K \) 개의 클러스터에 각각 배정하는 것이다. (물론 \( K \) 값은 미리 지정한다.)
- 간단하게 표기법을 보자면 \( D \) 개의 차원을 가지는 벡터를 \( {\bf u} \) 처럼 표기하고 (볼드체 주의),
- 이 벡터가 \( k \) 번 째 클러스터에 속하는 경우 \( {\bf u}_k \) 와 같이 표기한다.
- 이제 이 \( {\bf u}_k \) 벡터를 \( k \) 번째 클러스터의 정 중앙에 높여있는 벡터라고 생각해보자. (무게중심)
- \( {\bf u}_k \) 를 중심으로 해당 클러스터에 속하는 점들과의 거리의 총 합은, 클러스터에 속하지 않는 점들과의 거리의 총 합보다 작다.
-
우리의 최종 목표는 주어진 데이터 집합으로부터 이러한 중심점 \( {\bf u}_k \) 의 값들을 결정하는 것.
- 위와 같은 문제는 데이터 집합을 특정 클러스터에 할당하는 과정으로 표기하는 것이 좋다.
- 그러기 위해 우선 변수 \( r_{nk}\in {0,1} \) 을 정의한다.
- 이 때의 \( k \) 값은 당연히 \( k=1,…K \) 이다.
- 이는 어떤 \( n \) 번째 샘플 \( {\bf x}_n \) 가 \( k \) 번째 클러스터에 속하는 경우 \( r_{nk}=1 \) 이고 아닌 경우 0이 된다.
- 이건 이전에 봤던 1-to-K 코딩 방식이다.
- 이제 목적 함수를 정의한다. 이를 왜곡 측정( distortion measure ) 함수라고 한다.
- 이는 같은 클러스터에 속하는 각각의 점들로부터 그 클러스터의 평균과의 거리의 합을 제곱한 함수이다.
- 우리는 여기서 \( {r_{nk} } \) 와 \( {\bf \mu}_k \) 를 구해야 한다
- 이 때 함수 \( J \) 값이 최소가 될 때 각각의 값을 구해야 한다.
- 이를 위해 우리는 반복적인(iterative) 절차를 통해 이를 해결하는 방법을 살펴볼 것이다.
- \( r_{nk} \) 와 \( {\bf \mu}_k \) 를 구하기 위해 크게 2개의 단계로 나누게 된다.
- 먼저 \( {\bf \mu}_k \) 의 임의의 초기값을 설정한다.
- 첫번째 단계에서는 이 \( {\bf \mu}_k \) 값을 고정한 채로 \( J \) 를 최소화하는 \( r_{nk} \) 값을 구한다.
- 두번째 단계에서는 새롭게 얻어진 \( r_{nk} \) 를 고정하고 다시 \( {\bf \mu}_k \) 를 구한다.
- 두 값이 적당한 범위 내로 수렴할 때까지, 혹은 적당한 반복 횟수에 도달할 때까지 계속 반복한다.
- 각각의 두 단계를 \( E \) (expectation) 단계와 \( M \) (maximazation) 단계로 부르고 합쳐 \( EM \) 알고리즘이라고 한다.
- 이제 이러한 \( E \) 단계, \( M \) 단계를 이용한 K-means 알고리즘을 확인해보도록 하자.
- \( r_{nk} \) 를 구하는 과정을 먼저 살펴본다.
- \( J \) 가 \( r_{nk} \) 에 대해 선형 함수이므로 닫힌 형태(closed form)라고 볼 수 있다.
- 샘플은 모두 서로 독립적이므로 \( r_{nk} \) 도 각각의 \( n \) 에 대해 따로 최적화하면 된다.
- 즉, 다른 샘플과의 연관을 고려할 필요없이 현재 샘플에 대해 가장 타장한 \( r_{nk} \) 값을 선택하면 된다.
- 이 과정이 크게 어려운 것은 없다. 그냥 각 클러스터 중심과 샘플의 거리를 측정해서 가장 가까운 클러스터를 선택하면 된다.
- 이제 \( {\bf \mu}_k \) 를 구해보도록 하자. 물론 \( r_{nk} \) 는 고정한다.
- 목적함수 \( J \) 는 \( {\bf \mu}_k \) 에 대해서는 이차형식(quadratic)이다.
- 따라서 미분을 통해 최소값이 되는 지점을 얻을 수 있다.
- 이를 전개하면 다음을 얻을 수 있다.
- 결국 \( k \) 클러스터에 속한 점들의 평균을 구하게 된다. (k-means 라는 이름이 이런 이유이다.)
- 두 단계를 거치는 동안 데이터는 각각의 클러스터에 다시 할당이 되고,
- 이렇게 재할당된 데이터를 이용하여 평균 값을 다시 계산하는 과정을 반복하게 된다.
- 그림을 통해 K-means 가 수렴해가는 과정을 살펴보도록 하자.
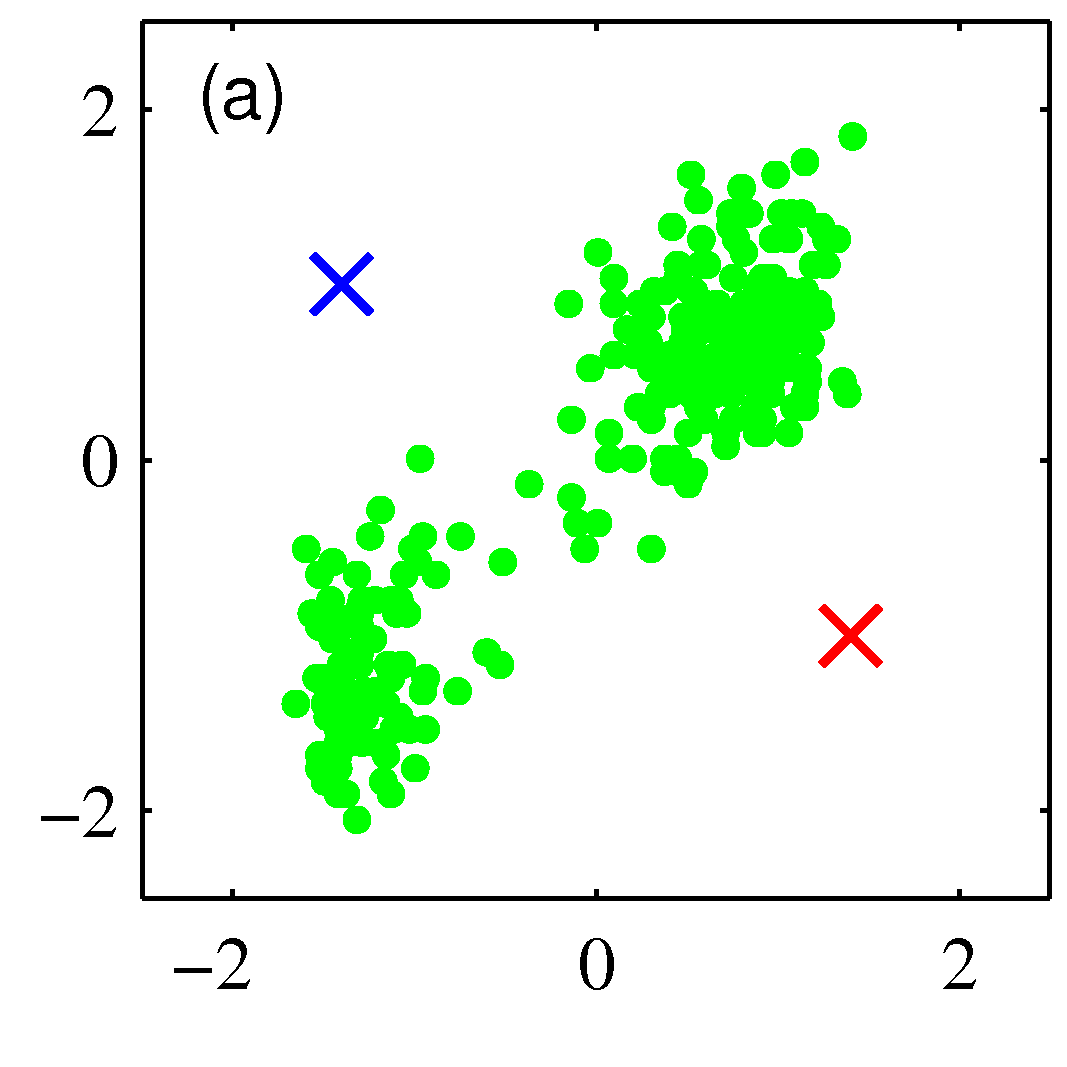
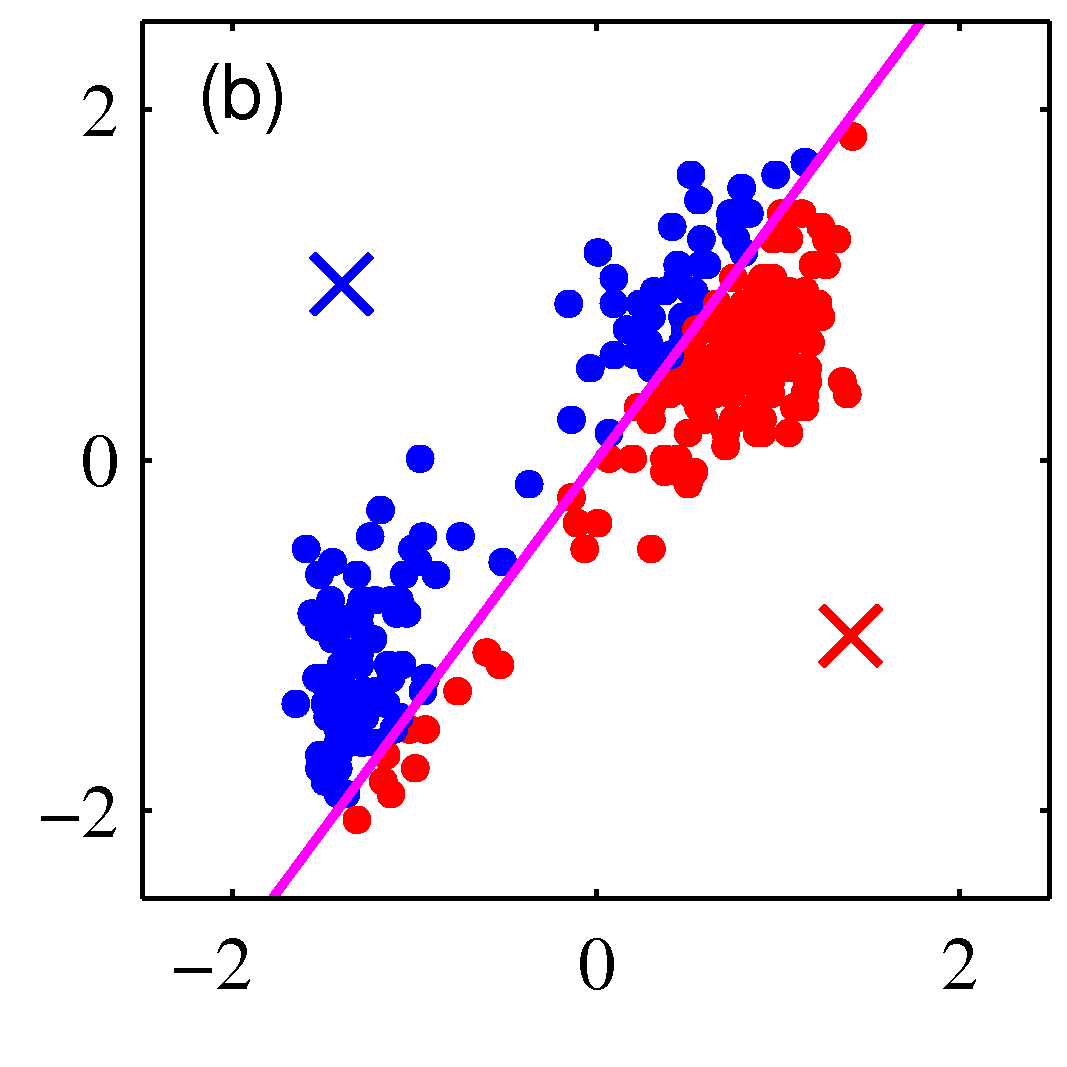
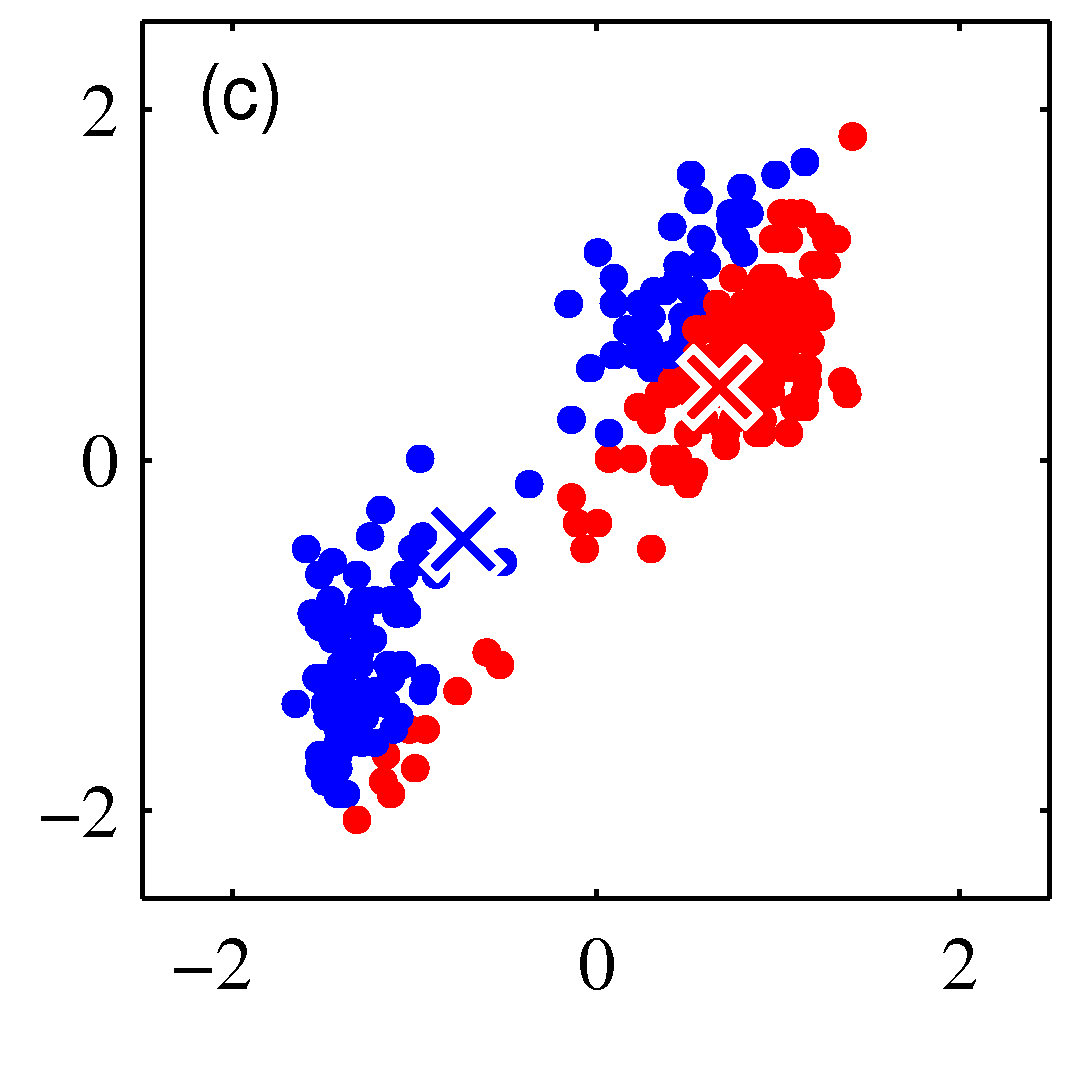
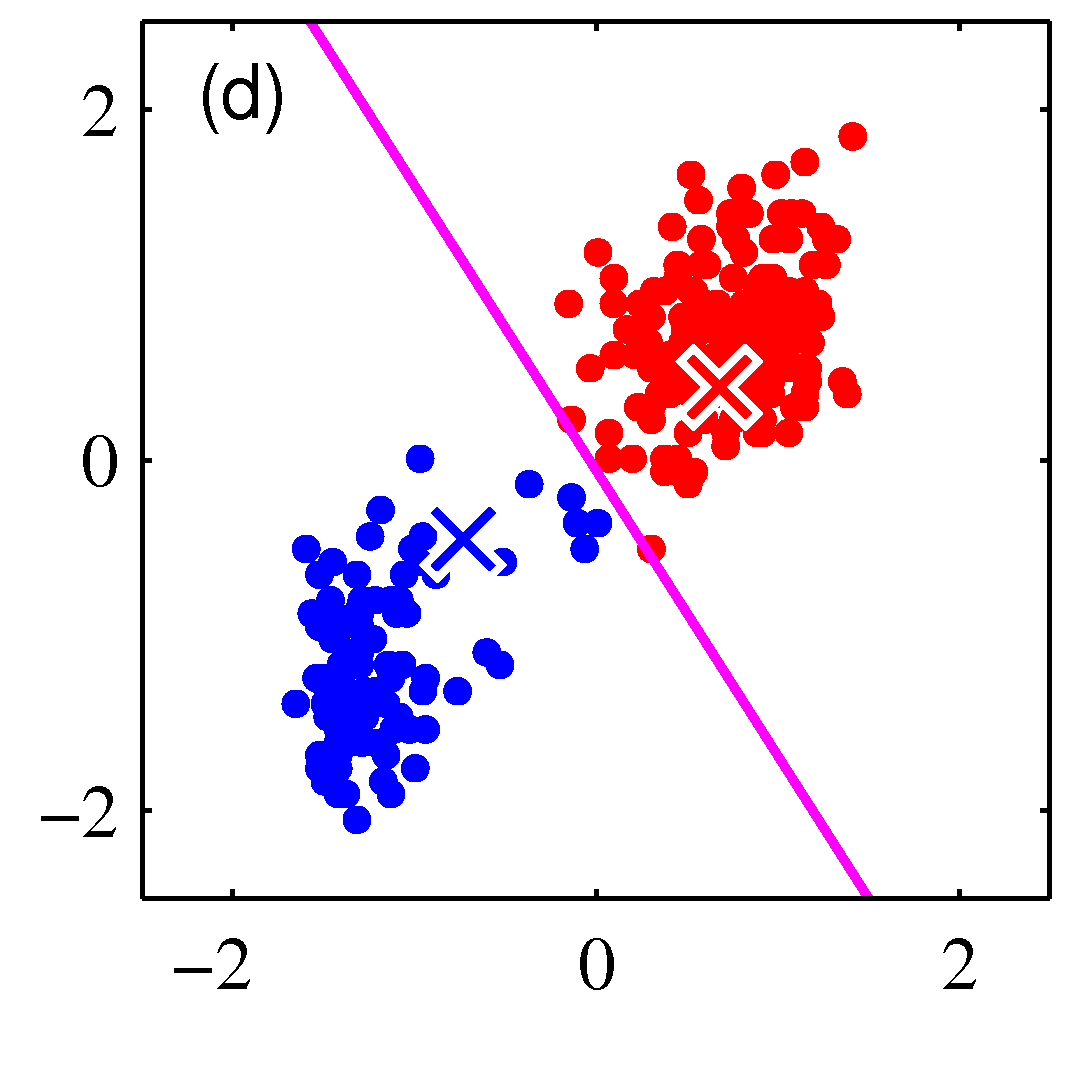
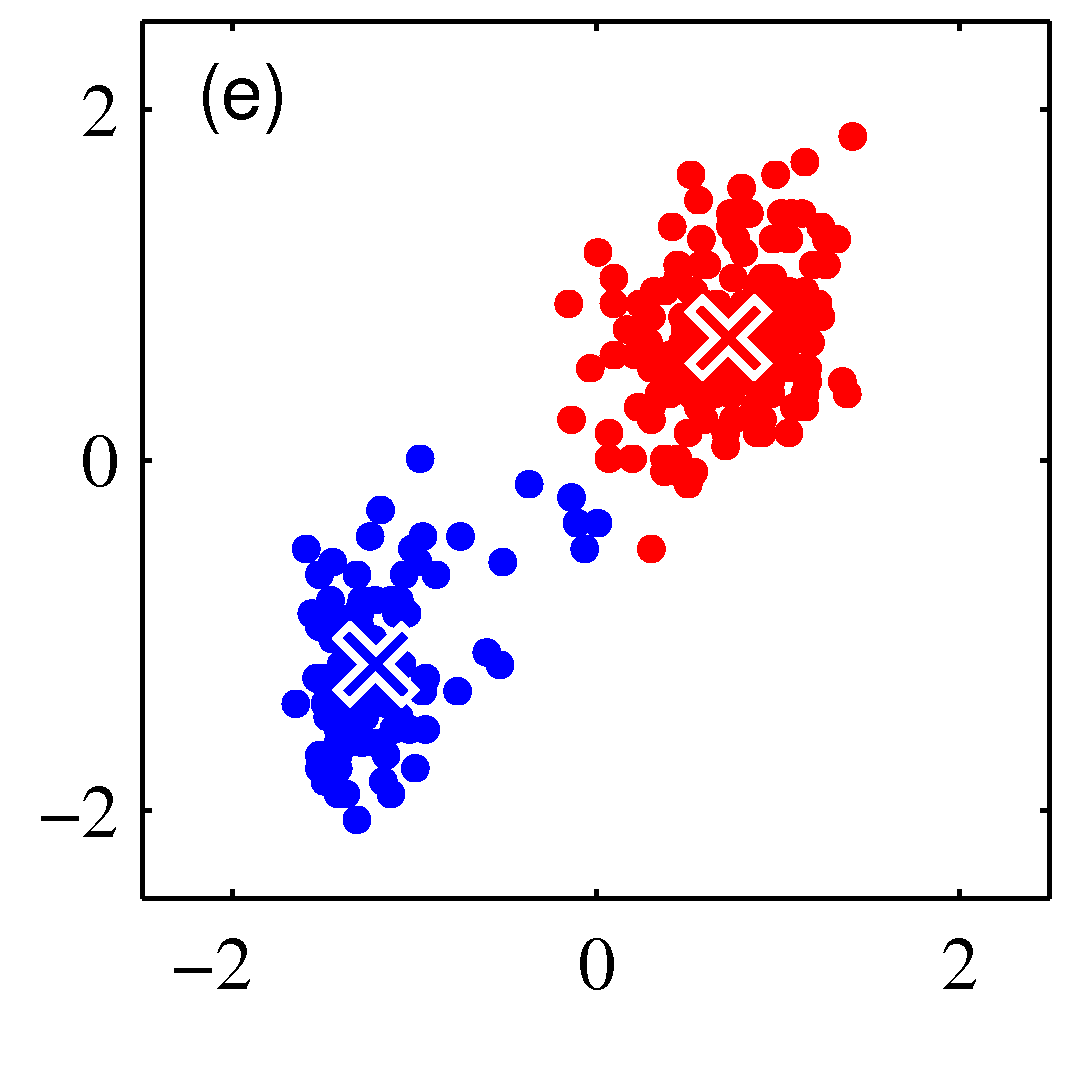
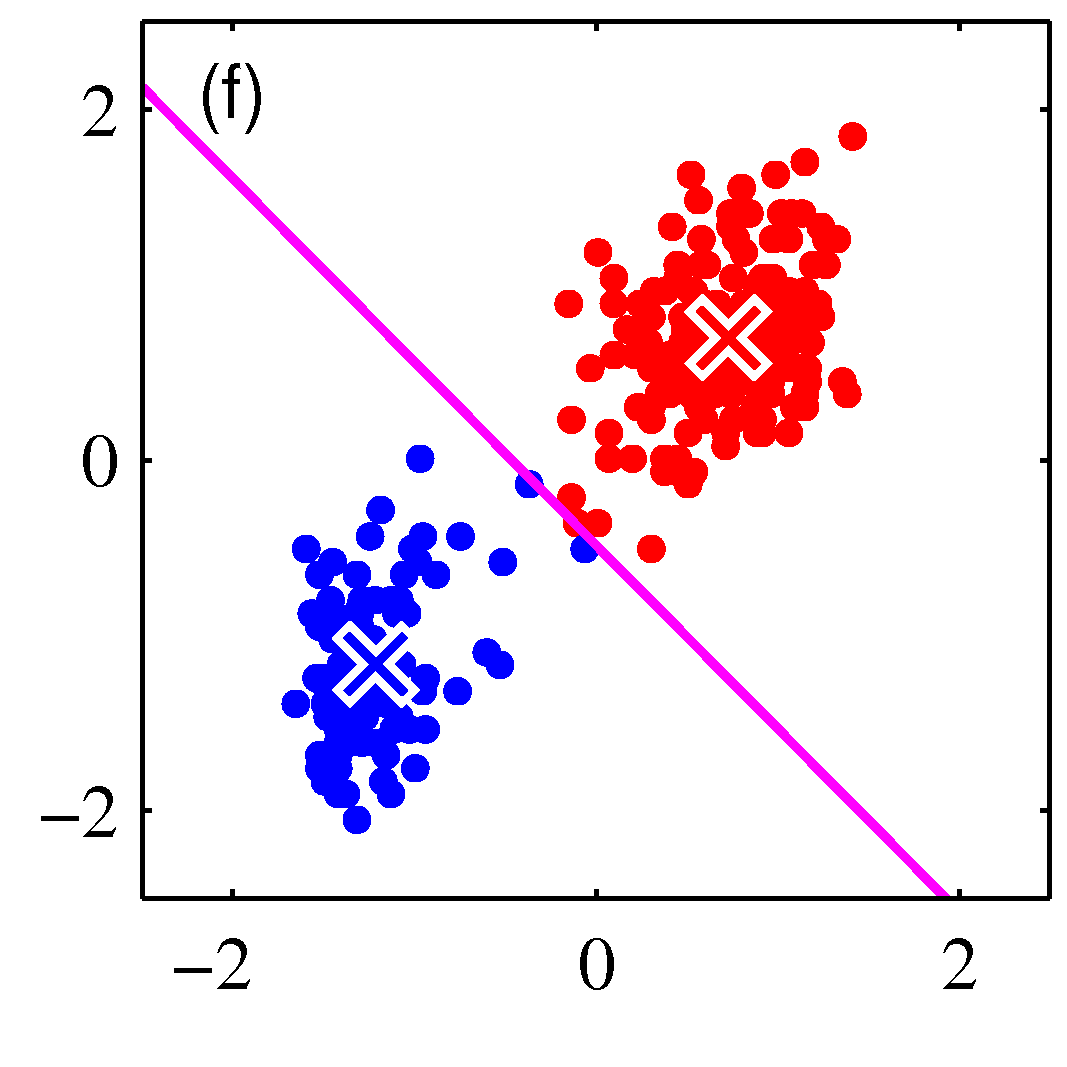
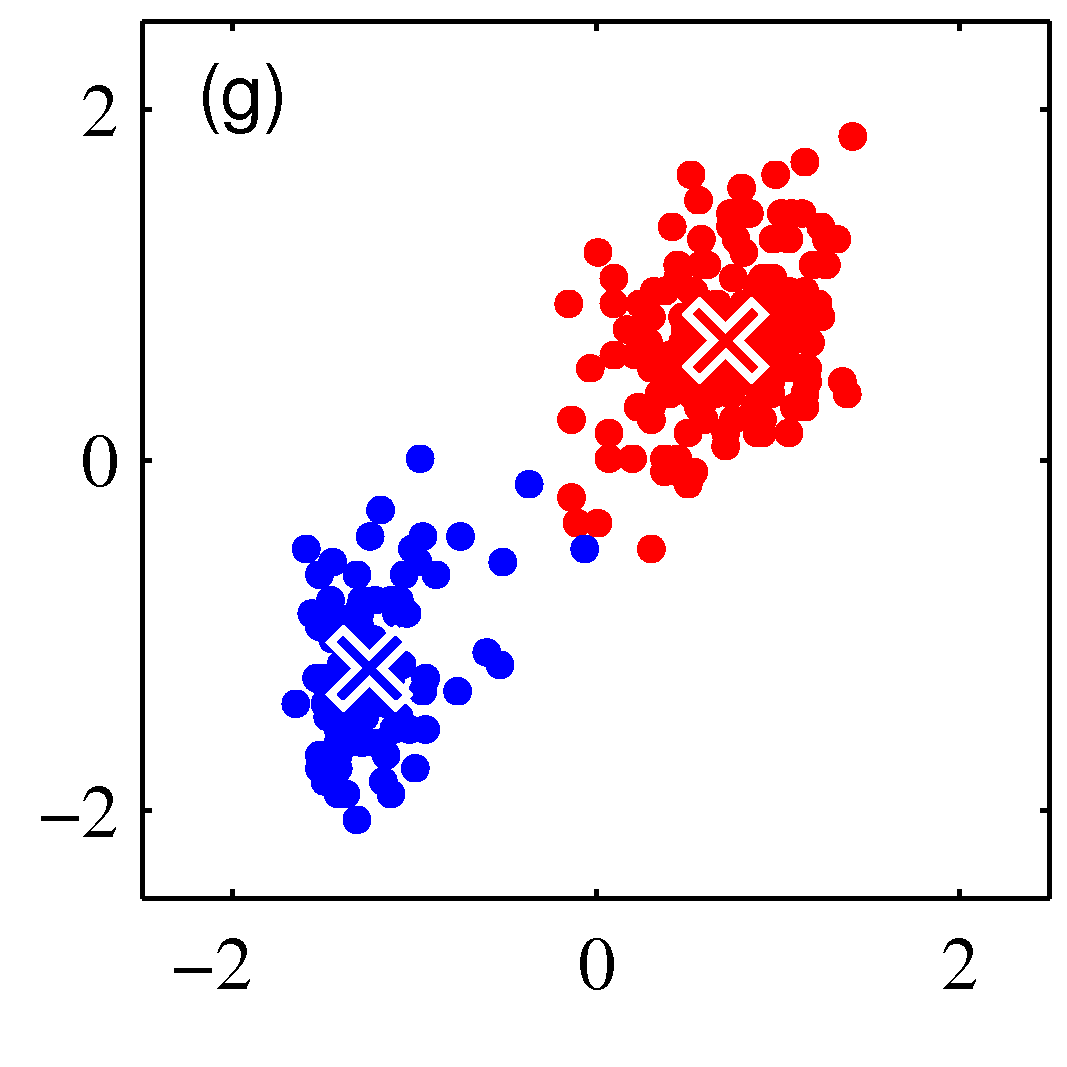
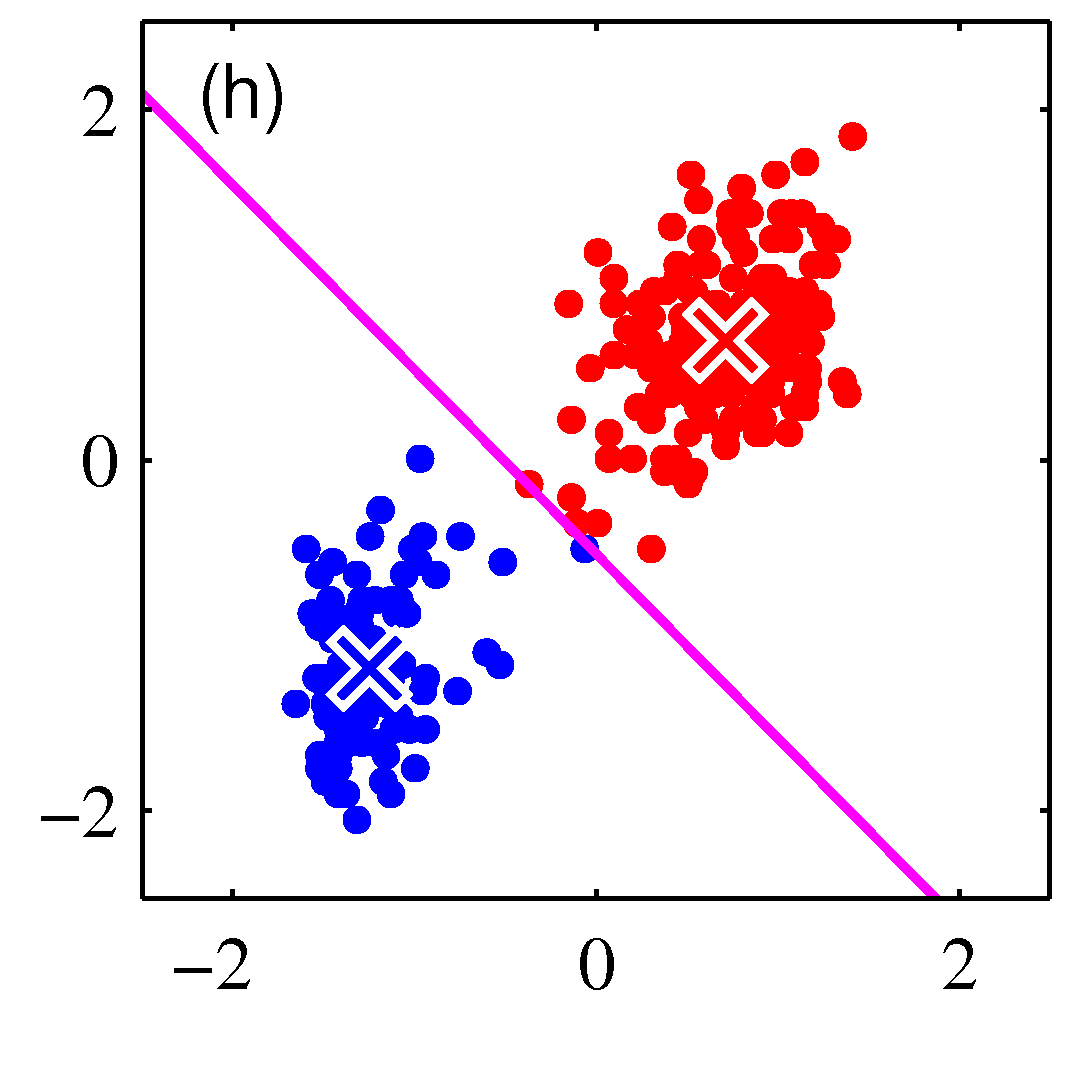
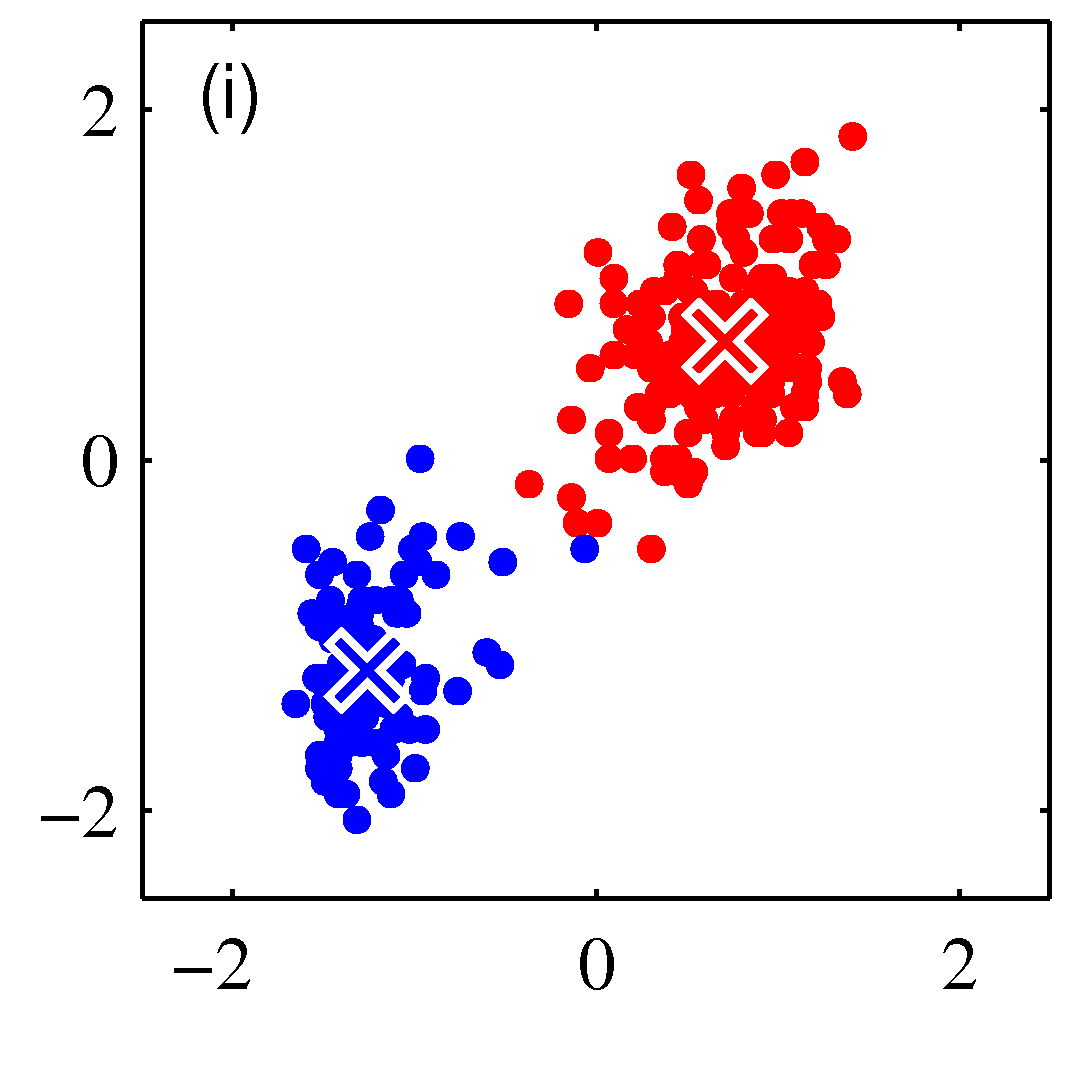
- 그림을 보면 쉽게 이해가 된다.
- 우선 2개의 클러스터를 구성한다고 결정한 상태이다.
- 임의의 2점을 평균 값으로 하여 \( EM \) 과정을 반복하게 된다.
- 그림 순서대로 평균 값을 계산한 뒤, 각각의 샘플에 대해 어느 클러스터에 속할지 다시 할당하고,
- 이렇게 할당된 데이터를 기준으로 다시 평균 값을 계산한다.
- 이를 수렴 조건이 만족할 때까지 반복한다.
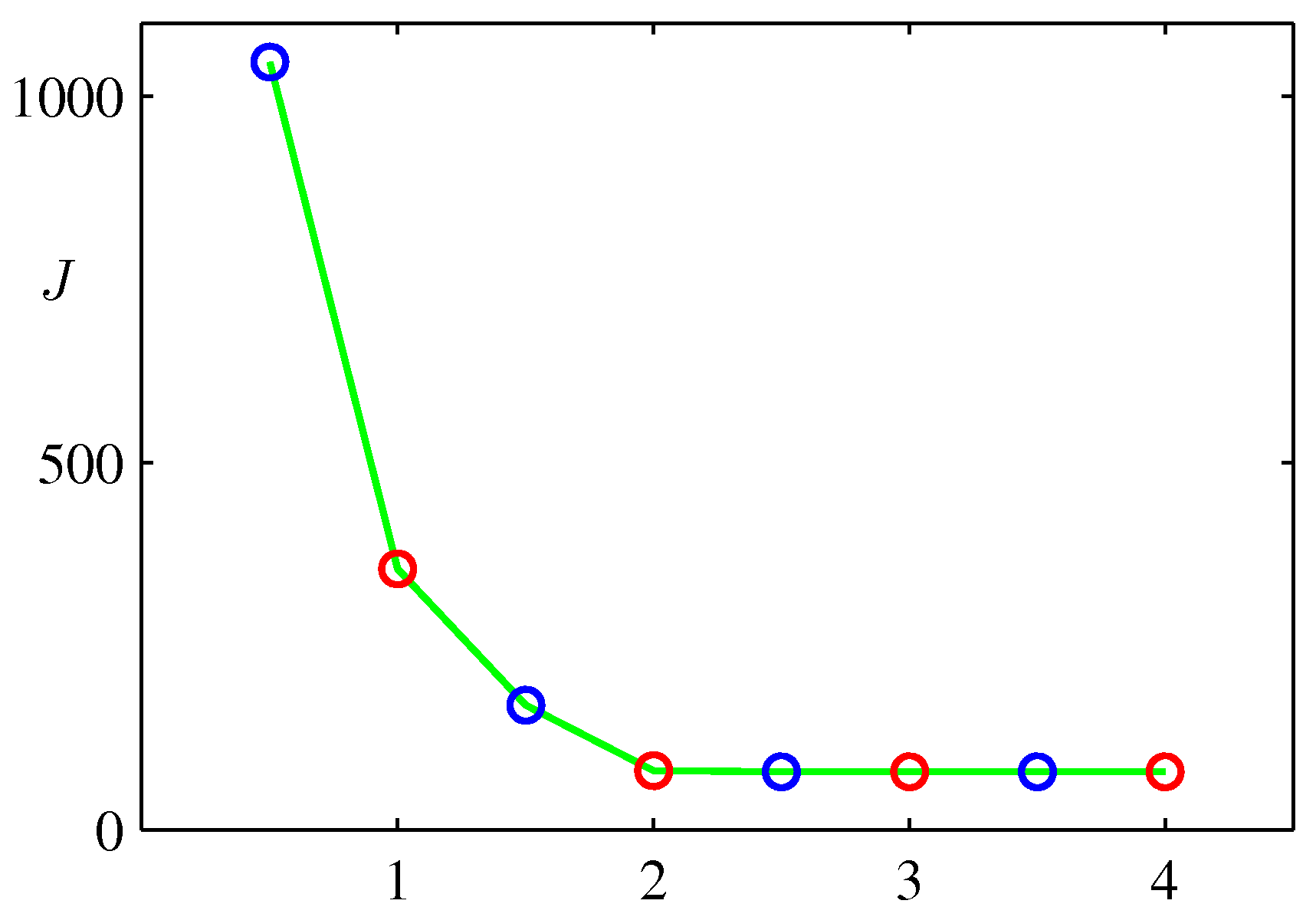
-
위 그림은 \( EM \) 과정을 반복할 때마다 함수 \( J \) 이 값이 줄어드는 것을 나타내는 그림이다.
-
사실 평균 \( {\bf \mu}_k \) 의 초기 값을 어디에 위치가는가에 따라 성능의 차이가 발생한다.
- 실제 반복 횟수의 차이가 크게 발생할 수 있기 때문이다.
- 초기 평균값을 정하는 적당한 방법 중 하나는 샘플 내에서 임의의 점들을 추출하여 평균을 구한 뒤 이를 초기 평균값으로 사용하는 것이다.
- 지금까지 언급한 방식대로 K-means를 구현한다면 성능이 크게 느릴 수 있는데 ,
- \( E \) 단계에서 평균과 모든 점들에 대해 비교를 하는 과정이 포함되어 있기 때문이다.
- 학습 속도를 높이기 위한 방법으로 여러 가지를 고려해볼 수 있다.
- 데이터를 트리 자료구조로 저장하여 사용하는 방법이 있다. (KD-트리 같은 방식)
- 삼각 부등식(triangle inequality) 방식을 사용하여 거리 계산을 하지 않는 방식도 있다고 한다.
- 지금까지는 배치(batch) 방식의 업데이트 기법을 살펴보았다.
- 온라인 업데이트 (online-update) 방식의 업데이트 기법도 있는데 (MacQueen, 1967)
- 정의한 \( J \) 함수에 대해 \( u_{k} \) 로 미분을 하면 회귀 함수가 얻어진다.
- 이에 대한 근(root) 값을 계산하는데 \( Robbins-Monro \) 알고리즘을 사용하는 방식이다.
- 이 식은 다음과 같은 식을 유도한다.
- 이 때 사용되는 학습 속도 비율(learning rate) \( \eta_n \) 는 식을 단조 감소하도록 만드는 값으로 사용해야 한다.
- K-means 알고리즘은 샘플과 평균간의 유클리디안 거리 측정 방식을 사용하기 때문에 데이터 타입에 제약이 존재한다.
- 유클리디안 거리를 사용할 수 있는 자료 타입이어야 한다.
- 예를 들어 특정 카테고리를 가지는 명목형 타입인 경우 거리를 측정할 수 없다.
- 또한 이상치(outlier)에 영향을 많이 받는 알고리즘이다.
- 평균을 사용하기 때문인데, 원래 평균값이 이상치에 취약하다.
- 따라서 이러한 제약을 없앨 수 있도록 K-means 알고리즘을 일반화한 알고리즘이 K-medoids 알고리즘이다.
K-medoids 알고리즘
- 유클리디안 거리 측정 함수 대신 \( \nu({\bf x}, {\bf x}’) \) 를 정의하여 사용한다.
- 이는 \( {\bf x} \) 와 \( {\bf x}’ \) 사이의 거리 개념을 나타내는 것이다.
- 즉, 거리를 구하는 식에 반드시 유클리디안 방식을 사용하지 않아도 된다.
- 목적 함수는 다음과 같다.
- \( E \) 스텝은 앞서 살펴본 방식과 동일한 방법으로 진행되며 따라서 이 때 필요한 연산량도 \( O(NK) \) 가된다.
- \( M \) 스텝은 단연히 달라지게 되는데,
- 두 점 사이의 상이함을 측정하는 단계이므로 (dissmilarity meature) \( \nu(\cdot) \) 의 비용이 이전보다 더 클수 있다.
- 그래서 연산량을 줄이기 위해 클러스터의 중심점을 클러스터에 속하는 데이터 중 하나로만 선정하기도 한다.
- 이러면 각 점들의 거리 계산을 중간에 좀 저장해 두고 다시 사용할 수 있다.
- 이 경우 \( \nu(\cdot) \) 를 계산하는 비용은 \( O(N_k^2) \) 이 필요하다.
- K-means 알고리즘은 계산 중에 하나의 점이 반드시 하나의 클러스터에 속하는 것으로 간주되어 계산되게 된다.
- 하지만 한 점이 여러 개의 클러스터의 중심으로부터 모두 비슷한 거리에 위치할 수도 있다.
- 이런 경우에는 이 점을 어떤 클러스터로 속하게 할지 애매하다.
- 확률적인 접근 방식을 이용하여 특정 클러스터에 대한 할당을 특정 클러스터에 포함될 확률값으로 계산할 수도 있다.
- 이러한 방식을 soft 대입 방식이라고 한다.
- 하지만 한 점이 여러 개의 클러스터의 중심으로부터 모두 비슷한 거리에 위치할 수도 있다.
9.1.1. 이미지 분할 및 압축 (Image segmentation and compression)
- K-means 알고리즘을 살펴보기 위해서 이미지를 분할하고 압축하는 예제를 살펴보도록 한다.
이미지 분할
- 목표 : 이미지 영역을 동질의 시각적 영역 단위로 나누는 작업
- 말이 좀 어렵긴한데 예제를 보면 쉽게 알 수 있다. 그냥 비슷한 색상들을 대표 색상으로 그룹화하는 작업.
- 이미지의 각 픽셀(pixel)을 하나의 데이터 포인트로 간주한다.
- 픽셀(pixel)
- 3차원 데이터 (RGB format : Red, Green, Blue)
- 이 때 각각의 색상의 범위를 정규화하여 [0, 1] 사이의 값만 가지도록 한다.
- 보통 한 색상을 0~255로 표현하는 경우도 많다. (R, G, B 각각에 대해)
- K-means 알고리즘을 적용하여 각 픽셀 데이터를 \( {R,G,B} \) 로 표현되는 중심 벡터 \( \mu_k \) 로 표현한다.








- 위의 그림은 이미지에 K-means를 적용한 결과이다.
- 각각의 점들을 얻어진 중심 픽셀의 대표 색으로 변경한 뒤에 다시 그림을 그렸을 때의 결과이다.
이미지 압축
- 분할 문제 뿐만 아니라 압축 문제에서도 K-means를 적용해 볼 수 있다.
- 물론 이 때 다루는 압축 방식은 손실 압축(lossy data compression) 방식을 의미한다.
- 압축 과정은 다음과 같다.
- \( N \) 개의 픽셀이 주어졌을 때 이를 \( K \) 개의 클러스터에 각각 할당한 뒤에
- 실제 각 점들을 다음과 같이 새로 저장한다.
- 각 점들이 할당된 클러스터의 식별자 \( K \) 를 만들고 (총 \( K \) 개)
- 각 점들에 대해 픽셀 색상이 아닌 이에 대응하는 식별자 값을 저장한다.
- 물론 이 때 식별자는 매우 작은 숫자이므로 좀 더 적은 저장 크기를 가지게 된다.
- 다음으로 \( K \) 에 대한 중심값 \( \mu_k \) 의 값을 저장.
- 이러한 방식을 벡터 양자화(vector quantization) 라고 한다.
- 그리고 이 때 사용된 \( \mu_k \) 를 코드북 벡터(code-book vector)라고 부른다.
- 사실 데이터 압축 문제를 데이터 분할 문제로도 다룰 수 있는데,
- 이미지를 분할하면 실제 이미지 압축 효과를 얻을 수 있기 때문
- 원본 이미지
- N 개의 픽셀
- 하나의 픽셀은 \( {R,G,B} \) 이며 한 색당 8bit 로 저장되므로 한 필셀은 24bit
- 따라서 전체 픽셀 저장에 필요한 크기는 \( 24N \) bit
- K-means가 적용된 이미지
- 하나의 픽셀을 \( \mu_k \) 의 id로 표현하게 된다.
- 이런 경우 하나의 픽셀은 \( log_2K \) bit 가 필요. 총 \( N \) 개의 픽셀은 \( Nlog_2K \) bit 가 필요.
- 코드북은 24bit 가 \( K \) 개 필요. 즉, 24K bit
- 총 필요한 저장 크기는 \( 24K + Nlog_2K \) bit
-
실제 \( K « N \) 이므로 저장 크기가 많이 줄어들 수 있다.
- 위의 그림에 대한 압축 비율을 살펴보도록 하자.
- 원본 이미지 : \( 240\times180 \) 픽셀이므로 \( 24\times43,200=1,036,800 \) bit 가 필요
- \( K=2 \) 인 경우 : \( 43,248 \) bit ( 원본의 4.2% )
- \( K=3 \) 인 경우 : \( 86,472 \) bit ( 원본의 8.3% )
- \( K=10 \) 인 경우 : \( 173,040 \) bit ( 원본의 16.7% )
- 물론 압축 정도와 이미지 품질간의 trade-off 가 존재한다.
- 좀 더 좋은 이미지 압축 방식을 고려한다면, 인접 픽셀 블럭 (예를 들어 \( 5\times5 \) 크기의 픽셀 블럭) 단위의 압축 등을 고려할 수 있다.