- 2.3 절의 가우시안 분포 내용이 너무 길어서 몇 개의 파트로 나누어 설명한다.
- 앞절의 내용은 Part.II 을 참고하기 바란다.
2.3.7. 스튜던트-t 분포 (Student’s t-distribution)
- 지금까지 우리는 가우시안 파라미터인 정확도(precision)의 공액 사전 분포(conjugate prior distribution)를 살펴보았다.
- 이 때 사용된 분포는 감마 분포의 꼴이었다.
- 주변 확률 분포 (marginal distribution)의 계산
- 감마 사전 분포 \( Gam(\tau|a,b) \) 를 가지는 단변량 가우시안 분포 \( N(x|\mu, \tau^{-1}) \)
- 이 때의 \( x \) 에 대한 주변 확률 분포(marginal distribution)를 구해보자. \( \tau \) 에 대해 적분한다.
- \( z = \tau[b+(x-\mu)^2/2] \) 로 놓고 식을 전개하면 다음을 얻게 된다.
- 교재에는 생략되어 있지만 전개 식을 간단히 정리해 놓는다.
- \( Z=b+(x-\mu)^2/2 \) 로 놓고 \( z=\tau Z \) 식을 전개한다.
- 또한 새로운 변수 \( v=2a \) 와 \( \lambda=a/b \) 를 이용한다.
- 이러한 분포를 스튜던트-t 분포라고 한다.
- 파라미터 \( \lambda \) : t-분포의 정확도(precision)
- 파라미터 \( v \) : 자유도(degree of freedom)
- 못 보던 개념인 자유도가 나왔다.
- 이 값에 따라 분포의 양상이 어떻게 달라지는지 확인해보자.
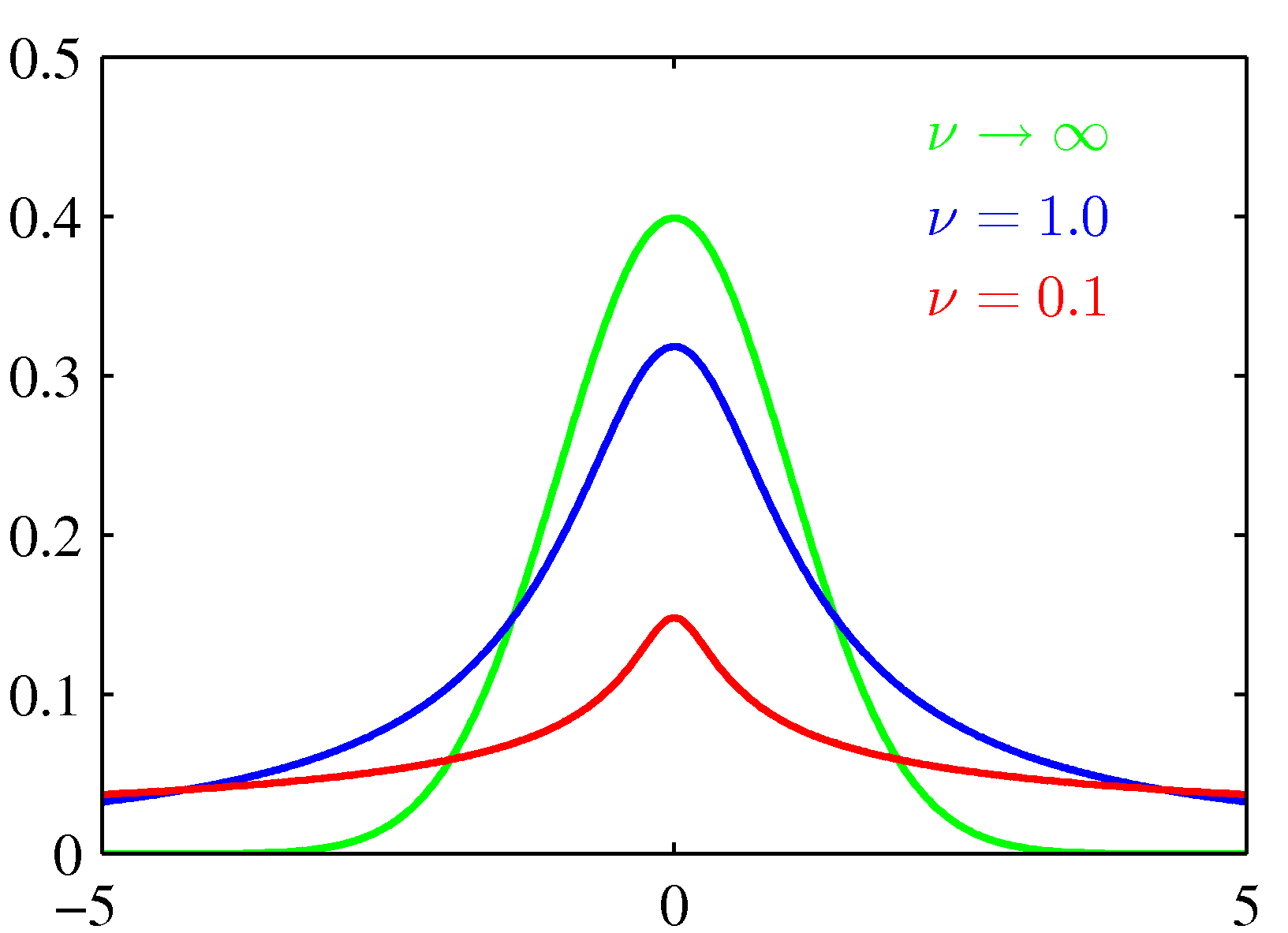
- \( \mu=0 \) 이고 \( \lambda=1 \) 인 환경에서 \( v \) 값만을 변화시켜 얻은 그래프이다.
- \( v\rightarrow\infty \) 인 경우 이 분포는 가우시안 분포 \( N(x|\mu, \lambda^{-1}) \) 가 되고,
- \( v=1 \) 인 경우 코시(Cauchy) 분포가 된다.
- 스튜던트-t 분포의 특징
- 가우시안 분포와는 달리 표본 집단에 대한 분포를 나타낼 때 사용한다.
- 표본의 크기와 자유도에 따라 모양이 달라진다.
- 자유도는 분포 내에서 (표본크기-1) 이므로 표본 크기가 많아질수록 모집단에 가까워진다.
- 스튜던트-t 분포는 가우시안 분포의 무한 혼합(infinite mixture)으로 해석될 수 있음.
- 가우시안 분포보다 꼬리가 긴 형태로 나오게 된다.
- 스튜던트-t 분포는 견고성(robustness) 이라는 중요한 특징을 가짐 - 특이값(outlier) 존재시 가우시안보다 덜 민감한 결과를 얻게 된다.
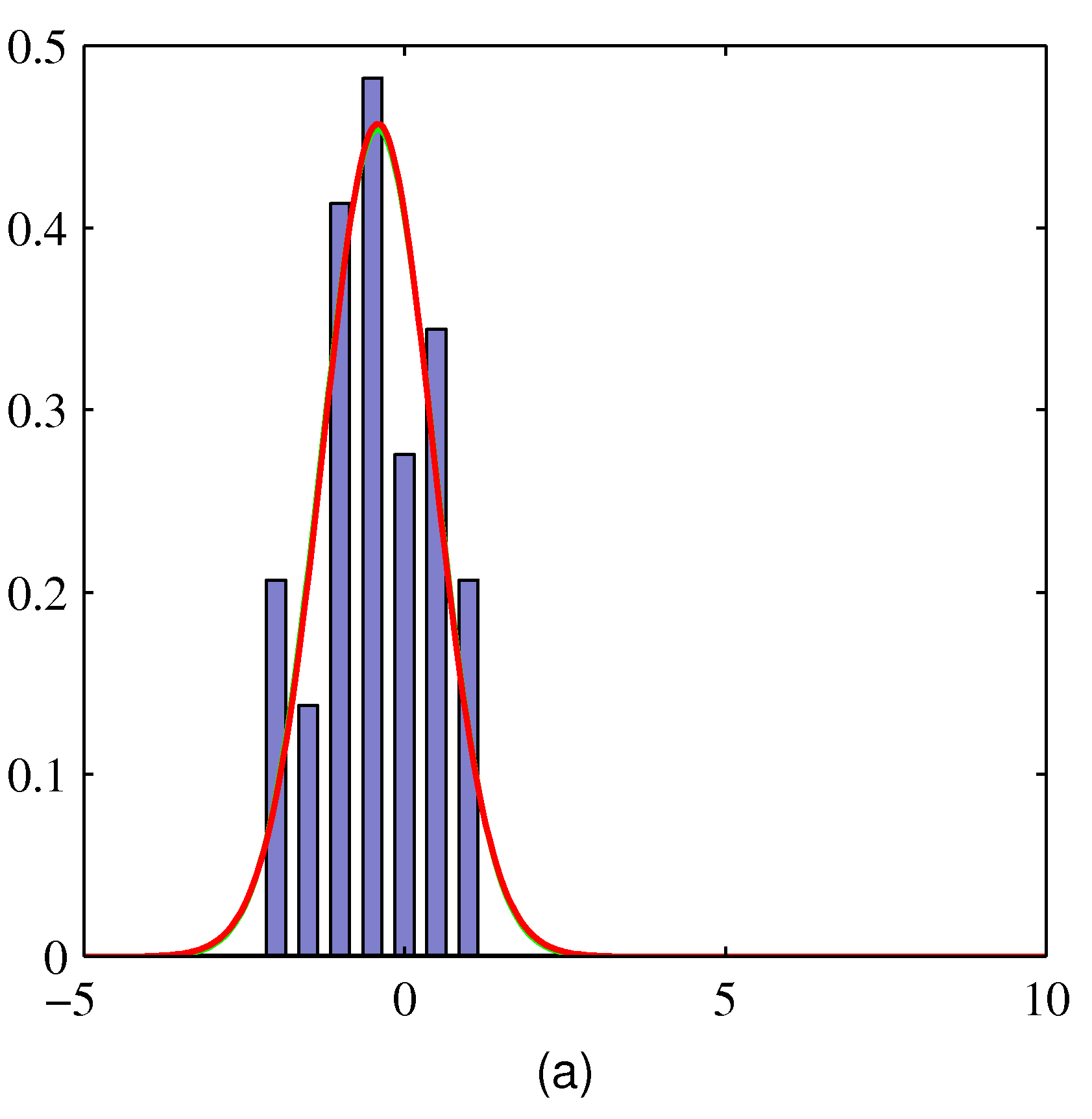
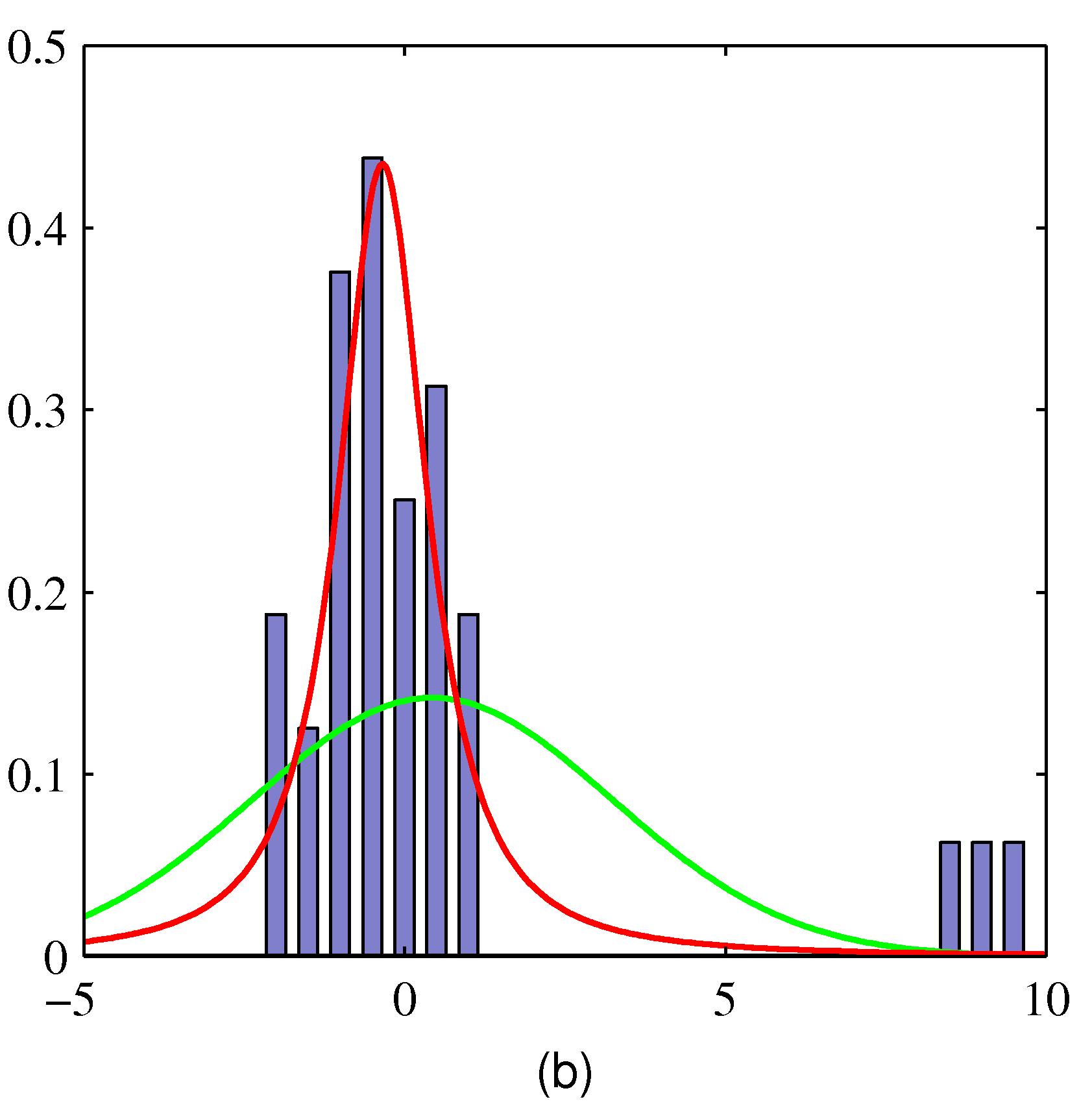
- 여기서 실제 데이터는 히스토그램으로 표현된다.
- MLE 를 이용하여 얻은 결과로 녹색 선은 정규분포, 적색 선은 t-분포이다.
- 오른쪽을 보면 가우시안이나 t-분포나 동일한 결과를 가진다.
- 하지만 왼쪽에 특이값(outlier) 데이터가 등장하는 경우 정규분포는 크게 치우치는 것을 알 수 있다.
- 반면 t-분포는 특이값(outlier)에 영향을 덜 받는다.
- 참고로 t-분포의 MLE 값은 EM 알고리즘을 이용하여 구하게 된다.
- t-분포 식 2.158 식에서 사용된 파라미터를 다음과 같은 값으로 사용하게 되면,
- \( v=2a \) , \( \lambda=a/b \) , \( \eta=\tau b/a \)
- 원래 t-분포와는 약간 다른 형태의 식을 얻을 수 있다.
- 물론 가우시안 분포를 다변량 가우시안 분포로 사용할 수도 있다.
- 앞서 보였던 방식대로 위의 식을 실제 적분하여 정리할 수 있다.
- 여기서 \( \nabla \) 는 다음과 같이 정의된다.
- 이 때의 평균과 분산, 최빈값(mode)는 다음과 같다.
- 전체 모양은 가우시안 분포와 마찬가지이므로 평균과 최빈값은 같다.
- 사실 스튜던트-t 분포는 전통적인 통계학에서 많이 사용되는 분포이다.
- 따라서 이 교재보다는 다른 통계학 교재가 훨씬 도움이 될 수 있다. - 여기서는 적은 샘플에 적용 가능하고 특이값에 대해 강건한(robust) 모델이라는 정도만 이해하고 우선 넘어가도 된다.
2.3.8. 주기성 변수들 (Periodic variables)
- 가우시안 분포가 어디에 가져다 놓아도 잘 써먹을 수 있는 훌륭한 분포이지만 특정 경우에서는 전혀 어울리지 않는 경우도 있다.
- 이번 절에서 다룰 주기성(periodic) 랜덤 변수가 이러한 경우에 대한 매우 적절한 예제이다.
- 주기성 변수라는 것은 일정한 단위를 두고 값이 반복되는 형태의 함수값인데 예를 들면 바람의 방향이나 지역 정보 등을 들 수 있다.
- 예제 1. 특정 위치(지리적)에서의 바람 방향
- 일정 기간동안 풍향을 예측한 뒤에 파라미터를 사용하는 분포를 이용하여 이를 요약하고자 할 때
- 예제 2. 하루 단위, 혹은 연간 단위의 주기를 가지는 모델
- 이런 경우에는 입력 단위를 극좌표 (polar) 단위로 전환한 뒤 표현 가능하다. ( \( 0 \le \theta \lt 2\pi \) )
- 또는 원점으로부터 어떤 방향을 축으로 삼아서 가우시안같은 분포를 이용하여 이런 반복적인 변수를 다룰수 있다.
- 그러나 실제로 이러한 접근 방식은 원점을 어디로 선택했느냐에 따라 결과가 크게 의존됨
- 예를 들어 현재 관찰값이 \( \theta_1=1^{\circ} \) 이고 \( \theta_2=359^{\circ} \) 인 경우
- 만약 원점을 \( 0^{\circ} \) 로 잡는 경우 이 표본의 평균은 \( 180^{\circ} \) 이고 표준편차는 \( 179^{\circ} \) 가 된다.
- 이제 원점을 \( 180^{\circ} \) 로 잡는 경우, 이 표본의 평균은 \( 0^{\circ} \) 이고 표준편차는 \( 1^{\circ} \) 가 된다.
- 원점 기준과 상관없이 언제나 동일한 결과를 얻을 수 있는 방법을 개발할 필요가 있다.
- 주기성 변수의 관찰 데이터가 \( D={\theta_1,…,\theta_N} \) 이라고 하자.
- 먼저 \( \theta \) 는 라디안 단위로 측정되는 데이터이다.
- 이 데이터를 단순 평균하는 값은 특정 좌표에 의존적이라는 것을 이미 확인했다.
- 따라서 상황에 따라 바뀌지 않는 강건한 평균 값을 구해야 한다.
- 이를 위해 우리는 관찰 데이터 \( \theta \) 를 각도로 가지는 단위 원 내 한 점으로 고려할 것이다.
- 단위 원 내 한 점이므로 \( |x_n|=1 \) 을 만족해야 한다.
- 각각의 점은 \( \theta \) 만큼의 각을 가지게 된다. 아래 그림을 참고하자.
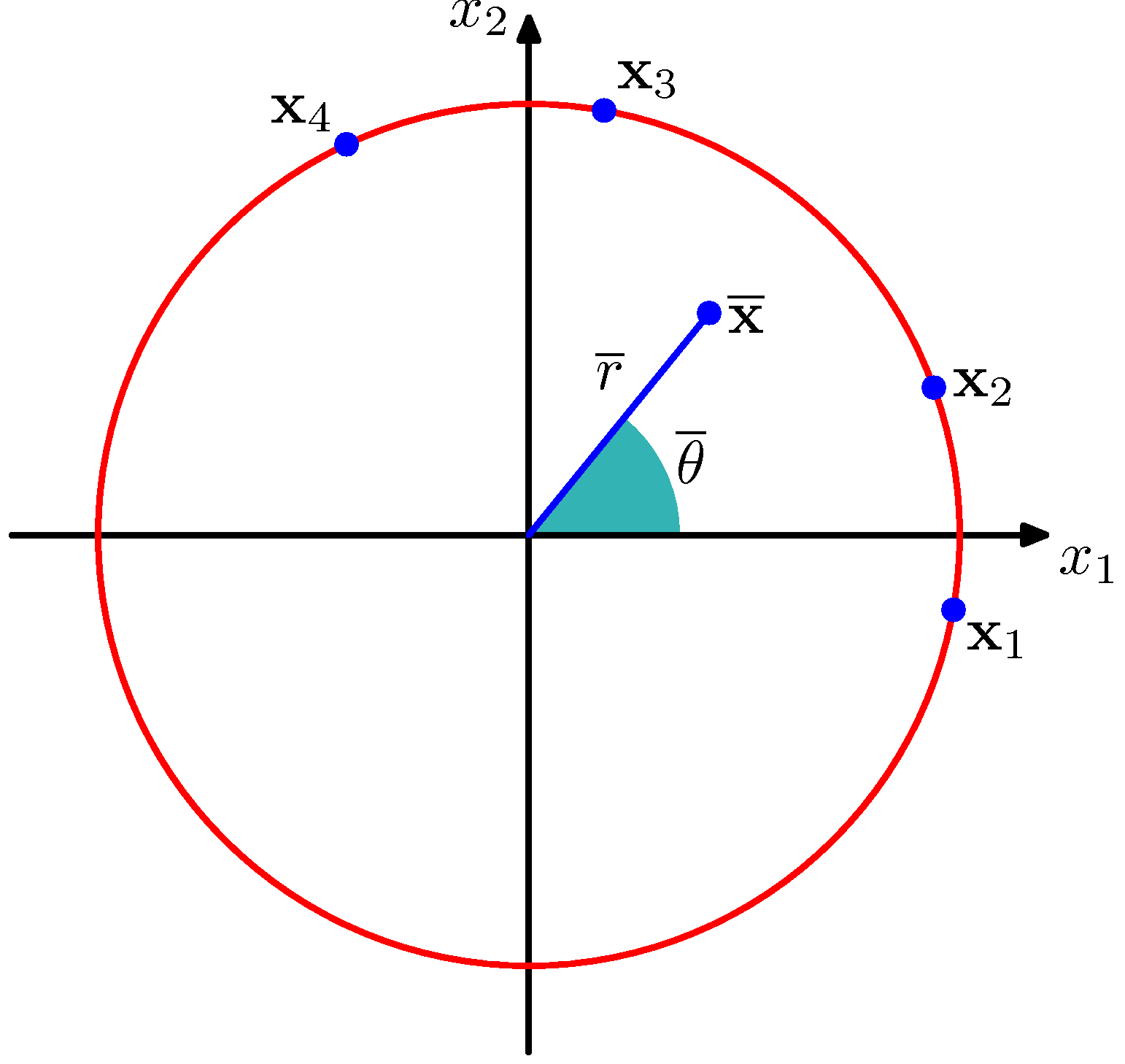
- 위의 그림을 보면 \( {\bf x}_n \) 데이터가 원 위에 위치하는 것을 알 수 있다.
- 따라서 이 점들에 대한 평균 값은 쉽게 구할 수 있다.
- 그림 내에서 \( \bar{ {\bf x}} \) 가 평균 값이 된다.
- 단위 원 빨간 선 위에 항상 평균 값이 위치하지 않는 이유는 이 때의 평균 값이 데카르트 좌표에 의한 값들의 평균이라서 그렇다.
- 너무 당연한 이야기지만 혹시나 잘못 이해하고 있을까해서 적어놓는다.
- 이제 관찰 값을 다시 데카르트 좌표로 변경하면 다음과 같다. \( {\bf x}_n=(\cos\theta_n, \sin\theta_n) \)
- 반지름의 길이를 \( 1 \) 로 강제했기 때문에 위와 같은 결과를 가진다.
- 데카르트 좌표로 전환된 관찰 데이터의 평균 값은 \( \bar{ {\bf x}}=(\bar{r}\cos\bar{\theta}, \bar{r}\sin\bar{\theta}) \) 이다.
- 이를 대입하여 전개하면,
- \( \tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}} \) 를 이용해서 \( \theta \) 에 대한 식으로 전개한다.
- 간단하게 미리 이야기를 해 보자면,위와 같은 결과가 주기성 변수에 대한 MLE 결과와 일치하는지 확인해 볼 것이다.
- 이제부터 우리는 가우시안 분포로 주기성 랜덤 변수에 대한 일반화 과정을 살펴볼 것이다.
- 이를 von Mises 분포라고 한다.
- 여기서는 단변량 가우시안 분포만을 고려하도록 하자.
- 사실 주기성 분포는 다차원의 공간 안에서도 발생할 수 있는 분포이다.
- 이와 관련된 사항이 궁금한 사람은 Mardia 와 Jupp 의 논문을 살펴보기를 바란다.
- 이제 변환을 위해 분포 \( p(\theta) \) 가 주기 \( 2\pi \) 의 랜덤 변수의 확률을 나타낸다고 해보자.
- 이때 \( \theta \) 에 대한 확률 밀도 \( p(\theta) \) 는 음수의 값을 가질 수 없다. (그리고 적분 값은 1이어야 한다.)
- 따라서 다음과 같은 조건을 만족해야 한다.
- 세번째 식에 의해 \( p(\theta+M2\pi)=p(\theta) \) 도 성립한다.
- 이제 2차원의 \( {\bf x}=(x_1,x_2) \) 변수에 대한 가우시안 분포를 고려해보자.
- 이 때 평균은 \( {\bf \mu}=(\mu_1,\mu_2) \) 이고 공분산은 \( \Sigma=\sigma^2I \) 로 가정한다.
- \( I \) 는 \( 2\times 2 \) 크기의 단위 행렬(Identity matrix)이다.
- 각 차원의 분산 값이 동일하므로 가우시안 컨투어(contour)는 원이 된다.
- 참고로 컨투어는 가우시안 분포에서 \( p({\bf x}) \) 의 값이 동일한 값을 가지는 영역을 선으로 연결한 것이다.
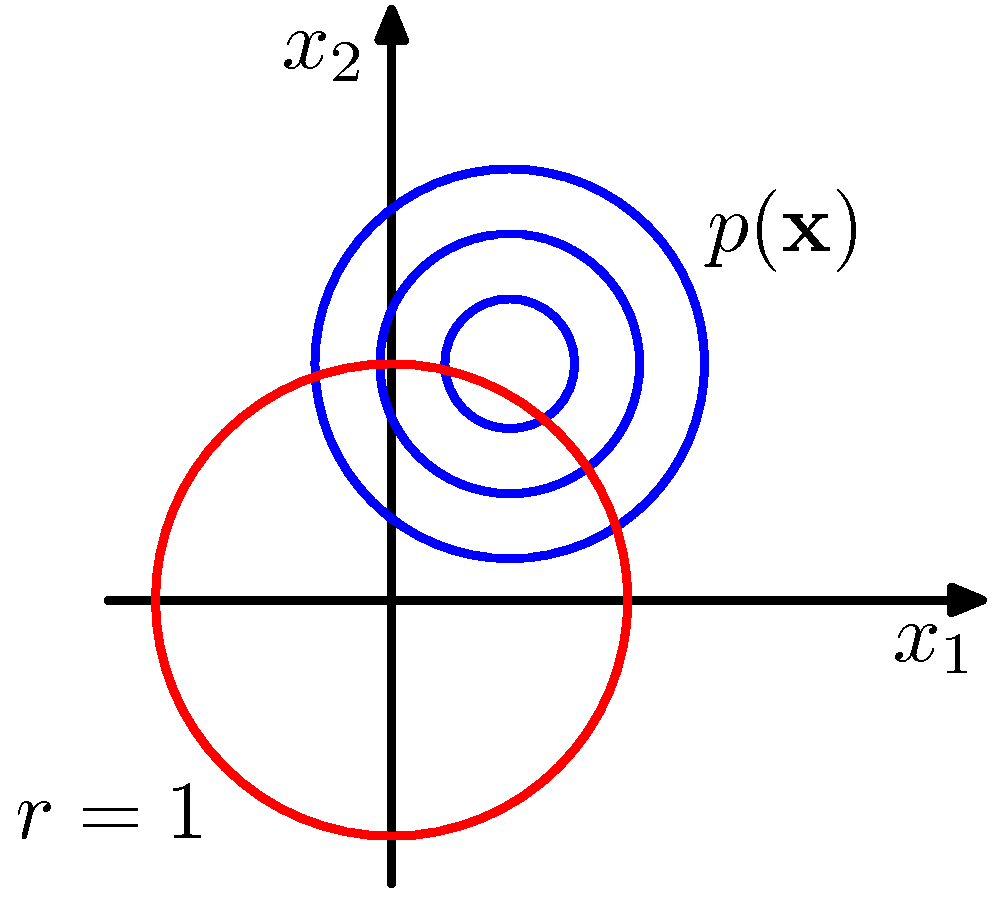
- 위의 그림에서 파란 색 컨투어는 \( p({\bf x}) \) 를 나타내는 그림이다. ( \( p(\theta) \) 가 아니다.)
- 붉은 색 선은 반지름의 길이가 \( 1 \) 인 경우를 의미한다.
- 이제 우리는 \( r \) 을 상수로 고정을 하고 이 때의 \( \theta \) 값을 살펴볼 것이다.
- 조금 부연하자면 위의 식은 2차원의 데카르트 좌표계를 2차원의 (반지름, 각도) 좌표로 변환하는 문제이다.
- 이 중에 \( \theta \) 에 대한 값만을 살펴보기 위해 일단 \( r \) 의 값을 고정한 것이라고 생각하면 된다.
- 이 때의 평균 값을 다시 극좌표계로 나타내어 보자.
- 사실 앞서 다루었던 예제와 동일한 문제를 풀고 있는 것이다.
- \( \theta \) 의 경우 주기성 랜덤 변수므로 이를 평균 측정이 가능한 데카트라 좌표로 변환하고,
- 이 때의 평균을 구한 뒤 다시 이 값을 \( \theta \) 에 대한 차원으로 변환하여 실제 평균값으로 사용
- 여기서는 이 때의 평균 값을 가우시안 분포에 대입하여 분포의 평균 값으로 사용할 것이다.
- 자 이제 \( {\bf x} \) 에 대한 가우시안 분포를 \( \theta \) 에 대한 식으로 전개해 보았다.
- 여기서 \( const \) 영역은 \( \theta \) 와는 독립적인 식이다.
- 이 식을 전개하기 위해 다음과 같은 식을 사용하였다.
- 이제 \( m=r_0/\sigma^2 \) 으로 정의하고 최종적인 식을 만들어보자.
- 단위 원인 \( r=1 \) 인 경우 다음과 같은 식이 유도된다.
- 이러한 분포를 \( von\;Mises \) 분포라고 한다.
- 기존의 가우시안 분포처럼 평균을 사용하고 분산 대신 \( m \) 을 사용하는 분포이다.
- 여기서 \( m \) 은 가우시안의 정확도(precision)와 유사하다.
- 여기서 사용되는 정규화 계수는 \( I_0(m) \) 으로 0차 제 1종 베셀 함수로 다음과 같이 표현된다.
- 어떤 식으로 유도되어 이렇게 전개되는지는 확인을 못했다.
- 위키피디아 등에 잘 정리되어 있으므로 참고하면 된다.
- 만약 \( m \) 이 충분히 크다면 이 분포는 가우시안 분포에 근접하게 된다.
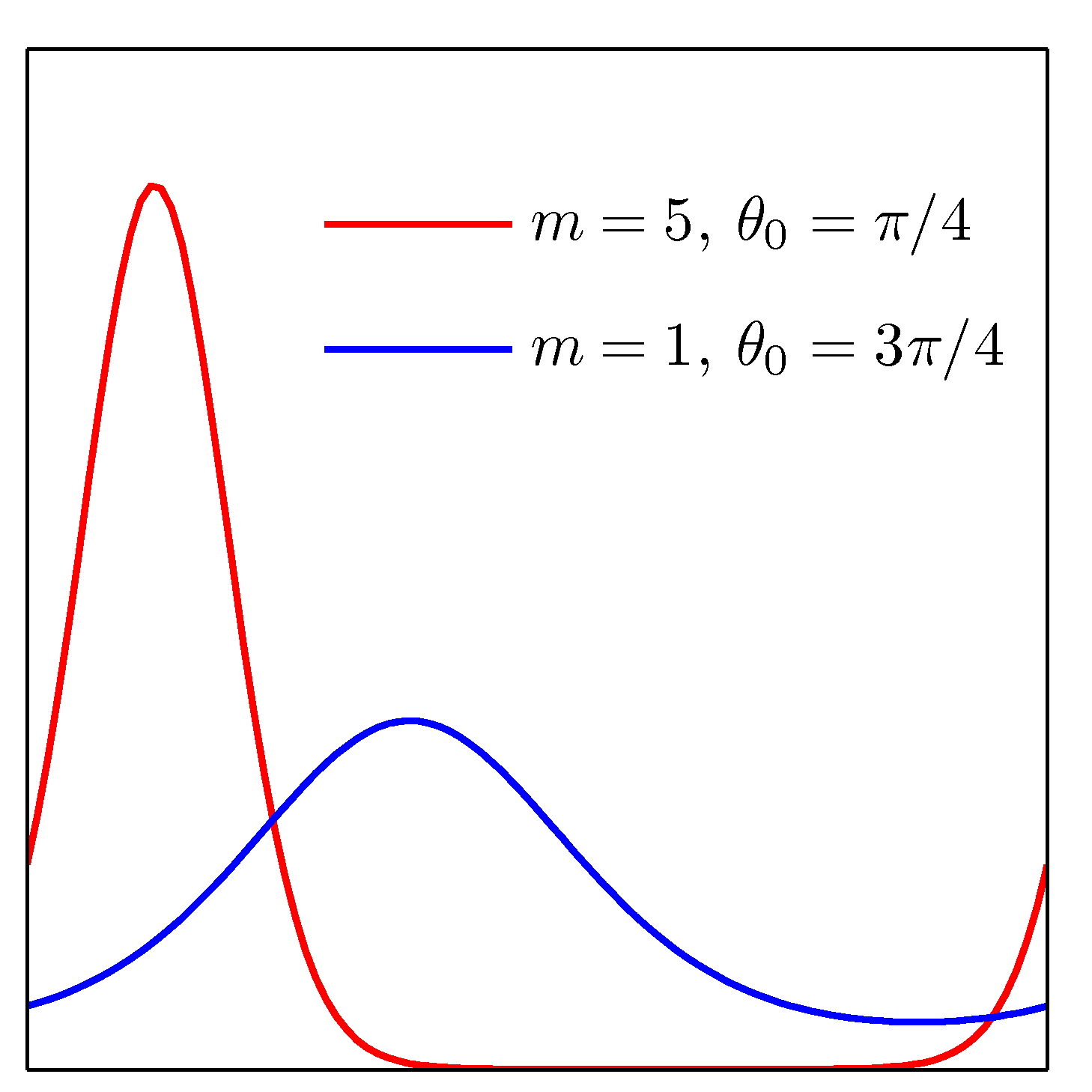
- 이 그림은 \( von\;Mises \) 분포를 그린 것이다.
- 주기성을 가지고 있다는 것을 확인할 수 있다.
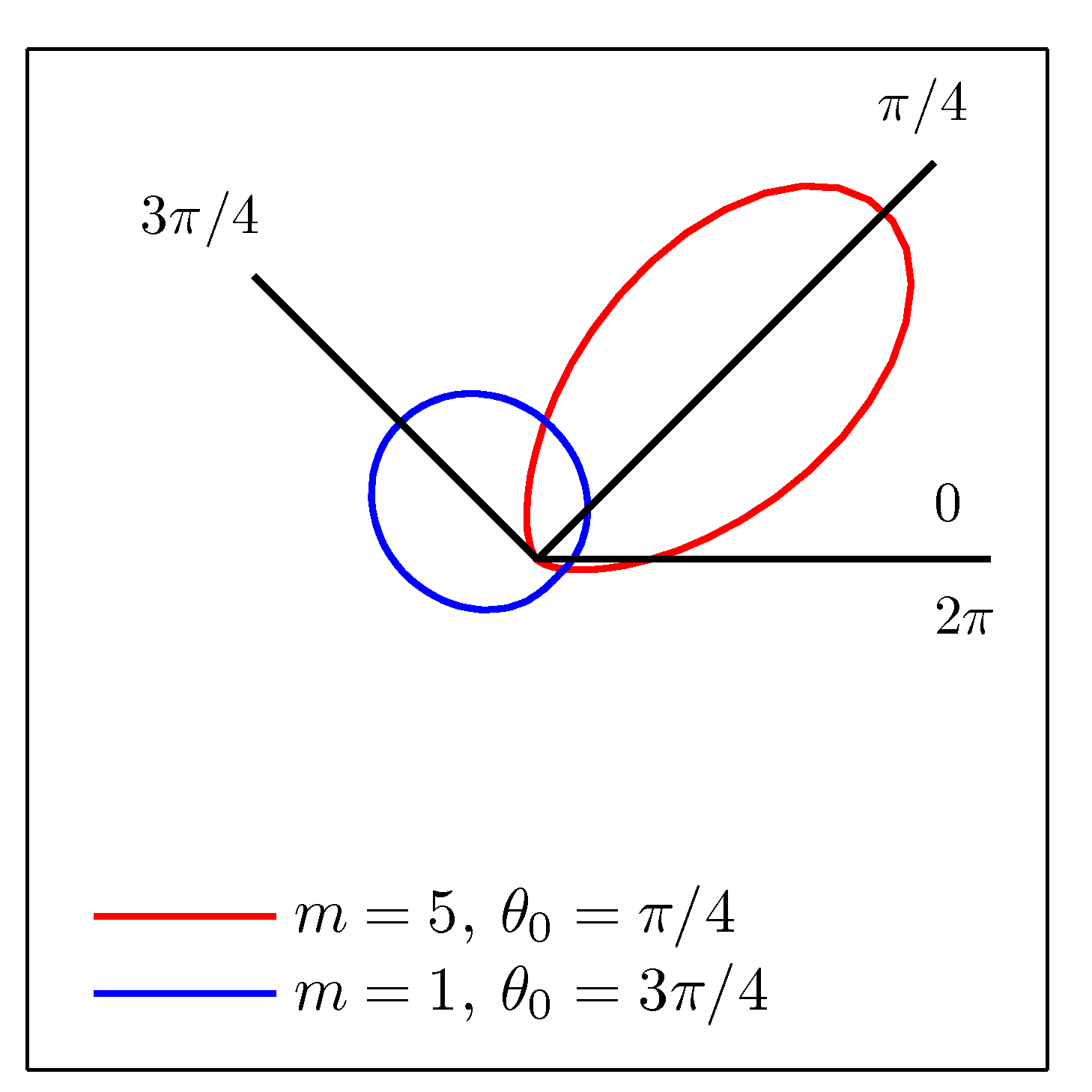
-
이 분포를 카르테시안 좌표계 (데카르트 좌표계)로 다시 그리면 위와 같은 그림이 된다.
-
\( I_0(m) \) 에 대한 그림은 다음과 같다.
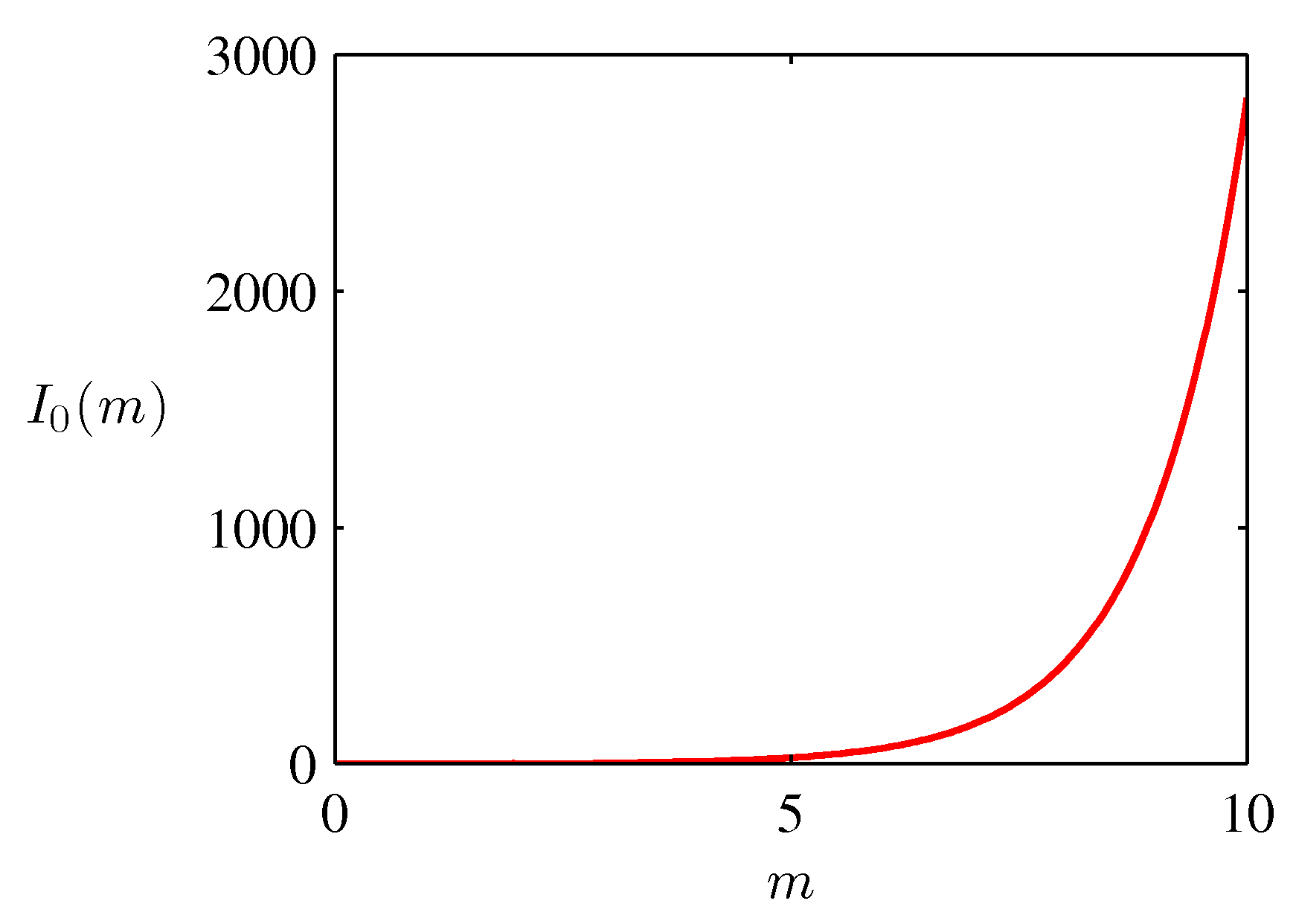
- 이제 이 분포의 파라미터 \( \theta_0 \) 와 \( m \) 의 MLE 값을 확인해보도록 하자.
- 우선 로그 가능도 함수(log likelihood function)는 다음과 같게 된다.
- 식을 보면 알겠지만 그냥 미분하면 MLE 값을 구할 수 있다.
- \( \theta \) 에 대해 미분하면 다음과 같은 결과를 얻게 된다.
- 마찬가지로 다음과 같은 삼각함수 공식을 사용한다.
- 이렇게 하면 다음의 식을 얻게 된다.
-
처음에 봤던 식과 동일한 결과를 얻게됨을 알 수 있다.
-
교재에 유도 과정은 생략되어 있다. 간단하게 정리해보자면,
- 파라미터 \( m \) 에 대해서도 MLE 값을 구할 수 있는데, 다음과 같은 식을 이용하면 구할 수 있다. ( \( I_0’(m)=I_1(m) \) )
- \( m \) 과 관련해서는 단순한 결과만을 기술하고 있다.
- 좀더 자세한 사항은 별도의 자료를 참고해야 할 듯.
- 이번 절이 다른 절과 크게 관련이 없는 영역이기도 해서 간단하게 교재에 나온 내용만 정리해 두도록 하자.
- 가우시안 분포에서와 마찬가지로 \( \theta \) 는 이미 얻어진 \( \theta_0^{ML} \) 값을 넣으면 된다.
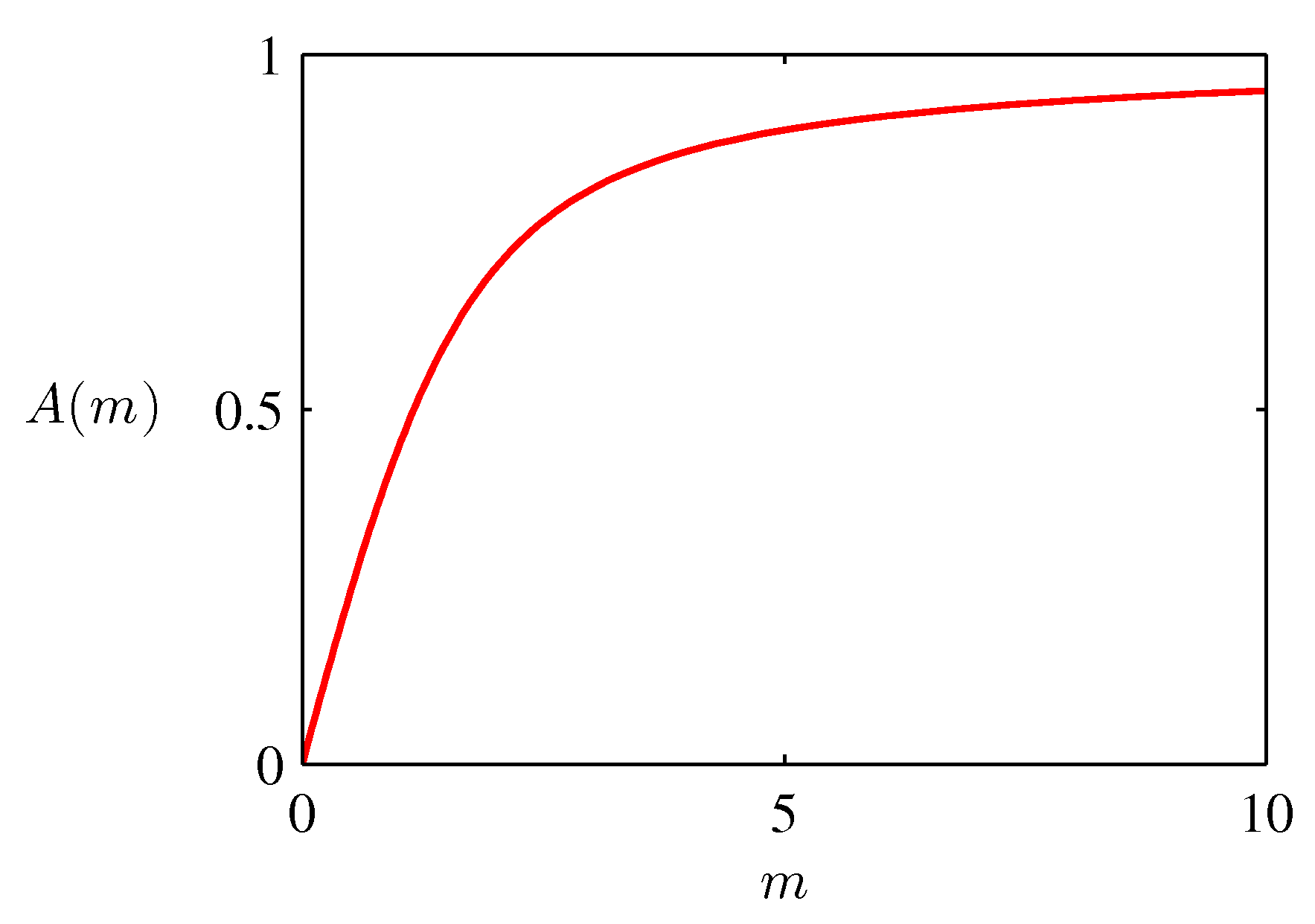
- \( m \) 에 대한 \( A \) 함수를 다음과 같이 정의한다.
- 그러면 다음과 같은 식을 얻을 수 있다.
- 이에 대한 그림은 다음과 같다.
- 간단하게 전개식을 정리해 놓는다. (교재에는 없다)
- 다음의 삼각 함수를 다시 사용해서 식을 전개한다.
- 최종 식은 다음과 같다.
- 주기 분포의 구조를 위한 몇가지 기법을 살펴보자.
- 가장 쉬운 방법은 Anglular 좌표를 고정된 크기의 bin 으로 분할되어 개수를 세는 히스토그램 방식
- 이러한 방식은 단순함과 유연성을 장점으로 가지지만 중요한 제약이 있다. 이는 2.5절에 서술할 것이다.
- 다른 접근 방식은 \( von\;Mises \) 분포처럼 유클리디안 공간에 가우시안 분포로 시작함
- Mardia 와 Jupp 의 방법으로 좀 더 복잡한 형태의 유도식을 제공하지만 여기서는 설명하지 않는다.
- 마지막으로 가우시안 분포와 같이 실수 범위에서 유효한 분포를 주기 분포로 전환하는 것
- \( 2\pi \) 내의 연속 구간을 주기성 변수 \( (0, 2\pi) \) 로 매핑하여 전환하는 것
- 단위 원 주의의 실수 축으로 매핑함
- 하지만 결과로 얻어지는 분포는 \( von\;Mises \) 분포보다 다루기가 어렵다.
- 여기서는 간단히 이런 것이 있다는 정도만 설명한다.
- 가장 쉬운 방법은 Anglular 좌표를 고정된 크기의 bin 으로 분할되어 개수를 세는 히스토그램 방식
2.3.9 가우시안 혼합 분포 (Mixtures of Gaussians)
- 가우시안 분포가 아주 흔하게 사용되는 분포이긴 하지만 현실세계가 그리 만만하지는 않다.
- 현실적으로 가우시안만을 적용하기 어려운 경우가 생겨나기도 한다.
- 아래와 같은 경우의 예제를 생각해보자.
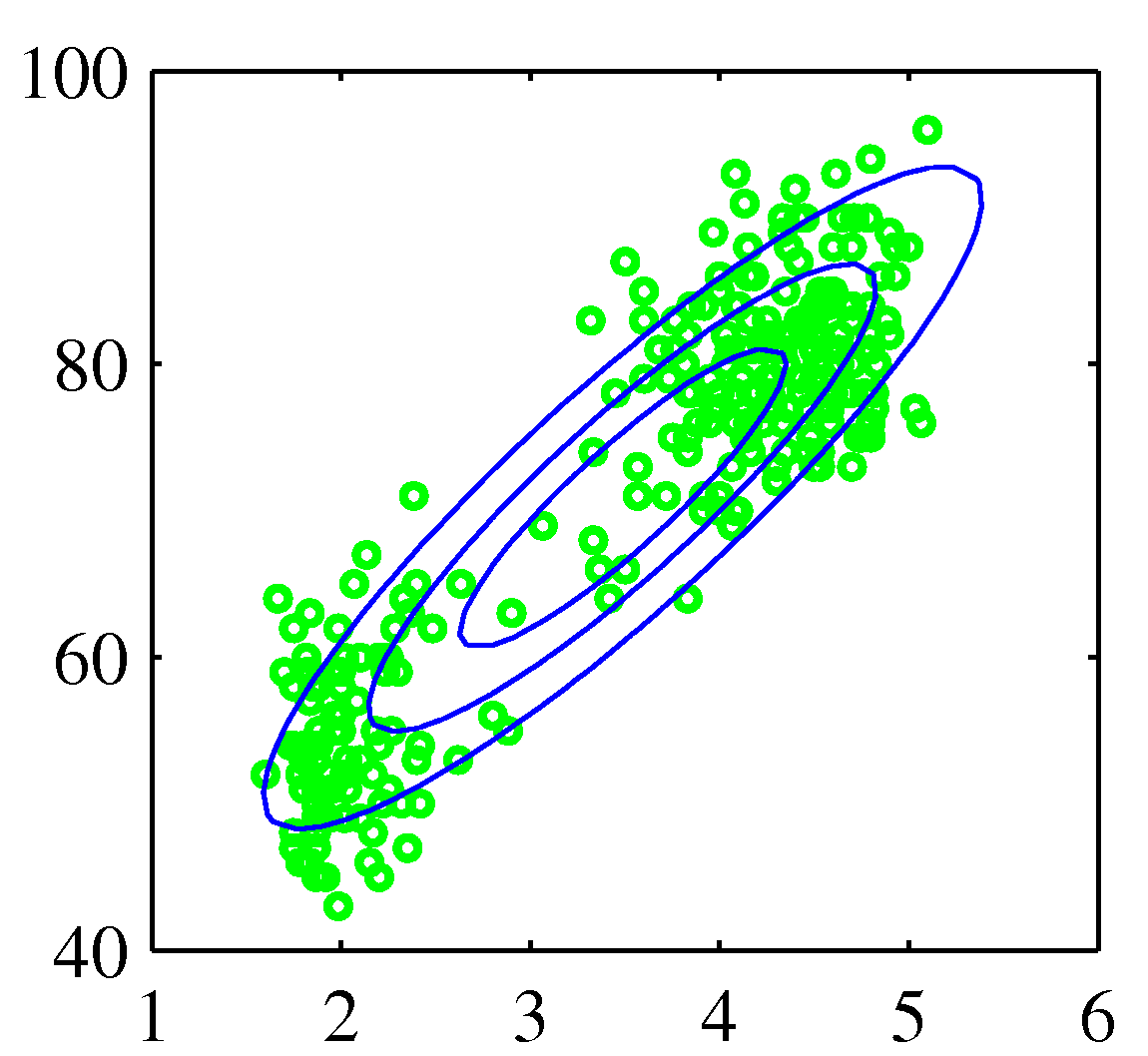
- 이 예제는 옐로스톤 국립공원에 있는 올드 페이스풀 간헐천의 화산 폭발에 대한 측정 데이터이다.
- 화산 폭발의 총 횟수는 272회이다.
- 각 측정은 폭발 지속 시간을 세로 축으로, 다음 폭발까지의 시간을 가로 축으로 구성한다.
- 데이터 집합은 크게 두 개의 지배적인 집단을 형성하고 있다.
- 가우시안 분포로는 이를 구성할 수 없다.
- 왼쪽의 그림을 보면 하나의 가우시안 분포로 데이터를 표현한 것으로 잘못된 결과라는 것을 직관적으로 알 수 있다.
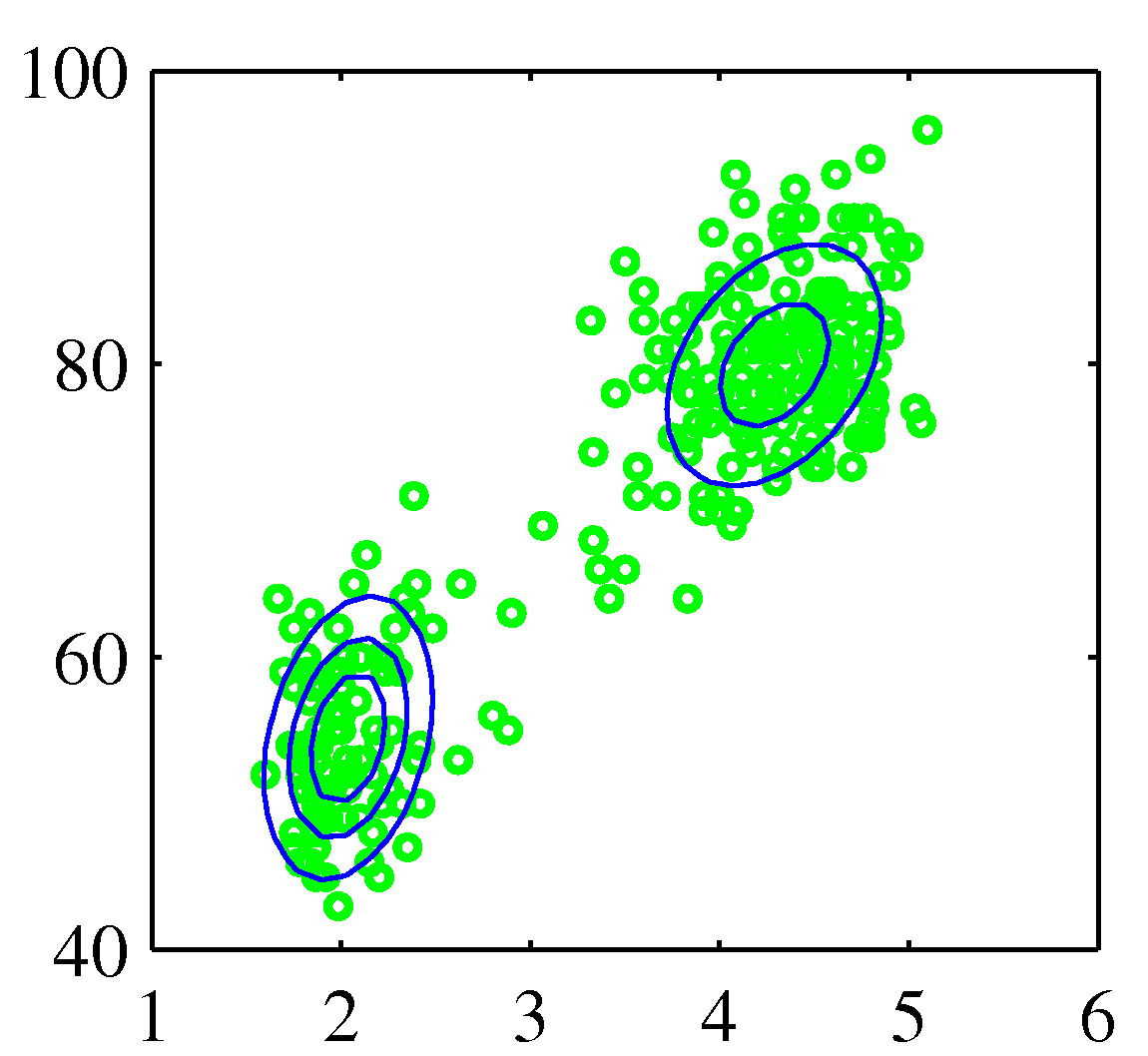
- 오른쪽 그림과 같은 구성을 위한 방법이 필요함.
- 두 개의 가우시안 선형 중첩은 더 나은 표현 방식이 될 수 있음.
- 이러한 문제를 해결하기 위해 이제부터 혼합 가우시안 모델 (Mixture Gaussian distribution) 을 제시한다.
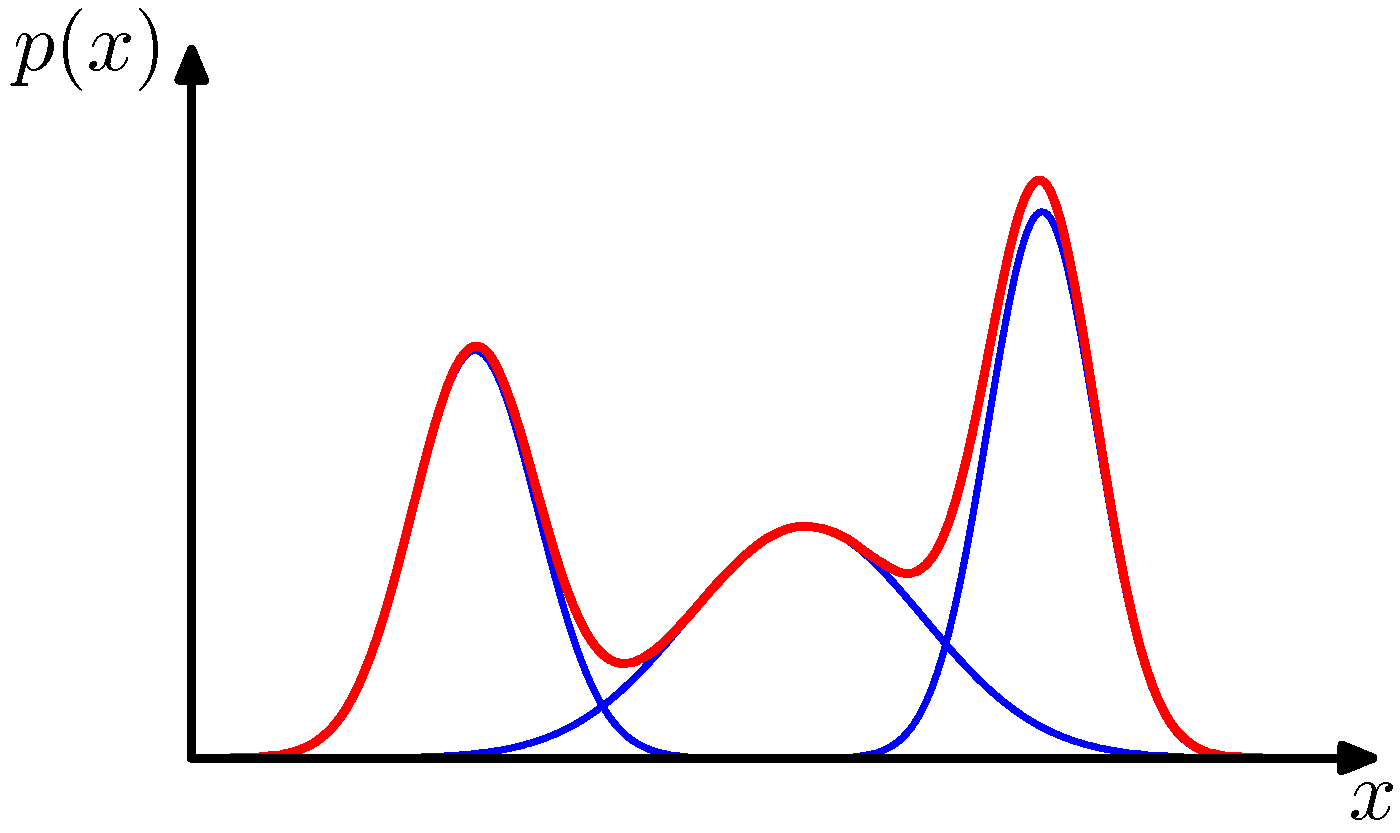
- 가우시안 선형 결합은 매우 복잡한 밀도를 표현할 수 있음
- 충분한 갯수의 가우시안 분포를 사용함으로써
- 선형 결합의 계수 뿐만 아니라 평균과 공분산 파라미터를 조절함으로써
- 거의 대부분의 연속 밀도를 임의의 정확도로 근사 가능함
- \( K \) 개의 가우시안 밀도의 중첩 형태는 다음과 같다.
- 이를 혼합 가우시안 (Mixture of Gaussians) 분포라고 한다.
- 이 때 각각의 가우시안 밀도 \( N({\bf x}|{\bf \mu}_k, \Sigma_k) \) 는 컴포넌트(component) 라고 부른다.
- 3개의 컴포넌트를 가지는 혼합 가우시안 분포의 컨투어와 표면의 예는 다음과 같다.
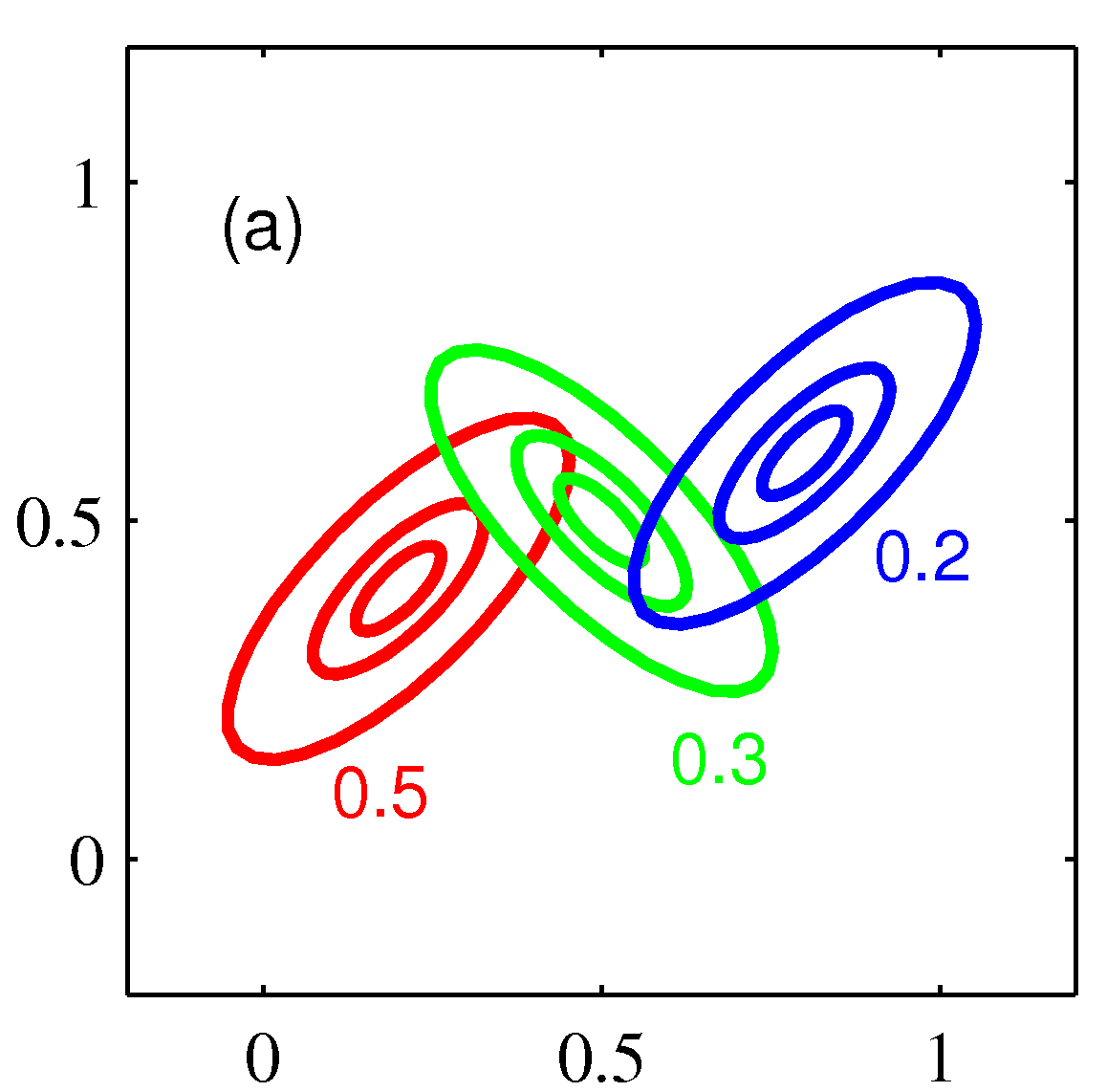
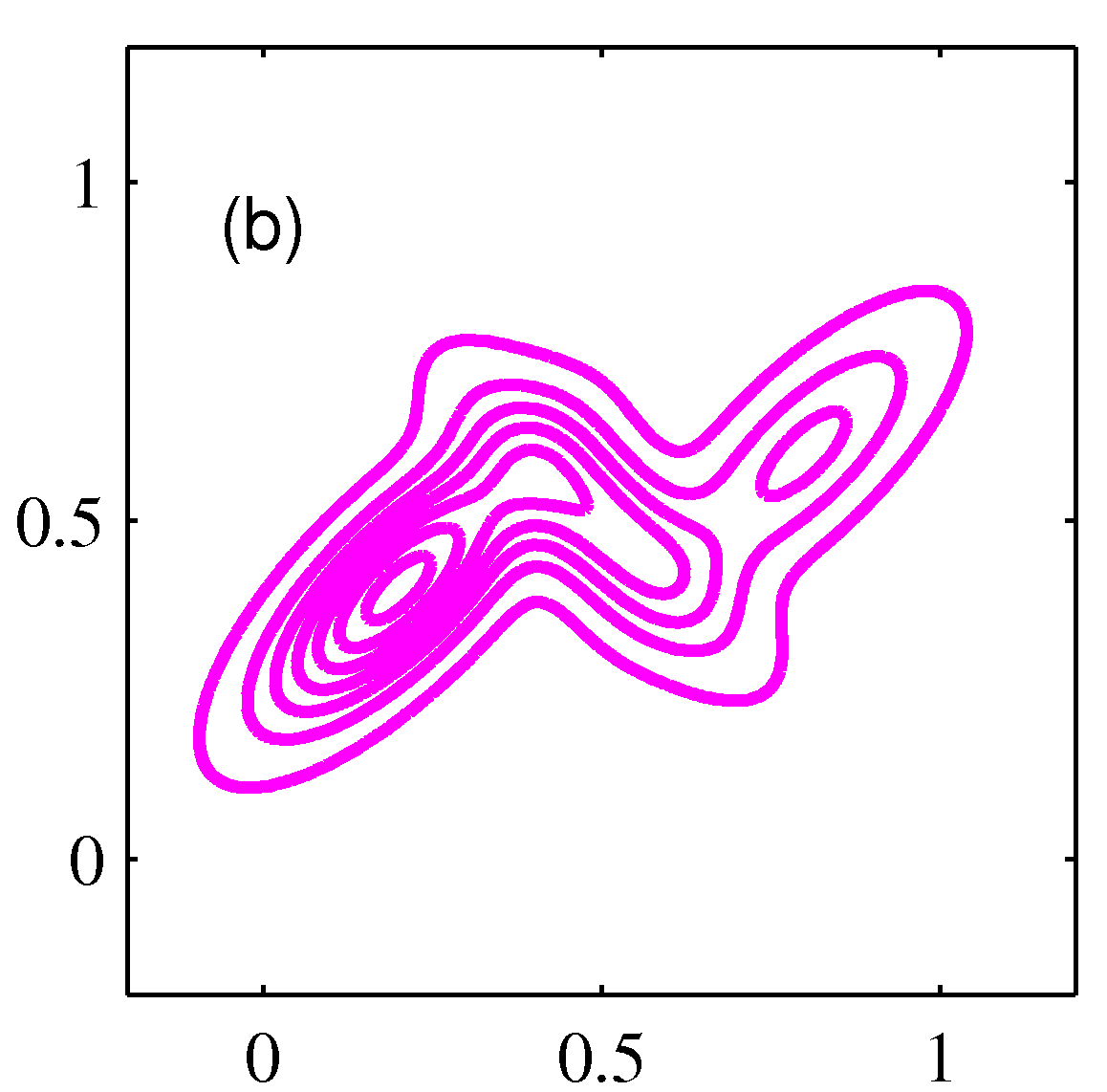
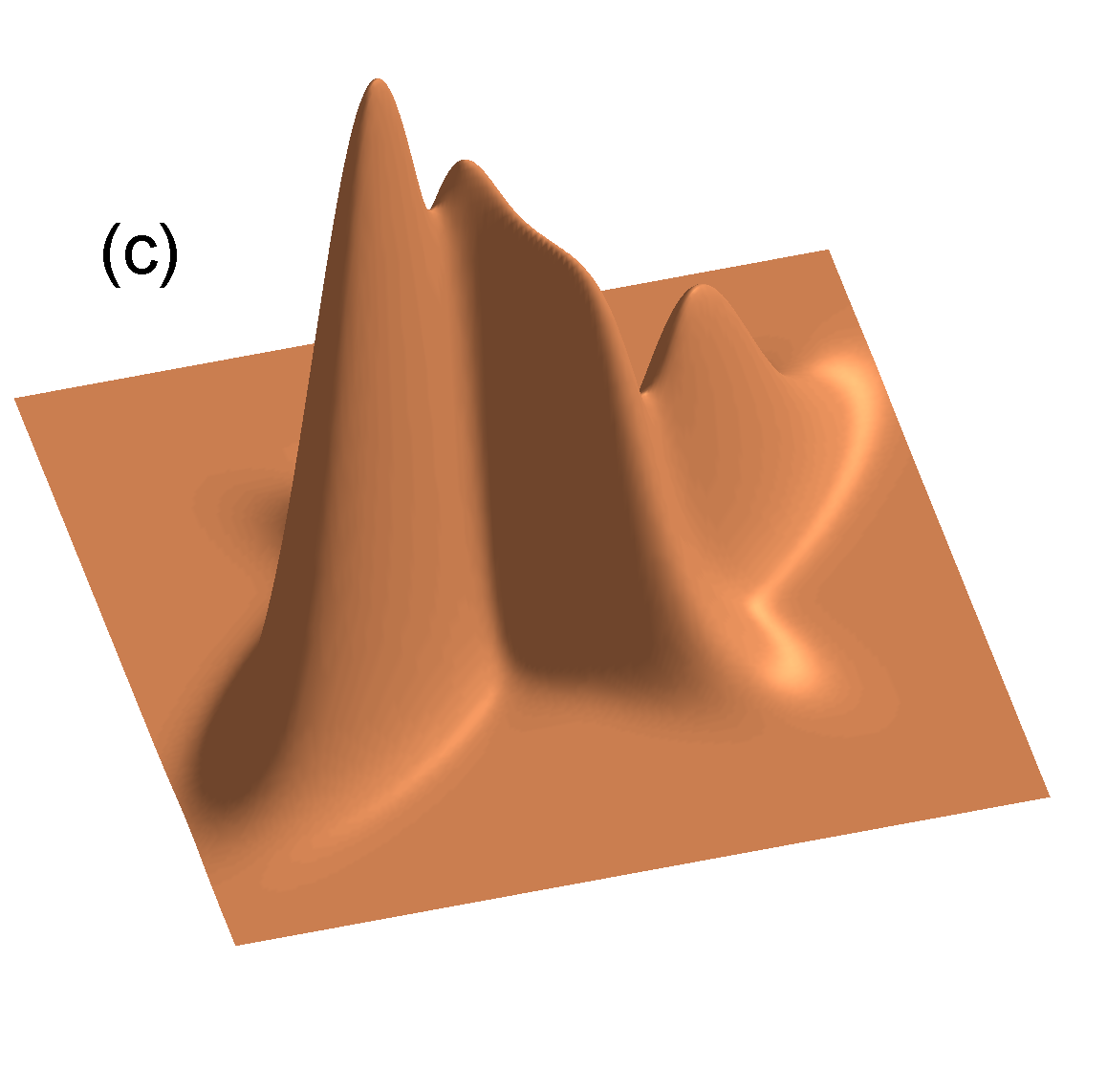
- 이번 절에서는 혼한 모델에서 사용하는 가우시안 컴포넌트에 대해 자세히 알아 볼 것이다.
- 사실 좀 더 일반화된 모델이라면 혼합 모델을 만들 때 서로 다른 분포를 혼합한 모델을 고려해 볼 수도 있다.
- 예를 들어 9.3.3 절에서는 이산 변수에 대해 베르누이 분포를 혼합한 모델을 사용할 것이다.
- 파라미터 \( \pi_k \) 는 혼합 계수 (mixing coefficients)이다.
- 각각의 컴포넌트 값들은 정규화 되어 있고 \( p({\bf x}) \) 도 정규화되어야 하므로 다음 조건을 만족한다.
- 또한 모든 분포는 \( N({\bf x}|{\bf \mu}_k, \Sigma_k) \ge 0 \) 이므로 \( p({\bf x})\ge 0 \) 을 만족해야 한다.
- 이런 조건들을 조합하면 다음을 얻을 수 있다.
- 합과 곱의 법칙을 이용하여 주변 밀도 (marginal density)를 전개한다.
- 이 식은 앞서 언급한 \( p({\bf x}) \) 와 같아야 한다.
- 따라서 \( \pi_k=p(k) \) 와 같은 식을 유도할 수 있음을 알 수 있다. 이는 \( k^{th} \) 번째의 컴포넌트의 사전 분포로 고려할 수 있다.
- 그리고 확률 밀도는 \( N({\bf x}|{\bf \mu}, \Sigma_k)=p({\bf x}|k) \) 로 생각하면 된다.
- 이후 responsibilities 라고 불리우는 사후 확률 \( p(k|{\bf x}) \) 의 중요성에 대해서도 살펴볼 것이다.
- 베이지안 이론에 의해 이 값은 다음과 같이 주어지게 된다.
- 이에 대한 내용은 챕터 9장에서 자세히 살펴 볼 것이다. (EM 알고리즘)
- 혼합 가우시안 분포의 파라미터는 \( \pi \) , \( {\bf \mu} \) , \( \Sigma \) 가 된다.
- 파라미터의 값을 설정하는 방법은 MLE 를 사용하는 것이다.
- 로그 가능도 함수는 다음과 같다.
- 입력 데이터는 \( {\bf X} = { {\bf x}_1,…,{\bf x}_N} \) 이다.
- 수식을 보자면 파라미터를 위한 MLE 식이 더 이상 닫힌 식(closed-form) 형태가 아니다.
- 따라서 단순히 미분을 취해 최대값을 가지는 모수를 찾는 방식이 아니라 반복적 수치 최적화 기법이 요구된다.
- 9장에서 EM 알고리즘을 통해 이를 확인하도록 하자.