1. Binary Variables

• 우선 가장 간단한 형태의 식으로 부터 논의를 시작한다.
• 랜덤 변수 \( x \) 가 \( x \in \{ 0,1 \} \) 인 상황(즉, 취할 수 있는 값이 단 2개)에서의 확률 분포를 살펴본다.
• 가장 간단한 경우가 바로 동전 던지기 예제인데, 동전을 던저 앞면이 나오면 \( x=1 \) , 뒷면이 나오면 \( x=0 \) 이다.
• 이 때 이 동전의 앞,뒷면이 나올 확률이 서로 동일하지 않다고 하면 앞면이 나올 확률은 다음과 같이 정의할 수 있다.

• 여기서 \( 0 \le \mu \le 1 \) 이다. ( 이 때 \(\mu \) 는 앞면이 나올 확률)
• \( x=0 \) 인 경우도 생각해야 하는데 확률식이므로 그리 어렵지 않게 정의할 수 있다.

• 이를 하나의 표현식으로 합쳐 만들어내면 다음과 같이 기술할 수 있다. ( \( x \) 의 값은 0 아니면 1이다.)

• 이것이 바로 베르누이(Bernoulli) 분포이다.
• 베르누이 분포의 평균과 분산값은 다음과 같다.

• 관찰 데이터 \( D={x_1,…,x_N} \) 이 주어졌다고 하면 이 관찰 값을 얻어낼 확률, 즉 가능도 함수를 다음과 같이 기술할 수 있다.

• 이것으로부터 MLE 를 구하게 될 것이니 로그를 취해보자. (로그 가능도 함수)

• 여기서 중요한 점 한 가지는 이 함수가 오로지 관찰된 데이터 \( x_n \) 의 개수 N에만 영향을 받는다는 것이다.
• 따라서 \( \frac{1}{N}\sum{x_n} \) 을 이 분포의 충분 통계량(sufficieant statistic)이라고 부른다.
  • 충분 통계와 관련된 내용은 이후에 다시 나올 것이다.
• 어쨌거나 이 식으로부터 모수(parameter)를 추정하는 것은 매우 간단하다. (그냥 미분해보면 된다.)

• 결국 MLE 로 모수의 추정값을 찾는 방법은 동전 앞면이 나온 횟수를 총 시행 횟수로 나누면 쉽게 구할 수 있다.

• 자 이제 이러한 추정 방식의 문제점을 살펴보자.
• 만약 동전을 3번 던졌는데 앞면만 3번이 나왔다면 MLE는 어떻게 될까?
• 이 때에는 \( \mu=1 \) 이 되며 앞으로 동전을 던졌을 때에는 무조건 앞면만 나온다고 판단하게 된다.
• 물론 이런 가정이 맞을 수도 있지만 (뭐, 앞면만 그려진 동전일 수도 있으니…) 일반적인 상황에서는 대개 틀린 결과이다.
  • 이런 경우를 오버피팅(over-fitting)되었다고 판단한다. 원래 MLE 방식은 관찰 데이터에 의해 오버피팅 되는 경향이 있다.
• 이후에는 \( \mu \) 에 대해 사전(prior) 분포를 도입해서 이런 문제(오버피팅)를 해결할 것이다.
• 이제 문제를 살짝 바꿔서 동전 던지기를 \( N \) 번 수행해서 앞면이 총 몇개가 나왔는지를 판단하는 문제를 고려해보자.
• 이런 분포를 이항 분포(binomial distribution)라고 부른다.
  • 베르누이와 이항 분포의 차이를 기억하자.

• \( N=10 \) 이고 \( \mu=0.25 \) 일 때의 결과를 살펴보자.

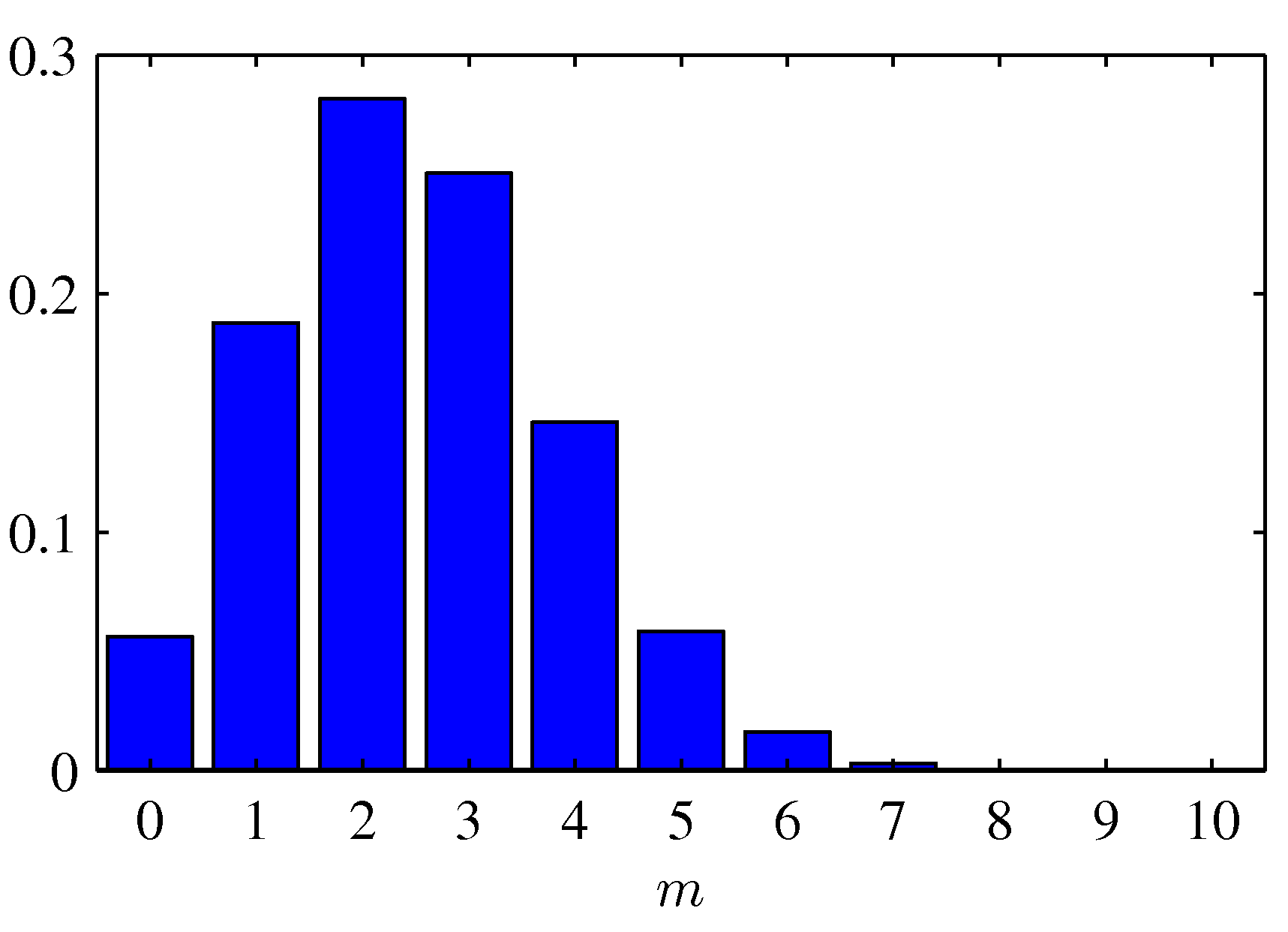
• 특별히 어려운 부분은 없다.
• 이 분포에 대한 평균과 분산 값은 다음과 같다.

• 식을 보면 베르누이의 확장판임을 쉽게 눈치챌 수 있다.
• 추가로 이 교재에서는 기본적인 확률 분포를 너무 간단하게 설명하고 있으므로 다른 교재를 함께 참고하도록 한다.

2.1.1. 베타 분포 (The beta distribution)

• 앞서 이항 분포에서 MLE 를 통해 얻어진 \( \mu \) 의 값이 샘플 평균임을 확인했다. ( \( \mu = \bar{x} \))
• 문제는 샘플 결과에 의존적이기 때문에 동전 던지기의 경우 만약 샘플의 결과가 모두 앞면이 나오면 \( \mu=1 \) 이 되어 오버피팅의 결과를 얻게 된다.
• 이제 이 문제를 확장하여 기존의 MLE가 아닌 베이지안 방식으로 파라미터를 추정하는 것을 살펴볼 것이다.
• 그 과정에서 필요하는 부분이 바로 파라미터의 사전(prior) 확률 값 \( p(\mu) \) 을 구하는 것이다.
  • 중요한 점은 \( p(\mu) \) 를 도입하되 여기서 \( \mu \) 는 랜덤 변수로 고려되게 된다.
    • 말이 좀 이상하긴 한데 확률 함수의 주 변수는 원래 랜덤 변수이다.
    • MLE 에서는 파라미터를 고정된 값이지만 알지 못하는 값으로 규정하고 이를 추정하는 문제로 해결했었다.
    • 전통적인 통계학에서는 이러한 방식의 한계점을 넘기 위해 구간 추정의 방식을 도입한다.
      • 즉, 파라미터를 하나의 값으로 추정하는 것이 아니라 어떤 범위 내에 존재하는 값으로 추정한다.
      • 얼핏 베이지언 방식과 비슷할 것 같지만 파라미터의 사전 확률 분포가 도입되는 것은 아니다.
    • 반면 베이지안 방식에서는 파라미터를 랜덤 변수로 고려하여 일반적인 확률 분포로 다루게 된다.
  • 그런데 무작정 사용할 파라미터를 랜덤 변수로 취급한다고 해서 모든 문제가 해결되는 것은 아니다.
  • 지금까지 살펴보았듯 가급적 이 값을 하나의 확률 분포로 고려를 했으면 하는데 파라미터에 대한 분포는 과연 어떤 분포를 가지는게 좋을까?
• 동전 던지기 문제에서는 가능도 함수의 형태가 \( \mu \) 와 \( (1-\mu) \) 의 지수의 곱으로 표현되고 있었다.
• 그리고 베이지안 방식에 에서는 가능도 함수 값을 최대로 하는 파라미터 값을 구하는 문제가 아니라,
  • 사후 분포(posterior)를 최대화하는 문제로 풀게 된다.    - 이 때 사후 분포는 가능도 함수로 유추된 \( p(x|\mu) \) 와 이 때의 \( p(\mu) \) 사전 분포의 곱에 비례한다.
    • \( p(\mu | x) \propto p(x|\mu)p(\mu) \)
  • 사후 분포는 확률 분포이다. 따라서 우리가 알고 있는 일반적인 분포의 형태로 만들어야 계산이 편하다. (예를 들면 정규분포, 이항분포 등)
  • 사전 분포도 확률 분포이다. 따라서 사전 확률 분포를 도입하되 이것 또한 우리가 알고 있는 분포로 만들어야 계산이 편하다.
    • 물론 실제로는 파라미터의 사전 분포 \( p(\mu) \) 가 실제 어떤 분포를 따라야 하는지는 사실 알아내기가 어렵다.
  • 근데 앞서 이야기한 대로 사전 분포도 쉬운 꼴로 되어 있어야 하고, 이에 가능도 함수를 곱한 것도 쉬운 분포 꼴로 나와야 한다.
  • 이런 경우 사후 분포와 사전 분포를 같은 분포의 형태로 만들어 사용하면 어떨까? 이러면 전체적으로 계산이 쉬워질 것이다.
  • 간혹 가능도 함수까지 유사한 분포 형태로 맞출수도 있다. 즉, 여기서는 \( \mu \) 와 \( (1-\mu) \) 의 지수의 곱 형태로 표현하는 것이다.
  • 이렇게 되면 사후 분포(posterior) 는 \( \mu \) 와 \( (1-\mu) \) 의 지수의 곱으로 표현될 것이고, 필연적으로 사전 분포도 이런 형태로 만들어져야 한다.
  • 결국 사용되는 사전 분포와 사후 분포의 형태가 같아진다.
• 이러한 속성을 공액(conjugacy)이라고 한다.
  • 여기서는 어떤 확률 분포들의 곱이 앞서 사용된 분포와 동일한 분포의 형태를 가지는 것을 의미하게 된다.
  • 사실 특별한 이유에서 분포를 고른다기보다 계산의 편리함이 우선시되는 방식이다. (즉, 마구잡이식 방법이다.)
  • 베이지언 방식에서는 사전 확률 분포와 사후 확률 분포의 형태를 동일하게 가져가는 방식을 취한다.
• 이런 이유에서 지금 소개할 베타 분포(Beta distribution)가 매우 유용하게 사용된다.
  • 이항 분포의 형태를 취하는 가능도 함수를 사용하는 경우 사전 확률로 베타 분포를 사용하면 베타 분포의 사후 확률을 얻을 수 있다.
  • 이는 이항 분포와 베타 분포가 서로 공액적 관계에 놓여있는 분포들이기 때문이다.
  • 즉, (베타분포 \( = \) 이항분포 \( \times \) 베타분포) 와 같은 형태의 식을 얻을 수 있다.
  • 베타 분포는 다음과 같다.

• 여기에 사용된 감마(Gamma) 함수는 다음과 같다. (이 함수는 감마 분포에서도 사용된다.)

• 베타 분포의 기본적인 성질은 다음과 같다.

• 식에서 사용된 베타 분포는 앞서 설명한 이항 분포의 공액 분포를 설명하는 것으로, 주 변수는 바로 이항 분포의 \( u \) 가 된다.
• 따라서 이 베타 분포의 모수 a, b는 초모수(hyper-paramter) 또는 하이퍼-파라미터라고 부른다.
  • 모수(paramter)의 모수(paramter) 이므로 하이퍼(hyper)를 붙인다.
  • 하이퍼-하이퍼-파라미터가 존재하는지 궁금하다면? 웃길것 같지만 존재하는 개념이며 계속 확장 가능함
• 그냥 지나치기 서운하므로 베타 분포의 모양을 좀 살펴보자.

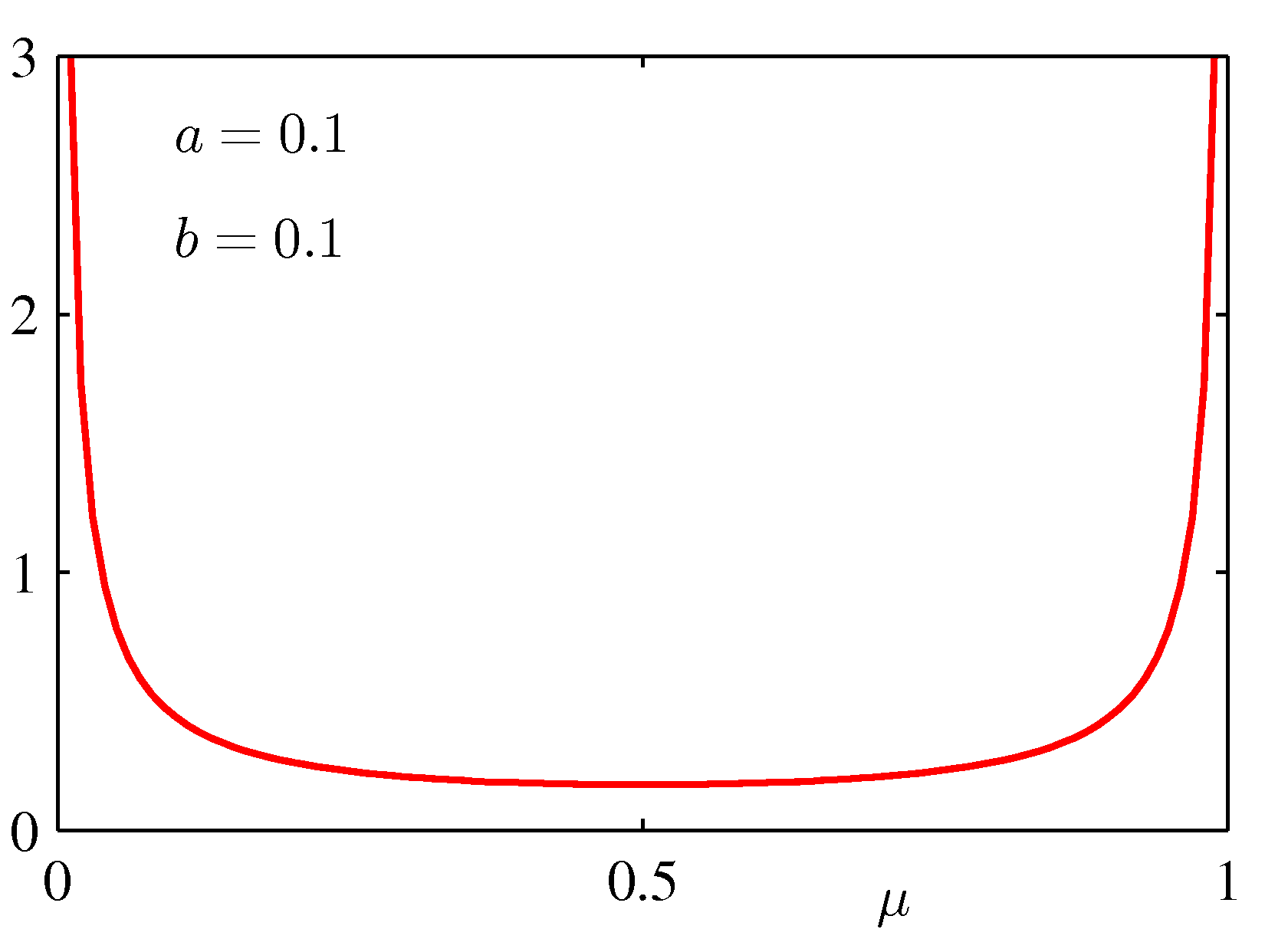
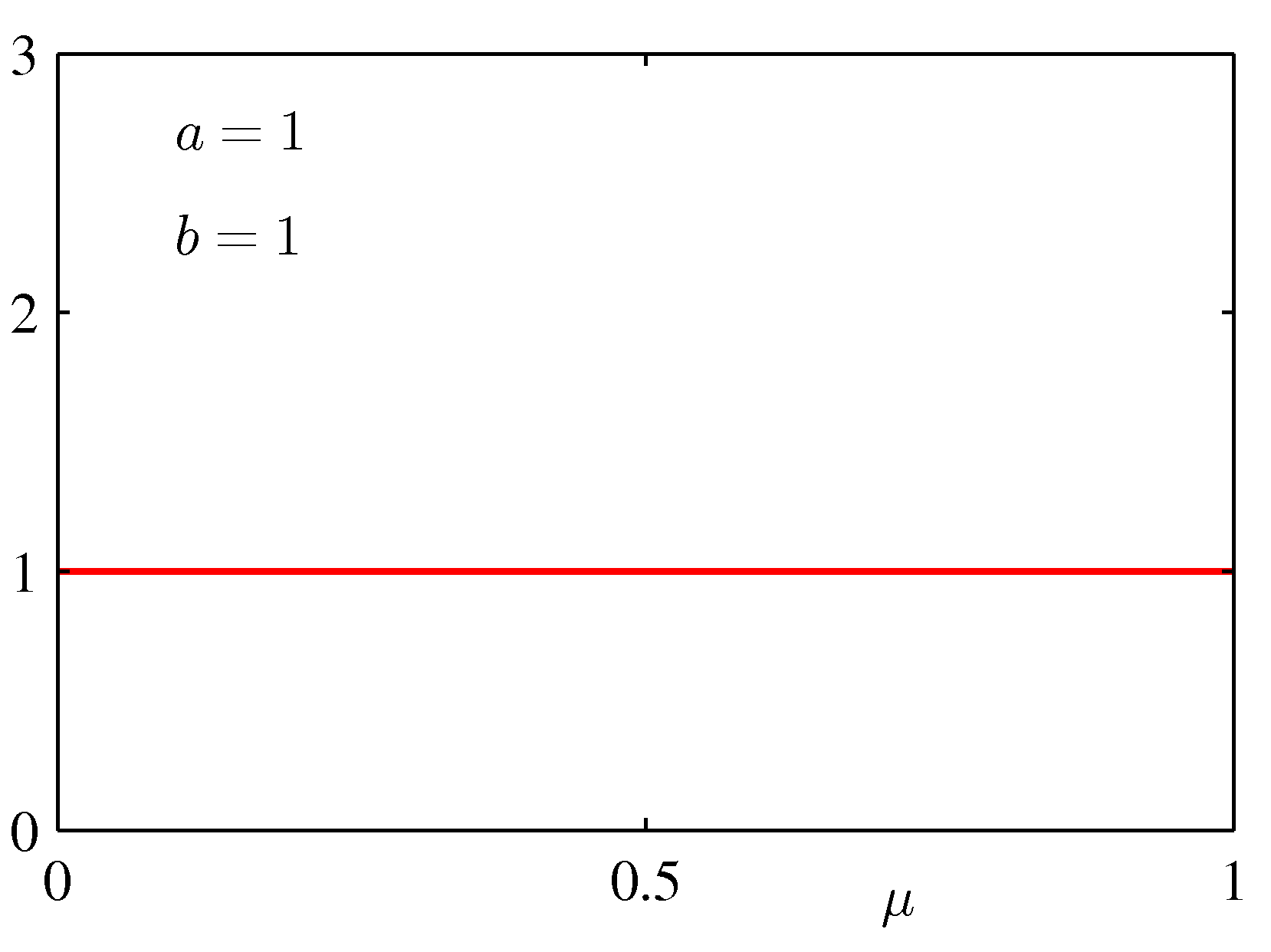
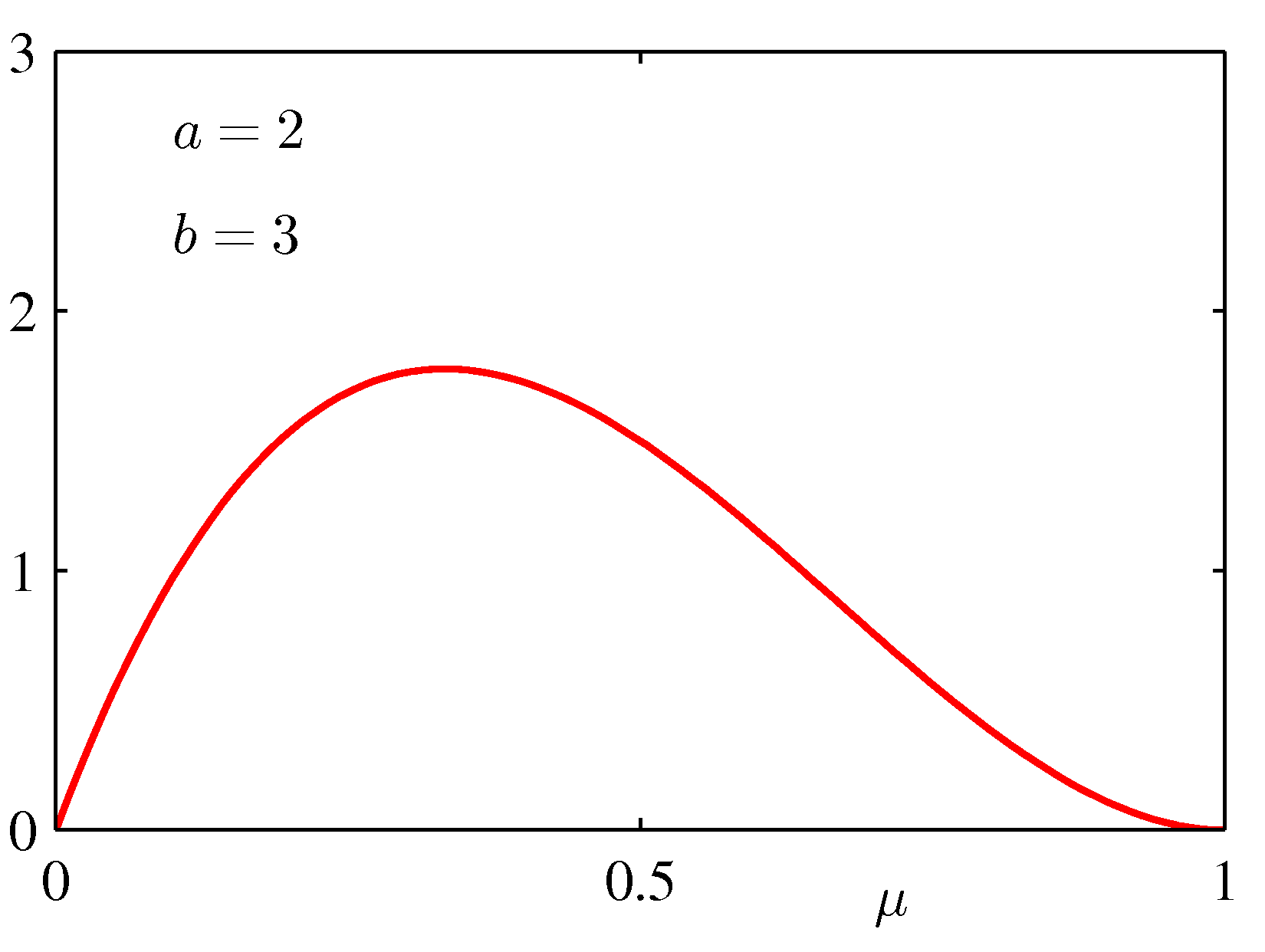
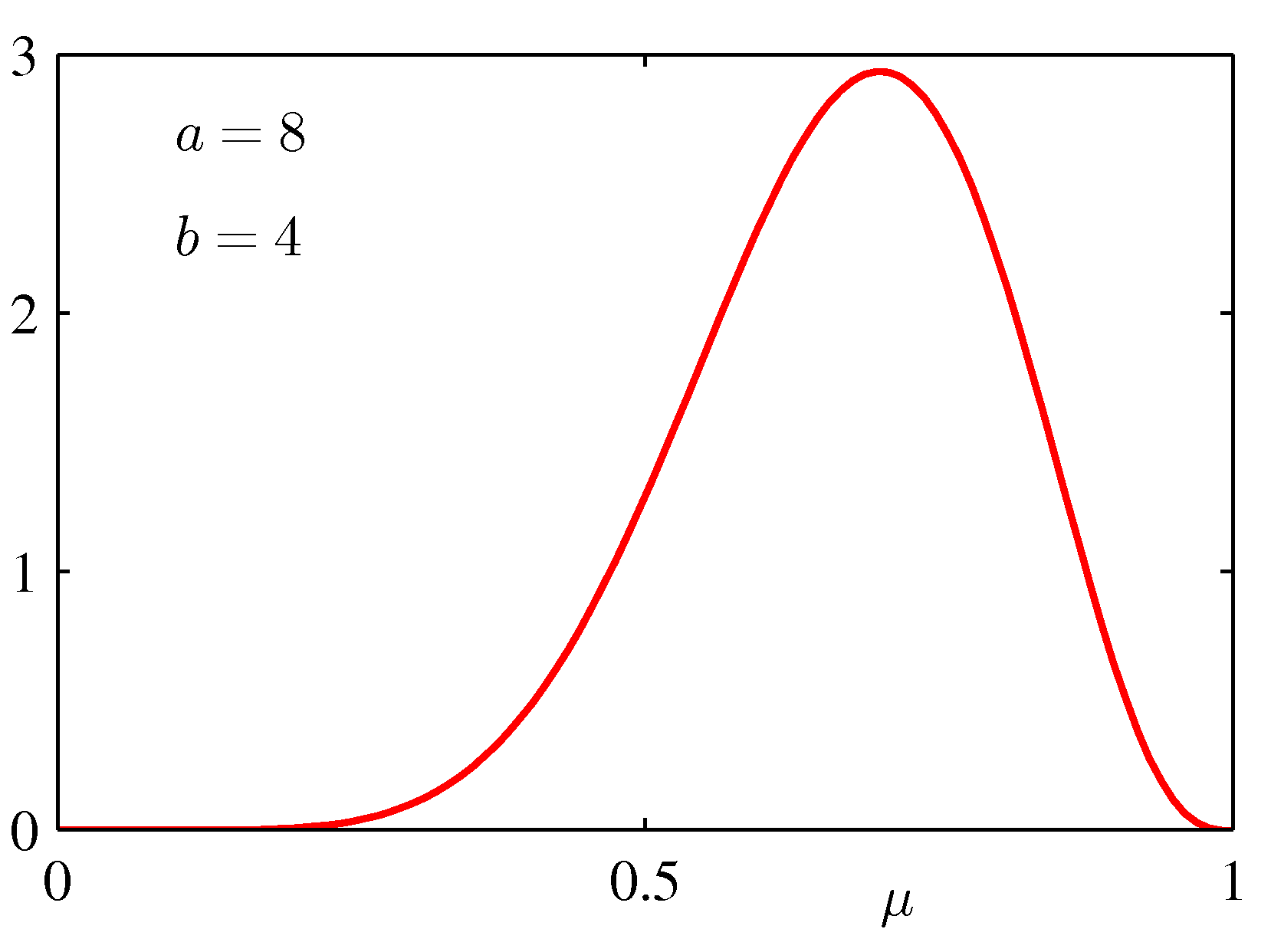
• 그럼 동전 던지기의 사후 분포(posterior) 는 어떤 모양이 될까?

• 오, 우리가 앞서 설명한 공액(conjugacy)적 특성이 나타나고 있다.
  • 쉽게 이야기하자면 모수의 사전 분포를 베타 분포로 썼더니 사후 분포도 베타 분포가 된다는 것.
• 만약 샘플이 충분해서 \( m, l \rightarrow \infty \) 라고 한다면 ( \( m \) 과 \( l \) 은 모두 가능도 함수로 구한 파라미터이다.) 이 결과는 MLE 와 동일해진다.

• 만약 샘플이 매우 작아 \( m, l \rightarrow 0 \) 에 가까운 값이라면, 이 분포는 사전 분포의 형태에 의존하게 된다.

• 이제 사후 확률 분포식을 살펴보도록 하자.

• 사후 분포도 베타 분포를 따른다.
• 위의 식에서 \( m \) 은 \( x=1 \) 인 경우의 횟수, \( l \) 은 \( x=0 \) 경우의 횟수를 의미한다.
• 이에 대응되는 \( a \) 와 \( b \) 는 앞면, 뒷면이 발생하는 사건에 대한 effective number of observations 이다.
  • 물론 \( a \) 와 \( b \) 가 모두 정수일 필요는 없다.
  • 하지만 이 값은 마치 사건이 일어나기 전에 해당 사건이 발현된 횟수처럼 고려될 수 있다.
  • 따라서 \( a \) 와 \( b \) 로 인해 지정된 총 횟수보다 실제 발생한 사건의 횟수가 더 적으면 사후 분포를 만들어내는 영역에서 사전 분포의 영향이 더 크다.
  • 반대로 실제 사건의 발생 횟수가 더 커지면 가능도 함수에 의해 만들어지는 조건부 분포의 영향이 커진다.
  • 결국 \( a \) 와 \( b \) 를 어떻게 지정하느냐에 따라 사후 확률을 계산하는데 영향을 미치게 되는 실제 데이터의 임계 크기를 결정할 수 있게 된다.
    • 여기서 effective number 의 의미를 유추할 수 있다.

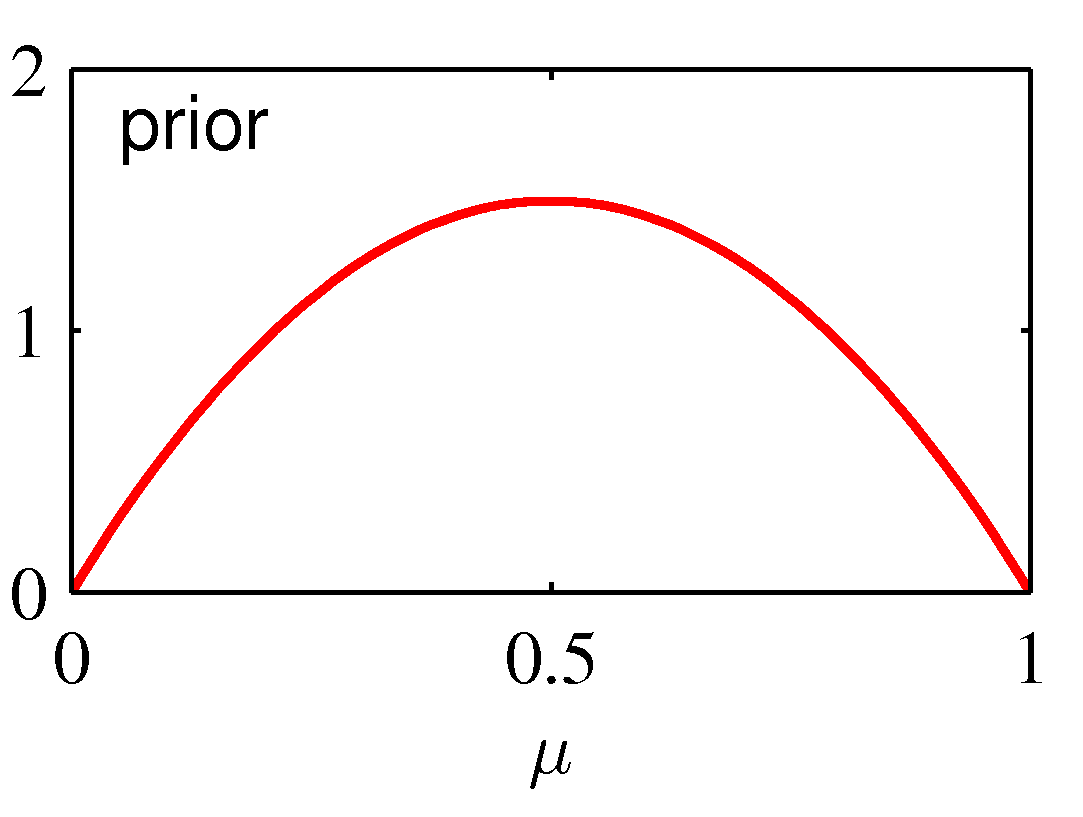
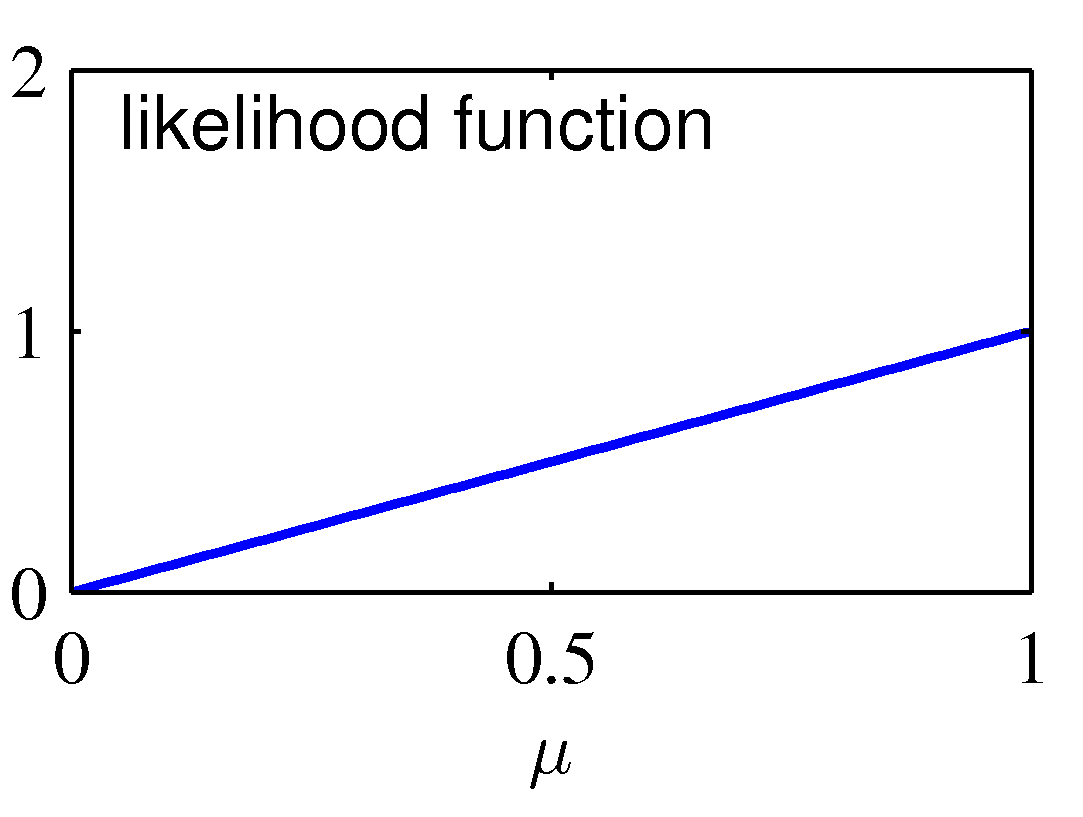
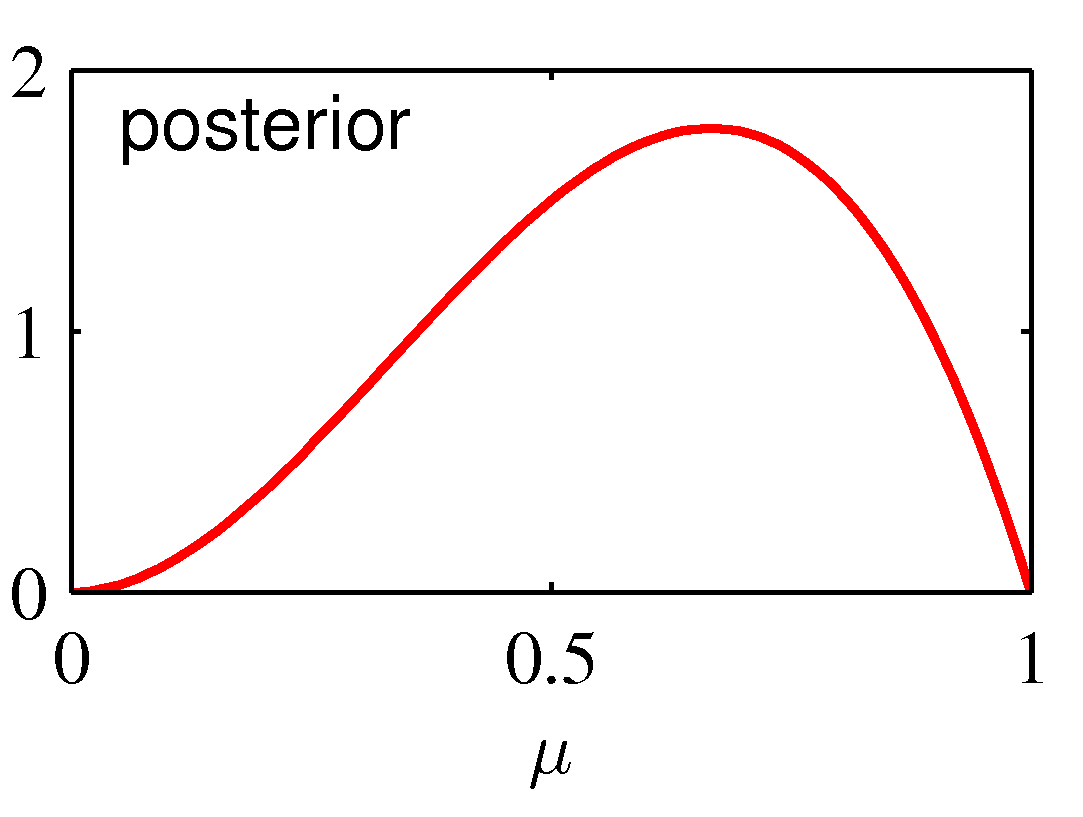
• 위의 그림은 연속된 베이즈 추론의 예로,
• 사전 분포로 베타 분포의 모수 값이 \( a=2 \) , \( b=3 \) 이 주어졌다. (즉, 총 5회 사건이 사전 분포로 지정된다.)
• 실제 발생한 사건은 1건으로 앞면이 나왔다. 이 경우 \( N=m=1 \) 이 되고 이를 모수에 관한 그림으로 표현하면 중간 그림이 된다.
• 최종 얻어지는 사후 확률은 맨 오른쪽이 된다.
  • 실제 발생한 사건은 동전의 앞면이 나온 한 가지 사건이지만,
  • 사전 분포의 영향으로 사후 분포의 모양이 사전 분포와 비슷하게 만들어지게 된다.
  • 물론 앞면이 한번 나왔기 때문에 \( \mu=1 \) 쪽으로 약간 치우치게 된다.

Sequential approach to learning

• 위의 그림에서도 잠시 언급하고 있지만 순차(sequential)적으로 확률 분포를 업데이트하는 모델을 고려해보자.
• 데이터가 한 건이라도 관찰될 때마다 사후 확률을 갱신할 수 있다.
• 사전 분포와 가능도 함수의 선택은 서로 독립적이고, 사전 분포와 사후 분포가 같은 모양의 함수 형태를 가지게 되므로,
  • 사전 분포가 베타 분포이고, 사후 분포도 마찬가지로 베타 분포가 되는 것을 이미 확인했다.
• 결국 사후 분포를 다음 사건이 발생할 때, 사전 분포로 활용을 해도 문제가 없게 된다.
• 이걸 극단적으로 반영하면 데이터 한 건 한 건 반영될 때 마다 업데이트 모델을 만들어낼 수 있다.

• 물론 몇개의 사건을 묶어 업데이트를 하는 mini-batch 형태의 모델도 적용 가능하다.

• 만약에 우리가 원하는 작업이 모수 값을 추정하는 것이 아니라.
• 새로운 데이터가 추가되었을 때 이를 결과에 대해 예측하는 것이 목적이라면,
  • 예를 들어 동전 던지기라면 임의로 던진 동전 한개가 앞면일지 뒷면일지 예측하는 문제.
  • 물론 부가적으로 모수값이 추정되어야만 앞면과 뒷면이 나올 확률값을 예측할 수 있지만, 어쨌거나 최종 필요한 것은 모수값은 아니다.
  • 이런 모델이 왜 좋나면 값이 고정된 모수를 선택해서 예측하는 것이 아니라 모수 자체를 확률 변수로 놓고 영향을 줄 수 있는 모든 모수의 가능성을 염두해 둔 수식을 만들어 원하는 예측값을 만들어낼 수 있다.
  • 결국 베이지안 방식에서의 예측 분포 모델을 돌려 설명한 것임.
• 식을 좀 정리해서 바로 이 확률값을 추정할 수 있는 식을 만들어낼 수 있다.

• 식을 보면 그냥 지금까지 예측된 데이터로 인해 만들어진 \( x \) 에 대한 평균값을 구하기만 하면 끝이다.
• 베타 분포의 평균값을 구하는 식은 이미 봤다.
  • \( E[\mu] = \frac{a}{a+b} \) (식 2.15)
• 이걸 사후 분포에 적용하면 다음과 같은 결과를 얻는다.

• 위 식에서 데이터가 매우 커져서 \( m,l \to \infty \) 가 되면 결국 이 식은 MLE 결과와 동일해진다.
  • 즉, 사후 분포에서 사전 분포의 영향력이 사라짐.
• 보통 데이터의 크기가 무한히 커지면 베이지안 추론 방식과 MLE 의 추론 방식이 같아지는 경우가 많다.
• 데이터의 크기가 유한한 경우 MLE 로 얻어진 모수와 사전 분포로 얻어진 모수의 중간 어딘가에 사후 분포로 예측한 모수값이 오게 된다.
• 데이터가 많아지면 많아질수록 사후 분포의 피크는 점점 날카롭게 오르게 된다.
  • 결국 분산 값이 작아지게 되고 Non-uniform 한 분포의 형태를 갖지게 된다.
• 만약 \( a\to\infty \) 또는 \( b\to\infty \) 인 경우 분산 값은 0이 되는 것을 알 수 있다.
  • 즉, 사전 분포의 \( \mu \) 가 고정된 값을 가지게 된다.
• 우리가 궁금한 점은 베이지언 방식을 취할 때 관찰 데이터가 많아질수록 사후 분포의 불확실성은 줄어들게 되는지 여부이다.
• 그림을 살펴보면 당연히 줄여든다는 것을 아는데, 이걸 수식적으로 좀 증명을 해보도록 하자.
  • 즉, 사후 분포는 사전 분포에 비해 더 높은 피크를 가지게 된다.
• 이를 확인하기 위해 빈도론자가 베이지언 방식을 어떻게 보고 있는지를 확인해야 한다.
  • 이 말이 좀 애매하기는 한데 빈도론자의 경우 가능한 모든 데이터를 모두 반영하여 식을 설계하고,
  • 베이지언 방식에서는 실제 일어난 사건만을 수식의 중심에 놓는다.
  • 따라서 빈도론자의 입장에서는 실제 여러 데이터가 발현되었을 때의 평균 값에 주목하게 된다.
    • 사실 이 부분은 이 교재에서 자세히 다루지 않는 부분이다.
    • 기존 통계학은 보통 관찰 데이터에 대한 점추정이 아닌 구간 추정을 한다.
    • 하지만 교재에서는 빈도론자적 입장에서는 점추정 방식의 MLE 만을 주로 다루고 있다.
• 만약 관찰 데이터 집합 \( D \) 의 파라미터 \( {\pmb \theta} \) 를 추론한다고 하자.
• 이 때 \( p({\pmb \theta}, D) \) 의 결합 분포로 인해 만들어지는 분포는 다음과 같게 된다.

• 이 때 각각의 식은 다음과 같다.

• 이 식이 어떻게 전개되었는지는 다음을 참고한다.

• 이 식을 Law of total expectation 이라고 한다.

• 마찬가지로 분산에 대해서도 이렇게 전개 가능하다.

• 마찬가지로 이 식을 Law of total variance 라고 부른다.
• 수식이 복잡해 보이지만 그리 중요한 것은 아니고 간단한 사실만 확인하고 넘어가도록 하자.
  • 왼쪽은 \( \theta \) 에 대한 사전 분산값이다.
  • 첫번 째 텀은 \( \theta \) 의 사후 분산값에 대한 평균이다.
  • 두번 째 텀은 \( \theta \) 의 사후 평균에 대한 분산이다.
  • 분산의 값은 양의 값을 가지기 때문에 첫번 째 텀은 왼쪽 값보다 작거나 같다.
• 결국 모수에 대해 왼쪽 값은 사전 분포의 분산, 오른쪽 첫번 째 텀은 사후 분포의 분산이 되므로,
• 모수에 대해 사후 분포의 값이 사전 분포보다 작다고 할 수 있다.