- 참고 사항
- 논문 저작자인 Max Jadeberg 가 이미 이와 관련되어 블로그에 따로 글을 올렸다.
- 아래 내용 중 일부 이미지는 이 블로그에서 발췌되었다.
Introduction
- 방향성 신경망(directed neural network)은 다음의 step을 가짐.
- 입력 데이터를 입력받아 순 방향으로 데이터를 진행하면 계산.
- 정의된 loss 함수로 나온 생성값을 역방향으로 전파. (backprop)
- 이 과정에 여러 가지 Locking이 생겨남.
- (1) Forward Locking : 이전 노드에 입력 데이터가 들어오기 전까지는 작업을 시작할 수 없다.
- (2) Update Locking : forward 과정이 끝나기 전까지는 작업을 시작할 수 없다. (예로 backprop)
- (3) Backwards Locking : forward와 backward 과정이 끝나기 전까진 작업을 시작할 수 없다.
- 위와 같은 제약으로 인해 신경망은 순차적으로 동기적 방식으로 진행된다.
- 학습이 이러한 과정이 당연해 보이지만 각 레이어에 비동기 방식을 도입하고 싶거나 분산 환경등을 고려하게 되면 이러한 제약이 문제가 된다.
- 이 논문의 목표는 위에서 설명한 모든 Locking 을 해결하는 것은 아니고 backprop 과정 중 발생하는 update locking을 제거하고자 하는 것.
- 이를 위해 레이어 \(i\) 의 weight \(w_i\) 를 backprop을 통해 업데이트 할 때 근사값을 사용하게 된다.
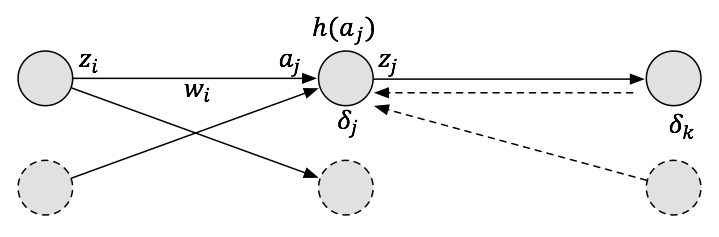
- 위의 식들은 논문 표기법을 좀 더 이해하기 쉬운 값으로 변경해 놓은 것이다. 그림을 참고하여 살펴보도록 하자.
- 이제 마지막 레이어로부터 backprop 계산을 위한 \(\delta\) 값을 살펴보도록 하자.
- 마지막 레이어가 \(k\) 라고 하고 하면,
- 중간 레이어에서의 \(\delta_j\) 도 이를 재귀적으로 이용하여 풀이할 수 있다.
- 이 논문은 이 수식을 다음과 같은 근사식으로 전환한다.
- 이 아이디어는 한 레이어에서 출력 값을 전달한 뒤 backprop 단계에서 전달되는 에러 값 \(\delta\) 를 기다리지 않고,
- 합성 그라디언트 (synthetic graidents) 값을 이용하여 바로 현재 레이어에서의 backprop 수행한다는 것이다. (Update Locking이 사라진다)
- 여기서 합성(synthetic)이란 표현은 그냥 비슷하게 gradient 값을 흉내낸 가짜 값을 의미한다. (바나나맛 우유에 바나나가 안들어있는 것처럼)
Decoupled Neural Interfaces (a.k.a DNI)
- 합성 그라디언트를 반환해주는 모듈을 아래와 같은 그림으로 표기한다.
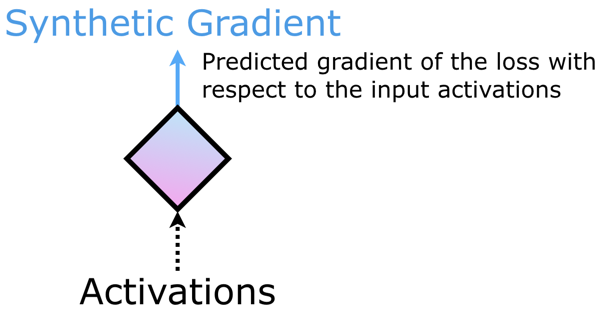
- 이러한 모듈을 DNI (Decoupled Neural Interfaces) 라고 부른다.
- 이를 이용하여 실제 어떻게 작업이 이루어지는지 살펴보자.
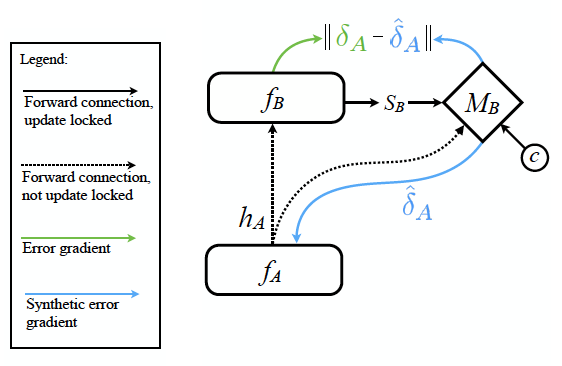
- 그림 설명
- \(f_A\) : 이전 레이어로 논문에서는 모듈이라고 부른다.
- \(h_A\) : 모듈 A가 출력하는 출력값이다.
- \(M_B\) : synthetic gradient 를 생성해주는 모듈이다.
- \(S_B\) : 모듈 B의 일부 상태 정보를 전달한다.
- \(c\) : 연산에 필요한 부가적인 정보를 그냥 묶어서 \(c\) 라고 표현한다.
- \(\|\delta_A - \hat{\delta}_A \|\) : \(\hat{\delta}_A\) 를 위한 Loss 함수이다.
- 이제 synthetic gradient 는 \(\hat{\delta}_A = M_B(h_A, s_B, c)\) 로 정의할 수 있다.
- 실제 동작은 아래 그림만 보면 바로 이해된다.
2.1 Synthetic Gradient for Feed-Forward Networks
- 이제 \(N\) 개의 레이어를 가진 feed-forward network에서 이를 활용하는 방법을 살펴보자.
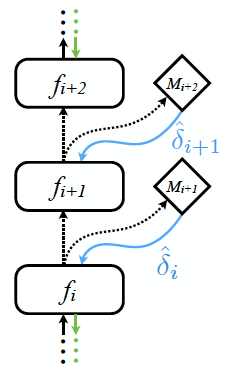
- 그림과 같이 여러 층의 레이어에 모두 적용 가능하다.
- 실제 동작되는 방식은 다음과 같다.
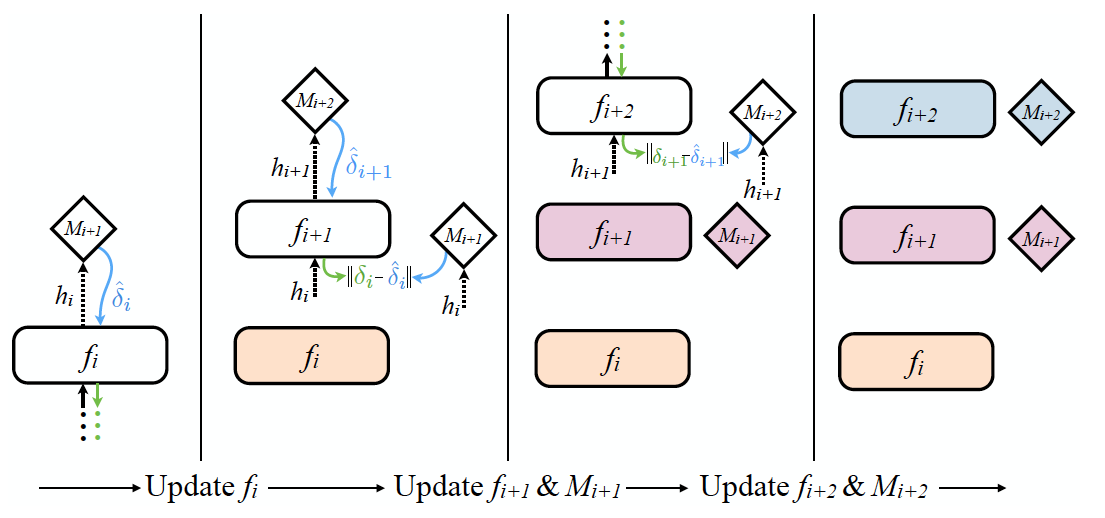
- 그냥 딱 봐도 어떻게 진행되는지 쉽게 알 수 있다.
- 일단 \(f_i\) 가 출력 \(h_i\) 를 \(M_{i+1}\) 에 전달하면 synthetic graident \(\hat{\delta}_i\) 를 바로 제공한다.
- \(f_i\) 는 forward 진행과는 무관하게 바로 backprop을 수행한다. (색상이 변경되었다.)
- 이제 \(h_i\) 를 입력으로 받은 \(f_{i+1}\)는 동일하게 \(h_{i+1}\) 을 \(M_{i+1}\) 을 전달하여 \(\hat{\delta}_{i+1}\) 을 얻는다.
- 사실 \(\delta_{i+1}\) 또한 synthetic gradient 이지만 이를 이용하며 바로 \(\delta_i\) 를 계산한뒤 \(M_{i+1}\) 을 업데이트 한다.
- 이 과정을 계속 반복한다.
Synthetic Gradient for Reccurrent Networks
- RNN 에도 이를 적용할 수 있다. 일단 무한히 전개되는 RNN 을 상상해보자.
- 즉, \(N \to \infty\) 가 되어 \(F_1^{\infty}\) 인 RNN이 된다.
- 이를 그림으로 나타내면 다음과 같다.

- 하지만 현실적으로는 이러한 모델을 계산하기 어렵다.
- 따라서 보통은 다음과 같은 형태로 제한하여 실제 계산을 수행하게 된다.

- 이를 식으로 표현해보자.
- \(N \to \infty\) 를 나타내는 식을 스텝 \(t\) 에서부터 \(T\) 까지의 식으로 나누어 tractable한 형태로 바꾼다.
-
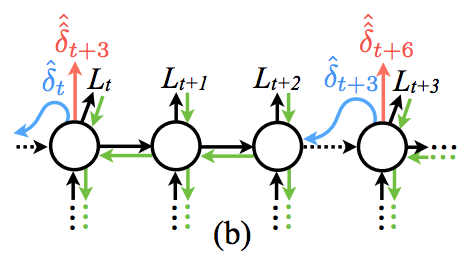
앞서 그림을 통해 설명했듯이 보통의 경우라면 이렇게 무한히 진행되는 RNN 계산이 어렵기 때문에 임의의 \(T\) 값을 정한 뒤 \(\delta_T=0\) 로 가정하고 식을 전개한다.
- 하지만 synthetic gradient 를 이용하면 그럴 필요 없다. \(\delta_T\) 를 근사할 수 있게 된다.
- 이와 관련된 내용도 다음의 그림을 보면 쉽게 이해할 수 있다.
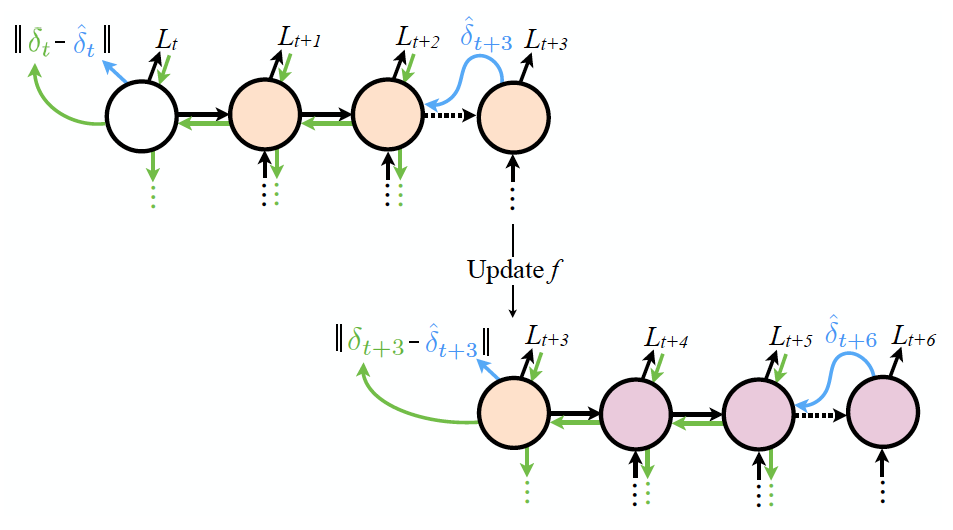
- 이것도 gif 파일로 보면 더 이해하기 쉬울 것이다.
Experiments
Feed-Forward Network
-
실험 결과를 살펴보자.
-
환경
- 데이터는 \(MNIST\) 와 \(CIFAR-10\).
- \(FCN\) 과 \(CNN\) 으로 각각 테스트.
- Hidden Layer의 수는 256 개로 고정
- 모든 Layer에 \(BN\) 과 \(ReLU\) 를 사용함.
- 모든 Layer에 \(DNI\) 적용.
- \(cDNI\) 는 \(DNI\) 에 이미지의 Label을 추가로 넣어 학습한 것을 의미.
- conditional DNI 라는 의미이다.
- 사용된 Label 은 one-hot representation 방식이다. ( \(MNIST\) 와 \(CIFAR\) 모두 10개의 class)
- CNN 에서는 이를 바로 넣기 힘드므로 \(C\) (channel) 에 one-hot 방식으로 mask를 추가하였다.
- 결국 10개의 추가 채널이 들어감.
- Optimizer 는 \(Adam\) 방식을 사용함.
- batch_size 는 256을 사용
- learning rate 는 초기값으로 \(3 \times 10^{-5}\) 를 사용하고 \(300K\) 와 \(400K\) 에서 10배 감소
- 사실 이러한 하이퍼 파라미터 값은 최적화 된 상태는 아니다.
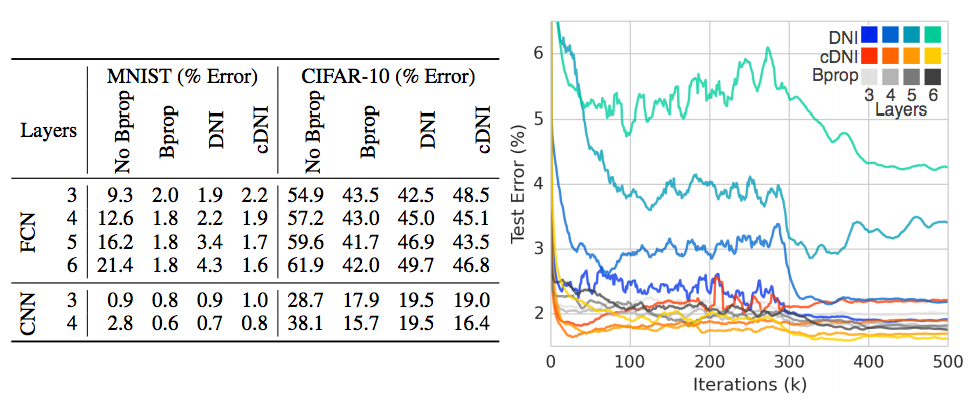
- 간단히 결과만 보면 \(cDNI\) 가 기존의 방식보다 정확도가 더 좋거나 비슷한 수준으로 보여짐.
- 가장 좋은 결과는 \(cDNI\) 모델에 linear synthetic graident 를 사용한 모델이다.
- synthetic gradient 도 단순한 신경망으로 구성한다. (여러 레이어로 테스트)
- 만약 0개의 Layer 인 경우 \(\widehat{\delta} = M(h) = \phi_w h + \phi_b\) 가 된다.
- 분류를 위한 Loss 함수는 cross-entropy 를 사용하였고 synthetic gradient 를 위한 Loss 함수는 \(L_2\) 를 사용하였다.
- 초기에 맨 마지막 레이어에서 내려오는 synthetic gradient 는 0으로 설정.
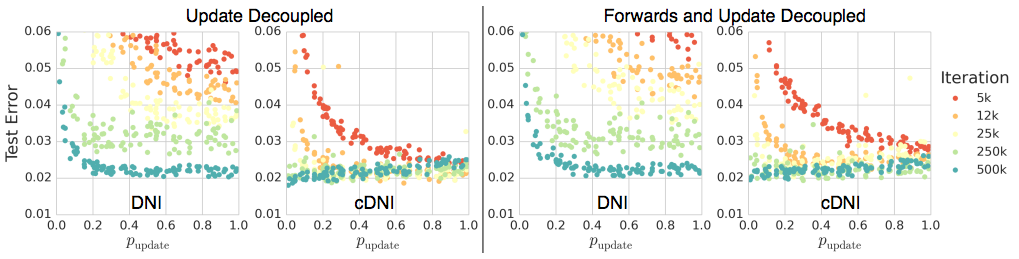
- 위 그림은 synthetic graident 가 실제 효과가 있는지를 확인하는 실험.
- \(x\) 축은 확률 값으로 \(p_{update}\) 확률을 나타낸다.
- 왼쪽 그림은 backprop 만 synthetic graident 를 적용한 것이고,
- 오른쪽 그림은 forward 도 synthetic graident 를 적용한 것이다.
- 따라서 완전히 async 로 동작하는 NN 이다.
- 이 때 확률 \(p_{update}\) 는 forward , backward 를 함께 선택하는 확률값으로 사용.
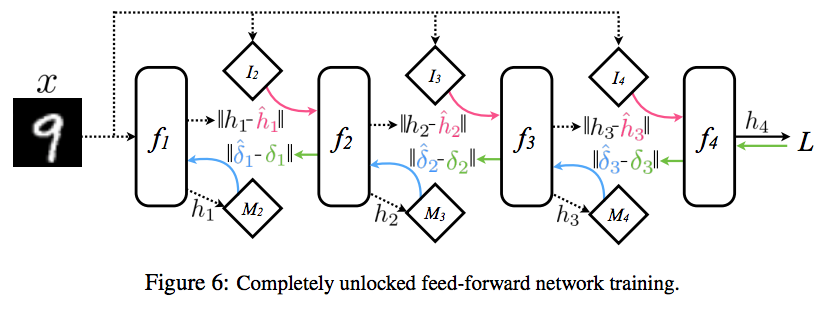
- Complete Unlock
- forward locking 도 없애도록 하여 완전하게 async 로 동작할 수 있는 모드를 의미한다.
- 이 모드는 모든 레이어에서 synthetic gradient 를 사용하는 것 뿐만 아니라 입력 또한 이런 방식으로 synthetic input 을 생성한다.
Recurrent Neural Net
- Reccerent 모델로 모두 \(LSTM\) 을 사용. 여기에 synthetic graident 를 적용한다.

- 문자열 복사 문제를 처리해본다.
- \(N\) 개의 문자열을 읽어 복사를 수행하는 연산이다.
- Repeat 모드의 경우 숫자 \(R\) 을 읽어 복사를 \(R\) 번 반복하게 된다.
- 위 수치값은 해당 \(T\) 를 사용하였을 때 실제 제대로 복원되는 Seq 의 길이를 의미함. (즉, 클수록 좋은 값이다)
-
단, Penn Treebank 는 에러값을 의미한다. (작을수록 좋은 값이다.)
- 여기서 Aux 는 다음과 같은 작업을 수행하는 보조 기능이다.