Swivel: Improving Embeddings by Noticing What's Missing

https://arxiv.org/abs/1602.02215

Word2Vec

  • word2vec 은 결국 matix factorization 과 동일한 원리이다. (참고)

  • 여기서는 아주 간단하게만 기초를 잡고 넘어가자.

  • 통계언어 모델은 (코퍼스 데이터를 입력으로 학습하여) 문장에 확률을 부여하는 모델.
    • 확률 값이 높은 문장이 확률 값이 낮은 문장에 비해 개연성이 있다고 본다.
    • curse of dimensionality 때문에 학습이 어렵다.
      • ocabulary의 차원도 높거니와 단어시퀀스 길이도 차원을 지수적으로 늘리는 역할을 한다.
    • 기존에는 이를 n-gram 모델로 처리했다.

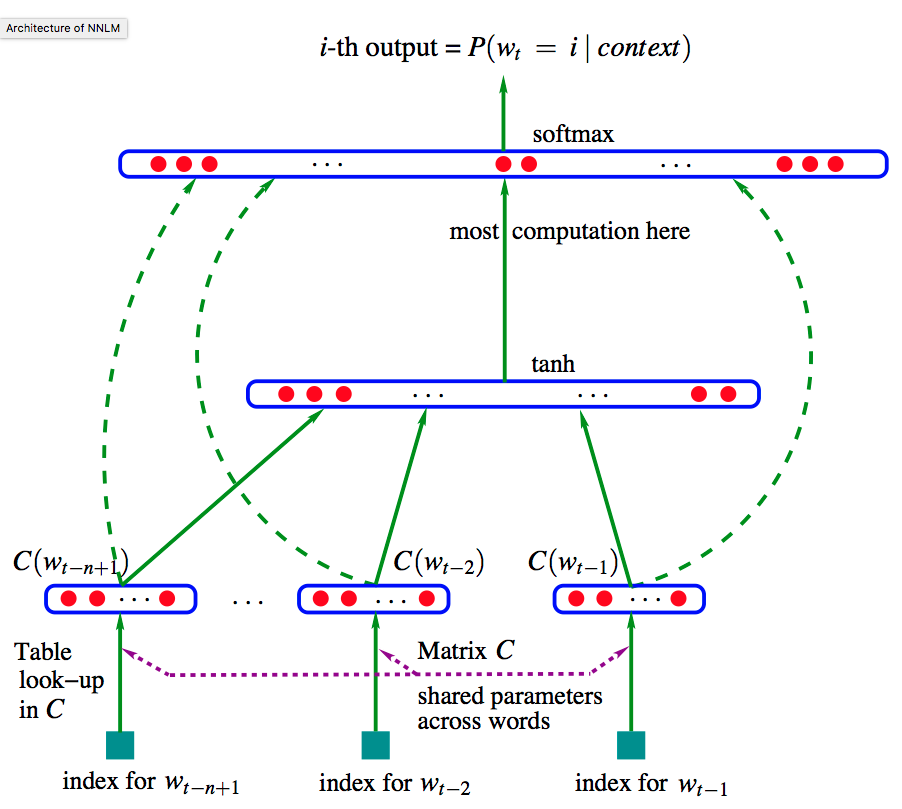
figure.1

  • NNLM
    • Bengio 가 2003년에 제시한 LM 모델로 일반적인 n-gram 모델보다 성능은 좋으나,
    • 학습 속도가 너무 느려 대규모 코퍼스에는 적용할 엄두를 내지 못했다.
      • vocabulary 크기에 선형적으로 학습 시간이 증가
    • 이 때 입력 단어를 embedding vector로 입력하게 된다.
      • 그리고 concept이 비슷한 단어는 비슷한 embedding vector값을 가진다.
    • 이후에 등장한 Mikolov 의 word2vec 은 사실 여기서 사용되는 word의 입력값을 생성하기 위한 방법.

Embedding Vector 를 표현하는 방법.

  • 앞서 비슷한 의미를 가지는 단어는 비슷한 embedding 을 가지는 형태로 값을 구해야 한다고 이야기 했다.
  • word 에 그냥 단순한 id 를 부여하게 되면 이런 구조를 만들어낼 수 없다. (‘모차르트’ 와 ‘모짜르트’는 유사하지만 id가 다르게 부여될 것이다.)
  • 그래서 대신 사용한 것이 co-occurrence 값을 word의 representation으로 취급.

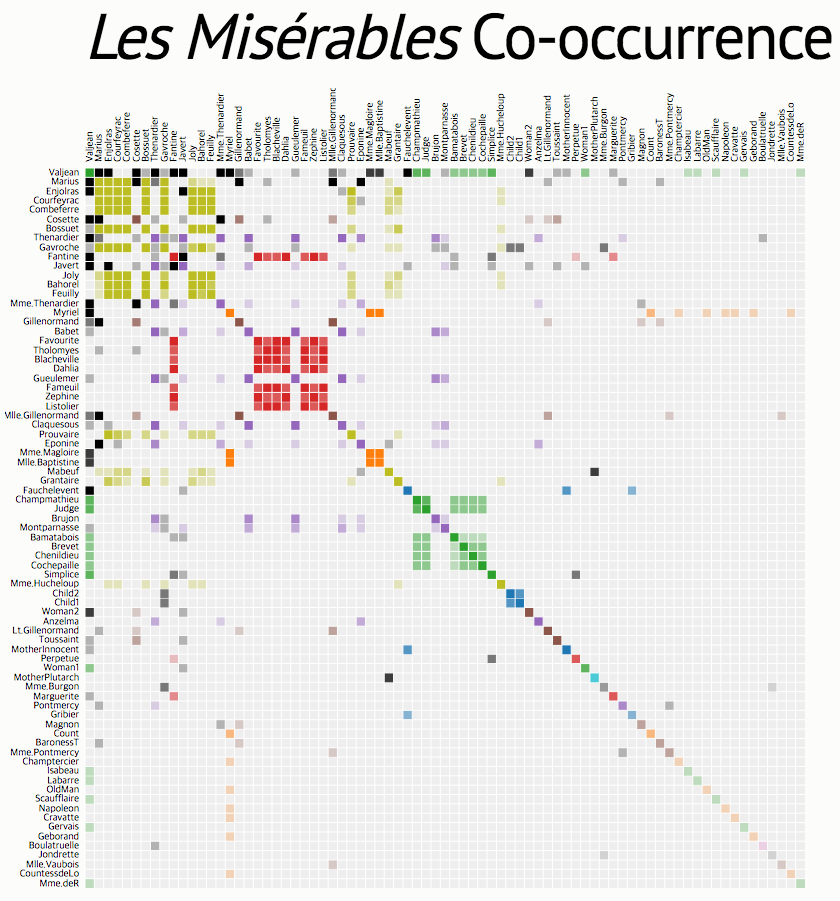
figure.2

  • co-occurrence 를 이용하여 word를 표현하는 경우 Dim 크기는 vocabulary 크기가 됨.
    • 표현해야 하는 데이터 집합의 크기가 너무 많다.
    • 게다가 지나칠 정도로 sparse 한 matrix가 된다.

Word Embeddings As Matrix Factorization

  • 결국 word vector에 대한 정보 축약의 문제로 귀결됨.
  • 이런 task에서 가장 손 쉬은 방식은 matrix factorization 방식.
    • 그래서 사실 word2vec은 PCA 나 SVD 와 그 성질이 유사하다.

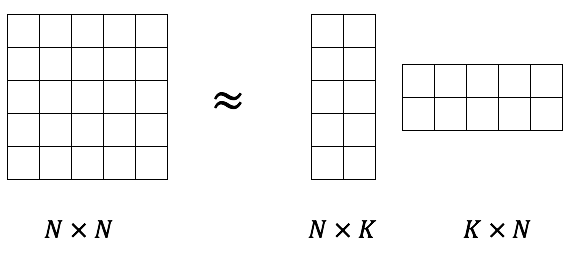
figure.3

\[M_{ij} = A_{i}^{T}B_{j}\]
  • word2vec 모델은 사전에 정해진 window size 내의 co-occurrence 를 근사하는 행렬을 찾는 모델.
  • 여기서 사실 행렬 \(A_{i}\) 와 행렬 \(B_{j}\) 를 동일하게 놓을 수도 있다.
    • 하지만 실제로는 두 행렬을 다른 행렬로 사용하는 것이 더 좋은 성능을 보인다.
  • 정리
    • 그럼 문서로 부터 co-occurrence matrix 만 생성하면 더 이상 문서를 살펴볼 필요가 없는가?
      • yes
    • 그런데 word2vec에서는 왜 dictionary 구축 후 다시 문서를 확인할까?
      • word2vec은 on-line 방식으로 문제를 풀이하는 모델.
      • co-occurrence 는 매우 큰 행렬이 될 수 있으므로 co-ocurrence를 만들지 않는다.
      • 대신 문서(doc)를 통해 co-occurrence matrix의 특정 elmt 만을 한번에 하나씩 살펴보는 효과 발생.
      • word2vec은 정확히는 co-occurrence count 를 근사하는 것이 아니다.

Swivel

  • 구글이 만든 word2vec 시스템.
  • 실제로는 Word2vec보단 Glove 모델과 더 유사하다.

  • GPU 를 활용한 분산 시스템에 특화.

  • 기본 아이디어.
    • word2vec은 원래 co-occurrence를 근사하는 행렬을 만들면 된다.
    • 하지만 co-occurrence를 메모리에 유지하면서 학습을 하기 어려우므로 word2vec은 이를 on-line방식으로 변경한 것이다.
    • 하지만 swivel 은 co-occurrence 행렬을 구하되 이를 분할하여 분산화시킨 모델을 고려.
  • co-occurrence 행렬의 구성
    • 일단 score 순으로 word를 정렬한다. (실제로는 pmi value)
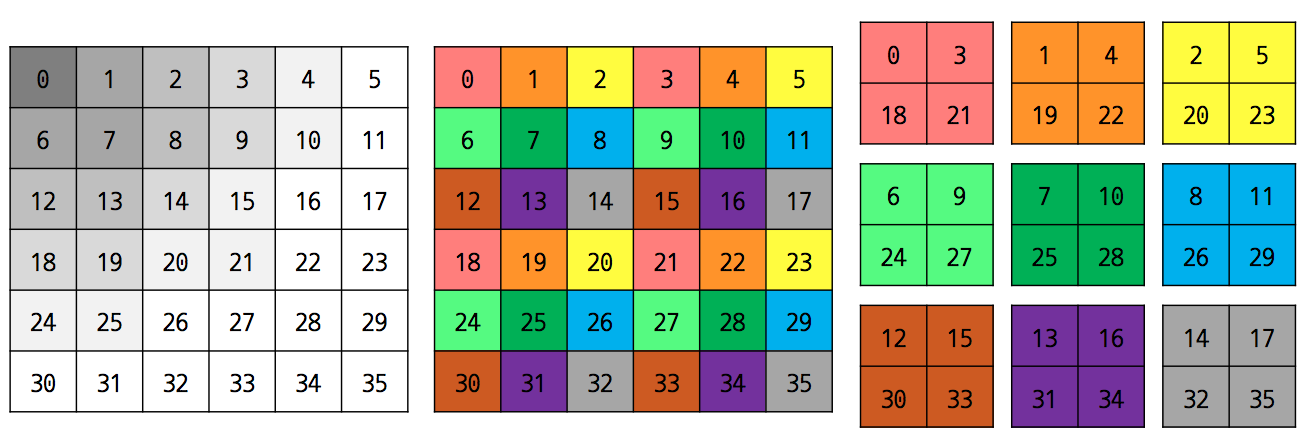
    • 이후 이 행렬을 분할하기 위해 전처리 과정을 진행한다.
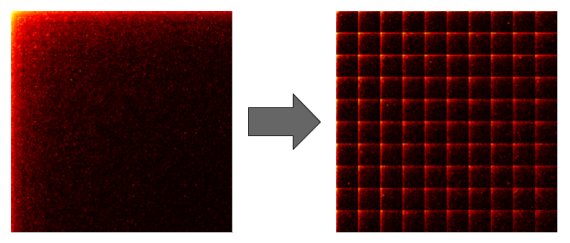
    • sparse 행렬의 데이터를 최대한 분산화시키는 구조로 행렬을 재구성한다.
    • 특정 크기의 블록으로 나눈 뒤 각각의 블록들을 병렬 처리하게 된다.

figure.4

figure.5

PMI (Point-wise mutual Information)

  • co-currence count 만으로 행렬을 만들면 Freq. 값이 높은 단어의 가중치가 너무 올라가게 된다.
    • 이런 경우 실제로는 의미없는 단어들의 가중치가 상대적으로 올라감.
    • 그래서 tf-idf 와 같은 concept으로 PMI value를 실제 값으로 사용하게 된다.
\[pmi(i, j) = \log{\frac{P(i,j)}{P(i)P(j)}} \qquad (1)\] \[pmi(i, j) = \log{\frac{x_{ij} |D|}{x_{i*}x_{*j}}} = \log{x_{i}} + \log{|D|} - \log{x_{i*}} - \log{x_{*j}} \qquad (2)\]
  • 단, \(x_{i*} = \sum_{j} x_{ij}\) , \(|D| = \sum_{i,j} x_{ij}\)
  • 만약 \(x_{ij}=0\) 인 경우 \(pmi\) 값이 \(-\infty\) 가 된다.
    • 이 경우를 위해 \(x_{ij}=0\) 인 경우에는 별도의 처리 작업을 수행한다. (뒤에 나옴)

Training

  • 실제 학습을 위해 \(d\)-dimensional embedding 행렬 2개를 사용한다.
    • \({\bf W} \in \mathbb{R}^{m \times d}\)
    • \(\tilde{\bf W} \in \mathbb{R}^{n \times d}\)
    • \(W_{i} \in {\bf W}\), \(\tilde{W}_{j} \in \tilde{\bf W}\)
  • 최종적으로 \( W_{i}\tilde{W_{j}}^{T}\) 를 부분 행렬 \(X_{ij}\) 에 근사하게 된다.

figure.6

  • 하나의 블록에 대해 근사하는 작업은 병렬적으로 진행되게 된다.
  • 하지만 완전한 병렬 구성은 어렵다.
    • 전체 계산을 위해서는 share 되는 블록이 필요하게 된다.
  • distbelief 모델
    • 최초 작성 버전은 구글의 distbelief 로 구현.
    • share되는 행렬을 ps(parameter server)에 두고 변경된 블록을 분산 환경의 머신에서 공유하는 방식으로 구현
    • async 모델을 사용하여 학습하는 형태. (하나의 weight 는 \(k \times k\) 크기의 블록)
    • 이 모델은 계산 및 네트워크 트래픽이 k에 비례하여 발생됨.
  • GPU 모델
    • 그래서 swivel 은 GPU를 활용하여 연산을 수행함.
    • GPU 에서는 행렬 곱이 상수 횟수의 연산으로 완료될 수 있다.
    • 실제 사용한 k 값은 4096.

Cost Function

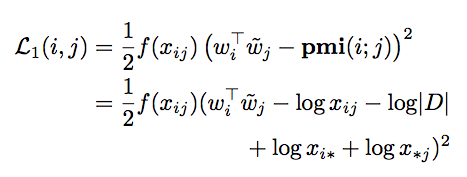
figure.7

  • 여기서 \(f(x_{ij})\) 함수는 사용자가 적당히 추가하는 보정 함수로 실험에서는 \(\sqrt{x_{ij}}\) 를 사용함.
  • 앞서 설명한대로 \(x_{ij}=0\) 인 경우에는 \(pmi\) 의 값이 \(-\infty\) 가 되므로 이를 처리해야 한다.
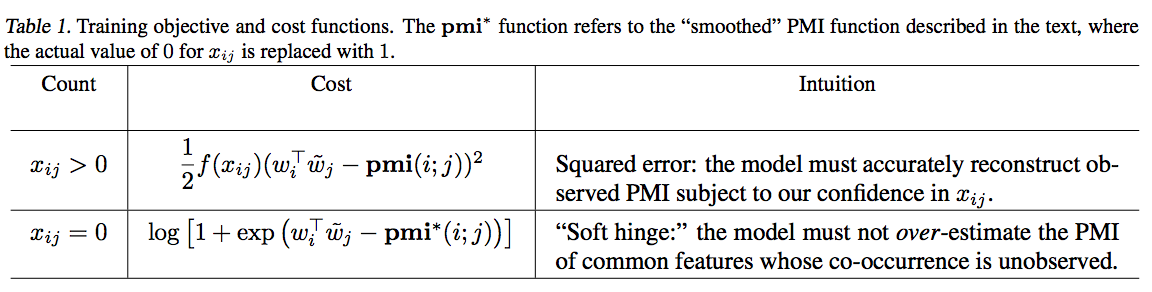
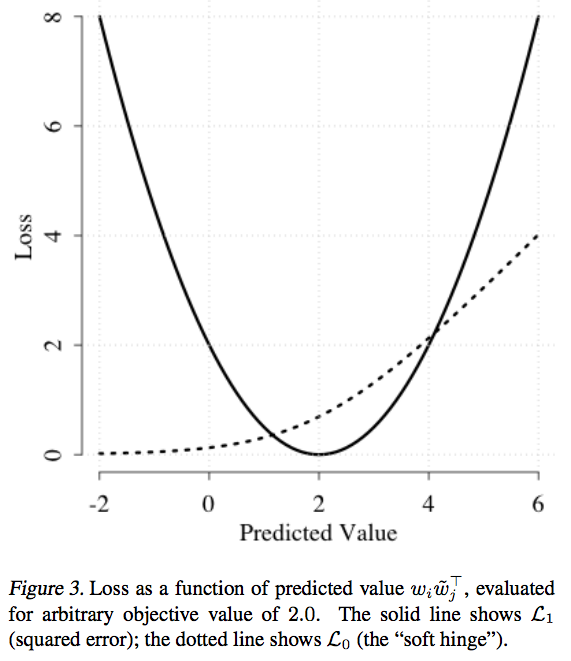
  • 따라서 \(x_{ij}=0\) 때의 Loss 를 다르게 처리함.
    • \(x_{ij} > 0\) 인 경우에는 \(L_{1}\) Loss를 사용하고 (squared error)
    • \(x_{ij} = 0\) 인 경우에는 \(L_{0}\) Loss를 사용 (soft hinge)

figure.8

  • 좀 더 고민해보자.
    • 단어 \(i\) 와 단어 \(j\) 가 Freq. 가 매우 낮은 단어라면 \(x_{ij}=0\) 는 학습 문서의 한계로 un-observed 상태라고 고려할수도 있음.
    • 반면 단어 \(i\) 와 단어 \(j\) 가 Freq. 가 높은 단어라면 이 경우에는 오히려 anti-correlated 의 증거라고 생각할 수 있다.
  • 이를 반영하기 위해 우리는 smoothing 기법을 도입한다.
    • 별거 없고 \(x_{ij} = 0\) 인 경우에 \(L_{0}\) Loss를 사용하되 \(x_{ij} = 1\) 로 취급
    • 이렇게 하면 Loss 는 다음과 같이 변경된다.

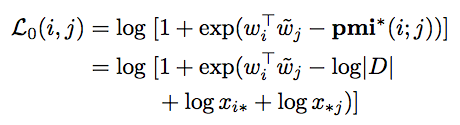
figure.9

  • 만약 \(i\) 와 \(j\) 가 고-빈도 word라고 생각해보자.
    • 그러면 \(\log{x_{i*}}\) 와 \(\log{x_{*j}}\) 의 값이 커지게 된다.
    • 이 경우 Loss 값을 작게 하는 방법은 \(w_{i}^T w_{j}\) 값을 작게 하거나 음수로 만들어야 한다.
    • 이 의미는 두 벡터의 co-occurrence 값을 anti-correlation 으로 간주하겠다는 의미가 된다.
  • 반대로 \(i\) 와 \(j\) 가 저-빈도 word라고 생각해보자.
    • 이 경우에는 \(\log{x_{i*}}\) 와 \(\log{x_{*j}}\) 의 값이 작으므로 \(w_{i}^T w_{j}\) 에 대한 제약이 없어진다.
    • 이런 경우에 사용하기 적당한 것이 soft hinge 이므로 이를 도입한 것.

figure.10

Experiments

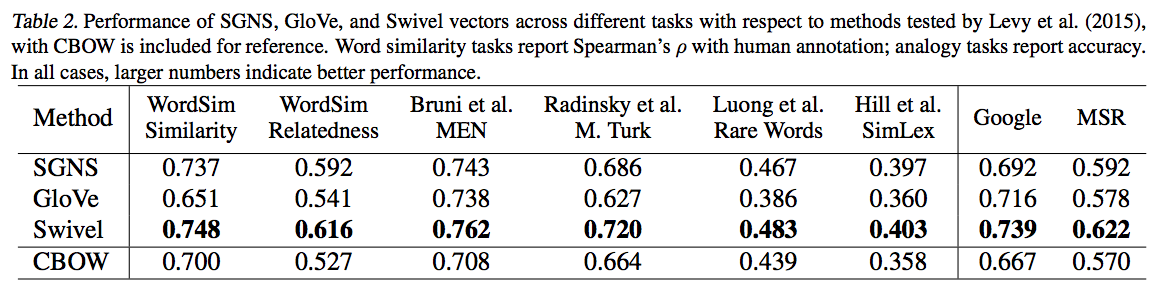
figure.11

  • 학습 데이터는 여러 종류의 데이터를 intrinsic 방식으로 해결.
  • Base-line 으로는 word2vec 모델과 Glove 모델을 사용.
    • word2vec
      • skipgram, neg-sampling size 는 5.
      • 65번 반복. rare set은 300 번 반복
      • Mikolov 가 사용한 방식대로 \(w_{i}\) 만 사용. (더 성능이 좋다.)
    • GloVe
      • GloVe 의 경우에는 두 embedding 벡터의 평균값을 사용한다. (이게 더 성능이 좋다.)
      • 100 반복. lr 은 0.05 tkdyd
      • cut-off alpha 값은 0.75
    • Swivel
      • 하모니 스케일 방식의 window 방식 사용.
        • 가장 가까운 word는 1점. 그 다음은 0.5점, 그 다음 word는 1/3점.
      • 100만 step 반복
      • 약 400,000 개의 단어. k=4096 사용. (블록 크기)
        • 이렇게 하면 약 100x100 개의 블록이 생성됨.
      • GloVe 와 마찬가지로 두 벡터의 평균을 사용.
      • 함수 \(f(x)\) 는 다음과 같다.
        • 최적의 값은 \(\alpha = 1/2\) 이고 \(b_0 = 0.1\), \(b=1/4\) 이다.
\[f(x_{ij}) = b_0 + b x_{ij}^{\alpha}\]
  • 실제 구현 코드가 제공된다. : 링크