Neural Turing Machine

튜링 머신 (Turing Machine)

튜링 머신(Turing machine)은 긴 테이프에 쓰여있는 여러 가지 기호들을 일정한 규칙에 따라 바꾸는 기계를 의미.
엘런 튜링이 제안한 머신으로 현대 컴퓨터의 초안이 됨.
이 논문은 뉴럴 튜링 머신 (Neural Turing Machine) 을 다루고 있기 때문에 당연히 먼저 튜링 머신을 알아야 한다.

튜링 머신의 이해

튜링 머신은 “계산 가능한 수에 대해, 수리 명제 자동 생성 문제의 응용” 이란 엘런 튜링의 논문에서 언급되었다.
이 논문이 나요게 된 배경부터 살펴보자.
1928년. 당시 수학계를 이끌던 다비트 힐베르트 (David Hilbert) 는 다음과 같은 의문을 제시하였다.
- 수학자들이 지금까지 해 왔던 일들을 정리해보니 몇 가지 추론 법칙을 조합하여 원하는 결과를 도출하는 것이 전부임.
- 그렇다면 몇 개의 추론 규칙을 제시하면 앞으로 수학자들이 증명할 명제 또한 모두 찾을 수 있지 않을까?
- 즉, 모든 수리 명제를 자동으로 만들어 낼 날이 올 수도 있겠구나.
- 힐베르트는 이러한 보편 규칙이 존재하는가에 대한 의문을 제시했다.
하지만 3년 후 독일의 신참 수학자 쿠르트 괴텔이 이는 불가능한 일임을 증명해버렸다.
- “기계적인 방식만으로는 수학의 모든 사실을 구성할 수 없다.”
- 이를 불완전성의 정리 (incompleteness theorem) 라 한다.
- 예를 들어 정수 무한대(∞)와 실수 무한대(∞)는 둘 다 무한대이지만 실수 무한대가 더 큰 범위.
  - 이러한 성질을 이용하면 카운터 예제를 만들어낼 수 있다고 한다. (정확한 내용은 잘 모르겠다.)
켐브릿지 대학을 갓 졸업한 앨런 튜링은 졸업 후 맥스 뉴먼의 강의에서 이를 증명하는 리뷰 수업을 듣게 된다.
- 그리고 곧바로 튜링은 자신만의 방식으로 괴텔의 논리를 증명하고자 했다.
튜링이 증명한 방식
- ‘기계적인 방식’이 무엇인지 정의하고 이를 구현하기 위한 보편 기계를 정의한다. (오로지 5개의 부품으로)
- 그리고 이 기계가 충분히 보편적이라는 것을 증명한다.
  - 여러가지 문제들을 제시하고 공통의 풀이 방식으로 해결한다.
- 마지막으로 이 기계로도 풀 수 없는 수학적 문제들을 제시하여 괴텔의 증명을 확인한다.
  - 예를 들어 앞서 설명한 카운터 예제 등은 보편 기계에서는 종료(halt)에 도달하지 못하는 상태가 되어 버린다.
그런데 사람들은 정작 보편 기계에 관심을 가지게 됨.
- 생각보다 현실적인 문제들을 해결할 수 있는 수단을 제공하고 있다.
- 튜링은 이 머신에 A-Machine 이란 이름을 붙였는데 이후 튜링 머신이 된다.
- 물론 튜링이 제시한 보편 기계는 당시에는 실제 동작하는 기계라기보단 개념에 가까웠음.
- 사실 튜링 머신은 우리가 알고 있는 오토마타의 일종일 뿐이다.
튜링 머신 구성 요소
- 테이프 (tape) : 일정한 크기의 Cell 로 나뉘어 있는 종이 테이프로 무한하다. (사실은 무한하다는 것 자체가 말이 안되긴 한다.)
- 헤드 (head) : 종이 테이프의 특정한 셀을 읽을 수 있는 헤드로 이동이 가능. (or 헤드가 고정되고 테이프가 움직여도 된다.)
- 상태 기록기 (state register) : 현재 튜링 머신의 상태를 저장
  - start state : 시작 상태 (상태 기록기가 초기화된 상태)
  - halt state : 작업 수행이 종료된 상태
- 액션 테이블 : 특정 상태에서 특적 기호를 읽었을 때 수행해야 할 행동을 지시하는 테이블
  - (예) 종이 테이프의 기호를 고치거나 지울 수 있다.
  - (예) 헤드를 오른쪽 또는 왼쪽으로 한칸 움직이거나 그냥 그 자리에 머문다.
  - (예) 상태 정보를 갱신한다. 혹은 그 상태 그대로 머물 수도 있다.
  - 테이프를 제외하고는 튜링 머신에 사용되는 상태와 액션 테이블은 유한한 크기를 가져야 한다.
많은 사람들이 취미로 튜링 머신을 구현한다.

figure.1

레고로도 만듬.

figure.2

Turing Machine Example

예를 통해 튜링 머신이 어떻게 동작하는지를 살펴보자.
아래 그림은 앞서 설명한 튜링 머신 구성 요소들을 그림으로 나타낸것이다.

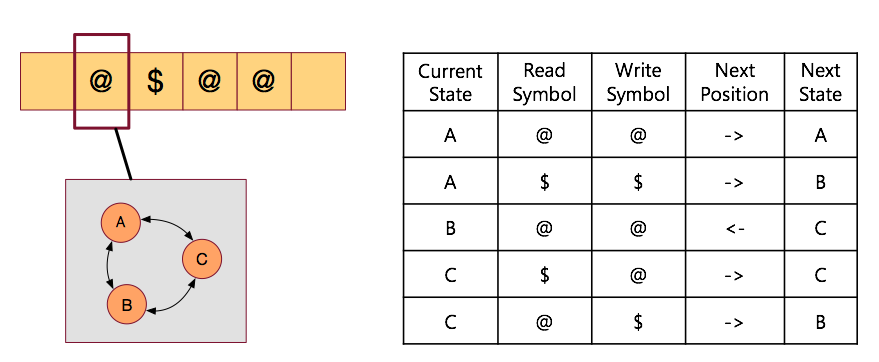
figure.3

위 튜링 머신은 $$$ 문자열을 맨 뒤로 옮기는 작업을 수행하는 튜링 머신이다.
이처럼 튜링 머신은 어떤 목적을 해결하기 위한 수단으로 작성된다.
이 때 사용되는 요소는 테이프, 헤드, 상태, 액션테이블 등이다.
그림에서 보면,
- 왼쪽 상단은 테이프를 의미한다. 여기에 데이터를 읽고 쓸 수 있다.
- 붉은 색 박스가 헤드(head)가 된다. 이를 움직여 테이프 위치를 지정할 수 있다.
- 왼쪽 하단의 박스가 상태(state)를 나타내는 상자이다. 현재 $\{A, B, C\}$ 중 하나의 상태에 매핑될 수 있다.
- 오른쪽이 액션 테이블로 각 상태에서 전이 가능한 행동들이 기술되어 있다.
- 이 테이블을 어떻게 작성하는가에 따라 우리가 해결해야 할 문제를 처리할 수 있음을 쉽게 알 수 있다.
그림만 봐도 대충 느낌이 오는데 그냥 전형적인 오토마타이다.
사실 현재 상태가 어떤 상태인지도 어딘가에 저장을 하고 있어야 하는데,
- 이것도 사실 테이프에 기록 가능하다.
- 현재 상태를 읽고 쓰는 방식도 마찬가지로 액션 테이블에 정의하고 테이프에 기록하면 된다.
감이 좀 올텐데 예를 들면 복사(copy)라던가 산술 연산 등을 오토마타로 구성할 수 있다.
- 이를 이용하여 실제 동작을 수행하는 튜링 머신을 구축할 수 있다.

Neural Turing Machine

이제부터는 뉴럴 튜링 머신을 살펴볼 것이다.

Introduction

컴퓨터 프로그램은 다음 3가지 요소로 구성됨.
- 기본 연산 (예를 들어 수학 연산들)
- 논리 흐름 컨트롤
- 외장 메모리 (연산의 결과를 쓰고 읽음)
튜링 머신은 현재 컴퓨터 구조의 기본 모델이라 생각할 수 있다.
- 이 구조를 차용하여 신경망 모델로 확장할 것이다.
RNN 은 딥러닝 모델 중 아주 성공적인 모델 중 하나이고 시간 t 를 기반으로 하고 있음.
- 사실 이러한 RNN 이 Turing-Complete 하다는 사실이 이미 알려져있음. (Siegelmann & Sontag, 1995)
- 따라서 튜링 머신으로 $RNN$ 을 흉내낼 수 있다.
뉴런 튜링 머신이 기존 튜링 머신과 다른 점은 $GD$ (gradient descent) 를 사용하여 학습이 가능하다는 점이다.
앞으로 뉴럴 튜링 머신 (Neural Turing Machine) 을 줄여 $NTM$ 이라 표기하도록 하자.
RNN
- $HMM$ 과 비슷하게 Sequence 모델이지만 $HMM$ 보다 더 크기가 충분한 메모리 및 연산량을 가짐.
- 그리고 최근에는 $LSTM$ 이 좋은 성능을 내고 있음. (Hochreiter & Schmidhuber, 1997)
- 문제는 vainshing & exploding 문제를 가지고 있다는 것.
  - 그래서 긴 Sequence 를 가지는 문제를 잘 해결하지는 못한다.
- 여기서 이러한 이야기를 하는 이유는 $NTM$ 이 이러한 문제를 더 잘 해결하고 있기 때문.

NTM (a.k.a Neural Turing Machine)

$NTM$ 은 2개의 컴포넌트를 가지고 있음. : 컨트롤러(controller) 와 메모리 (memory)
컨트롤러는 입력, 출력 버퍼(벡터)를 통해 메모리와 통신을 한다.
- $NTM$ 은 기본 튜링 머신과는 다르게 입출력 연산을 통해 직접 메모리에 접근할 수도 있다.
- 그리고 이때 사용되는 연산의 내부 파라미터(weights)를 헤드 (head)로 취급하게 된다.
모든 컴포넌트들은 미분 가능한 함수로 구성된다.
- 그래야 $GD$ 를 사용할 수 있다.
- 그리고 “blurry” 라고 정의한 (어떤 영국 밴드가 떠오른다) 읽기, 쓰기 기능으로 메모리와 반응하는 범위를 만들어 낼 수 있다.
  - 보통 일반적인 튜링 머신에서는 주소 찾기 (addressing) 과정으로 이를 처리하게 된다.
전체적인 도식은 다음과 같다.

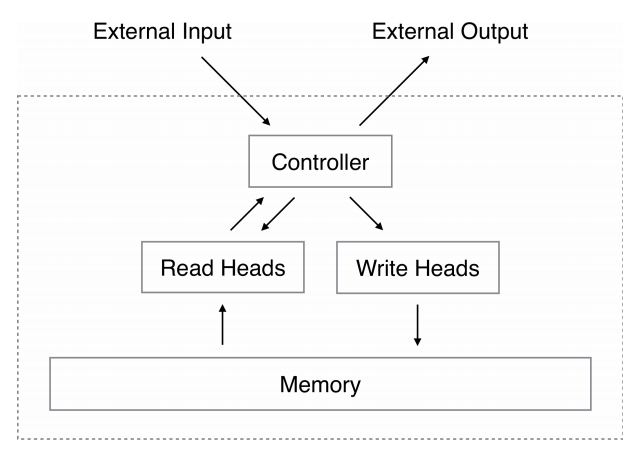
figure.4

그리고 이 때의 controller 는 신경망으로 구성된다.
이제 구성 요소들을 하나씩 살펴보도록 하자.

Memory

메모리는 그냥 우리가 알고 있는 메모리와 개념이 같다.
- 하지만 좀 더 간단하게 Matrix 로 표현됨.
기본 구조는 다음과 같다.

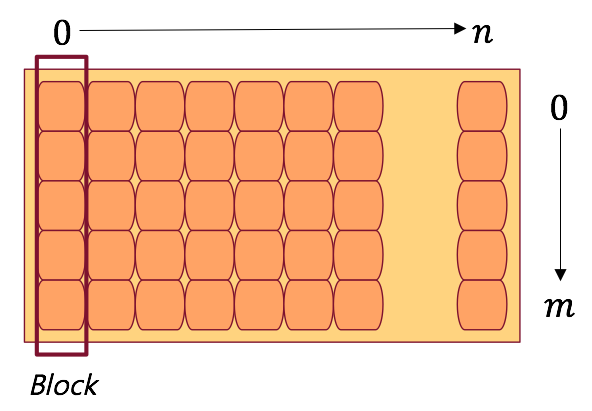
figure.5

한 메모리 내에 의미있는 정보는 블록 (Block) 단위로 나누어진다.
현재 메모리 크기는 n 이고 블록 크기는 m 으로 정의한다.
- 읽고 쓰는 메모리 단위는 Block 단위가 된다.

Reading

이제 메모리 읽기 연산 read 를 정의한다.
보통의 경우라면 헤더에 메모리 주소를 저장한 뒤 데이터를 바로 읽어내는 과정으로 작성되겠지만 $NTM$ 은 (당연히) 다르다.
시간 t 일 때 어떤 정보들을 담고있는 상태의 메모리를 Mt 라고 정의힌다.
- 이 메모리의 크기는 $N \times M$ 으로 정의된다.
이제 weight 벡터 ${\bf w}_t$ 를 추가한다. 이는 시간 $t$ 일때 읽어야할 메모리 주소 헤더를 반환해주는 벡터가 된다.
이 때의 ${\bf w}_t$ 는 다음의 조건을 가진다. (이 때 $i$ 는 메모리 row 인덱스를 의미하게 된다.)

$\sum_i w_t(i) = 1,\;0 \le w_t(i) \le 1,\;\forall i\qquad{(1)}$

블록 크기가 $M$ 인 메모리로부터 실제 읽은 정보를 담는 벡터를 ${\bf r}$ 벡터로 정의한다.
이 벡터는 인덱스 $i$ 위치의 메모리 블럭 $M_t(i)$ 와 convex 결합으로 구성되는 크기 $M$ 의 벡터로 정의된다.
${\bf r}_t \leftarrow \sum_{i} w_t(i)M_t(i)\qquad{(2)}$
말로 설명하면 어려운데 그림으로 보면 좀 쉽다.

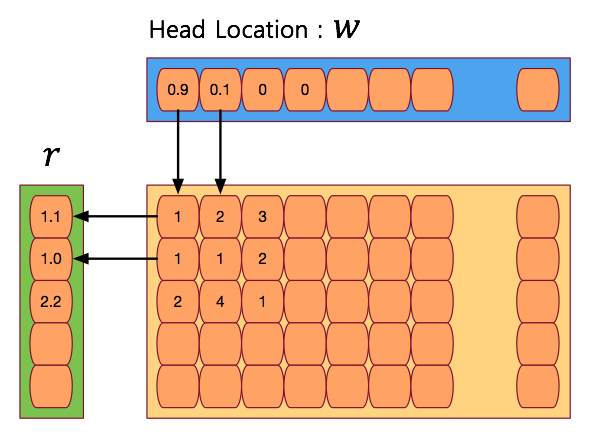
figure.6

그림을 보면 알 수 있듯 $w_t(i)$ 값이 높은 메모리 블록의 정보들을 많이 반영하여 얻어진 값을 최종 값으로 사용한다.

Writing

LSTM 으로부터 얻은 영감을 write 연산에 적용해본다.
- 즉, 쓰기 작업을 erase 와 add, 두 개의 작업으로 분리하여 생각할 것이다.
시간 $t$ 에 write 용 헤드가 출력하는 weight 를 ${\bf w}_t$ 라 하자.
그리고 이 때 삭제를 위해 사용되는 erase 벡터 et 도 정의한다.
- 이 벡터의 값은 $0$ ~ $1$ 사이의 값만 넣을 수 있다. (실수값이다.)
현재 time step 의 바로 전 step 의 메모리 상태를 $M_{t-1}$ 라 한다면 삭제 연산을 다음과 같이 정의한다.

$\tilde{M}_t(i) \leftarrow M_{t-1}(i)\left[1 - w_t(i) {\bf e}_t\right]\qquad{(3)}$

만약 erase 벡터 ${\bf e}$ 가 모두 $1$ 을 가진다면 결국 $w$ 값 중 큰 값을 가진 메모리가 0에 가까운 값을 가지게 된다. (삭제 효과)
역시나 말로 하면 이해가 잘 안되므로 그림으로 살펴보자.
- 최종 결과는 메모리에 저장됨을 확인하자.

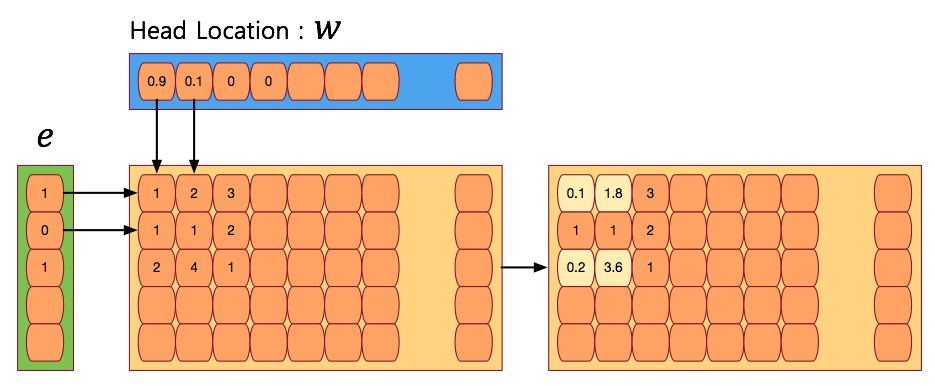
figure.7

이제 add 연산을 보도록 하자.
- 당연히 삭제와 비슷하게 add 용 벡터 ${\bf a}$ 가 추가된다.

$M_t(i) \leftarrow \tilde{M}_t(i) + w_t(i){\bf a}_t\qquad{(4)}$

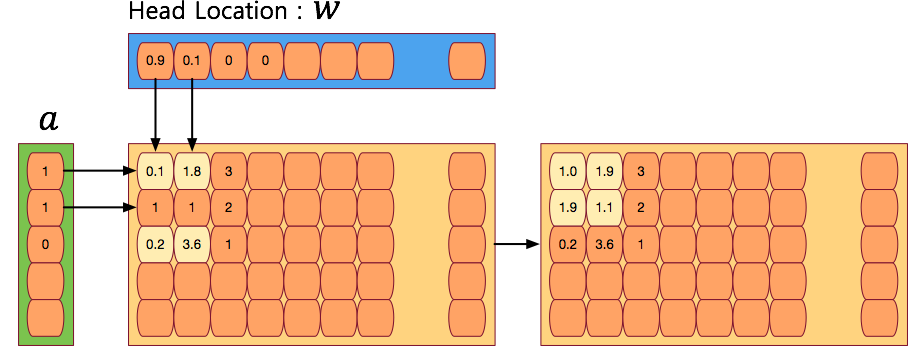
figure.8

Addressing Mechanisms

지금까지 메모리에 데이터를 읽고 쓰는 방법을 살펴보았다.
이제부터는 어떻게 주소를 지정할 수 있는지를 살펴 볼 것이다.
- 주소를 지정하기 위해 필요한 것은 무엇인가?
- 앞서 살펴본 읽기, 쓰기 작업에서 힌트가 나오기는 했는데 실제 주소를 접근하는데 사용되는 요소는 바로 벡터 ${\bf w}$ 이다.
- 즉, ${\bf w}$ 의 값을 변화시켜 주소를 지정하게 된다.
이를 어떻게 지정할지를 알아봐야 하는데 메모리 접근 방식과 마찬가지로 아주 일반화된 형태로 w 값을 만들어낼 수 있는 방법을 제안한다.
- 힌트를 주자면 이후 목적에 맞게 이러한 ${\bf w}$ 값을 학습하게 될 것이다.
w 의 값을 정하는 방법에는 두 가지 관점이 포함되어 있다.
- content-based addressing
- location-based addressing
content-based addressing
- 이 방식은 신경망에서 Hopfield 가 제안한 방식(1982년)이다.
- 이 방식은 매우 간단한 방식으로 동작한다.
- 우리가 찾고자 하는 값의 위치를 아주 간단한 방법들 통해 대락적인 근사 값으로 반환해준다.
- 하지만 모든 주소 지정 방식을 content-based addressing 로 풀 수 있는 것은 아니다.
location-based addressing
- 앞서 설명을 했듯 모든 주소 지정 방식을 content-based addressing 로만 해결할 수 있는 것은 아니다.
- 예를 들어 수치 연산과 관련된 문제들을 살펴보자.
- 두개의 변수 $x$ 와 $y$ 가 있다고 하고 연산 $f(x, y)=x \times y$ 를 정의한다.
- controller 가 이 연산을 수행하고자 하면 두 개의 변수 값을 메모리에 읽어와 결과를 반드시 어느 메모리 공간에 기록해야 한다.
  - 실수 값의 영역은 매우 크고, 실제 결과 또한 결정적인 수치 값이므로 content-based addressing 방식으로는 처리가 어렵다.
- 사실 이러한 방식은 내재된 content 를 사용하는 작업이 아닌 메모리 저장 위치인 location 에 제약을 가지는 작업이기 때문이다.
결론적으로 보면 content-based addressing 는 location-based addressing 보다는 좀 더 일반화된 주소 지정 방식이라 이야기할 수 있다.
- 왜냐하면 content-based addressing 내에 location-based addressing 방식을 포함시킬 수 있기 때문이다. (반대는 불가능하다.)
- 우리는 이러한 방식을 채택하여 location-based addressing 도 가능한 content-based addressing 방식을 사용할 것이다.

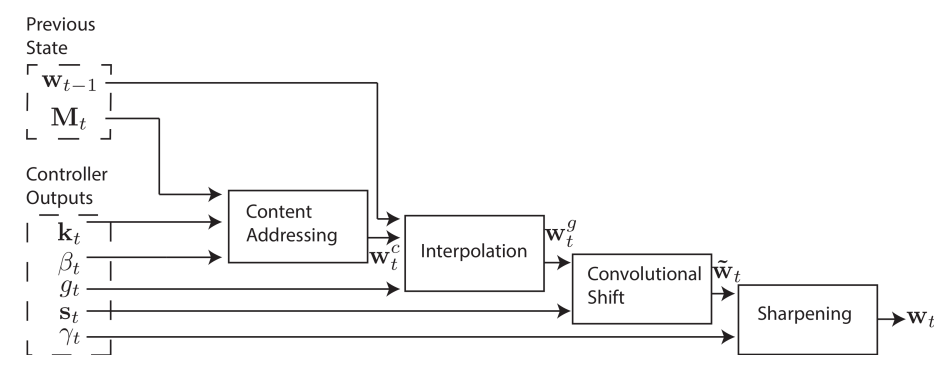
figure.9

위의 그림은 NTM 한 step에서 다음 step으로 전환시 찾아 갈 주소 값을 만들 수 있는 식을 도식화한 그림이다.
- 결국 이전의 메모리 $M_{t-1}$ 와 ${\bf w_{t-1}}$ 를 이용하여 위의 특정 연산들을 수행하면 다음 주소를 얻을 수 있도록 하기 위한 ${\bf w}_t$ 를 만들 수 있다는 이야기.
- 특정 연산들이 바로 content 와 location 주소 지정 방식을 가능케 하는 열쇠.
- 당연히 연산 사이에 들어간 weight 들은 이후 입력 데이터를 통해 학습하게 될 파라미터가 된다.
- 막연히 생각해보자면 $RNN$ 과 동일한 작업을 하게 될 것인데 $RNN$ 에서는 과거의 정보를 hidden 레이어로 넘겼다면 $NTM$ 에서는 메모리에 저장을 하게 될거란 이야기.
- 게다가 정확한 값을 기억하는 것이 아니라 신경망의 특성을 이용하여 embedding 된 정보로 저장을 하게 될 것이다.
- 이제 주소 지정을 위한 각각의 연산들이 무엇을 의미하는지 살펴보도록 하자.

Focusing by Content

content 주소 지정 방식을 먼저 설명한다.
- 앞서 간단히 개념을 언급하긴 했지만 centent 주소 지정 방식이란 어떤 입력 값을 넣어 그 값을 저장하고 있는 주소 값을 반환하는 작업을 의미한다.
- 물론 이를 통해 얻어지는 주소 값을 이용해 실제로 값을 메모리에서 읽어오면 이 값은 원래 입력 값과 정확히 일치하는 값이 아니라 근사값을 얻게 된다.
  - 이게 바로 content-based addressing 를 의미하는 것이다.
- 신경망에서 auto-encoder 같은 걸 떠올리면 좀 더 쉽게 이해가 될 것이다.
- 이를 어떻게 구현할 수 있는지 식을 살펴보자.

$w_t^c(i) \leftarrow \frac{\exp\left( \beta_{t} K\left[ {\bf k}_t, M_t(i) \right] \right)}{ \sum_j \exp\left( \beta_{t} K\left[ {\bf k}_t, M_t(j) \right] \right)}\qquad{(5)}$

$K[{\bf u}, {\bf v}] = \frac{ {\bf u} \cdot {\bf v} }{ \|{\bf u}\| \cdot \|{\bf v}\| }\qquad{(6)}$

식만 봐도 그냥 softmax 임을 알 수 있다.
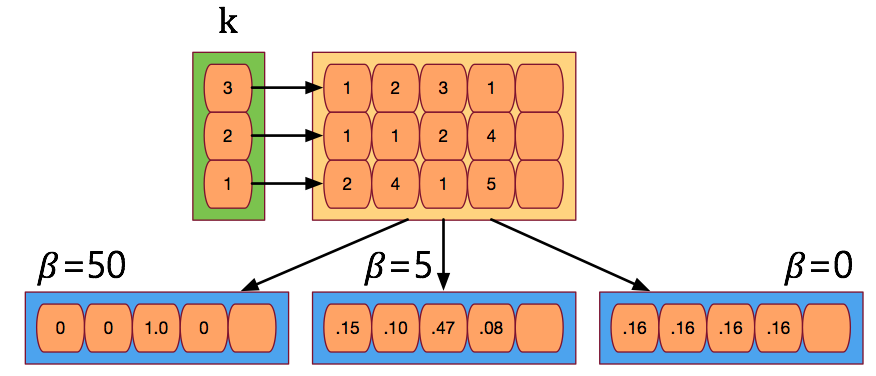
먼저 길이가 $M$ 인 키(key) 벡터 $k_t$ 가 주어지면 이를 유사도 측정 함수인 $K$ 함수에 대입하여 $w_t^c$ 를 구하게 된다.
유사도 함수 $K$ 는 그냥 코사인(cosine) 유사도 함수이다.
결국 의미하는 바는 키(key) 벡터 $k_t$ 를 메모리와 비교하여 코사인 유사도가 높은 위치에 높은 확률 값을 부여하는 형태.
이 때 추가적으로 $\beta_t$ 를 사용하는데 이 값을 적절히 조절하면 확률 강도(퍼짐 정도)를 조절할 수 있다.

figure.10

Focusing by Location

앞서 이야기한대로 어떤 작업의 경우 단순히 location 방식의 주소 지정 방식으로 처리를 해야할 경우가 있다.
그리고 메모리 위치에 접근하는 작업은 반복적으로 접근하는 방법과 랜덤한 접근 둘 다 가능하도록 구현되어야 한다.
일단은 현재 접근하는 메모리 위치에서 1만큼 오른쪽으로 (혹은 왼쪽으로) 이동한다던가 하는 작업을 할 수 있어야 한다.
하지만 이미 우리는 앞 단계에서 content 정보로 주소 지정을 하는 기능을 사용하고 있다.
- 따라서 location 을 위한 주소 지정 방식을 사용하기 위해서는 content 와 location 을 선택할 수 있는 방법이 필요하다.
다음과 같은 과정을 추가하여 두 과정을 적절히 선택할 있도록 한다.

${\bf w}_t^g \leftarrow g_t{\bf w}_t^{c} + (1-g_t){\bf w}_{t-1}\qquad{(7)}$

여기서 gt 는 게이트를 의미한다. 게이트는 0 ~ 1 사이의 실수 값을 가진다.
- ${\bf w}_t^c$ 는 이전 content 연산을 통해 얻어진 주소 값이다.
- ${\bf w}_{t-1}$ 는 이전 step 의 ${\bf w}$ 값을 의미한다.
만약 게이트 gt=0 인 경우에는 앞서 사용한 content 정보를 전혀 사용할 수 없게 된다.
- 따라서 $g_t=0$ 인 경우 이전 step 에 사용되었던 주소 값이 그대로 전달되게 된다.
반대로 게이트 $g_t=1$ 인 경우에는 content 를 위한 주소 정보만 사용되고 이전에 담겨 있던 값은 의미가 없어진다.
이 과정을 interpolation 이라 한다.
- $\{0,1\}$ 값 중에 하나를 선택하는 것이 아니라 실수 값을 선택한다.
- 그런 이유로 interpolation 이라는 용어가 사용된다. 따라서 이 둘의 결과를 섞을 수도 있다.
- $LSTM$ 에서 사용되던 게이트들을 생각해보자.

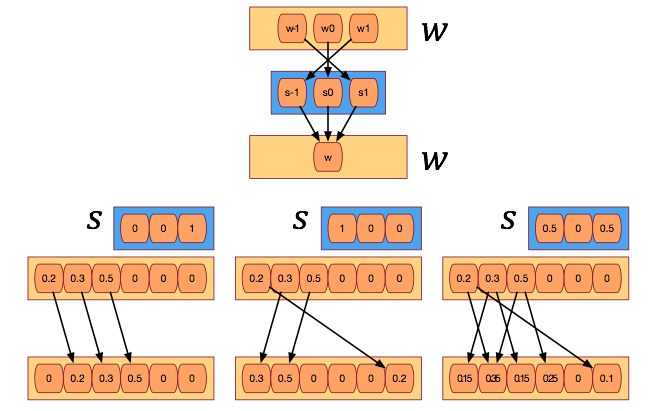
이제 shift weighting 을 살펴보도록 하자.
이 작업은 주소 값을 좌 혹은 우로 이동을 할 수 있는 연산이다.
이를 위한 변수로 st 를 제공한다.
- ${\bf s}_t$ 는 시작과 끝 값을 가지는 벡터로 구성되며 현재 위치에 대한 상대 인덱스가 저장된다.
- 그리고 그 크기는 그 사이의 정수 개수만큼 된다.
- 예를 들어 시작 값이 $-1$ 이고 끝 값이 $1$ 인 경우 $\{-1, 0, 1\}$ 인 요소들을 가지게 된다.
실제 값을 만들어내는 가장 쉬운 방법은 softmax 를 사용하는 것이다.
- 사실 다른 방법도 실험을 해보긴 했다. 예를 들어 특정 실수 값을 출력하여 이를 이용하여 st 값을 만들어봤다.
  - 예를 들어 controller 가 예측한 이동 값이 $6.7$ 이라면 $s_t(6) = 0.3$ , $s_t(7)=0.7$ 로 하고 나머지 값은 모두 0으로 등.

$\tilde{w}_t(i) \leftarrow \sum_{j=0}^{N-1}w_t^g(j)s_t(i-j) \qquad{(8)}$

그림을 보면 쉽게 이해할 수 있다.

figure.11

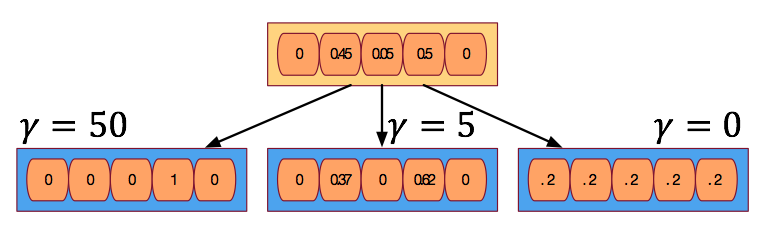
식(8) 을 통하게 되면 약간 문제가 있는데 확률적인 비율로 값이 분배되는 효과가 있기 때문에 특정 주소를 딱 집어야 하는 경우에는 좀 맞지 않을 수 있다.
이를 보정하기 위해 sharping 과정을 추가한다.
- 확률이 더 높은 위치의 값을 boosting하는 효과를 가진다.
- 물론 값을 어떻게 조정하느냐에 따라 값을 더 뭉갤수도 있다.

$w_t(i) \leftarrow \frac{\tilde{w}_t(i)^{\gamma_t}}{\sum_j \tilde{w}_t(j)^{\gamma_t}}\qquad{(9)}$

figure.12

Controller Network

지금까지 여러 파라미터 값들을 제어하여 $NTM$ 을 동작하는 것을 확인했다.
위의 작업들을 조합하면 메모리 읽기, 쓰기, 주소 지정 동작을 수행할 수 있다.
$LSTM$ 의 경우 모델 내에 메모리를 유지하면서 동작을 하게 되는데 동일하지만 $NTM$ 을 이용하면 외부에 메모리를 두는 형태로 구현이 가능하다.
실험을 통해 $RNN$ 으로 작업했던 일들을 $NTM$ 으로 동작해보고 더 좋은 성능을 얻을 수 있음을 확인해보도록 하겠다.

Experiment

여기서는 아주 기본적인 작업에 대한 실험만을 진행해 볼 것이다.
- 데이터를 복사하는 작업
- 데이터를 정렬하는 작업
모든 실험에는 다음 세 가지 모델을 사용한다.
- feedforward 방식을 사용하는 $NTM$ controller
- $LSTM$ 을 사용하는 $NTM$ controller
- 그냥 $LSTM$

Copy

여기서는 아주 긴 시퀀스를 가지는 데이터 구조를 복사하는 실험을 할 것이다.
사실 이런 문제는 $RNN$ 에서 많이 다루어졌다.
실험 환경
- 입력값은 랜덤한 이진 벡터의 시퀀스이다. (8bit)
- 길이는 랜덤하게 $1$ ~ $20$ 사이의 값을 가진다.
- 시퀀스의 마지막 입력은 구분자(delimiter)를 사용.

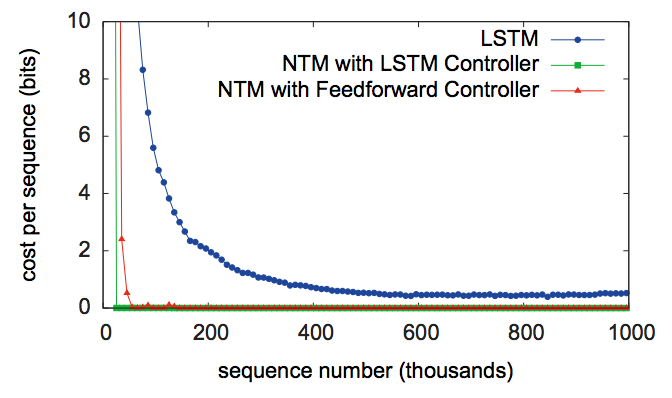
figure.13

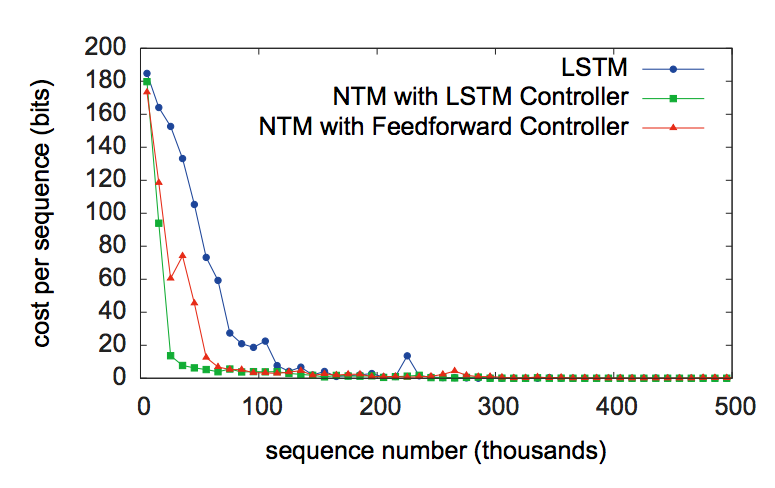
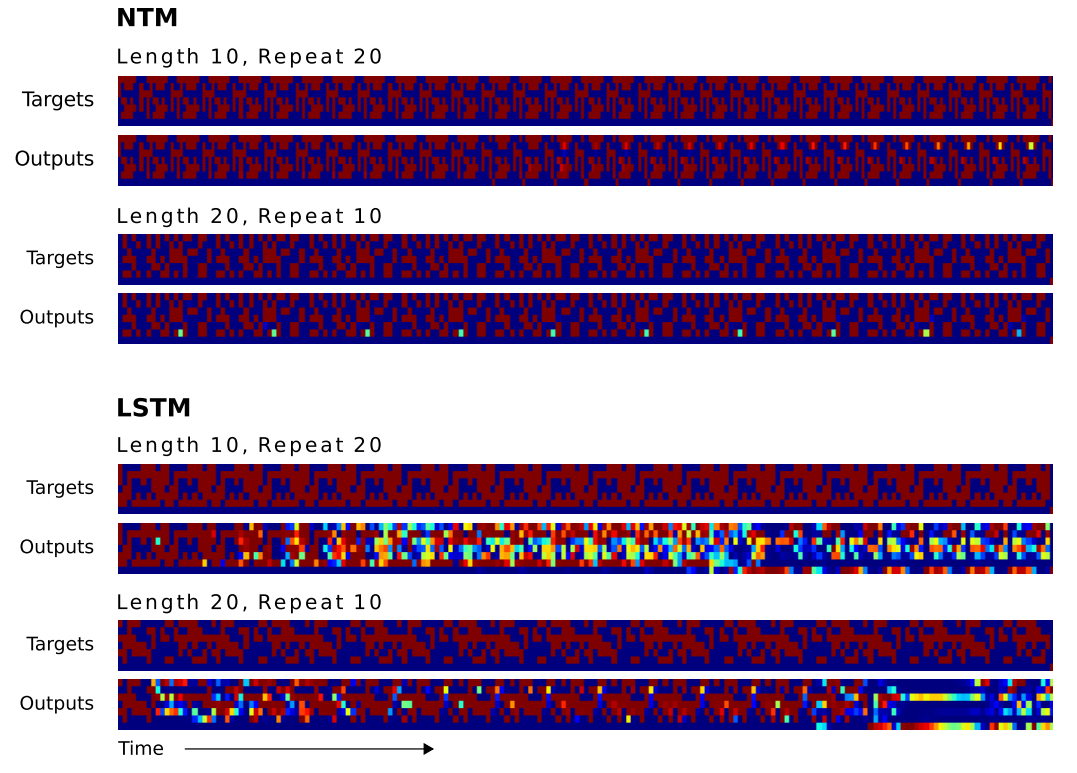
위의 그림은 $NTM$ 이 $LSTM$ 을 단독으로 사용하는 것보다 훨씬 빠르다는 것을 보여주는 지표이다.
시퀀스 길이를 늘려가면서 단위 시퀀스당 비용을 보여준다. (근데 cost의 의미를 모르겠다. 시간인가?)
게다가 더 긴 시퀀스에 대해서도 $NTM$ 이 더 잘 학습한다는 것을 알 수 있었다.
NTM 은 LSTM 과 다르게 완전하게 복사하는 알고리즘을 학습하고 있다는 사실을 알 수 있다.
- 이를 확인하기 위해서 우리는 학습된 상태에서 controller 와 memory 사이의 작업 과정을 분석하였다.
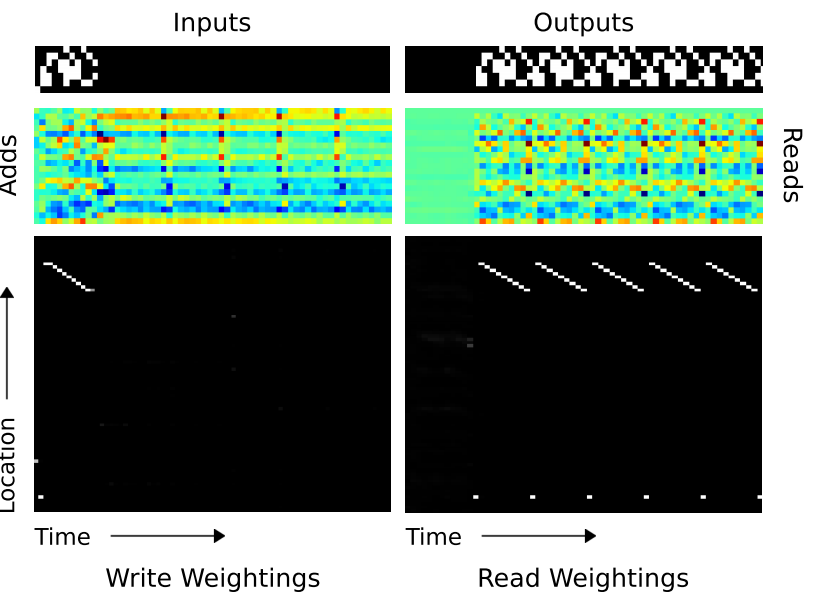
- 대충 아래와 같은 방식으로 돌아가게 된다.

초기화 : 헤드를 시작 위치로 옮긴다.

while 구분자(delimeter)가 아닐때 까지 반복 do
  입력 벡터를 받음
  입력 벡터를 헤더 위치에 기록
  헤더의 위치를 1만큼 증가
end while

헤더 위치를 다시 맨 처음 시작 위치로 이동

while true do
  헤더 위치로부터 출력할 벡터를 읽음
  읽은 백터를 외부로 방출(emit)
  헤더의 위치를 1만ㅊ큼 증가
end while

실험 결과를 살펴보자.

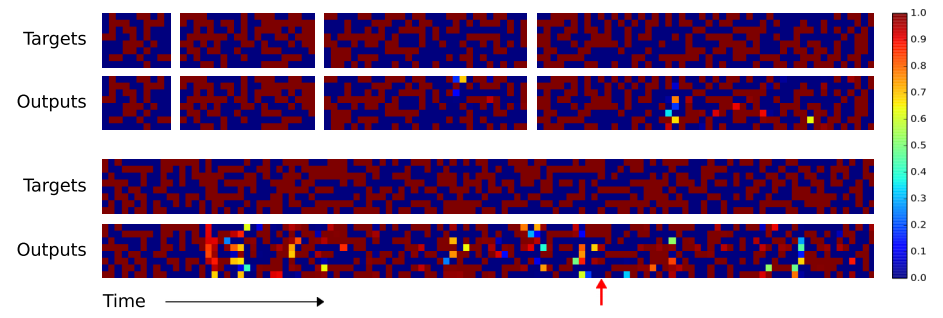
figure.14

먼저 상단의 4개의 상자는 입력 길이가 각각 10, 20, 30, 50 인 시퀀스를 넣는 것을 의미한다. 바로 아래는 120 길이의 입력을 의미한다.
색상은 출력 값을 나타낸다. (1이면 붉은색, 0이면 파란색이고 그 사이의 값은 색상 스펙트럼으로 표현한다.)
길이가 20일 때까지는 100% 정확하게 동작한다. 50일 때까지도 꽤나 정확하게 동작한다는 것을 알 수 있다.
참고로 $LSTM$ 의 결과는 어떤지 확인해보자.

figure.15

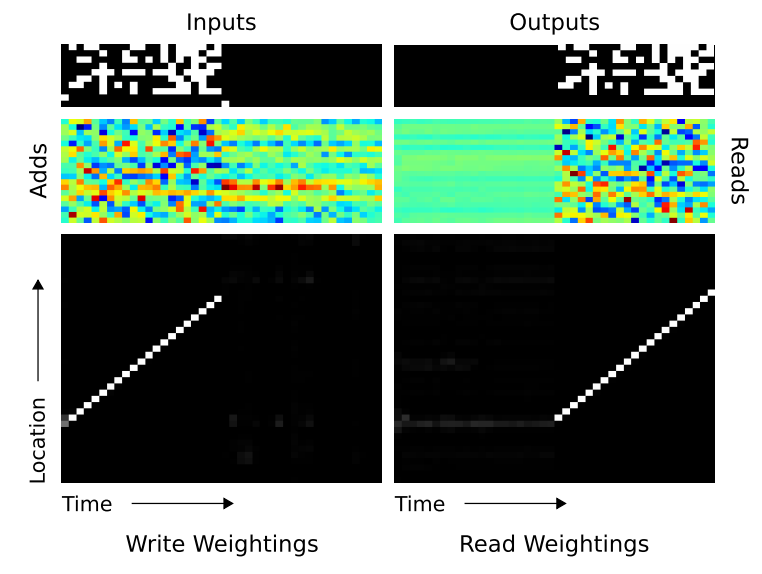
NTM 이 복사 작업을 진행할 때의 add 메모리 값과 위치를 위한 wt 벡터 값을 보도록 하자.
- $w_t$ 의 경우 $1$ 이 하얀색, $0$ 이 검은색으로 중간은 회색의 스케일을 가지게 된다.

figure.16

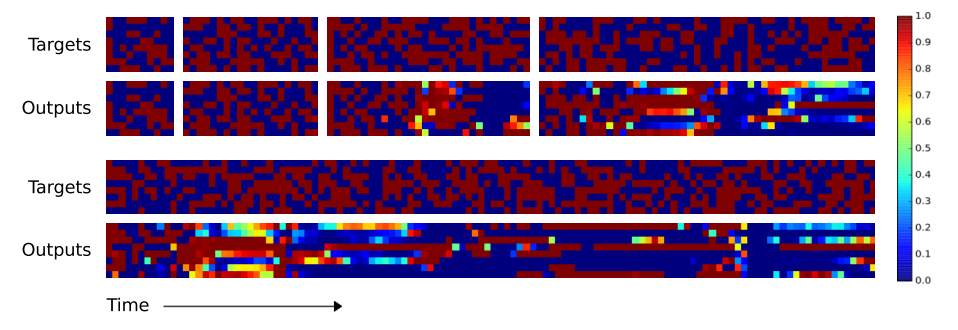
Repeat Copy

반복 복사는 그냥 복사 기능을 확장한 것이다.
추가적인 기능으로 입력이 종료되는 시점부터 실제 복사가 발생되도록 구현한다. 그것도 원하는 만큼 $n$ 회 반복 할 수 있다.
이를 통해 $NTM$ 이 for loop 기능을 수행할 수 있는지를 알수 있다.
입력은 임의의 크기의 이진 시퀀스 데이터를 입력한 뒤 반복할 숫자를 입력한다.
- 이 때 입력할 숫자값은 이진 시퀀스 데이터와 같은 채널을 사용하지 않고 다른 채널을 사용하게 된다.
복사(Copy)와 마찬가지로 성능을 좀 보자.

figure.17

실제 결과도 눈으로 보는게 가장 빠르다.

figure.18

figure.19

Associative Recall

앞에서 살펴본 알고리즘은 무척이나 간단한 알고리즘이다.
이제 좀 더 복잡한 문제들을 다루어보도록 하자.
진행
- 입력은 delimeter 를 이용하여 두 개의 데이터를 입력하게 된다. (두개의 delim 등장마다 하나의 요청 단위가 된다.)
- 입력은 6 bit 크기의 이진 데이터 3개를 하나의 묶음으로 하여 다른 sub delimeter 로 여러 개를 입력한다.
  - 데이터가 6 bit 인 것은 실제로는 8 bit 데이터인데 2개를 delimeter 로 사용하기 때문이다.
- 이 때 첫번째 delim 입력이 끝나고 두번째 데이터를 입력하고 나면, 최종 출력은 첫번째 입력 내에서 두번째와 매칭되는 시퀀스를 찾아 그 다음 시퀀스를 출력해주는 것이 목표.
- 그냥 그림으로 보는게 이해가 빠르다.

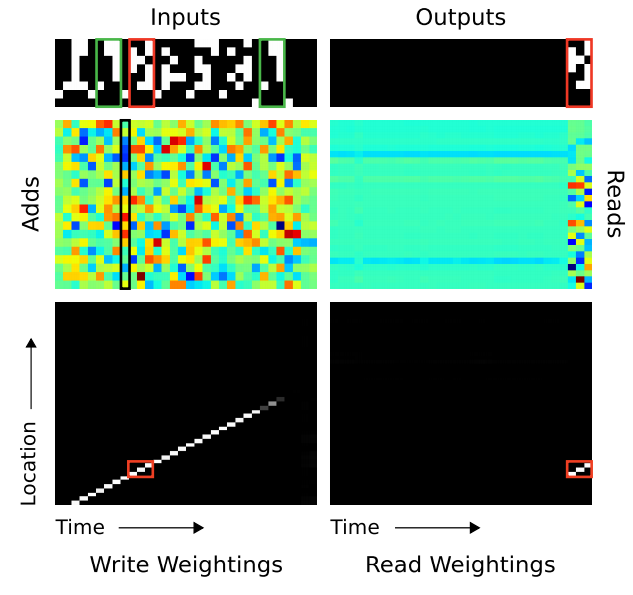
figure.20

그림을 보면 3 bit 입력 후 sub-delimeter 를 확인할 수 있다.
그리고 최종 출력된 결과를 보면 정확히 원하고자 하는 위치 이후의 3 bit 가 출력됨을 확인할 수 있다.

Dynamic N-Grams

n-gram 문제는 $NTM$ 이 예측 분포 문제를 얼마나 빨리 적응하는지를 확인하는 예제이다.
말은 화려한데 그냥 어떤 분포를 통해 생성된 데이터들의 패턴을 파악하여 다음 값을 에측하는 문제이다.
굳이 n-gram 이란 용어를 쓴 이유는 이를 활용하면 전이 확률 정보를 메모리에 저장 하는 형태로 익히 알려진 N-gram 모델을 구현해 낼 수 있기 때문이다.
여기서는 이진 6-Gram 을 사용한다. 이 말은 앞의 5-bit 를 확인한 뒤 현재 bit 를 예측한다는 의미이다.
- 이 때의 확률 값을 다음과 같이 정의한다.

$P(B=1\|N_1, N_0, c) = \frac{N_1+\frac{1}{2}}{N_1+N_0+1}\qquad{(10)}$

여기서 $c$ 는 윈도우 크기로 현재 $6$ 으로 설정되어 있다. (앞서 5개의 bit를 살펴봄)
$N_0$ 는 $c$ 이내의 bit 중 $0$ bit 인 경우를 의미하고, $N_1$ 은 $1$ bit 를 의미한다.

figure.21

Priority Sort

마지막으로 정렬 알고리즘을 살펴본다.
랜덤하게 이진 데이터 벡터를 입력받아 이를 정렬한다. 이 때의 우선 순위는 균등하게 생성된다.
20개의 이진 데이터를 입력받은 뒤 (이 때 priority 도 함께 받는다.) 이 중 priority가 높은 순으로 16개의 이진 벡터를 출력한다.
- 크기를 16으로 제한한 이유는 $NTM$ 이 깊이(depth) `4의 이진 힙소트 문제 처리가 가능한지를 확인하기 위해 사용되었기 때문이다.

figure.22

figure.23

뭐 결과는 이렇다는데 자세한 내용이 없어서 생략하도록 하자.

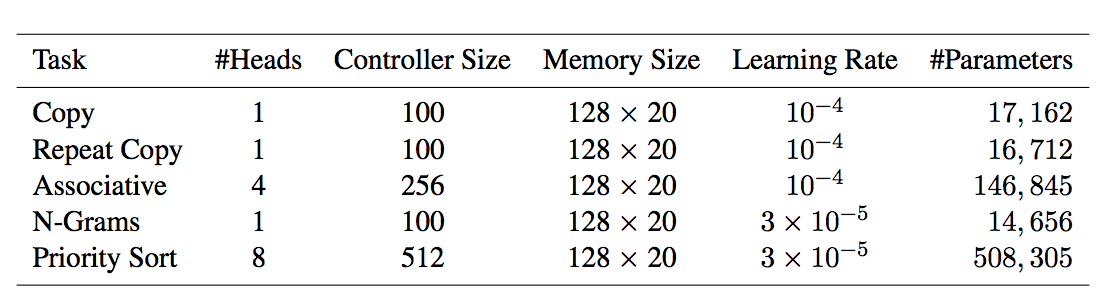
Experimental Settings

$NTM$ with Feeadforward

figure.24

$NTM$ with $LSTM$

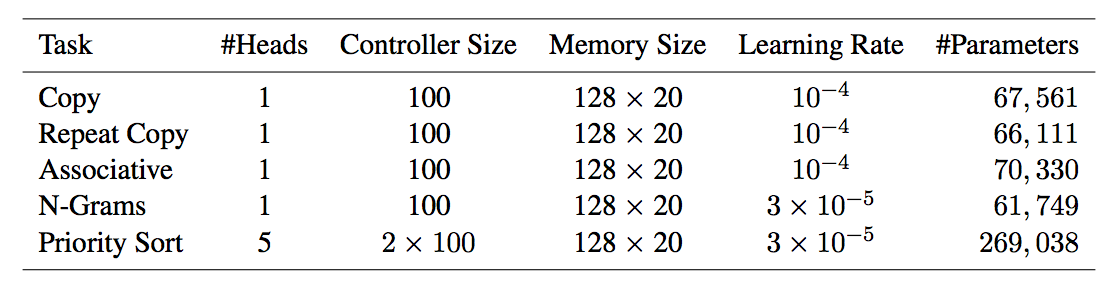
figure.25

$LSTM$

figure.26

Neural Turing Machine

https://arxiv.org/abs/1410.5401

튜링 머신 (Turing Machine)

튜링 머신의 이해

Turing Machine Example

Neural Turing Machine

Introduction

NTM (a.k.a Neural Turing Machine)

Memory

Reading

Writing

Addressing Mechanisms

Focusing by Content

Focusing by Location

Controller Network

Experiment

Copy

Repeat Copy

Associative Recall

Dynamic N-Grams

Priority Sort

Experimental Settings

참고자료