MultiGrain: a unified image embedding for classes and instances.

https://arxiv.org/pdf/1902.05509.pdf

Introduction

  • 이미지 인식(Image recognition)은 컴퓨터 비젼의 핵심이며 매년 새로운 기법들이 쏟아져 나오고 있다.
    • 하지만 대부분 인식 분야의 특정 영역에만 국한하여 문제를 해결한다.
  • 각 단계의 문제들을 예를 통해 알아보자. (좀 더 큰 단위에서 작은 단위의 순서로…)
    1. 어느 클래스에 속하는지를 찾는 문제 (intra-clas variation 에 상관 없이…)
    2. 보여지는 상태에 상관없이 인스턴스 단위로 특정 객체가 무엇인지를 찾아내는 문제
    3. 약간 수정된 이미지를 가지고 복사 여부를 확인하는 문제
  • 특화된 영역에서는 좋은 성능을 모델을 만들 수 있지만 몇몇 분야에서는 이게 어려울 수 있다.
  • 예를 들어 이미지 검색 (image retieval)등이 있다.
    • 최종 목표는 질의 이미지를 대규모 데이터베이스로부터 최적의 다른 이미지를 매칭하는 문제이다.
    • 어떤 경우 동일한 데이터베이스를 여러 입도(multi-granularites) 단위로 검색을 해야 할 수도 있다.
    • 왜냐하면 이미지 검색 시스템의 성능은 사용하는 이미지 임베딩(embedding)의 크기에 크게 영향받기 때문이다.
    • 결국 데이터베이스의 크기를 어떻게 가져갈 것인가에 대한 문제가 된다.
    • 동일 데이터베이스에 대해 여러 임베딩 데이터를 준비하게 되면 그만큼 리소스 비용 부담이 커지게 된다.
  • 이 논문에서는 이미지에 대한 새로운 표현(representation) 방식을 소개한다.
  • MultiGrain 이라 명명한 이 방식은 3가지 문제를 함께 처리한다.

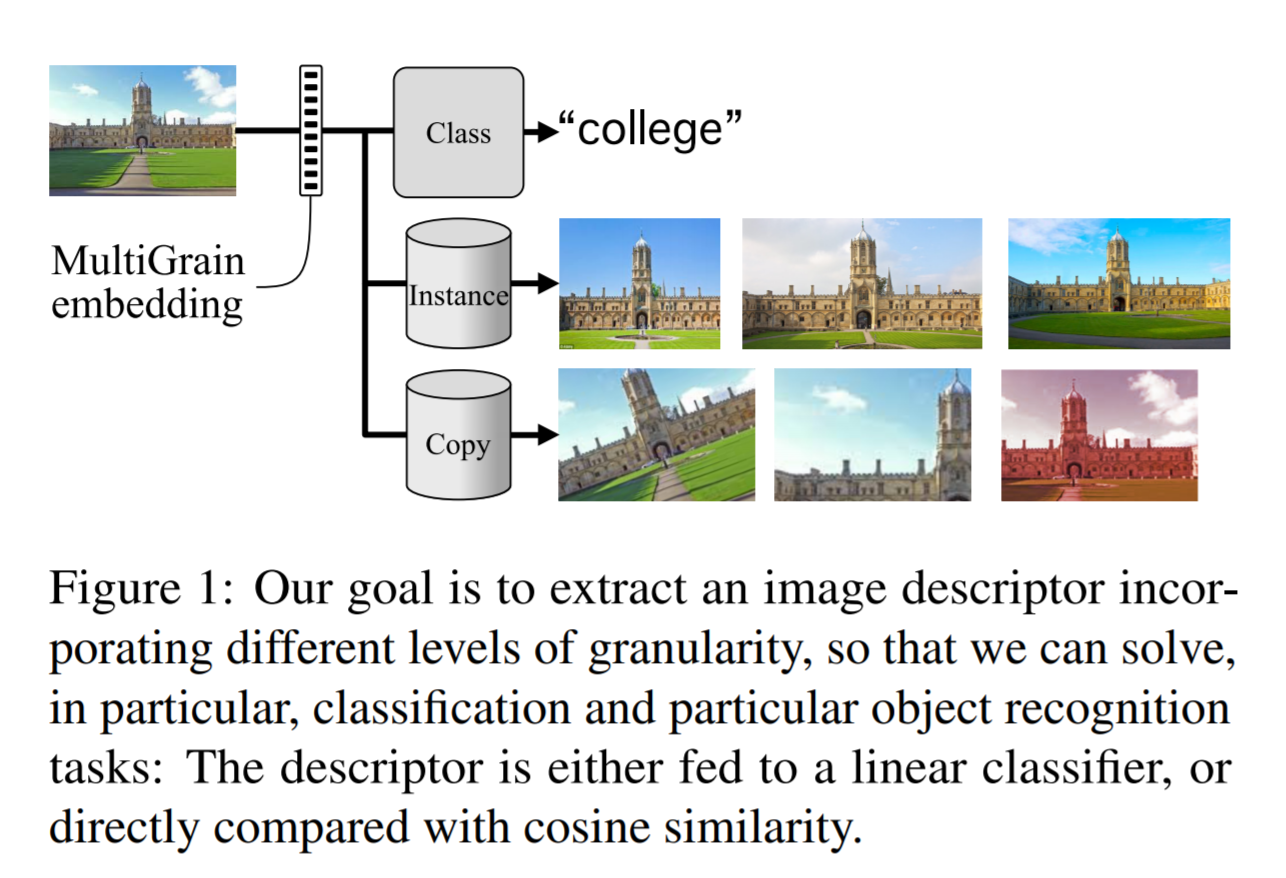
Figure.1

  • 여기에서는 3가지 태스크를 한번에 학습한다.
    • 입도 수준이 다른 3가지 태스크를 한번에 학습하여 좋은 성능을 낸다. (개별적으로 학습한 것보다 성능이 좋다.)
  • 인스턴스 단위의 이미지 검색은 다양한 형태로 실제 산업에서 사용된다.
    • (저작권이 있는) 복사된 이미지를 검출한다던지 처음 본 이미지를 인식한다던가 등
    • 대용량 이미지를 처리하는 경우 여러 문제를 다룰 수 있는 이미지 임베딩을 얻는 것이 중요하다.
      • 예를 들어 이미지 저장 플랫폼은 특정 분류를 수행하는 것 뿐만 아니라 동시에 복사본 여부 판별을 수행할 수도 있다.
      • 이러한 방법은 이미지를 저장하고 계산하는 실제 비용을 크게 감소시킬 수도 있다. (한번에 처리하니까)
  • 이 관점에서 본다면 분류만을 위한 CNN 모델은 범용성은 쌈싸먹은 Feature 추출기라 할 수 있다.
  • 분류 및 검색 둘다 잘 동작하는 임베딩을 학습할 수 있는 사실은 놀랍지만 서로 모순되는 것은 아니다.
    • 실제로 두 태스크 사이에는 논리적인 의존성이 존재한다.
    • 동일한 인스턴스를 포함하는 이미지는 정의에 따라 동일한 클래스에 속하게 된다.
    • 또한 복사된 이미지는 동일한 인스턴스를 가지고 있다.
  • 일단 시작은 기존에 존재하는 분류용 CNN 네트워크를 활용한다. (자세한 내용은 뒤에서 보자)
  • 분류와 검색은 cross-entropy 와 contrastive loss 를 사용한다.
    • 중요한 것은 인스턴스 인식 부분은 별도의 instance 레이블을 가진 학습 데이터를 요구하지 않는다는 것이다.
  • 요약하자면,
    • 이 논문에서는 MultiGrain 구조를 설명한다. 이 모델은 서로 다른 입도를 가지는 태스크에 잘 동작하는 임베딩을 제공한다.
    • 좋은 배치(batch) 전략을 사용하여 성능 이득을 얻는 것을 확인한다.
    • 이미지 검색 기법에서 영감을 받은 pooling layer 기법을 활용하여 정확도를 올린다.
  • 간단하게 기술하고 넘어가자.
  • image classification
    • ImageNet-2012 버전의 강자는 AmoebaNet-B (557M param., 480x480 input)
    • 이 논문에서는 ResNet-50 사용 (26M)
  • image seaarch (from local feature to CNN)
    • 임베딩 유사도 문제로 문제를 해결한다.
    • 객체 검색을 위한 특별한 아키텍쳐
      • PCA-whitening
      • R-MAC image descriptor
  • data augmentation
    • RA (repeated augmentation)

Table.1

아키텍쳐

  • 일단 목표는 이미지 분류와 검색을 둘 잘 하는 모델을 만드는 것이다.

Spatial pooling operators

  • 여기서는 global spatial pooling layer 를 다룬다.
  • 보통의 경우 pooling 을 사용하면 max pooling 을 사용하게 된다.
  • 반면 global spatial pooling 은 3d tensor 에 적용되는 pooling 기법이다.
  • 분류
    • LeNet-5 나 AlexNet 에는 마지막 레이어에 spaital pooling 적용한다. 이는 위치 특성을 반영한다.
    • 하지만 ResNet, DenseNet 등은 average pooling 을 사용하고 있다.
  • 이미지 검색
    • 이미지 검색의 경우 지역적 정보를 요구한다.
    • 특정 객체가 비주얼 적으로 유사한 경우 유사도가 높아야 한다.
    • 따라서 pooling 사용시 지역적(local) 특성을 담을 수 있는 pooling 을 사용해야 ㅎ나다.
  • GeM (Generalized mean pooling)
    • 참고로 \(p \) 가 \(\infty\) 가 되면 max pooling
    • \(p\) 가 \(1\) 이 되면 avg. pooling
    • 여기서 \(p\) 는 학습이 되는 weight 또는 수동으로 지정 가능하다.
    • 분류에서는 avg. pooling 을 사용하고 검색에서는 근사 max pooling 을 사용한다. (R-MAC 등)
\[e = \left[\left(\frac{1}{|\Omega|}\sum_{u \in \Omega}{x^{p}_{cu}}\right)^{\frac{1}{p}}\right]_{c=1..C}\qquad{(1)}\]
  • 이 논문에서는 처음으로 분류 문제에서도 GeM 을 활용한다.

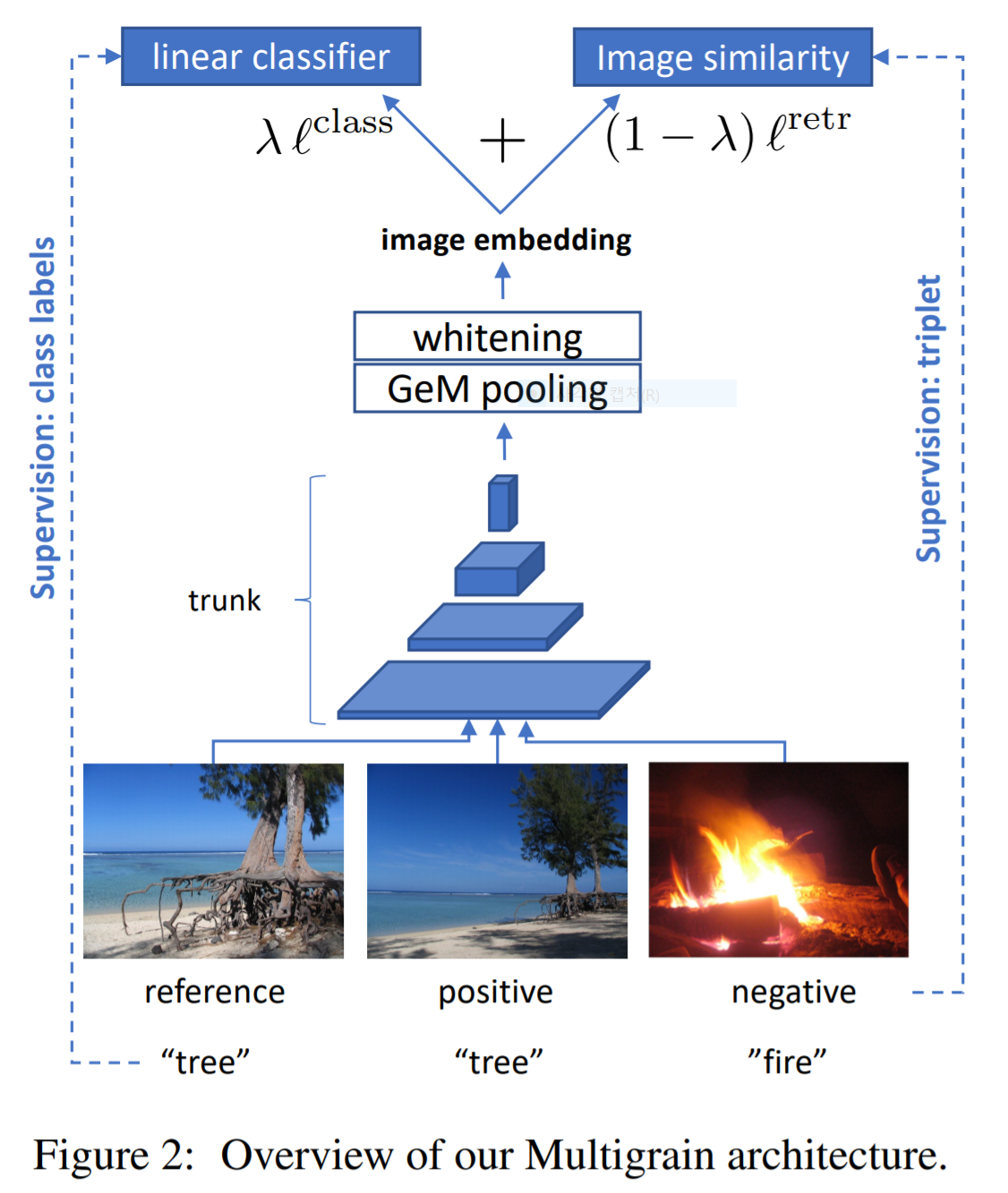
Figure.2

목적 함수

  • 검색과 분류를 결합하기 위해 각각의 목적 함수를 만들고 이를 결합하여 사용한다.

분류 Loss 함수

  • \({\bf e}_i \in R^d\) : 이미지 임베딩 벡터
  • \({\bf w}_c \in R^d\) : 클래스 \(c \in {1,…,C}\) 를 위한 선형 분류기 파라미터
  • \(y_i\) : GT
  • \({\bf W} = [{\bf w}_c]_{c=1..C}\) 를 간단하게 표기
\[L^{class}({\bf e}, {\bf W}, y_i) = -\langle{\bf w}_{y_i}, {\bf e}_i \rangle + \log{\sum_{c=1}^{C}{\exp\langle{\bf w}_c,{\bf e}_i\rangle}}\qquad{(2)}\]

검색용 Loss 함수

  • 이미지 검색에서는 두개의 매칭 이미지를 사용한다. (positive pair)
  • 이 경우 임베딩 값이 매칭되지 않은 이미지들보다 거리상으로 더 가까워야 한다.
  • contrastive loss 는 positive pair 간의 거리를 최소 threshold 보다 더 가깝게 놓아두는 방법을 사용한다.
  • 반면 triple loss 는 positive pair 를 negative pair 보다 더 가깝도록 구성한다.
  • triple loss 의 경우 데이터를 구성하기가 매우 어렵다.
  • 배치(batch) 단위의 이미지 처리를 하기 때문에 실제 구현이 까다롭다.
    • Wu 는 이런 어려움을 극복하고자 새로운 방법을 제안했다.
    • 주어진 배치 이미지들로부터 각 이미지의 임베딩을 단위 백터로 normalize 한 다음 margin loss 를 이용하여 거리 계산을 수행한다.
    • 이미지를 단위 구 (unit sphere) 공간에 사상하여 margin loss 를 만들어낸다.
\[L^{retr}({\bf e}_i, {\bf e}_j, \beta, y_{ij}) = \max\left\{0, \alpha+y_{ij}(D({\bf e}_i,{\bf e}_j)-\beta)\right\}\qquad{(3)}\]
  • 여기서 \(D\) 는 Euclidean 거리이다. (물론 이미 normalize 되어 있다.)
    • \(D({\bf e}_i,{\bf e}_j)=||\frac{e_i}{||e_i||} - \frac{e_j}{||e_j||} ||\)
    • \(y_{ij}\) 는 두 이미지가 매칭되는 경우 1, 아닌 경우 -1
    • \(\alpha\) 는 hyper parameter이고 \(\beta\) 는 parameter 이다.
  • 위에서 사용되는 loss 함수는 샘플링을 통해 얻어진 positive, negative 쌍의 subset 으로 계산된다.
\[\begin{align} &P_+(B)=\left\{ (i, j) \in B^2 : y_{ij}=1\right\}, \\ &P_-(B)=\left\{ (i, j^*) : (i, j) \in P_+(B), j^* ~ p(\cdot|i)\right\}, \\ &P(B) = P_+(B) \cup P_-(B) \end{align} \qquad{(4)}\]
  • 단 negative \(j\) 에 대한 확률 값은 다음과 같다.
\[p(j|i) \propto \min{(\tau, q^{-1}(D({\bf e}_i, {\bf e}_j)))\cdot 1_{y_{ij}=-1}},\;where\;\tau > 0\] \[q(z) \propto z^{d-2}(1-z^2/4)^{\frac{d-3}{2}}\]
  • 데이터가 shere 에 놓여있을 때 임의의 두 점 사이의 거리에 대한 확률 함수식이라 생각하면 된다.

  • 여기서 \(z\) 는 \(i\) 와 \(j\) 의 거리를 나타내는 변수이다. (물론 \(d\)는 demension을 의미한다.)

  • 위의 수식 표기가 정확하게 뭘 의미하는지 애매하다.
    • 느낌적 느낌으로는 positive 는 Batch 내 모든 동일 클래스 이미지를 뽑고,
    • negative는 positive 와 동일한 갯수로 weighted sampling 을 하여 추출한다.
      • Uniform 하게 뽑으면 구 공간 내에서는 특정 거리 (예를 들어 \(\sqrt{2}\)) 정도의 거리를 가지는 샘플이 많이 뽑히게 되므로 이를 보정하기 위해 분포를 고려한 샘플링을 수행한다.
    • Wu의 논문을 참고할 것

Joint loss and architecture

\[\frac{\lambda}{|B|}\cdot \sum{L^{class}({\bf e}_i, {\bf w}, y_i)} + \frac{1-\lambda}{|P(B)|}\cdot\sum_{(i,j) \in P(B)}{L^{retr}({\bf e}_i, {\bf e}_j, \beta, y_{ij})}\qquad{(5)}\]

Batching with repeated augmentation (RA)

  • 여기서는 이미지 분류를 위한 학습 데이터만을 사용하고 이미지 검색을 위한 학습 데이터를 구성하기 위해 augmentation 을 수행하는 방법을 다룬다.
  • 이 방법은 별도의 데이터 정제 작업을 추가하지 않는다.
  • 여기서는 SGD와 data augmentation을 이용하여 학습할 때 사용되는 샘플링 방식을 다룬다.
  • RA (repeated augmentations)
    • 이미지 배치 (\(B\)) 에서 \(\lceil |B|/m\rceil\) 만큼 샘플링을 한다.
    • 이 데이터를 \(m\) 번 변환하여 사용한다. (transform)
  • 결국 총 반복 횟수는 기본 epoch 에 \(m\) 배 늘어난 만큼 수행해야 한다.

PCA whitening

  • 학습 마지막 단에 PCA whitening 을 적용한다.
\[\Phi({\bf e}) = S\left(\frac{ {\bf e} }{\| {\bf e} \|} -{\bf \mu}\right)\] \[\langle {\bf w}_c, {\bf e}\rangle = \langle {\bf w}_c , \Phi^{-1}(\Phi({\bf e}))\rangle = \| {\bf e} \| ( \langle {\bf w}^{'}_c , \Phi ({\bf e})\rangle + b^{'}_c )\]

입력 크기

  • 분류의 경우 전통적인 방식의 \(224 \times 224\) 방식 사용
    • 물론 center crop 이 포함된 방식
  • 검색의 경우 800 이나 1024가 사용되기도 한다. (긴축 기준)
    • 그리고 center crop 같은 건 안 쓴다.
  • 여기서는 기본적인 \(224 \times 224\) 방식을 사용한다.
    • 큰 이미지는 test time 에서만 사용한다.
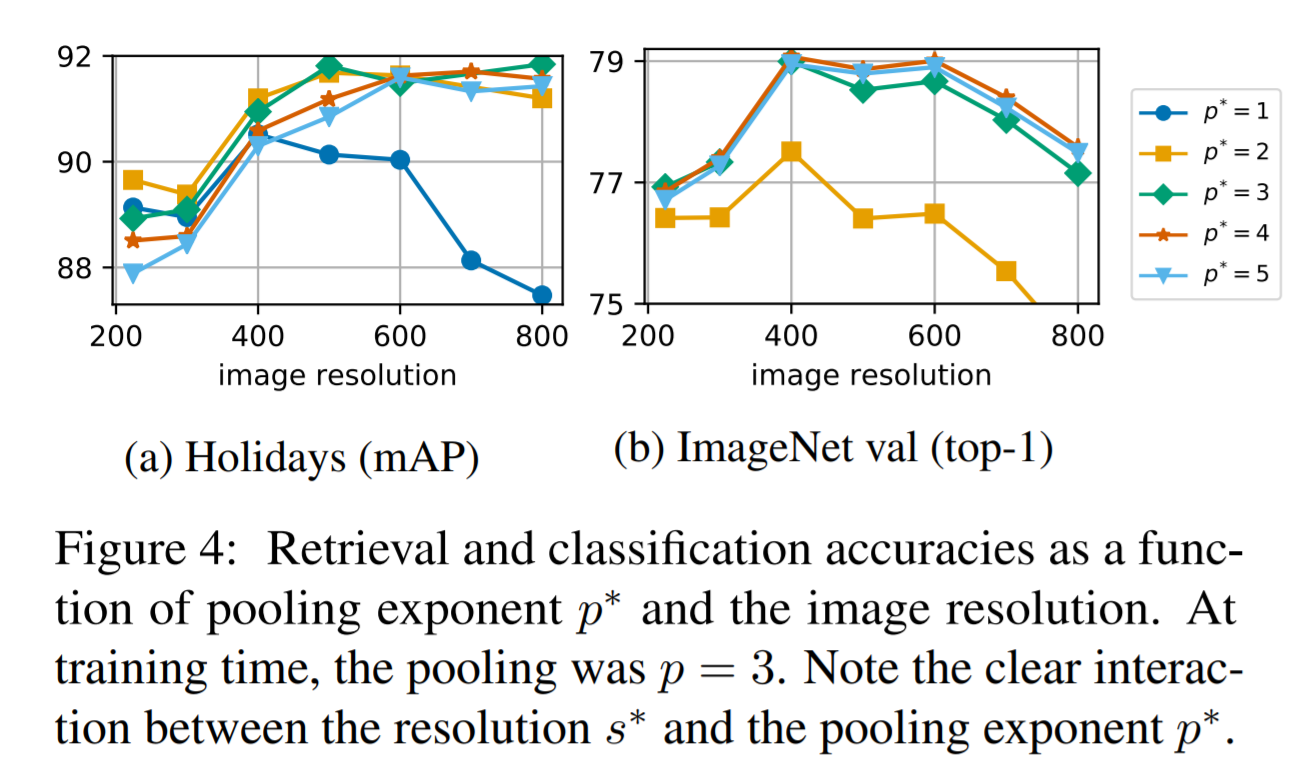
    • 대신 큰 이미지가 들어오면 사용되는 \(p\) 값 (GeM 내 pooling 의 \(p\) 값) 도 키운다.

Proxy task for cross-validation of p

  • 모든 태스크에 사용할만한 적당한 값 \(p\) 를 선정하기 위해 간단한 합성 데이터를 구성하여 실험한다.
    • 2000개의 이미지를 ImageNet 에서 선별 (각 클래스별 2개)
    • 각각에 대해 5개의 augment 이미지를 생성 후 실험

Etc.1

  • 최적의 \(p^*\)는 검색과 분류 모두 잘 되는 수준.

Figure.3

실험

  • 시간이 없는 관계로 (^^;) 대충 살펴보자.

실험 세팅

  • 기본 구조
    • ResNet-50
    • lr : 0.2 (30, 60, 90 마다 감소. 총 120 epoch)
    • 배치 크기 \(|B|=512\)
    • RA 는 \(m=3\)
    • 기타 논문 참고
  • Data augmentation
    • 표준 flip, random crop, random lighting noise, color jittering of brightness, contrast, saturation
  • Pooling exponent
    • \(p=1\) 또는 \(p=3\) 사용
    • 그림 3 참고
  • Input size & cropping
    • 분류 : \(224 \times 224\), crop
    • 검색 : \(s^*=224, 500, 800\), no crop
  • Margin loss & batch sampling
    • RA 는 \(m=3\) 사용
    • 기본 margin loss 사용
    • 4개의 GPU 에서 학습
  • 데이터셋
    • ImageNet-2012, 1000개의 레이블
    • 분류를 위한 평가셋은 50,000 ro
    • 검색을 위해서는 Holidays 데이터셋을 사용. (mPA 로 측정)
    • UKB object detection 도 확인
    • PCA whitening 을 위해서 20K 의 이미지를 사용 (YFCCD100M 사용)

pooling expanding

  • pooling expoint \(p^*\) 는 3으로 사용.

Figure.4

Tradeoff 파라미터

  • 파라미터 \(\lambda\) 값을 선정하는 문제
  • 사실 둘이 동등한 관계는 아니다. (0.5 로 사용한다고 해서 동등한 가중치를 가진다는 것은 아니다.)
    • 분류와 검색용 term 에 대해서 실제 중요도를 분석하였다.
    • graident back-propagation 의 avg. norm 값을 측정하는 방법을 통해 유추

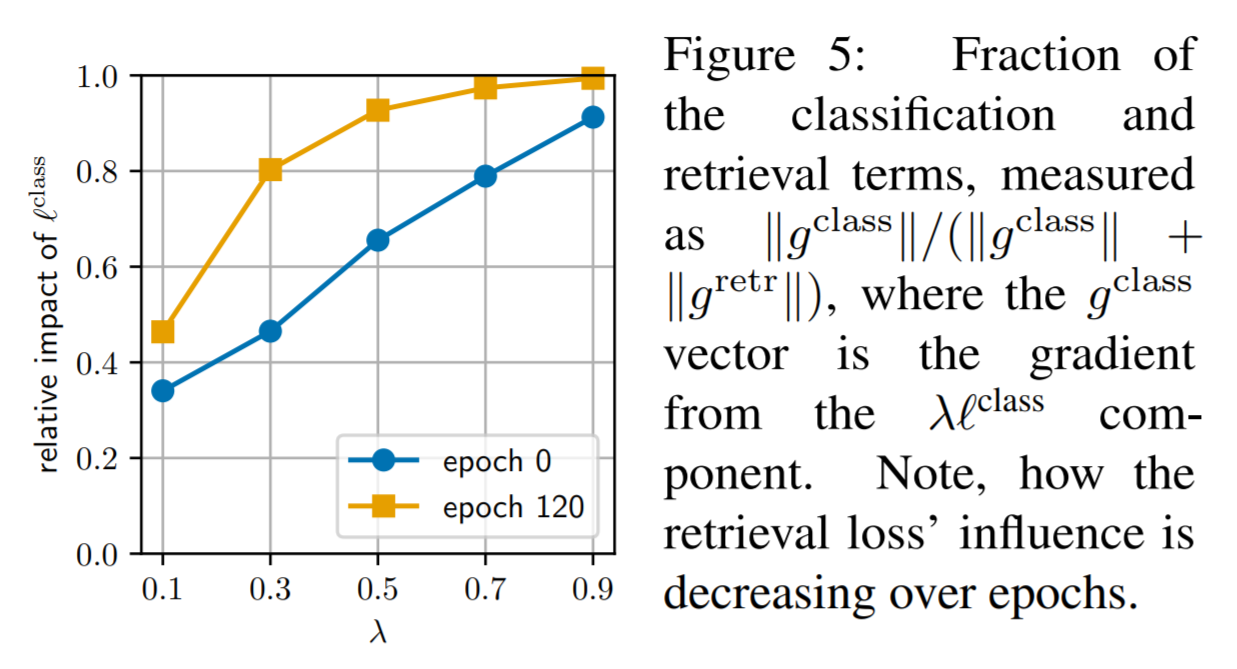
Figure.5

  • 만약 \(\lambda=0.1) 인 경우 분류 성능이 매우 안 좋다.
  • 또한 \(\lambda=1\) 보다는 \(\lambda=0.5\) 일 때 분류 성능이 더 좋다.
  • Table.2 를 참고할 것.
  • 논문에서는 최종 결과로 \(\lambda=0.5\) 를 사용. (\(s^*\) 는 224와 500 사용.)

분류 결과

  • MultiGrain 을 위해 \(s=224\) 에 대해 \(p=1\) 또는 \(p=3\)으로 비교 실험
  • 각 평가마다 \(s^*=224, 500, 800\) 으로 결과 확인
  • Table.2 를 참고할 것
  • AA는 auto-gugment 기법을 사용한 방법을 의미한다. (다른 논문에 제시되어 있다.)

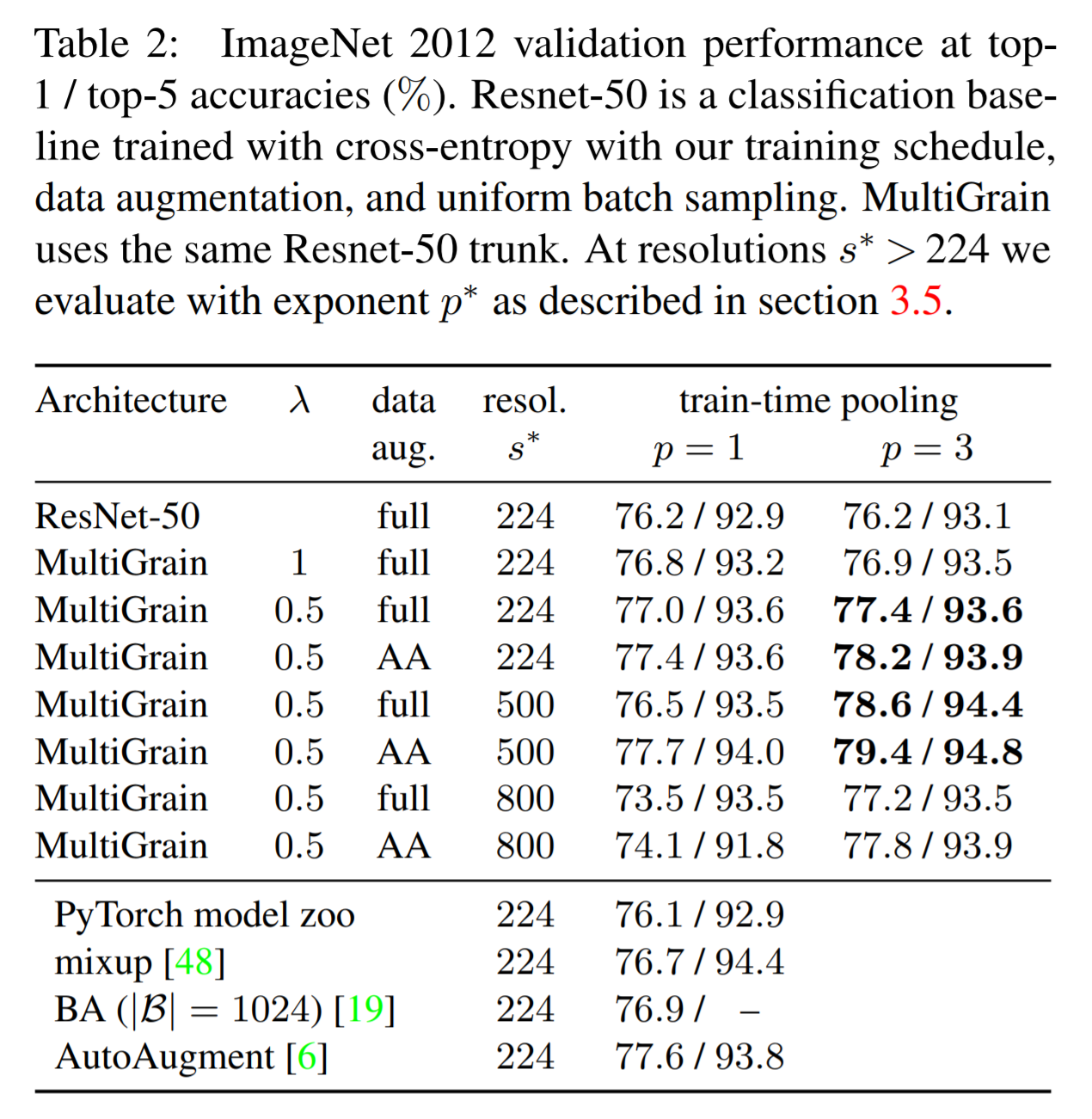
Table.2

  • AA 를 적용하느 경우 더 오랜 시간을 학습해야 효과가 있음을 확인하였다.

검색 결과

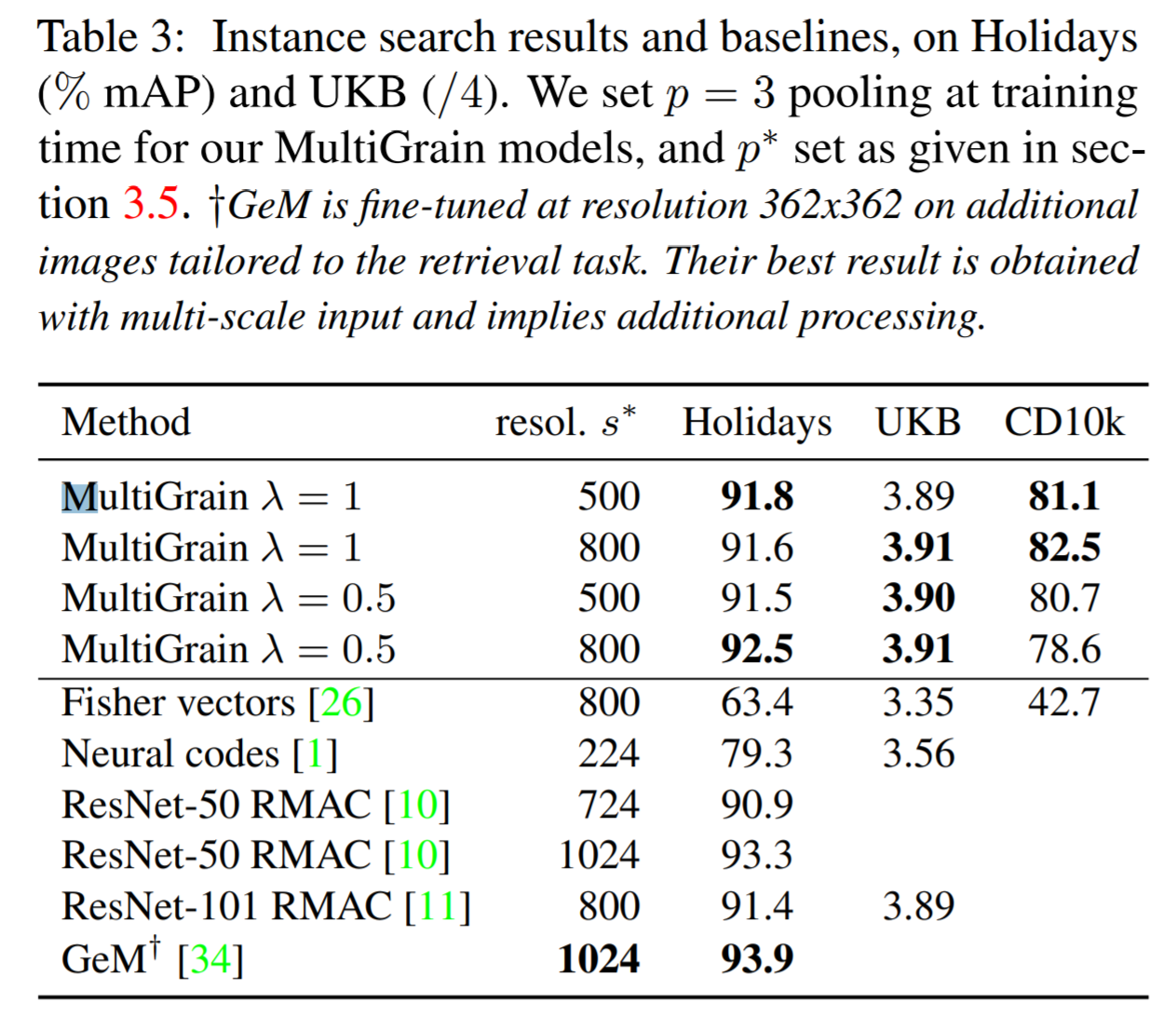
  • Table.3 을 참고하자.
  • RA 가 효과가 좋다.
  • GeM 에서 사용된 논문은 93.9% 로 성능이 가장 좋지만 입력 크기로 1024를 요구한다.
  • MultiGrain 은 500으로 충분하다.

Table.3