Benchmarking neural network robustness to common corruptions and perturbations
Introduction
- 인간의 눈은 강건(robust)하지만 컴퓨터 비전은 그렇지 못하다.
- 그냥 입력 변화에 취약하지 않은가, 취약한가의 차이
- 인간의 경우 입력의 작은 변화에 의해 최종 판단 결과가 달라지는 경우는 거의 없다.
- 딥러닝의 경우 강건함(robust)과 관련된 연구가 오로지 adversarial attack 쪽으로만 연구되었다.
- 반면 이 논문에서는 조금 다른 형태의 강건함을 다루는 두 개의 데이터셋을 제안한다.
- ImageNet-C : curruption robustness 를 측정할 수 있는 데이터셋
- ImageNet-P : perturbation robustness 를 측정할 수 있는 데이터셋
- ImageNet-C
- 75개 집합의 일반적인 visual corruption 을 다루고 이를 ImageNet 데이터셋에 적용한다.
- image corruption 을 측정하는 데이터셋이 되기를 희망한다.
- ImageNet-P
- perturbation 집합을 소개하고 이를 ImageNet 데이터셋에 적용한다.
- 이 평가지표를 이용해서 네트워크의 안정성을 측정한다.
- 또한 corruption 안정성으로 올리면 perturbation 강건성도 함께 상승함을 확인한다.
- Adversarial Example
- adversaial image란 이미지에 약간의 distortion 을 가해 분류기를 혼동하도록 만들어낸 이미지를 말한다.
- 야주 약간의 이미지 변화만으로도 분류기가 크게 결과를 혼동할 수 있음을 확인하였다.
- Robustness in Speech
- 음성 인식 분야는 adversarial 예제와 같은 문제보다는 일반적인 환경에서의 corruption 에 대한 강건성을 요구한다.
- 일반적인 음성 corruption 은 “거리의 소음”, “주변 소음”, “바람 소리” 등이 있다.
- 이를 위한 noisy 환경의 데이터 집합들이 존재한다.
- 입력 전처리 작업을 통해 이러한 것들을 보정하기도 한다.
- ConvNet Fragility Studies
- 많은 연구를 통해 CNN 이 약간의 corruption 에도 취약하다는 것을 확인하였다.
- 가우시안 노이즈, 블러를 사용해서 Google Vision API 가 잘 동작하지 않음을 확인. (Hosseini et al.)
- 기타 등등. 주요하지 않은 것 같아 생략.
- Robustness Enhancements
- 강건성(robust)을 모델에 추가하기 위한 방안으로 blur 이미지를 학습 데이터에 추가. (Vasiljevic et al.)
- Zheng et al. 은 노이즈를 추가한 이미지로 fine-tuning 하면 underfitting 이 되는 현상을 확인
- 소프트맥스 값을 그대로 사용하기 보다는 noise 를 추가한 소프트맥스가 더 좋은것도 확인
Corruptions, Perturbations, Adversarial Perturbations
- 여기서는 corruption 과 perturbation 에 대한 robustness 를 정의하고 이것이 adversarial perturbation 과 어떻게 다른지 확인한다.
- 시작하기에 앞서 분류기 \(f:\mathcal{X}\rightarrow\mathcal{Y}\) 는 분포 \(\mathcal{D}\) 에 의해 생성된 학습 데이터로 학습되었다고 하자.
- curruption 함수 집합은 \(\mathcal{C}\)로 표기하고 perturbation 함수 집합은 \(\mathcal{E}\) 로 표기한다.
- 이제 \(P_{\mathcal{C}}(c)\) 와 \(P_{\mathcal{E}}(\varepsilon)\) 를 실 세계의 corruption, perturbation 의 빈도로 생각한다.
- 대부분류기는 \(\mathcal{D}\) 에 의해 제공된 학습 데이터로 accuracy 를 측정한다. (\(P_{(x,y)\sim\mathcal{D}}(f(x)=y)\))
- 이 논문에서는 분류기의 corruption robustness 를 측정할 수 있는 방법을 제안한다.
- \(\mathbb{E}_{c\sim C}[P_{(x,y)\sim\mathcal{D}}(f(c(x))=f(x))]\)
- 이는 adversarial robustness 의 식인 \(\min_{||\delta||_{p} < b}P_{(x,y)\sim\mathcal{D}}(f(x+\delta)=y)\) 와 대조대는 식이다.
- 결국 corruption robustness 는 분류기가 corruption \(C\) 에 대한 평균 강건성을 측정하는 방식으로 결정한다.
- 마찬가지로 perturbation robustness 도 다음과 같이 정의한다.
- \(\mathbb{E}_{c\sim C}[P_{(x,y)\sim\mathcal{D}}(f(\varepsilon(x))=f(x))]\)
- 최종적으로 이 논문은 실제 공통으로 적용 가능한 corruption 과 perturbation 을 선정하여 이를 기준으로 평가를 할 수 있도록 제안한다.
- 이를 각각 ImageNet-C, ImageNet-P 의 형태로 제공한다.
ImageNet-C, ImageNet-P robustness benchmarks
ImageNet-C 디자인

- ImageNet-C 는 ImageNet에 15개의 corruption 타입이 적용한 데이터이다.
- 대표적인 4개의 카테고리로 noise, blur, weather, digital 을 사용한다. (그림 1 참고)
- 모든 corruption 타입은 5단계의 레벨이 존재한다. Appendix.A 에서 예제를 제공한다.
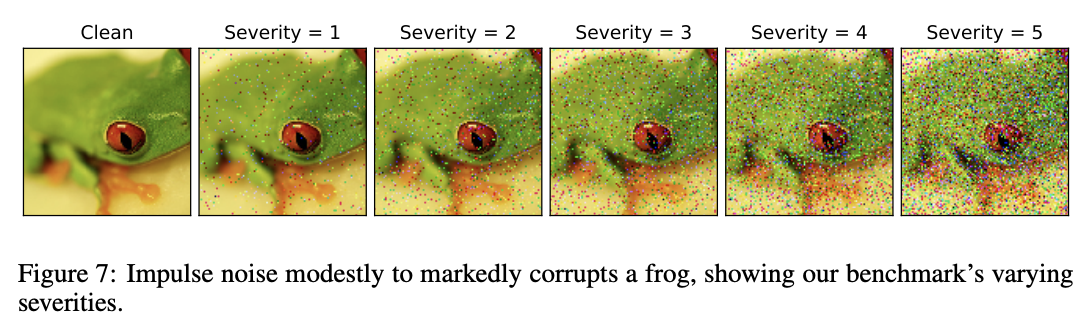
- 실제 세계의 corruption 을 반영하기 위해 intensity 에서도 여러 변형체가 존재할 수 있다.
- 이런 것들을 반영하기 위해 예를 들어 fog cloud 같은 경우 모든 이미지마다 unique 한 corruption을 추가하였다.
- 알고리즘을 활용하여 이를 ImageNet 데이터에 적용한다. 이렇게 얻어진 데이터를 ImageNet-C 로 명명한다.
- https://github.com/hendrycks/robustness
- 중요한 점은 실제 구현하는 모델을 이 데이터로 학습하면 안된다는 것이다.
- 학습은 ImageNet 으로 하고 평가시에만 이를 활용하도록 한다.
- 추가로 CIFAR-10-C, Tiny-ImageNet-C, ImageNet64x64-C 도 제공한다.
- Inception 모델을 위한 버전도 존재한다. (입력 크기가 다르므로)
- 최종 75종류의 corruption 이 적용된 ImageNet-C 를 제공한다.
일반적인 corruption 들
- Gaussian noise는 low-lighting 환경에서 발생할 수 있다.
- Shot noise 는 Possion noise 라 불리우는데 빛이 쪼개진다는(discrete) 본질적인 현상에 의해 발생되는 전자적인 노이즈이다.
- Impulse noise 는 salt-and-pepper noise로 bit 에러 등으로 발생될 수 있다.
- Defocus blur 는 사진 포커싱이 나가면 발생되는 현상이다.
- Frosted Glass Blur 는 창문등에 의해 발생한다. (반투명 유리 등)
- Motion blur 는 카메라를 움직이면서 찍을 때 발생한다.
- Zoom blur 는 사진을 찍을 때 물체가 그 앞으로 빠르게 지나갈 때 발생한다.
- Snow 는 시각적 판단을 흐리게 하는 요소이다.
- Frost 는 창문이나 렌즈에 서리가 끼면 발생할 수 있다.
- Fog 는 물체를 가린다.
- diamond squre 알고리즘으로 그릴 수 있다.
- Brightness 는 일광의 강도에 따라 달라진다.
- Contrast 는 조명의 상태나 피사체의 색상에 의해 달라질 수 있다.
- Elastic 변형은 이미지의 작은 영역을 찍을 때 발생한다.
- Pixelation 은 낮은 해상도로 찍은 이미지를 큰 사이즈로 변경할 때 발생한다.
- JPEG 는 압축 알고리즘으로 압축시 발생하는 artifact 가 생겨난다.
ImageNet-P 디자인

- 두번째로, 분류기를 위한 perturbation robustness 테스트셋을 제공한다.
- perturbation 에 약한 분류기는 상황에 따라 다른 결과를 제공하므로 사용자의 신뢰를 낮추게 된다.
- ImageNet-C 와 비슷하게 ImageNet-P 에서는 noise, blur, weather, digital-distortion 으로 구성된다.
- 또한 이전과 마찬가지로 난이도를 제공한다. (어려움의 정도)
- 동일하게 CIFAR-10-P, Tiny-ImageNet-P, ImageNet64x64-P 도 제공한다.
- ImageNet-P 데이터는 ImageNet-C 데이터에서 시작해서 여기에 perturbation을 추가한다. (그림 2 예제 참고)
- 각 시퀀스에는 30개가 넘는 프레임으로 구성된다. 데이터 크기에 문제가 될 수 있으므로 10개의 perturbation만을 적용한다.
일반적인 Perturbation 들
- ImageNet-C 보다 미묘하게 발생되는 Gaussian noise perturbation 은 깨끗한 ImageNet 데이터로 시작한다.
- 시퀀스 내의 프레임은 동일한 이미지로 구성되지만 미세한 Gaussian noise perturbation이 적용된다.
- 이 시퀀스 디자인은 shot noise perturbation 시퀀스와 유사하다.
- 하지만 그 나머지 perturbation은 시간성(temporality)을 가진다.
- 이 경우 이전 프레임에 대해 perturbation 을 가해 현재 프레임을 만든다.
- 가해진 perturbation 이 작기 때문에 여러번 반복해서 적용해도 원래 분포에 크게 바뀌지는 않는다.
- 예를 들어 translation perturbation 시퀀스의 경우 한번에 한 픽셀씩 왼쪽으로 이동한 이미지를 만든다.
- 따라서 입력은 여전히 고품질 이미지이다.
- 시간성에 영향을 받는 perturbation 시퀀스는…
- motion blur, zoom blur, snow, brightness, translate, rotate, tilt, scale 이다.
평가 메트릭
ImageNet-C Metrics
- Gaussian noise 와 같은 일반적인 corruption 의 경우 심각도에 따라 괜찮을수도 나쁠수도 있다.
- 좀 더 종합적인 평가를 위해 5개의 단계로 나누고 이를 집계한다.
- 가장 먼저 분류기 \(f\) 에 대해 순수한 top-1 에러를 측정한다. (\(E_{clean}^{f}\))
- 두번째로 corruption type \(c\) 에 대한 에러를 측정한다.
- 이 때 각 유형 단계(severities)별 오류를 계산한다. (\(E_{s,c}^{f}\)), (\(1 \le s \le 5\))
- 각 유형에 따른 corruption 정도가 다른 수준의 난이도를 만들기 때문에 이에 대한 보정을 적용한 뒤 계산하는 방법이 필요하다.
- 예를 들어 Fog 문제는 brightness 보다 class 값을 더 애매하게 만들어낸다.
- 이를 해결하기 위해 base 모델를 두어 normalize 를 수행한다.
- 여기서는 baseline 모델로 AlexNet 을 사용한다.
\[CE_c^f = \frac{\left(\sum_{s=1}^5{E_{s,c}^f}\right)}{\left(\sum_{s=1}^5{E_{s,c}^{AlexNet}}\right)}\]
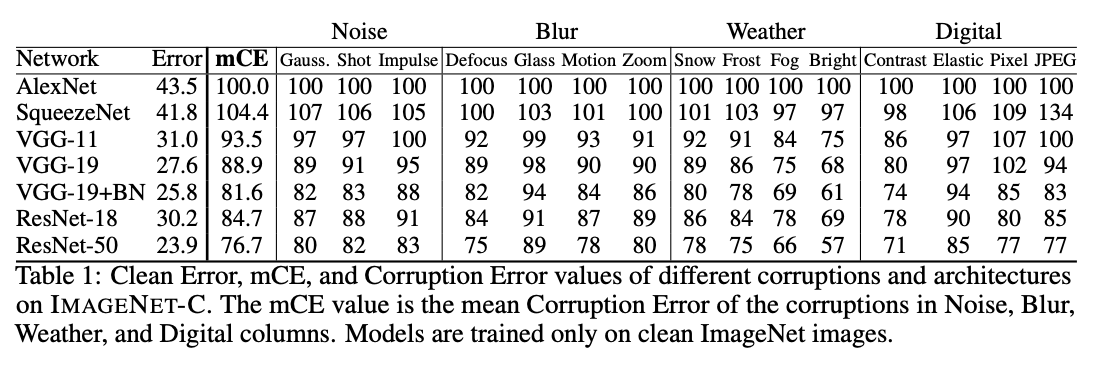
- 이제 15개의 corruption error 를 측정하면 15개의 \(CE\) 를 만들 수 있다.
- \(CE_{Gaussian Noise}^{f}\), \(CE_{Shot Noise}^{f}\), …, \(CE_{JPEG}^{f}\),
- 이를 평균내면 \(mCE\) 가 된다.
- 이제 더 미묘한 경우의 corruption robustness 를 측정하기 위한 방법을 제안한다.
- 어떤 분류기가 대부분의 corruption 을 잘 처리하고 있다면 ImageNet 과 ImageNet-C 사이의 corruption 에러 차이는 적다.
- 이와 대조하여 어떤 분류기는 clean 데이터보다 ImageNet-C 에 대해 급격하게 에러 값이 커질 수 있다.
- 하지만 현재 수식으로는 전자가 더 큰 \(mCE\) 를 가질수 있다.
- 이에 대한 보정을 수행한다.
\[CE_c^f = \frac{\left(\sum_{s=1}^5{E_{s,c}^f-E_{clean}^f}\right)}{\left(\sum_{s=1}^5{E_{s,c}^{AlexNet}-E_{clean}^{AlexNet}}\right)}\]
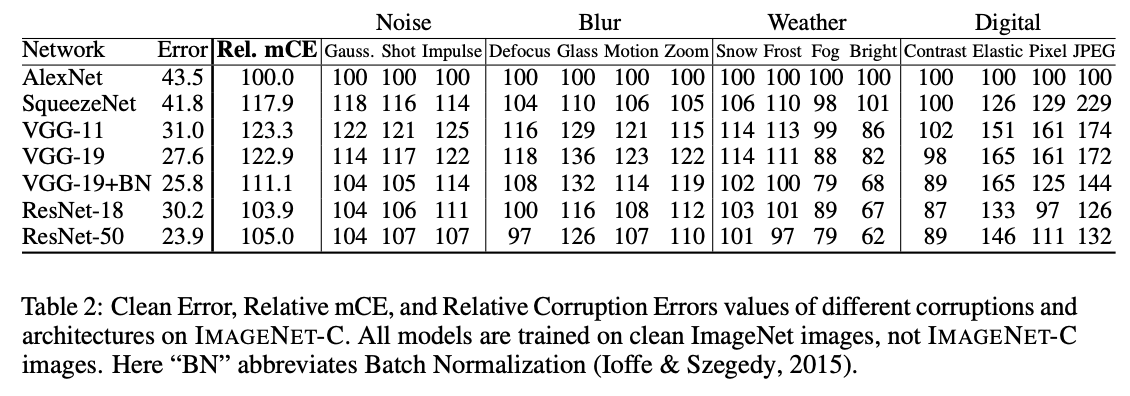
- 이에 대해 평균을 낸 값을 \(Relative\;mCE\) 라고 부른다.
ImageNet-P Metrics
- 직관적으로 생각해보면 다음 식으로 perturbation을 측정할 수 있다.
\[\mathbb{E}_{\varepsilon \sim \mathcal{E}}[P_{(x,y)\sim\mathcal{D}}(f(\varepsilon(x))\neq f(x))]\]
- 사실 수식에 대한 명확한 정의가 되어 있지 않다. (\(n\) 이 정확히 무슨 의미라던가…)
- 이제 각 perturbation \(p\) 에 대해 \(m\)은 perturbation 시퀀스의 갯수로 정의한다.
- 이게 뭘까 고민해봤는데 예를 들어 translation 같은 perturbation은 여러 방향으로의 이동이 있을 것 같다.
- 이렇게 되면 하나의 perturbation에 대해 여러가지 시퀀스를 만들어 낼 수 있음.
- 그런데 실제 구현 코드에서는 이런 식으로 구현되어 있지 않다. 그래서 \(m\) 이 평가 이미지 갯수일 수도 있겠다는 생각.
- 어떻게 판단해도 수식상 문제가 없어 보여서 실제 어떤 의미인지 잘 모르겠음.
- 여기에 시퀀스 \(S=\{(x_{1}^{(i)}, x_{2}^{(i)},…, x_{n}^{(i)})\}_{i=1}^{m}\)이다.
- \(n\) 이 명확하지 않는데 아마도 시퀀스 길이로 hyperparamter 가 아닐까 한다.
- 보통 31개를 쓰는 것 같은데 \(p\)에 따라 달라지는 듯 하다. (첫번째는 원본, 그 다음은 perturbation을 가한 이미지.)
- 이제 ‘Flip Probabilty’ 네트워크를 고려해 보자. ( \(f:\mathcal{X}\rightarrow \{1,2,…,1000\}\) )
- 시퀀스 \(S\) 에 대해 다음과 같은 식을 고려할 수 있다.
\[FP_{p}^{f} = \frac{1}{m(n-1)}\sum_{i=1}^{m}{\sum_{j=2}^{n}{\mathbb{1}\left(f(x_j^{(i)})\neq f(x_{j-1}^{(i)})\right)}} = P_{x\sim S}\left(f(x_j)\neq f(x_{j-1})\right)\]
- 만약 시계열(temporal) 속성이 필요없는 경우 (예를 들어 noise perturbation 같은..) 식을 좀 더 간단히 사용할 수 있다.
- \(x_1^{(i)}\) 는 clean 데이터이고, \(x_j^{(i)}\) 는 \(x_1^{(i)}\) 의 perturbation 으로 구성해도 된다. (단, \(j > 1\))
- 이 경우 식을 다음과 같이 만들 수도 있다.
\[FP_p^{f} = \frac{1}{m(n-1)}\sum_{i=1}^{m}{\sum_{j=2}^{n}{\mathbb{1}\left(f(x_j^{(i)})\neq f(x_1^{(1)})\right) = P_{x\sim S}\left(f(x_j) \neq f(x_1) \;|\; j>1 \right)}}\]
- 그 다음 \(FP_p^f=\frac{FP_p^f}{FP_p^{AlexNet}}\) 을 적용한다.
- 이에 대한 평균 값을 사용한다. 이를 \(mFR\) 이라 한다.
- \(mFR\) 의 경우 \(Relative\) 속성의 평가 지표는 없다.
- top-1 은 이런 식으로 할 수 있는데 top-5 의 경우 측정이 애매해진다.
- 이를 위해 top-5 측정용 식을 추가한다.
- 새로운 함수 \(\tau(x)\) 를 추가한다.
- 예를 들어 Toucan 은 97번째 라벨이고, Pelican 은 145번째 라벨이라고 하자.
- 어드 입력에 대해 1등 결과가 Toucan 이 나오고 2등 결과가 Pelican 인 경우를 가졍하면,
- \(\tau(x)(97)=1\) 이고 \(\tau(x)(144)=2\) 가 나온다.
\[d\left(\tau(x), \tau(x')\right) = \sum_{i=1}^{5}{\sum_{j=\min(i, \sigma(i))+1}^{max(i, \sigma(i))}{\mathbb{1}(1 \le j-1 \le 5)}}\]
- 단, \(\sigma = \left(\tau(x)\right)^{-1}\tau(x’)\) 이다.
- 만약 \(\tau(x)\) 와 \(\tau(x’)\) 가 동일하다면 \(d\left(\tau(x), \tau(x’)\right)=0\) 이다.
\[uT5D_p^f = \frac{1}{m(n-1)}\sum_{i=1}^{m}{\sum_{j=2}^{n}{d\left(\tau(x_j), \tau(x_{j-1})\right)}} = P_{x\sim S}\left(d\left(\tau(x_j), \tau(x_{j-1})\right)\right)\]
- noise perturbation 에 대해서는 \(uT5D_p^f = \mathbb{E}_{x\sim S}[d(\tau(x_j), \tau(x_{1}))|j>1]\) 을 사용한다.
- 표준화를 위해 \(T5D_p^f = \frac{uT5D_p^f}{uT5D_p^{AlexNet}}\) 을 사용한다.
- 마지막으로 전체 평균값을 \(mT5D\) 로 사용한다.
Preserving metric validity
- ImageNet-C 와 ImageNet-P 의 최종 목표는 모델의 강건성을 평가하는 것이다.
- 이 논문은 다음과 같은 프로토콜을 제공한다.
- 먼저 학습자는 ImageNet 과 기타 본인이 원하는 학습 데이터로 학습을 한다.
- 학습시 corruption과 perturbation 을 제거하기 위해 어떤 방식을 사용했는지 명시해야 한다.
- 하지만 이런 학습 방식은 별로 권하지 않는다. (섹션2를 살펴봐라)
- 다른 distortion 들은 허용한다.
- 예를 들어 uniform noise 라던가 표준화된 data augmentation (i.e. cropping, mirroring)
- 그 다음 ImageNet-C 혹은 ImageNet-P 데이터에 대해 평가한다.
- 추가적으로 제공된 ImageNet-C와 ImageNet-P 에 대한 validation set 도 테스트할 수 있다.
실험
아키텍쳐 강건성
- 현재 모델 발전 방향이 강건성을 달성하고 있는가? YES
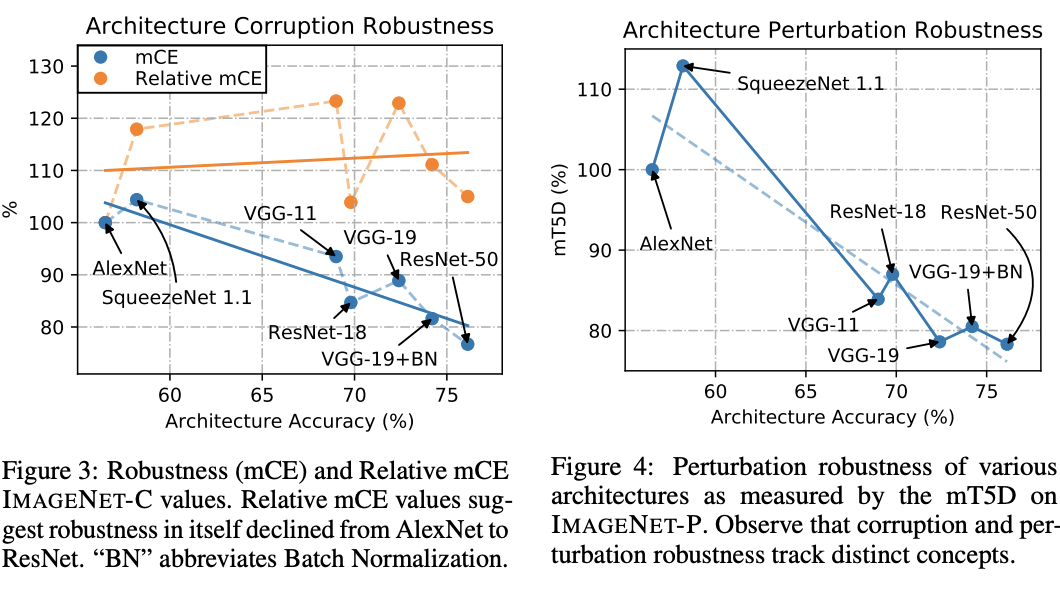
- 그림.3을 보면 아키텍처가 향상됨에 따라 mCE 지표도 나아지고 있다.
- 아키텍쳐는 점점 성공적으로 진화하고 있다.
- 원래 데이터에서 비슷한 오류율을 가지고 있는 모델은 CE 값도 비슷하다.
- 문제는 Relative mCE 를 보면 알수 있듯 정확도(accuracy)에만 치중된 평가 방식으로 인해 후속 모델임에도 mCE가 떨어지는 경우도 있다.
- 그림.3에서 Relate mCE 를 살펴보면 후속 모델임에도 AlexNet보다 떨어지는 경우가 있다.
- 결과적으로 AlexNet 에서 ResNet 까지 corruption 문제는 개선되지 않았다.
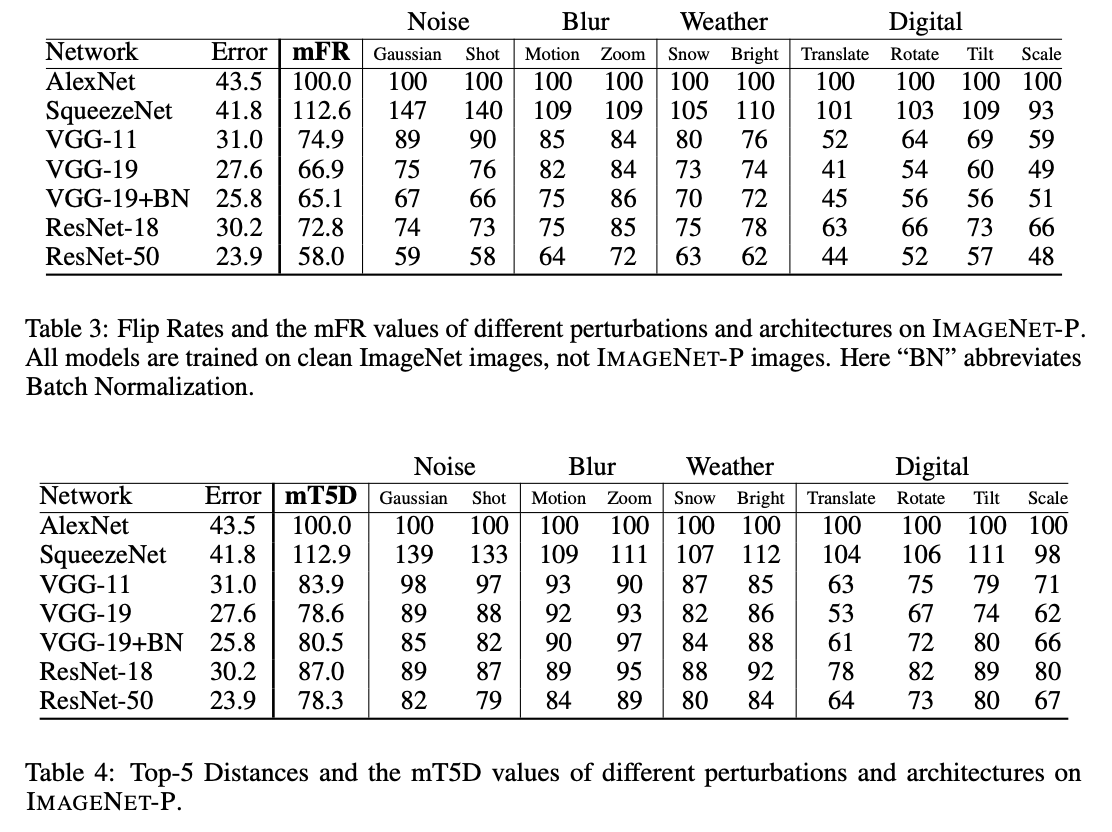
- 놀랍게도 VGG 가 ResNet 보다 성능이 더 않좋다.
- BN 에 따라 결과가 다르긴 하지만 (corruption 과 perturbation 사이의 상관 관계상) 실제 상충 관계가 있다고 말하기는 어렵다.






