Google's Neural Machine Translation System.

https://arxiv.org/abs/1609.08144

  • 구글이 만든 신경망 번역 시스템으로 GNMT (Google Nueral Machine Translation) 라고 부른다.
    • 당연히 end-to-end 구조이다.
    • 예전 방식인 phrase-based 번역 모델에 비해 짱 좋다.
    • 그리고 참고로 일반적인 신경망 번역 시스템을 NMT 라고 부른다.
  • 물론 NMT 계열의 모델도 단점이 있다.
    • 연산량이 무지 높다.
    • 큰 모델을 사용하려면 많은 데이터가 필요하다.
  • 실제로 서비스하려면 정확도와 속도가 생명.
  • 구글이 사용한 GNMT 모델을 잠시 소개하자면,
    • 8개의 LSTM encoder 와 8 개의 LSTM docoder (게다가 Attention 모델)
    • 학습시 속도를 올리기 위해 low-precision 연산 처리.
    • 드문드문 발생하는 단어들도 잘 좀 처리해보자는 의미에서 wordpiece 를 사용.
    • 빠른 검색을 위한 beam-search 는 local-normalization 기법을 사용함.

Introduction

  • NMT 가 각광을 받는 이유는 당연하게도 기존 모델에 비해 아주 간단하면서도 좋은 성능을 내주기 때문.
  • 하지만 만능은 아닌 것이 다음과 같은 제약사항이 존재한다.
    • (1) 느린 학습(training) 속도와 느린 추론(inference) 속도
      • 데이터가 크니 느린건 당연지사.
      • 추론 속도도 보통 phrase-based 방식보다 느린데 이는 모델 파라미터가 너무 많아 단위 연산 비용이 높기 때문.
    • (2) 드물게 등장하는 단어에 대한 부정확도
      • 아주 드물게 등장하는 단어는 추론(inference)시 사전에 없을 수 있다.
      • 이 경우 <unk> 등의 태그로 처리한다.
      • *Copy Model 이란 방식으로 해결할 수 있긴 한데 그냥 모르는 단어는 번역 후에도 그냥 그대로 사용하는 것이다.
        • 이 경우에도 적절한 위치에 해당 단어가 놓아지게 된다.(alignment)
        • 물론 이게 항상 좋은 결과를 주는 것은 아니다.
    • (3) 가끔씩 전체 입력 문장에 대해 다 번역을 하지 않는 경우가 생긴다.
      • 이 경우 번역 결과는 개판이 된다.
  • NMT 이전에는 SMT (Statistical Machine Translation) 모델이 주류였음. ( 참고 동영상 )
  • 현실적은 구현 방법은 Phrase-based Model 였다. (단어들을 구 단위로 묶어 번역 처리함)
  • 이 논문은 NMT 와 관련된 논문이니 예전 것들은 접어두고 NMT 에만 집중하자.

Model Architecture

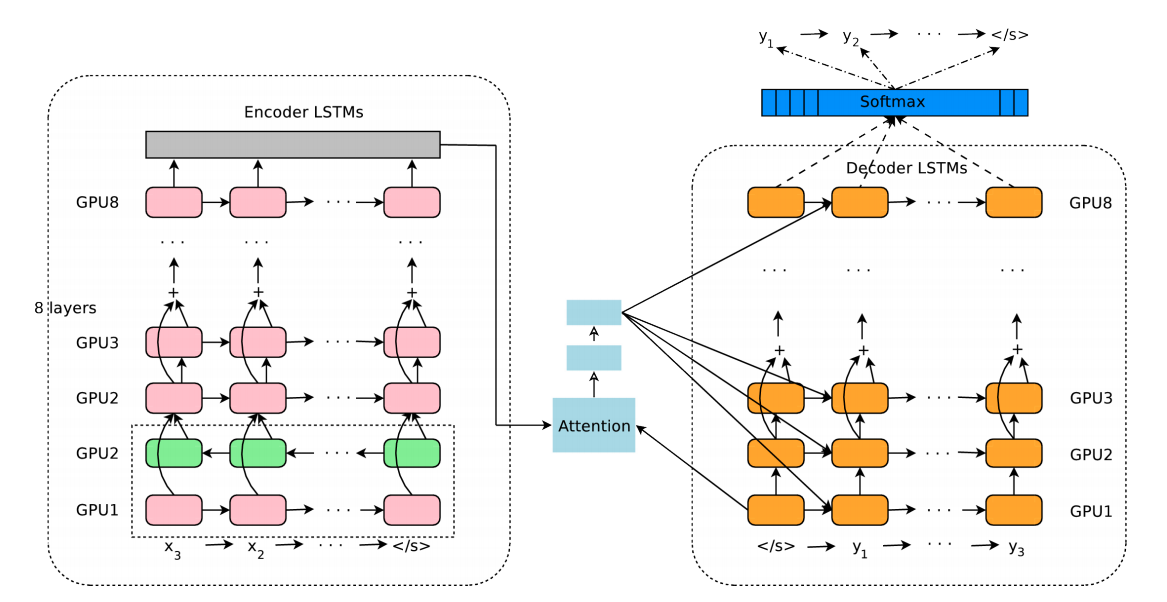
figure.1

  • [그림.1] 만 봐도 attention 기능이 들어간 기본적인 seq-to-seq 모델임을 알 수 있다.
  • seq-to-seq 를 잘 모르는 분들을 위해 2014 NIPS 에서 Ilya Sutskever 가 발표한 최초의 모델을 잠시 보자.

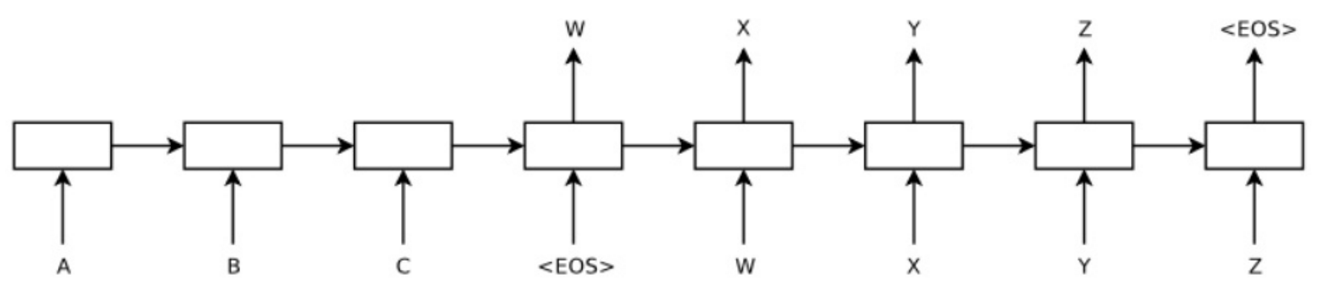
figure.2

  • 다시 GNMT 로 돌아와서…
  • 이 모델은 크게 3가지 영역으로 나눌 수 있다.
    • 입력 문자열을 처리하는 encoder 네트워크.
    • 출력 문자열을 처리하는 decoder 네트워크.
    • 그리고 attention 네트워크.
  • 표기법을 좀 살펴보도록 하자.
    • 볼드체 소문자는 벡터(vector)를 의미 (ex) \({\bf v}, {\bf o}_i\)
    • 볼드체 대문자는 행렬(matrix)을 의미 (ex) \({\bf U}, {\bf V}_i\)
    • 필기체 대문자는 집합(set)을 의미 (ex) \(\mathcal{V}, \mathcal{T}\)
    • 그냥 대문자는 문자열을 의미 (ex) \(X, Y\)
    • 그냥 소문자는 문자열 내에 속한 심볼을 의미 (ex) \(x, y\)
  • \(M\) 개의 길이를 가지는 입력 문자열 : \(X = \{ x_1, x_2, …, x_M \} \)
  • \(N\) 개의 길이를 가지는 출력 문자열 : \(Y = \{ y_1, y_2, …, y_N \} \)
\[{\bf x}_1, {\bf x}_2, ..., {\bf x_M} = EncoderRNN(x_1, x_2, ..., x_M) \qquad{(1)}\]
  • 이 때 \({\bf x}_1, {\bf x}_2, …, {\bf x_M}\) 는 고정된 크기를 가지는 벡터.
    • 이 벡터의 개수는 \(M\) 개라는 것을 유의하자.
\[P(Y|X) = P(Y|{\bf x}_1, {\bf x}_2, ..., {\bf x_M}) = \prod_{i=1}^{N} P(y_i | y_0, y_1, y_2, ..., y_{i-1};{\bf x}_1, {\bf x}_2, ..., {\bf x_M}) \qquad{(2)}\]
  • 유심히 볼 것이 하나 있는데 바로 \(y_0\) 이다. 특별한 심벌로 문장의 시작을 나타내는 심볼이다.
  • 실제 추론 단계에서는 결국 다음 심볼의 확률값을 계산하는 문제로 생각하면 된다.
\[P(y_i | y_0, y_1, y_2, ..., y_{i-1};{\bf x}_1, {\bf x}_2, ..., {\bf x_M}) \qquad{(3)}\]
  • decoder 단계에서는 RNN (LSTM) 과 소프트맥스(softmax) 레이어를 사용한다.
    • softmax 를 이용하여 출력할 단어를 결정하게 된다.

  • 보통 LSTM 이 깊어질수록 (레이어를 올릴수록) 성능이 좋다는 보고가 있는데 여기서도 마찬가지였다.

  • attention 모델은 사실 이 논문 을 따라한 것이다.
\[\begin{align}s_t &= AttentionFunction({\bf y}_{i-1}, {\bf x}_t)\;\;\forall{t},\;\;1 \le t \le M \\ p_t &=\frac{\exp{(s_t)}}{\sum_{t=1}^{M} \exp{(s_t)}}\;\;\forall{t},\;\;1 \le t \le M \\ {\bf a}_i &= \sum_{t=1}^{M} p_t \cdot {\bf x}_t \end{align} \qquad{(4)}\]

Residual Connections

  • 정확도를 올리고자 residual 노드를 넣는다. (LSTM stack에다가)
  • residual 을 넣지 않고 일반적인 stacked LSTM 을 쌓아 사용하면 학습 속도가 너무 느리게 된다.
    • 게다가 잘 알고 있는대로 exploding 과 vanishing gradient 문제가 발생한다.
  • 경험상 번역 모델에 기본적인 LSTM 모델을 사용하면 4개 층까지는 잘 동작하지만 6개부터는 문제가 발생하고 8개는 제대로 동작하지 못한다.

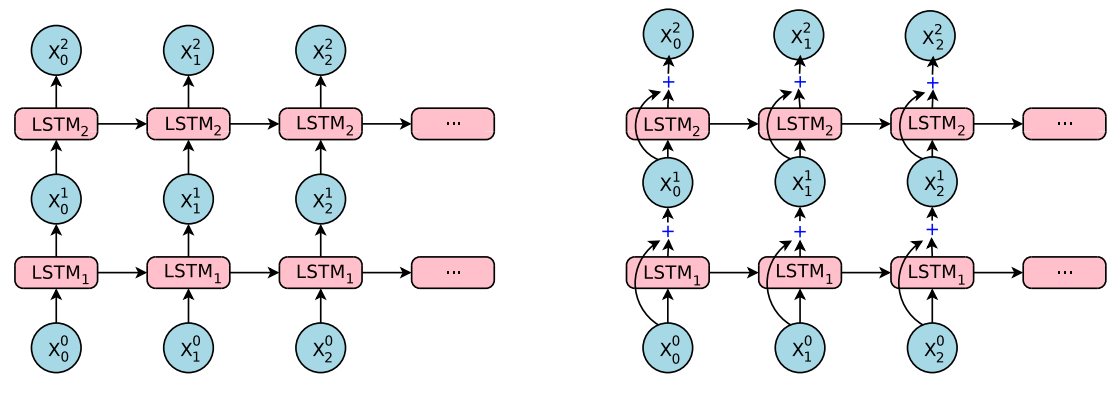
figure.3

  • 일반적인 LSTM 모델의 수식은 다음과 같다.
\[\begin{align}{\bf c}_{t}^{i}, {\bf m}_{t}^{i} &= LSTM_i({\bf c}_{t-1}^{i}, {\bf m}_{t-1}^{i}, {\bf x}_{t}^{i-1};{\bf W}^{i}) \\ {\bf x}_{t}^{i} &= {\bf m}_{t}^{i} \\ {\bf c}_{t}^{i+1}, {\bf m}_{t}^{i+1} &= LSTM_{i+1}({\bf c}_{t-1}^{i+1}, {\bf m}_{t-1}^{i+1}, {\bf x}_{t}^{i};{\bf W}^{i+1}) \end{align}\quad{(5)}\]
  • 이 때 \({\bf x}_{t}^{i}\) 는 \(LSTM\) 의 스텝 \(t\) 일 때의 입력 값으로 사용된다.
  • \({\bf m}_{t}^{i}\) 와 \({\bf c}_{t}^{i}\) 는 각각 \(LSTM\) 의 Hidden 상태와 메모리 값을 의미한다.
  • 여기에 redidual 을 추가한 모델은 다음과 같다.
\[\begin{align}{\bf c}_{t}^{i}, {\bf m}_{t}^{i} &= LSTM_i({\bf c}_{t-1}^{i}, {\bf m}_{t-1}^{i}, {\bf x}_{t}^{i-1};{\bf W}^{i}) \\ {\bf x}_{t}^{i} &= {\bf m}_{t}^{i} + {\bf x}_{t}^{i-1} \\ {\bf c}_{t}^{i+1}, {\bf m}_{t}^{i+1} &= LSTM_{i+1}({\bf c}_{t-1}^{i+1}, {\bf m}_{t-1}^{i+1}, {\bf x}_{t}^{i};{\bf W}^{i+1}) \end{align}\quad{(6)}\]
  • 아주 간단한 변경만으로도 엄청난 효과를 낸다.
  • 실험 결과 8 레이어의 \(LSTM\) 이 가장 효과가 좋았다. (encoder, decoder 각각)

Bi-directional Encoder for First Layer

  • 번역 시스템에서는 번역을 제대로 하기 위해 입력 쪽 데이터를 양 방향에서 살펴보아야 할 필요가 있다.
    • 보통 입력 쪽 언어의 정보는 왼쪽에서 오른쪽으로 이동되는 것이 보통인데 이게 출력 쪽 언어에서는 서로 분할되어 다른 위치에 등장해야 하는 경우도 많다.
    • 컨텍스트를 충분히 살펴보기 위해 encoder 단계에서는 bi-directional RNN 을 사용하게 된다.
    • 아래 그림을 참고하도록 하자.

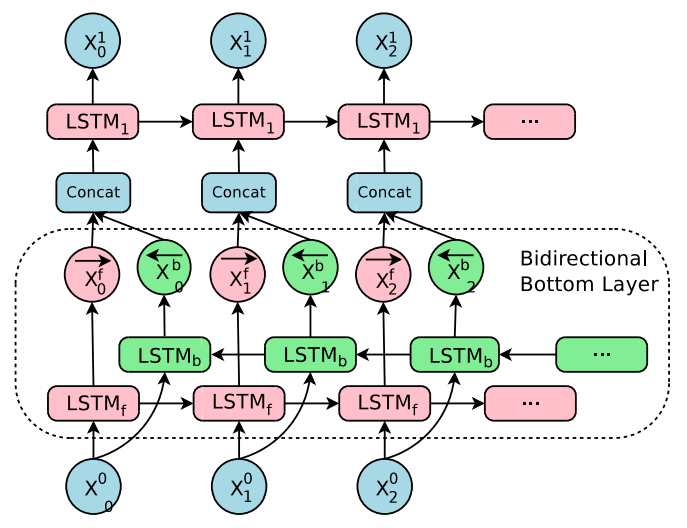
figure.4

Model Parallelism

  • 모델이 복잡하기 때문에 병렬 모델을 사용할 수 밖에 없다.
    • 모델 병렬화(model parallelism)와 데이터 병렬화(data parallelism)를 모두 사용한다.
  • 데이터 병렬화를 위해 사용한 방식은 Downpour SGD 이다.
    • \(n\) 개로 복사된 장비가 동일한 모델 파라미터를 공유한다.
    • 그리고 각각 독립적으로 파라미터를 업데이트한다. (asynchronously update)
  • 실험에서는 약 10개의 장비( \(n=10\) )로 실험하였다.
    • 모든 장비는 \(m\) 개의 문장을 mini-batch 로 사용한다.
    • 실험에서는 주로 \(m=128\) 을 사용하였다.
  • 추가로 모델 병렬화 (model parallelism)을 사용해서 성능을 더 올린다.
    • 다중 GPU 환경으로 모델을 구성한다. (장비당 8개의 GPU를 사용한다.)
    • 각 레이어 층마다 서로 다른 GPU를 할당하여 처리하게 된다.
    • 이렇게 하면 \(i\) 번째 레이어의 작업이 모두 종료되기 전에 \(i+1\) 번째 작업을 진행할 수 있다.

  • softmax 레이어도 분할하여 사용한다.

  • 현재 bi-directional LSTM 은 첫번재 레이어에만 적용한다.
    • 병렬화를 위해 최대한 효율적으로 구성하기 위해서이다.

Segmentation Approaches

  • NMT 방식은 고정된 단어 사전 집합을 사용하게 된다.
  • 하지만 이런 방식은 단어 사전에 포함되지 않은 단어가 등장했을 때 처리가 애매하다는 문제가 있다. (OOV : Ouf of Vocabulary)
  • 이를 해결하기 위한 가장 쉬운 방식은 copy 모델이다.
    • 해석이 되지 않는 단어는 그냥 입력으로부터 출력으로 전달해버리는 방식.
  • 우리는 이를 좀 더 개선하기 위해 sub-word unit 을 만드는 방식을 추가한다.
  • 이는 work/character 방식을 혼합한 방식이라 생각하면 된다.

Wordpiece Model

  • OOV 문제를 해결하기 위해 sub-word unit 방식의 WPM (wordpiece model)을 개발함.
  • 이는 일본어, 한국어 (응?) 세그멘테이션(segmentation) 문제를 해결하기 위해 개발한 방법을 응용한 것이다.
  • 문자 단위의 시퀀스에서 분할 가능한 단어 별로 나누어내는 과정이 들어간다. (우리는 한국 사람이니까 형태소 분석을 생각하자.)
  • 아래 예제를 보면 대충 어떤 것인지 짐작이 갈 것이다.
    • Word: Jet makers feud over seat width with big orders at stake
    • wordpieces: _J et _makers _fe ud _over _seat _width _with _big _orders _at _stake
  • 보면 알겠지만 “Jet” 이라는 단어는 “_J” 과 “et” 로 나누어지게 된다.
  • 마찬가지로 “feud” 는 “_fe” 와 “ud” 로 나누어진다.
  • “_” 는 시작 문자라는 의미로 붙인다.
  • 이 방식은 language-model likelihood 값을 최대화하는 방식으로 학습을 하여 구성한다.
    • 이 문서 를 참고하라고 한다.
    • 위 논문과 다르게 구현된 내용은 시작 심볼(start symbol)은 사용하였지만 종료 심볼(end symbol)은 사용치 않는다고.
  • 지나치게 세세하게 나누면 사전에 포함되어야 할 단어 수가 너무 많아지므로 적당한 수준으로 나눈다.
    • 실험에서는 wordpiece 조각을 약 8k ~ 32k 에서 좋은 결과를 얻었다. (BLEU 기준)
  • 이러한 방식으로도 얻을 수 없었던 단어(rare word)들은 앞서 언급한대로 copy model 을 사용하였다.

Mixed Word/Character Model

  • 두번째 접근 방식으로 혼합된 단어/문자 모델 (mixed word-characer model)을 사용한다.
  • 단어 모델에서는 고정된 단어 사전을 사용한다.
    • 하지만 이것만 사용하면 OOV 문제가 발생함을 앞서 설명했다.
  • 보통 OOV 단어로 판명되면 <UNK> 태그를 붙이게 되는데 여기서는 이것 대신 문자 단위로 나우어 처리한다.
    • 단어를 문자 단위로 나누되 태그를 붙인다.
    • 시작 문자인 경우 <B>, 중간 문자인 경우 <M>, 끝 단어인 경우 <E> 를 붙인다.
    • 예를 들어 Mike 라는 단어는 <B>M <M>i <M>k <E>i 로 나누어진다.
  • 전체 작업 과정에서는 이 prefix 를 유지한채로 학습하고 후처리 단계에서 이 태그가 남아있는 경우 해당 태그들을 다시 삭제한다.

Traning Criteria

  • 주어진 \(N\) 개의 입력 출력 쌍 문장을 \(\mathcal{D} \equiv \{ {\bf X}^{(i)}, {\bf Y}^{*(i)}\}_{i=1}^{N}\) 라고 하자.
  • 기본적인 maximum-likelihood 학습 방식은 로그 확률 값을 최대화하는 목적 함수를 사용하는 것이다.
\[\mathcal{O}_{ML}({\bf \theta}) = \sum_{i=1}^{N}\log P_{\theta}({\bf Y}^{*(i)}|{\bf X}^{(i)}) \qquad{(7)}\]
  • 이 함수의 가장 큰 문제는 BLEU 평가 지표가 목적 함수와 바로 부합되지 않는다는 사실.
  • (참고) BLEU 평가란?
\[BP=\left\{\begin{array}{11}1 & if\; c \gt r\\e^{1-r/c} & if\; c \le r\end{array}\right.\] \[p_n = \frac{\sum_{C \in Candieates}\sum_{ngram \in C} Count_{clip}(ngram)}{\sum_{C \in Candieates}\sum_{ngram' \in C'} Count_{clip}(ngram')}\] \[BLEU = BP\cdot\exp\left( \sum_{n=1}^{N} w_n\log p_n \right)\]
  • 이를 위해 조금 다른 목적 함수를 도입한다.
  • 강화학습에서 사용되던 Reward 개념을 도입하여 보상 기대값을 목적 함수로 사용하게 된다.
\[\mathcal{O}_{RL}({\bf \theta}) = \sum_{i=1}^{N}\sum_{Y \in \mathcal{Y}} P_{\theta}({\bf Y}|{\bf X}^{(i)}) r({\bf Y}, {\bf Y}^{*(i)}) \qquad{(8)}\]
  • 여기서 \(r({\bf Y}, {\bf Y}^{*(i)})\) 은 문장 단위 점수를 나타낸다.
    • 즉, 출력한 문서와 실제 문서와의 차이를 점수로 환산하게 된다는 것이다.
  • 이 때 사용하는 점수 지표는 BLEU 가 아니고 GLEU 이다.
  • GLEU 는 우리가 만든 지표인데 대충 다음과 같다.
    • 출력 문자열과 정답 문자열을 일단 1 ~ 4 까지의 토큰 문자열로 만든다.
    • 출력 문자열을 기준으로 recall과 precision 을 구한다.
    • 이 중 가장 작은 값을 GLEU 값으로 정한다.
    • 실제 값은 0 ~ 1 사이의 값을 가지게 된다.
  • 최종 평가 함수는 ML 방식과 RL 방식을 합쳐 목적 함수로 사용한다.
\[\mathcal{O}_{mixed}(\theta) = \alpha \times \mathcal{O}_{ML}(\theta) + \mathcal{O}_{RL}(\theta) \qquad{(9)}\]
  • 우리가 사용한 \(\alpha\) 값은 \(0.017\) 이다.

Quantizable Model and Quantized Inference

  • NMT 의 가장 큰 단점 중 하나로 연산량이 너무 높아 추론(inference) 시간이 길게 걸린다는 것이 있다.
  • 좋은 결과를 내려면 더 많은 연산을 해야 한다.
  • 이를 해결하기 위해 Quntized inference 를 수행한다.
    • 수치 정확도를 낮추어 더 빠른 연산을 수행하게 된다.
  • 이미 많은 연구에서 Quantize 에 대한 연구를 진행하고 있다. (CNN 분야 등)
  • stacked RNN 구조에서는 아직 이를 적용한 분야가 없는데 여기서 해본다.
  • 사실 우리가 사용한 방식은 구글 내부에서 사용하는 하드웨어에 최적화된 방식이다.
  • quantize 로 인한 에러를 최소화하기 위해 학습시 모델에 약간의 제약을 가한다.
    • 그리고 이러한 quantize 로 인한 에러가 거의 없음을 확인하였다.
  • 학습시 가한 제약으로 학습을 하고 나면 추론시에 별도의 추가 작업 없이도 이 quantize를 사용하는 효과.
  • 앞서 살펴보았던 LSTM 식을 떠올려보자. 이를 약간 수정한 형태이다.
\[\begin{align}{\bf c}_{t}^{'i}, {\bf m}_{t}^{i} &= LSTM_i({\bf c}_{t-1}^{i}, {\bf m}_{t-1}^{i}, {\bf x}_{t}^{i-1};{\bf W}^{i}) \\ {\bf c}_{t}^{i} &= \max(-\delta, \min(\delta, {\bf c}_{t}^{'i})) \\ {\bf x}_{t}^{'i} &= {\bf m}_{t}^{i} + {\bf x}_{t}^{i-1} \\ {\bf x}_{t}^{'i} &= \max(-\delta, min(\delta, {\bf x}_{t}^{'i}) \\ {\bf c}_{t}^{i+1}, {\bf m}_{t}^{i+1} &= LSTM_{i+1}({\bf c}_{t-1}^{i+1}, {\bf m}_{t-1}^{i+1}, {\bf x}_{t}^{i};{\bf W}^{i+1}) \\ {\bf c}_{t}^{'i+1} &= \max(\delta, min(\delta, {\bf c}_{t}^{'i+1})) \end{align}\qquad{(10)}\]
  • 식 10은 \(LSTM\) 내부 게이트 로직에서 사용되게 된다.
  • 참고로 \(LSTM\) 내부 식을 살펴보도록 하자.
\[\begin{align}{\bf W} &= [{\bf W}_1, {\bf W}_2, {\bf W}_3, {\bf W}_4, {\bf W}_5, {\bf W}_6, {\bf W}_7, {\bf W}_8 ] \\ {\bf i}_t &= sigmoid({\bf W}_1{\bf x}_t + {\bf W}_2{\bf m}_t) \\ {\bf i'}_t &=tanh({\bf W}_3{\bf x}_t + {\bf W}_4{\bf m}_t) \\ {\bf f}_t &= sigmoid({\bf W}_5{\bf x}_t + {\bf W}_6{\bf m}_t) \\ {\bf o}_t &= sigmoid({\bf W}_7{\bf x}_t + {\bf W}_8{\bf m}_t) \\ {\bf c}_t &= {\bf c}_{t-1} \odot {\bf f}_{t} + {\bf i}_{t}^{'} \odot {\bf i}_{t} \\ {\bf m}_t &= {\bf c}_{t} \odot {\bf o}_{t} \end{align}\qquad{(11)}\]
  • quantized 시에 사용된 모든 실수 값은 (식 10과 11에서) 모두 8-bit 또는 16-bit 실수 값으로 처리된다.
  • 위에서 사용된 weight 행렬 \({\bf W}\) 는 사실 8-bit 정수 행렬 \({\bf WQ}\) 로 변환하여 사용한다.
\[\begin{align}s_i &= \max(abs({\bf W}[i,:])) \\ {\bf WQ}[i,j] &= round({\bf W}[i,j] / {\bf s}_i \times 127.0) \end{align}\qquad{(12)}\]
  • \({\bf c}_t^i\) 와 \({\bf x}_t^i\) 는 모두 16-bit 정수 값으로 표현 가능하다.
    • 이를 위해 \([-\delta, \delta]\) 범위를 사용한 것이다.
  • 모든 weight 행렬은 (위에서 언급한 것과 같이) 8-bit 정수로 처리된다.

  • 그리고 \(sigmoid, tanh\) 등의 함수와 element-wise 연산인 \( (\odot, +) \) 등도 모두 정수에 대한 연산으로 수행된다.

  • (참고) TensorFlow 에 포함된 Quantization 을 참고하도록 하자.
  • 마지막으로 이 논문에서 사용한 log-linear softmax 레이어를 살펴보자.
  • 학습 과정 동안 decoder RNN 에서는 출력 값 \({\bf y}_t\) 를 내어놓게 된다.
    • 이를 이용하여 확률 \({\bf p}_t\) 를 만든다.
\[\begin{align}{\bf v}_t &= {\bf W}_s \times {\bf y}_t \\ {\bf v}_t^{'} &= \max(-\gamma, min(\gamma, {\bf v}_t)) \\ {\bf p}_t &= softmax({\bf v}_t^{'})\end{align}\qquad{(13)}\]
  • 마찬가지로 여기서도 \({\bf W}_s\) 는 8-bit 의 정수값 행렬이다.

  • clipping 을 위한 계수 \(\gamma\) 는 실험에서는 25를 사용하였다.

  • 학습시 성능을 좀 살펴보자.

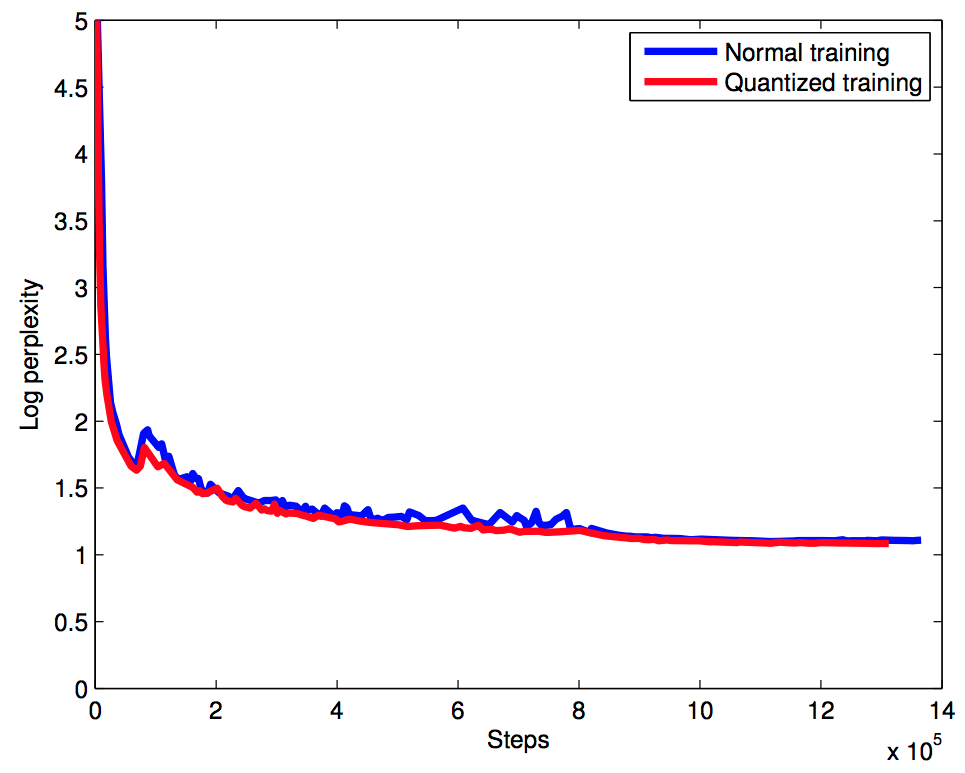
figure.5

  • perplexity 는 거의 차이가 없다는 것을 알수 있다. (오히려 quantized model 이 더 성능이 좋다.)
  • 다음으로 전체 지표이다. TPU 가 정말 좋다는 것을 알수 있다. (TPU는 구글 자체 머신)

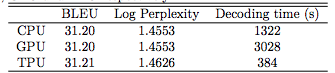
figure.6

Decoder

  • 최종 출력 문자열 \({\bf Y}\) 를 만들기 위해 빔서치(beam search)를 사용한다.
  • 점수 함수 \(s({\bf Y}, {\bf X})\) 는 학습시 주어진다.
  • 여기서는 빔서치를 최적화하기 위한 두 가지 기법을 소개한다.
    • coverage penalty
    • length normalization
\[\begin{align}s({\bf Y}, {\bf X}) &= \log(P({\bf Y}|{\bf X}))/lp({\bf Y}) + cp({\bf X};{\bf Y}) \\ lp({\bf Y}) &= \frac{(5+|{\bf Y}|)^{\alpha}}{(5+1)^{\alpha}} \\ cp({\bf X};{\bf Y}) &= \beta * \sum_{i=1}^{|{\bf X}|} \log(\min(\sum_{j=1}^{|{\bf Y}|}p_{i,j}, 1.0)), \end{align}\qquad{(14)}\]
  • 먼저 Length Normalization 은 길이가 평가시 긴 문장의 확률 값이 더 작아지므로 이를 보정하기 위한 방법.
    • 이를 위해 하이퍼 파라미터인 \(\alpha\) 를 사용한다.
    • \(\alpha\) 는 보통 \(0\) ~ \(1\) 사이의 값을 사용한다. (실험에서는 \(0.6\) ~ \(0.7\) 사용)
  • Coverage penalty 는 잘 모르겠음.
    • \(p_{i,j}\) 는 출력 단어 \(y_j\) 에서의 (즉, \(j\) 번째 위치에서의) attention 확률이 된다.
    • encoder 에서의 확률 normalization 과 같다고 보는데 좀 더 확인이 필요하다.
  • 영어를 프랑스어로 바꿀 때 \(\alpha\) 와 \(\beta\) 값을 실험. (결과는 BLEU 값)
    • RL 방식이 아니라 ML 방식임.

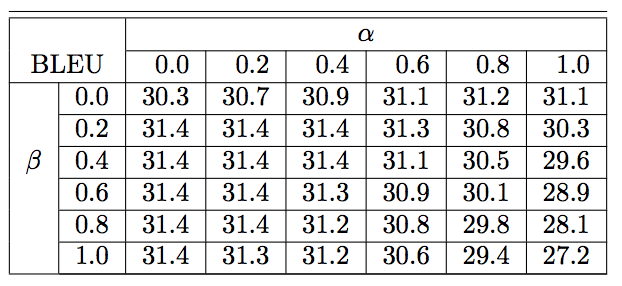
figure.7

  • ML 방식을 쓰고 다시 RL 방식으로 튜닝한 방법.

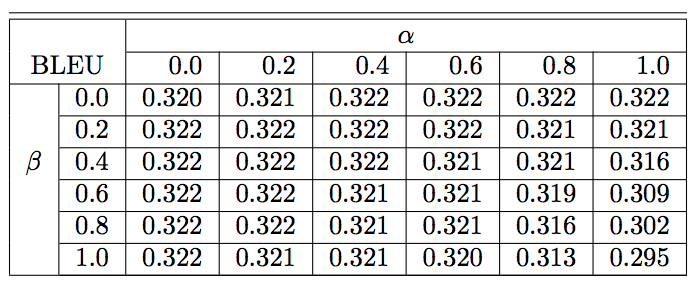
figure.8

Experimetns & Results

  • 사용한 데이터는 \(WMT\) \(En \to Fr\) 과 \(WMT\) \(En \to De\) 이다.
    • \(WMT\) \(En \to Fr\) : 35M 쌍의 문자열.
    • \(WMT\) \( En \to De\) : 5M 쌍의 문자열.

평가방식

  • BLEU 점수. (Moses 에서 구현한 BLEU 점수 측정 방식을 사용)

학습 방법

  • TensorFlow 로 구현하여 사용
  • 병렬화 적용함. (12개의 독립 머신)
  • 파라미터는 모두 공유되고(shared) 업데이트 방식은 asynchronous 방식.
  • 모든 파라미터들은 \([-0.04, 0.04]\) 범위의 값으로 초기화하고 시작.
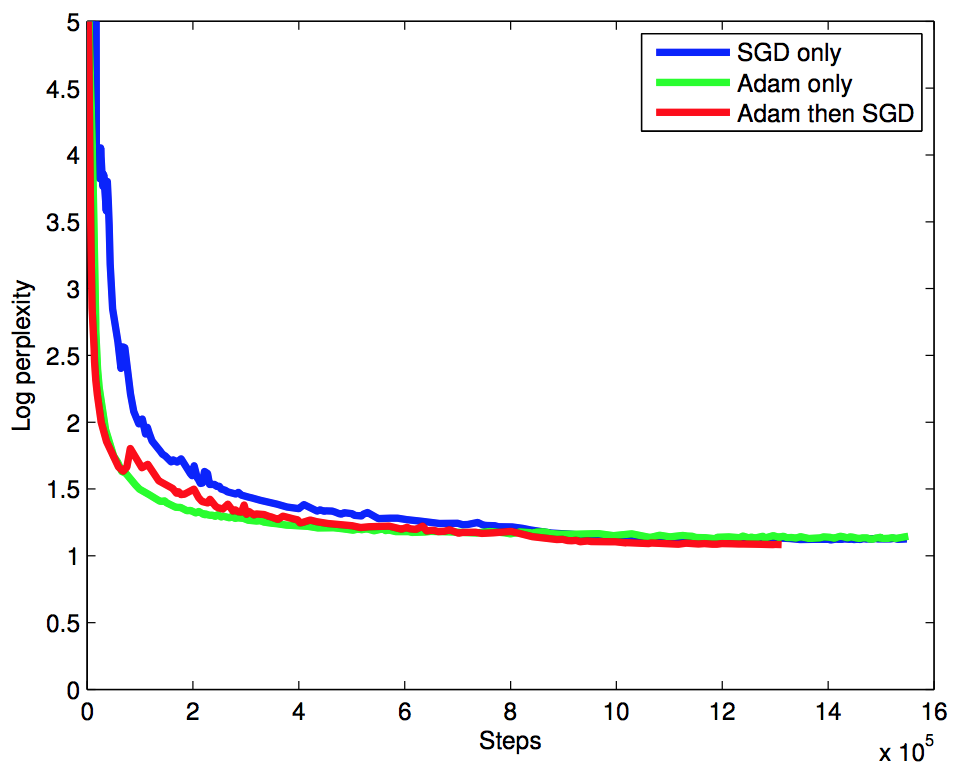
  • Adam 옵티마이져와 기본 SGD 방식을 혼합해서 사용.
    • 먼저 60K step 만큼은 Adam 방식을 사용하고 그 다음부터는 기본 SGD를 돌림.
    • 우리가 해보니까 초기 학습 속도를 올리는데에는 Adam 이 짱인데 끝이 별로다. 그래서 뒷 부분은 SGD로 바꿈.

figure.9

  • \(lr\) 은 \(0.5\) 를 사용하였다.
    • \(1.2M\) 까지 그대로 사용하다가 그 이후는 \(200k\) 단위마다 반씩 줄여가면서 \(800k\) 까지 학습.
  • 총 96대의 K80 GPU 장비에서 6일 걸림.
  • 오버피팅(overfeating)을 막기 위해 드롭아웃 쓴다. (\(0.2 ~ 0.3)\) 정도의 비율.
    • 근데 이건 ML 모델에서만 사용하고 RL 모델에서는 안 씀.
  • 그 외 실험 결과는 생략한다.