페이스북(facebook)이 공개한 Convoutional Seq2Seq 모델.
자료
- 코드는 여기에 공개되어 있다.. (torch 구현체로 루아 코드임)
- 추가로 아래에 정리한 논문 이전에 발표된 논문이 존재한다.
Introduction
- Seq2Seq 모델은 기계번역 영역에서 매우 성공적인 모델이었음.
- 2014년 NIPS에서 Sutskever가 이를 발표. 엄청난 인기를 모음.
- Sutskever가 최초의 Seq2Seq 발명자로 알고 있는 사람이 많은데 실은 조경현 교수가 먼저 발표한 모델. (링크)
- 현재 Seq2Seq에서 일반적으로 사용하는 모델은 Bi-directional RNN 모델.
- 여기에 soft-attention 을 추가하면 금상첨화.
- 반면 CNN 모델을 이용하여 이런 시도를 하던 사람도 있긴 있었음.
- 고정된(fixed) Conv 크기를 가져야 한다는 단점이 있진 하지만 (RNN에 비해) 생각보다 CNN의 장점도 많다.
- RNN보다 더 많은 stack을 쌓을 수 있다.
- 이전 step에 영향을 받는 구조가 아니므로 병렬화에 유리하다.
- 고정된(fixed) Conv 크기를 가져야 한다는 단점이 있진 하지만 (RNN에 비해) 생각보다 CNN의 장점도 많다.
- Multi-layer CNN은 hierarchical representation 을 갖는다.
- 이런 구조는 RNN 방식보다 정보를 더 오랫 시간동안 유지할 수 있는 힘의 원천.
- 이 논문에서는 CNN 만을 활용하여 Seq2Seq 연산을 어떻게 제공하는지를 다룸.
Seq2Seq with RNN
- 논문에서는 아주 간단하게 RNN을 활용한 Seq2Seq를 소개함. 하지만 여기서는 아주 간단하게만 보자.
- 어쨌거나 최근 Sequence Task의 기본 base라 할 수 있을만큼 대세인 방식.
- 관련 이론으로 RNN계열로 GRU나 LSTM 정도만 알고 있으면 될 듯 하다.
- Attention을 추가로 알고 있으면 좋다.
- 보통 최종 출력되는 output 에 대한 식은 다음과 같이 정의된다.
- 여기에 attention 모델을 추가하면 다음과 같은 식을 사용하게 된다.
- 논문에서 생략한게 너무 많은 거 같다. 간단하게 적어보자.
- \(c_i\) 는 decoder 에 들어가는 입력 값. 결국 \(a_{i:}\) 에 많은 영향을 받게 될 것이다.
- \(z_j\) 는 encoder 의 출력값. encoder 의 max 크기에 영향을 받게 된다. (\(m\))
- \(d_i\) 는 Seq 연산 중에 다음 attention 영역 계산시 사용되는 요소이다.
- 식을 잘보자. 모든 \(i\) 와 \(j\) 에 대해 연산을 해야 한다. (\(j\) 는 encoder 길이. \(i\)는 decoder 길이가 된다.)
- 출력에 대한 seq 정보를 얻어 다음에 바라봐야 할 attention 영역을 만들어낼 때 사용되는 값으로,
- 일단 \(W_d h_i + b_d\) 는 \(g_i\) 와의 크기를 맞추기 위한 선형 변환이고,
- \(g_i\) 는 이전 decoder 의 출력값이다.
- 결국 attention \(a_{ij}\) 는 encoder 의 출력값에 대해 실제 decoder 의 이전 출력 seq 를 따라가면서 집중해야 할 영역을 찾아내는 과정이라는 것.
- 설명이 어렵지만 attention 을 한번이라도 살펴봤던 사람이라면 대충 느낌적 느낌은 떠오를 것이다.
- (참고) Seq2Seq Encoder-Decoder 방식에 대한 내용이 잘 설명된 자료 : 링크
Convolutional Architecture
- 표기
- 입력 문자열 : \({\bf x} = (x_1, …,x_m)\)
- 입력에 대한 Embedding 벡터 : \({\bf w} = (w_1, …,w_m)\)
- 입력에 대한 Position 벡터 : \({\bf p} = (p_1, …,p_m)\)
- 실제 입력 벡터 : \({\bf e} = (w_1 + p_1, …,w_m + p_m)\)
- Decoder로부터 얻어지는 Feed-back 벡터 : \({\bf g} = (g_1, …,g_m)\)
- Encoder 출력 벡터 : \({\bf z^l} = (z_1^l, …,z_m^l)\)
- Decoder 출력 벡터 : \({\bf h^l} = (h_1^l, …,h_m^l)\)
- Convolution 커널의 크기 : \(k\)
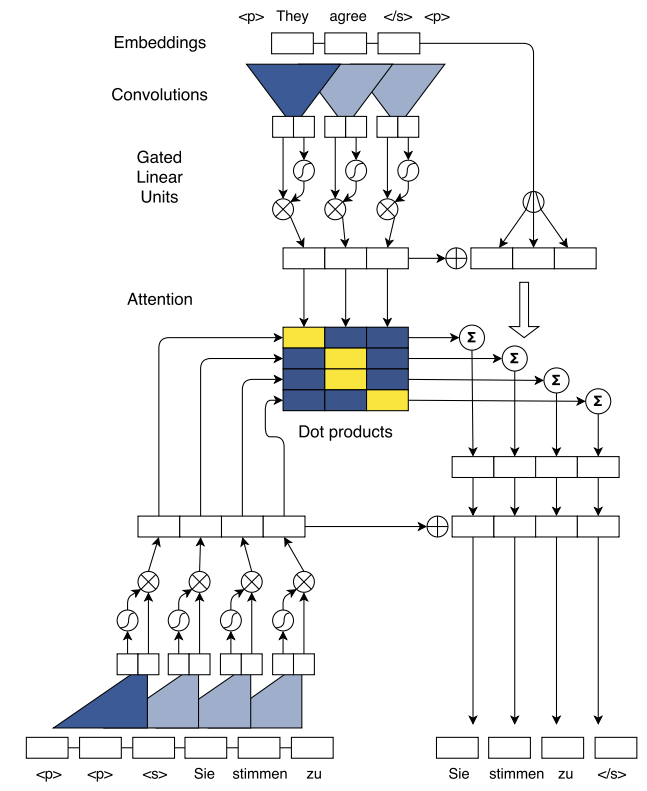
- Convolutions
- 내맘대로 표기법. (논문의 표기가 복잡하게 되어 있음)
- word embedding \(e_j^{(d)} = w_j^{(d)} + p_j^{(d)}\).
- input block \(X^{(kd)} = [ e_{j}^{(d)},…,e_{j+k-1}^{(d)} ]\)
- convolution 출력 \(conv_o^{(2d)} = W^{(2d \times kd)} X_k^{(kd)}\)
- 참고로 convolution을 구성할 때에는 문장의 양 끝에 \(k-1\) 갯수만큼 패딩을 추가한다.
- 이렇게하면 입력과 출력의 차원이 같아진다.
- GLU (Gated Linear Units)
- 공동 저자인 Dauphin이 제안한 모델. (이 논문을 참고하자.)
- CNN 을 이용한 Seq 모델에서 사용하는 gate 로 LSTM 내의 gate와 유사. (하지만 훨씬 간단하다.)
- 저자의 주장으로는 이런 간단한 모델로도 성능이 좋다고..
- 여기서 \(A\) 와 \(B\) 는 각각 d 차원의 크기를 가진다. ( \(A, B \in {\mathbf R}^d\) )
- \(\otimes\) 는 point-wise 곱을 의미한다.
- 따라서 \(v\) 또한 \(v([A, B]) \in {\mathbf R}^d\) 를 만족한다.
- 이전 연구에서 Oord 가 \(tanh\) 를 이용하여 이런 모델을 만들긴 했었다.
- Dauphin 은 이전 논문에서 \(tanh\) 보다 \(\sigma\) 가 언어 모델링 쪽에서는 더 성능이 좋다는 것을 보였다.
- Deep한 모델을 설계할 때 Residual Connection을 사용하면 성능이 더 좋아진다.
- 따라서 여기서는 모든 Convolution 레이어마다 Residual connection을 추가한다.
- 이 말은 Convolution 층이 하나가 아니라 여러 층이라는 것.
- 마찬가지로 GLU도 각 층마다 추가한다.
- 이제 Convolution에 대해 일반화된 식으로 다시 기술하면 다음과 같다.
- 앞서 설명한대로 입력쪽의 경우 Encoder 출력의 크기가 입력과 동일하기 때문에 이런 방식의 구현에 문제가 없다.
- 하지만 Decoder 의 출력 개수는 알수가 없다. (보통 RNN에서는 end-tag 혹은 max margin 값에 다다르면 종료)
- 이제 지금까지 설명한 내용을 그림으로 보자.
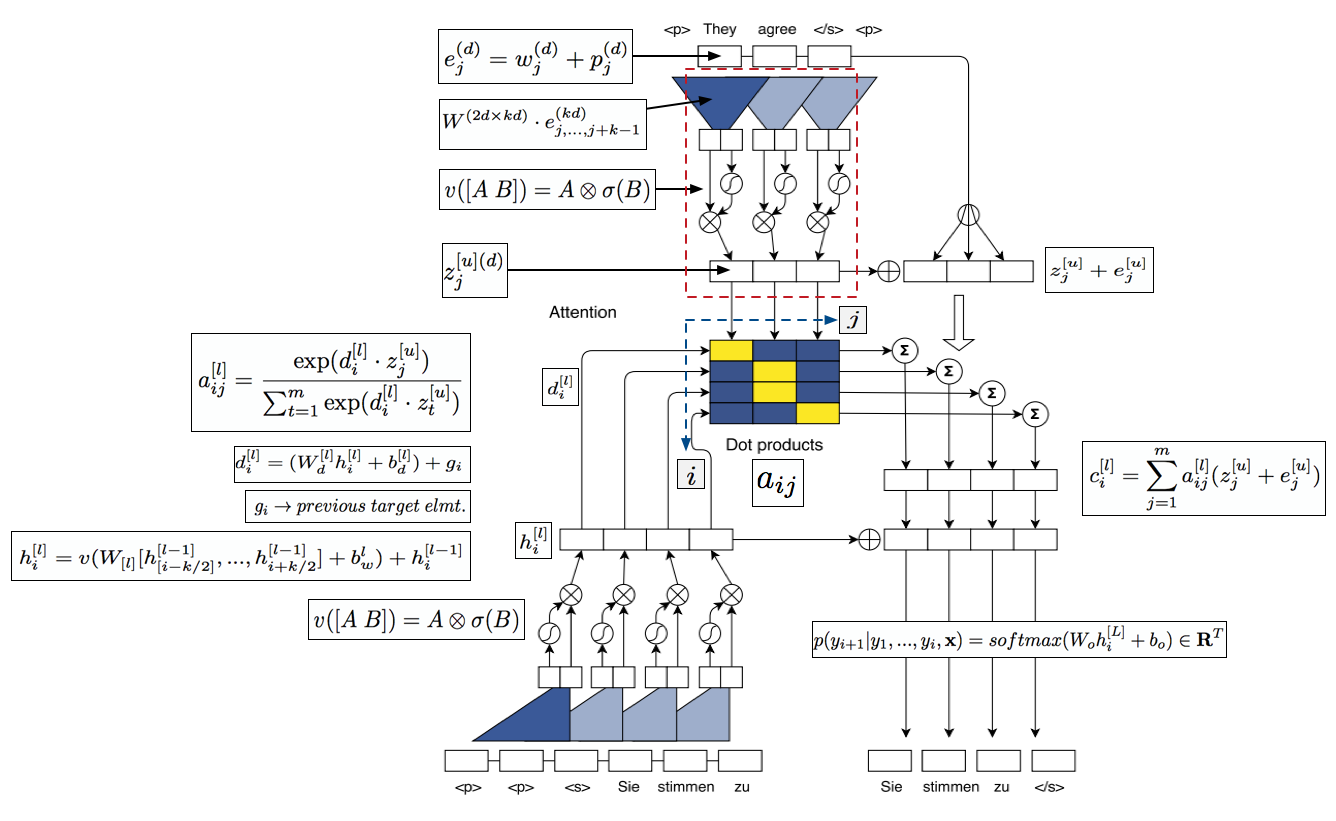
- Decoder 가 Multi layer 구조인 경우엔 위의 그림만으로는 부족하다.
- 아래 gif 이미지를 참고하자.

Normalization 전략
- Weight Normalization
- 우선, 이 논문에서는 Batch Normalization은 사용하지 않는다.
- 이전 논문들에서 이미지의 경우 CNN에서 BN이 좋은 성능을 보이지만 문서와 관련된 CNN에서는 별로 품질이 좋지 않다는 것을 확인했다고 한다.
- 그래서 대신 여기서는 Weight Normalization이란 기법을 쓴다.
- BN은 Batch 에 포함된 Sample에 영향을 받는데 WN은 그런 방식은 아니다.
- 가중치(W)를 정규화
- CNN의 경우 RNN에 비해 W 갯수가 적다. 이런데 유리하다.
- 보통 BN에 대해 저연산비용을 들이면서 근사를 할 수 있는 모델로 알려져 있다.
- 관련해서 참고할만한 자료 : 링크
- 우선, 이 논문에서는 Batch Normalization은 사용하지 않는다.
- Weight Initialization
- W를 초기화하는 방법은 참 여러가지인데 가장 간단한 방법은 0에 가까운 값을 random 설정하는 것.
- 여기서는 아주 진지 하게 분산을 고려하여 초기 W 바운드를 검증한다.
- 이전부터 이런 류의 초기화 방식에 관련된 논문들이 많았었다.
- cs231n 자료에도 이와 비슷한 내용이 나오기도 한다. (링크)
- 여기서도 이를 비슷한 방식으로 증명하여 초기값 범위를 설정함.
- 논문 뒷 부분에 수식 풀이가 기술되어 있으니 호기심에 밤잠을 못이룰 것 같으면 읽고 자도록 하자. (잠 잘올듯)
Experiments
- 실험 결과는 간단하게 정리하자.
- 사용되는 데이터는 주로 WMT 데이터 (링크)
- 2006년부터 시작된 workshop으로 매년 데이터 set을 제공하는 듯 하다. (task 진행)
- ACL 행사 때 함께 진행되는 task인 듯.
- WMT16은 영어를 불가리아어, 치코어, 독일어, 스페인어, 바스크어, 네덜란드어, 포르투칼어 등으로 번역 (IT 관련 자료임)
- 사용된 모델의 파라미터 정리
- encoder, decoder 에 사용된 hidden layer 크기는 512
- Nesterov Gradient Method (링크) 사용
- momentum : 0.99
- lr : 0.25
- batch size : 64 문장 단위
- GPU 메모리에 맞춘 크기
- Dropout 사용 (입력 convolution 영역)
- 구현
- Torch 로 구현되어 있음.
- M40 GPU 장비 (single)
- 영어-프랑스어(WMT14) 번역에는 Multi-GPU 사용 (single machine)
- 평가
- Word-base 방식과 BPE 방식을 사용
- Word-base 방식은 Voca 를 구축하고 OOV가 발생하면 Copy를 한다.
- BPE (Byte Pair Encodeing) 은 다음 논문을 참고하자.
- 56개는 복합어, 21개는 이름. 6개는 외래어였다.
- 아 OOV에 대해서는 쪼개어서 subword를 구성하면 성능이 좋아질 수 있겠구나.
- 그냥 “
lower단어 같은 걸low+er등으로 나누어볼 수 있다” 정도로 받아들이도록 하자.
- Word-base 방식과 BPE 방식을 사용
- 성능
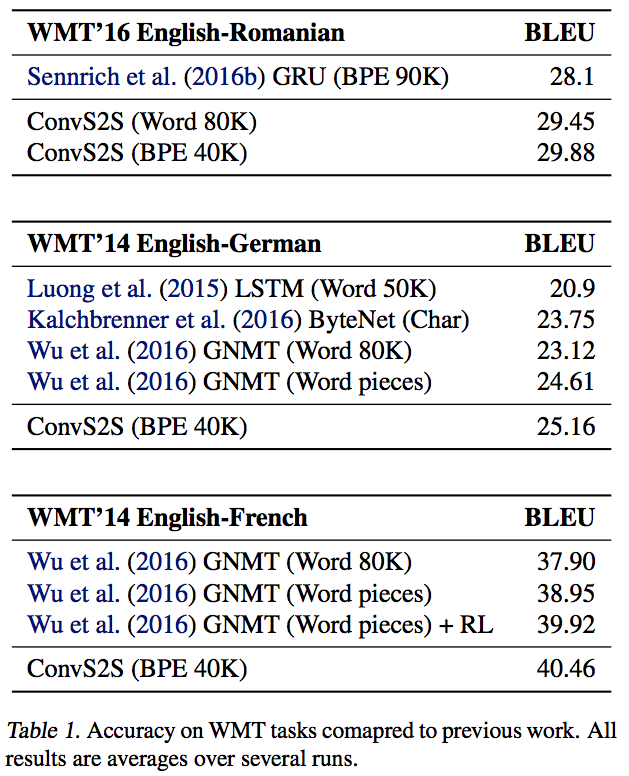
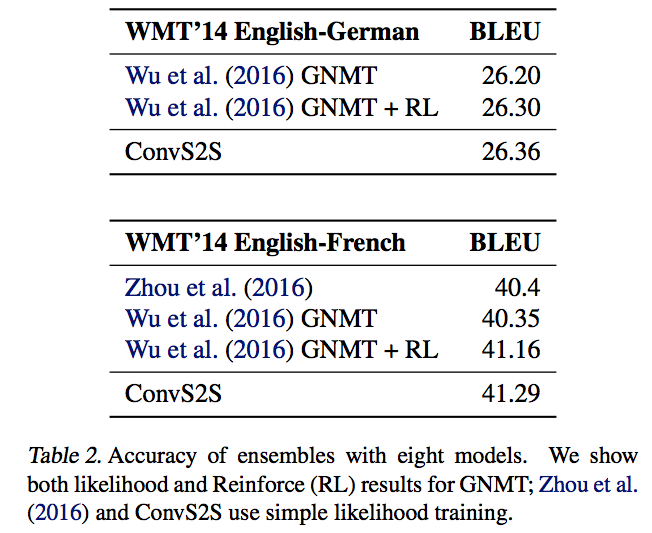
- 앙상블
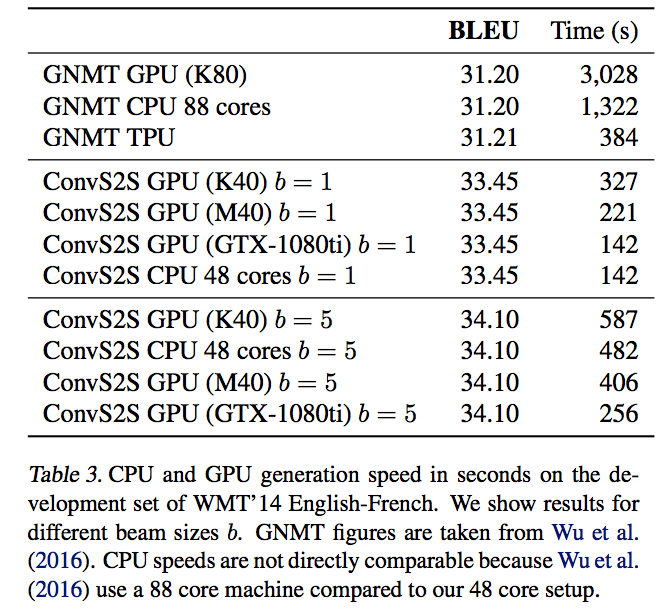
- 시간 성능 측정
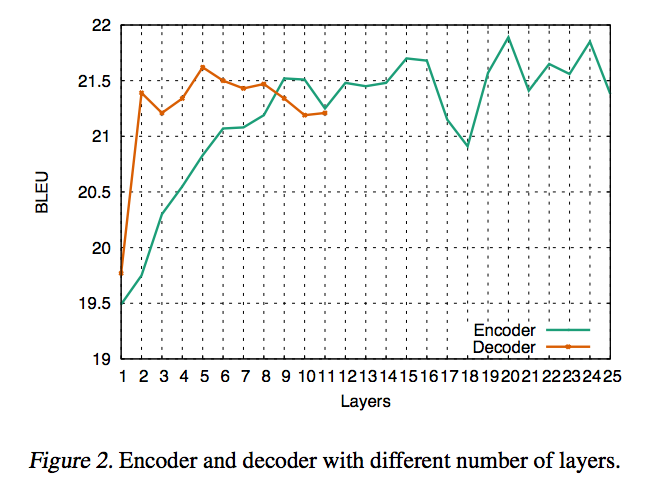
- Attention Layer
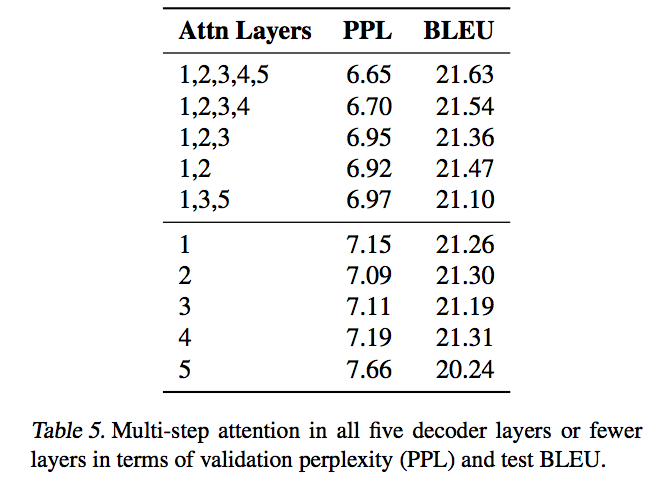
- Layer Count