- (참고) 나온지 얼마 되지도 않은 논문인데 벌써 여러군데 참고할만한 글들이 올라온다. (링크)
- 아마 압도적인 성능 때문에 큰 이슈가 되는 듯.
Introduction
- ConvNet 의 성능을 올리기 위해 scaling up 을 시도하는 것은 매우 일반적인 일.
- 우리가 잘 알고 있는 ResNet 은 ResNet-18 부터 ResNet-200 까지 망의 깊이(depth)를 늘려 성능 향상을 이루어냄.
- 아주 자연스럽게 망이 깊어질수록 성능이 좋아진다는 것을 이해할 수 있다.
- 최근 GPipe 를 사용한 모델은 이미지넷 top-1 을 84.3% 까지 끌어올렸다.
- scale-up 방식이 성능을 올리는데 주요한 요소라는 것은 알았지만 아직까지 scaling up 에 대한 연구는 부족한 상황.
- 크게 3가지 방식의 scale-up 이 있다.
- 망의 depth 를 늘리는 것
- channel width 를 늘리는 것
- 입력 이미지의 resolution 을 올리는 것
- 이 논문에서는 이 세가지 방법에 대한 최적의 조합을 어떻게 찾을 수 있는지를 연구한다.
- 중요한 것은 제한된 resource 범위 내에서 최적의 조합을 고려한다.
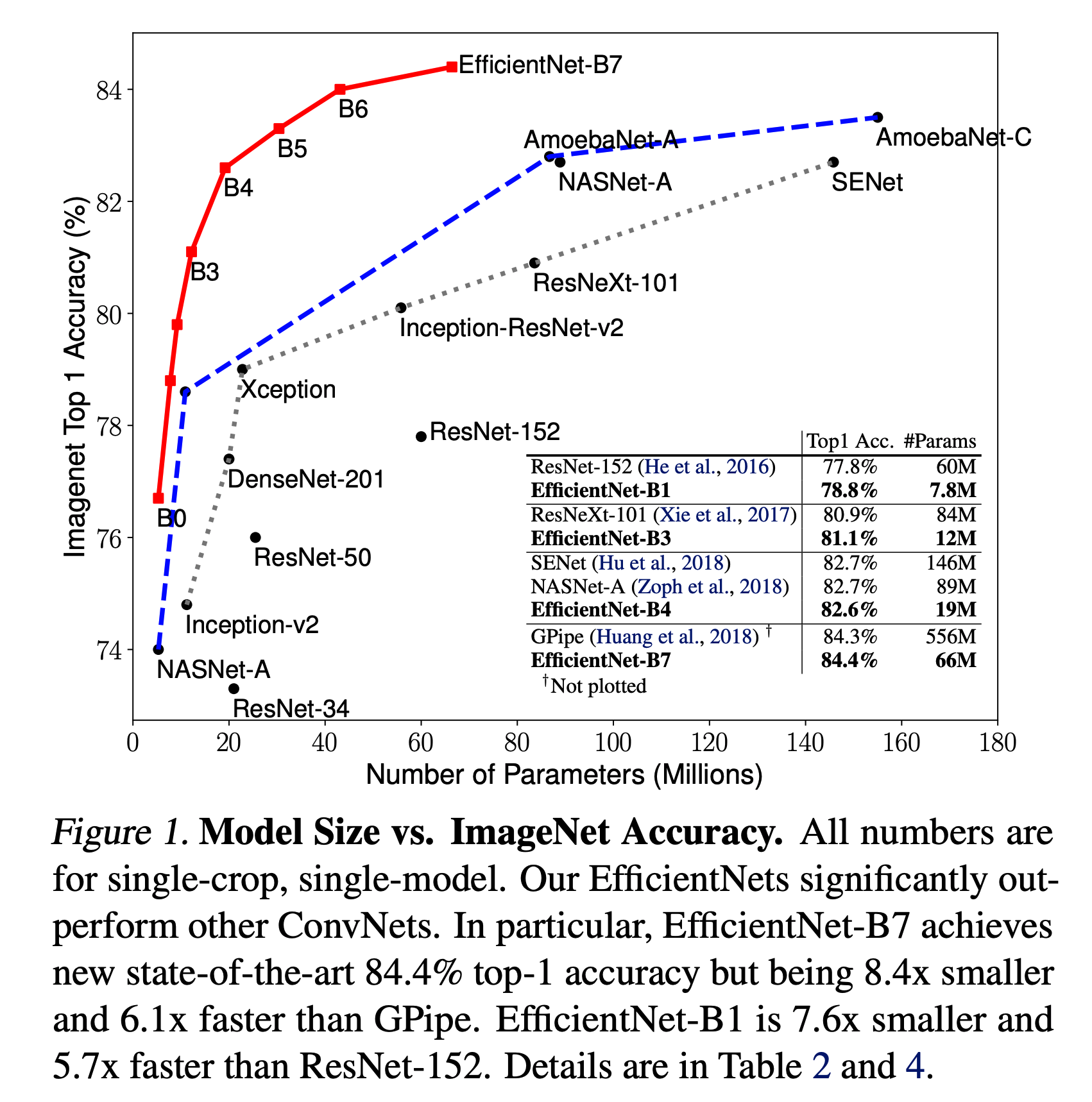
- 아래 그림을 보면 정말 압도적으로 적은 Parameter 수로 어마어마한 성능을 낼 수 있음을 알 수 있다.
- 이제 이 결과가 블러핑이 아닌 것만 확인된다면 이미지 분류의 새로운 장이 열릴수도 있다.
- 다음은 세가지 scale-up을 나타내는 그림이다.
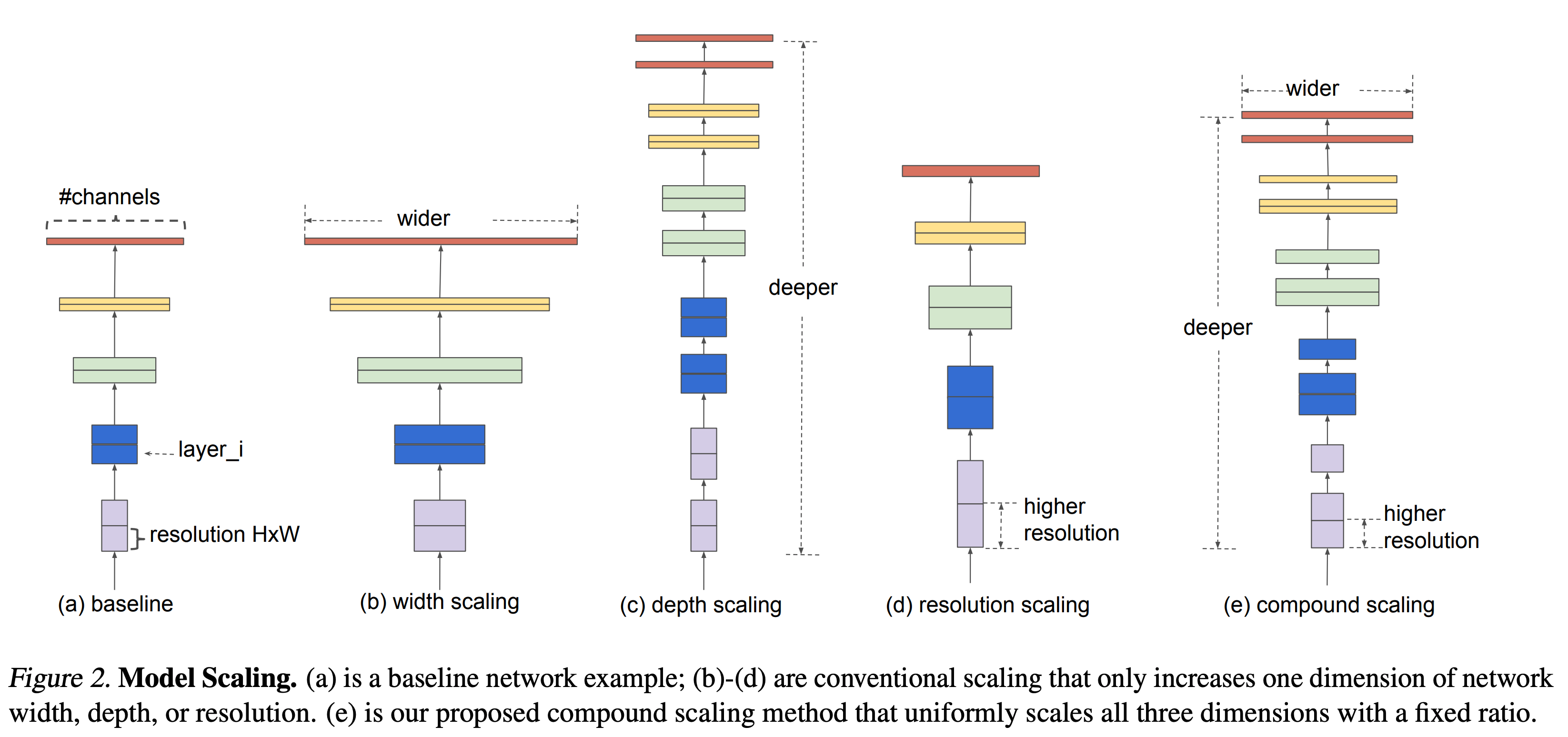
- 이 논문의 목적은 그림 맨 오른쪽에 있는 compound scaling 을 잘 해보겠다는 것이다.
- 직관적으로 생각해보면 compound scale up을 잘 만들기 위한 가장 손쉬운 방법은 depth/width/resolution 을 모두 다 크게 키우는 것이다.
- 당연히 이 논문에서 이를 검증해 본다.
- 논문에서는 MobileNet 과 Resnet 을 이용하여 이를 확인한다. (이름은 EfficientNet 으로 지었다.)
- 그림.1 에서 알 수 있듯 EfficientNet-B7 이 GPipe 를 눌렀다.
- 그럼에도 불구하고 파라미터의 사용량은 1/8 수준이다.
- 실제 Inference 시간도 6배 빠르다.
Compound Model Scaling
-
여기서는 compound model scaling 을 어떻게 수행하는지를 다룬다.
- 표기법
- 신경망 : \(Y_i = F_i(X_i)\)
- \(F_i\) 는 연산자, \(Y_i\) 는 출력 텐서, \(X_i\) 는 입력 텐서.
- \(X_i\) 의 크기는 \(<H_i, W_i, C_i>^1\)
- \(N\) 는 레이어의 결합체
- \(N=F_k \odot …\odot F_2 \odot F_1(X_1)=\bigodot_{j=1,…k}F_j(X_1)\)
- 신경망 : \(Y_i = F_i(X_i)\)
- 일부 망들은 전체 레이어(layer)를 몇개의 스테이지(stage)로 나눌 수 있다.
- ResNet 은 5개의 stage 로 구분된다.
- 모든 stage 는 모두 동일한 conv 연산을 수행한다.
- 단, stage의 첫번째 layer 는 조금 다르게 downsampling 기능이 추가되어 있다.
-
참고로 그림 2(a) 에서 입력 크기는 \(<224, 224, 3>\) 이고, 출력 크기는 \(<7, 7, 512>\) 이다.
-
이제 최종 목표를 간단하게 식으로 정리해보자.
- 이 문제의 어려운점은 \(d, w, r\) 이 서로 독립적인 관계가 아닌데다가 resource 의 제약도 존재한다는 것.
- 이런 어려움으로 인해 지금까지는 하나의 factor 에 대해서만 변화를 가하는 작업들이 이루어졌다.
- Depth(d)
- 가장 흔한 scale-up 방법으로 깊은 망은 더 높은 성능을 내는 것은 이미 잘 알려진 사실.
- 하지만 망을 계속 깊게 쌓는 것은 한계가 있다. ResNet-1000 은 ResNet-101 과 거의 비슷한 성능을 가지게 된다.
- Width(d)
- width 를 제어하는 모델은 대개 작은 크기의 모델들이었다.
- 기존의 연구에 따르면 width 를 넓게 할수록 미세한 정보 (fine-grained feature)들을 더 많이 담을 수 있다는 것이 알려져있다
- Resolution(d)
- 입력에 더 큰 이미지를 넣으면 성능이 올라간다.
- 이전의 다른 연구에서 입력 크기가 \(224 \times 224\) 인 모델보다 \(331 \tims 331\) 이미지를 사용했을 때 더 좋은 성능을 냄을 확인하였다.
- 최신 연구인 GPipe 에서는 \(480 \times 480\) 크기를 사용한다.
- 또한 object-detection 영역에서는 \(600 \times 600\) 을 사용하면 더 좋은 성능을 보임을 확인했다.
- 관찰.1
- width/depth/resolution 을 키우면 성능이 올라가지만 점점 커질수록 얻어지는 이득이 적어진다.
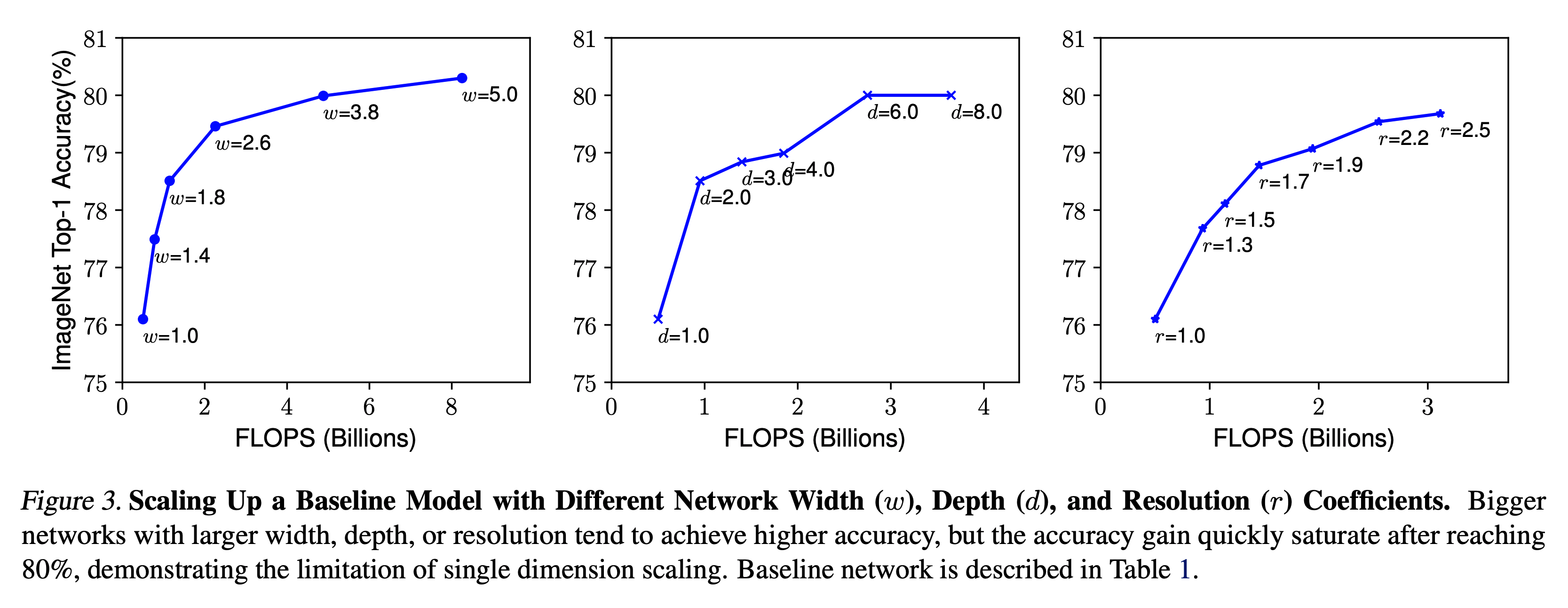
Compound Scaling
- depth/resolution 을 고정한 채로 width 값을 변하시키면서 테스트.
- 이 때 다양한 크기의 depth/resolution 을 테스트하여 확인.
-
동일한 FLOPS 에서 width/depth/resolution 조합에 따라 다양한 성능 차이를 보이게 된다.
- 관찰.2
- 최고의 정확도를 갖기 위해서는 가장 최적의 with/depth/resolution 조합을 찾아내야 한다.
- 사실 이전에도 이런 연구가 없었던 것은 아니다.
- 하지만 이를 수동으로 찾는 작업으로 시도했다.
- 이 논문에서는 새로운 방식의 compound scaling method를 제안한다.
- \(\alpha, \beta, \gamma\) 는 상수이고 grid search 를 이용하여 찾는다.
- \(\phi\) 는 사용자가 제어할 수 있는 factor 로 가용한 resource 에 따라 적당한 값을 취한다.
- 제곱의 식이 들어가 있는 이유는 FLOPS 의 배수 문제 때문.
- depth 는 2배가 되면 2배의 FLOPS 가 되지만,
- width, resolution 은 2배가 되면 4배의 FLOPS가 된다.
- 최종적인 FLOPS는 \(\left(\alpha, \beta^{2}, \gamma^{2}\right)^{\phi}\) 에 의해 결정된다.
- 이 논문에서는 \(\alpha \cdot \beta^2 \cdot \gamma^2 \simeq 2\) 라는 제약을 사용한다.
- 최종 FLOPS는 \(2^{\phi}\) 정도가 된다.
EfficientNet 구조
- base 모델이 어떤 모델이냐에 따라 기본 성능 차이가 많이 발생하므로 좋은 base 모델을 사용하는 것이 중요하낟.
- 이 논문에서는 기존에 알려진 좋은 모델을 사용한다.
- MNasNet 에서 영감을 받아 accuracy 와 FLOPS를 고려하는 최적화 방식을 사용한다.
- MNasNet과 동일한 search space 를 사용하였다.
- \(ACC(m)\times[FLOPS(m)/T]^{w}\) 를 최적화 식으로 사용함.
- 여기서 \(m\)은 모델을 나타낸다.
- 대신 이 논문에서는 응답시간(latency) 대신 FLOPS 를 최적화하였다.
- FLOPS 를 최적화하는 것이 특정 device 에 덜 영향을 받는다고 생각하였다.
- MNasNet 에서 영감을 받아 accuracy 와 FLOPS를 고려하는 최적화 방식을 사용한다.
- 이렇게 사용된 기본 모델을 EfficientNet-B0 로 명명하였다.
- MNasNet 과 거의 같으나 더 큰 FLOPS target을 설정하였으므로 모델이 좀 더 크다. (FLOPS 가 약 400M)
- 여기에 SE(Squeeze-and-Excitation) block 도 추가하였다.
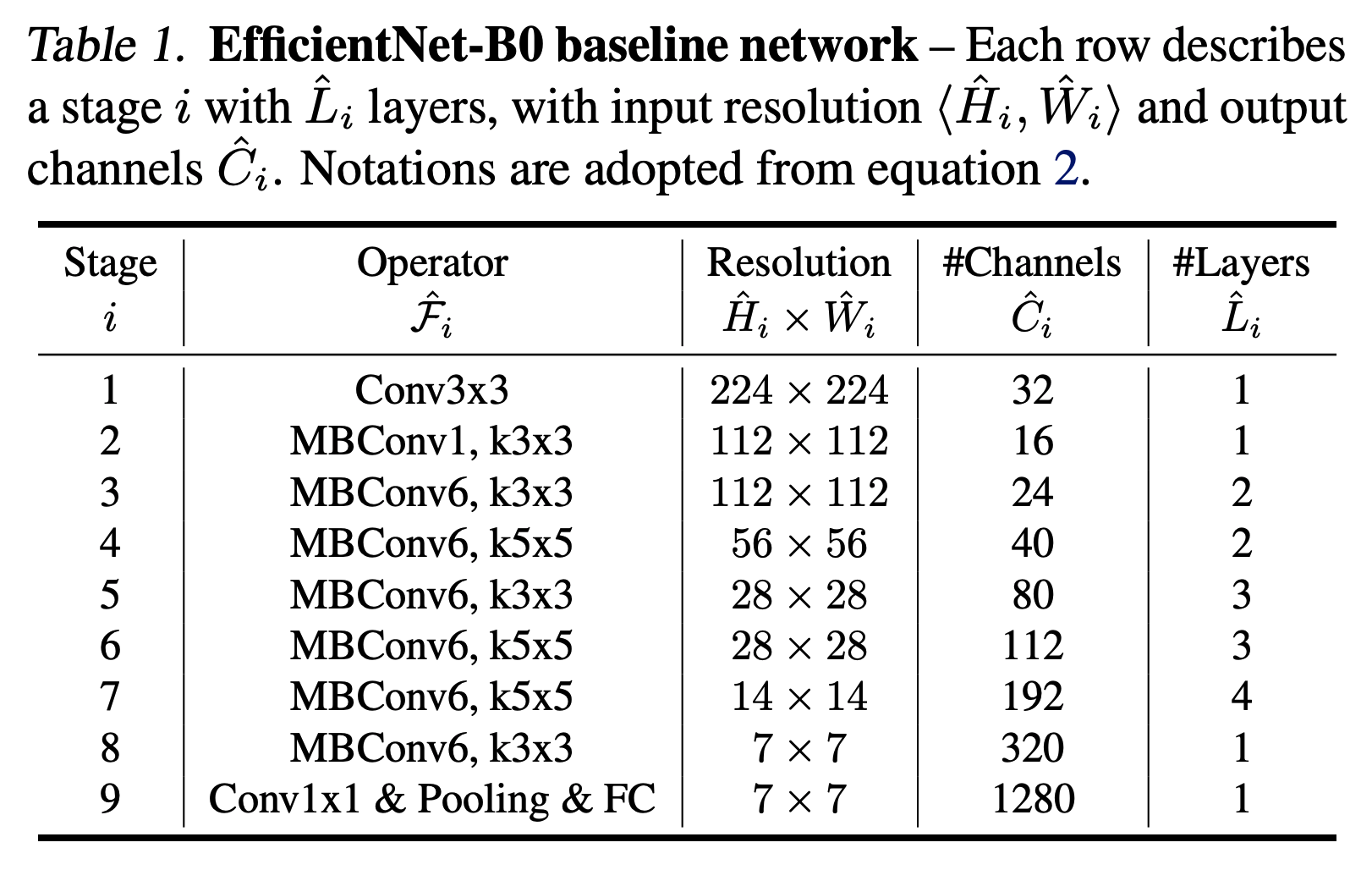
-
EfficientNet-B0 을 시작으로 다음 순서에 따라 scale 을 확장한다.
- STEP.1
- 먼저 \(\phi=1\) 로 고정한 뒤 grid search 를 수행하여 \(\alpha, \beta, \gamma\) 값을 찾는다. (식 2,3을 이용)
- EfficientNet-B0 에 대해 논문에서 찾은 값은 \(\alpha=1.2, \beta=1.1, \gamma=1.15\) 였다.
- 이 값은 \(\alpha \cdot \beta^2 \cdot \gamma^2 \simeq 2\) 를 만족한다.
- STEP.2
- \(\alpha, \beta, \gamma\) 값을 고정한 뒤 서로 다른 \(\phi\) 값을 조절한다. (식3 참고)
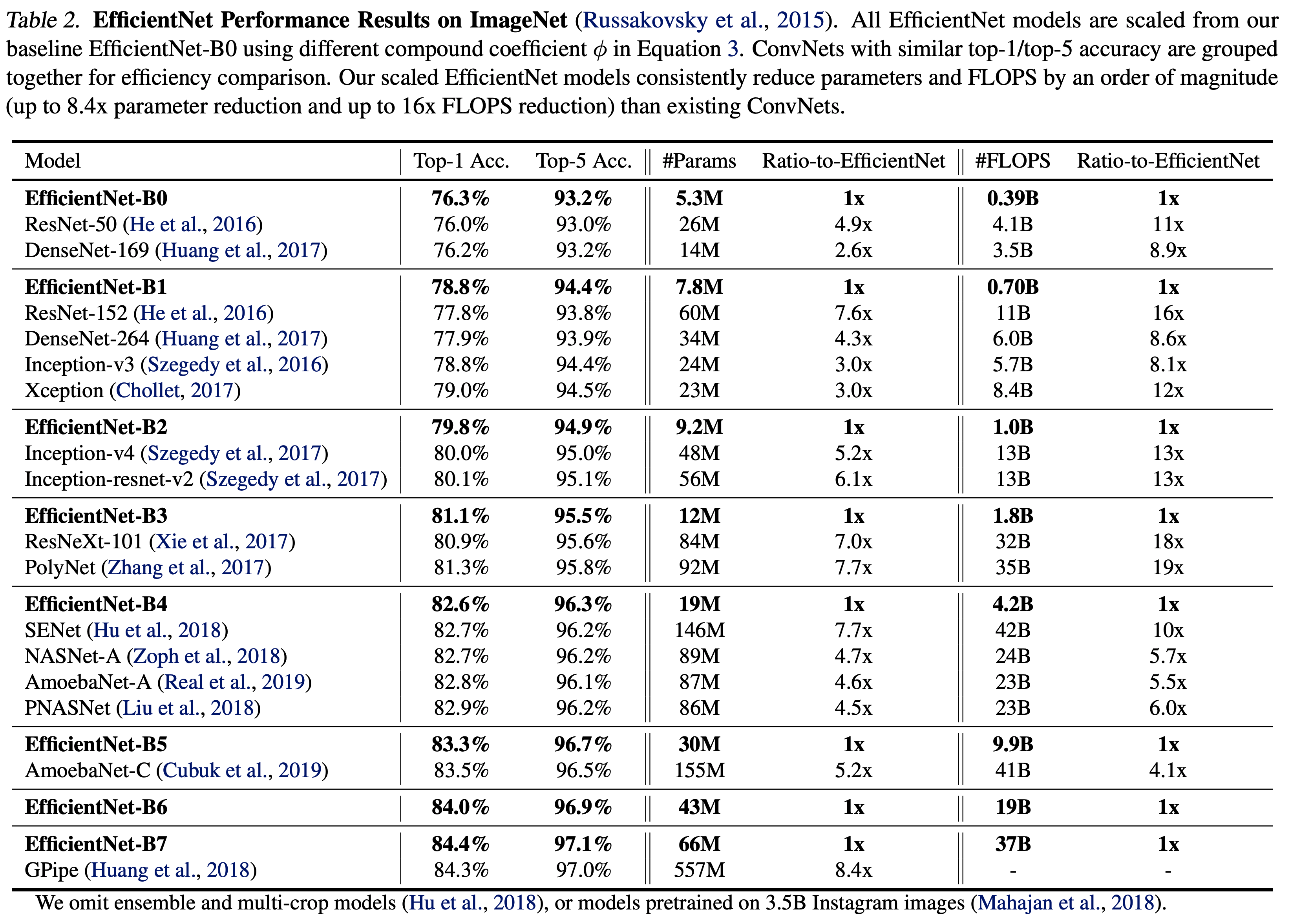
- 이렇게 해서 얻어진 결과가 EfficientNet-B1 ~ B7 까지이다.
- 자세한 사항은 Table.2 를 참고하자.
- \(\alpha, \beta, \gamma\) 값을 고정한 뒤 서로 다른 \(\phi\) 값을 조절한다. (식3 참고)
실험
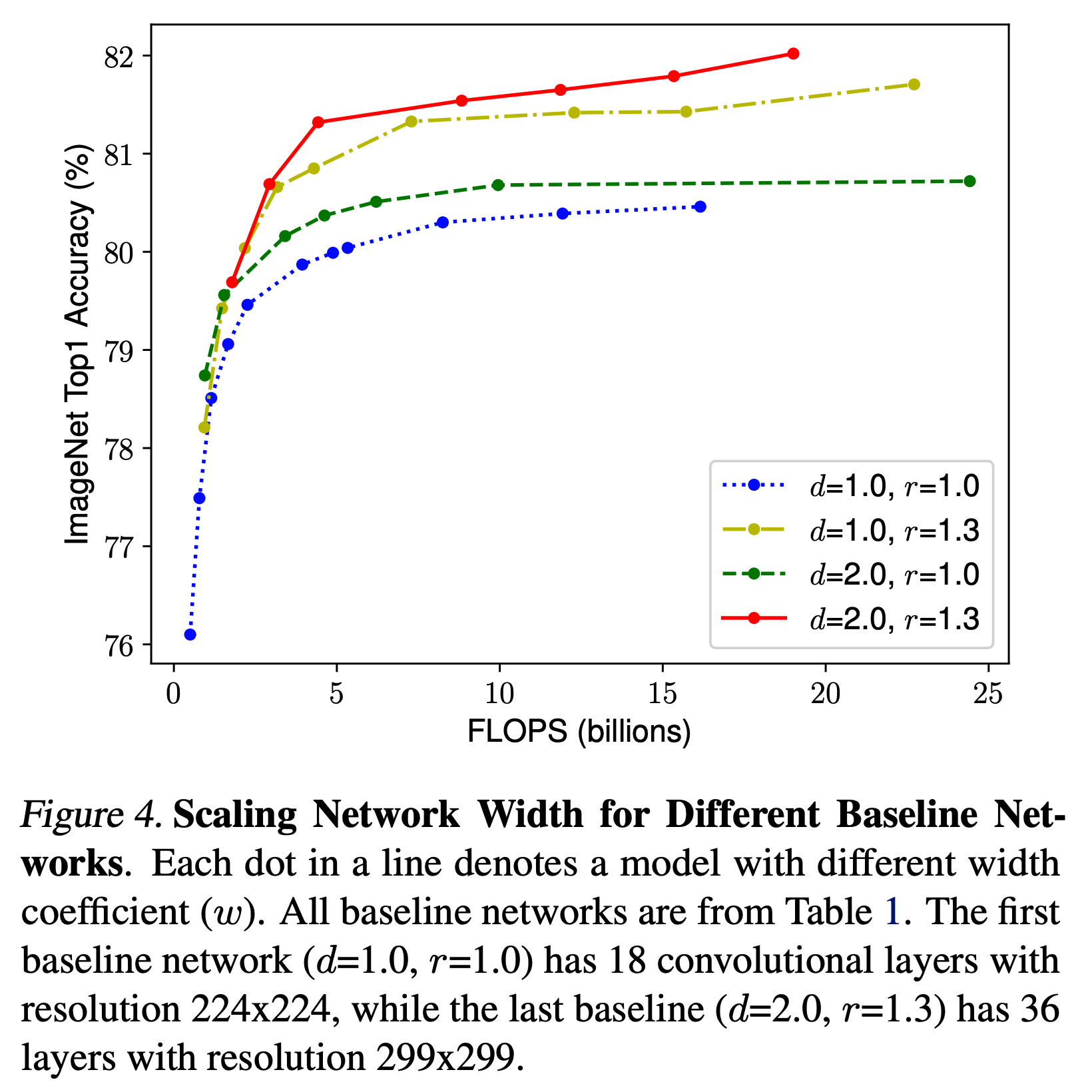
- 제시한 방법이 타당한지 확인하기 위해 MobileNet 과 ResNet 에도 적용하여 scale-up 해보기
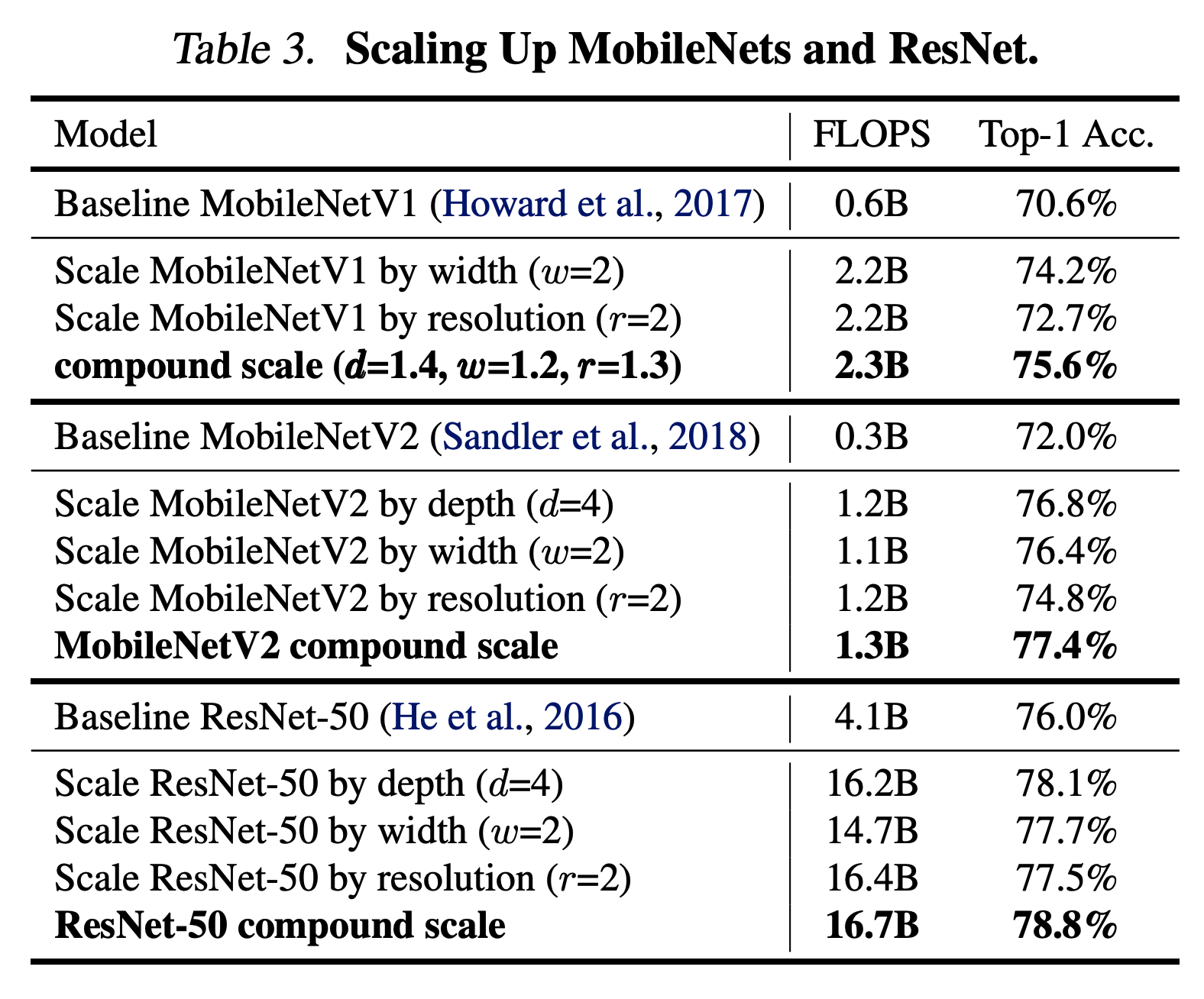
- 표에서 보면 알 수 있듯 단순히 scale 을 독립적으로 증가시키는 것 보다 compound scale 에서 얻어진 결과로 scale-up 하는 것이 효과가 더 좋다.
ImageNet 결과
- EfficientNet 을 ImageNet 기반으로 학습.
- RMSProp optimizer (decay: 0.9, momentum: 0.9)
- batch-norm momenterm: 0.99
- weight decay: 1e-5
- init lr: 0.256 (decay: 0.97, every 2.4 epochs)
- swish activation 사용 (링크)
- stochastic depth with drop ratio:0.3 (링크)
- 보통 큰 모델은 좀 더 강한 regularization 이 필요하다.
- 그래서 EfficientNet-B0 에는 0.2 의 dropout을, EfficientNet-B7 에는 0.5의 dropout 을 적용.
- 잠깐 다시 그림.1 을 소환해보자.

- 그림.5는 그림.1 과 거의 같으나 model size 말고 FLOPS를 기준으로 그린 그림이다.
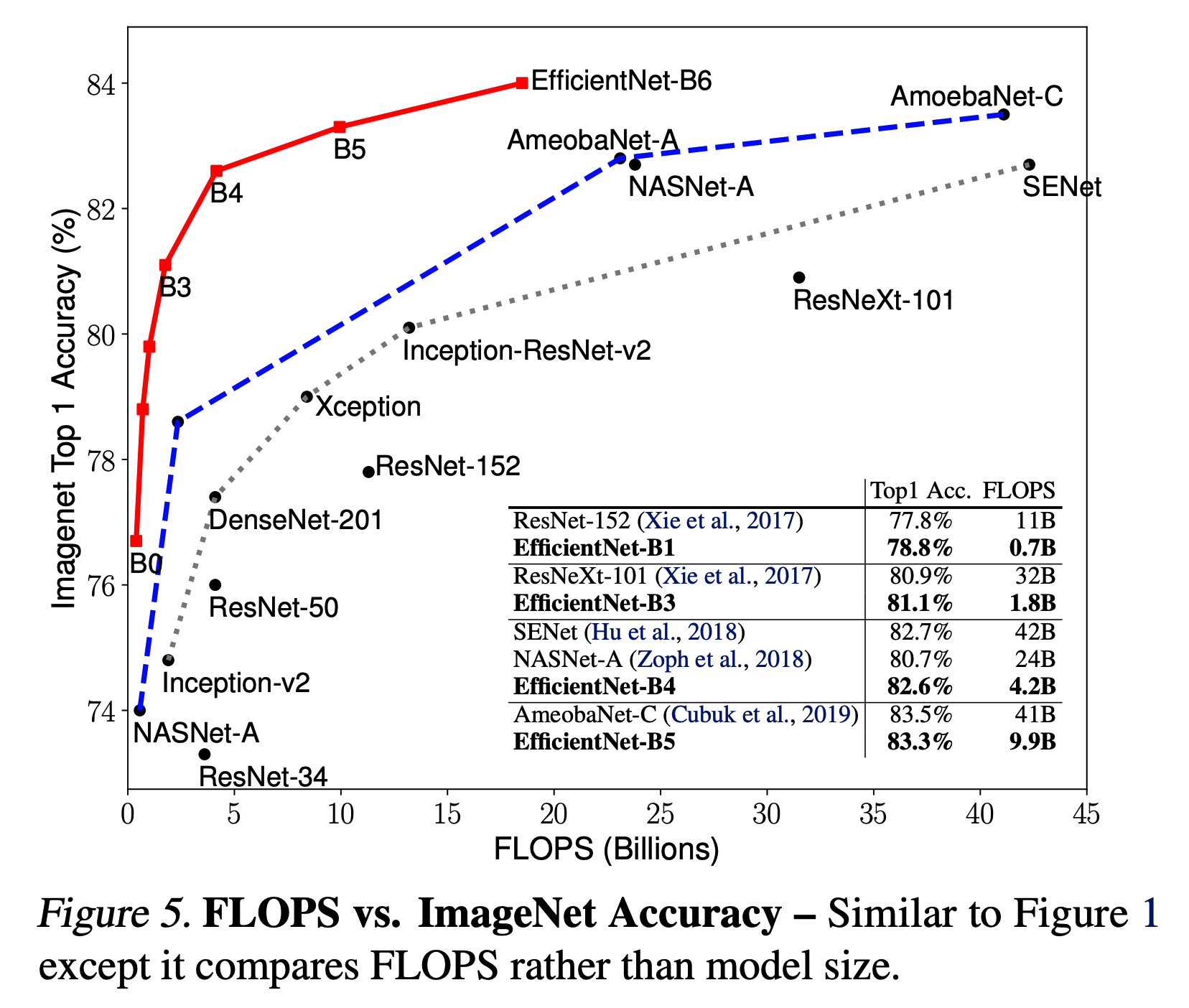
- 어짹거나 결과를 보면 애부 적은 수의 FLOPS 를 가진다.
- 실제 성능을 확인하기 위해 CPU 에서 이를 테스트해본다.
- FLOPS는 GPU보다 CPU 응답속도에 잘 비례한다.

- (의견) 뭐 EfficientNet 이 당연히 FLOPS 가 적으니 빠르겠지만서도, 실제 그렇게 빠른 것인지는 의문이다.
- 어쨌거나 CPU 에서 20회 측정 후 평균을 낸 값이라고 한다.
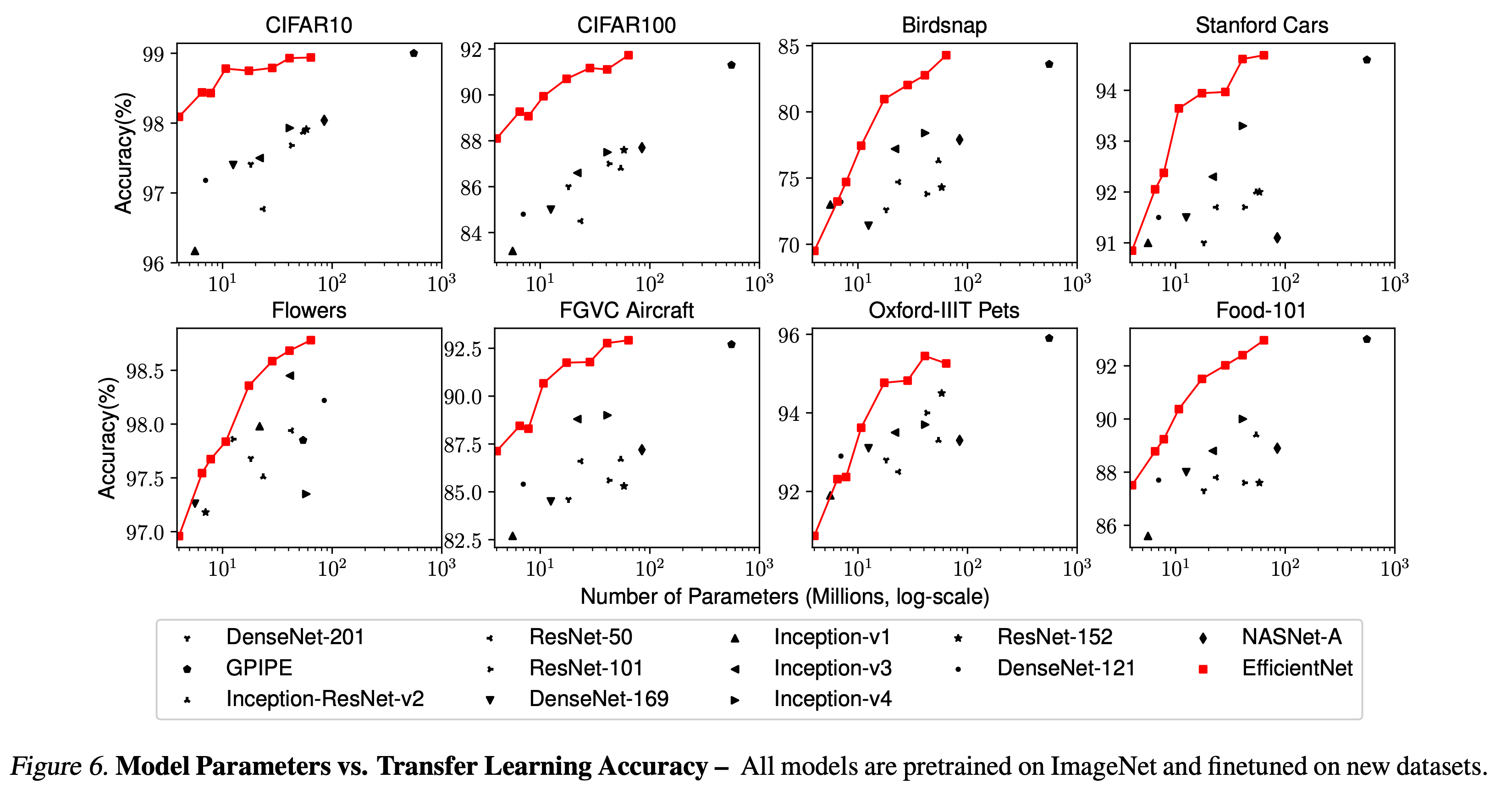
Transfer Learning 결과
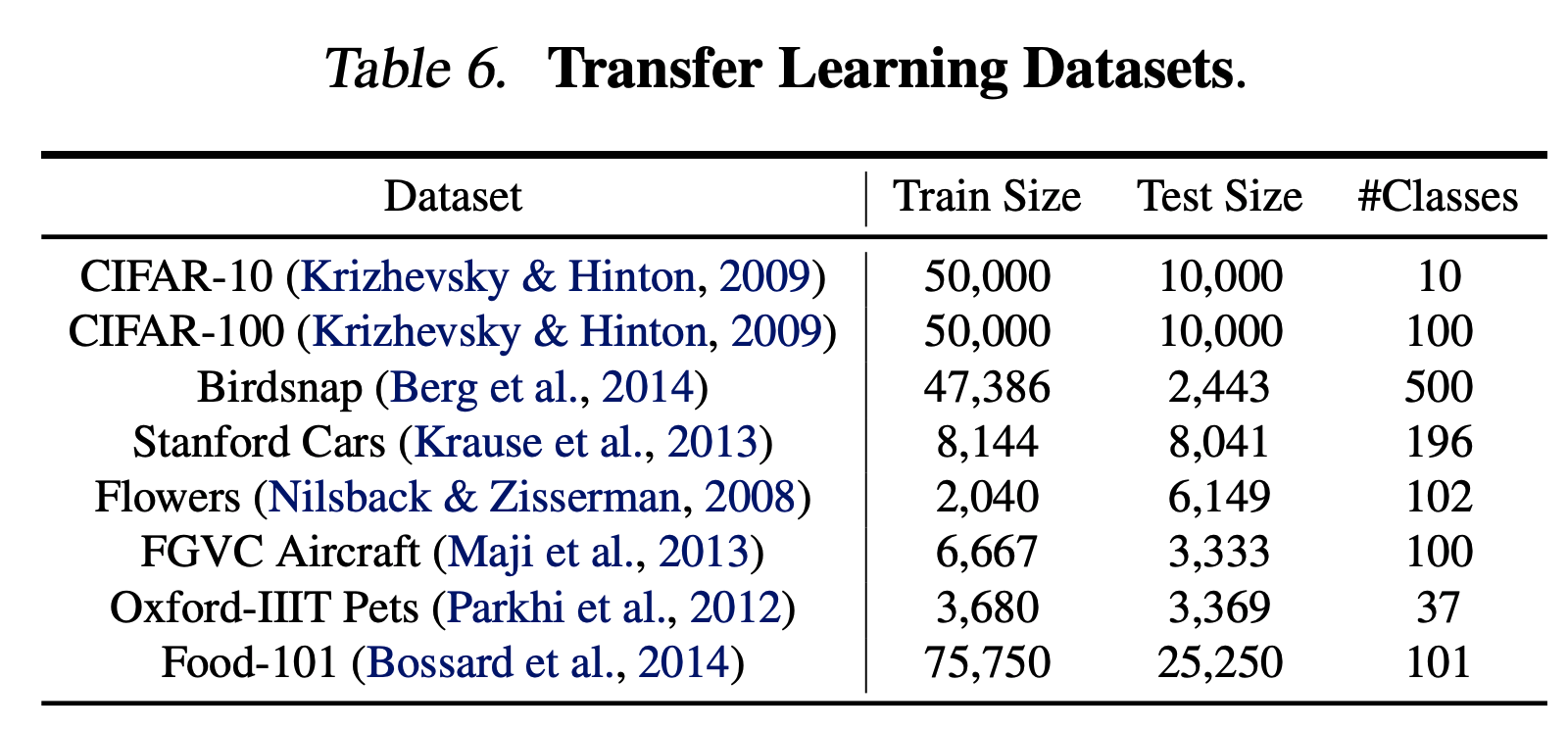
- 다음 데이터에 대한 Transfer learning 을 실험하였다.
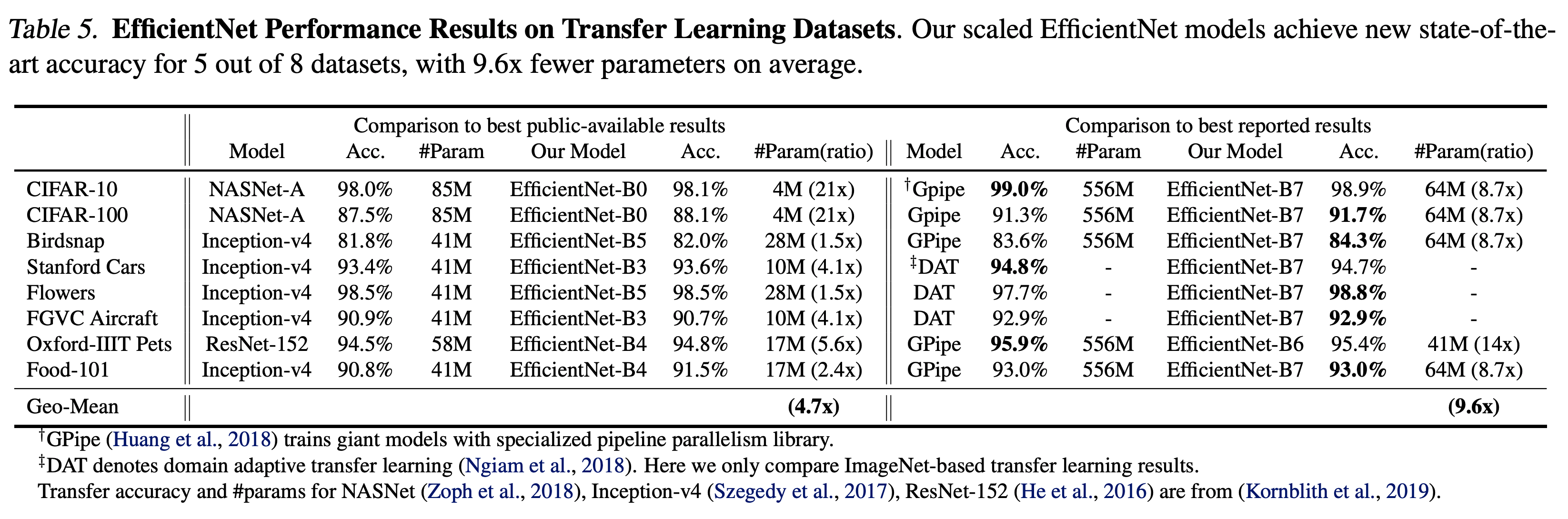
- Table.5 는 NASNet-A 와 Inception-v4 등 다른 모델과의 transfer learning 성능을 비교한다.
- 파라미터 수와 성능을 요약한 그림은 다음과 같다.
토의
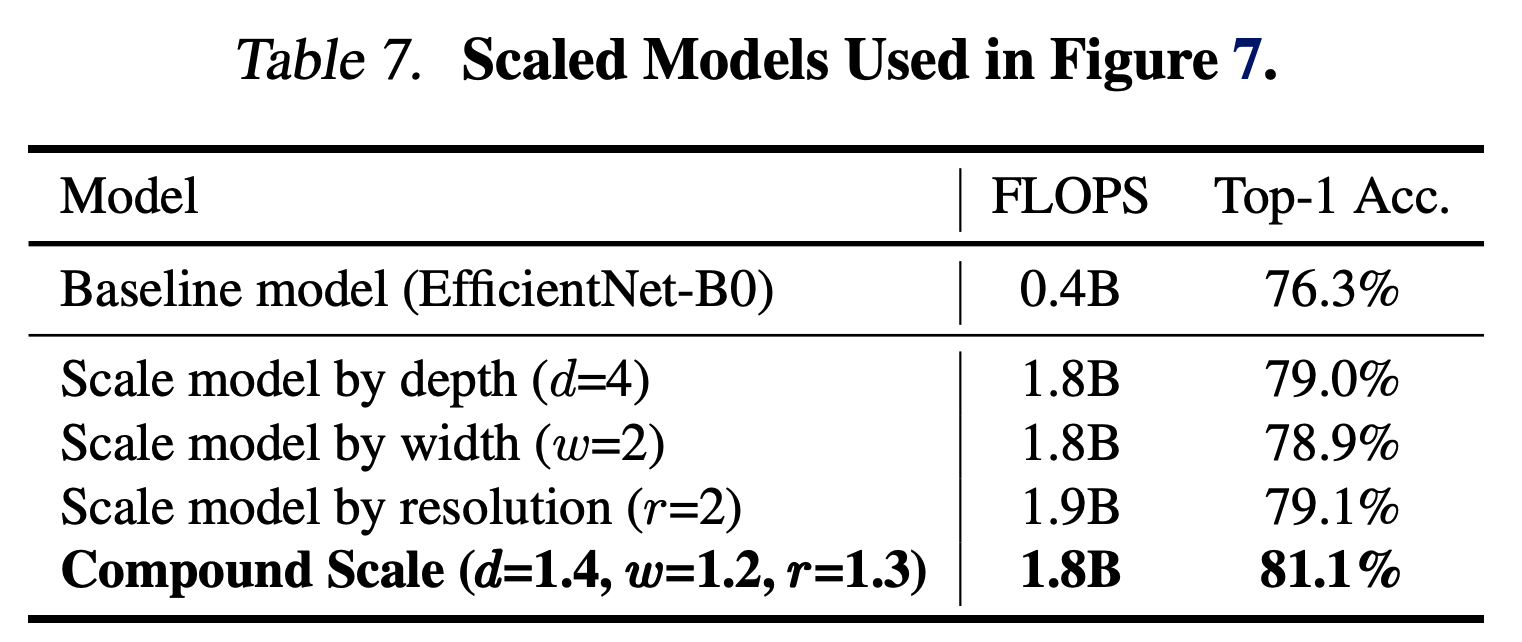
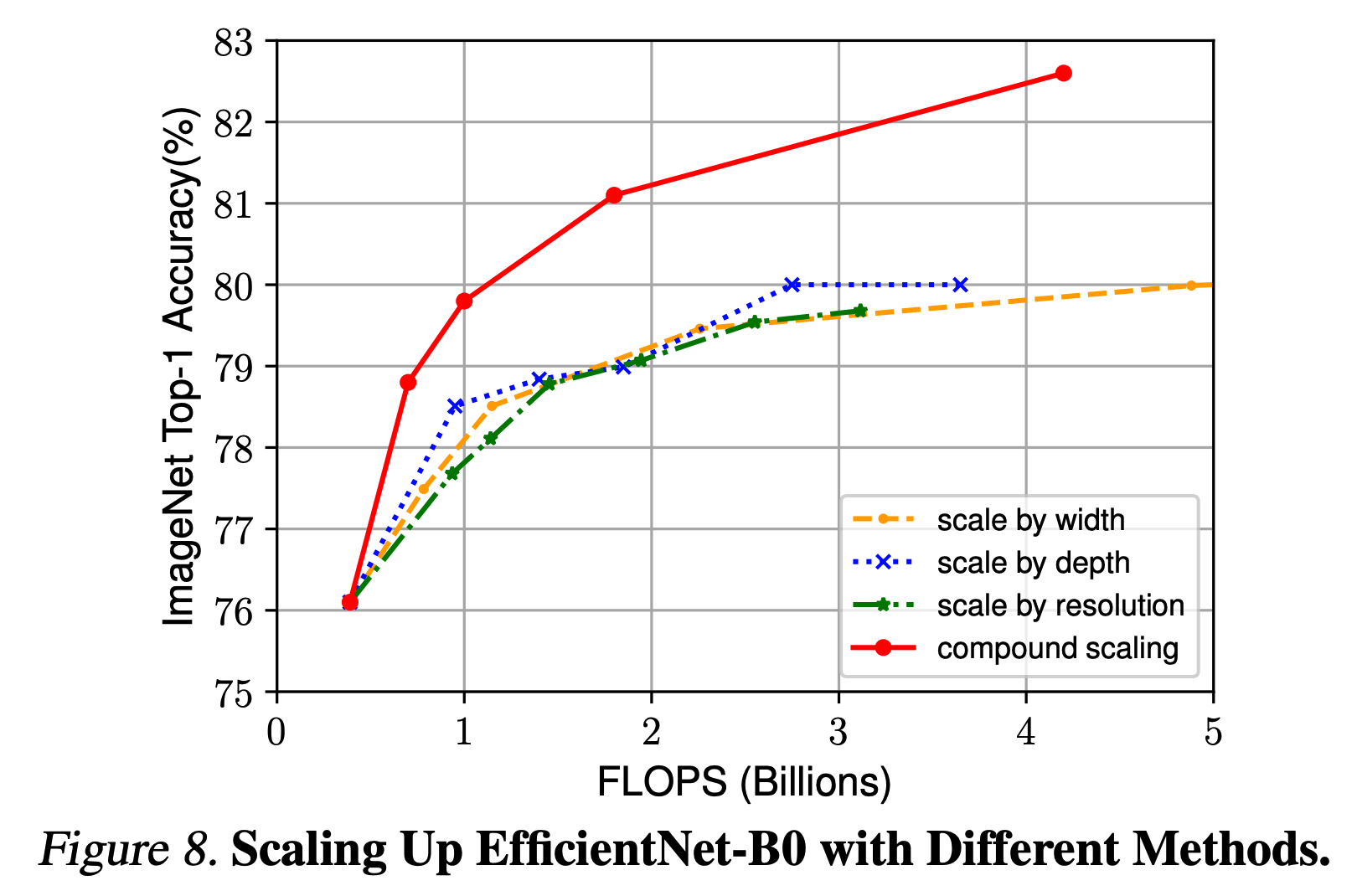
- 논문이 제시한 방식이 맞는지 확인하기 위해 서로 다른 scale 로 평가한 ImageNet 성능은 다음과 같다.
- 그림만 봐도 compound scale 방식이 좋다.
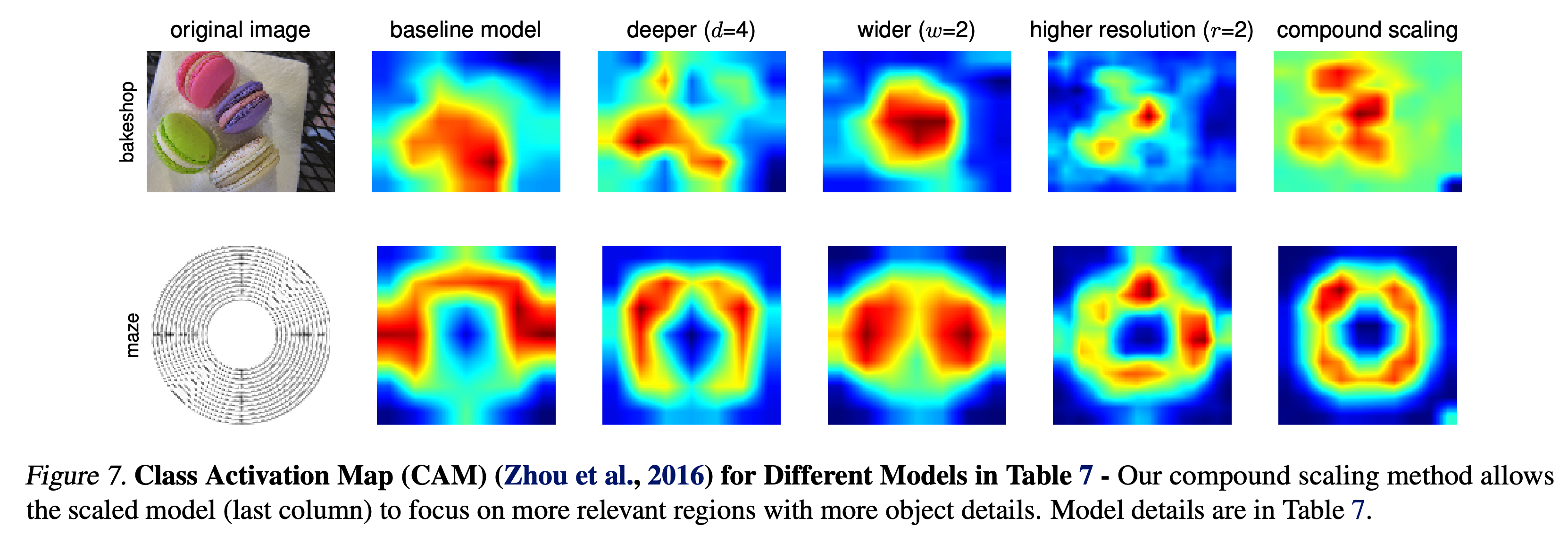
- 실제 더 좋은 결과를 가져오는지 확인하기 위해 activation map 도 확인하였다.
- 당연히 compound scale이 더 좋다.