개론
- 최근 연구에 따르면 CNN 을 활용하여 이미지의 유사도를 측정하고자 하는 시도가 많았음.
- 유사도 계산을 위한 방법을 모델 안에서 직접 학습하는 것을 Metric Learning 이라고 함.
- 지금까지 다양한 방법들이 제시되어 왔음.
- 이 논문에서는 앞서 사용되었던 방법들을 고찰하고 Facility Location 이라는 방법을 제안함.

관련 연구
- CNN을 활용한 연구 중 semantic embedding 을 활용하는 기법들을 순서대로 확인해보자.
Contrastive Embedding
- 샴(Siamese) 네트워크를 활용한 방법. 한 쌍(pair)으로 이루어진 데이터 집합이 필요하다. \( \{({\bf x}_{i},{\bf x}_{j}, y_{ij})\} \)
- Positive 샘플에 대해 거리를 0에 가깝게 하고, Negative 샘플에 대해서는 특정 threshold 이상의 거리를 유지하도록 학습
- Loss 함수는 다음과 같이 정의된다.
- 여기에서 \(f(\cdot)\) 는 CNN 망으로부터 얻어진 feature 라고 정의한다.
- 그리고 두 feature 에 대한 거리는 \(D_{i,j} = ||\;f({\bf x}_{i}) - f({\bf x}_{j})\;||\) 로 정의한다.
- \(y_{i,j}\) 는 indicator 로 \(y_{i,j} \in \{ 0, 1\}\) 이며, 한 쌍의 데이터가 동일한 클래스이면 1, 아니면 0 의 값을 가지게 된다.
- \([\cdot]_{+}\) 는 Hinge Loss 함수를 의미한다. 즉, \(\max(0, \cdot)\) 과 동일한 의미가 된다.
- Contrastive Embedding 방식의 장점과 단점
- (장점) 비교적 쉽게 학습 집합을 구성해서 진행할 수 있다.
- (단점) 학습 속도를 올리기 위해서는 학습 데이터 집합을 잘 선정해야 한다.
- (단점) 모든 데이터에 대해 상수 margin \(\alpha\)를 선택해야 한다.
- (단점) 클래스 단위이므로 시각적으로 다른 구조를 가지는 동일 클래스 데이터가 동일한 공간에 Embedding되게 된다.
Triplet Embedding
- Triplet 방식은 Metric Learning 에서 가장 자주 쓰이는 기법이다. (참고논문)
- 학습을 위해 3개의 쌍이 필요하다. \( \{({\bf x}_{a}^{(i)},{\bf x}_{p}^{(i)}, {\bf x}_{n}^{(i)})\} \)
- 여기서 \( ({\bf x}_{a}^{(i)},{\bf x}_{p}^{(i)}) \) 은 같은 클래스에서 나온 쌍이고, \( ({\bf x}_{a}^{(i)}, {\bf x}_{n}^{(i)}) \) 는 다른 클래스에서 나온 쌍이다.
- Loss 함수는 다음과 같이 정의된다.
- 여기서 \(D_{ia,jp} = ||\;f({\bf x}_{i}^{a}) - f({\bf x}_{i}^{p})\;||\) 이고 \(D_{ia,jn} = ||\;f({\bf x}_{i}^{a}) - f({\bf x}_{i}^{n})\;||\) 이다.
- \([\cdot]_{+}\) 는 Hinge Loss 함수를 의미한다. 즉, \(\max(0, \cdot)\) 과 동일한 의미가 된다.
- Hinge Loss 를 사용한다는 것이 중요하다 !!! (MSE 등은 왜 안될까!!!)
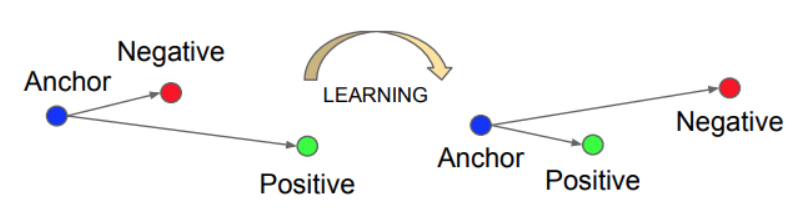
- Triplet Embedding의 장점 및 단점
- (장점) Contastive Embedding 보다 더 좋은 성능을 낸다.
- (장점) Loss 함수가 Convex 함수이다.
- (장점) Embedding 공간이 임의로 왜곡되는 것을 허용함. (margin \(\alpha\) 는 상대적인 개념으로 적용됨)
- (단점) 학습 시간이 오래 걸린다.
- 학습이 진행되어 Converge 되면 Negative Margin 을 위반하는 학습 집합이 거의 등장하지 않게 되어 학습이 거의 진행되지 않는다.
- (참고) FaceNet 에서 사용하는 Semi-Hard Negative Sampling
- Batch 단위 내에서 Anchor 샘플과 이에 대한 Positive, Negative 샘플을 추출함.
- 이 때 학습이 잘 이루어질만한 Negative 샘플을 선정하여 사용.
Lifted Structured Feature Embedding
- 관련논문 : Deep Metric Learning via Lifted Structured Feature Embedding
- 모든 positive pair가 모든 negative pair에 대해 거리를 비교하는 모델
- 이 논문은 정말 대충 보았으므로 틀리게 서술된 내용이 있을 듯함. (참고 바람)
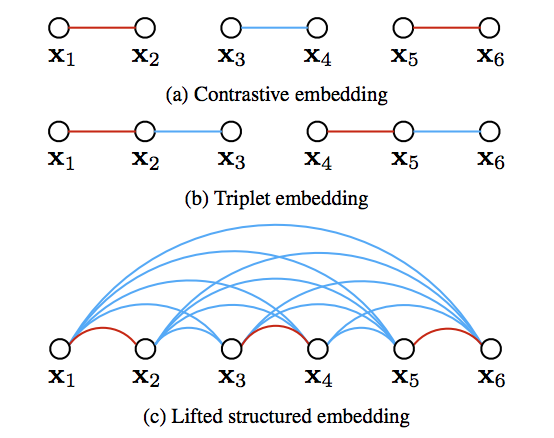
- Loss 함수는 다음과 같이 정의된다.
- 아이디어는 간단하다. 다만 몇 가지 문제가 존재한다.
- 문제
- non-smooth.
- All Pairs 에 대해 여러번 전체 연산을 수행해야 한다.
- 해결방안
- non-smooth는 upper bound 식을 도입하여 해결한다. (관련 링크 : LogSumExp)
- All Pairs 문제는 이전 연구에서 했던 것들과 유사하게 importance sampling 으로 푼다.
- Loss 함수를 다음과 같이 재정의한다.
- 샘플링 방식은 간단하게 적자면,
- 일단 positive pair 쌍들을 랜덤하게 선정 후,
- 적당히 Batch 데이터 안에 포함하도록 구성한다.
- 이후 Batch 내부에서 positive pair 에 포함된 각각의 샘플에 대해 hard negative 샘플을 구함.
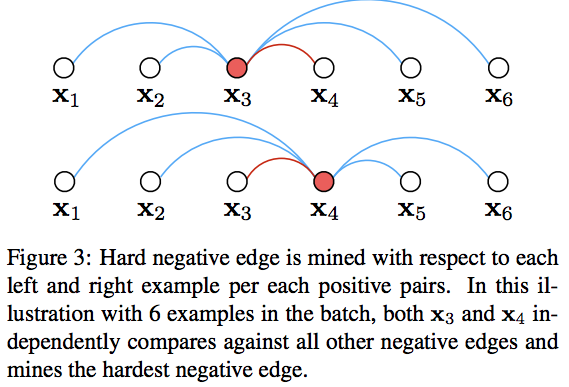
- 최종적으로 다음과 같은 효과가 있다.
N-Pair Loss
- 관련논문 : Improved Deep Metric Learning with Multi-class N-pair Loss Objective
- Triplet 구조를 일반화하여 (N+1)-Tuplet 네트워크를 제안함.
- 1 Anchor, 1 Positive, (N-1) Negative Samples
- N=2 인 경우 Triplet 과 동일한 모델이 된다.
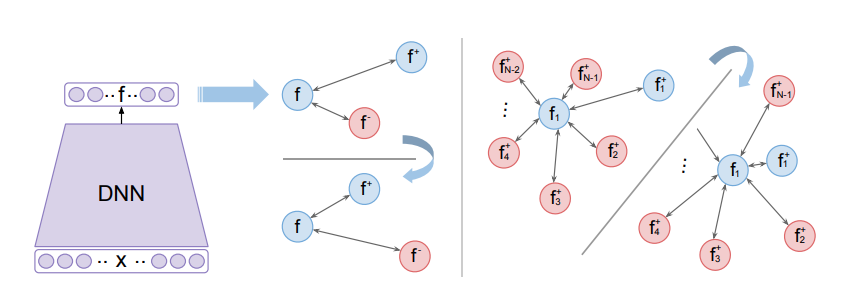
- Loss 함수는 다음과 같다.
- 이 때 \(f(\cdot)\) 은 CNN 을 통과하여 얻은 feature 값이다. (논문에서는 Embedding Kernel 이라 표현)
- \(\log(\cdot)\) 항은 다음과 같이 풀어서 작성할 수 있다.
- 수식 구조를 보면 Multi-class Logistic Loss 즉, Softmax Loss와 그 모양이 유사하다.
학습 집합의 구성
- 빠른 학습을 위해 효과적인 배치 구성이 필요하다.
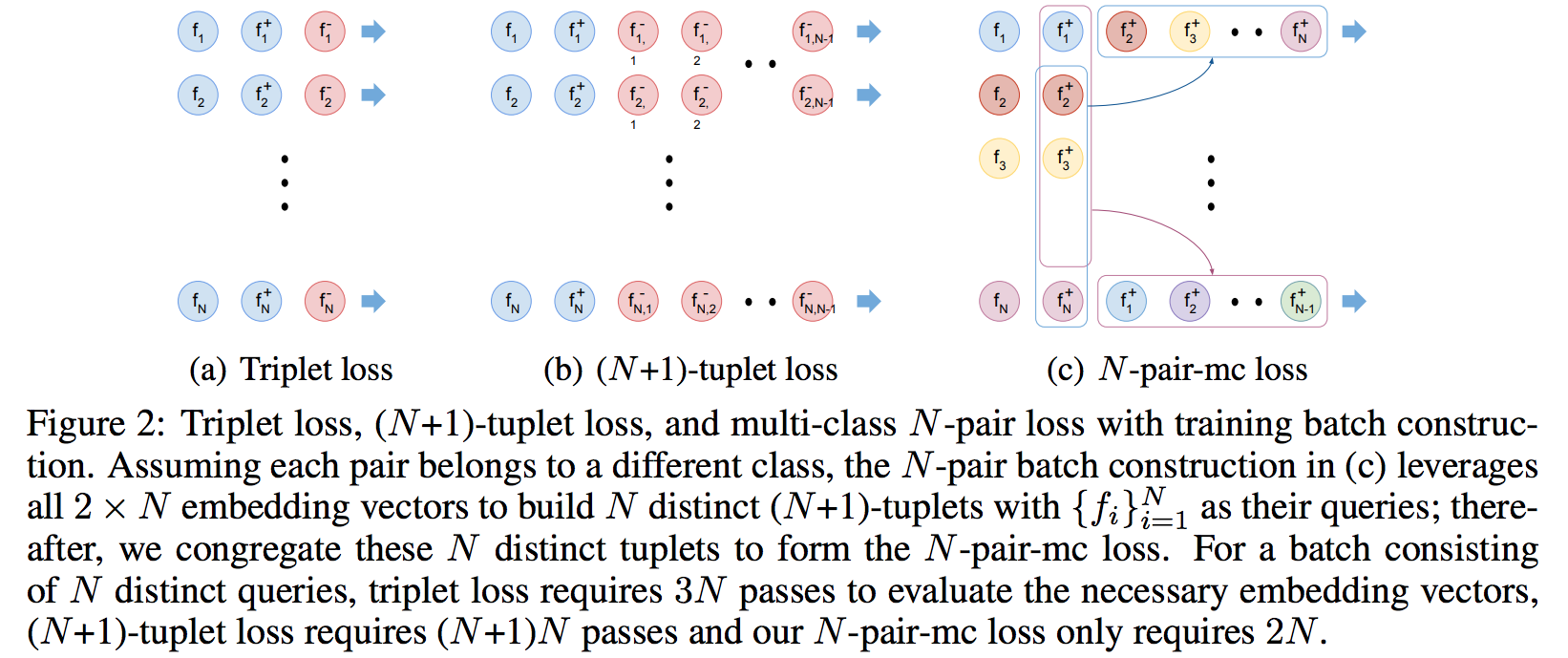
- N-pair-mc loss
Facility Location
- 기존에 사용되던 Metric Loss 들은 Mini-Batch 안에서의 Pairs/Triplets 로 정의되어 있음.
- 따라서 Global Structure 에 대한 정보는 고려되지 못함.
- 게다가 데이터 준비 과정도 매우 힘들다. (학습셋 구축이 가장 어려운 일이다.)
- 본 연구에서는 Clustering Quality Metric (NMI)로 바로 최적화 시키는 기법을 적용함.
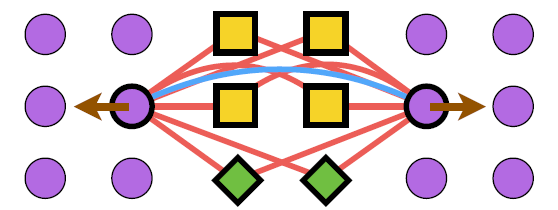
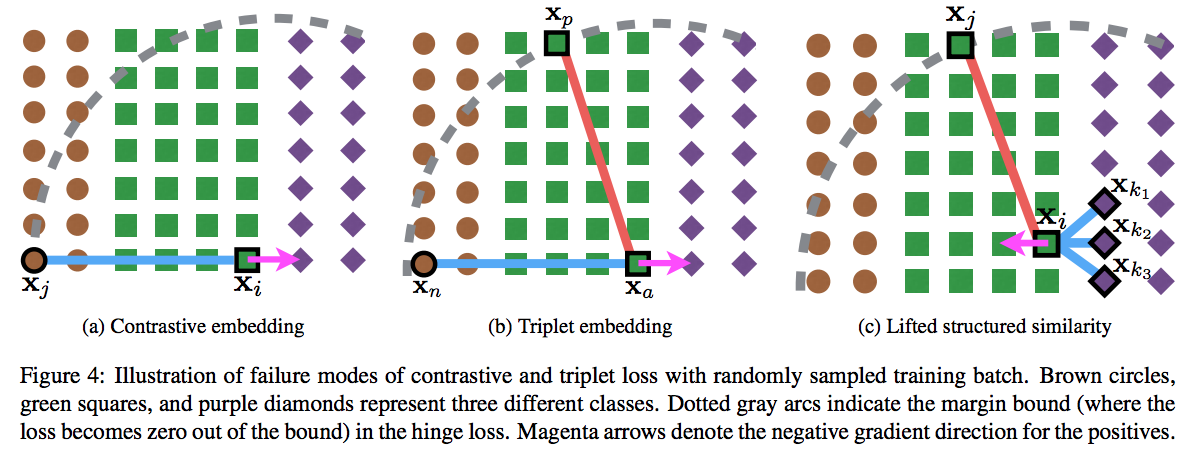
- 위 그림은 앞서 사용된 Loss 방식으로도 해결이 되지 않는 카운터 예제이다.
- 여기서 파란색 선은 positive pair 이고 붉은 색 선은 negative pair 를 의미한다.
- 이 경우 동일한 클래스에 속한 positive pair (여기서는 보라색 점)에 척력(repulsion)이 작용됨.
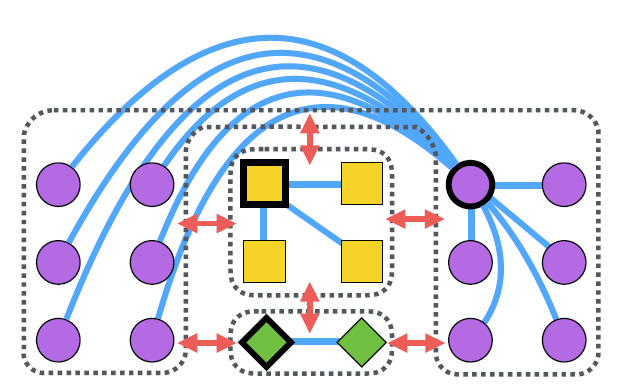
- Facility Location 방법을 대략적으로 나타낸 그림.
- 여기서 파란색 선은 positive pair, 볼드(bold) 표시된 노드는 medoid 이다.
- 서로 다른 클래스는 클러스터 단위로 척력이 적용된다.
Facility location problem
- 입력 데이터 (\(i\) 는 샘플 인덱스): \(X_i\)
- 이에 대한 Embedding 함수 결과 (출력은 \(K\) 차원) : \(f(X_i;\Theta)\)
- 랜드마크(Landmark) 집합 \(S\)
- \(S \subseteq V\) 이고 \(V\)는 \(V = \{1,…|X|\}\)
- 즉, S 는 샘플 갯수 N 이하의 정수로만 이루어진 집합의 부분 집합.
- Facility location function 정의
- Facility Location 함수는 어떤 score를 생성하는 함수이다.
- \(S\) 는 어쨌거나 일단 정해져 있어야 한다. (이 함수의 입력 파라미터이다.)
- 모든 샘플에 대해서 \(S\) 에 속한 값을 인덱스로 가지는 샘플들과의 거리를 계산한 뒤 최소 거리를 가지는 값만을 누적한다.
- 최종 결과는 (\(-\)) 부호로 인해 음수 값이다. (따라서 이후에 이 값을 최대로 만드는 식을 설계할 것이다.)
- 이 식의 의도를 쉽게 알 수 있는데 가장 적합한 집합 \(S\), 즉 좋은 medoid 집합을 선정하는 문제로 전개해 나갈 것이다.
- 결국 \(S\) 인덱스를 가지는 데이터 집합이 클러스터를 대표하는 medoid 가 된다는 것이다.
- 사실 가장 좋은 집합 \(S\) 를 구하는 문제는 NP-hard 문제이다.
- 물론 최악의 경우 그렇다는 것이고 통상적으로 Greedy 솔루션이 존재한다.
- 이제 새로운 함수를 정의한다. 이를 오라클(oracle) 함수라고 정의한다.
- \(V\) 집합 원소 중 샘플이 특정 클래스 \(k\) 에 속하는 경우의 해당 샘플 인덱스 집합을 \( \{i;{\bf y}^*[i]=k \}\) 와 같이 표기한다.
- 수식이 혼동이 좀 될수 있는데 위 식이 하고자 하는 것은 비교적 간단하다.
- 일단 특정 클래스에 속한 데이터 내에서 최적의 medoid 를 선정하는 것을 목표로 한다.
- 따라서 클래스마다 1개의 medoid를 찾게 된다.
- 이 작업을 최종적으로 모든 클래스에 대해 수행하게 된다. 결과는 클래스 독립적이다.
- 최종적으로 얻어지는 것은 score 값이다.
Loss function
- Loss 함수를 살펴보자.
- 일단 수식 \(\gamma \Delta(g(S), {\bf y}^*)\) 는 Margin 값이므로 나중에 고민해보자.
- 앞서 등장한 Facility Location은 전체 데이터를 대상으로 얻어진 점수이다.
- 이 때 원래의 클래스 수와 동일한 medoid 개수라는 제한을 준 상태에서 최적의 \(F\) 값을 구하게 된다.
- 예를 들어 실제 클래스가 5개이면 사용가능한 medoid 개수는 정확히 5개라는 뜻이다.
- 결국 레이블 수와 같은 크기의 mediod를 가지도록 최적의 클러스터링을 구성하게 된다.
- 이 때 원래의 클래스 값은 고려되지 않는다는 것이 중요하다.
- 이 때 원래의 클래스 수와 동일한 medoid 개수라는 제한을 준 상태에서 최적의 \(F\) 값을 구하게 된다.
- 통상적으로 학습 초기에는 정답 클래스를 고려하지 않는 Facility Score 점수가 정답 클래스를 고려하는 Oracle Score 보다 더 좋다.
- 이 경우 (Margin은 잠시 잊고 Score Function의 출력 부호를 고려하면) Loss는 0보다 큰 값이 만들어진다.
- 결국 이 둘 사이의 차이를 없애야 하고 파라미터를 조절하여 Oracle Score가 클러스터링 Score 보다 좋아지도록 학습해야 한다.
- 당연히 Oracle Score는 단 한번만 만들어내는 것이 아니다. (즉, 고정값이 아니다.)
- 학습을 진행하면 파라미터 \( \Theta \) 가 갱신되게 되므로 이것도 Iteration 마다 계산되어야 한다.
- 결국 식(6)은 Oracle score \(\tilde{F}\) 가 cluster score \(F\) 보다 커지도록 \(f(\cdot;\Theta)\) 가 학습된다는 의미이다.
- 그림 (1) 이 이를 나타낸 것이다.
- 이제 Margin \(\gamma \Delta(g(S), {\bf y}^*)\)를 고민해보자.
- 먼저 구조화된 Margin 함수 \(\Delta({\bf y}, {\bf y}^*)\) 를 정의한다.
- 이 때 \({\bf y}\) 는 \(y = g(S)\) 를 사용하게 된다.
- Margin Term 은 클러스터링 품질을 측정하는 것이다.
- \(y\) 와 \(y^*\) 가 일치하는 경우 이 값은 0이 된다.
- 그리고 1인 경우 최악의 경우를 의미한다. (서로 아무런 상관없이 값이 발현)
- 식은 다음과 같다.
(참고)
- Mutual Information 은 다음과 같이 정의된다.
- NMI (Normalized Mutual Information)
- NMI는 피어슨 상관 계수와 비슷한 형식으로 두 확룔 함수가 완전하게 독립이면 0 을 갖게 된다.
- 반대로 완전한 상관성을 가지게 되면 1을 갖게 된다.
- 여기서 확률 값을 계산하는 방법은 (이산값이므로) 다음의 방식을 사용한다.
Backpropagation subgradient
- 앞서 정의한 Loss 함수를 사용하기 위해서는 파라미터로 미분한 식이 필요하다.
- 적절히 전개하면 가능하다고 한다.
- 여기서 \(S_{PAM}\) 은 식(6) 부분에서 앞쪽 영역의 식을 의미하는 것이다.
- 이 부분은 3.4 절을 참고하자.
- 전개식은 다음과 같다.
Loss augmented inference
- 식(6) 중 앞의 식을 푸는 방법을 기술한다. 여기서는 생략하도록 하자.
Implementation details
-
구현체가 이미 TensorFlow contrib 에 포함되어 있다. (참고링크)
- 환경
- Inception (w/ batch norm) (Pretrained Model ILSVRC2012)
- Random Crop, Single Center Crop
- N-Pair
- Multiple Random Crop (Avg. Embeding Vector)
- Embedding Size :64 (다른 논문과의 비교를 위해)
- RMSProp
- 논문에서 언급했듯 정제된 학습셋이 필요하지는 않다. (Triplet 같은 데이터가 필요 없음)
- 대신 배치 크기 \(m\) 만큼의 샘플을 랜덤하게 뽑아 쓴다.
- 이러한 이유로 다음과 같은 범위로 학습 데이터가 구성될 수도 있다.
- 배치 내 모든 샘플이 동일 클래스 : 이 경우 하나의 클러스터가 생성
- 배치 내 모든 샘플이 모두 다 다른 클래스 : 이 경우 각자의 샘플이 모두 개별 클러스터
- 제약을 두어 학습이 잘 되도록 한다. 배치 내에 포함되는 Unique 클래스의 갯수를 \(C\) 라 정의한다.
-
그런 다음 \(\frac{C}/m=\{0.25, 0.50, 0.75\}\) 로 배치 샘플을 구성해서 테스트를 수행하였다.
- 한 클래스에서 데이터가 많이 뽑힐 수 있기 때문에 다음과 같은 조건을 둔다.
- 클래스가 \(C\) 개라고 하면 \(\frac{C}{m}=\{0.25, 0.50, 0.75\}\)
- 최종적으로 실험 데이터마다 적합한 비율을 선정하여 사용하였다.
- CUB-200-2011, Cars196 : \(\frac{C}{m}=0.25\)
- Stanford Online Products : \(\frac{C}{m}=0.75\)
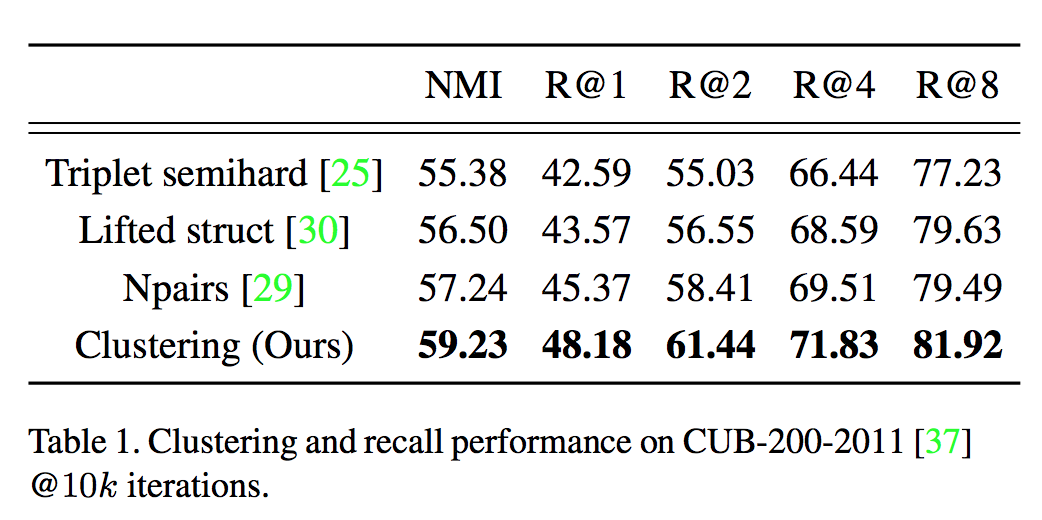
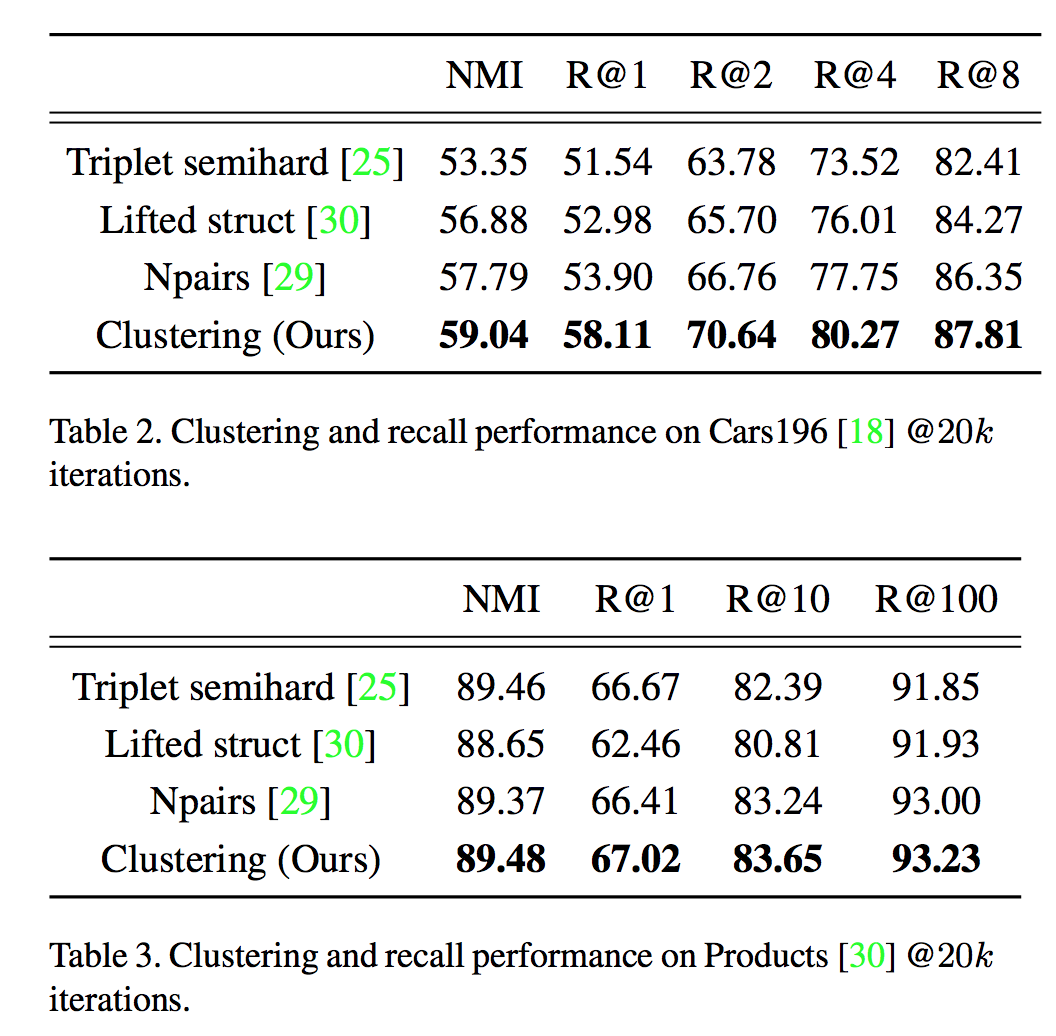
실험 결과