CBAM: Convolutional Block Attention Module

• 저자가 한국인이다. 그래서 한글 설명 자료가 있다.
  • 참고 문서 : 링크
  • 사실 따로 문서를 작성할 필요도 없이 그냥 이 자료를 보면 된다.
• BAM 논문 : 링크
• CBAM 논문 : 링크

이미지에서의 Attention.

• 이미지 처리(즉, CNN) 쪽에서 사용되는 Attention 는 주로 VQA 나 Captioning 분야였다.
  • Show, Attend and Tell: Neural Image Caption Generation with Visual Attention
• 즉, Attention은 Sequence 구조를 채용하는 모델에서 Seq. 진행 중 집중을 해야 하는 Local 영역의 Context 를 찾기(attention)위한 기법으로 사용되었다.
  • 따라서 VQA 나 Captioning 등 이미지와 문장(Sentence)을 함께 사용하는 Task 에서나 관심을 받은게 사실이다.
• 단일 이미지를 입력받는 Task 에서는 자연스럽게 Attention 을 사용할 이유가 없었음.
  • 대신 동영상은 이미지의 Seq. 로 취급될 수 있으므로 당연히 관심을 가지게 됨.
• Self-Attention 의 등장으로 Attention 의 개념이 확장됨. (?)
  • Seq. 구조를 탈피하여 무언가 집중(진짜 attention)한다는 의미로 사용된다는 느낌.
  • 전통적인 image classification / detection 에서도 적용이 되기 시작함.
  • Self-Attention 참고할만한 자료 : 링크

Method and Results

• 입력 : Conv feature (3-dim feature, HWC)
• 이에 대한 element 단위 attention 을 계산. (element-wise 곱)
  • sigmoid 를 사용하여 weighting 연산

• 여기서 $F$ 는 conv feature 이고 $M$ 은 Attention Map 을 생성하는 함수이다.
• 이런 아이디어는 이미 RAN (Residual Attention Networks) 과 같은 논문에서 제시.
  • encoder-decoder 방식을 사용하여 3D Attention Map을 만들어낸다.
  • 단점은 연산량이 너무 많다.
  • 대신 성능 향상은 1~2 % 수준
• 비슷한 효과를 내면서 아주 가벼운 연산만을 추가 사용하는 방안을 고민.
  • 게다가 기존 모델을 그대로 사용하여 반영 가능.

BAM (Bottlenect Attention Module)

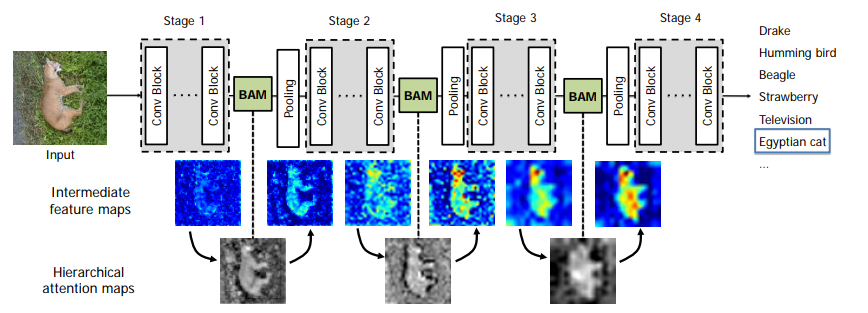
• Attention 모듈은 각 네트워크의 bottlenect 영역에 위치
  • 즉, pooling 이 일어나는 위치 앞단에 BAM 모듈을 추가함.
  • Resnet 은 4개의 bottlenect 모듈이 존재

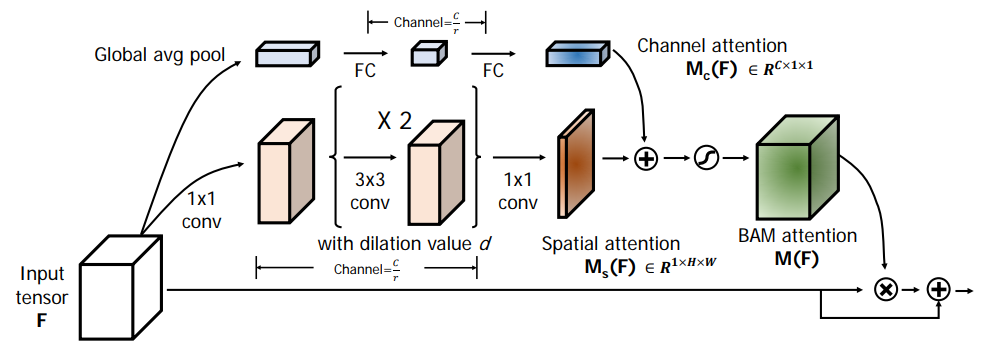
• 위의 그림이 BAM 의 상세 내용을 요약한 그림.
  • $d=4$ 와 $r=16$ 을 사용. (실험을 통해)
• BAM 은 입력으로 3D 크기의 feature map $F$ 를 입력받는다. ($F \in R^{C \times H \times W}$)

• 여기서 $\otimes$ 는 element-wise 곱을 의미한다.
• 여기에 residual 개념을 적용해서 attention map 을 합치는 구조이다.
• 다음으로 효율적인 모델 구성을 위해 2개의 attention 을 구분한다.
  • 바로 Channel attetion $M_c(F)$ 와 Spatial attention $M_s(F)$.

• 최종 출력은 $R^{C \times H \times W}$ 이다.

• Channel attention branch

• Spatial attention branch

• 여기서 $f$ 는 convolution 연산이고 BN 은 batch normalization 이다.
• 윗첨자 값은 filter 크기를 나타낸다.
• 여기에는 2개의 $1x1$ conv 가 사용되었고 $3x3$ 크기의 dilated conv 도 사용되었다.
  • dilated conv 는 atrous conv 라고도 알려져있는데 넓은 영역의 context 를 응축하는데 더 좋다고 알려져있어 사용했다고 한다.

• Channel 과 Spatial Attention map 의 결합

  • 결국 서로 다른 크기를 가지는 두 $M_c$ , $M_f$ 를 결합하여 최종 형태를 구성해야 한다.
  • 만들어야 하는 크기는 $R^{C \times H \times W}$ 이다.
  • 다음과 같은 방법을 고려해 볼 수 있다.
    • element-wise summation, multiplication, or max operation
  • 실제 사용한 것은 element-wise summation. (효율성)

BAM 실험 결과

• 여러가지 hyper parameter 테스트.

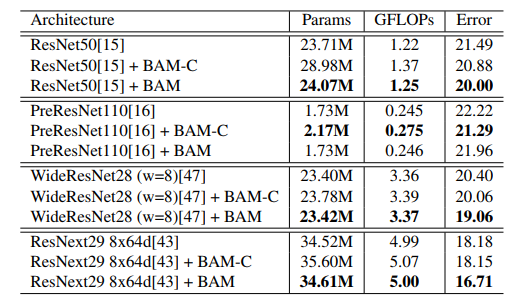
• BAM 블록을 bottlenect 에 놓는 것이 좋은지 conv 내에 포함시키는 것이 좋은지 확인.

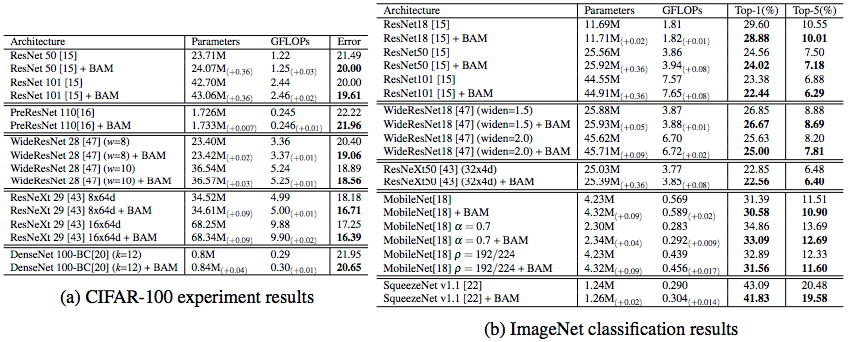
CBAM (Convolutional Block Attention Module)

• Attention Map 을 channel 과 spatial 로 구분한다는 것은 동일하다.
• 하지만 연산을 더 줄임.

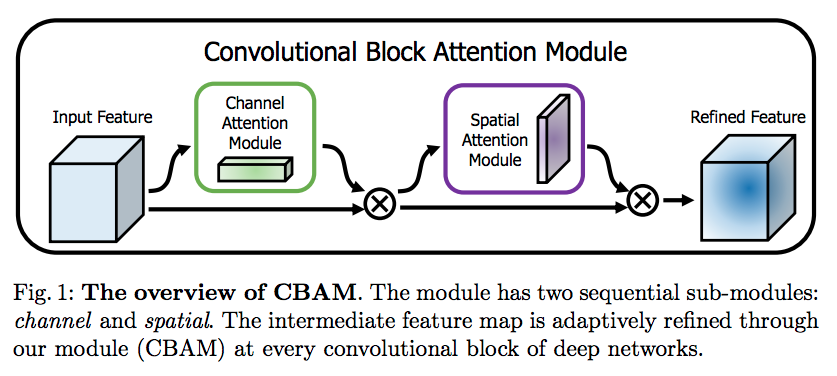
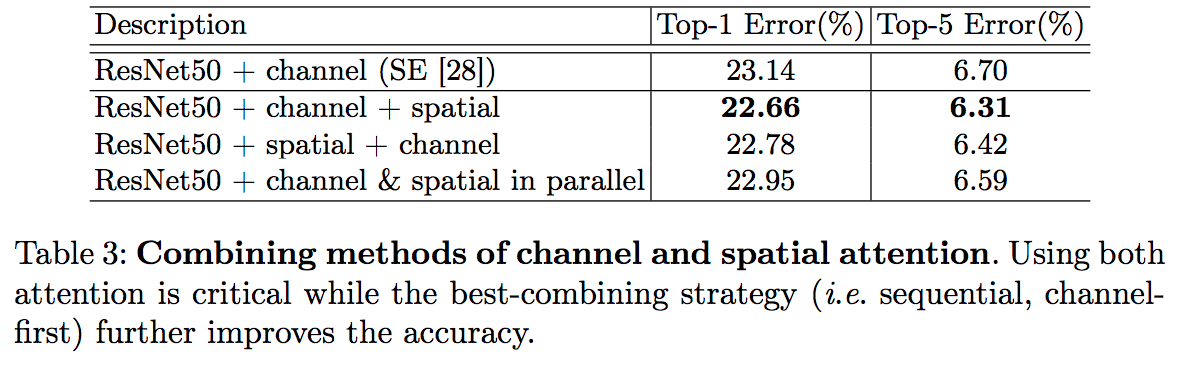
• BAM 은 channel 과 spatial 을 동시에 진행하여 합치는 구조이지만, CBAM 은 순차 적용 방식을 사용함.
  • channel 을 먼저 적용하는 것이 성능이 좋다.

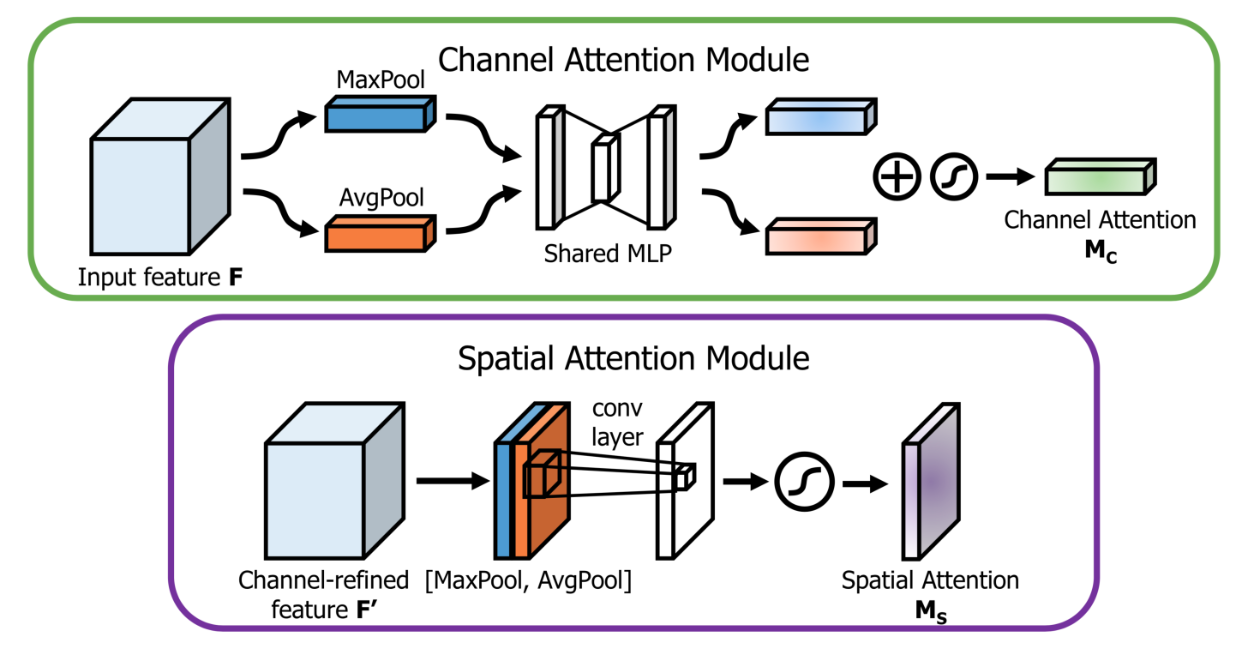
• Channel attention branch
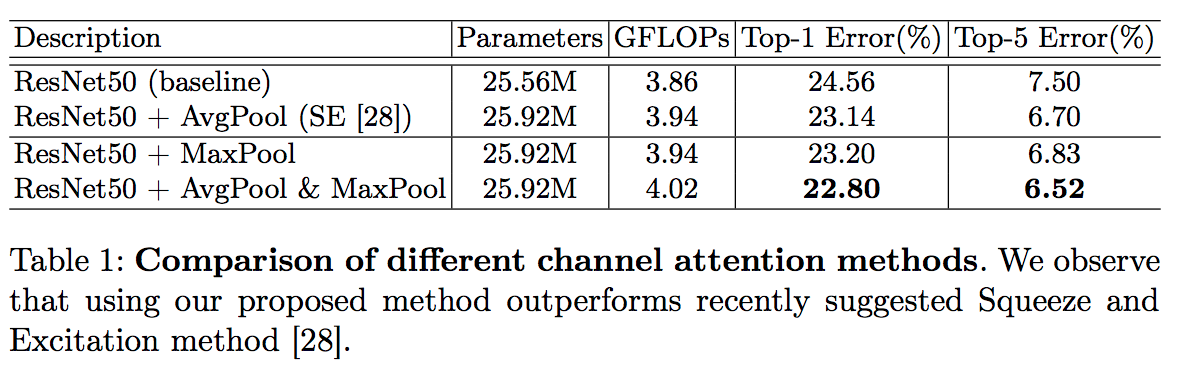
  • Max Pooling 이냐 Avg Pooling 이냐 고민을 하다가 둘 다 사용함.
  • 실험적으로 둘 다 사용하는 것이 더 좋다는 것을 확인했다.

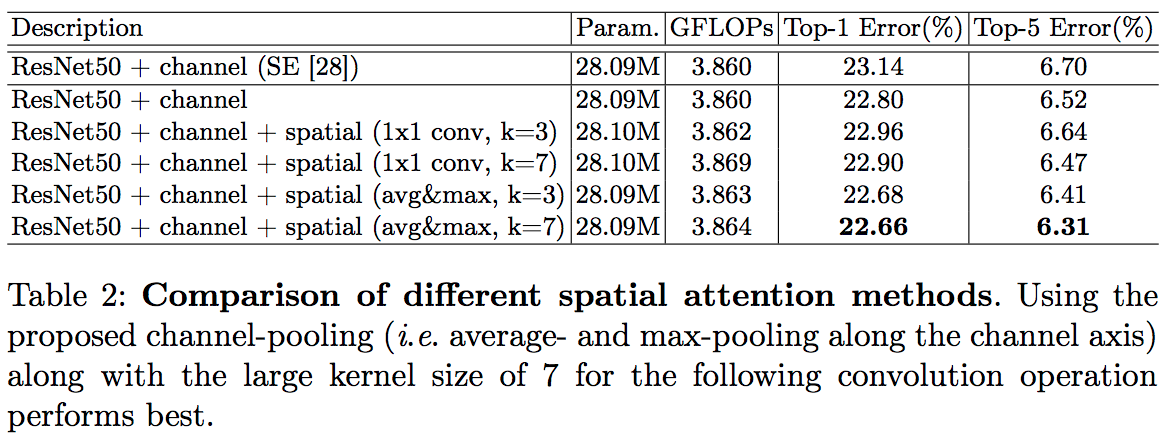
• Spatial attention branch
  • spatial attention 이 channel attention 과 다른 점은 정보가 어디(where)에 있는지를 중점으로 둔다는 것이다.

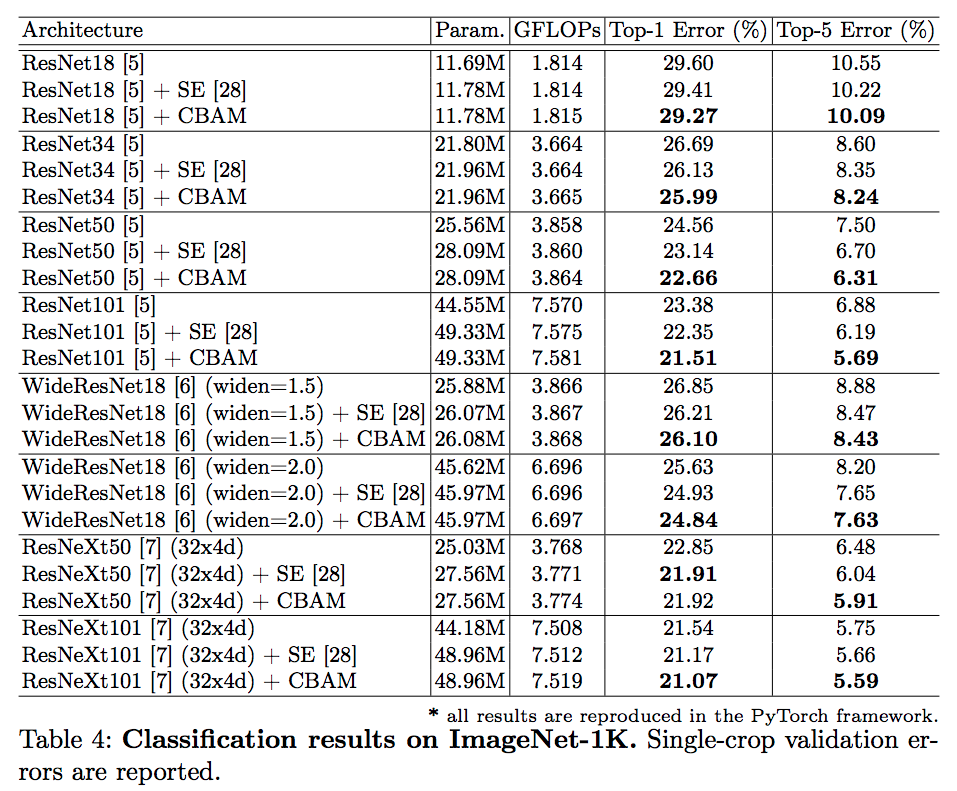
실험