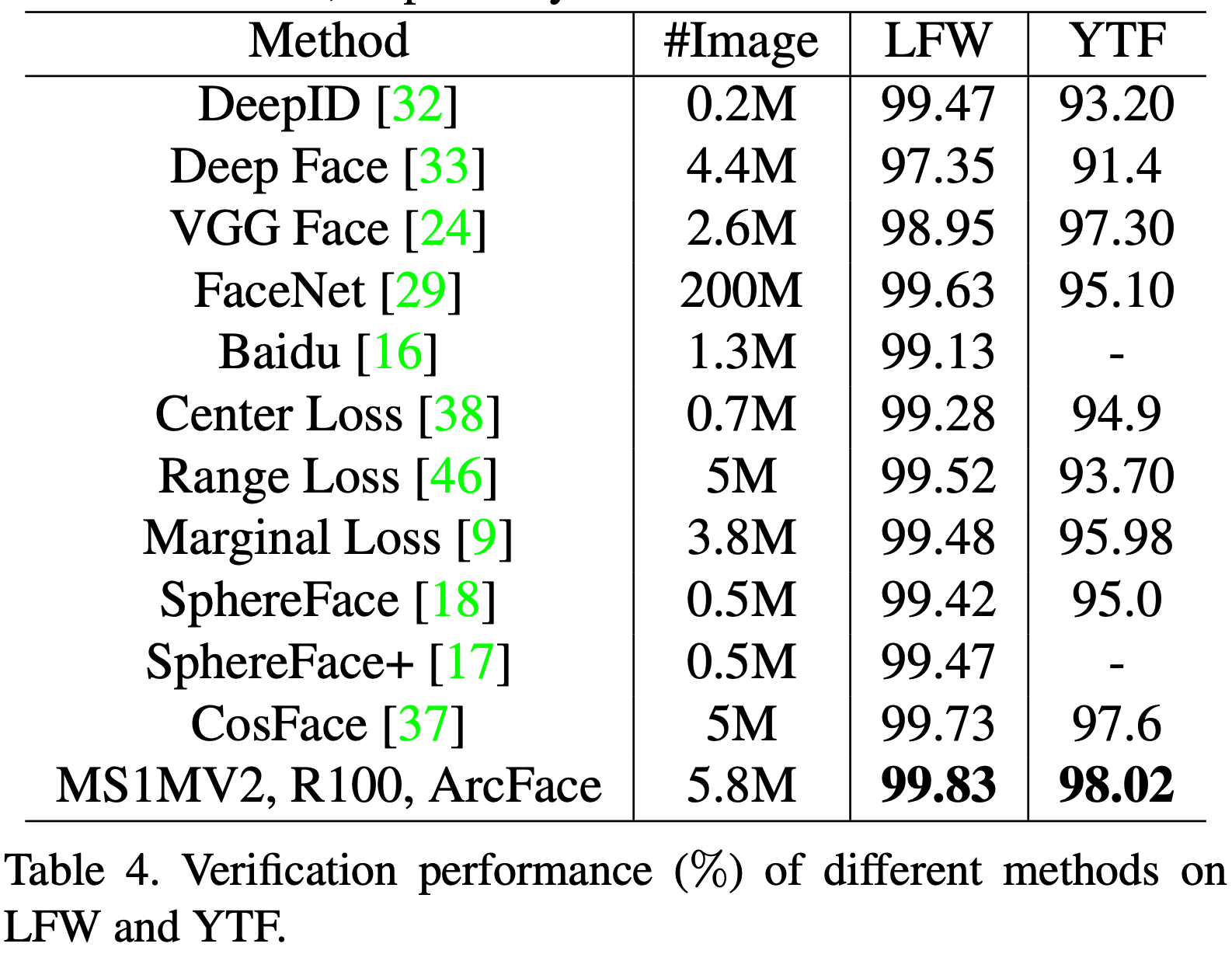
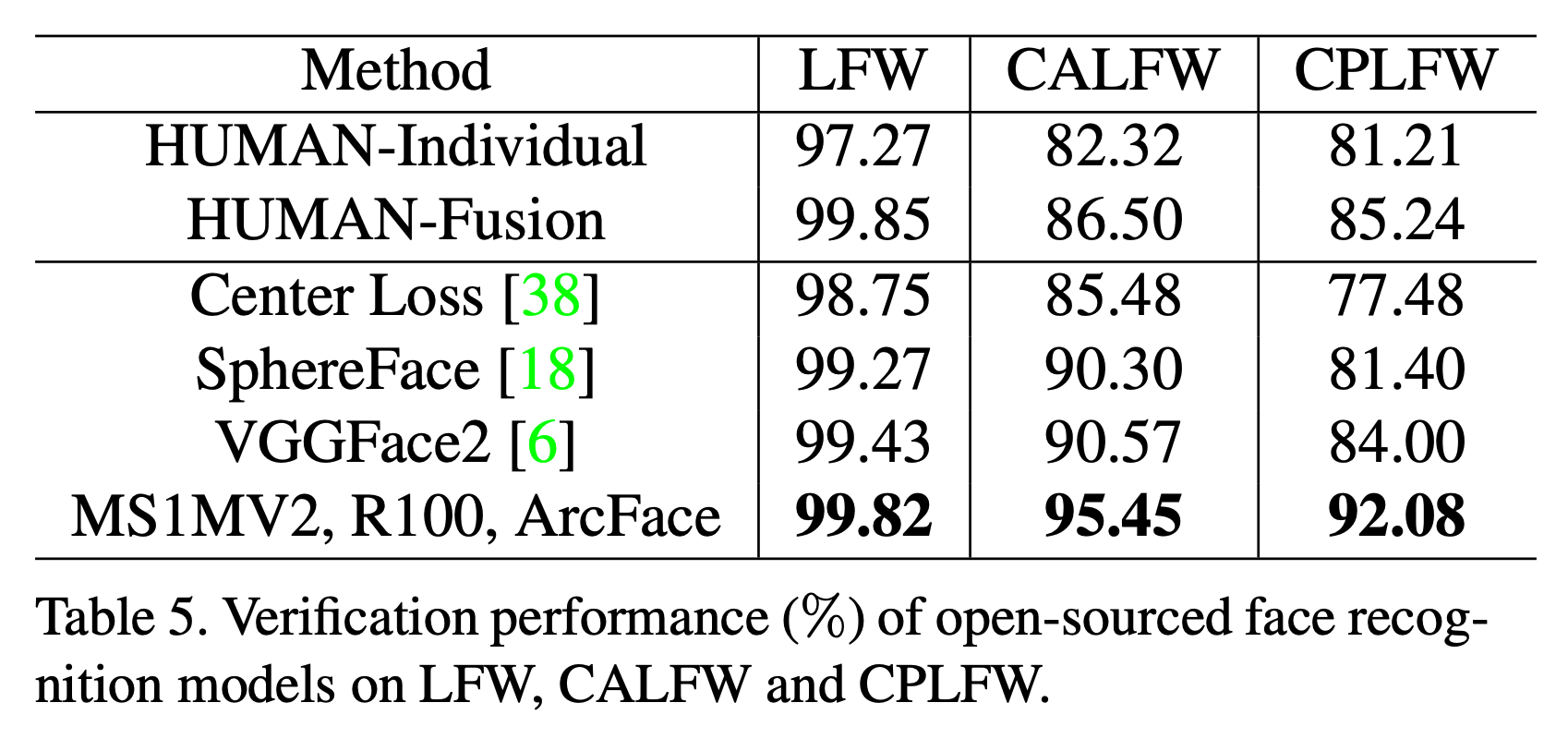
- 얼굴 인식 관련 논문이지만 얼굴 인식 내용을 다루려고 하는 것은 아니다.
- Softmax 함수를 대체하기 위한 새로운 Loss 함수를 살펴보도록 하자.
- Metric Learning 을 위해 Euclidean 방식의 Loss 를 Augular 기반의 Loss 로 변경
- 관련 논문들
Introduction
- 얼굴 인식(face recognition, FR) 성능을 올리기 위한 새로운 Loss 함수를 제안.
-
물론 기존에 알려진 Loss 함수를 개선하는 것.
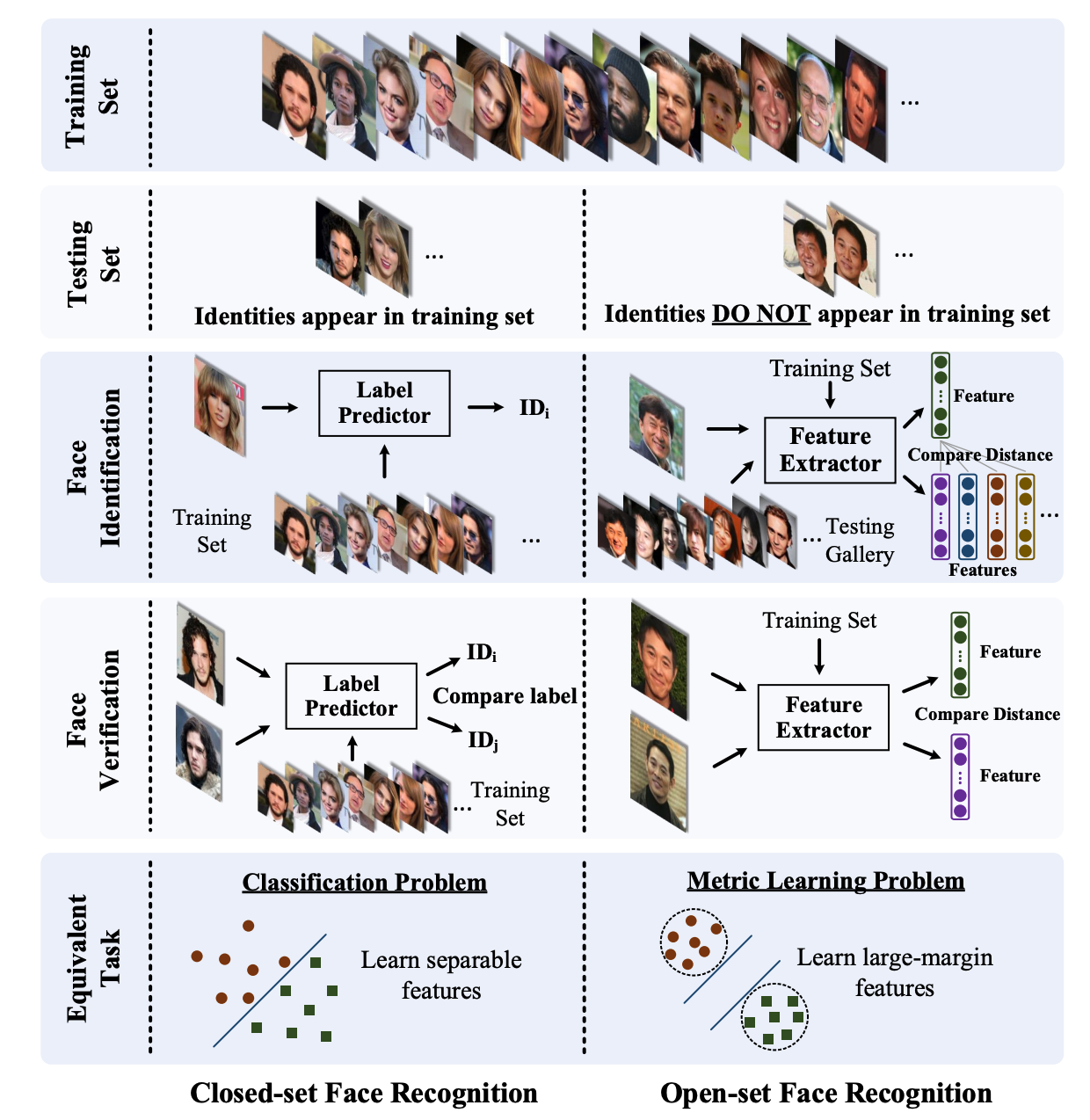
- FR에서 왜 Metric Learning 이 필요한가?
- 보통 분류 문제는 classification 으로 해결. 유사 이미지 검색(IR)의 경우 Metric Learning을 사용.
- FR 문제도 IR로 해결할 수 있다. (Closed-set vs. Open-Set)
Related Work
Angular Loss
- triplet loss, n-pair loss 와 같이 Metric Learning Loss 에서 Angular Loss 를 사용하는 것.
- 기존 Metric Learning 에서는 각 샘플간의 거리로만 학습을 진행.
- 문제는 scale 변화에 민감하다. 단순히 margin 등만을 사용하는 비교는 intra-class variation 스케일을 무시하는 것.
- 수학적으로도 Metric space 의 sub-optimal 로 수렴을 한다고 함. (이건 찾아보지는 않았음)
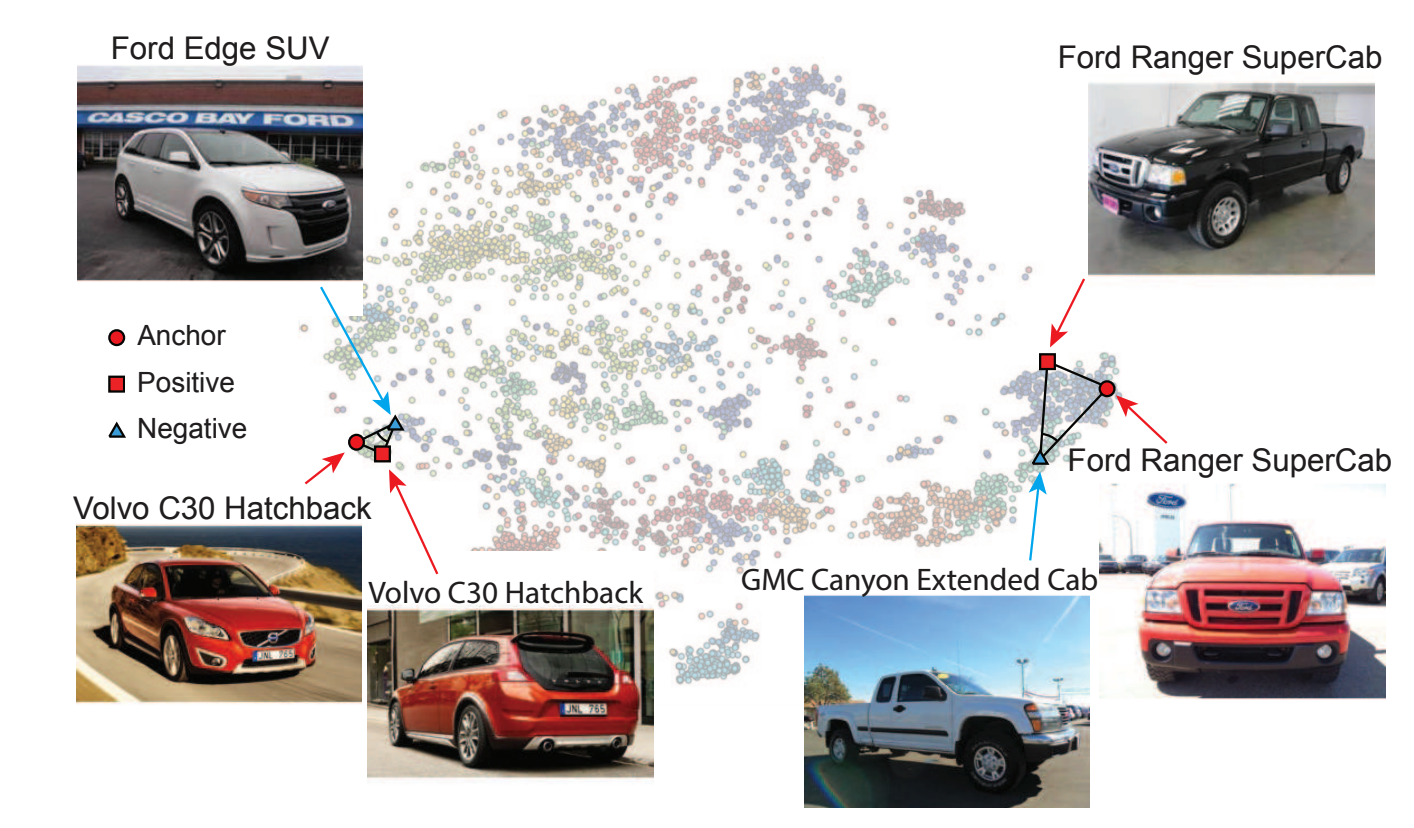
- Angular 기반으로 Metric Learning 을 해보자.
-
각도의 경우 rotaion-invariant, scale-invarint 속성이 보장된다.
- 기본적인 triplet loss 의 학습 방식
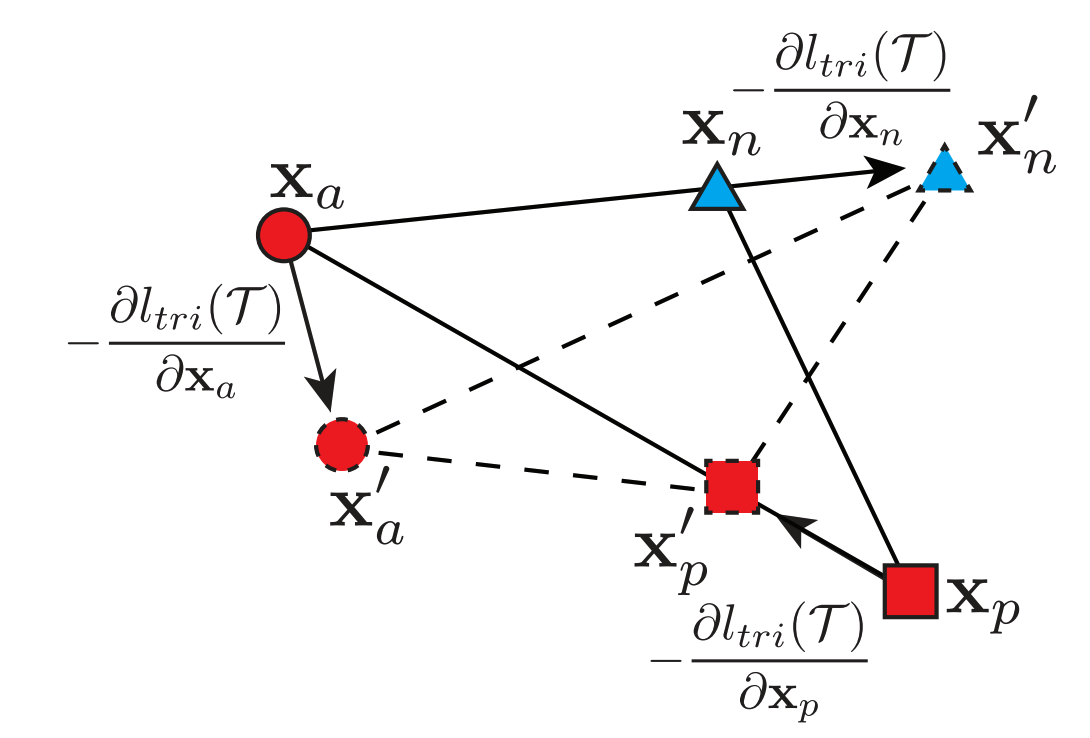
- Angular loss 의 적용 (AMC-Loss)
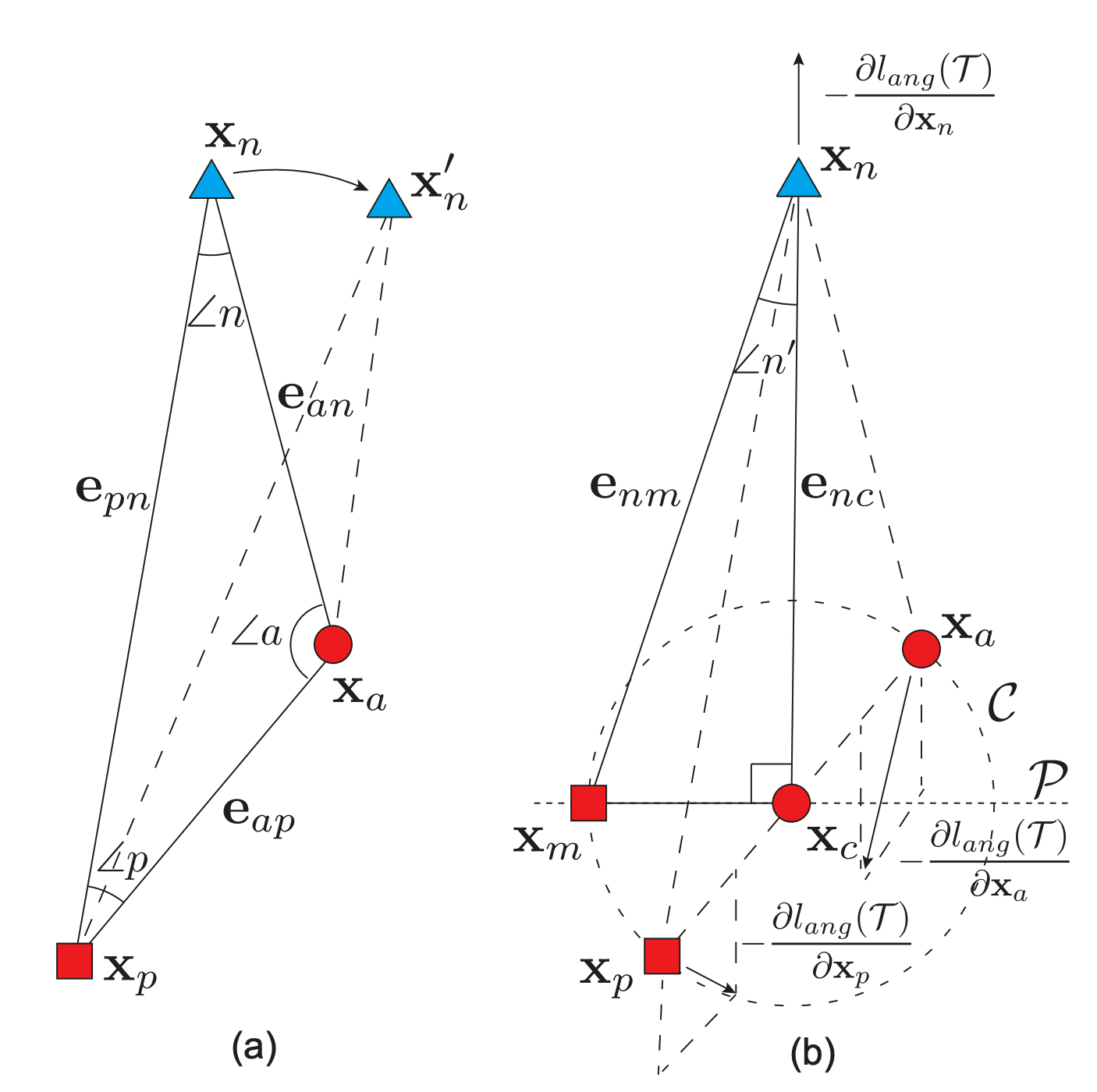
SphereFace
- Softmax 에 Angular 를 적용해볼 수는 없을까?
- 이러면 분류 문제에서도 이를 적용해볼 수 있을 것 같다.
- SphereFace 에서 사용하는 Loss 는 Angular-Softmax. 이를 그냥 A-Softmax 라고 부른다.
- “Softmax 함수에 Angular Margin 을 넣어보자.”

- Vanilla Softmax Loss
- 여기서 제약 조건으로 wegith vector \(\bf{W}\) 의 크기를 강제로 1로 고정.
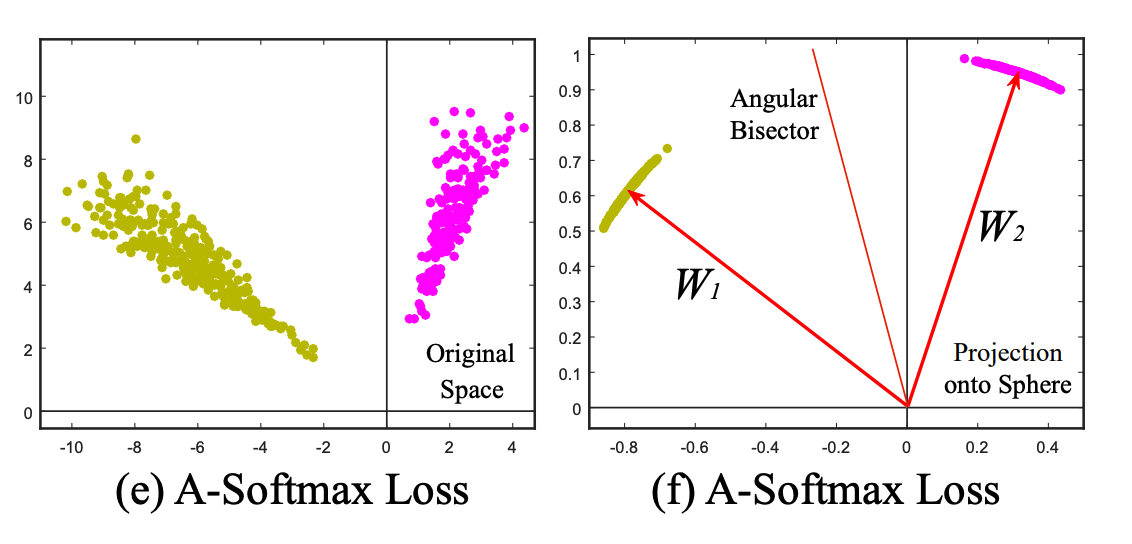
- 위 그림에서 Modified Softmax Loss 는 끝단 FC 영역을 2-dim logit 영역이라고 보면 된다.
- 여기서 \(|\bf{W}|\) 를 1로 고정하면 결국 각 클래스에 대한 분리는 각도(angular)로만 결정되게 된다.
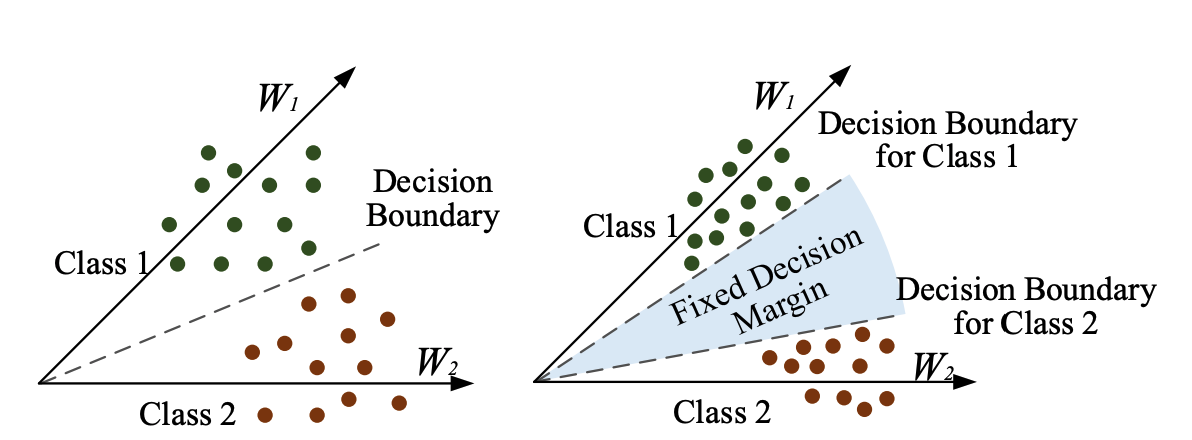
- 여기에 추가로 Margin 을 두어 각 클래스 사이의 거리를 멀게 하도록 추가 제약을 가하는 것이다.
- 여기서 margin 은 \(m\) 을 의미한다.
- 실제로는 별로 좋지 못한 식인데 \(m\) 을 정수로 제한하고 사용한다 하더라도 수식 전개가 복잡하다.
- 최종 결과는 아래와 같이 된다.
Additive Margin Softmax
- SphereFace 와 동일한 개념이지만 구현상의 어려움을 피하기 위해 만든 Softmax.
- 동일하게 \( \| \bf{W} \| =1\) 이고 Angular margin 을 추가한다.
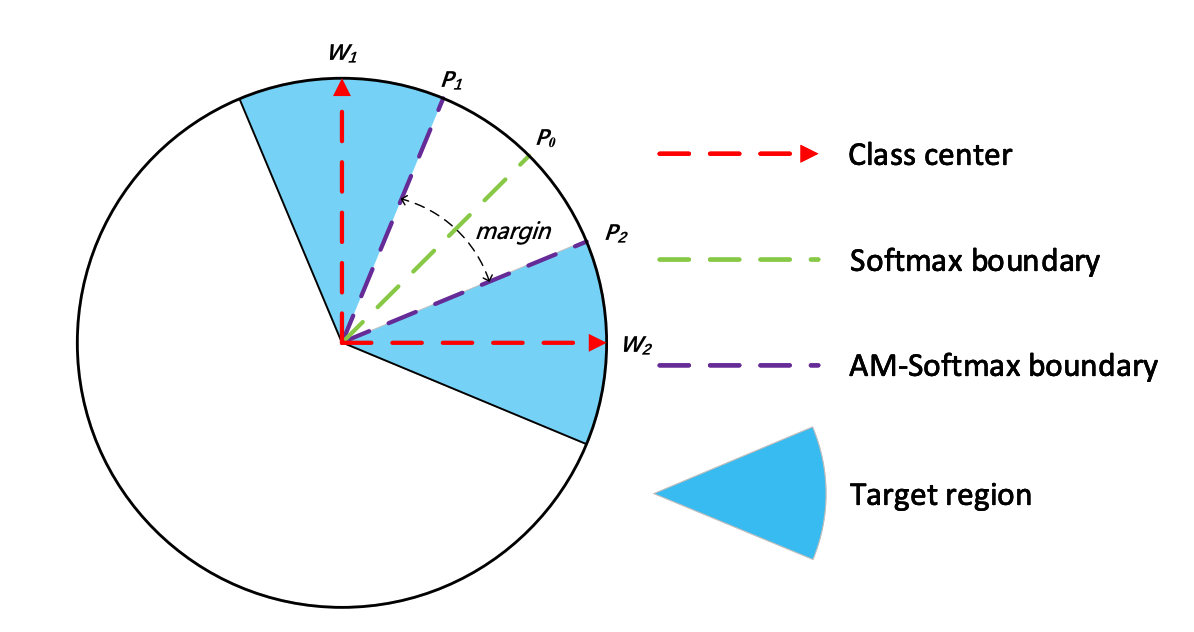
CosFace
- 왜 그런지 모르겠으나 Additive Margin softmax 방식과 동일한 Loss 를 사용한다.
- 논문이 동시에 나온 것인지 모르겠다.
ArcFace
- 마찬가지로 Angular Margin Loss 를 사용한다.
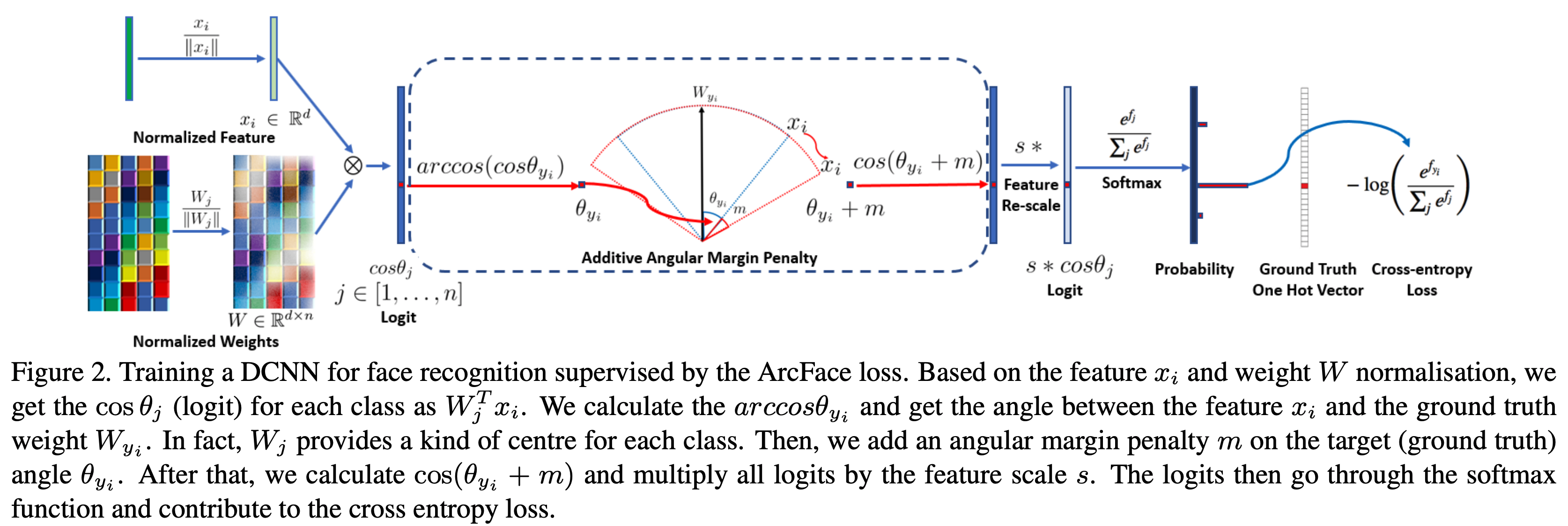
- 구현은 간단하게 할 수 있다.

- ArcFace 의 장점
- 직접적으로 margin 을 두어 최적화한다.
- 구현이 매우 쉽다.
- 성능이 매우 좋다.
- (토이 예제) 아주 간단한 형태의 샘플을 확인해보았다.
- 클래스 당 약 1,500개의 이미지로 구성된 8개의 클래스
- 2D Embedding 데이터로 각각 Softmax 와 ArcFace 로 실험

SphereFace, CosFace 와의 비교
- 수학적 유사성
- 3가지 방식 모두 intra-class 의 compactness 를 강화하고 inter-class 의 diversity 를 증가시킨다.
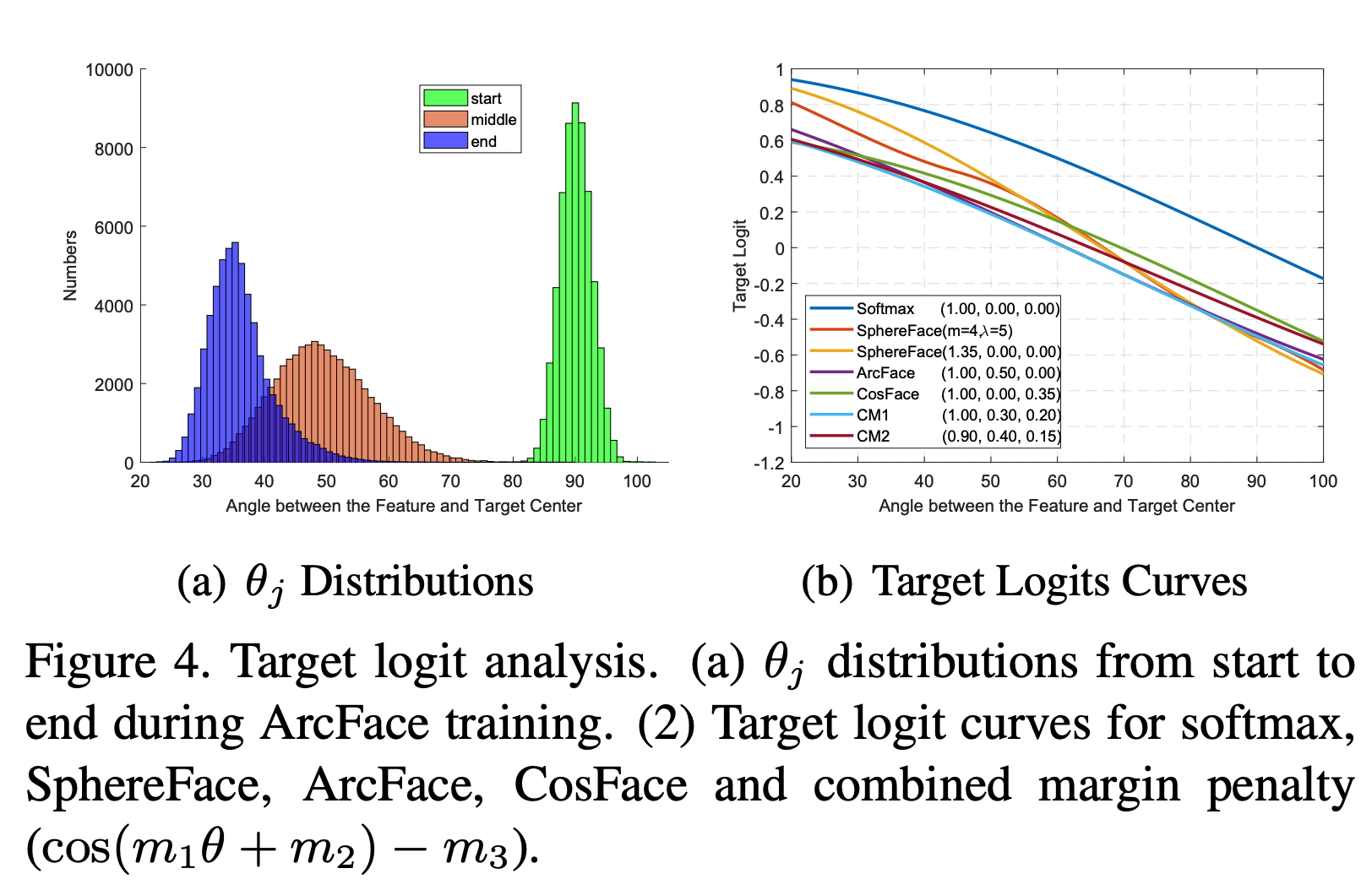
- (추가적으로) 사실 3개의 방법을 혼합하여 사용할 수도 있다.
- \(m_1\) : multiplicative angular margin
- \(m_2\) : additive angular margin
-
\(m_3\) : additive cosine margin
- Geometric Difference
- 수학적 유사성에도 불구하고 ArcFace 가 더 좋은 이유는,
- 더 좋은 geometric attribute 를 가지고 있기 때문. (주장)
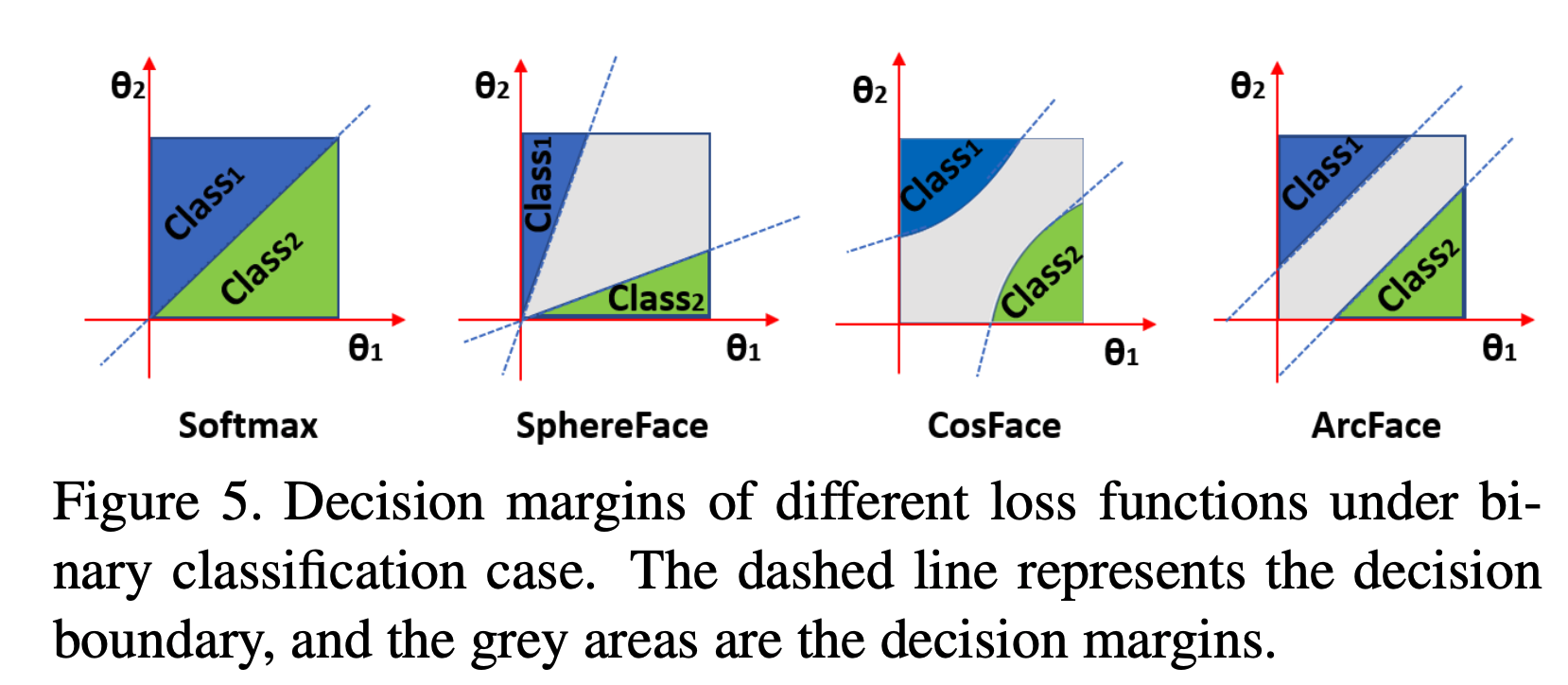
실험
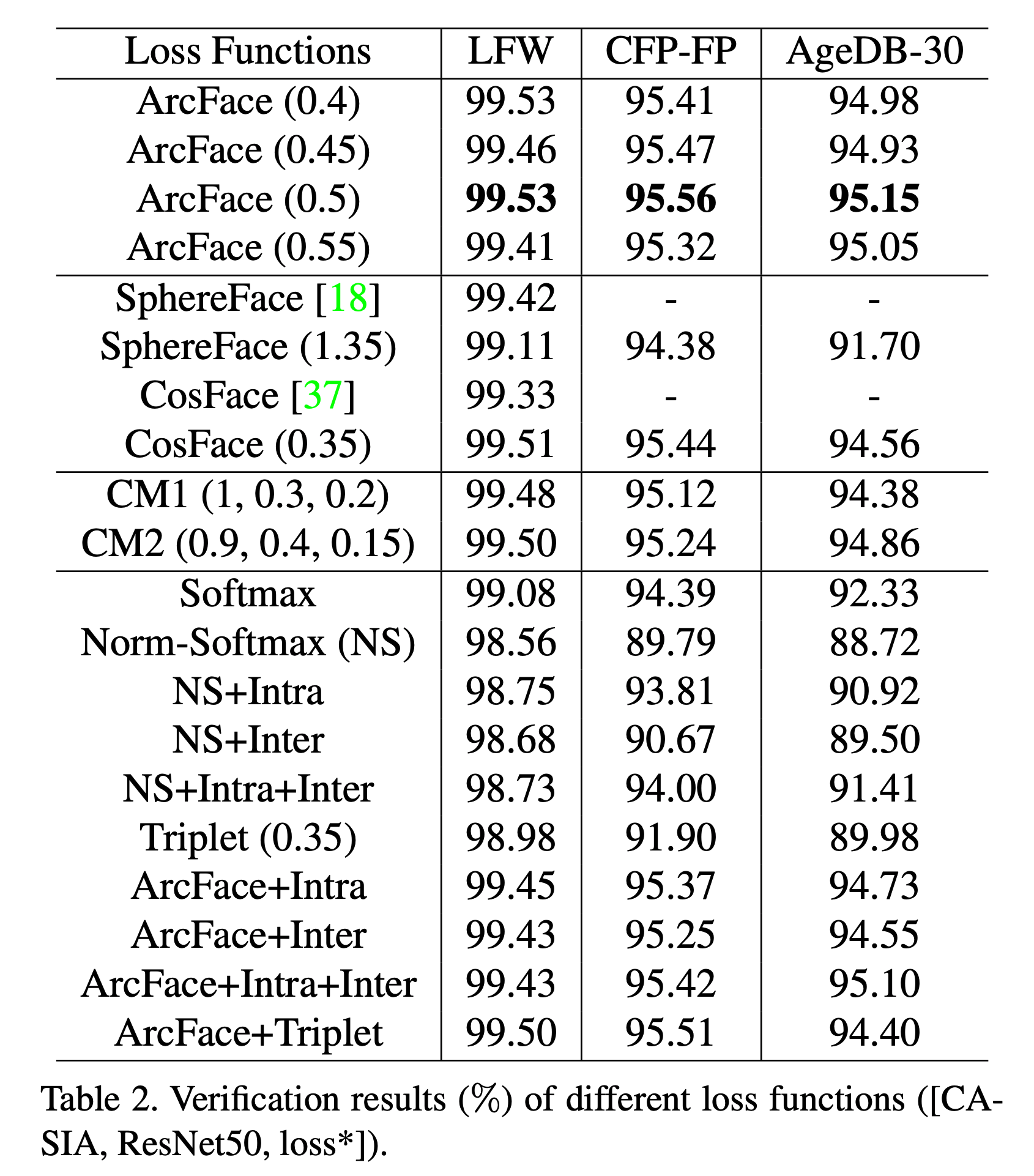
- 동일한 Backbone 하에서 학습 후 실험.
- (참고) CM : combined margin.
- LFW, CFP-FP, AgeDB-30
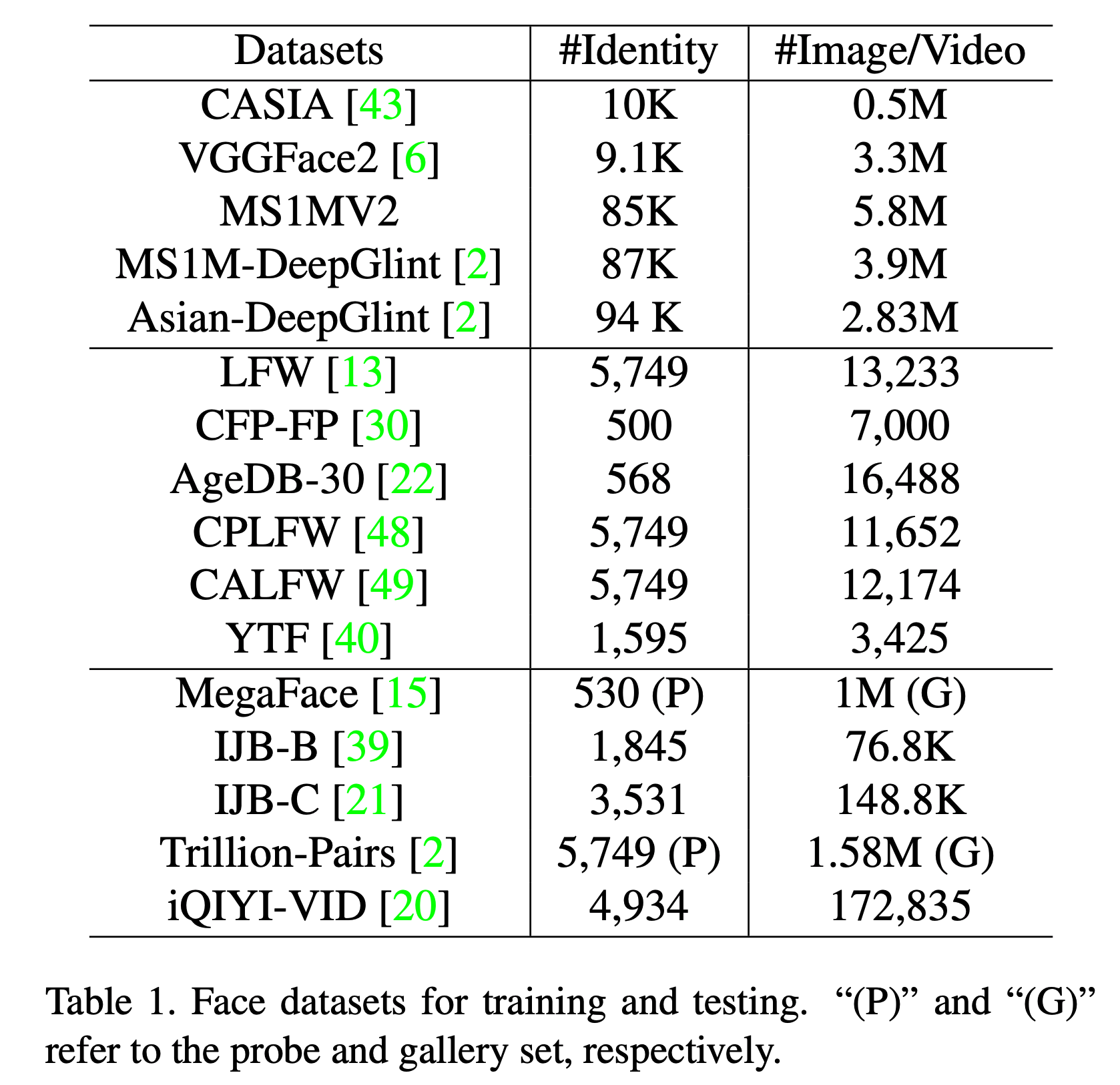
Other FR benchmark dataset